Investigation of Polarization Division Multiplexed CVQKD Based on Coherent Optical Transmission Structure

Abstract

Employing commercial off-the-shelf coherent optical transmission components and methods to design a continuous variable quantum key distribution (CVQKD) system is a promising trend of achieving QKD with high security key rate (SKR) and cost-effectiveness. In this paper, we explore a CVQKD system based on the widely used polarization division multiplexed (PDM) coherent optical transmission structure and pilot-aided digital signal processing methods. A simplified pilot-aided phase noise compensation scheme based on frequency division multiplexing (FDM) is proposed, which introduces less total excess noise than classical pilot-aided schemes based on time division multiplexing (TDM). In addition, the two schemes of training symbol (TS)-aided equalization are compared to find the optimal strategy for TS insertion, where the scheme based on block insertion strategy can provide the SKR gain of around 29%, 22%, and 15% compared with the scheme based on fine-grained insertion strategy at the transmission distance of 5 km, 25 km, and 50 km, respectively. The joint optimization of pilot-aided and TS-aided methods in this work can provide a reference for achieving a CVQKD system with a high SKR and low complexity in metropolitan-scale applications.

1. Introduction

Quantum key distribution (QKD) provides a novel approach to sharing secret keys between two communicating parties, which can achieve unconditional security when combined with the ‘one-time pad’ [1,2]. Although QKD technology has made considerable strides toward practical implementation over the past several decades, it still faces challenges that hinder further development, the most prominent of which are cost and the secure key rate (SKR). On one hand, the integration of QKD with deployed optic fiber network infrastructures has not yet met expectations, resulting in the high cost of current commercial QKD equipment [3]. On the other hand, the SKR of current commercial QKD devices remains at the Kbps level, far below the Tbps capacity of modern communication systems [4]. Continuous variable (CV) QKD is considered a promising solution for addressing the two issues mentioned above due to its high key rate over metropolitan area and compatibility with commercial off-the-shelf components [5].

In a typical CVQKD protocol, Alice modulates key information on the quadratures of coherent states and sends it to Bob through a lossy channel. Then Bob recovers the raw keys from the received signal by using coherent detection such as homodyne or heterodyne detection [6,7]. This structure of CVQKD shows high similarity to the widely deployed coherent optical transmission systems, indicating the prospect of high-performance and cost-effective QKD system once the state-of-the-art methods of existing coherent optical transmission systems can be effectively adopted for CVQKD [8,9]. Actually, the research on CVQKD schemes is just developing in this direction. For example, compared with the early proposed Gaussian-modulated coherent states (GMCS) protocol, the discrete-modulated coherent states (DMCS) protocol uses more efficient modulation formats such as quadrature amplitude modulation (QAM) and thus can be implemented with more efficient forward error correction (FEC) algorithms as well as fewer quantization bits for digital-to-analog converters (DACs) and analog-to-digital converters (ADCs) [10]. In addition, it has been attractive to use traditional continuous wave (CW) light instead of pulsed light to support a higher SKR and a more accurate track of the phase noise [11]. Moreover, the emergence of schemes based on a local local oscillator (LLO) also shows advantages over transmitted local oscillator (TLO) schemes, making it feasible to directly use integrated coherent receivers [12]. With the progress of research, the SKR of CVQKD system has been increased from the Kbps level to the Mbps level over the past few years, and it is worth noting that the experimental demonstrations of the CVQKD system based on the CW light and LLO have achieved sub-Gbps or even higher within metropolitan area [7,13,14].

The main factor that restricts the further increasing of SKR in CVQKD implementations lies in the ultra-low power of transmitted QKD signal, which means that the classical digital signal processing (DSP) methods may be inefficient to recover the raw keys signal from the weak and noisy QKD signal. As a result, it is more attractive to design efficient DSP methods to enhance the performance of CVQKD systems by using a reference signal. For instance, pilot tone or training symbols can be added to the QKD signal to compensate the phase noise by using signal division multiplexing methods such as TDM, FDM, and PDM, which are widely used in optical communication [15,16,17]. In addition, regarding the pursuit of higher-SKR CVQKD, PDM can not only be employed to transmit reference signals but it can also transmit QKD signals in both polarization states, which can achieve a potential SKR at the Gbps level and shows promising feasibility mainly because the hardware structure of the classical dual-polarization coherent optical transmission system can be well migrated with only slight adjustment [8,9]. The investigation of such PDM CVQKD systems was initially used in TLO systems [18]. More recently, PDM CVQKD systems based on the CW-LLO scheme have been an attractive option. However, the performance of DSP methods in PDM CVQKD systems has not yet been systematically evaluated. On the one hand, an efficient pilot-aided phase noise compensation scheme should be designed to fit the needs of the system. On the other hand, the PDM CVQKD induced extra impairments such as polarization noise [19,20], thus corresponding DSP algorithms should be designed to compensate these impairments. The influences of these algorithms on the performance of CVQKD need to be analyzed.

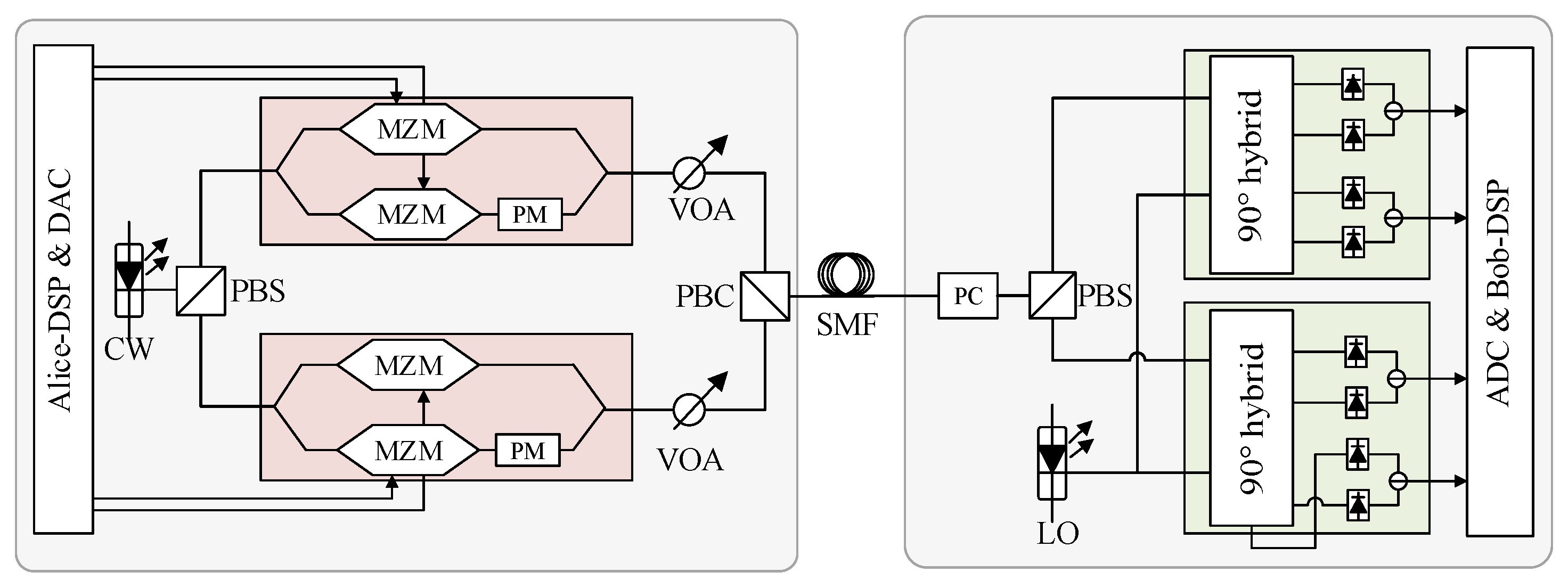
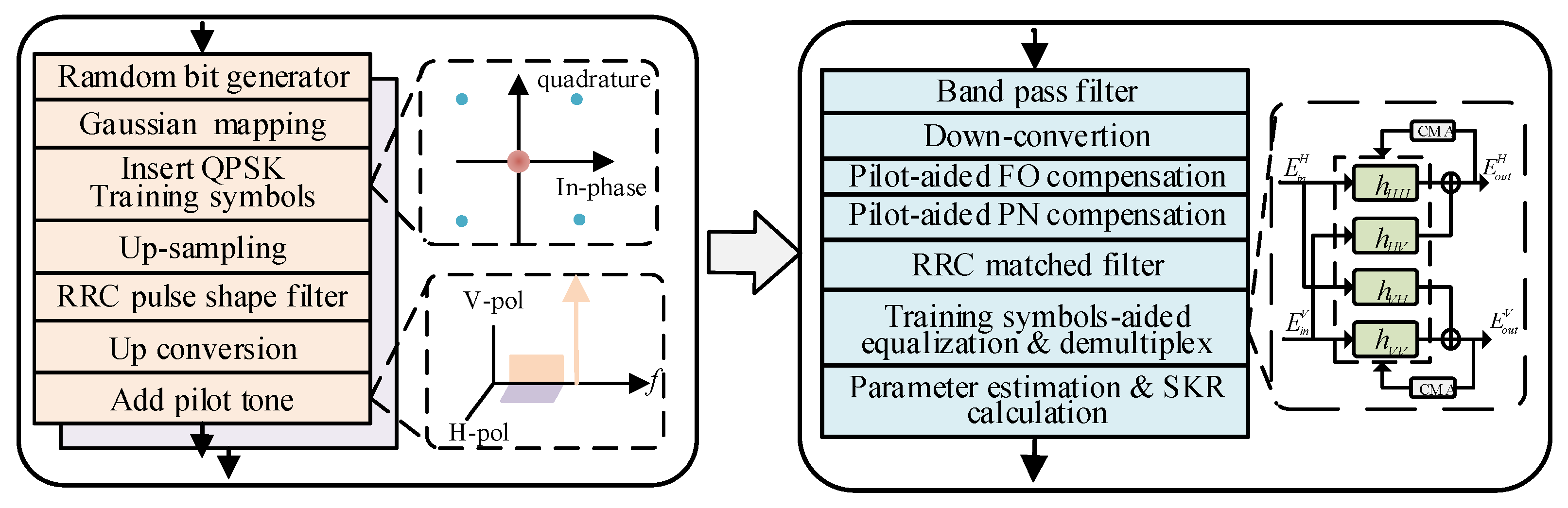
In this paper, we investigate PDM-CVQKD based on the structure of the classical coherent optical transmission system, where the CW-GMCS-LLO scheme is applied. Firstly the structure of the PDM-CVQKD system is established and the main DSP methods for the system are introduced. Then, a simplified FDM pilot-aided signal processing scheme is proposed for carrier frequency offset (FO) estimation and phase noise (PN) compensation. The excess noise corresponding to the FDM pilot-aided scheme is also modeled in comparison with the traditional TDM pilot-aided scheme. In addition, the two strategies of the TS-aided equalization scheme are compared to find the optimal option of the insertion of TS depending on the channel situation. Lastly, the SKR of the PDM-CVQKD system at different transmission distances is evaluated based on the joint optimization of the setup of pilot-aided PN compensation and TS-aided equalization.

2. System Architecture and Digital Signal Processing Methods

2.1. Transmission Structure

Figure 1 shows the structure of the PDM-CVQKD system based on coherent optical transmission components. On the transmitter side, Alice exploits a CW laser source to generate the optical carrier. A polarization beam splitter (PBS) is then used to divide the optical carrier into two orthogonal polarization states. For each polarization, an in-phase-and-quadrature (IQ) modulator consisting of two Mach–Zehnder modulators (MZM) and a phase modulator (PM) modulates the baseband electrical signal generated by the transmitter side digital signal processing (Tx-DSP) onto the optical carrier, followed by a variable optical attenuator (VOA) to modify the output power of the modulated signal to make sure that the mean photon number of each optical pulse is sufficiently small for security. Later, the output signals of two VOAs are multiplexed by a polarization beam combiner (PBC) and transmitted over a single mode fiber (SMF) channel. On the receiver side, the PDM signal firstly passes through a polarization controller (PC) to initially eliminate the rotated state of polarization (RSOP) during fiber transmission and is then separated by a PBS into two separate parts. Here, Bob exploits another CW laser source to supply the LO signal of polarization-diversity coherent receiver, which consists of two heterodyne detectors. Subsequently, the outputs of PBS are demodulated by the heterodyne detectors and lastly processed in the receiver side (Rx) DSP module to further compensate the impairments of the demodulated baseband electrical signal and distill secret keys.

2.2. DSP Methods of Transmitter and Receiver

For the PDM-CVQKD system in Figure 1, it is similar to classical coherent optical transmission that some impairments will be induced by the imperfections during the transmission. For example, the frequency offset between two lasers of Alice and Bob as well as the linewidth of two lasers will induce phase noise. In addition, the polarization mode dispersion and RSOP in fiber will cause crosstalk between the signals of two polarizations [21]. As we already pointed out, CVQKD signal is transmitted under very low SNR, thus is vulnerable to these impairments. In this case, it is essential to propose corresponding signal processing schemes. As mentioned in Section 1, the common scheme follows the approach of transmitting the quantum signal together with the pilot signal using signal division multiplexing methods such as TDM, FDM, and PDM. In our work, we propose a pilot-aided DSP scheme that is based on frequency division multiplexing, as shown in the lower left inset of Figure 2. In this scheme, a single frequency pilot tone with different frequency bands of quantum signal is used for compensating the phase noise, where only one pilot tone in the vertical polarization (V-pol) is needed for both the quantum signals of vertical polarization and horizontal polarization (H-pol), which can be simplified for the DSP at transmitter and reduce the crosstalk of pilot to QKD signal compared to the classical schemes that add pilot tone in both two polarization states. In addition, since the pilot tone is in the different frequency band of the QKD signal, the polarization crosstalk can not be efficiently compensated by using the pilot tone. As a result, Quadrature Phase-Shift Keying (QPSK) training symbols with higher power can be inserted into the QKD symbols for channel equalization and polarization de-multiplexing, as shown in the upper left inset of Figure 2.

To perform the pilot-aided scheme, the DSP flow is designed as follows: at the transmitter (Alice) side, for each polarization, random bits are generated and mapped into Gaussian distributed symbols, then the QPSK modulated training symbols are inserted into the signal. The signal is then up-sampled and pulse shaped using a Root-Raised Cosine (RRC) filter to minimize inter-symbol interference (ISI). Subsequently, the baseband signal is then up-converted to an intermediate frequency to reduce the low frequency noise and the pilot tone is added. At the receiver (Bob) side, two independent bandpass filters are employed to isolate the quantum signal and the pilot tone, ensuring minimal cross-talk and out-of-band noise interference. The filtered QKD signal is then down-converted to baseband. Subsequently, the FO between Alice’s and Bob’s lasers is estimated by performing a fast Fourier transform (FFT) on the pilot signal and estimated with the following:

$${\widehat{f}}_o=f_{peak}-f_p$$

(1)

where $f_{peak}$ is the peak frequency of the FFT spectrum, $f_p$ is the frequency of transmitted pilot tone. Then, based on the measured $f_{peak}$, the PN can be estimated as

$${\widehat{\theta }}_n={\widehat{\theta }}_{drift}+{\widehat{\theta }}_{channel}+{\widehat{\theta }}_{error}=\mathrm{angle}\left({\alpha }_p{e}^{-i2\pi f_{peak}t}\right),$$

(2)

where ${\widehat{\theta }}_{drift}$ and ${\widehat{\theta }}_{channel}$ are the phase drift caused by the linewidth of lasers as well as the phase drift occurring during the channel transmission, respectively. ${\widehat{\theta }}_{error}$ is the estimation error induced by the noise on the pilot tone. ${\alpha }_p$ is the complex pilot symbols after bandpass filtering. It is noteworthy that in our FDM-based pilot scheme, ${\widehat{\theta }}_{drift}$ and ${\widehat{\theta }}_{channel}$ of the pilot tone and quantum signal are identical, which can be well compensated. Whereas the estimation error ${\widehat{\theta }}_{error}$ will induce residual phase noise, resulting in an excess noise in practice. After the pilot-aided FO and PN compensation, an RRC matched filter is employed to initially eliminate ISI. Subsequently, the QPSK training symbols-aided (TS-aided) equalization and polarization demultiplexing is operated to compensate the ISI that is caused by the polarization-dependent impairments. The most dominant polarization-dependent impairment that undermines the performance of PDM-CVQKD system is the RSOP, which can be described using Jones Matrix as

$$J_{RSOP}=\left[\begin{array}{cc}{e}^{-j\delta /2}& 0\\ 0& e^{j\delta /2}\end{array}\right]\left[\begin{array}{cc}cos\varphi & -sin\varphi \\ sin\varphi & cos\varphi \end{array}\right]$$

(3)

where $\delta$ is the phase difference of two polarization, $\varphi$ is the polarization state rotation angle, which is time-varying during transmission and induce excess noise. To compensate the RSOP impairment, butterfly adaptive equalizers can be used to achieve the inverse matrix of $J_{RSOP}$, defined by

$$H=\left[\begin{array}{cc}{h}_{HH}& h_{HV}\\ h_{VH}& h_{VV}\end{array}\right]$$

(4)

where $h_{HH}$, $h_{HV}$, $h_{VH}$, $h_{VV}$ are the coefficients of four finite impulse response (FIR) filters. The structure of the equalizer is shown in the right insert of Figure 2, where a butterfly filter structure is employed to construct the matrix in Equation (2). Depending on the difference of cost function of the equalizer and the filter coefficients update function, numerous algorithms have been derived, among which the constant modulus algorithm (CMA) is the most widely used [22]. In our scheme, the TDM-based TS-aided equalization based on CMA is utilized. As for the insertion of TS in QKD symbols, there are mainly two schemes that are widely used. Scheme A employs a fine-grained insertion strategy, as shown in Figure 3a, where TS and QKD symbols are alternatively transmitted, i.e., inserting one TS before each QKD symbol. Such an interleaving scheme can provide the optimal compensation of RSOP, especially in rapidly varying channels. However, this scheme exhibits several drawbacks. On the one hand, the high density of TS symbols in this scheme results in high overhead, thus limiting the SKR. On the other hand, it is rather challenging to achieve rapid and precise control over the power level of TS and QKD symbols in CW system. Scheme B operates a block-based TS insertion which offers the trade-off between RSOP compensation and spectral efficiency, as shown in Figure 3b, where the N received symbols of each blocklength are divided into k sequences of M symbols, each set of M symbols are then divided into $\alpha M$ training symbols and $(1-\alpha )M$ QKD symbols. For each M symbol, the TS are utilized to make the equalizer’s coefficients converge to be optimal. These optimized parameters are then employed as the initial settings for processing the QKD symbols. The value of parameter k and $\alpha$ can be adaptive according to the actual channel situation. Compared with scheme A, scheme B can be more simplified in hardware implementation and DSP operation, as it reduces the need for rapid control of the modulator and the complexity of data acquisition at receiver. What is more, scheme B may provide sub-optimal equalization performance but higher spectral efficiency and more flexibility in implementation. A detailed and comparative analysis of the two schemes’ performance will be presented in Section 4. After the TS-aided equalization, critical system parameters such as channel transmittance and excess noise are estimated to evaluate the performance of quantum channel and SKR is evaluated using the estimated parameters and the covariance matrix in entanglement-based (EB) model [23,24].

2.3. Noise Configure and SKR Calculation

After Bob’s detection as well as the DSP of the noisy quantum signal, the symbols that Bob obtained can be expressed as

$$y_k=\sqrt{{\displaystyle \frac{\eta T}{2}}}{x}_k+w_k,$$

(5)

where $y_k$ are the transmitted symbols with modulation variance $V_A$. T is the transmittance of optical link and $\eta$ is the quantum efficiency of heterodyne detector. $w_k$ is the additive noise with variance $N_0+{\nu }_{el}+{\displaystyle \frac{\eta T}{2}}\epsilon$, where $N_0$ is the shot noise. Note that $N_0=1$ when signals are normalized to shot noise unit (SNU). $\epsilon$ is the excess noise corresponding to the Alice side, which is mainly composed of the noise corresponding to the imperfection of transceiver, channel, and residual impairment after receiver’s DSP operations. ${\nu }_{el}$ is the electronic noise of detectors. To establish the security of the protocol, it is normally assumed that Eve controls the transmittance T and the excess noise $\epsilon$. The security of CVQKD is evaluated by the lower bound of the information that Alice and Bob can obtained, i.e., the SKR, which can be expressed in asymptotic regime as

$$R=R_S(1-\alpha )(\beta I_{AB}-{\chi }_{BE}),$$

(6)

where $R_S$ is the symbol rate, $\alpha$ is the proportion of pilot symbols, $I_{AB}$ denotes the mutual information between Alice and Bob, $\beta$ is the reconciliation efficiency and ${\chi }_{BE}$ is the Holevo information that eavesdroppers can obtain from Bob. The detailed expression of the SKR for the GMCS protocol is derived in [23], which is also employed for the numerical simulation in this work. Note that the value of $I_{AB}$ and ${\chi }_{BE}$ are determined by the value of parameters such as $V_A$, T, $\eta$, ${\nu }_{el}$ and $\epsilon$, which means that it is essential to precisely estimate these parameters to evaluate the actual SKR. In particular, the calibration of $V_A$ can be rather important for the initial setup of the commercial CVQKD system, whose accuracy determines whether the transmitted QKD signal remains in a valid quantum state. In addition, the varying of circumstances can result in the change of these parameters in time, which should also be taken into account in practical implementation.

3. The Effects of FDM Pilot-Aided Scheme on Security Parameter Estimation

As previously mentioned, a critical prerequisite for secure key generation in the QKD system is the accurate estimation of security parameters at the receiver. In practical operation, the security parameters such as $N_0$, $\eta$, ${\nu }_{el}$ can be calibrated at receiver and regarded as fixed when the system is stable. However, the estimation of parameters such as $V_A$, T and $\epsilon$ may be affected by the imperfections of the transceiver, such as impairments induced by the pilot tone as well as the non-optimization of DSP algorithms. In this section, we focus on the impact of the proposed FDM-based pilot-aided DSP schemes on the estimation of security parameters. First of all, a numerical simulation system based on the scheme in Figure 1 and Figure 2 is established. The main parameter setup is shown in

Table 1. Main parameter setup of the numerical simulation.

Parameter	Value
Blocklength N	1 × 105
Symbol rate $R_S$	2 GBaud
Roll-off factor	0.2
Up-convertion frequency	1.5 GHz
Pilot frequency $f_p$	3.5 GHz
Frequency offset $f_o$	1 MHz
$V_{\pi }$ of MZM	3 V
Modulation variance $V_A$ in SNU	5
Central frequency of lasers	193.4 THz
Optical fiber loss coefficient	0.2 dB/km
Bandwidth of receiver	12 GHz
Quantum efficiency $\eta$	0.8
Reconciliation efficiency $\beta$	0.95
Electronic noise variance ${\nu }_{el}$ (in SNU)	0.1

, where the symbol rate of quantum signal is set to 2 Gbaud, the central frequency of quantum signal is up-converted to 1.5 GHz to avoid low-frequency noise, and the frequency of the pilot tone is set to 3.5 GHz to reduce the crosstalk in the frequency domain. Note that the shot noise as well as the electronic noise is regarded as Gaussian white noise with a variance of $N_0+{\nu }_{el}$. For convenience of analysis, we assume that the shot noise variance $N_0$ of each heterodyne detector are equal, which can be given by

$$N_0={\displaystyle \frac{e^2\eta B_{det}{P}_{LO}}{h\nu }},$$

(7)

where e is the elementary charge, $B_{det}$ is the bandwidth of receiver, $P_{LO}$ is the optical power of LO, h is the Planck constant, $\nu$ is the central frequency of lasers. In practice, the value of $N_0$ is crucial for the security analysis because all the parameters estimation at receiver side are based on the calibrated $N_0$. Normally, $N_0$ is calibrated together with the electronic noise variance ${\nu }_{el}$ by the following steps: firstly turn off the LO input and cut off the input of received signal, the measured variance is ${\nu }_{el}$; then turn on the LO input and measure the total noise variance; later, $N_0$ can be estimated by the difference of the two measured variances. $N_0$ can also be calibrated with “one-time” methods to realize the real time estimation without cutting off the optical link [5].

Firstly, extra impairments will be induced by the pilot tone at the transmitter. For example, the calibration of modulation variance $V_A$ may be effected because the nonlinear effects of MZMs may be amplified when a strong pilot is used. Normally, the value of $V_A$ can be calculated by $V_A=2\langle n\rangle$, where $\langle n\rangle$ is the average photon number of the transmitted optical signal, which can be estimated by measuring the output optical power at transmitter. In our scheme, the output signal of H-pol only consists of a QKD signal, so $V_A$ can be estimated directly from the output power. Whereas for V-pol, the output signal consists of both the QKD signal and the pilot tone, resulting in the inability to directly measure the output power of the QKD signal. Here we define the power ratio of pilot tone to quantum signal by $r_{pq}={\left(V_p\right)}^2/{\left(V_q\right)}^2$, where $V_p$ and $V_q$ are the mean voltage of electronic quantum signal and electronic pilot tone assigned to MZM. As a result, $V_A$ of V-pol can be indirectly estimated by

$$V_A={\displaystyle \frac{2\langle n\rangle }{r_{pq}+1}},$$

(8)

$V_A$ can also be estimated at receiver in back to back (B2B) situation, i.e., under a fixed transmittance of $T_0=1$. In this case, once $N_0$ is calibrated, $V_A$ can be estimated as

$$V_A={\displaystyle \frac{2{\langle xy\rangle }^2}{\eta T_0\langle x^2\rangle }},$$

(9)

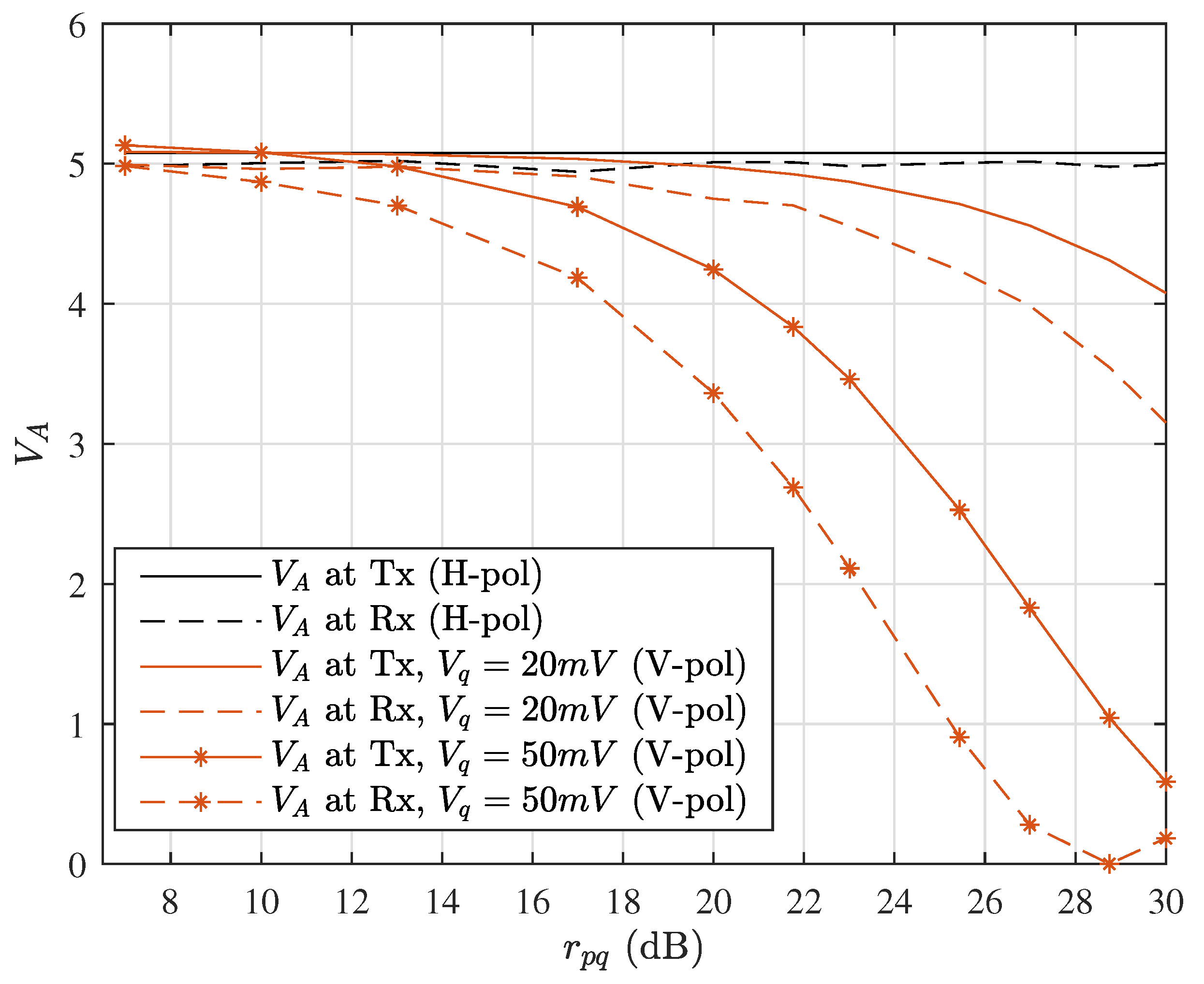
where x is the transmitted symbols that is not normalized to SNU, y is the received symbols that is normalized to SNU. Figure 4 shows the $V_A$ of V-pol and H-pol estimated at transmitter/receiver with different $r_{pq}$ (in dB), where the initial $V_A$ of each polarization are set to 5 in SNU. Note that the QPSK training symbols are not inserted here for simplicity and the results are averaged over 20 acquisitions of received symbols for enough precision. The results indicated that the estimated $V_A$ of H-pol is matched either estimated at the transmitter or receiver. However, for V-pol, $V_A$ estimated at transmitter is no longer accurate with the increase of $r_{pq}$, mainly because the $r_{pq}$ used in Equation (8) is the power ratio of baseband electrical pilot tone and quantum signal, which is not the actual $r_{pq}^{\prime }=P_p/P_q$ of the output optical signal due to the nonlinear effect of IQ modulators when the power of pilot tone is high. In particular, the nonlinearity grows more pronounced with the increasing of $V_q$, as depicted by the star-marked yellow curve in Figure 4. As a result, it is feasible to calibrate $V_A$ at the transmitter when $r_{pq}$ is at a relatively low level, whereas it is more appropriate to perform the calibration of $V_A$ at the receiver when $r_{pq}$ is high in practical implementation.

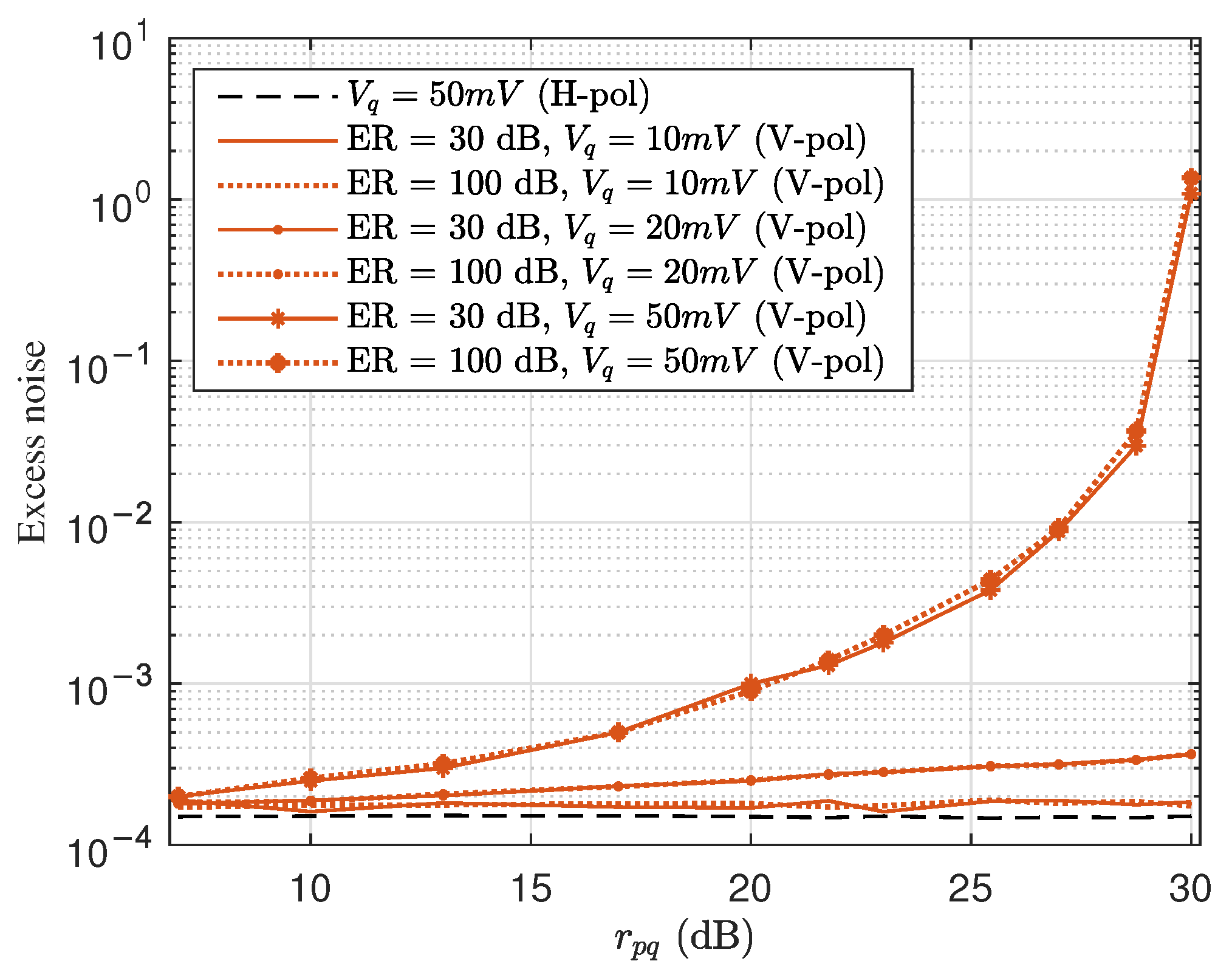
The modulation-related excess noise under the impact of pilot tone is also evaluated as shown in Figure 5, where the nonlinearity as well as limited dynamic range of MZM is taken into account. Note that the $V_A$ at each $r_{pq}$ are all normalized to 5 for the convenience of comparison and the transmission distance is 20 km. The nonlinear effect of MZM can induce the excess noise of ${\epsilon }_{mod-H}$ = 1 × 10⁻⁴ when no pilot is added. Whereas when the pilot is modulated together with QKD signal, the excess noise increases, especially with the increasing of $V_q$ and $r_{pq}$. For example, the excess noise of ${\epsilon }_{mod-V}$ = 9 × 10⁻⁴ is induced at the typical $V_q$ of 50 mV and $r_{pq}$ of 20 dB. It means that the FDM pilot tone can cause extra modulation-related excess noise which can not be ignored, which is more dominant compared to the schemes without using FDM pilot. As for the effect of limited dynamic range of MZM, it has been shown that the limited extinction ratio (ER) of the amplitude modulator may cause the increase in excess noise for the pilot-aided schemes based on TDM [18]. The simulation results in Figure 5 show that the limited ER of MZM will not lead to extra excess noise in the FDM pilot-aided scheme.

Another important factor that affects security parameter estimation of pilot-aided scheme lies in the interference of the pilot tone on the quantum signal due to the employing of non-ideal band-pass filter. For the pilot-aided scheme in Figure 2, the filtered quantum signal of V-pol will contain residual pilot tone components, resulting in parameter estimation errors and an increase in excess noise in the system. In our simulation, the band-pass filter we adopt is a classical FIR filter based on Hamming window. Figure 6 gives the curve of estimated T and excess noise of each polarization with respect to the bandwidth of band-pass filter after 20 km transmission, where the filter order is set to be 20 for the curves unmarked and 50 for the curves using dot marks. The simulation results indicate that there exists an optimal bandwidth of FIR filter that can achieve the unbiased estimation of T = 0.4 (20 km). The excess noise induced by the non-ideal filter is about ${\epsilon }_{filter-V}$ = 5 × 10⁻⁴ for V-pol and ${\epsilon }_{filter-H}$ = 0.5 × 10⁻⁴ for H-pol.

Furthermore, as mentioned before, the implement of pilot-aided PN estimation and compensation can not be perfect in practice because of the estimation error ${\widehat{\theta }}_{error}$ in Equation (2). According to the research in [12], the residual excess noise induce by ${\widehat{\theta }}_{error}$ in TDM pilot-aided schemes can be estimated by

$${\epsilon }_{pn-tdm}={\displaystyle \frac{V_A(\chi +1)}{|{\alpha }_p{|}^2}}={\displaystyle \frac{\chi +1}{r_{pq}^{\prime }}},$$

(10)

where $\chi =(2+2{\nu }_{el}-\eta T)/\eta T+\epsilon$ is the total noise of the pilot tone, ${\alpha }_p$ is the amplitude of the pilot tone in SNU. However, for FDM pilot-aided scheme, the total noise of pilot tone is not equal to that of QKD signal because the noise bandwidth of received pilot tone and QKD signal are different. In this case, ${\epsilon }_{pn}$ is given by

$${\epsilon }_{pn-fdm}={\displaystyle \frac{{\chi }^{\prime }+1}{r_{pq}^{\prime }}},$$

(11)

where ${\chi }^{\prime }\approx \chi (B_p/B_q)$ is the total noise of FDM pilot tone, $B_p$ and $B_q$ are the bandwidth of filtered QKD signal and filtered pilot tone, respectively. In TDM pilot-aided system, $B_p$ and $B_q$ are equal, while $B_p$ is much less than $B_q$ in FDM pilot-aided system when narrow-band filter is used to filter the pilot tone. As a result, ${\epsilon }_{pn-fdm}$ is much less than ${\epsilon }_{pn-tdm}$. The total excess noise induced by pilot tone in each polarization can be eventually calculated as

$${\epsilon }_{pilot-V\left(H\right)}={\epsilon }_{mod-V\left(H\right)}+{\epsilon }_{filter-V\left(H\right)}+{\epsilon }_{pn-fdm},$$

(12)

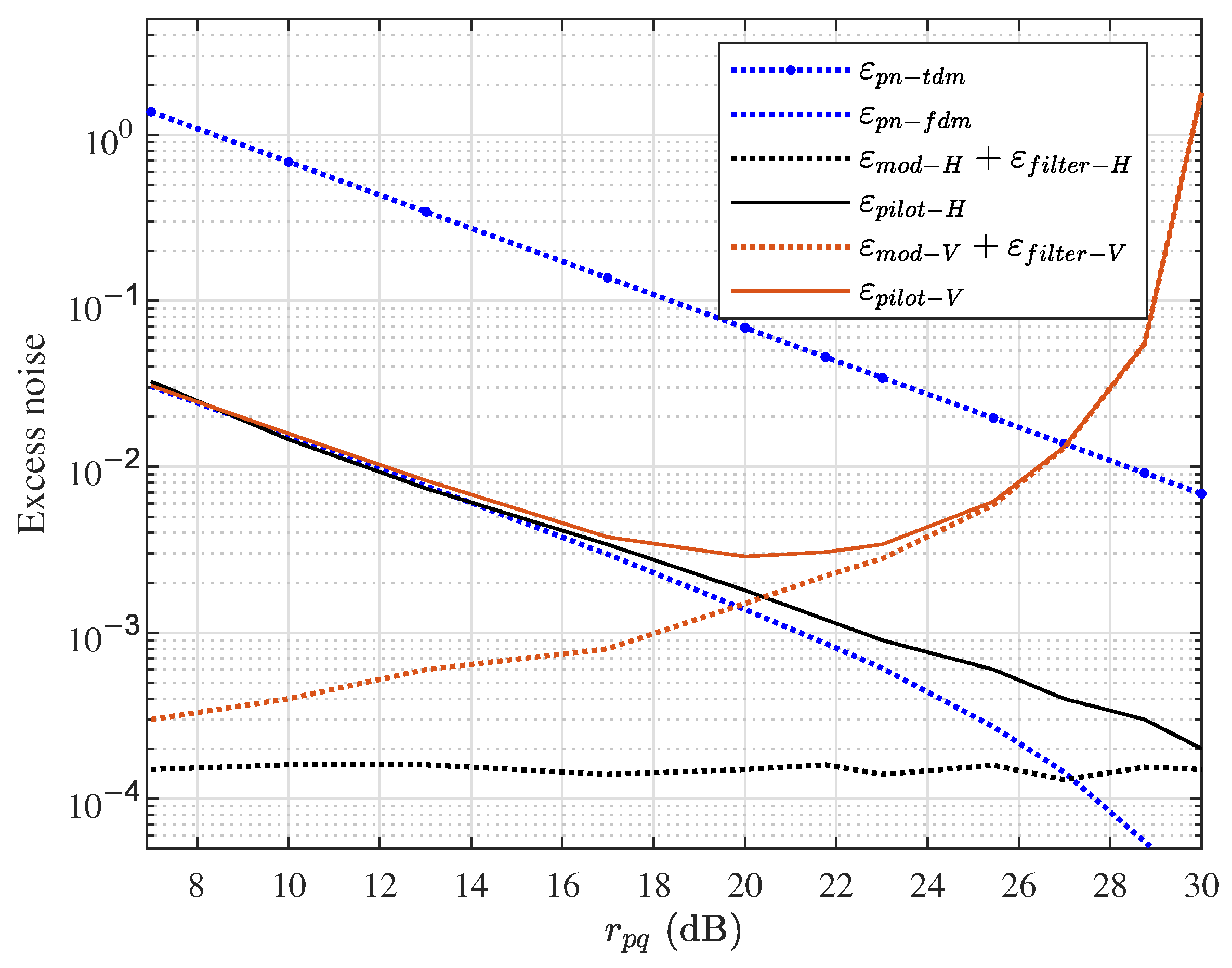
Figure 7 shows the excess noises mentioned in (12) with respect to $r_{pq}$ at the transmission distance of 20 km. The total linewidth of CW and LO are set to 1 × 10⁴ Hz, the bandwidth of bandpass filter is set to be approximately 2.75 GHz for QKD signal and 55 MHz for pilot tone. The result shows that the ${\epsilon }_{pilot-V}$ is minimized to 2.8 × 10⁻³ at the $r_{pq}$ of 20 dB. The corresponding ${\epsilon }_{pilot-H}$ is 1.5 × 10⁻³. The estimated ${\epsilon }_{pn-fdm}$ is 1.4 × 10⁻³ for both polarization states, which is almost 50 times less than ${\epsilon }_{pn-tdm}$. Note that ${\epsilon }_{mod-V\left(H\right)}$ and ${\epsilon }_{filter-V\left(H\right)}$ are neither related to transmission distance, whereas ${\epsilon }_{pn-fdm}$ is increased as the transmission distance increases. It means that the most dominant excess noise induced by pilot tone is ${\epsilon }_{mod-V\left(H\right)}+{\epsilon }_{pn-fdm}$ for V-pol and only ${\epsilon }_{pn-fdm}$ for H-pol.

4. Strategy Optimization of TS-Aided Equalization

Compared to the FDM pilot-aided phase noise compensation, the TDM-based TS-aided equalization and demultiplexing scheme achieves RSOP compensation at the expense of reduced QKD spectral efficiency. Therefore, to achieve the optimal SKR, it is necessary to optimize the equalizer parameters while adaptively selecting the optimal TS rate $\alpha$ depending on the channel conditions. In this section, the performance of two TS-aided equalization schemes shown in Figure 3 are numerically compared to find the optimal strategy of TS insertion, thereby optimize the SKR of QKD system taking into account the impacts of pilot-aided scheme analyzed in Section 3. For scheme A, the parameter $\alpha$ is fixed to 0.5, as a result, only the equalizer’s parameters such as the tap number $n_{tap}$ and step size u of CMA algorithm are needed to be optimized. Figure 8 shows the excess noise of scheme A with respect to different $n_{tap}$ and u, where the RSOP is set to be 1 × 10⁴ rad/s and the transmission distance is 20 km. Note that only the excess noise related to equalization is analyzed here, so that the parameters corresponding to the pilot tone are set to be ideal to make ${\epsilon }_{pilot-V\left(H\right)}=0$. It can be observed that the lowest excess noise of ${\epsilon }_{eq-V}$ = 4 × 10⁻³ can be achieved with $n_{tap}=81$ and u = 2 × 10⁻⁴. Based on the same parameter setup of equalizer, the lowest excess noise of ${\epsilon }_{eq-H}$ = 4.1 × 10⁻³ can be achieved as well. Apparently, scheme A can effectively compensate RSOP once the parameter of equalizer is optimized.

As for scheme B, each N symbol is divided into k blocks of length M and $\alpha M$ TS are then used for the convergence of CMA equalizer. For each $(1-\alpha )M$ symbols, the lowest excess noise can be achieved by jointly optimizing the value of $\alpha$, $n_{tap}$ and u. The total excess noise related to equalizer, denoted by ${\epsilon }_{eq-V\left(H\right)}$, can be obtained by averaging the excess noise of k blocks. 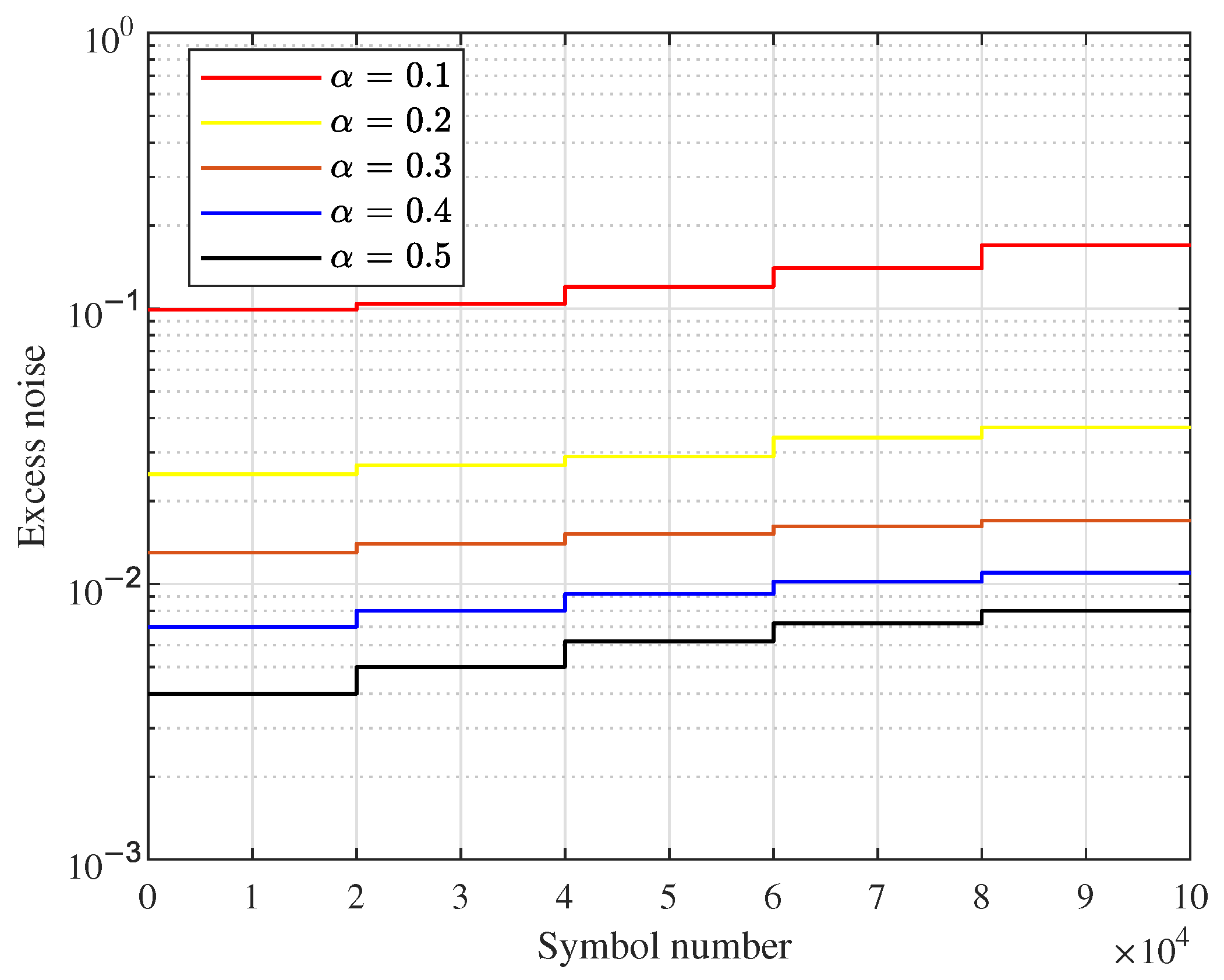Following this strategy, the ${\epsilon }_{eq-V}$ of each k blocks with different $\alpha$ are simulated as shown in Figure 9, where the blocklength N is set to 1 × 10⁵ and k is set to a fixed value of 5 for simplicity. To maintain consistency with scheme B, the parameters of equalizer are set by $n_{tap}=81$ and u = 2 × 10⁻⁴ for both TS and QKD symbols. The results show that for each value of $\alpha$, ${\epsilon }_{eq-V}$ increases with the increasing of symbol number, mainly because of the accumulation RSOP effect over time. It can also be seen that the mean value of ${\epsilon }_{eq-V}$ decreases with the increasing of $\alpha$, specifically, the mean value of ${\epsilon }_{eq-V}$ when $\alpha =0.5$ is 6 × 10⁻³ for scheme B, which is higher than the value of 4 × 10⁻³ for scheme A.

Since the value of $\alpha$ in Scheme A is fixed to 0.5, its ${\epsilon }_{eq-V\left(H\right)}$ and SKR are constant at a specific distance. However, the value of $\alpha$ in scheme B can be adapted to achieve the highest SKR. As a result, the strategy of scheme B can be optimized by traversing the total excess noise of each polarization with different $\alpha$ to find the highest SKR, where the total excess noise of each polarization is defined by

$${\epsilon }_{total-V\left(H\right)}={\epsilon }_0+{\epsilon }_{pilot-V\left(H\right)}+{\epsilon }_{eq-V\left(H\right)},$$

(13)

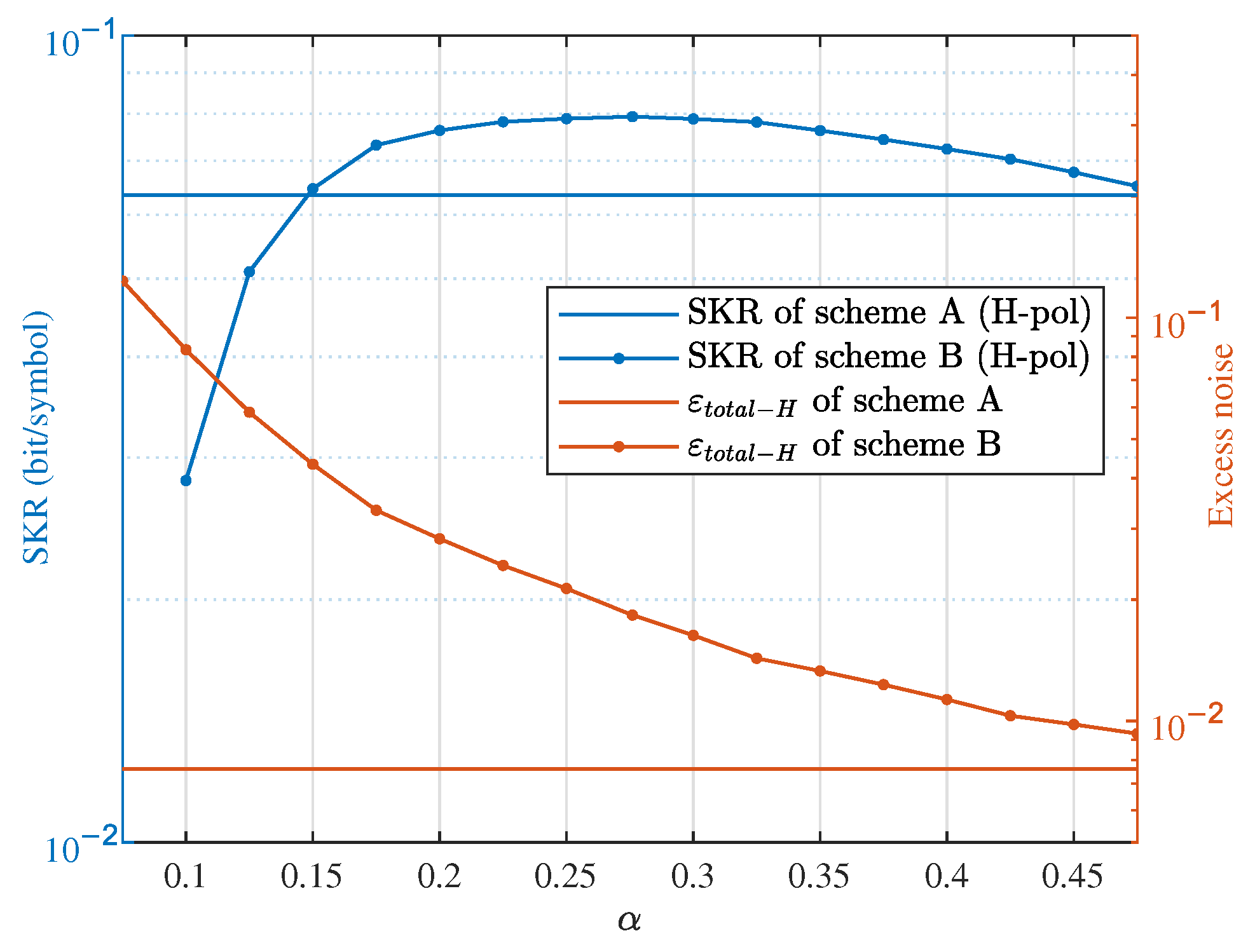
where an original system excess noise of ${\epsilon }_0=0.002$ is added to simulate the fixed excess noise contributed by the noise relative intensity noise of lasers, quantisation noise of ADC, nonlinear noise of the MZM, etc. Note that the ${\epsilon }_{pilot-V\left(H\right)}$ is given by the value in Figure 7. Figure 10 shows the ${\epsilon }_{total-V}$ and SKR of scheme B with respect to different $\alpha$, with the transmission distance is 20 km. The ${\epsilon }_{eq-V\left(H\right)}$ and SKR of scheme A are also given to compare the performance of the two schemes. The results in Figure 10 confirm that at the transmission distance of 20 km, scheme B can achieve higher SKR than scheme A by choosing the optimal $\alpha$, even though the excess noise is much higher.

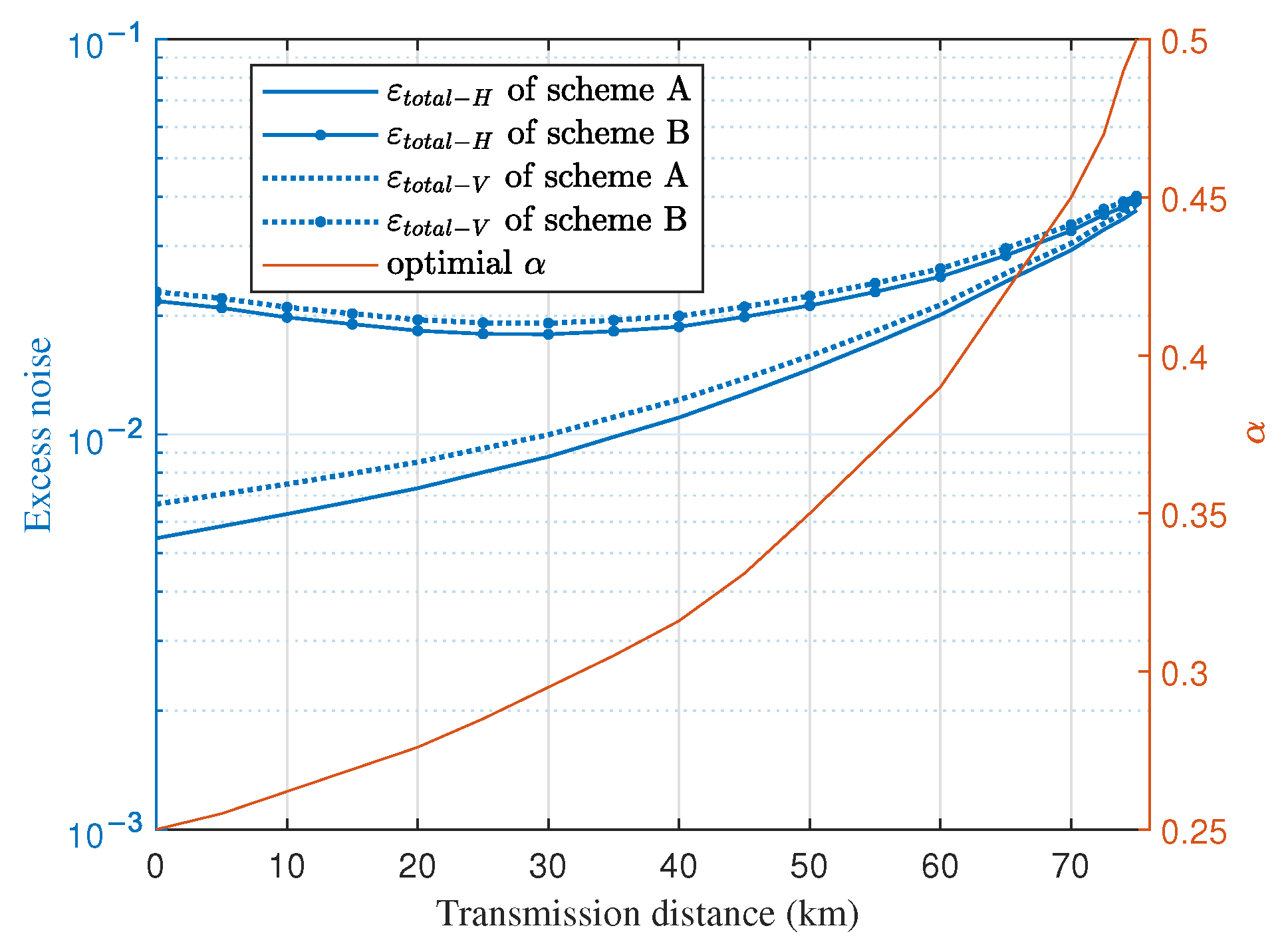
Based on the optimized strategy, the total excess noise and the corresponding optimal $\alpha$ that maximize the SKR of scheme B at different transmission distances for both H-pol and V-pol can be obtained, as shown in Figure 11, where the ${\epsilon }_{total-V\left(H\right)}$ of scheme A are also depicted for comparison. For scheme A, ${\epsilon }_{total-V\left(H\right)}$ increases with the increase of transmission distance and the proportion of ${\epsilon }_{eq-V\left(H\right)}$ and ${\epsilon }_{pilot-V\left(H\right)}$ are equivalent because scheme A can achieve the minimum excess noise induced by RSOP. Whereas for scheme B, ${\epsilon }_{total-V\left(H\right)}$ exhibits a trend of first decreasing and then increasing with distance, and ${\epsilon }_{eq-V\left(H\right)}$ dominates the total excess noise because of the non-optimal compensation of RSOP compared to scheme A. The occurrence of the trend for scheme B is primarily because that the increasing of $\alpha$ results in the fast decreasing of ${\epsilon }_{eq-V\left(H\right)}$ for short transmission distances while the slow decreasing of ${\epsilon }_{eq-V\left(H\right)}$ for long transmission distances, which can also be seen from the results in Figure 10. Meanwhile, ${\epsilon }_{total-V}$ is higher than ${\epsilon }_{total-H}$ for both scheme A and scheme B because of the extra excess noise induced by the pilot tone in V-pol. In addition, the optimal $\alpha$ also increases with the increase of transmission distance.

Finally, to evaluate the overall security of the system, the SKR (in bit/symbol) of scheme A and scheme B at different transmission distances are given in Figure 12, where the SKR of H-pol and V-pol are calculated both individually and summed. The results show that scheme B can obtain higher SKR than scheme A for the transmission distances less than 55 km and lower SKR for the transmission distances more than 55 km. For example, the total SKR of around 0.67 bit/sample, 0.11 bit/sample, 0.015 bit/sample can be achieved for scheme B and 0.52 bit/sample, 0.09 bit/sample, 0.013 bit/sample for scheme A at the transmission distances of 5 km, 25 km, and 50 km, respectively. Considering the baud rate of 2 Gbaud, the corresponding SKR in bps are 1340 Mbps, 220 Mbps, 30 Mbps for scheme B and 1040 Mbps, 180 Mbps, 26 Mbps for scheme A at the transmission distances of 5 km, 25 km and 50 km, respectively. It can be figured out that scheme B can realize the SKR gain of around 29%, 22%, and 15% compared to scheme A at the transmission distance of 5 km, 25 km, and 50 km, respectively, which are significant for metropolitan-scale applications. Note that the aim of the simulation in this work is to compare the performance of different DSP schemes in PDM CVQKD system, therefore the SKR obtained under the system setup is just typical value for reference. It means that in practical experiments, even higher SKR can be achieved by increasing the baud rate and choosing the optimal parameters of the system. In practical implementation, the noise level and the parameters may vary a lot, but the results show a strategy of realizing the optimal performance with a simplified DSP method. In addition, as shown in the inset of Figure 12, the extra excess noise induced by the pilot tone in V-pol results in insignificant SKR loss compared with H-pol, which further proves that the FDM-based pilot-aided scheme contributes few impact on the performance of the system.

5. Discussion

• The calibration of $V_A$ in pilot-aided CVQKD systems is an important issue worthy of discussion, mainly because the method of calibrating $V_A$ in B2B is infeasible in commercial application.
• The GMCS protocol encodes information by modulating the quadratures (amplitude and phase) of coherent states with a Gaussian distribution, which is optimal for achieving the theoretical channel capacity. GMCS has been complete in security proof so that is widely used in commercial CVQKD systems. The main drawback of GMCS are the reconciliation efficiency of the post-processing stage. In contrast, the DMCS protocol simplifies the preparation by using a small, finite set of non-Gaussian states, typically four coherent states arranged symmetrically in phase space (e.g., a constellation similar to a QPSK modulation). The key advantage of DMCS is its significant simplification for implementation and compatibility in classical coherent optical transmission systems. However, the universal security proof of DMCS protocol is not complete up to now, which limits its employment in practice. In conclusion, only DMCS is considered in the simulation of this work because the security proof of GMCS is more complete compared to that for DMCS. In the future, we will consider DMCS protocol as well.
• In this work, the finite-size effect is not taken into account for simplicity. However, in our work, we focus on the performance comparison of two pilot-aided phase noise compensation schemes as well as the comparison of two TS-aided equalization schemes. As a result, the impact of the finite-size effect on the concrete value of SKR can be insignificant because we mainly consider the SKR difference of different schemes. For example, assume that the SKR of scheme A and scheme B in finite-size regime are $R_{fin}^A$ and $R_{fin}^A$, the corresponding SKR in are $R_{asy}^A$ and $R_{asy}^B$. We could have $R_{asy}^B-R_{asy}^A=R_{fin}^A-R_{fin}^A$ because the decrease of SKR induced by finite-size effect are the same for both of the schemes.

6. Conclusions

In this paper, we investigate PDM-CVQKD based on the structure of classical coherent optical transmission system, where the CW-GMCS-LLO scheme is applied. We propose a simplified FDM-based pilot-aided scheme which can be more efficient and induces less excess noise compared with the traditional TDM-based pilot-aided scheme. In addition, we analyze the effects of pilot-aided scheme on the security parameters of QKD system, the numerical results show that the FDM pilot tone will cause the nonlinear effect of MZM, thus induce excess noise, whereas the FDM pilot-aided PN compensation can be more accurate compared to traditional TDM or PDM pilot-aided PN compensation schemes. Furthermore, the performance of two TS-aided equalization schemes are compared. Assuming the typical linewidth of 1 × 10⁴ Hz and RSOP of 1 × 10⁴ rad/s, scheme B can achieve higher SKR than scheme A by optimizing the value of $\alpha$, $n_{tap}$ and u when the transmission distances are less than 55 km. It means that for short distance QKD, scheme B can be more efficient by offering the trade-off between excess noise and spectral efficiency. The work of this paper aims at offering a reference for the implementation of CVQKD with high SKR and low complexity.