Vector Vortex Beams: Theory, Generation, and Detection of Laguerre–Gaussian and Bessel–Gaussian Types
Abstract
1. Introduction
2. Theoretical Analysis
2.1. Theoretical Models for Generating LGVB and BGVB
2.2. Generation of VVBs
2.3. Characterizing the Properties of the VVB
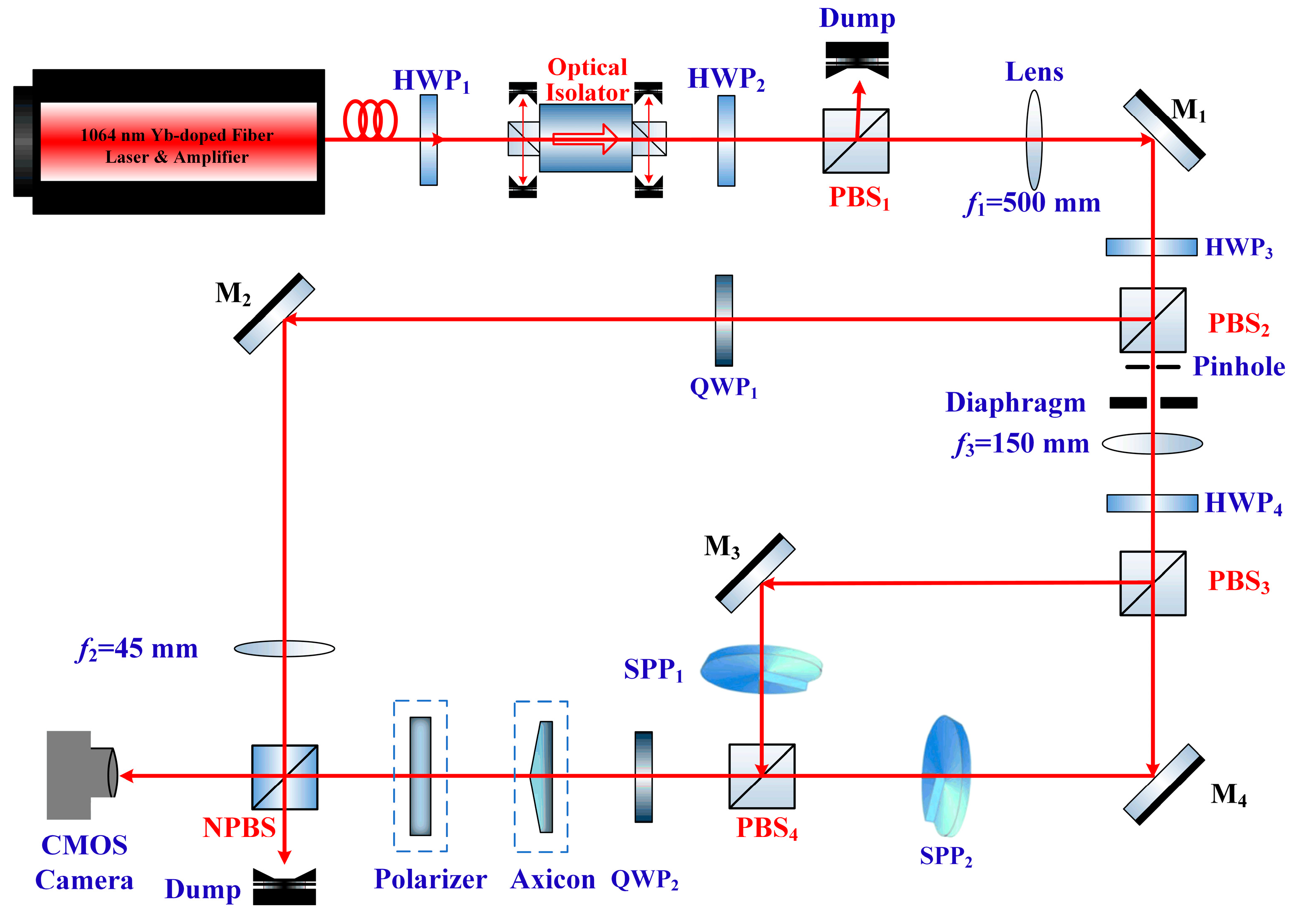
3. Experimental Setup
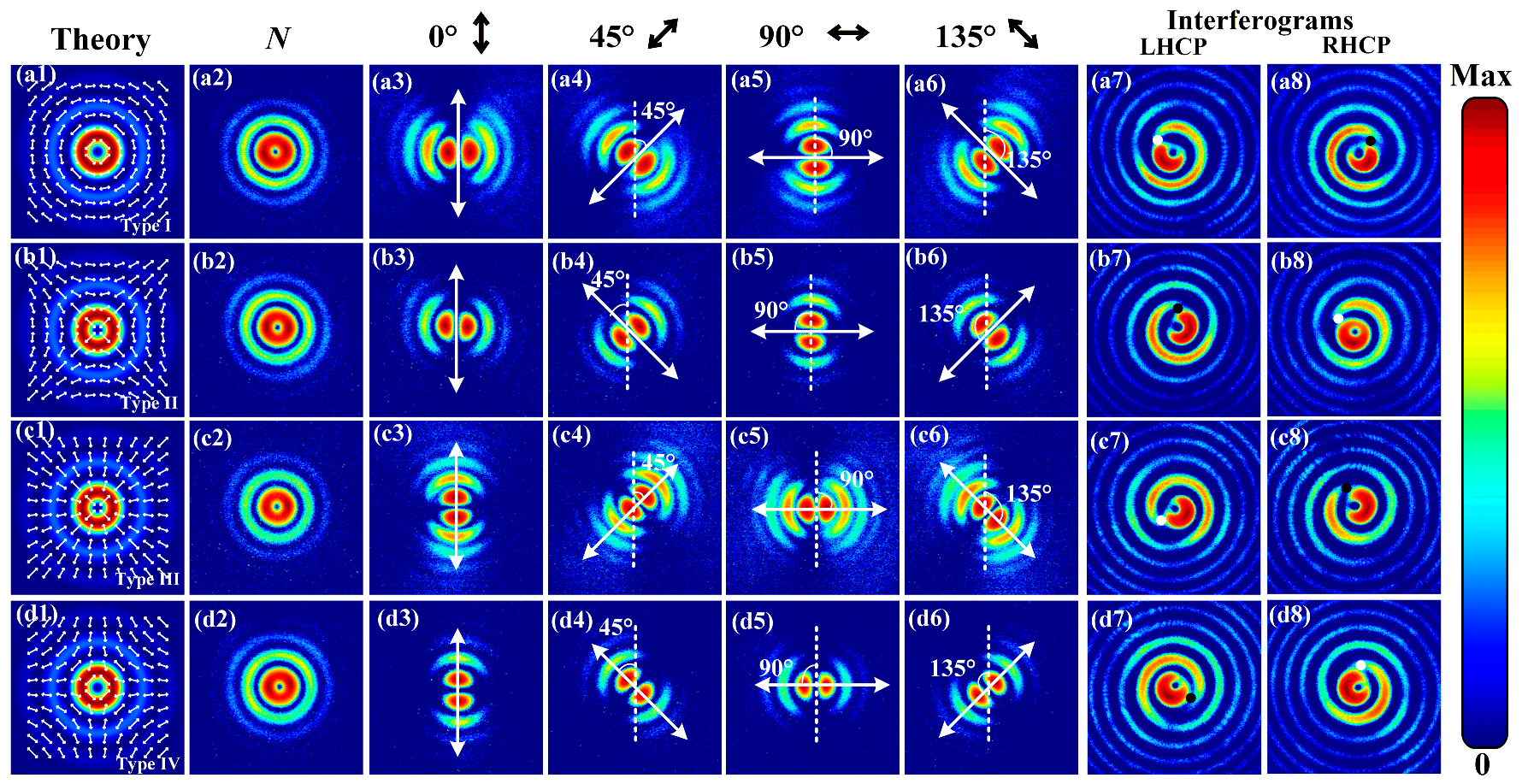
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Gbur, G.J. Singular Optics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Wang, C. Generation and expansion of Laguerre-Gaussian beams. J. Opt. 2022, 51, 910–926. [Google Scholar] [CrossRef]
- Yu, T.; Xia, H.; Xie, W.; Xiao, G.; Li, H. The generation and verification of Bessel-Gaussian beam based on coherent beam combining. Results Phys. 2020, 16, 102872. [Google Scholar] [CrossRef]
- Tao, X.; Liang, Y.; Zhang, S.; Li, Y.; Guo, M.; Li, P. Generation of perfect vortex beams with complete control over the ring radius and ring width. Photonics 2023, 10, 1382. [Google Scholar] [CrossRef]
- Guo, M.H.; Yan, X.; Wu, Z.K.; Gu, Y.Z.; Li, P. Analytical frequency-doubled HG modes in astigmatic mode converters for composite vortex beam generation. Opt. Express 2025, 33, 42206–42220. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Wan, Z.; Shen, Y.; Wang, Z.; Shi, Z.; Liu, Q.; Fu, X. Divergence-degenerate spatial multiplexing towards future ultrahigh capacity, low error-rate optical communications. Light Sci. Appl. 2022, 11, 144. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liu, J.; Li, S.; Zhao, Y.; Du, J.; Zhu, L. Orbital angular momentum and beyond in free-space optical communications. Nanophotonics 2021, 11, 645–680. [Google Scholar] [CrossRef] [PubMed]
- Willner, A.E.; Song, H.; Zou, K.; Zhou, H.; Su, X. Orbital angular momentum beams for high-capacity communications. J. Light. Technol. 2022, 41, 1918–1933. [Google Scholar] [CrossRef]
- Ruan, Z.; Wan, Y.; Wang, L.; Zhou, W.; Wang, J. Flexible orbital angular momentum mode switching in multimode fibre using an optical neural network chip. Light Adv. Manuf. 2024, 5, 296–307. [Google Scholar] [CrossRef]
- Gao, H.; Yang, D.; Liu, Z.; Yang, Z. Microscopic imaging method based on spatial phase-shifted interference of single-interferograms using vortex beams. Opt. Laser Technol. 2025, 189, 113150. [Google Scholar] [CrossRef]
- Wang, B.; Shi, J.; Zhang, T.; Xu, X.; Cao, Y.; Li, X. Improved lateral resolution with an annular vortex depletion beam in STED microscopy. Opt. Lett. 2017, 42, 4885–4888. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, C.; Liu, T.; Ren, Y. Generation of spiral optical vortex with varying OAM for micro-manipulation. Opt. Commun. 2022, 524, 128767. [Google Scholar] [CrossRef]
- Mallick, N.S. Vortex beam assisted generation and manipulation of structured light. J. Opt. Soc. Am. B 2024, 41, 2085–2091. [Google Scholar] [CrossRef]
- Qiu, S.; Liu, T.; Ding, Y.; Liu, Z.; Chen, L.; Ren, Y. Rotational Doppler effect with vortex beams: Fundamental mechanism and technical progress. Front. Phys. 2022, 10, 938593. [Google Scholar] [CrossRef]
- Cheng, T.Y.; Wang, W.Y.; Li, J.S.; Guo, J.X.; Liu, S.; Lv, J.Q. Rotational Doppler effect in vortex light and its applications for detection of the rotational motion. Photonics 2022, 9, 441. [Google Scholar] [CrossRef]
- Galvez, E.J. Vector beams in free space. In The Angular Momentum of Light; Andrews, D.L., Babiker, M., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 51–70. [Google Scholar]
- Yue, Z.; Lu, P.; Xu, J.; Li, Z.; Teng, S. Vector beams encoded by diverse orthogonal polarization states and their generation based on metasurfaces. New J. Phys. 2023, 25, 013018. [Google Scholar] [CrossRef]
- Vyas, S.; Kozawa, Y.; Sato, S. Polarization singularities in superposition of vector beams. Opt. Express 2013, 21, 8972–8986. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, C.; Lu, P.; Xu, J.; Yue, Z.; Teng, S. Generation of vector beams with different polarization singularities based on metasurfaces. New J. Phys. 2022, 24, 043022. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, L.; Jiang, X.; Zhu, L.; Shi, Q. Optical force effects of Rayleigh particles by cylindrical vector beams. Nanomaterials 2024, 14, 691. [Google Scholar] [CrossRef]
- Weng, X.; Du, L.; Shi, P.; Yuan, X. Creating adjustable uniform optical cages through polarization shaping in a low NA optical system. Appl. Opt. 2017, 56, 1046–1051. [Google Scholar] [CrossRef]
- Man, Z.; Bai, Z.; Li, J.; Zhang, S.; Li, X.; Zhang, Y.; Ge, X.; Fu, S. Optical cage generated by azimuthal- and radial-variant vector beams. Appl. Opt. 2018, 57, 3592–3597. [Google Scholar] [CrossRef]
- Zhu, M.; Fu, S.; Man, Z. Linear and angular momentum properties induced by radial- and azimuthal-variant polarized beams in a strongly focused optical system. Opt. Express 2022, 30, 41048–41060. [Google Scholar] [CrossRef]
- Xian, M.; Xu, Y.; Ouyang, X.; Cao, Y.; Lan, S.; Li, X. Segmented cylindrical vector beams for massively-encoded optical data storage. Sci. Bull. 2020, 65, 2072–2079. [Google Scholar] [CrossRef]
- Hong, J.; Li, J.; Chu, D. Dynamic phase and polarization modulation using two-beam parallel coding for optical storage in transparent materials. Sensors 2022, 22, 9010. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.Z.; Pan, Y.; Zhao, M.D.; Zhang, G.L.; Zhang, Y.; Tu, C.; Li, Y.; Wang, H.T. Focusing behavior of the fractal vector optical fields designed by fractal lattice growth model. Opt. Express 2018, 26, 1597–1614. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Xiao, X.; Gao, Y.; Li, J.; Hoenders, B.J.; Cai, Y.; Yuan, Y. Signal quality enhanced and multicast transmission via cylindrical vector beams with adaptive optics compensation in free space optical communications. Appl. Phys. Lett. 2023, 123, 211102. [Google Scholar] [CrossRef]
- Zhang, L.; Qiu, X.; Li, F.; Liu, H.; Chen, X.; Chen, L. Second harmonic generation with full Poincaré beams. Opt. Express 2018, 26, 11678–11684. [Google Scholar] [CrossRef]
- Liu, H.; Li, H.; Zheng, Y.; Chen, X. Nonlinear frequency conversion and manipulation of vector beams. Opt. Lett. 2018, 43, 5981–5984. [Google Scholar] [CrossRef]
- Wu, H.J.; Yang, H.R.; Rosales-Guzmán, C.; Gao, W.; Shi, B.S.; Zhu, Z.H. Vectorial nonlinear optics: Type-II second-harmonic generation driven by spin-orbit-coupled fields. Phys. Rev. 2019, 100, 053840. [Google Scholar] [CrossRef]
- Yang, C.; Zhou, Z.Y.; Li, Y.; Li, Y.H.; Liu, S.L.; Liu, S.K.; Xu, Z.H.; Guo, G.C.; Shi, B.S. Nonlinear frequency conversion and manipulation of vector beams in a Sagnac loop. Opt. Lett. 2019, 44, 219–222. [Google Scholar] [CrossRef]
- Fu, S.; Gao, C. Vector Beams and Vectorial Vortex Beams. In Optical Vortex Beams: Fundamentals and Techniques; Springer Nature: Singapore, 2023; pp. 277–333. [Google Scholar]
- Liu, S.; Qi, S.; Zhang, Y.; Li, P.; Wu, D.; Han, L.; Zhao, J. Highly efficient generation of arbitrary vector beams with tunable polarization, phase, and amplitude. Photonics Res. 2018, 6, 228–233. [Google Scholar] [CrossRef]
- Yu, W.; Yan, J. Modelling and analysis of vector and vector vortex beams reflection for optical sensing. Photonics 2024, 11, 729. [Google Scholar] [CrossRef]
- Wu, H.; Qiu, J.; Wang, P.; Shang, Y.; Zhang, L.; Wei, H.; Pang, F. Cylindrical vector beam for vector magnetic field sensing based on magnetic fluid. IEEE Photonics Technol. Lett. 2021, 33, 703–706. [Google Scholar] [CrossRef]
- Ndagano, B.; Nape, I.; Cox, M.A.; Rosales-Guzman, C.; Forbes, A. Creation and detection of vector vortex modes for classical and quantum communication. J. Light. Technol. 2017, 36, 292. [Google Scholar] [CrossRef]
- Cheng, M.; Dong, K.; Shi, C.; Mohammed, A.A.H.T.; Guo, L.; Yi, X.; Wang, P.; Li, J. Enhancing performance of air-ground OAM communication system utilizing vector vortex beams in the atmosphere. Photonics 2023, 10, 41. [Google Scholar] [CrossRef]
- He, H.; Friese, M.E.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 1995, 75, 826. [Google Scholar] [CrossRef]
- Ling, X.; Zhou, X.; Huang, K.; Liu, Y.; Qiu, C.W.; Luo, H.; Wen, S. Recent advances in the spin Hall effect of light. Rep. Prog. Phys. 2017, 80, 066401. [Google Scholar] [CrossRef] [PubMed]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313. [Google Scholar] [CrossRef]
- Ndagano, B.; Perez-Garcia, B.; Roux, F.S.; McLaren, M.; Rosales-Guzman, C.; Zhang, Y.; Mouane, O.; Hernandez-Aranda, R.; Konrad, T.; Forbes, A. Characterizing quantum channels with non-separable states of classical light. Nat. Phys. 2017, 13, 397. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P. Generation of light fields with controlled non-uniform elliptical polarization when focusing on structured laser beams. Photonics 2023, 10, 1112. [Google Scholar] [CrossRef]
- Qasim, M.; Liu, Y.; Tao, S. Non-uniform phase distribution of a tightly focused elliptically polarized vortex beam. Phys. Scr. 2024, 99, 115508. [Google Scholar] [CrossRef]
- Chen, B.; Pu, J. Tight focusing of elliptically polarized vortex beams. Appl. Opt. 2009, 48, 1288–1294. [Google Scholar] [CrossRef] [PubMed]
- Nivas, J.; Allahyari, E.; Cardano, F.; Rubano, A.; Fittipaldi, R.; Vecchione, A.; Paparo, D.; Marrucci, L.; Bruzzese, R.; Amoruso, S. Surface structures with unconventional patterns and shapes generated by femtosecond structured light fields. Sci. Rep. 2018, 8, 13613. [Google Scholar] [CrossRef] [PubMed]
- Borodaenko, Y.; Syubaev, S.; Gurbatov, S.; Zhizhchenko, A.; Porfirev, A.; Khonina, S.; Mitsai, E.; Gerasimenko, A.; Shevlyagin, A.; Modin, E.; et al. Deep subwavelength laser-induced periodic surface structures on silicon as a novel multifunctional biosensing platform. ACS Appl. Mater. Interfaces 2021, 13, 54551. [Google Scholar] [CrossRef]
- Nivas, J.J.; Allahyari, E.; Amoruso, S. Direct femtosecond laser surface structuring with complex light beams generated by q-plates. Adv. Opt. Technol. 2020, 9, 53. [Google Scholar] [CrossRef]
- Varlamova, O.; Costache, F.; Reif, J.; Bestehorn, M. Self-organized pattern formation upon femtosecond laser ablation by circularly polarized light. Appl. Surf. Sci. 2006, 252, 4702. [Google Scholar] [CrossRef]
- Fraggelakis, F.; Stratakis, E.; Loukakos, P.A. Control of periodic surface structures on silicon by combined temporal and polarization shaping of femtosecond laser pulses. Appl. Surf. Sci. 2018, 444, 154. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, X.; Naidoo, D.; Fu, X.; Forbes, A. Structured ray-wave vector vortex beams in multiple degrees of freedom from a laser. Optica 2020, 7, 820–831. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, H.; Liu, Q.; Fu, X.; Shen, Y. Ultra-degree-of-freedom structured light for ultracapacity information carriers. ACS Photonics 2023, 10, 2149. [Google Scholar] [CrossRef]
- He, C.; Shen, Y.; Forbes, A. Towards higher-dimensional structured light. Light Sci. Appl. 2022, 11, 205. [Google Scholar] [CrossRef] [PubMed]
- Naidoo, D.; Roux, F.S.; Dudley, A.; Litvin, I.; Piccirillo, B.; Marrucci, L.; Forbes, A. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photonics 2016, 10, 327–332. [Google Scholar] [CrossRef]
- Sroor, H.; Huang, Y.W.; Sephton, B.; Naidoo, D.; Vallés, A.; Ginis, V.; Qiu, C.-W.; Ambrosio, A.; Capasso, F.; Forbes, A. High-purity orbital angular momentum states from a visible metasurface laser. Nat. Photonics 2020, 14, 498–503. [Google Scholar] [CrossRef]
- Oh, Y.J.; Park, J.S.; Park, E.J.; Kim, J.W.; Jeong, H. Diode-pumped Nd:YVO4 lasers with cylindrical vector vortex output in continuous-wave and Q-switched operation. Opt. Laser Technol. 2023, 164, 109483. [Google Scholar] [CrossRef]
- Wang, H.; Ma, Z.; Dou, J.; Fan, L.; Li, B.; Hu, Y. Hybrid-order Poincaré sphere beam fiber laser. Opt. Express 2025, 33, 26272–26285. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Rao, A.S.; Omatsu, T. Generation of V-point polarization singularity using single phase encoding with a spatial light modulator. Sci. Rep. 2023, 13, 315. [Google Scholar] [CrossRef]
- Li, R.; Zhu, X.; Tu, Y.; Lin, Z.; Liu, Z.; Liu, T.; Ren, Y. Generation of high radial node vector vortex beams based on digital micromirror device. Opt. Laser Technol. 2024, 171, 110457. [Google Scholar] [CrossRef]
- Gou, Y.; Tian, H.W.; Wang, Z.X.; Zhang, T.Y.; Sun, S.; Zheng, S.; Cui, T.J.; Ma, H.F. Generation of arbitrarily programmable vector vortex beams based on spin-independent metasurface. Laser. Photonics Rev. 2024, 18, 2400700. [Google Scholar] [CrossRef]
- Yao, J.; Wu, S.; Li, X.; Liu, J.; Zhan, Q.; Wang, A. Generation of arbitrary vector vortex beam using a single Q-plate. Laser Photonics Rev. 2025, 19, 2402290. [Google Scholar] [CrossRef]
- Harrison, J.; Mphuthi, N.; Mabena, C.; Naidoo, D. High-energy generation of arbitrary cylindrical vector vortex beams using a modified Mach-Zehnder interferometer. Appl. Opt. 2025, 64, C60–C68. [Google Scholar] [CrossRef] [PubMed]
- Stoyanov, L.; Zhekova, M.; Stefanov, A.; Stefanov, I.; Paulus, G.G.; Dreischuh, A. Zeroth- and first-order long range non-diffracting Gauss-Bessel beams generated by annihilating multiple-charged optical vortices. Sci. Rep. 2020, 10, 21981. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Zhang, W.; Wang, L.; Li, W.; Gong, L.; Cheng, W.; Chen, H.; Gruska, J. Propagation and self-healing properties of Bessel-Gaussian beam carrying orbital angular momentum in an underwater environment. Sci. Rep. 2019, 9, 2025. [Google Scholar] [CrossRef]
- Diao, L.; Wang, M.; Zhang, J.; Wang, W.; Ma, C. Self-healing, transmission, and communication properties of Bessel-Gaussian vortex beam in the underwater environment. IEEE J. Quantum Electron. 2025, 61, 8000108. [Google Scholar] [CrossRef]
- Dudley, A.; Li, Y.; Mhlanga, T.; Escuti, M.; Forbes, A. Generating and measuring nondiffracting vector Bessel beams. Opt. Lett. 2013, 38, 3429–3432. [Google Scholar] [CrossRef] [PubMed]
- Baltrukonis, J.; Ulčinas, O.; Orlov, S.; Jukna, V. High-order vector Bessel-Gauss beams for laser micromachining of transparent materials. Phys. Rev. Appl. 2021, 16, 034001. [Google Scholar] [CrossRef]
- Zhou, Z.; Tan, Q.; Jin, G. Cylindrically polarized vortex beams generated by subwavelength concentric Al metallic gratings. J. Opt. 2011, 13, 075004. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.A.; Cottrell, D.M. Production, detection, and manipulation of vortex beams and radially polarized beams. In Optics and Photonics for Information Processing VII; SPIE: Bellingham, WA, USA, 2013; Volume 8855, p. 885502. [Google Scholar] [CrossRef]
- Wakayama, T.; Higashiguchi, T.; Oikawa, H.; Sakaue, K.; Washio, M.; Yonemura, M.; Yoshizawa, T.; Tyo, S.; Otani, Y. Determination of the polarization states of an arbitrary polarized terahertz beam: Vectorial vortex analysis. Sci. Rep. 2015, 5, 9416. [Google Scholar] [CrossRef]
- He, Y.; Liu, J.; Xie, Z.; Zhang, X.; Cai, Y.; Su, M.; Chen, S.; Li, Y. Independently detect the spiral phase of cylindrical vector vortex beams. In Proceedings of the 2017 Opto-Electronics and Communications Conference (OECC) and Photonics Global Conference (PGC), Singapore, 23–27 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Wang, Z.; Jian, S. Vectorial vortex beam detection using plasmonic interferences on a structured gold film. Opt. Laser Technol. 2019, 109, 241. [Google Scholar] [CrossRef]
- Zhang, C.; Min, C.; Zhang, Y.; Fu, Y.; Li, L.; Wang, Y.; Yuan, X. Detection of cylindrical vector beams with chiral plasmonic lens. Chin. Opt. Lett. 2022, 20, 023602. [Google Scholar] [CrossRef]
- Qi, J.; Yi, W.; Fu, M.; Liu, J.; Zhu, M.; Zhu, S.; Chen, X.; Zhang, H.; Zhang, H.; Shi, B.; et al. Continuously adjustable cylindrical vector and vortex beams by programming vortex half-wave plates and detection based on coaxial or small-angle interference. Phys. Rev. Appl. 2022, 18, 034086. [Google Scholar] [CrossRef]
- Kumar, P.; Nishchal, N.; Omatsu, T.; Rao, A. Self-referenced interferometry for single-shot detection of vector-vortex beams. Sci. Rep. 2022, 12, 17253. [Google Scholar] [CrossRef] [PubMed]
- Longman, A.; Fedosejevs, R. Mode conversion efficiency to Laguerre-Gaussian OAM modes using spiral phase optics. Opt. Express 2017, 25, 17382–17392. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, P.; Ma, J.; Zhang, S.; Gu, Y. Generation and detection of optical vortices with multiple cascaded spiral phase plates. Photonics 2022, 9, 354. [Google Scholar] [CrossRef]
- Ruffato, G.; Massari, M.; Romanato, F. Generation of high-order Laguerre-Gaussian modes by means of spiral phase plates. Opt. Lett. 2014, 39, 5094–5097. [Google Scholar] [CrossRef]
- Jarutis, V.; Paškauskas, R.; Stabinis, A. Focusing of Laguerre-Gaussian beams by axicon. Opt. Commun. 2000, 184, 105–112. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K. Generation of high-order Bessel beams by use of an axicon. Opt. Commun. 2000, 177, 297–301. [Google Scholar] [CrossRef]
- Topuzoski, S.; Janicijevic, L. Conversion of high-order Laguerre–Gaussian beams into Bessel beams of increased, reduced or zeroth order by use of a helical axicon. Opt. Commun. 2009, 282, 3426–3432. [Google Scholar] [CrossRef]
- Parsa, S.; Fallah, H.R.; Ramezani, M.; Soltanolkotabi, M. Generation of pulsed Bessel-Gaussian beams using passive axicon: Theoretical and experimental studies. Appl. Opt. 2012, 51, 7339–7344. [Google Scholar] [CrossRef]
- Sun, C.; Pi, H.; Kiang, K.S.; Ou, J.Y.; Yan, J. Arbitrary hybrid and higher-order Poincaré sphere beam generation by metasurfaces via a unified design framework. Adv. Photonics Nexus 2025, 4, 016015. [Google Scholar] [CrossRef]
- Lei, Q.; Tu, S.; Gong, H.; Zhao, L.; Ren, Y.; Cai, Y.; Zhao, Q. Construction of vector vortex beams on hybrid-order Poincaré sphere through highly scattering media. Opt. Express 2024, 32, 21506–21516. [Google Scholar] [CrossRef]
- Aadhi, A.; Vaity, P.; Chithrabhanu, P.; Reddy, S.G.; Prabakar, S.; Singh, R.P. Non-coaxial superposition of vector vortex beams. Appl. Opt. 2016, 55, 1107–1111. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N. Vortex beams with high-order cylindrical polarization: Features of focal distributions. Appl. Phys. B 2019, 125, 100. [Google Scholar] [CrossRef]
- Rashid, M.; Maragò, O.M.; Jones, P.H. Focusing of high order cylindrical vector beams. J. Opt. A Pure Appl. Opt. 2009, 11, 065204. [Google Scholar] [CrossRef]
- Stalder, M.; Schadt, M. Linearly polarized light with axial symmetry generated by liquid-crystal polarization converters. Opt. Lett. 1996, 21, 1948–1950. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Allegre, O.J.; Perrie, W.; Abrams, K.; Ouyang, J.; Fearon, E.; Edwardson, S.P.; Dearden, G. Dynamic modulation of spatially structured polarization fields for real-time control of ultrafast laser-material interactions. Opt. Express 2013, 21, 25333–25343. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Khonina, S.N.; Ivliev, N.A.; Churin, E.G.; Kirilenko, M.S. Polarization-sensitive patterning of azopolymer thin films using multiple structured laser beams. Sensors 2023, 23, 112. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Tao, X.; Guo, M.; Zhou, C.; Chen, J.; Shang, G.; Li, P. Vector Vortex Beams: Theory, Generation, and Detection of Laguerre–Gaussian and Bessel–Gaussian Types. Photonics 2025, 12, 1029. https://doi.org/10.3390/photonics12101029
Yan X, Tao X, Guo M, Zhou C, Chen J, Shang G, Li P. Vector Vortex Beams: Theory, Generation, and Detection of Laguerre–Gaussian and Bessel–Gaussian Types. Photonics. 2025; 12(10):1029. https://doi.org/10.3390/photonics12101029
Chicago/Turabian StyleYan, Xin, Xin Tao, Minghao Guo, Chunliang Zhou, Jingzhao Chen, Guanyu Shang, and Peng Li. 2025. "Vector Vortex Beams: Theory, Generation, and Detection of Laguerre–Gaussian and Bessel–Gaussian Types" Photonics 12, no. 10: 1029. https://doi.org/10.3390/photonics12101029
APA StyleYan, X., Tao, X., Guo, M., Zhou, C., Chen, J., Shang, G., & Li, P. (2025). Vector Vortex Beams: Theory, Generation, and Detection of Laguerre–Gaussian and Bessel–Gaussian Types. Photonics, 12(10), 1029. https://doi.org/10.3390/photonics12101029




