High-Performance NIR Laser-Beam Shaping and Materials Processing at 350 W with a Spatial Light Modulator
Abstract
1. Introduction
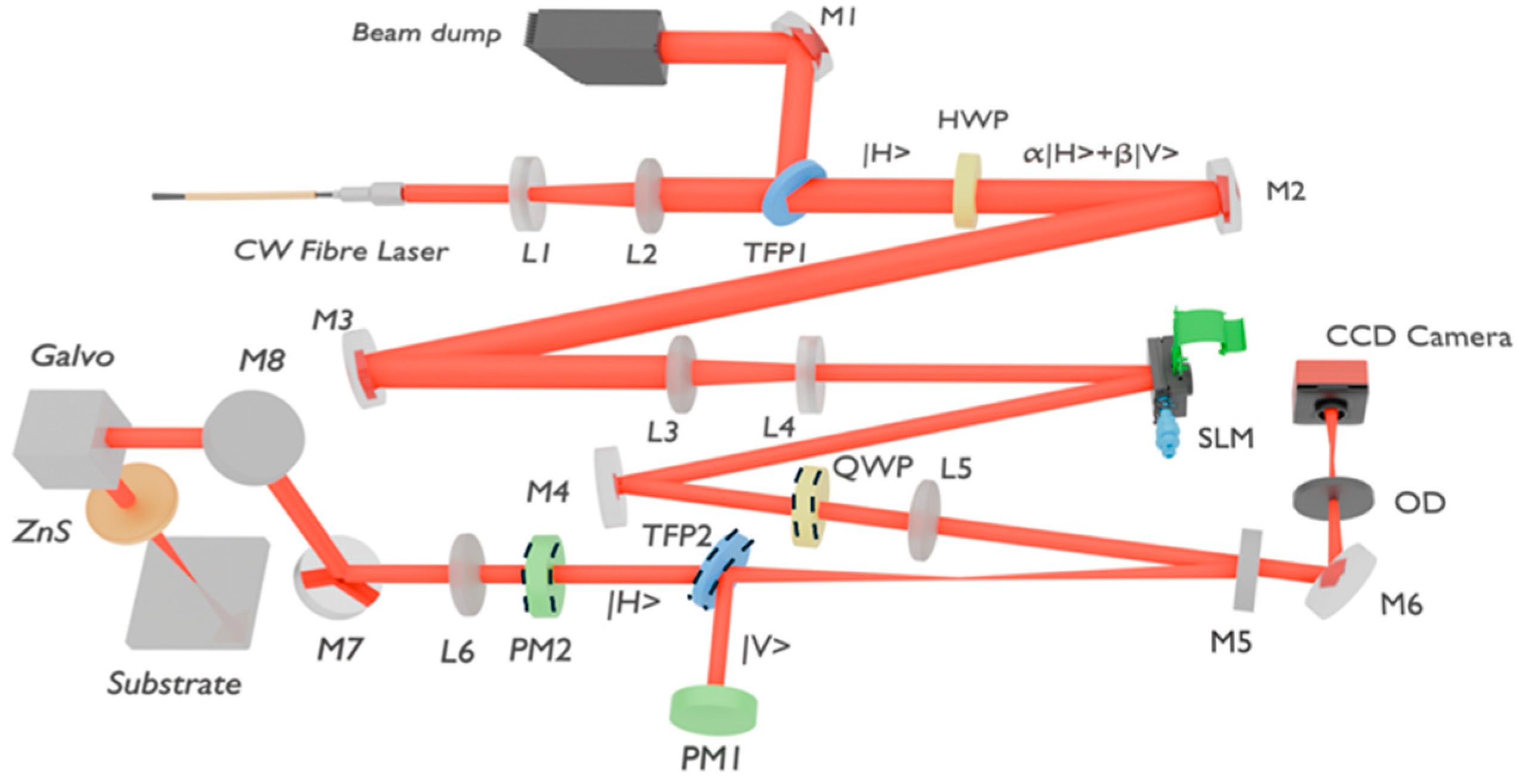
2. Materials and Methods
3. Results
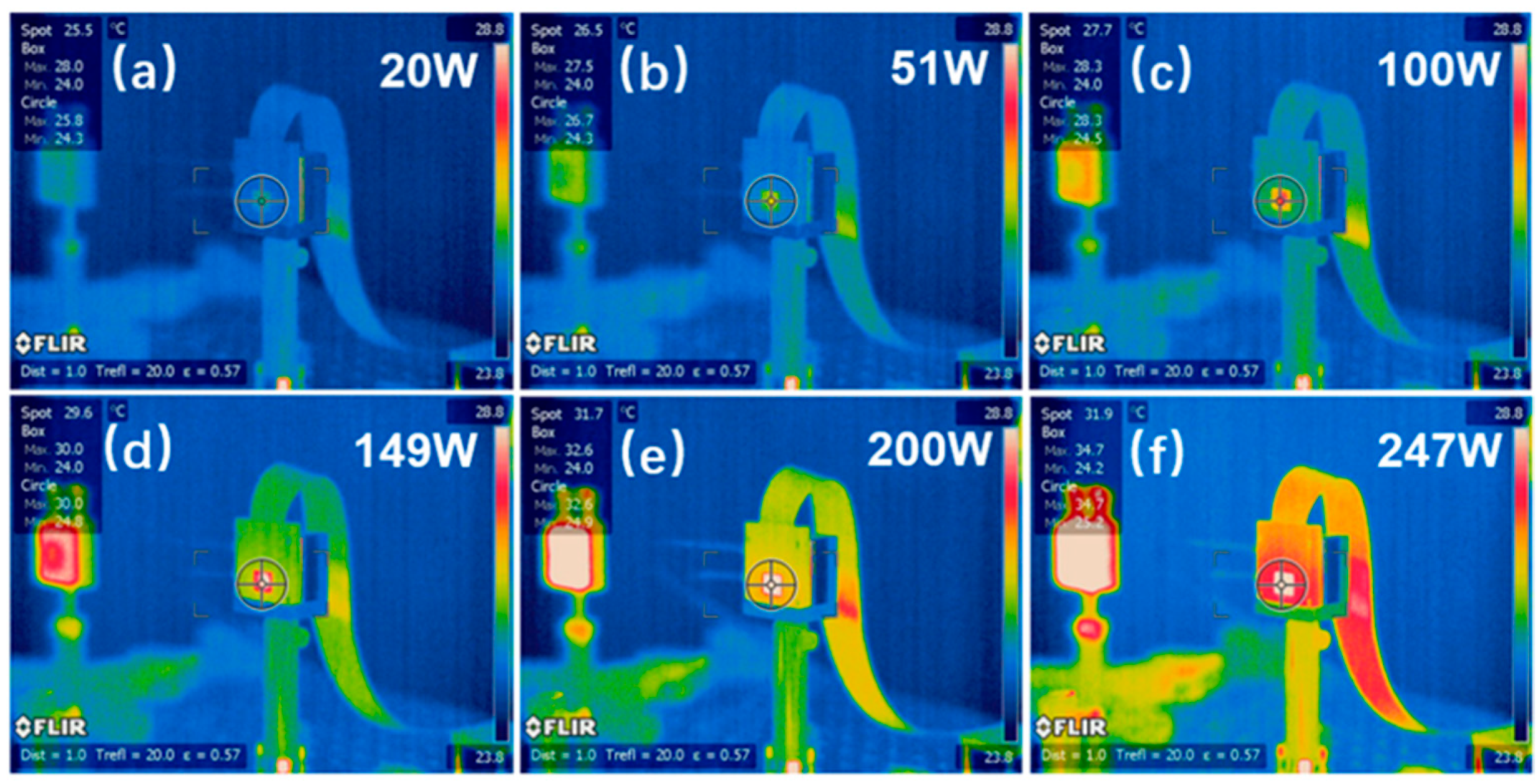
3.1. Chip Temperature with Exposure
3.2. Numerical Modelling of SLM Chip Temperature with Laser Exposure
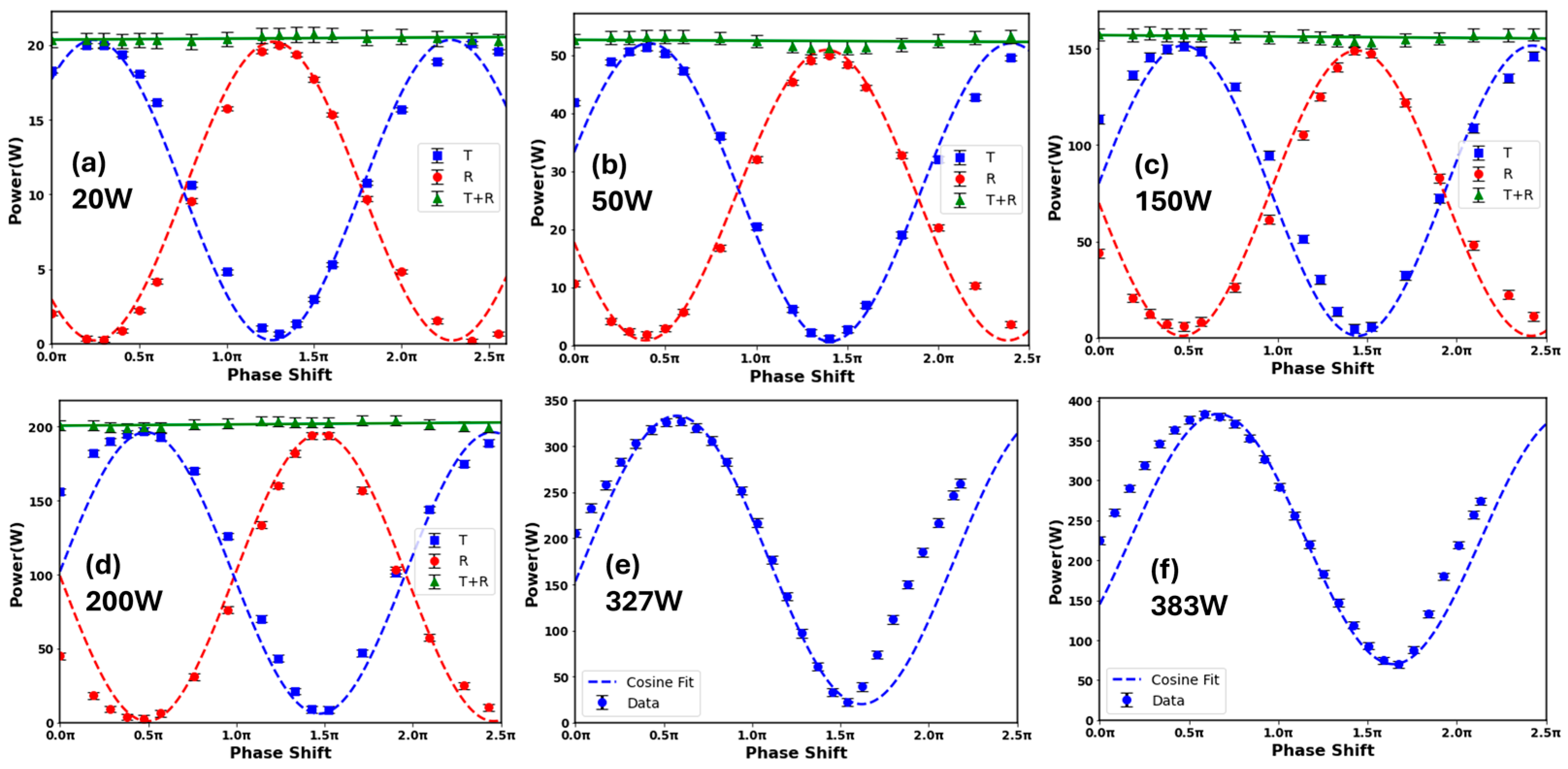
3.3. Phase Response with Exposure
3.4. Multi-Spot Blind Drilling, Mild Steel
3.5. Multi-Beam Surface Scanning, Mild Steel
3.6. Vortex Beam Processing, Mild Steel
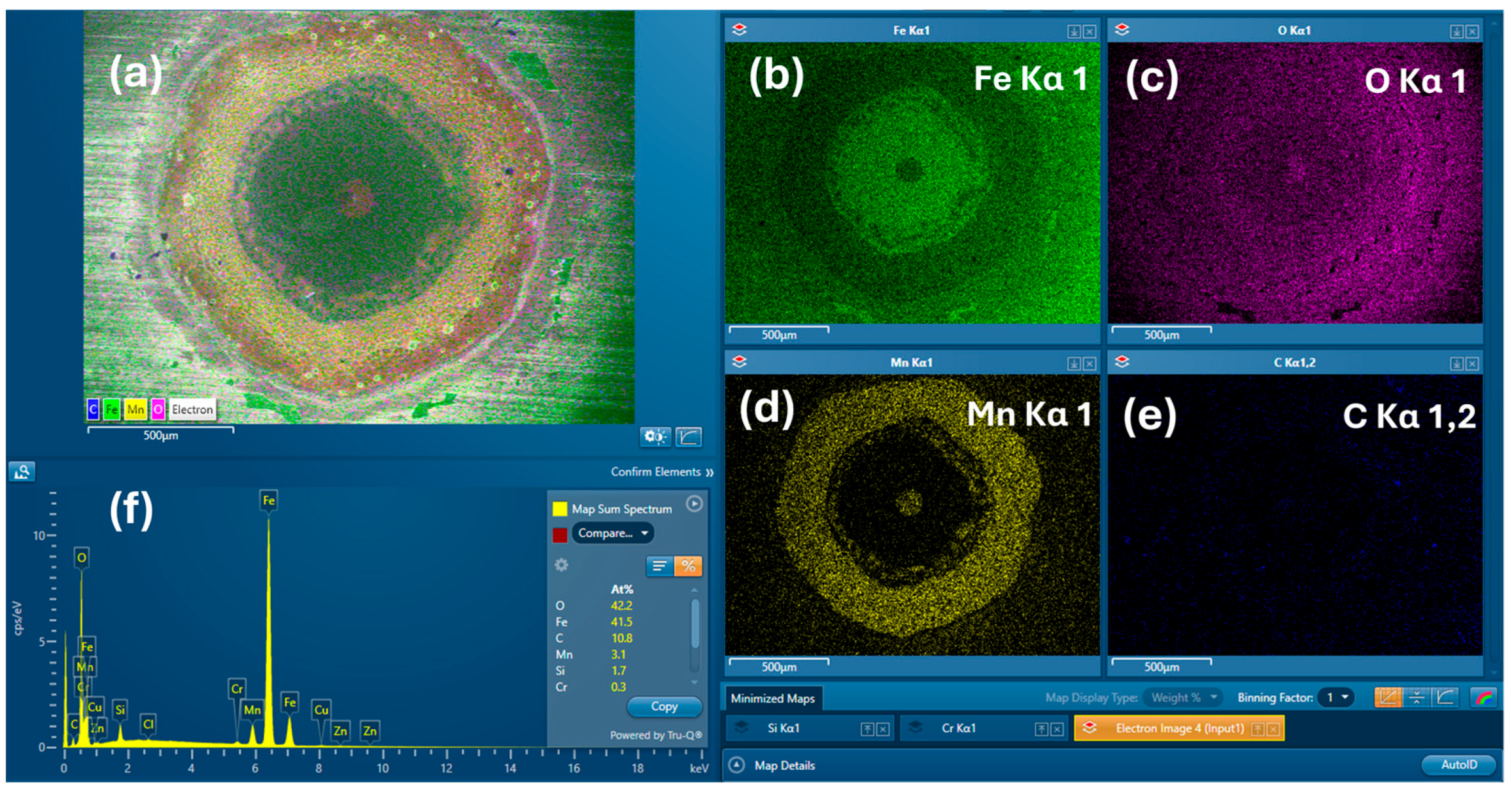
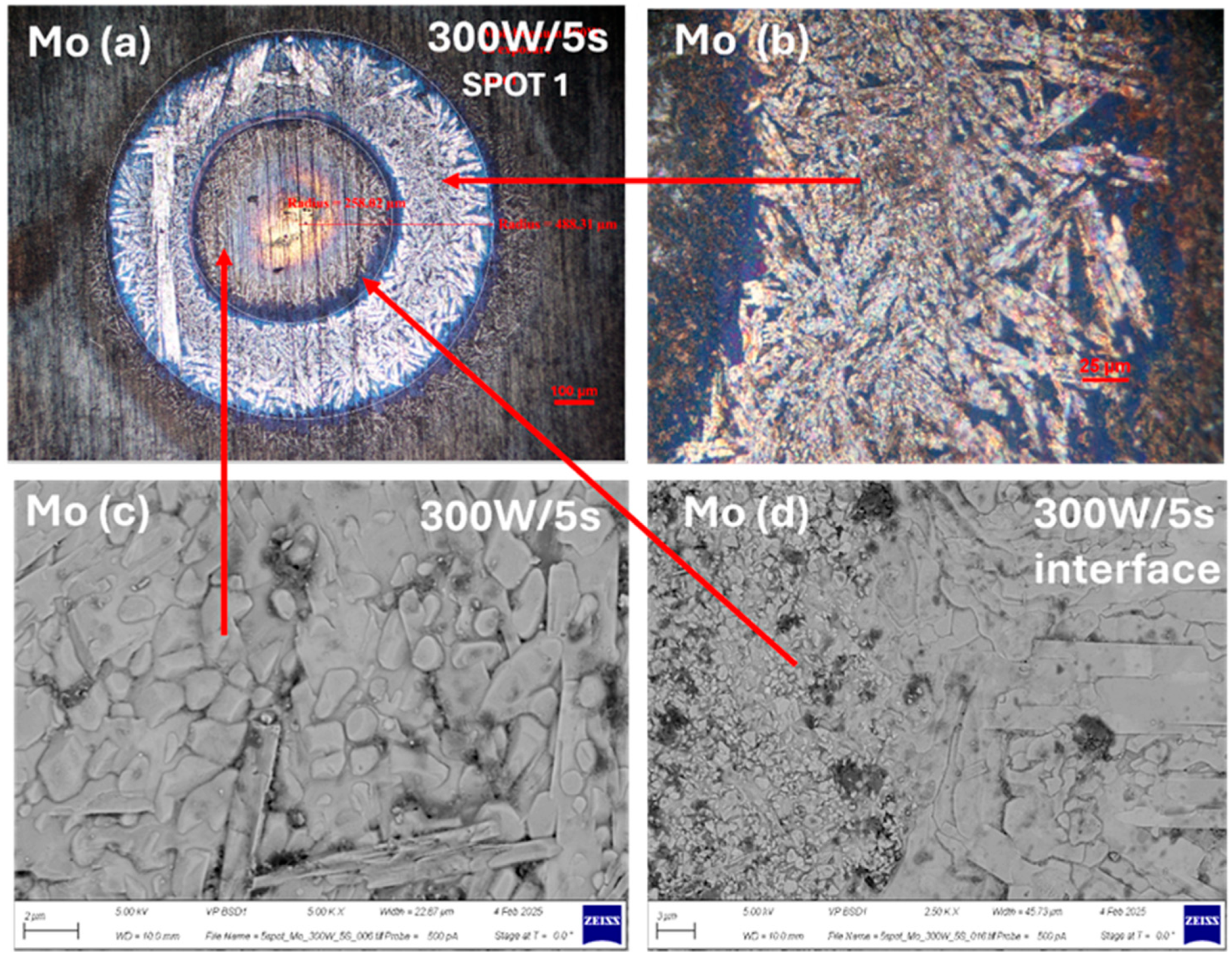
3.7. Multi-Beam Exposure, Molybdenum
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwab, K. World Economic Forum. In The Fourth Industrial Revolution; Portfolio Penguin: New York, NY, USA, 2017; ISBN 978-1-944835-00-2. [Google Scholar]
- Takiguchi, Y.; Tanaka, H.; Watanabe, T.; Asaine, H.; Mukozaka, N.; Ohtake, Y.; Toyoda, H. High laser power resistance phase-only spatial light modulator for laser processing cyber-physical system. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXVI; SPIE: Bellingham, WA, USA, 2021; Volume 11673, p. 1167305. [Google Scholar] [CrossRef]
- Shen, Y.; Zhan, Q.; Wright, L.G.; Christodoulides, D.N.; Wise, F.W.; Willner, A.E.; Zou, K.; Zhao, Z.; Porras, M.A.; Chong, A.; et al. Roadmap on spatiotemporal light fields. J. Opt. 2023, 25, 093001. [Google Scholar] [CrossRef]
- Forbes, A.; Aiello, A.; Ndagano, B. Classically entangled light. In Progress in Optics; Visser, T.D., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 64, pp. 99–153. [Google Scholar] [CrossRef]
- Nape, I.; Sephton, B.; Ornelas, P.; Moodley, C.; Forbes, A. Quantum structured light in high dimensions. APL Photonics 2023, 8, 051101. [Google Scholar] [CrossRef]
- Forbes, A. Structured light from lasers. Laser Photonics Rev. 2019, 13, 1900140. [Google Scholar] [CrossRef]
- Chen, J.; Kong, L.; Zhan, Q. Demonstration of a vectorial optical field generator with adaptive close loop control. Rev. Sci. Instrum. 2017, 88, 125111. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Hu, Z.; Bento, D.M.; Ali, A.A.I.; Patel, M.; Lavery, M.P.J.; Ellis, A.D. Enhanced atmospheric turbulence resiliency with successive interference cancellation DSP in mode division multiplexing free-space optical links. J. Light. Technol. 2022, 40, 7769–7778. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Maurer, C.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. What spatial light modulators can do for optical microscopy. Laser Photonics Rev. 2011, 5, 81–101. [Google Scholar] [CrossRef]
- Matsumoto, N.; Konno, A.; Inoue, T.; Okazaki, S. Aberration correction considering curved sample surface shape for non-contact two-photon excitation microscopy with spatial light modulator. Sci. Rep. 2018, 8, 9252. [Google Scholar] [CrossRef]
- Sinjab, F.; Liao, Z.; Notingher, I. Applications of spatial light modulators in Raman spectroscopy. Appl. Spectrosc. 2019, 73, 727–746. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Liu, Z.; Ding, L.; Du, P.; Chen, Y.I.; Zheng, Z.; Ba, D.; Dong, Y.; Yuan, H.; et al. High-quality near-field beam achieved in a high-power laser based on SLM adaptive beam-shaping system. Opt. Express 2015, 23, 681–689. [Google Scholar] [CrossRef]
- Li, S.; Ding, L.; Du, P.; Liu, Z.; Wang, Y.; Zhou, L.; Yan, X. Using the spatial light modulator as a binary optical element: Application to spatial beam shaping for high-power lasers. Appl. Opt. 2018, 57, 7060–7064. [Google Scholar] [CrossRef] [PubMed]
- Bahk, S.W.; Fess, E.; Kruschwitz, B.E.; Zuegel, J.D. A high resolution, adaptive beam shaping system for high-power lasers. Opt. Express 2010, 18, 9151–9163. [Google Scholar] [CrossRef] [PubMed]
- Awwal, A.A.S.; Orth, C.; Tse, E.; Matone, J.; Paul, M.; Hardy, C.; Brunton, G.; Herman, M.; Yang, S.; DiNicola, J.M.M.; et al. Image processing and control of a programmable spatial light modulator for spatial beam shaping. Proc. SPIE 2013, 8613, 86130F. [Google Scholar] [CrossRef]
- Salter, P.S.; Booth, M.J. Adaptive optics in laser processing. Light Sci. Appl. 2019, 8, 100. [Google Scholar] [CrossRef]
- Hayasaki, Y.; Onodeara, R.; Kumagai, K.; Hasegawa, S. Automatic generation of a holographically shaped beam in an actual optical system for use in material laser processing. Opt. Express 2023, 31, 1982–1991. [Google Scholar] [CrossRef]
- Hasegawa, S.; Hayasaki, Y. Polarization distribution control of parallel femtosecond pulses with spatial light modulators. Opt. Express 2013, 21, 12987–12995. [Google Scholar] [CrossRef]
- Hasegawa, S.; Hayasaki, Y. Dynamic control of spatial wavelength dispersion in holographic femtosecond laser processing. Opt. Lett. 2014, 39, 478–481. [Google Scholar] [CrossRef]
- Tang, Y.; Perrie, W.; Sierra, D.R.; Li, Q.; Liu, D.; Edwardson, S.P.; Dearden, G. Laser–Material Interactions of High-Quality Ultrashort Pulsed Vector Vortex Beams. Micromachines 2021, 12, 376. [Google Scholar] [CrossRef]
- Jin, Y.; Allegre, O.J.; Perrie, W.; Abrams, K.; Ouyang, J.; Fearon, E.; Edwardson, S.P.; Dearden, G. Dynamic modulation of spatially structured polarization fields for real-time control of ultrafast laser-material interactions. Opt. Express 2013, 21, 25333–25343. [Google Scholar] [CrossRef]
- Lutz, C.; Roth, G.L.; Rung, S.; Esen, C.; Hellmann, R. Efficient ultrashort pulsed laser processing by dynamic spatial light modulator beam shaping for industrial use. J. Laser Micro/Nanoeng. 2021, 16, 2021. [Google Scholar] [CrossRef]
- Tang, Y.; Perrie, W.; Schille, J.; Loeschner, U.; Li, Q.; Liu, D.; Edwardson, S.P.; Forbes, A.; Dearden, G. High-quality vector vortex arrays by holographic and geometric phase control. J. Phys. D Appl. Phys. 2020, 53, 465101. [Google Scholar] [CrossRef]
- Häfner, T.; Strauß, J.; Roider, C.; Heberle, J.; Schmidt, M. Tailored laser beam shaping for efficient and accurate microstructuring. Appl. Phys. A 2018, 124, 111. [Google Scholar] [CrossRef]
- McArthur, S.R.; Thomson, R.R.; Ross, C.A. Investigating focus elongation using a spatial light modulator for high-throughput ultrafast-laser-induced selective etching in fused silica. Opt. Express 2022, 30, 18903–18913. [Google Scholar] [CrossRef]
- Silvennoinen, M.; Kaakkunen, J.; Paivasaari, K.; Vahimaa, P. Parallel femtosecond laser ablation with individually controlled intensity. Opt. Express 2014, 22, 2603–2608. [Google Scholar] [CrossRef]
- Flamm, D.; Jenne, M.; Zimmermann, F.; Kleiner, J.; Kaiser, M.; Hellstern, J.; Tillkorn, C.; Kumkar, M. Beam shaping for ultrafast materials processing. In Laser Resonators, Microresonators and Beam Control XXI; SPIE: Bellingham, WA, USA, 2019; Volume 109041G. [Google Scholar] [CrossRef]
- Fang, Z.; Zhou, T.; Perrie, W.; Bilton, M.; Schille, J.; Loeschner, U.; Edwardson, S.P.; Dearden, G. Pulse burst generation and diffraction with spatial light modulators for dynamic ultrafast laser materials processing. Materials 2022, 15, 9059. [Google Scholar] [CrossRef]
- Mauclair, C.; Saint-Pierre, D.; Desrus, H. Advances in Spatial Light Shaping for Ultrafast Laser Surface Functionalisation. In Proceedings of the Lasers in Manufacturing Conference, Munich, Germany, 26–29 June 2017. [Google Scholar]
- Mauclair, C.; Pietroy, D.; Di Maio, Y.; Baubeau, E.; Colombier, J.P.; Stoian, R.; Pigeon, F. Ultrafast laser micro-cutting of stainless steel using a modulated line of multiple foci formed by spatial beam shaping. J. Laser Appl. 2015, 67, 212–217. [Google Scholar] [CrossRef]
- Lamprecht, B.; Satzinger, V.; Schmidt, V.; Perharz, G.; Wenzl, F.P. Spatial light modulator based laser microfabrication of volume optics inside solar modules. Opt. Express 2018, 26, A227–A239. [Google Scholar] [CrossRef]
- Mauclair, C.; Cheng, G.; Huot, N.; Audouard, E.; Rosenfeld, A.; Hertel, I.V.; Stoian, R. Dynamic ultrafast laser spatial tailoring for parallel micro-machining of photonic devices in transparent materials. Opt. Express 2009, 17, 3531–3542. [Google Scholar] [CrossRef]
- Wang, J.; Sun, S.; Zhang, H.; Hasegawa, S.; Wang, P. Holographic femtosecond laser parallel processing method based on the fractional Fourier transform. Opt. Laser Technol. 2021, 146, 106704. [Google Scholar] [CrossRef]
- Hauschwitz, P.; Palkova, Z.; Vachova, L.; Bicistova, R.; Prochazka, M.; Plocek, V.; Tarant, I.; Pathak, S.; Brajer, J.; Muzika, J.; et al. Rapid laser-induced nanostructuring for yeast adhesion-reducing surfaces using beam shaping with SLM. J. Mater. Res. Technol. 2025, 35, 193–198. [Google Scholar] [CrossRef]
- Hasegawa, S.; Nozaki, K.; Tanabe, A.; Hashimoto, N.; Hayasaki, Y. Holographic femtosecond laser processing using 6.3kHz pulse-to-pulse spatial light modulation with binary phase masks. J. Laser Appl. 2024, 176, 111014. [Google Scholar] [CrossRef]
- Pan, H.; Sapkota, D.; McIlvenny, A.; Lu, A.; Picksley, A.; Woodley, A.; Zorba, V.; Gonsalves, A.; Zhou, T.; van Tilborg, J. High throughput homogenisation of a quasi-Gaussian ultrafast laser beam using a combined refractive beam shaper and spatial light modulator. Opt. Eng. 2024, 63, 094103. [Google Scholar] [CrossRef]
- Gillner, A.; Finger, J.; Gretzski, P.; Neissen, M.; Bartels, T.; Reininghaus, M. High power laser processing with ultrafast and multi-parallel beams. J. Laser Micro/Nanoeng. 2019, 14, 129–137. [Google Scholar] [CrossRef]
- Beck, R.J.; Parry, J.P.P.; MacPherson, W.N.; Waddie, A.; Weston, N.J.; Shephard, J.D.; Hand, D.P. Application of cooled spatial light modulator for high power nanosecond laser micromachining. Opt. Express 2010, 18, 17059–17065. [Google Scholar] [CrossRef]
- Klerks, T.; Eiffel, S. Flexible beam shaping for next generation of process development. In Proceedings of the 9th International Conference on Photonics (LANE), Fürth, Germany, 19–22 September 2016. [Google Scholar]
- Kaakkunen, J.J.J.; Lakso, P.; Kujanpaa, V. Adaptive multibeam laser cutting of thin steel sheets with fibre laser using spatial light modulator. J. Laser Appl. 2014, 26, 032008. [Google Scholar] [CrossRef]
- Bernard, O.; Audouard, E.; Schops, B.; Delaigue, M.; Dalla-Barba, G.; Mishchik, K.; Honninger, C.; Mottay, E. Efficient micro processing with high power femtosecond lasers by beam engineering and modelling. Procedia CIRP 2018, 74, 310–314. [Google Scholar] [CrossRef]
- Zhu, G.; Whitehead, D.J.; Perrie, W.; Allegre, O.J.; Olle, V.; Li, Q.; Tang, Y.; Dawson, K.; Jin, Y.; Edwardson, S.P.; et al. Investigation of the thermal and optical performance of a spatial light modulator with high average power picosecond laser exposure for materials processing applications. J. Phys. D Appl. Phys. 2018, 51, 095603. [Google Scholar] [CrossRef]
- Tang, Y.; Li, Q.; Fang, Z.; Allegre, O.J.; Perrie, W.; Zhu, G.; Whitehead, D.J.; Li, L.; Edwardson, S.P.; Dearden, G. Extending the operational limit of a cooled spatial light modulator exposed to 200W average power for holographic picosecond laser processing. Opt. Laser Technol. 2025, 181, 111589. [Google Scholar] [CrossRef]
- Takiguchi, Y.; Tanaka, H.; Watanabe, T.; Kato, N.; Uchida, K.; Takumi, M.; Otsu-Hyodo, T.; Nakamura, K.; Toyoda, H. Development of High-power Infrared Laser Capable Phase-only Spatial Light Modulator. J. Laser Micro/Nanoeng. 2023, 18, 115–120. [Google Scholar] [CrossRef]
- Blair, D.; Cleva, F.; Man, C.N. Optical absorption measurements in monocrystalline sapphire at 1 μm. Opt. Mater. 1997, 8, 233–236. [Google Scholar] [CrossRef]
- Grunewald, J.; Prudlik, R.; Holla, V.; Kopp, P.; Off, R.; Stoll, T.; Kollmannsberger, S.; Wudy, K. Generating brick-like melt pools for Laser-Based Powder Bed Fusion using flexible beam shaping: A proof of concept on bead-on-plate single tracks. Procedia CIRP 2024, 124, 746–750. [Google Scholar] [CrossRef]
- Kippels, M.; Pratzsch, N.; Lantzsch, T. Flexible Beam Shaping Platform Optimises LBPF Processes. Fraunhofer Institute for Laser Technology, 16 November 2024. Aachen [Press Release]. Available online: https://www.ilt.fraunhofer.de/en/press/press-releases/2024/11-7-beamshaping-platform-optimises-lpbf-processes.html (accessed on 1 April 2025).
- Cailabs. Available online: https://www.cailabs.com (accessed on 19 April 2025).
- Harrison, J.; Naidoo, D.; Forbes, A.; Dudley, A. Progress in high-power and high-intensity structured light. Adv. Phys. X 2024, 9, 2327453. [Google Scholar] [CrossRef]
- Hamamatsu Photonics. Available online: https://www.hamamatsu.com (accessed on 19 April 2025).
- Wittenberg, A.M. Total hemispherical emissivity of sapphire. J. Opt. Soc. Am. 1965, 55, 432–435. [Google Scholar] [CrossRef]
- Optoman. Available online: https://www.optoman.com (accessed on 19 April 2025).
- Stubenvoll, M.; Schäfer, B.; Mann, K. Measurement and compensation of laser-induced wavefront deformations and focal shifts in near IR optics. Opt. Express 2014, 22, 25385–25396. [Google Scholar] [CrossRef]
- Faas, S.; Förster, D.J.; Weber, R.; Graf, T. Determination of the thermally induced focal shift of processing optics for ultrafast lasers with average powers of up to 525 W. Opt. Express 2018, 26, 26020–26029. [Google Scholar] [CrossRef]
- Ream, S.; Zhang, W.; Firestone, G.; Walters, C. Zinc sulphide optics for high power laser applications. In Proceedings of the 26th International Congress on Applications of Lasers and Electro-Optics (ICALEO 2007), Orlando, FA, USA, 29 October–1 November 2007; pp. 903–909. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Sheffield Gauge Plate Ltd. Available online: https://sheffieldgaugeplate.co.uk (accessed on 19 April 2025).
- Di Leonardo, R.; Ianni, F.; Ruocco, G. Computer generation of optimal holograms for optical trap arrays. Opt. Express 2007, 15, 1913–1922. [Google Scholar] [CrossRef]
- Royal Society of Chemistry. Molybdenum. Periodic Table. Available online: https://periodic-table.rsc.org/element/42/molybdenum (accessed on 19 April 2025).
- American Elements. Available online: https://www.americanelements.com (accessed on 19 April 2025).
- Hay, B.; Beaumont, O.; Failleau, G.; Fleurence, N.; Grelard, M.; Razouk, R.; Davée, G.; Hameury, J. Uncertainty assessment for very high temperature thermal diffusivity measurements on molybdenum, tungsten and isotropic graphite. Int. J. Thermophys. 2022, 43, 2. [Google Scholar] [CrossRef]
- Lindemann, A. Measurement of the Thermophysical Properties of Pure Molybdenum; NETZSCH-Gerätebau GmbH: Selb, Germany, 2009. [Google Scholar]
- Wikipedia Contributors. Molybdenum Trioxide. In Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Molybdenum_trioxide (accessed on 19 April 2025).
- Camacho-López, S.; Cano-Lara, M.; Camacho-López, M. Fast growth of multi-phase MoOx synthesized by laser direct writing using femtosecond pulses. Crystals 2020, 10, 629. [Google Scholar] [CrossRef]
- Cano-Lara, M.; Camacho-López, S.; Esparza-García, A.; Camacho-López, M.A. Laser-induced molybdenum oxide formation by low energy (nJ)–high repetition rate (MHz) femtosecond pulses. Opt. Mater. 2011, 33, 1648–1653. [Google Scholar] [CrossRef]
- National Center for Biotechnology Information. Molybdenum Blue. PubChem Compound Summary. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/Molybdenum-blue (accessed on 19 April 2025).
- Civan Advanced Technologies. Civan Laser. Available online: https://www.civanlaser.com (accessed on 19 April 2025).
- Hönninger, C.; Audouard, E. Multi-100W fs laser perspectives. Laser Tech. J. 2018, 15, 40–43. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Roecker, C.; Loescher, A.; Bienert, F.; Holder, D.; Weber, R.; Onuseit, V.; Graf, T. High power ultrafast thin disk multi-pass amplifiers for efficient laser-based manufacturing. Adv. Opt. Technol. 2021, 10, 251–256. [Google Scholar] [CrossRef]
- Nubbemeyer, T.; Kaumanns, M.; Ueffing, M.; Gorjan, M.; Alismail, A.; Fattahi, H.; Bron, J.; Pronin, O.; Barros, H.G.; Major, Z.; et al. 1 kW, 200 mJ, picosecond thin disk laser system. Opt. Lett. 2017, 42, 1381–1384. [Google Scholar] [CrossRef]
- Padgett, M.; Courtial, J.; Allen, L. Light’s orbital angular momentum. Phys. Today 2004, 57, 35–40. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, M. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Cao, Y.; Zhu, T.; Lv, H.; Ding, W. Spin controlled orbital motion in tightly focussed high order Laguerre- Gaussian beams. Opt. Express 2016, 24, 3377–3384. [Google Scholar] [CrossRef]
- Weber, R.; Wagner, J.; Peter, A.; Hagenlocher, C.; Spira, A.; Urbach, B.; Shekel, E.; Vidne, Y. Basic properties of high-dynamic beam shaping with coherent combining of high-power laser beams for materials processing. J. Manuf. Mater. Process. 2025, 9, 85. [Google Scholar] [CrossRef]
- Hasegawa, S.; Hayasaki, Y. Adaptive optimisation of a hologram in holographic femtosecond laser processing. Opt. Lett. 2009, 34, 22–24. [Google Scholar] [CrossRef]
- Christopher, P.J.; Mouthaan, R.; Kadis, A.; Gabbani, N.; O’Neill, W.; Wilkinson, T.D. Thermal compensation for high load spatial light modulators in real-time. In CLEO: Science and Innovations; Optical Society of America: Washington, DC, USA, 2020; p. ATu4K.5. [Google Scholar] [CrossRef]
- Christopher, P.J.; Gordon, G.S.D.; Wilkinson, T.D. Benchmarking the Gerchberg–Saxton algorithm. arXiv 2020, arXiv:2005.08623. [Google Scholar]
- Corda, R.; Giusto, D.; Liotta, A.; Song, W.; Perra, C. Recent advances in the processing and rendering algorithms for computer-generated holography. Electronics 2019, 8, 556. [Google Scholar] [CrossRef]
- Schroff, P.; La Rooij, A.; Haller, E.; Kuhr, S. Accurate holographic light potentials using pixel crosstalk modelling. Sci. Rep. 2023, 13, 3252. [Google Scholar] [CrossRef] [PubMed]
- Buske, P.; Hofmann, O.; Bonnhoff, A.; Stollenwerk, J.; Holly, C. High fidelity laser beam shaping using liquid crystal on silicon spatial light modulators as diffractive neural networks. Opt. Express 2024, 32, 7064–7078. [Google Scholar] [CrossRef]






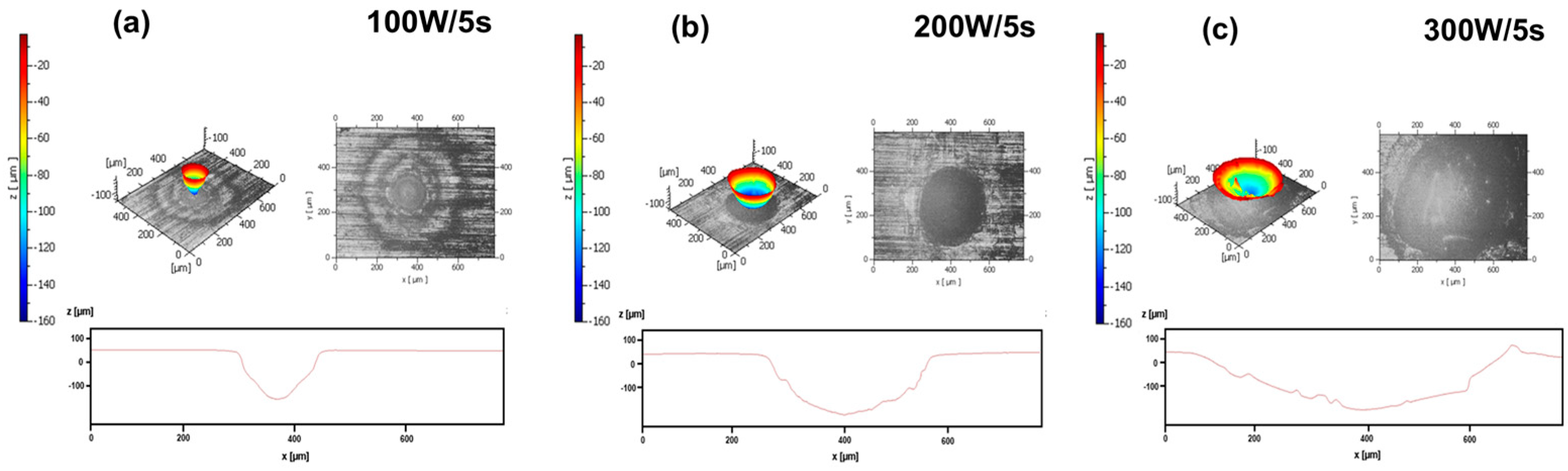




| P(W) | <ε>1–5 = (Rmin/Rmax) | (δV/δt)/W [μm3W−1s−1]/Spot |
|---|---|---|
| 50 | 0.88 ± 0.04 | 25.5 ± 20.3 |
| 100 | 0.84 ± 0.05 | 309 ± 70 |
| 200 | 0.82 ± 0.04 | 2221 ± 690 |
| 250 | 0.90 ± 0.05 | 4618 ± 1471 |
| 300 | 0.94 ± 0.04 | 4429 ± 1208 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, S.; Wang, S.; Pulham, C.; Tang, Y.; Perrie, W.; Allegre, O.J.; Tang, Y.; Sharp, M.; Leach, J.; Whitehead, D.J.; et al. High-Performance NIR Laser-Beam Shaping and Materials Processing at 350 W with a Spatial Light Modulator. Photonics 2025, 12, 544. https://doi.org/10.3390/photonics12060544
Zuo S, Wang S, Pulham C, Tang Y, Perrie W, Allegre OJ, Tang Y, Sharp M, Leach J, Whitehead DJ, et al. High-Performance NIR Laser-Beam Shaping and Materials Processing at 350 W with a Spatial Light Modulator. Photonics. 2025; 12(6):544. https://doi.org/10.3390/photonics12060544
Chicago/Turabian StyleZuo, Shuchen, Shuai Wang, Cameron Pulham, Yin Tang, Walter Perrie, Olivier J. Allegre, Yue Tang, Martin Sharp, Jim Leach, David J. Whitehead, and et al. 2025. "High-Performance NIR Laser-Beam Shaping and Materials Processing at 350 W with a Spatial Light Modulator" Photonics 12, no. 6: 544. https://doi.org/10.3390/photonics12060544
APA StyleZuo, S., Wang, S., Pulham, C., Tang, Y., Perrie, W., Allegre, O. J., Tang, Y., Sharp, M., Leach, J., Whitehead, D. J., Bilton, M., Mirihanage, W., Mativenga, P., Edwardson, S. P., & Dearden, G. (2025). High-Performance NIR Laser-Beam Shaping and Materials Processing at 350 W with a Spatial Light Modulator. Photonics, 12(6), 544. https://doi.org/10.3390/photonics12060544







