Abstract
Automatic mode-locking is a crucial approach for achieving ultrashort pulses in fiber lasers. Here, a random search algorithm was developed, and an automatic mode-locked laser was constructed. Numerical simulations of an automatic mode-locked Yb-doped fiber laser were conducted, and both continuous-wave, as well as mode-locked pulse states, were successfully obtained. The laser utilized a squeezer-type electrically controlled polarization controller to adjust the mode-locking states and enabled the controllable output of 532.71 fs dissipative solitons and 23.87 ps noise-like pulses, with search times of 14.19 s and 2.37 s, respectively. The center wavelengths were 1034 nm and 1038 nm, with signal-to-noise ratios of 63.1 dBm and 51.2 dBm, respectively. This work effectively addresses the polarization state drift caused by temperature and vibration, enhancing the laser’s environmental adaptability through adaptive monitoring.
1. Introduction
Fiber lasers have emerged as a significant research focus in modern laser technology due to their high efficiency, superior beam quality, compact structure, and excellent thermal management capabilities [1,2]. In recent years, remarkable advancements have been achieved in regards to output power, beam quality, and wavelength coverage [3,4], driving continuous expansion of their application domains. In industrial manufacturing, high-power fiber lasers are widely employed for precision cutting, welding, and additive manufacturing [5]. In telecommunications, Er-doped fiber amplifiers [6] and Raman fiber lasers [7] provide critical technological support for high-speed optical communication networks. In scientific research, ultrafast fiber lasers offer stable and reliable pulsed light sources for nonlinear optics and spectroscopy experiments [8].
Automatic mode-locking is one of the key technologies for achieving ultrafast lasers, which have developed rapidly in recent years, with remarkable achievements. To date, automatic mode-locking has emerged as a hotspot in the field of ultrafast lasers, demonstrating significant research value and application potential. In 2019, Pu et al. [9] achieved fundamental mode-locking in an Er-doped fiber laser within just 1.01 s using a genetic algorithm. By 2023, Zhu et al. [10] had combined particle swarm optimization with genetic algorithms to realize controllable dual-pulse outputs with intervals of 2.01 ns, 7.10 ns, and 12.36 ns. In 2024, Yan et al. [11] integrated machine learning with genetic algorithms to achieve dual-wavelength soliton mode-locking. Tong et al. [12] implemented automatic search for rectangular pulses in Yb-doped fiber lasers, while Kokhanovskiy et al. [13] utilized soft actor critic algorithms to achieve searching up to the 11th harmonic. Automatic mode-locking has undergone multiple algorithmic updates, significantly enhancing the intelligence level and mode-locking speed of the lasers. Its applications have expanded from fundamental mode-locking to the generation of specific pulses, such as multi-wavelength and harmonic types. However, algorithmic evolution has introduced greater complexity in system design and control logic, imposing higher demands on hardware and computational power. Previous research has primarily focused on single states, but actual lasers may exhibit combinations of multiple states, including continuous wave (CW), Q-switching, dissipative soliton (DS), noise-like pulse (NLP), and bound-state soliton states. Accurately identifying these states presents a new challenge.
This paper presents theoretical simulations and experimental investigations of the nonlinear polarization-rotating (NPR) automatic mode-locked fiber lasers. In the theoretical simulation section, phase shifts were introduced in two distinct directions to simulate a squeeze-type electrically controlled polarization controller (EPC), achieving CW and DS pulses with durations of 8.28 ps and 16.08 ps, respectively. In the experimental study, a random search algorithm was designed to identify and distinguish DS and NLP. DS, with a duration of 532.71 fs, and NLP, with a duration of 23.87 ps, centered at wavelengths of 1034 nm and 1038 nm, with signal-to-noise ratios of 63.1 dBm and 51.2 dBm, respectively, were achieved.
This paper is divided into six sections. Section 1 outlines the research background and reviews key prior studies; Section 2 introduces theoretical models; Section 3 presents numerical simulation results; Section 4 details the experimental setup, workflow, and random search algorithm; Section 5 reports experimental findings; Section 6 concludes with a summary and analysis of the entire study.
2. Theoretical Model
A simplified model of the automatic mode-locked fiber laser is shown in Figure 1, where SMF and YDF denote single-mode fibers and Yb-doped fibers. The analyzer only transmits horizontally polarized light. The OC is an output coupler with an output ratio of 1:9.

Figure 1.
Simplified model of the automatic mode-locked NPR fiber laser.
The polarization state of the light is typically represented using the Poincaré sphere [14]. With the horizontal direction of the fiber cross-section defined as the x-axis, reported works by other groups indicate that fiber compression manifests as rotation around an axis on the Poincaré sphere [15]. Compression at 0° relative to the x-axis corresponds to rotation around the S1 axis, while 45° compression corresponds to rotation around the S2 axis. Therefore, two compressions separated by 45° can achieve arbitrary polarization state adjustment, as shown in Figure 2.
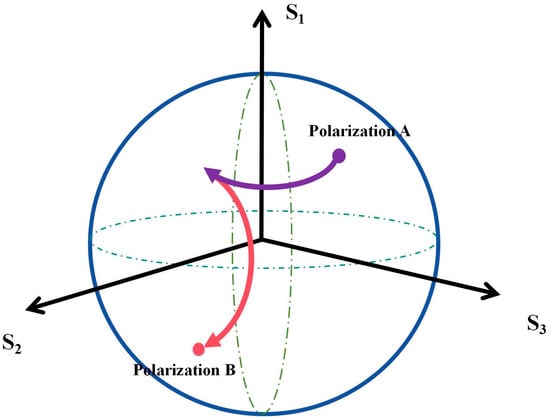
Figure 2.
Diagram of EPC adjustment (purple curve: squeezing in the 0° direction; red curve: squeezing in the 45° direction).
When the fiber is squeezed in the 0° direction, the transmission matrix can be expressed as [16]
where represent the birefringence phase shift generated by squeezing at the 0° direction.
When the fiber is squeezed in the 45° direction, the transmission matrix can be expressed as [16]
represent the birefringence phase shift generated by squeezing in the 45° direction. Therefore, the transmission matrix for a complete polarization state adjustment by the EPC can be expressed as
By introducing different and values, we can adjust the phase difference between the two orthogonal components of the light, which directly determines the polarization state. Subsequently, the polarizer can convert it into selective intensity loss, thereby achieving saturable absorption.
3. Simulation Results
We employed MATLAB R2024a for numerical simulations. To simplify the iterative process, the continuous-wave pump was replaced by a 100 ps, 0.01 pJ seed pulse. Under different phase shifts, the simulation results are as follows. When introducing the 0 phase shift in the 0° direction and the π/6 phase shift in the 45° direction, the output is mode-locked state 1, with a duration of 16.08 ps and a spectral width of 10.62 nm, as shown in Figure 3a,b. Figure 3c depicts the temporal evolution of the pulse over multiple round trips in the cavity. When introducing 0.637π in the 0° direction and π/6 in the 45° direction, the output is mode-locked state 2, with a duration of 8.25 ps and a spectral width of 18.35 nm, as shown in Figure 3d,e. Figure 3f depicts the temporal evolution of the pulse. Under positive dispersion, states 1 and 2 both exhibit Gaussian pulse shapes, with steep spectral edges, indicating that they are DS pulses. The difference in spectral width stems from the NPR equivalent filter bandwidth modulation caused by phase shift variations. Near the filter cutoff frequency, nonlinear effects significantly intensify, greatly promoting the generation and resonance of dispersion waves, thereby forming sidebands. Different phase shifts alter the phase-matching conditions between the main pulse and dispersion waves, affecting resonance intensity. Thus, Figure 3e exhibits more pronounced sidebands. Compared to the slender vertical bright lines in Figure 3f, Figure 3c exhibits a slight distortion in the details. This is because the DS characteristics of state 2 are more pronounced, resulting in greater pulse stability during evolution.
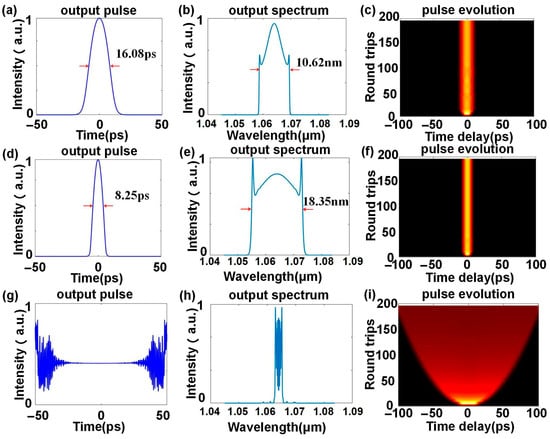
Figure 3.
Simulation results for different EPC setups. Mode-locking state 1: (a) pulse; (b) spectrum; (c) pulse evolution. Mode-locking state 2: (d) pulse; (e) spectrum; (f) pulse evolution. Continuous wave: (g) pulse; (h) spectrum; (i) pulse evolution.
When 0.955π is introduced in the 0°direction and π/6 is introduced in 45° direction, the resulting pulse and spectra are shown in Figure 3g,h. The pulse cannot be stably propagated within the laser and gradually degrades into CW as the number of evolution cycles increases, as shown in Figure 3i. This phenomenon occurs because the polarization state deviates from the optimal operating point for mode-locking, resulting in a modulation depth decrease in the equivalent saturable absorber and making it difficult to suppress the CW oscillations.
To investigate the dynamic evolution process, we introduced phase shifts ranging from 0 to 2π in the 0° and 45° directions. The spectral width variation due to phase shifting is shown in Figure 4a, where the purple region corresponds to significant spectral broadening, indicating that the system is in a mode-locked state. The pulse duration variation is depicted in Figure 4b, with the green region corresponding to pronounced pulse compression, similarly signifying the presence of mode-locking.
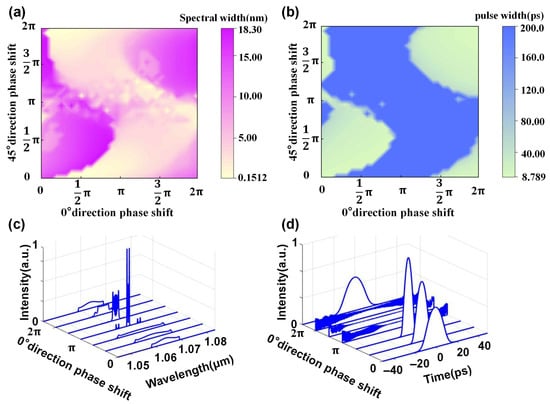
Figure 4.
Dynamic output via EPC adjustment. (a) Spectral bandwidth variation under two directions; (b) pulse width variation under two directions; (c) variation of optical spectrum under 0° direction alone; (d) variation of pulse under 0° direction alone.
By fixing the phase shift at 45° to π/6 and introducing phase variations from 0 to 2π at 0°, the dynamic evolution of pulse and spectral morphology can be observed, as shown in Figure 4c,d. Within the range of 0 to 0.637π, the pulse-narrowing induced by NPR becomes increasingly pronounced, accompanied by a corresponding broadening of the spectrum. This is because adjusting the polarization state increases the modulation depth of the equivalent saturable absorber. Between 0.637π and 1.592π, the pulse cannot be sustained, and the output degrades into CW. this is because the deviation of the polarization state from the optimal operating point leads to a reduction in the modulation depth. From 1.592π to 2π, the pulsed output is restored. this is due to the re-emergence of the optimal operating point.
4. Experimental Setup and Algorithm Design
The experimental setup is shown in Figure 5a, primarily consisting of an NPR Yb-doped fiber laser and an automatic mode-locking feedback control system. The pump source utilizes a 976 nm semiconductor laser with a maximum output power of 650 mW. The gain medium consists of a 20 cm section of ytterbium-doped fiber (YB-1200, Liekki, Tokyo, Japan), with the remainder constructed using single-mode fiber (HI1060, Corning, Corning, NY, USA), resulting in a total cavity length of 8.5 m. The EPC is a four-channel electrically controlled polarization controller (HS-3307A, HUASMART, Zhongshan, China), whose working mechanism is shown in Figure 5b. Channel 1 applies 0° squeezing, while Channel 2 applies 45° squeezing. OC1 is a 1:9 fiber coupler, and OC2 is a 5:5 fiber coupler. At 1040 nm, the net dispersion within the laser cavity is estimated to be 0.17 ps2. The control section comprises a photodetector (818-BB-35F, Newport, Franklin, MA, USA, 15 GHz), an oscilloscope (DPO70604C, Tektronix, Beaverton, OR, USA, 6 GHz), a spectrometer (AQ6370C, YOKOGAWA, Tokyo, Japan), and a computer (Y7000, Lenovo, Morrisville, NC, USA). Together with the laser, they form a complete closed-loop system.
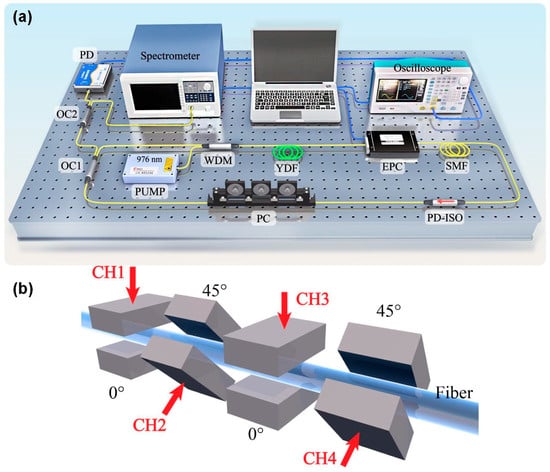
Figure 5.
(a) Experimental setup. WDM: wavelength division multiplexer; YDF: Yb-doped fiber; SMF: single-mode fiber; PD-ISO: polarization-dependent isolator; PC: polarization controller; PD: photodetector. (b) Diagram of the EPC working principle: the fiber is compressed from the 0° and 45° directions.
The automatic mode-locking process is shown in Figure 6a. Under a 400 mW pump, the EPC receives signal to compress the fiber. Subsequently, the oscilloscope and spectrometer capture time-domain and frequency-domain signals, then transmit them to the computer. The computer first calculates the average signal intensity and variance of the pulse sequence, along with the width and average slope of the upper and lower edges for the spectrum. It then compares these measured values with the nominal values to determine the mode-locking state and type. Finally, it issues new commands to the EPC, completing one feedback adjustment cycle.
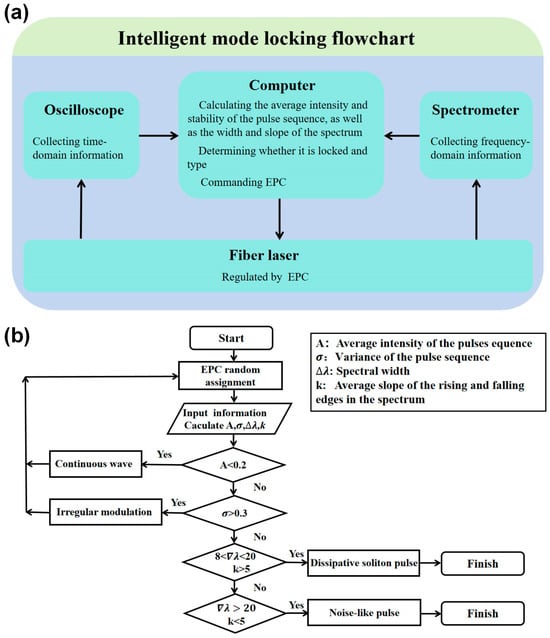
Figure 6.
(a) Flowchart of automatic mode-locking; (b) diagram of random search algorithm.
The random search algorithm is illustrated in Figure 6b. The EPC employs an 8-bit digital-to-analog converter to map the birefringence phase shift ranging from 0 to 2π onto an integer interval of 0 to 255. During the search process, the computer randomly selects integer values from this interval and transmits them to the EPC, thereby introducing the corresponding phase shift. Through extensive data collection and analysis of the output, we identified four primary operating modes for this laser: The CW exhibits only background noise in the time-domain signal (A < 0.2); irregular modulation shows some signal intensity in the time-domain, but remains largely chaotic ( > 0.3); the DS features spectral broadening with sharp rising and falling edges (8 < < 20, k > 5), while the NLP exhibits significant spectral broadening with smoother edges (20 < < 30, k < 5). The algorithm employs these characteristics as key diagnostic criteria. The method of determining the type of the pulse through spectral characteristics displays certain universality. For example, traditional solitons exhibit Kelly sidebands, and self-similar pulse spectra are rectangular.
5. Experimental Results
When channel 1 is set to 87 (0° phase shift of 0.682π) and Channel 2 is set to 144 (45° phase shift of 1.129π), we successfully obtained DS pulses. The pulse sequence is presented in Figure 7a, demonstrating excellent temporal stability with an interval of 41.35 ± 0.05 ns. The spectrum is shown in Figure 7b, with a central wavelength of 1034.00 ± 0.02 nm (corresponding to the emission peak of Yb3+ near 1030 nm) and a spectral width of 10.07 ± 0.02 nm. The ratio frequency (RF) spectrum is shown in Figure 7c, with a repetition frequency of 24.19 ± 0.01 MHz and a signal-to-noise ratio of 63.1 ± 0.1 dBm. The autocorrelation trace of the pulse after extracavitary compression is shown in Figure 7d, with a duration of 532.71 ± 0.05 fs due to the fact that the DS requires precise balancing of the nonlinear and dispersion effects. Therefore, its search is challenging [17]. The process involved 32 iterations, taking 14.19 s (multiple tests have shown that the search time for DS is 11 to 16 s).
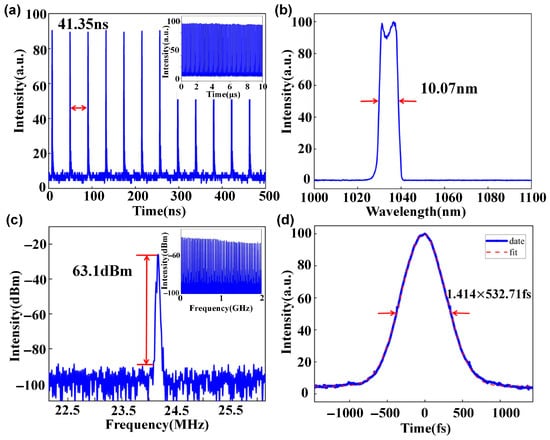
Figure 7.
Output characteristics of dissipative solitons (a) Pulse sequence (inset: 10 µs long range); (b) spectrum; (c) radio frequency spectrum (inset: 2 GHz long range); (d) autocorrelation trace.
Compared to DS, the NLP is more readily formed in Yb-doped fiber lasers [18]. When Channel 1 was set to 157 (0° phase shift of 1.231π) and Channel 2 was set to 11 (45° phase shift of 0.086π), we successfully obtained the NLP. As shown in Figure 8a, the pulse sequence appears notably disordered. The spectrum depicted in Figure 8b exhibits smooth edges, with a contour that is approximately arc-shaped. The central wavelength is 1038.00 ± 0.02 nm (similarly corresponding to the emission peak of Yb3+ near 1030 nm), and the spectral width is 36.79 ± 0.02 nm. The RF spectrum is shown in Figure 8c, and distinct sidebands are present on both sides of the main frequency, with a signal-to-noise ratio of 51.2 ± 0.1 dBm. The autocorrelation trace shown in Figure 8d exhibits typical NLP characteristics, including a broad base with a duration of 23.87 ± 0.01 ps and a narrow peak of 290.66 ± 0.05 fs. The search process for this noise-like pulse required only six iterations, taking 2.37 s (multiple tests have shown that the search time for NLP is 1 to 4 s).
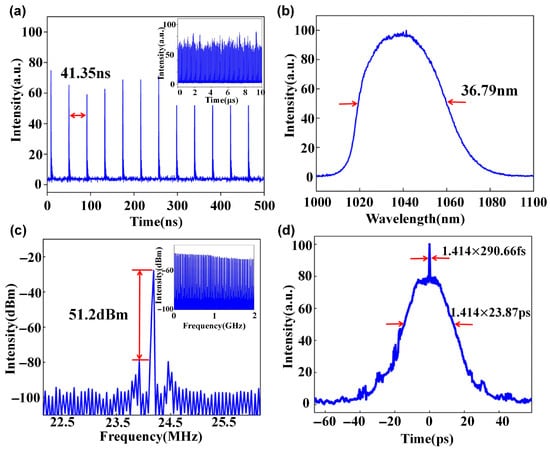
Figure 8.
Output characteristics of noise-like pulses. (a) Pulse sequence (inset: 10 µs long range); (b) spectrum; (c) radio frequency spectrum (inset: 2 GHz long range); (d) autocorrelation trace.
To observe the dynamic evolution process, we fixed the phase shift of Channel 2 to 0 and sequentially varied the values of Channel 1 within the range of 0–255, thereby obtaining the spectral evolution diagram corresponding to the EPC regulation process.
We excluded portions in which the output was a continuous wave and selected valid data from Channel 1 with values between 60 and 200 (phase shift of 0.47π–1.57π) for analysis. The results are shown in Figure 9a. When Channel 1 was set to 80, broadening appeared at the bottom of the spectrum, indicating that the output was transitioning from a continuous wave to mode-locked pulses. At a value of 100, the spectrum exhibited typical dissipative soliton characteristics. At 120, the spectral baseline smoothed out, indicating an intermediate state transitioning from a dissipative soliton to noise-like behavior. This transitional state can be accessed through bidirectional approximation. Within the 140–160 range, the spectrum exhibited typical noise-like characteristics. At 180, distinct interference fringes appeared in the spectrum, revealing that the noise-like mode-locking was becoming unstable. By 200, the output completely degraded into a continuous wave.
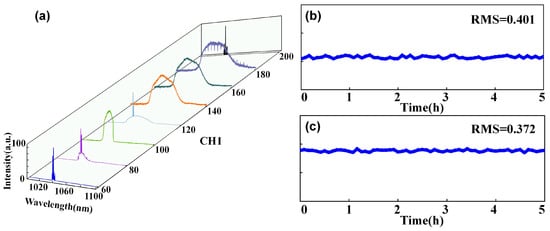
Figure 9.
(a) Dynamic process of automatic mode-locking; (b) stability of dissipative soliton output; (c) stability of noise-like pulse output.
In addition, the laser also displays other working states. At a pump power of 230 mW, Q-switched mode-locking can be achieved. At a pump power of 480 mW, dual-pulse mode-locking and high-order harmonics (up to the fourth harmonic) can be achieved. We will continue to pay close attention to and study these phenomena.
At a constant temperature of 20 °C, we measured the output power stability under two states over 5 h. The results are shown in Figure 9b,c. The average power of the dissipative soliton output is 11.50 mW, with a root mean square (RMS) of 0.401, while the average power of the noise-like output is 17.65 mW, with an RMS of 0.372. Both states exhibit good power stability. The higher noise-like power is attributed to the fundamental nature of noise-like pulses as a pulse packet containing numerous random fs-scale spikes. This structure distributes peak power across countless small spikes, thereby avoiding destructive nonlinear effects (such as pulse fragmentation) that could arise from a single high-intensity peak. Consequently, the NLP as a whole can carry significantly higher single-pulse energy than can the dissipative soliton.
The relationship between output power and pump power is shown in Figure 10. The system exhibits three distinct states across different power ranges. The laser’s threshold for light emission is 40 mW. When the pump power ranges from 40 mW to 140 mW, the laser operates in a continuous wave. Between 140 mW and 300 mW, the system enters a mode-locked state, with stable pulsed output. The output power exhibits an overall linear increase, achieving a slope efficiency of 4.96% (the red dashed line represents the fitted curve). Between 300 mW and 500 mW, the output power saturates and stabilizes between 17–18 mW. This can be attributed to the saturation of effective gain, which represents a dynamic equilibrium state between stimulated emission and population inversion.
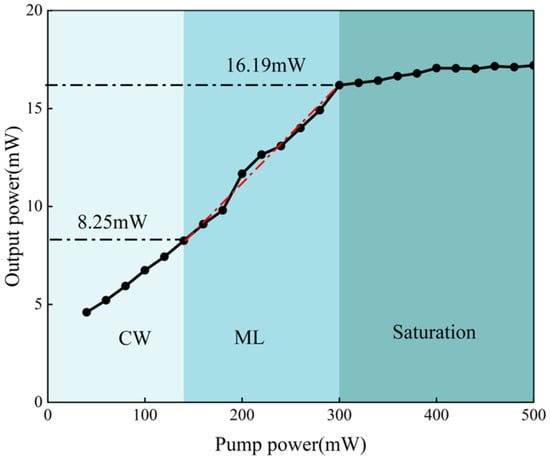
Figure 10.
Output power versus pump power. CW: continuous-wave mode; ML: mode-locked mode (red dashed line: linear fitting curve).
6. Conclusions and Discussion
In summary, we theoretically simulated an auto-locking fiber laser and proposed a random search algorithm for experimental implementation, successfully achieving an automatic search for dissipative soliton pulses and noise-like pulses. The simulation employed the stepwise Fourier method to solve nonlinear Schrödinger equations, combined with transmission matrix descriptions to characterize the tuning effects of squeeze-type polarization controllers, presenting simulation results for continuous and locked-mode light. In the experiment, the algorithm achieved a dissipative soliton mode-locking search in 14.19 s and a noise-like mode-locking search in 2.37 s by discriminating between low disorder and sharp spectral edges in dissipative soliton pulse sequences versus high disorder and smooth spectral edges in noise-like pulse sequences. We believe that this work holds significant potential in fields requiring stable light sources, such as high-speed optical communications, optical coherence tomography, fluorescence microscopy imaging, and optical frequency combs.
When the dimension of the control parameters increases or the target pulse becomes more complex, the basic random search is often inefficient and needs to be upgraded. We compared the main research achievements in recent years as shown in Table 1 and found that there are mainly the following optimization directions: First, Bayesian optimization is adopted, which builds a probabilistic proxy model by combining the attempted parameters with their corresponding results, thereby narrowing the search range. Second, based on genetic algorithms, the parameter combinations are iteratively evolved through selection, crossover, and mutation, gradually approaching the global optimal solution. Third, a physical correlation between the control parameters and the nonlinear dynamic characteristics of the laser is established, which constructs an interpretable mapping model, thereby achieving predictable and clearly guided intelligent mode-locking.

Table 1.
Comparison with previous studies (TA: traversal algorithm; HA: human-like algorithm; GA: genetic algorithm; SAC: soft actor critic; RSA: random search algorithm).
Author Contributions
Methodology, P.Y.; Software, P.Y.; Validation, P.Y.; Data curation, L.M. and R.Y.; Writing—original draft, P.Y.; Writing—review & editing, P.Y. and Y.S.; Supervision, Y.S.; Funding acquisition, P.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peng, K.; Feng, S.; Li, Y.; Ni, L.; Yu, J.; Xiang, H.; Leng, X.; Lin, A. 5-kW narrow-linewidth single-mode fiber laser based on homemade ultra-low absorption LMA-30/400 Yb-doped fiber. Opt. Laser Technol. 2025, 192, 113583. [Google Scholar]
- Zhang, L.; Fu, S.; Sheng, Q.; Luo, X.; Zhang, J.; Shi, W.; Yao, J. Wavelength extension of Er-doped fluoride fiber laser to above 3800 nm. J. Light. Technol. 2024, 42, 8435–8441. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, S.; Sheng, Q.; Zhou, Z.; Zhang, L.; Shi, W.; Yao, J. High-power continuous-wave mid-infrared 2.8 μm Er-doped fiber lasers: A review. Opt. Laser Technol. 2025, 181, 112024. [Google Scholar] [CrossRef]
- Jing, X.; Zhang, X.; Shen, C.; Huang, J. Tm fiber laser in-band pumped Ho:YLF/SrWO4 intracavity mid-infrared Raman laser at 2550 nm. Opt. Laser Technol. 2025, 189, 113033. [Google Scholar]
- Zou, J.; Liu, T.; Kong, H.; Xie, S.; Fang, C.; Wu, Q. Plume active control in high-power fiber laser welding based on high-speed shielding gas microbeam. Opt. Laser Technol. 2025, 180, 111535. [Google Scholar]
- Inoue, K. Quantum-limited transmission distance of optically repeating systems using a hybrid EDFA/Raman amplifier. Opt. Lett. 2024, 49, 5360–5362. [Google Scholar]
- Vatnik, I.D.; Gorbunov, O.A.; Churkin, D.V. Generation of narrow modes in random Raman fiber laser based on multimode fiber. Photonics 2024, 11, 2. [Google Scholar]
- Li, F.; Zhao, W.; Fu, Y.; Xing, J.; Wen, W.; Wang, L.; Li, Q.; Cao, X.; Zhao, H.; Wang, Y. High-power GHz burst-mode all-fiber laser system with sub 300 fs pulse duration. Photonics 2024, 11, 570. [Google Scholar]
- Pu, G.; Yi, L.; Zhang, L.; Hu, W. Genetic algorithm-based fast real-time automatic mode-locked fiber laser. IEEE Photon. Technol. Lett. 2020, 32, 7–10. [Google Scholar]
- Zhu, Q.; Zhang, Z.; Tong, L.; Li, T.-J.; Geng, M.-M.; Xu, W.-C.; Zhang, Z.-R.; Luo, Z.-C. Auto-setting multi-soliton temporal spacing in a fiber laser by a hybrid GA-PSO algorithm. Opt. Express 2023, 31, 40498–40507. [Google Scholar]
- Yan, Q.; Tian, Y.; Zhang, T.; Lv, C.; Meng, F.; Jia, Z.; Qin, W.; Qin, G. Machine learning based automatic mode-locking of a dual-wavelength soliton fiber laser. Photonics 2024, 11, 47. [Google Scholar] [CrossRef]
- Tong, L.; Li, T.; Zhu, Q.; Liu, M.; Zhang, Z.-R.; Luo, Z.-C. Intelligent multi-parameter control of a rectangular pulse in a passively mode-locked fiber laser. Opt. Express 2024, 32, 43214–43223. [Google Scholar] [CrossRef]
- Kokhanovskiy, A.; Kuprikov, E.; Serebrennikov, K.; Mkrtchyan, A.; Davletkhanov, A.; Bunkov, A.; Krasnikov, D.; Shashkov, M.; Nasibulin, A.; Gladush, Y. Multistability manipulation by reinforcement learning algorithm inside mode-locked fiber laser. Nanophotonics 2024, 13, 2891–2901. [Google Scholar] [CrossRef]
- Tudor, T.; Voitcu, G. Revisiting Poincaré sphere and Pauli algebra in polarization optics. Photonics 2024, 11, 379. [Google Scholar] [CrossRef]
- Chen, J.-I.; Chang, S.-C. Fiber full-polarization-state controller. J. Light. Technol. 1989, 7, 700–705. [Google Scholar] [CrossRef]
- Sakai, J.; Kimura, T. Birefringence and polarization characteristics of single-mode optical fibers under elastic deformations. IEEE J. Quantum Electron. 1981, 17, 1041–1051. [Google Scholar] [CrossRef]
- Singh, P.; Senthilnathan, K. A review on dissipative optical solitons: A route to photo-bot. Opt. Laser Technol. 2025, 187, 112647. [Google Scholar] [CrossRef]
- Kobtsev, S.; Komarov, A. Noise-like pulses: Stabilization, production, and application. J. Opt. Soc. Am. B 2024, 41, 1116–1127. [Google Scholar] [CrossRef]
- Radnatarov, D.; Khripunov, S.; Kobtsev, S.; Ivanenko, A.; Kukarin, S. Automatic electronic-controlled mode locking self-start in fibre lasers with non-linear polarization evolution. Opt. Lett. 2013, 38, 34–36. [Google Scholar]
- Shen, X.; He, B.; Zhao, J.; Liu, Y.; Bai, D.; Yang, K.; Wang, C.; Liu, G.; Luo, D.; Liu, F.; et al. Repetition rate stabilization of an erbium-doped all-fiber laser via opto-mechanical control of the intracavity group velocity. Appl. Phys. Lett. 2015, 106, 031117. [Google Scholar] [CrossRef]
- Woodward, R.I.; Kelleher, E.J.R. Genetic algorithm-based control of birefringent filtering for self-tuning, self-pulsing fiber lasers. Opt. Lett. 2017, 42, 2952–2955. [Google Scholar] [PubMed]
- Pu, G.; Yi, L.; Zhang, L.; Hu, W. Intelligent programmable mode-locked fiber laser with a human-like algorithm. Optica 2019, 6, 362–369. [Google Scholar]
- Xian, A.; Cao, X.; Liu, Y.; Wang, Y.; Yin, X.; Liu, G.; Zhou, W.; Wang, H.; Huang, H.; Tang, D.; et al. Adaptive genetic algorithm-based 2 μm intelligent mode-locked fiber laser. OSA Contin. 2021, 4, 2747–2756. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).