Universal Phase Correction for Quantum State Transfer in One-Dimensional Topological Spin Chains

Abstract

Gap-protected topological channels are a promising way to realize robust and high-fidelity state transfer in quantum networks. Although various topological transfer protocols based on the Su-Schrieffer-Heeger (SSH) model or its variants have been proposed, the phase accumulation during the evolution, as an essential aspect, is underestimated. Here, by numerically studying the phase information of quantum state transfer (QST) in one-dimensional (1D) topological spin chains, we uncover a universal phase correction ${\varphi }_0=(N-1)\pi /2$ for both adiabatic and diabatic topological schemes. Interestingly, the site-number-dependent phase correction satisfies ${\mathbb{Z}}_4$ symmetry and is equally effective for perfect mirror transmission in spin chains. Our work reveals a universal phase correction in 1D topologically protected QST, which will prompt a reevaluation of the topological protection mechanism in quantum systems.

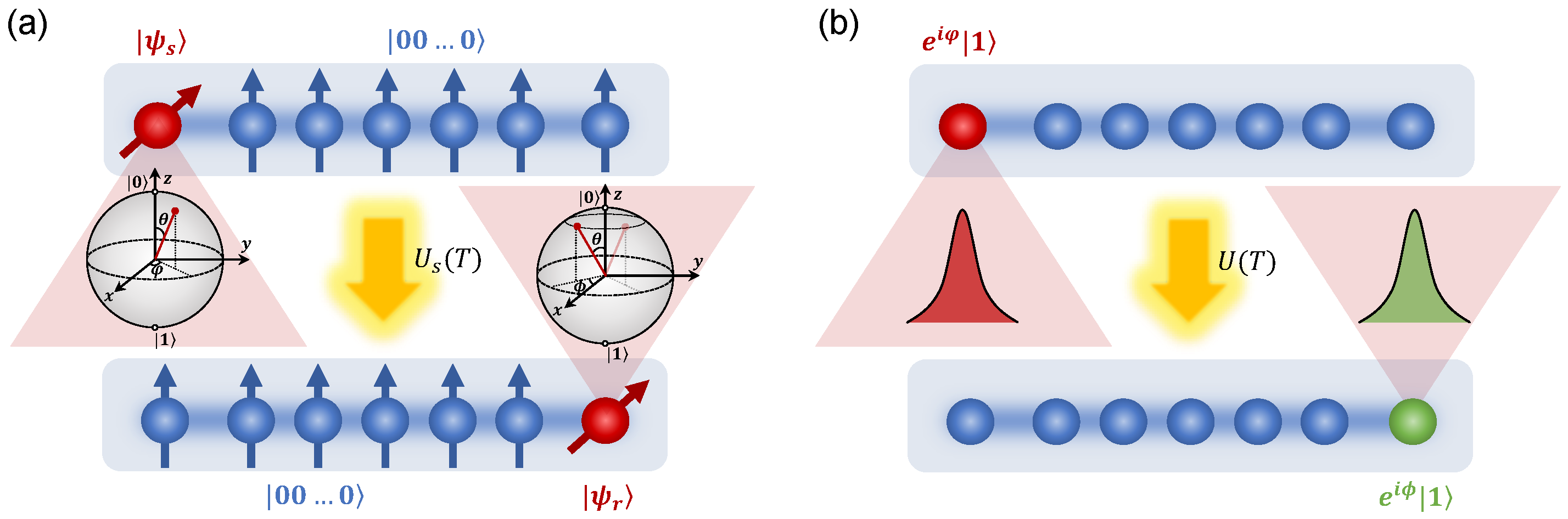
1. Introduction

Realization of high-fidelity quantum state transfer (QST) from a sender to a receiver node is an essential requirement for quantum communication and quantum computation [1]. For short distance QST, how to construct transfer channels through a network of qubits in a quantum processor is a critical problem. Originating from an unmodulated spin chain [2,3], various QST schemes have been reported in the last two decades [4,5,6,7]. Among these, the notable protocols of perfect state transfer [8,9,10] in multi-qubit networks have been demonstrated in quantum systems including nuclear spins [11], photonic waveguides [12,13,14], nanomechanical oscillators [15] and superconducting qubits [16]. However, these transfer schemes depend on precise individual couplings and accurate timing of dynamical evolution. Practical imperfections in quantum networks and timing errors in manipulation degrade the transfer fidelity. This motivates the need to realize robust high-fidelity QST.

Due to the disorder-immunity property of edge state transport, a series of gap-protected topological transfer mechanisms have been proposed in recent years [17,18,19,20,21,22,23,24,25,26,27,28,29]. These mechanisms require qubits to be coupled in specific topological configurations that form chain-like structures, along with temporal modulation to achieve robust, high-fidelity state transfer. Crucially, the temporal evolution of any quantum state under a Hamiltonian inevitably induces phase accumulation [2,26,30,31,32], which subsequently compromises transfer fidelity. However, discussions of accumulated phases remain notably absent from current protocols for topologically protected QST. Advances in microwave control and nanofabrication technologies have enabled superconducting systems to demonstrate significant advantages in qubit scaling and coupling control. These advantages have been validated across quantum simulation, precision measurement, and quantum computing applications. In particular, superconducting qubits have been widely adopted as a platform for implementing spin chains, enabling investigation of QST [16], topological pumping [33], and topological edge states [34,35].

Here, we first revisit QST in spin chains, elucidating the critical role of the phase of transition amplitude and the equivalence within the single-excitation subspace. We then numerically investigate transport processes in various topological transport protocols, focusing on the phase and magnitude of the transition amplitude under disorder perturbations. Our findings reveal that, upon completion of a full transfer period, a universal phase factor accumulates at the receiving site, which depends solely on spin numbers and exhibits ${\mathbb{Z}}_4$ symmetry. Remarkably, this phase relationship remains valid even for non-adiabatic topological transport protocols. Importantly, we reveal that the accumulated phase in the 1D topological transports originates from the topological zero-energy modes of the Su-Schrieffer-Heeger (SSH) model. Finally, we briefly discuss the feasibility of implementing our findings within a superconducting system.

2. Phase Accumulation of QST

We consider the transfer of a quantum state $|{\psi }_s\rangle =cos{\displaystyle \frac{\theta }{2}}|0\rangle +e^{i\phi }sin{\displaystyle \frac{\theta }{2}}|1\rangle$ from the sender to the receiver qubit in a spin chain. As shown in Figure 1a, the initial state of this spin system is $|\mathsf{\Psi }\left(0\right)\rangle =cos{\displaystyle \frac{\theta }{2}}|\mathbf{0}\rangle +e^{i\phi }sin{\displaystyle \frac{\theta }{2}}|\mathbf{1}\rangle$, where $|\mathbf{0}\rangle =|000\dots 0\rangle$ corresponds to the ground state with an eigenenergy of $E_0=0$ and $|\mathbf{1}\rangle =|100\dots 0\rangle$ corresponds to the first spin pointing upward while all other spins remain downward. After a specific evolution time t governed by the Hamiltonian

$$H=\sum _n{J}_n[{\sigma }_n^x{\sigma }_{n+1}^x+{\sigma }_n^y{\sigma }_{n+1}^y],$$

(1)

the quantum state of the N-th (receiver) spin is [2]

$$|{\psi }_r\left(t\right)\rangle =cos{\displaystyle \frac{\theta }{2}}|0\rangle +A\left(t\right)e^{i\phi }sin{\displaystyle \frac{\theta }{2}}|1\rangle ,$$

(2)

where ${\sigma }^{x,y}$ are the Pauli matrices and $A\left(t\right)=\langle \mathbf{N}|e^{-iHt}|\mathbf{1}\rangle$ is the transition amplitude for an excitation from the sender to the receiver.

Assuming that after time $t=T$, the quantum state at the receiver $|{\psi }_r\left(T\right)\rangle$ approaches the input state $|{\psi }_s\rangle$. Considering all pure states in the Bloch sphere as initial states, one obtains the average transfer fidelity [2,3,32]

$$\mathcal{F}={\displaystyle \frac{1}{2}}+{\displaystyle \frac{{\left|A\left(T\right)\right|}^2}{6}}+{\displaystyle \frac{\left|A\right(T\left)\right|cos\gamma }{3}},$$

(3)

where $\gamma =arg\left\{A\right(T\left)\right\}$. It is evident that achieving high transfer fidelity requires not only the magnitude of the transition amplitude to approach 1 but also the phase of the transition amplitude to be either integer multiples of $2\pi$ or a predetermined fixed value [2,30,32]. Therefore, when implementing topological transport protocols for QST in spin chains, the phase accumulation of the transition amplitude $\gamma$ must be a predetermined fixed value. Otherwise, even if $\left|A\right|=1$, the average fidelity would be limited to the classical threshold of $\mathcal{F}=2/3$ due to the random phase $\gamma$. However, this critical requirement remains underexplored in existing protocols, especially under disorder-induced perturbations.

We stress that an equivalent approach is adopted in the subsequent research process: the problem of single-qubit state transfer in spin chains is mapped to the excitation transfer in a spinless lattice [2,3,32]. This methodology was widely employed in previous studies on topological transport schemes [21,22,23,24,25,27]. The core principle of this approach lies in the fact that regardless of how the Hamiltonian H varies, the component of the initial state $|\mathbf{0}\rangle$ will always be perfectly transferred to the receiver qubit. Therefore, we only need to consider the transfer of the excitation $|\mathbf{1}\rangle$ within an $N\times N$ subspace. In the single-excitation subspace, the Hamiltonian of the spinless chain is

$$H\left(t\right)=\sum _n{J}_n\left(t\right)(a_n^{†}{a}_{n+1}+a_{n+1}^{†}{a}_n).$$

(4)

The transition amplitude is $A\left(T\right)=\langle N\left|U\right(T\left)\right|1\rangle$ for an excitation from the sender site to the receiver, where $U\left(T\right)=\mathcal{T}exp[-i{\int }_0^{T}d\tau H\left(\tau \right)]$ is the time-evolution operator, and $|n\rangle$ stands for the excitation at the n-th site, as shown in Figure 1b. Similarly, disorder in the nearest-neighbor spin couplings in Equation (1) is equivalently described as a disorder in the hopping terms between adjacent sites in the single-excitation subspace of the spinless lattice. In all numerical calculations discussed below, the total transfer time T is discretized into sufficiently small time intervals $\mathsf{\Delta }t=T/S$ (S is an integer) via the Trotter-Suzuki decomposition, during which the Hamiltonian in Equation (4) is treated as approximately constant. Thus, the full time-evolution operator is approximated using the expression $U\left(T\right)\approx e^{-iH\left(t_S\right)\mathsf{\Delta }t}\cdots e^{-iH\left(t_2\right)\mathsf{\Delta }t}{e}^{-iH\left(t_1\right)\mathsf{\Delta }t}$.

3. Results

3.1. Normal SSH Transport

As shown in Figure 2a, we consider an adiabatic topological scheme based on the standard SSH model [36]. Notably, this chain contains even sites and two alternating hopping terms $J_n=J_{\mathrm{o}}\left(t\right)=(1-ϵ){sin}^2(\pi t/T)$ ($n\in \mathrm{odd}$) and $J_n=J_{\mathrm{e}}\left(t\right)=1$ ($n\in \mathrm{even}$) in Equation (4). This time-dependent scheme is first reported to configure topological quantum networks for state transfer between distant qubits [20]. Here, we choose $N=20$ sites and set the total evolution time T sufficiently large to realize the high-fidelity transport. Figure 2b and Figure 2c show the gap-protected energy bands and the evolution results, respectively.

To evaluate robustness, we introduce time-independent random hopping disorders $\delta J_n\in [-\mathsf{\Delta },\mathsf{\Delta }]$ in the topological structure. For each disorder strength $\mathsf{\Delta }$, we generate 200 disorder realizations to analyze the transition amplitude. Figure 2d,f and Figure 2e,g show the magnitude and the phase of the transition amplitude, respectively. Evidently, as disorder strength increases, the average magnitude of the transition amplitude gradually decreases. Interestingly, when the disorder strength is below 0.1, the accumulated phase across 200 disorder configurations remains unchanged for each disorder strength. Importantly, through a numerical analysis of transport processes with various numbers of lattice sites (see Figure A1 in Appendix A), we reveal the relationship between the accumulated phase and the lattice site number

$$\gamma =\left\{\begin{array}{cc}\pi /2,\hfill & \hfill N\equiv 0mod4\\ -\pi /2,\hfill & \hfill N\equiv 2mod4\end{array}\right.$$

(5)

under weak disorders.

When the disorder strength exceeds ${\mathsf{\Delta }}_c=0.1$, the transition amplitude phase $\gamma$ randomly assumes discrete values of $-\pi /2$ or $\pi /2$, while its magnitude $\left|A\right|$ exhibits stochastic variations spanning the full interval $[0,1]$. These results indicate that the scheme is no longer viable for QST when the disorder strength exceeds the critical disorder strength ${\mathsf{\Delta }}_c$. In numerical calculations, the critical disorder strength decreases with the number of lattice site N in the transport.

3.2. Edge-Defect Topological Transport

Different from the standard SSH chain with even sites, some topological transfer protocols based on the edge-defect SSH model are proposed [21,24]. As shown in Figure 3a, an unpaired cell appears at the edge of the SSH model, therefore, the total number of lattice sites N is odd. We set $N=19$ and the hopping parameters satisfy $2J_{\mathrm{o}}\left(t\right)=1-cos(\pi t/T)$, $2J_{\mathrm{e}}\left(t\right)=1+cos(\pi t/T)$ and make the transfer period T large enough to keep adiabaticity. Figure 3(b1,c1) displays the energy bands and the excitation transmission under this kind of cosine modulation. In the presence of random disorder $\delta J_n\in [-\mathsf{\Delta },\mathsf{\Delta }]$, the transfer probability can still approach unity even under extremely large disorder strength, while the accumulated phase at the receiver node remains fixed despite disorder-induced interference, as demonstrated in Figure 3(d1–g1).

Figure 3(b2,c2) exhibit energy bands and excitation transmission of another edge-defect topological transport protocol with exponential modulation [24]. In the topological scheme, $J_{\mathrm{o}}\left(t\right)=(1-e^{-\alpha t/T})/(1-e^{-\alpha })$ and $J_{\mathrm{e}}\left(t\right)=[1-e^{-\alpha (1-t/T)}]/(1-e^{-\alpha })$. We set the coefficient $\alpha =6$. By comparing Figure 3(d1,f1) and Figure 3(d2,f2), it is evident that the exponentially modulated protocol outperforms the cosine-modulated scheme under identical disorder strength. Importantly, both mechanisms exhibit site-number-dependent phase accumulation in the presence of disorder, as shown in Figure 3(e1,e2,g1,g2) and Figure A2.

By numerical calculations, we further investigate the relationship between the number of lattice sites (N) and the accumulated phase in this edge-defect topological model. Importantly, we find the relation

$$\gamma =\left\{\begin{array}{cc}0,\hfill & \hfill N\equiv 1mod4\\ \pi ,\hfill & \hfill N\equiv 3mod4\end{array}\right.$$

(6)

persisting under strong disorder.

Combining with Equation (5), we can readily conclude that the accumulated phase at the receiver follows a ${\mathbb{Z}}_4$ symmetry group $\{e^{-i\pi /2},e^{i\pi /2},e^{i\pi },1\}$ for different site numbers in 1D topological transport protocols. As we discussed above, the site-number-dependent accumulated phase provides the precise phase correction

$${\varphi }_0={\displaystyle \frac{N-1}{2}}\pi$$

(7)

for QST in these topologically protected spin chains. Next, we check the validity of the phase correction in other 1D topological transfer schemes.

3.3. Topological Interface Transport

Beyond edge states, another class of gap-protected QST channels is the topological interface [23,25]. As shown in Figure 4a, the intra-cell hopping at the m-th cell is $J_{\mathrm{o}}^m\left(t\right)=sin(\pi t/2T)\sqrt{(N_c-m+1)/N_c}$ while the inter-cell hopping is $J_{\mathrm{e}}^m\left(t\right)=cos(\pi t/2T)\sqrt{m/N_c}$. Therefore, there is an interface position (indicated by the purple arrow) separating topologically trivial ($J_{\mathrm{o}}^m>J_{\mathrm{e}}^m$) and non-trivial regions ($J_{\mathrm{o}}^m<J_{\mathrm{e}}^m$). Moreover, these two interaction terms are modulated by sinusoidal and cosinusoidal functions, respectively. This time-modulated inhomogeneous coupling distribution emulates the square-root operator form between Fock states [25,37,38], thereby resulting in completely flat energy bands, see Figure 4b. Under adiabatic conditions, the initial excitation of the sender site is perfectly transported to the receiver through adiabatic evolution guided by time-modulated topological interface states, as shown in Figure 4c.

To numerically study the robustness of the transition amplitude, we introduce stochastic noise to the coupling strengths. Like the foregoing process, the effective coupling strengths become $J_{\mathrm{o},\mathrm{e}}^m\left(t\right)+\delta J_n$, where $\delta J_n\in [-\mathsf{\Delta },\mathsf{\Delta }]$ depends solely on spatial position. We set the adiabatic transfer period as $T=1000$, analyzing 200 independent disorder realizations at each disorder strength. Figure 4d,f demonstrate the remarkable robustness of this mechanism against disorder perturbations. The phase of transition amplitude also satisfies the aforementioned phase relation (Equation (6)), as shown in Figure 4e,g. These results indicate that implementing this topologically protected transfer mechanism in spin chains enables robust high-fidelity QST.

Figure 5a illustrates another topological interface model [23,39,40], which includes two topologically non-trivial SSH chains with Gaussian modulations $J_{\mathrm{o}}\left(t\right)=exp[-{(t-\delta /2-T/2)}^2/w^2)]$ and $J_{\mathrm{o}}^{\prime }\left(t\right)=exp[-{(t+\delta /2-T/2)}^2/w^2)]$. Similarly, the initial excitation adiabatically follows the gap-protected channel displayed in Figure 5b from the sender to the receiver. The entire evolution process is shown in Figure 5c. Due to the special structure, the total number of sites satisfies $N\equiv 3mod4$. Figure 5d,e demonstrates the robustness evaluation for the transfer protocol with $N=19$. It is clear that the accumulated phase remains $\pi$ across the 200 independent disorder realizations at each disorder strength, even when the transition amplitude magnitude becomes negligible.

3.4. Rice-Mele Transfer Schemes

In addition to the SSH model, another prominent example of a topological system is the Rice-Mele lattice [41]. As shown in Figure 6a, there is a stagger potential energy $\lambda$ and $-\lambda$ across lattice sites. Reference [22] puts forward a topological transfer scheme based on the three-stage modulated Rice-Mele model. In particular, the nearest neighbor coupling

$$J_{\mathrm{o}}\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1-ϵ}{2}}\left(1-cos{\displaystyle \frac{\pi t}{\tau }}\right),\hfill & \hfill 0<t<\tau \\ 1-ϵ,\hfill & \hfill \tau <t<\tau +{\tau }_z\\ {\displaystyle \frac{1-ϵ}{2}}\left(1-cos{\displaystyle \frac{\pi t}{\tau -{\tau }_z}}\right),\hfill & \hfill \tau +{\tau }_z<t<T\end{array}\right.$$

(8)

and the on-site potential

$$\lambda \left(t\right)=\left\{\begin{array}{cc}{\lambda }_0,\hfill & \hfill 0<t<\tau \\ {\lambda }_0-\alpha (t-\tau )/2,\hfill & \hfill \tau <t<\tau +{\tau }_z\\ -{\lambda }_0,\hfill & \hfill \tau +{\tau }_z<t<T\end{array}\right.$$

(9)

Here, the parameters ${\tau }_z=T-2\tau$ and $\alpha =4{\lambda }_0/{\tau }_z$. We choose $ϵ=0.1,\tau =200,{\tau }_z=T-2\tau$, and ${\lambda }_0=0.2$ to calculate the energy bands and the transmission process in Figure 6b,c. It is obvious that the initial excitation at the sender site can be perfectly transferred to the receiver without noise.

In the presence of disorder perturbations at nearest-neighbor couplings, we numerically investigate the transition amplitude of this transport mechanism. As demonstrated in Figure 6d,e, it is evident that under weak disorder conditions, while the magnitude of the transition amplitude retains high values, its phase exhibits stochastic behavior instead of remaining fixed. Therefore, this topologically protected transport mechanism is unsuitable for QST in spin chains, but is better suited for propagating classical excitations, particularly in scenarios where phase information is not considered.

3.5. Non-Adiabatic Topological Transfer

To satisfy the adiabaticity requirement of the topologically protected mechanism, the transfer period T typically needs to be extremely long. For real quantum systems with finite lifetimes, it is challenging to implement these adiabatically modulated topological mechanisms. Recently, we proposed a non-adiabatic topological transfer without introducing additional modulation [27]. Specifically, for the aforementioned topological interface transport scheme in Figure 4, non-adiabatic transitions between energy levels are utilized to accelerate excitation transport.

We numerically calculate the transfer probability at the receiving terminal under varying transfer periods, as shown in Figure 7a. Within the regime significantly below the adiabatic threshold, the transfer probability exhibits a critical period in which the transfer probability approaches unity. For the system size $N=21$, we select the critical period $T_c=52$ (indicated by a green triangle) and plot the transport dynamics in Figure 7b. Compared to Figure 4b, the dynamic trajectory of Figure 7b exhibits probability distribution at even sites due to non-adiabatic transitions, a characteristic further confirmed in Figure 8c,e.

Furthermore, to examine the robustness of non-adiabatic topological transfer, we investigate two chains with $N=21$ and $N=19$. For each disorder strength, we compute results from 500 random disorder configurations. Comparing Figure 7c,e and Figure 4d,f, it is apparent that non-adiabatic topological transfer is more susceptible to disorder perturbations compared to its adiabatic counterpart. However, under weak disorder conditions, non-adiabatic topological transport still shows noise-resistant behavior. More significantly, the accumulated phase of the transition amplitude in this regime adheres to the site-number-dependent relationship previously proposed in Equation (6), as shown in Figure 7d,f.

Significantly, although the robustness against disorder noise in the non-adiabatic regime does not exceed that of the adiabatic regime, our calculations reveal that the time consumption of non-adiabatic transfer is shorter than that of adiabatic transport by a factor of twenty (see Figure 4 and Figure 7). These findings suggest that non-adiabatic topological transfer demonstrates superior potential for QST in spin chains.

3.6. Origin of Phase Accumulation

We summarize the phase accumulation of different 1D topological transport schemes in

Table 1. Summary table of phase accumulation across different 1D topological transport mechanisms.

Model	Modulation Form	Number of Sites	Accumulated Phase $\mathit{\gamma }$
normal SSH [Figure 2]	adiabatic, cosine [20]	$N\in$ even	$\left\{\begin{array}{cc}\pi /2,\hfill & N\equiv 0mod4\hfill \\ -\pi /2,\hfill & N\equiv 2mod4\hfill \end{array}\right.$
edge-defect SSH [Figure 3]	adiabatic, cosine [21]	$N\in$ odd	$\left\{\begin{array}{cc}0,\hfill & N\equiv 1mod4\hfill \\ \pi ,\hfill & N\equiv 3mod4\hfill \end{array}\right.$
	adiabatic, exponential [24]
interface SSH [Figure 4, Figure 5 and Figure 7]	adiabatic, square-root [25]	$N\in$ odd	$\left\{\begin{array}{cc}0,\hfill & N\equiv 1mod4\hfill \\ \pi ,\hfill & N\equiv 3mod4\hfill \end{array}\right.$
	non-adiabatic, square-root [27]
	adiabatic, Gaussian [23]
Rice-Mele [Figure 6]	adiabatic [22]	$N\in$ even	Random

. According to our numerical results, the transport mechanism based on the Rice-Mele model is ineffective for QST. In the remaining adiabatic and non-adiabatic transport schemes based on the SSH model, the final phase accumulation follows ${\mathbb{Z}}_4$ symmetry. To trace the origin of phase accumulation, we define a quantity

$$P_i\left(t\right)=|\langle {\psi }_i{\left(t\right)|\psi \left(t\right)\rangle |}^2$$

(10)

to quantify the i-th energy band contribution to the transport process, where $|{\psi }_i\left(t\right)\rangle$ is the eigenstate of the i-th energy band and $\left|\psi \right(t)\rangle$ is the evolved state in the single-excitation subspace. We note that the eigenstates $|{\psi }_i\rangle$ are labeled with indices $i=\cdots ,-2,-1,0,1,2,\cdots$ based on sorting their corresponding eigenenergies in ascending order. It is evident from Figure 8a–f that these transport mechanisms primarily depend on topological zero-energy modes because $P_0\left(t\right)\approx 1$.

Owing to the chiral symmetry of the SSH model, all energy bands exhibit symmetry about zero energy, where each eigenstate possesses a chiral counterpart [42]. Consequently, dynamical phases are inherently eliminated at every instant during any transport protocol. Actually, the accumulated phase originates from the gap-protected zero-energy states. The chiral symmetry constrains topological zero modes to localize exclusively on one sublattice of the SSH chain [42]. This spatial distribution enforces a $\pi$-phase difference between adjacent sublattice sites. Under different transport schemes, time-dependent modulations merely alter the probability distribution of zero modes, i.e., transitioning from complete localization on the leftmost site to the rightmost site. Throughout this evolution, the $\pi$-phase difference between sublattice sites remains topologically preserved. Taking adiabatic topological interface transport as an example, we plot its time-varying zero-energy mode in Figure 8g. Based on the phase difference, we sequentially cycle through the labeling of phases 0 ($2\pi$), $-\pi /2$ ($3\pi /2$), $\pi$ and $\pi /2$ on the lattice. Throughout the evolution of transport dominated by topological zero-energy modes, this geometric information is transferred to the receiving qubit. Consequently, the phase accumulation in the final state depends solely on the number of lattice sites and satisfies ${\mathbb{Z}}_4$ symmetry.

As shown in Figure 3(b1,b2), Figure 4b and Figure 5b, the topological transport schemes with odd sites exhibit a robust zero-energy mode in the energy gap even under strong disorders [see Figure 8h]. On the contrary, for the transport protocol with even sites [see Figure 2b], the two zero-energy modes (labeled as $|{\psi }_{0L}\rangle$ and $|{\psi }_{0R}\rangle$) are hybridized and easily broken by disorders. Consequently, within 1D SSH-based topological transports, implementations utilizing even-numbered lattice sites exhibit reduced noise robustness compared to odd-numbered configurations. This conclusion agrees well with the above numerical results.

4. Summary and Discussion

Through revisiting QST in spin chains, we demonstrate that phase accumulation during excitation transmission constitutes a crucial factor that cannot be neglected. Furthermore, we numerically investigate various 1D topologically protected QST mechanisms, including SSH chains with cosine, Gaussian, exponential, and square-root modulation profiles (see Table 1). Remarkably, all these 1D topological transfer mechanisms share a universal site-dependent phase accumulation that satisfies ${\mathbb{Z}}_4$ symmetry. Under weak disorder conditions, this relationship between accumulated phase and site number persists even in non-adiabatic topological transfer protocols. Finally, we demonstrate that the phase accumulation in topological transport primarily originates from the fixed phase difference of zero-energy modes, which is caused by the chiral symmetry of the SSH model. Surprisingly, this phase relationship also manifests in perfect mirror transmission mechanisms [9,15], which impose no constraints on spin numbers and possess a static, non-topological Hamiltonian.

Based on these findings, we uncover a universal phase correction ${\varphi }_0=(N-1)\pi /2$ for QST in 1D topological spin chains. Specifically, once the number of participating spins is determined, a compensatory phase gate

$$\begin{array}{c}\hfill C_P\left({\varphi }_0\right)=\left[\begin{array}{cc}1& 0\\ 0& e^{i\pi {\displaystyle \frac{N-1}{2}}}\end{array}\right]\end{array}$$

(11)

can be applied at the receiving qubit to faithfully reconstruct the initial quantum state. Additionally, our work reveals that in Rice-Mele model-based topological transfer, the phase factor at the receiving qubit becomes completely randomized under noise, rendering this scheme unsuitable for QST applications. As previously analyzed in our introduction to the origin of the universal phase, its applicability is grounded in various 1D topological transport mechanisms based on the SSH model. For transport mechanisms in two or higher dimensions, the applicability of this phase should be approached with caution, since distinct transport mechanisms inherently entail different manners of phase accumulation.

For superconducting multi-qubit processors, the experimentally achievable decoherence time is larger than the adiabatic requirement of the 1D topological transports, which has been evaluated in Reference [21]. We focus on the relation between coherence times and the universal phase correction in Equation (11). Similar to other single-qubit phase gates (such as S gate, T gate), the compensatory phase gate $C_P\left({\varphi }_0\right)$ implemented here essentially requires the final spin state to undergo a rotation around the z-axis of the Bloch sphere by a specific angle ${\varphi }_0$. For superconducting qubits, there is an easy experimental method to realize z rotation, called virtual Z gates [43,44]. That is, altering the phase of subsequent driving pulses addressing the receiver qubit is effectively equivalent to imposing a phase shift of $e^{i{\varphi }_0}$ on the qubit state in the computational basis (energy basis), where the pulses act on the $|0\rangle$-$|1\rangle$ transition. This approach avoids spending additional time accumulating a dynamical phase difference between the two states of the qubit, thus introducing no additional decoherence error.

Finally, following general phase correction, what is the robustness of these topological transport mechanisms associated with the 1D SSH model against timing errors? We present the relevant results in Figure 9. It can be observed that the transfer fidelity for these adiabatic protocols exhibits remarkable robustness against timing errors. For non-adiabatic transfer [Figure 9a], however, considerable caution is required when selecting the transmission time. In practice, non-adiabatic transfer presents a trade-off between decoherence time and timing error, as it achieves significantly shorter transmission times compared to adiabatic mechanisms.