Abstract
The emergence of metalenses has opened new possibilities for miniaturizing optical systems. However, the limited group delay provided by meta-atoms restricts their aperture size under broadband operation. This challenge has stimulated the development of hybrid refractive–metalens systems, which overcome the performance limitations of individual metalenses while achieving a more compact form factor than conventional refractive lens assemblies. Here, we propose a design methodology for hybrid lenses that combines ray tracing with full-wave simulation. We analyze key aspects of the metalens within the hybrid system for a wide wavelength band—specifically, dispersion and transmission efficiency. Based on this approach, we designed a high-resolution hybrid lens operating in the 435–656 nm visible band with a 35° field of view. The results demonstrate that the proposed lens achieves imaging performance equivalent to that of conventional refractive systems while reducing the total track length by 29%. This validates the effectiveness of our design method, indicating its strong potential for application in compact and lightweight optical systems.
1. Introduction
The rapid advancement of imaging sensor technology has intensified the need for optical systems that deliver exceptionally high resolution while conforming to stringent size, weight, and power constraints, particularly in applications such as unmanned aerial vehicles and next-generation consumer electronics. Conventional refractive lenses form images by gradually bending light through curved surfaces, relying on cumulative phase accumulation as waves propagate through media of different refractive indices. To correct various optical aberrations, an intricate combination of multiple, precisely crafted lens elements is required to precisely manipulate the optical path differences and phase accumulation across both the aperture and the spectrum. This systematic correction, while effective, fundamentally compromises the core goals of miniaturization and cost efficiency, leading to increased volume, weight, and manufacturing complexity.
The emergence of metasurfaces, planar metamaterials engineered with subwavelength nanostructures, has heralded a paradigm shift, promising unprecedented control over the phase, amplitude, and polarization of light [1]. These ultra-thin platforms offer exceptional design freedom, enabling high-performance metalenses [2,3,4], polarization-selective devices [5,6,7,8], and holography [9,10,11] within dramatically reduced form factors. Recent advancements, such as nonlocal metasurfaces utilizing multilayer coupling, further open pathways toward ideal wavefront manipulation and system integration [12,13,14]. However, the promise of metasurfaces is tempered by formidable challenges. The design and simulation complexity escalate prohibitively for large-aperture metalenses. While dispersion can be tailored using nanostructures with specific group delays, this approach imposes stringent fabrication constraints, requiring extreme alignment precision and deeply subwavelength features, often at the expense of efficiency and practical manufacturability [15,16,17,18].
In this landscape, a synergistic approach emerges: the hybrid refractive–metalens system (HRMS). By marrying the robust light-bending capabilities of conventional refractive lenses with the nanoscale wavefront manipulation of metasurfaces, HRMS offers a compelling path to compact, aberration-corrected optics [19]. This synergy reduces both the number of refractive elements required and the fabrication complexity demanded of the metasurface [20,21,22]. More recently, several innovative approaches to hybrid lens design have been proposed. A metalens integrated onto substrates with variable height has been designed to achieve broadband imaging capabilities in the near-infrared regime [23]. For visible-light imaging, hybrid lenses incorporating nonlinear materials have demonstrated the ability to convert near-infrared wavelengths into the visible range for detection and imaging purposes [24]. Yet, current explorations of HRMSs remain limited, predominantly focused on infrared wavelengths and on-axis performance at normal incidence, with wide-field imaging scenarios and critical factors like metasurface-induced transmission loss often overlooked.
Here, we present a comprehensive design methodology for a visible-spectrum HRMS that addresses these critical gaps. Our work emphasizes the optimization of optical transmission and the effective mitigation of chromatic aberration across the entire visible band. We outline fundamental principles for intelligently distributing optical power between refractive and metasurface components. This strategy not only simplifies the lens system, minimizing the number of elements, particularly challenging aspheric lenses, but also relaxes the fabrication tolerances for the metasurface without compromising its diffraction efficiency. The metasurface is specifically engineered to provide chromatic compensation, leveraging the complementary advantages of both technologies. To validate our framework, we designed and tested an exemplary HRMS. The results demonstrate a significant reduction in the total track length (TTL) compared to conventional refractive designs, alongside relaxed manufacturing requirements and a simplified metasurface architecture. This work provides a practical and efficient strategy for realizing broadband, achromatic imaging in next-generation compact optical systems, bridging the gap between high performance and stringent size, weight, and power (SWaP) constraints.
2. Design Principles
The design of an HRMS leverages the exceptional phase manipulation freedom offered by metasurfaces, which surpasses the limitations of conventional freeform optics in both achievable phase profiles and practical manufacturability. On the one hand, for chromatic aberration correction, the metalens and the refractive lens possess opposite dispersion characteristics, which effectively counteracts the axial chromatic aberration introduced by the refractive lens. On the other hand, to address off-axis aberrations (e.g., coma, astigmatism) induced by wide-angle incidence, the metasurface offers unparalleled phase control freedom. Its phase profile can be precisely designed as a function of position, wavelength, and angle of incidence, enabling the simultaneous synthesis of a phase front that compensates for large-angle aberrations. This enhanced freedom is key to simultaneously reducing the TTL and improving the modulation transfer function (MTF) across the field.
The design workflow of the HRMS is illustrated in Figure 1. A key challenge in such systems lies in bridging the macroscopic optical layout with the microscopic behavior of meta-atoms. Macroscopic optical simulations typically rely on ray tracing, whereas the response of individual meta-atoms requires full-wave vectorial simulation methods, which are not directly applicable to large-scale systems. To address this multiscale problem, we adopt a combined approach integrating ray tracing and full-wave electromagnetic simulations. Although the light propagation through a metalens is governed by vectorial Maxwell’s equations, the deflection of light at the metalens interface follows generalized Snell’s law. This makes it feasible to derive the phase gradient point by point and reconstruct a continuous phase profile. By treating the metalens as a phase surface in ray-tracing software, it becomes possible to co-optimize the metalens with conventional refractive elements, thereby bridging macro- and microscale optical design. Note, however, that this phase-surface abstraction ignores effects such as diffraction efficiency and higher-order diffraction. It is therefore essential that the actual phase response of the fabricated metalens closely match the ideal phase profile.
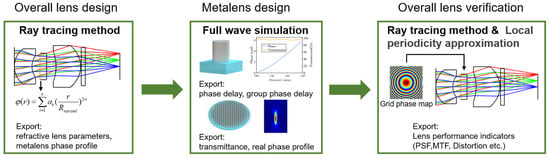
Figure 1.
Design flowchart of the HRMS.
The first step involves using ray-tracing software to optimize the entire optical system by representing the metalens as a phase surface. Here, the commercial software ZEMAX (Zemax OpticStudio 19.4) is used for optical design. The optimization procedure mirrors that of conventional refractive lenses, involving the selection of appropriate variables and operands to minimize aberrations. To achieve high imaging quality across a wide field of view (FOV), different from the parabolic profile used in axial focusing, an even-order polynomial phase profile is adopted in the design [25]. Consistent with the methodology used in single-layer metalens designs for large FOV applications [26], this approach enables effective aberration correction through the optimization of the even-order coefficients. Special attention is also paid to the angles of incidence and dispersion at the phase surface to ensure the manufacturability of the metalens.
In the second step, the metalens is designed at the meta-atom level. Full-wave simulations are performed to characterize the optical response of individual meta-atoms; here, the finite-difference time-domain method (FDTD) is used for simulating the optical performance of the metalens. By scanning their geometric parameters, a phase and transmission library is obtained. The target phase profile obtained from ray tracing is then used to optimize the arrangement of meta-atoms across the surface, resulting in a physically realizable metasurface layout.
The third step is the validation of the HRMS. The actual phase profile of the manufactured metalens is either discretized into a grid phase matrix based on the local periodicity approximation or fitted with a new set of polynomial coefficients. These representations are re-imported into the ray-tracing software for approximate simulation, enabling performance verification before physical fabrication.
Throughout the optimization of the metalens, two key performance metrics are emphasized: focusing efficiency and polychromatic MTF across the entire FOV. High focusing efficiency directly contributes to an improved signal-to-noise ratio in the captured images, while the full-field MTF indicates the imaging resolution of the system under real-world conditions. Many existing single-layer metasurface designs for achromatic operation achieve color correction at the cost of reduced focusing efficiency and often only optimize the MTF for on-axis incident light. As a result, although compact, such systems tend to exhibit lower imaging signal-to-noise ratios and degraded off-axis performance. To overcome these limitations and achieve higher overall image quality, our design simultaneously prioritizes both focusing efficiency and full-field MTF, ensuring that the metalens performs robustly with high resolution across varied practical imaging scenarios.
Building upon the design workflow and figure of merit outlined previously, we now delve into the specific characteristics of the metalens. The operation of metasurfaces is governed by diffraction; they exhibit dispersion behavior analogous to that of conventional diffractive lenses. This similarity allows well-established design methodologies for diffractive optics to be informatively applied to metalenses. In the ray tracing design, a broadband light source is employed, while the metalens is set in Zemax as a wavelength-independent binary phase profile. This phase profile is defined by an even-order polynomial independent of wavelength, which can be written as
where an denotes phase coefficients of the even-order polynomial, r is the radial coordinate of the metalens, and rnormal is the normalized radius, respectively. Note that the phase profile here is wavelength-independent; when different incident wavelengths are taken into account, the phase profile can be depicted as follows:
In Equation (2), the phase coefficient an is transformed into a quantity that is related to the wavelength. It can be observed that the phase profile exhibits a linear relationship with the reciprocal of wavelength, which is consistent with the phase response of the meta-atom across different wavelengths. Therefore, the meta-atom dimension at a given position of the metalens can be determined by matching both the phase value at the central wavelength and the group delay to the target phase profile. It is also essential to maintain high transmission efficiency over the operating bandwidth to ensure the overall performance of the metalens. A wavelength-dependent constant c(λ) can be into Equation (2), and intelligent algorithms such as particle swarm optimization can be used to achieve better matching between the meta-atom and the phase profile [27]. If the required group delay is excessively large, a quasi-achromatic approach based on folding the group delay in the time domain can be employed [28]. By folding the group delay with respect to the frequency difference, the requirement on its range is relaxed, thereby enabling achromatic performance across a broader bandwidth. On the other hand, based on Equation (2), the metalens could maintain chromatic aberration in the HRMS. To better illustrate the chromatic behavior, we consider a representative single-layer metalens designed at a central wavelength of 550 nm to compare the focal length variation between FDTD simulation and ZEMAX. Figure 2a illustrates the schematic of the meta-atoms composed of niobium oxide (Nb2O5) nanopillars with cylindrical, square, and hexagonal cross-sections on a 350 nm period silica substrate with a height of 700 nm. In order to ensure stable and reproducible fabrication, the minimum lateral size of all three nanostructure geometries was set to 100 nm, while the maximum lateral dimension was constrained to 250 nm. As shown in Figure 2b, each geometry exhibits distinct transmittance and phase responses. Achieving high overall transmission requires not only accurate phase modulation but also high transmittance at the meta-atom level, necessitating a diverse set of structural options. Figure 2c presents the focal length shift across wavelengths obtained through full-wave simulation. The metalens, designed for 550 nm, exhibits progressively shorter focal lengths as wavelength increases. Figure 2d compares full-wave simulation results with ZEMAX simulations using a binary 2 surface, revealing a consistent trend. This agreement confirms that the metalens preserves certain chromatic properties that can be utilized by sharing the same phase profile across multiple wavelengths.
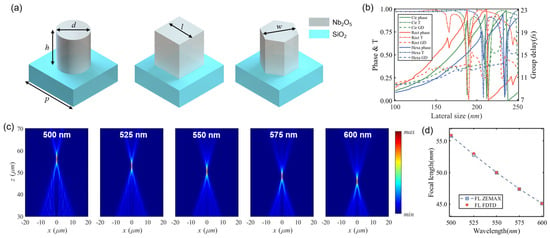
Figure 2.
Verification of the chromatic aberration of the metalens. (a) Schematic diagram of the meta-atom. (b) Transmittance, phase retardation, and group delay with meta-atoms of different shapes and lateral sizes. (c) Intensity at axial plane at different wavelengths using the FDTD method. (d) Focal length for FDTD simulation results with Zemax simulations.
Unlike single metalens imaging systems [29], the hybrid design allows the use of a broadband source during ray-tracing optimization. The opposite signs of chromatic aberration between refractive and meta-diffractive elements enable effective chromatic compensation within the HRMS. Consequently, a satisfactory polychromatic MTF can be achieved through co-optimization, demonstrating the potential of the HRMS in correcting chromatic aberrations.
In addition to chromatic aberration, transmittance is another critical performance metric for metasurfaces. High transmittance helps reduce stray light and ensures a high signal-to-noise ratio in the resulting images. During the design process, the period of the meta-atoms must be carefully chosen to satisfy the Nyquist sampling criterion under oblique illumination in the whole wavelength range. As the angle of incidence increases, the effective normal wavevector decreases; thus, the period should be small enough to suppress higher-order diffraction and stray light under large angle incidence. As illustrated in Figure 3a, which analyzes cylindrical meta-atoms at 550 nm under tilted incidence, a notable decrease in transmittance is observed beyond 30° incidence [30]. Furthermore, the optical power distribution of the metalens must be properly allocated. As the numerical aperture (NA) increases, the focusing efficiency tends to decrease [31], which means a higher optical focal degree will reduce the diffraction efficiency of the metalens. Figure 3b shows the focusing efficiency, defined as the ratio of energy within three times the full width at half maximum (FWHM) to the total incident energy, for metalenses with a diameter of 50 μm at 550 nm. It is evident that the focusing efficiency declines with increasing NA. Therefore, a balanced co-design of refractive and meta optics is essential to achieve both high image quality and device miniaturization.
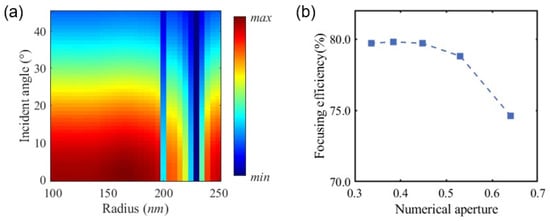
Figure 3.
Incident angle analysis of the metalens. (a) Transmittance of the circular meta-atom with different incident angles at a wavelength of 550 nm. (b) Focusing efficiency of the metalens with different numerical apertures.
3. Specific Design, Fabrication, and Characterization
To validate the proposed design methodology, an HRMS operating across the visible spectrum from 430 nm to 650 nm was designed for an 8-megapixel sensor. The specifications are summarized in Table 1. The lens provides a 35° full FOV, a focal length of 15 mm, and an F-number of 1.67. Key performance metrics include a polychromatic MTF exceeding 0.4 at 120 lp/mm over the entire field and distortion controlled below 5%. To realize a compact system, the TTL was minimized and the number of elements reduced without employing any aspheric surfaces.

Table 1.
Specifications for the HRMS.
As illustrated in Figure 4a, the system incorporates one metalens and five spherical lenses, achieving a TTL of 22.4 mm. As shown in the layout diagram, light rays passing through the metalens do not exhibit pronounced bending, implying that the optical power introduced by the metalens is relatively small, and its primary role lies in aberration correction. In comparison, a conventional refractive design with equivalent performance requires four spherical and two aspherical glass lenses, resulting in a TTL of 31.5 mm, as shown in Figure 4c. The reduction in the total track length (TTL) is primarily achieved through the unique advantages of metalenses in off-axis aberration correction. In conventional systems, correcting off-axis aberrations often requires multiple aspheric elements to maintain manufacturability. Metalenses, however, overcome this limitation by enabling arbitrary phase manipulation with subwavelength structures, thereby integrating the functionality of multiple aspheric surfaces into a single flat optical element. Consequently, the HRMS significantly shortens the TTL without compromising optical performance. It should be noted that if all elements in a system already employ aspheric surfaces, the potential for further TTL reduction using a metalens becomes more limited. Figure 4b presents the MTF curves of the lens at 0°, 12.25°, and 17.5° field angles obtained through ray-tracing simulation. The MTF values at 120 lp/mm for the three fields are 0.67, 0.52, and 0.44, respectively, indicating sufficient image resolution across the FOV. It is worth noting that the system operates effectively under broadband visible light (430–650 nm) without significant degradation in imaging performance, demonstrating its robustness over a wide spectral range. For comparison, the MTF of the refractive lens is presented in Figure 4d, showing performance nearly identical to that of the HRMS lens. However, to correct aberrations in the peripheral field of view, the refractive design requires a longer optical path, resulting in a greater total lens length. Figure 4e illustrates the variation in focal length with wavelength across the visible spectrum. The focal shift is less than 2 μm, and the depth of focus for the central wavelength calculated based on the Rayleigh criterion is 6 μm, which indicates the achromatic performance of the system. This effect stems from the complementary chromatic aberration contributions between the refractive elements and the metalens. Furthermore, the point spread function (PSF) and back focal distance under on-axis illumination were simulated at different wavelengths, as summarized in Figure 4d. It is noted that the RMS diameters of the PSF at five wavelengths are 2.71 μm, 2.43 μm, 2.74 μm, 2.68 μm and 2.46 μm, which remain small across all wavelengths, ensuring high imaging resolution.
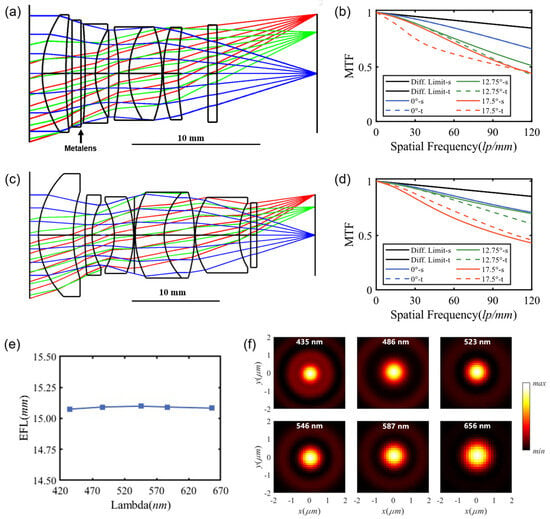
Figure 4.
Design results of the HRMS. (a) Optical layout of the HRMS of the visible spectrum. (b) Simulated MTF for both tangential and sagittal at 0 field, 0.7 field, and 1 field of the HRMS. (c) Optical layout of the refractive lens. (d) Simulated MTF for tangential and sagittal at 0 field, 0.7 field, and 1 field of the refractive lens. (e) Effective focal length of the HRMS with different wavelengths. (f) Simulated PSF at different wavelengths of the HRMS.
Subsequently, the designed HRMS was fabricated. Figure 5a shows the overall appearance of the metalens. The refractive lens part, consisting entirely of spherical surfaces, was manufactured using conventional precision grinding and polishing techniques. The metasurface was fabricated via electron-beam lithography (EBL). Specifically, a 700 nm thick Nb2O5 layer was deposited on a glass substrate using plasma-enhanced chemical vapor deposition (PECVD). The refractive index of the film, measured by spectroscopic ellipsometry (HORIBA Scientific UVISEL, Paris, France), was 2.32 at the central wavelength of 550 nm. The sample was spin-coated with ma-N2405 electron-beam resist (Micro Resist Technology, Berlin, Germany). The metalens pattern was exposed using EBL (Raith Voyager, Dortmund, Germany) and developed in ma-D525 (Micro Resist Technology, Berlin, Germany). Inductively coupled plasma reactive ion etching (Samco RIE-230IP, Kyoto, Japan) was employed to transfer the pattern into the niobium oxide layer. Finally, the residual resist was removed via plasma etching. Figure 5b show the optical image of the fabricated metalens whilescanning electron microscopy (SEM) images of the fabricated metasurface are shown in Figure 5c. Owing to the reasonable distribution of optical power in the design, the required group delay for chromatic compensation is relatively modest, which allows most nanostructures to take the form of cylindrical pillars. For system assembly, dedicated mechanical mounts are designed to secure each lens element, minimizing misalignment-induced performance degradation. Since the metalens is fabricated on a square substrate, it is integrated into the optical assembly using UV-curing adhesive. The fabricated HRMS is experimentally characterized using the setup illustrated in Figure 5d. The FOV and MTF were evaluated by imaging a standard checkerboard target. As shown in Figure 5e, the captured image exhibits clearly resolved grid lines across the entire field, confirming a wide and effective FOV. Quantitative analysis of the image further indicates a diagonal FOV exceeding 35°. And it also can be seen from the picture that the distortion of the HRMS is low. The MTF was measured using the slanted-edge method (SFR) at three representative field positions: on-axis, 0.7 field, and full field. The results are summarized in Figure 5f. At 120 lp/mm, the measured MTF values were 0.46, 0.41, and 0.40, respectively. Although these values are slightly lower than the design predictions, they still meet the specified performance requirements. The minor degradation can be attributed to fabrication imperfections in both the refractive lenses and the metalens, as well as alignment tolerances during assembly. And the focusing efficiency of the HRMS was also characterized by illuminating the system with collimated white light and measuring the energy of the focused spot at the focal plane. The focusing efficiency was determined by comparing this focused energy with the incident light intensity. Based on this method, the fabricated HRMS was found to exhibit an efficiency of 82.3% across the visible spectrum. This can be attributed to the well-designed configuration and high-precision fabrication process employed in the device.

Figure 5.
Characterization and testing of the HRMS. (a) Schematic of a prototype HRMS. (b) Optical microscope image and (c) scanning electron microscope image of the metalens in the designed HRMS. (d) Experimental platform for resolution test characterization. (e) Image of a checkerboard captured by the designed HRMS using halogen lamps for lighting. (f) Measured MTF curve at 0 field, 0.7 field, and 1 field.
To evaluate the imaging performance of the fabricated HRMS for color applications, we captured images of pictures projected on a screen, as shown in Figure 6a–d. Compared to a monolayer achromatic metalens design, the HRMS demonstrates higher resolution and reduced chromatic aberration. However, a slight color shift is observed in the captured images, which mainly stems from the wavelength-dependent transmission efficiency of the metalens. This issue can be effectively addressed through neural network-based image enhancement algorithms. The integration of computational optics presents a significant opportunity for performance enhancement. For instance, the PSF of the HRMS can be characterized across the field of view. A neural network can then be employed to perform spatially variant deconvolution, leveraging the estimated PSF to restore image clarity and compensate for residual aberrations across the entire image, even without a co-designed optical encoder. For instance, generative adversarial networks can be employed to further reduce chromatic aberrations and improve image sharpness. Notably, AI-based image processing offers a promising solution to compensate for such optical imperfections and enhance overall image quality [32]. Alternatively, in projection systems, a neural network can be used to pre-correct the input image, thereby compensating for optical imperfections and achieving superior imaging quality [33]. Such a combination of meta-optical design and computational imaging offers a powerful pathway toward high-fidelity, compact imaging systems, making the HRMS particularly promising for applications in wearable devices and other portable technologies.

Figure 6.
(a–d) Color images displayed on a screen captured by the HRMS.
4. Conclusions
In summary, we developed a versatile design methodology for broadband, high-resolution hybrid optical systems with wide field-of-view capabilities. As shown in Table 2, the HRMS designed in this work features a large aperture while maintaining high resolution and efficiency across the visible spectrum. The effectiveness of this approach is validated through the design and characterization of a high-resolution HRMS operating in the visible spectrum. Within a design framework combining ray-tracing and full-wave simulation, we analyzed both macroscopic requirements and microscopic characteristics of the metalens. It is shown that the metalens should assume low optical power and operate under small angles of incidence within the HRMS, while its chromatic behavior can be treated similarly to that of diffractive optical elements. Based on this theoretical foundation, we designed and fabricated a hybrid refractive–metasurface lens working in the visible band, which achieves a full-field MTF above 0.4 at 120 lp/mm. Compared to conventional refractive lenses, the proposed system significantly simplifies the architecture and reduces the TTL. The presented theory and design framework are expected to accelerate the adoption of HRMSs in practical applications. We envision that such systems may progressively replace traditional multi-element refractive lenses, thereby advancing the development of compact and lightweight optical systems.

Table 2.
Performance of this work compared with other HRMSs.
Author Contributions
Conceptualization, Y.M. and X.L.; modeling and simulation, X.L. and P.S.; fabrication, Y.X. and X.L.; experimental characterization, P.W. and X.Y.; data analysis, X.L. and Y.M.; writing—original draft preparation, X.L. and P.W.; writing—review and editing, X.L. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a National Key Research and Development Program of China grant (2023YFF0613000); National Natural Science Foundation of China (NSFC) grant (62222511); Natural Science Foundation of Zhejiang Province China grant (LR22F050006); and STI 2030–Major Projects grant (2021ZD0200401).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
All data that support the findings of this study are included within the article.
Acknowledgments
The author would like to acknowledge Weige Lv, Liying Chen, and Wei Wang from the State Key Laboratory for Extreme Photonics and Instrumentation and the College of Optical Science and Engineering, Zhejiang University, for their assistance in the experiments.
Conflicts of Interest
The authors X.L., Y.X., P.S. and X.Y. are from Hangzhou Najing Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HRMS | Hybrid refractive–metalens system |
| SWaP | Size, weight, and power |
| MTF | Modulation transfer function |
| FOV | Field of view |
| NA | Numerical aperture |
| PSF | Point spread function |
| EBL | Electron-beam lithography |
| PECVD | Plasma-enhanced chemical vapor deposition |
| SEM | Scanning electron microscopy |
References
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Ren, X.; Wang, S.; Su, V.-C.; Chen, M.-K.; Chu, C.H.; Kuo, H.Y.; Liu, B.; Zang, W. Metalens-array–based high-dimensional and multiphoton quantum source. Science 2020, 368, 1487–1490. [Google Scholar] [CrossRef]
- Ossiander, M.; Meretska, M.L.; Hampel, H.K.; Lim, S.W.D.; Knefz, N.; Jauk, T.; Capasso, F.; Schultze, M. Extreme ultraviolet metalens by vacuum guiding. Science 2023, 380, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Balthasar Mueller, J.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Rubin, N.A.; D’Aversa, G.; Chevalier, P.; Shi, Z.; Chen, W.T.; Capasso, F. Matrix Fourier optics enables a compact full-Stokes polarization camera. Science 2019, 365, eaax1839. [Google Scholar] [CrossRef]
- Xiong, B.; Liu, Y.; Xu, Y.; Deng, L.; Chen, C.-W.; Wang, J.-N.; Peng, R.; Lai, Y.; Liu, Y.; Wang, M. Breaking the limitation of polarization multiplexing in optical metasurfaces with engineered noise. Science 2023, 379, 294–299. [Google Scholar] [CrossRef]
- Fu, B.; Zhou, X.; Li, T.; Zhu, H.; Liu, Z.; Zheng, S.; Zhou, Y.; Yu, Y.; Cao, X.; Wang, S.; et al. Miniaturized high-efficiency snapshot polarimetric stereoscopic imaging. Optica 2025, 12, 391–398. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Zhang, H.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.-W.; Qiu, C.-W. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4, 2808. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Shi, Y.; Wang, Z.; Wan, S.; Li, Z.; Li, Z. Azimuth-Resolved On-Chip Meta-Hologram. Laser Photonics Rev. 2025, e01642. [Google Scholar] [CrossRef]
- Overvig, A.C.; Malek, S.C.; Yu, N. Multifunctional nonlocal metasurfaces. Phys. Rev. Lett. 2020, 125, 017402. [Google Scholar] [CrossRef] [PubMed]
- Malek, S.C.; Overvig, A.C.; Alù, A.; Yu, N. Multifunctional resonant wavefront-shaping meta-optics based on multilayer and multi-perturbation nonlocal metasurfaces. Light Sci. Appl. 2022, 11, 246. [Google Scholar] [CrossRef]
- Li, T.; Liu, M.; Hou, J.; Yang, X.; Wang, S.; Wang, S.; Zhu, S.; Tsai, D.; Wang, Z. Chip-scale metaphotonic singularities: Topological, dynamical, and practical aspects. Chip 2025, 3, 100109. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Chen, M.-K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.-T.; Wang, J.-H. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef]
- Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Yu, N. Broadband achromatic dielectric metalenses. Light Sci. Appl. 2018, 7, 85. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Yang, W.; Ji, Z.; Jin, L.; Ma, X.; Song, Q.; Boltasseva, A.; Han, J.; Shalaev, V.M. High-efficiency broadband achromatic metalens for near-IR biological imaging window. Nat. Commun. 2021, 12, 5560. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sisler, J.; Huang, Y.-W.; Yousef, K.M.; Lee, E.; Qiu, C.-W.; Capasso, F. Broadband achromatic metasurface-refractive optics. Nano Lett. 2018, 18, 7801–7808. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Zhao, W.; Wang, Y.; Huo, P.; Zhang, H.; Lu, Y.Q.; Xu, T. Achromatic and coma-corrected hybrid meta-optics for high-performance thermal imaging. Nano Lett. 2024, 24, 7609–7615. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Wen, L.; Li, H.; Wang, S.; Xia, R.; Mei, Z.; Yang, Z.; Zhao, M. Aberration-corrected hybrid metalens for longwave infrared thermal imaging. Nanophotonics 2024, 13, 3059–3066. [Google Scholar] [CrossRef]
- Li, A.; Chen, J.; Liu, M.; Wei, W.; Duan, H.; Jia, H.; Hu, Y. Fundamental design framework of hybrid refractive-metalens system for axial aberrations correction and its validation in LWIR band. Opt. Express 2025, 33, 27535–27547. [Google Scholar] [CrossRef]
- Balli, F.; Sultan, M.; Lami, S.K.; Hastings, J.T. A hybrid achromatic metalens. Nat. Commun. 2020, 11, 3892. [Google Scholar] [CrossRef]
- Karepov, S.; De Angelis, C.; Ellenbogen, T. Hybrid Nonlinear Metasurface Refractive Lens. Nano Lett. 2025, 25, 8103–8109. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Li, X.; Xing, Y.; Wang, J.; Zheng, W.; Wang, Z.; Ma, Y. Broadband Achromatic Hybrid Metalens Module with 100° Field of View for Visible Imaging. Sensors 2025, 25, 3202. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, F.; Pu, M.; Guo, Y.; Li, X.; Ma, X. Recent advances of wide-angle metalenses: Principle, design, and applications. Nanophotonics 2021, 11, 1–20. [Google Scholar] [CrossRef]
- Ou, K.; Yu, F.; Li, G.; Wang, W.; Miroshnichenko, A.E.; Huang, L.; Wang, P.; Li, T.; Li, Z.; Chen, X. Mid-infrared polarization-controlled broadband achromatic metadevice. Sci. Adv. 2020, 6, eabc0711. [Google Scholar] [CrossRef]
- Chen, Q.; Gao, Y.; Pian, S.; Ma, Y. Theory and fundamental limit of quasiachromatic metalens by phase delay extension. Phys. Rev. Lett. 2023, 131, 193801. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, F.; Lu, X.; Xie, T.; Pu, M.; Guo, Y.; Wang, Y.; Luo, X. Single-layer metalens for achromatic focusing with wide field of view in the visible range. J. Phys. D Appl. Phys. 2022, 55, 235106. [Google Scholar] [CrossRef]
- Yun, J.-G.; Kang, H.; Lee, K.; Jeong, Y.; Lee, E.; Kim, J.; Choi, M.; Koo, B.; Kim, D.; Choi, J. Compact eye camera with two-third wavelength phase-delay metalens. Nat. Commun. 2025, 16, 7299. [Google Scholar] [CrossRef] [PubMed]
- Egede Johansen, V.; Gür, U.M.; Martínez-Llinás, J.; Fly Hansen, J.; Samadi, A.; Skak Vestergaard Larsen, M.; Nielsen, T.; Mattinson, F.; Schmidlin, M.; Mortensen, N.A. Nanoscale precision brings experimental metalens efficiencies on par with theoretical promises. Commun. Phys. 2024, 7, 123. [Google Scholar] [CrossRef]
- Wei, J.; Huang, H.; Zhang, X.; Ye, D.; Li, Y.; Wang, L.; Ma, Y.; Li, Y. Neural-network-enhanced metalens camera for high-definition, dynamic imaging in the long-wave infrared spectrum. ACS Photonics 2025, 12, 140–151. [Google Scholar] [CrossRef]
- Chen, Q.; Zhou, J.; Pian, S.; Xu, J.; Li, X.; Li, B.; Lu, C.; Wang, Z.; Jiang, Q.; Qin, S. Hybrid Meta-Optics Enabled Compact Augmented Reality Display with Computational Image Reinforcement. ACS Photonics 2024, 11, 3794–3803. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).