Fractional-Order Modeling of a Multistable Erbium-Doped Fiber Laser
Abstract
1. Introduction
2. Mathematical Model of the Erbium-Doped Fiber Laser
2.1. General Model and Parameters
2.2. Inclusion of Pump Modulation and Simulation Parameters
2.3. Nondimensionalization of the Erbium-Doped Fiber Laser Model
2.4. Rescaling the Erbium-Doped Fiber Laser Model
3. Fractional Derivative Laser Model
3.1. Two-Stage Fractional Runge–Kutta Method
3.2. Local Stability Analysis
- -
- The system is stable if and only if for all eigenvalues .
- -
- The system is asymptotically stable if and only if for all eigenvalues .
- -
- The system is unstable if for at least one eigenvalue .
3.3. Global Stability Analysis
4. Experimental Results
4.1. Experimental Setup and Parameters
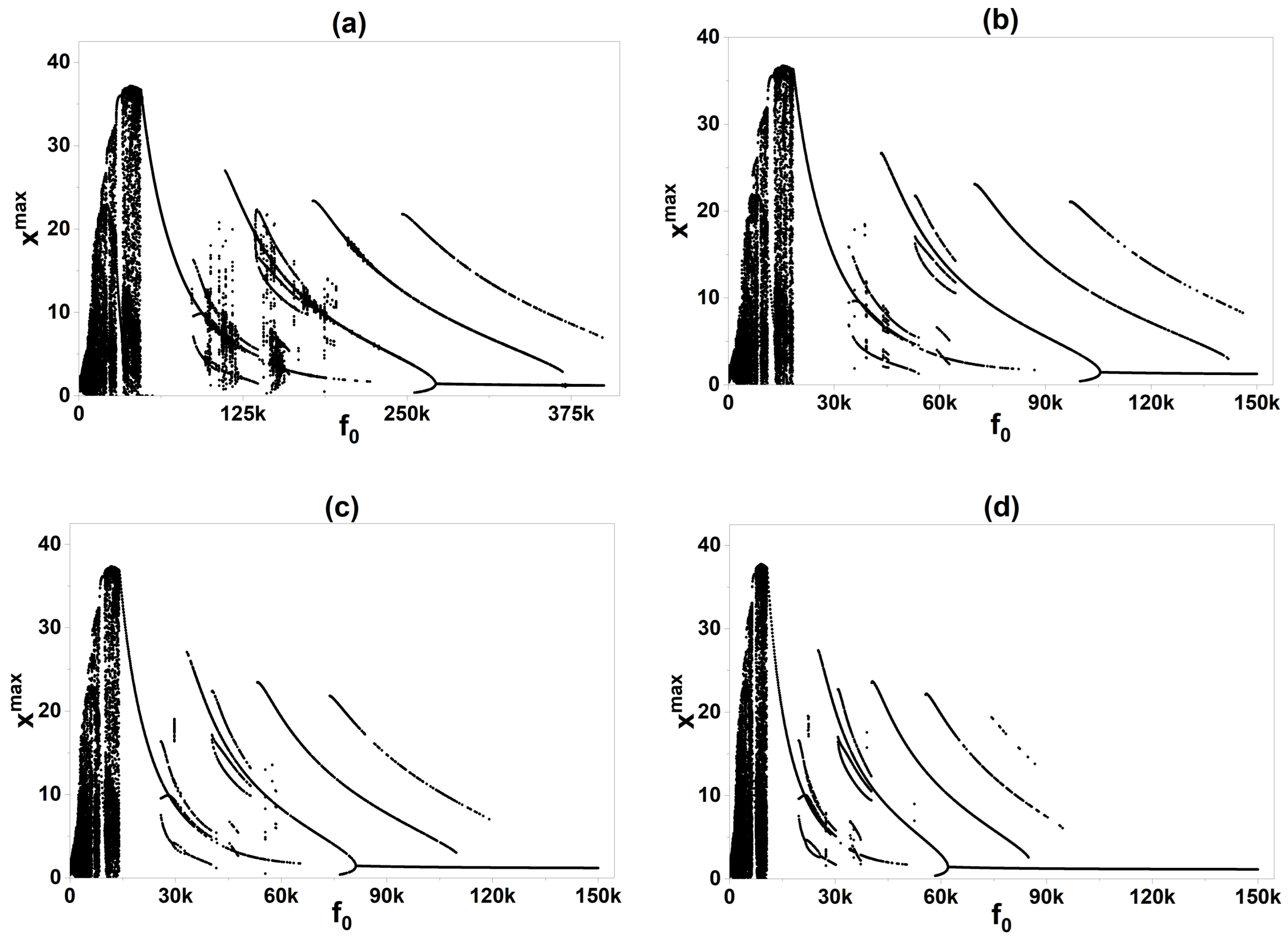
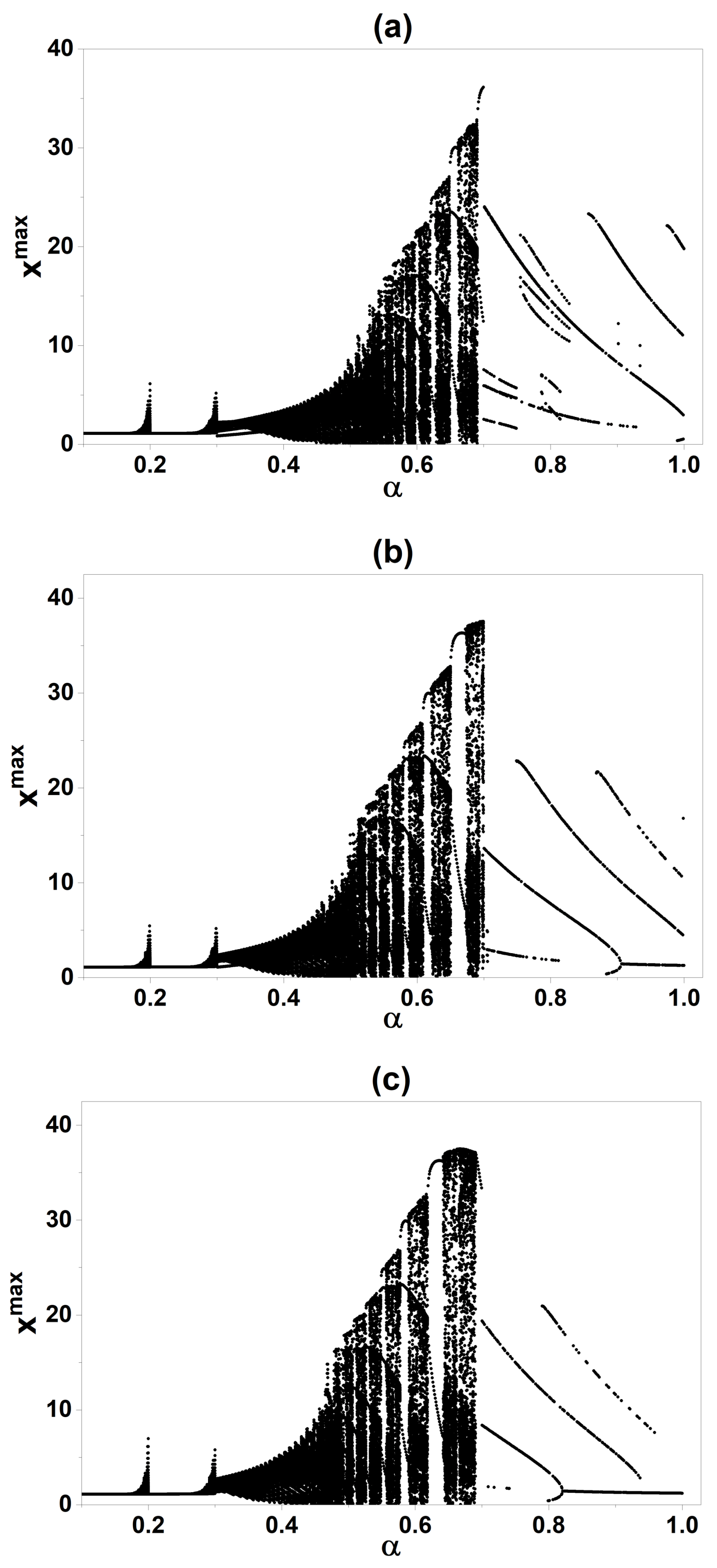
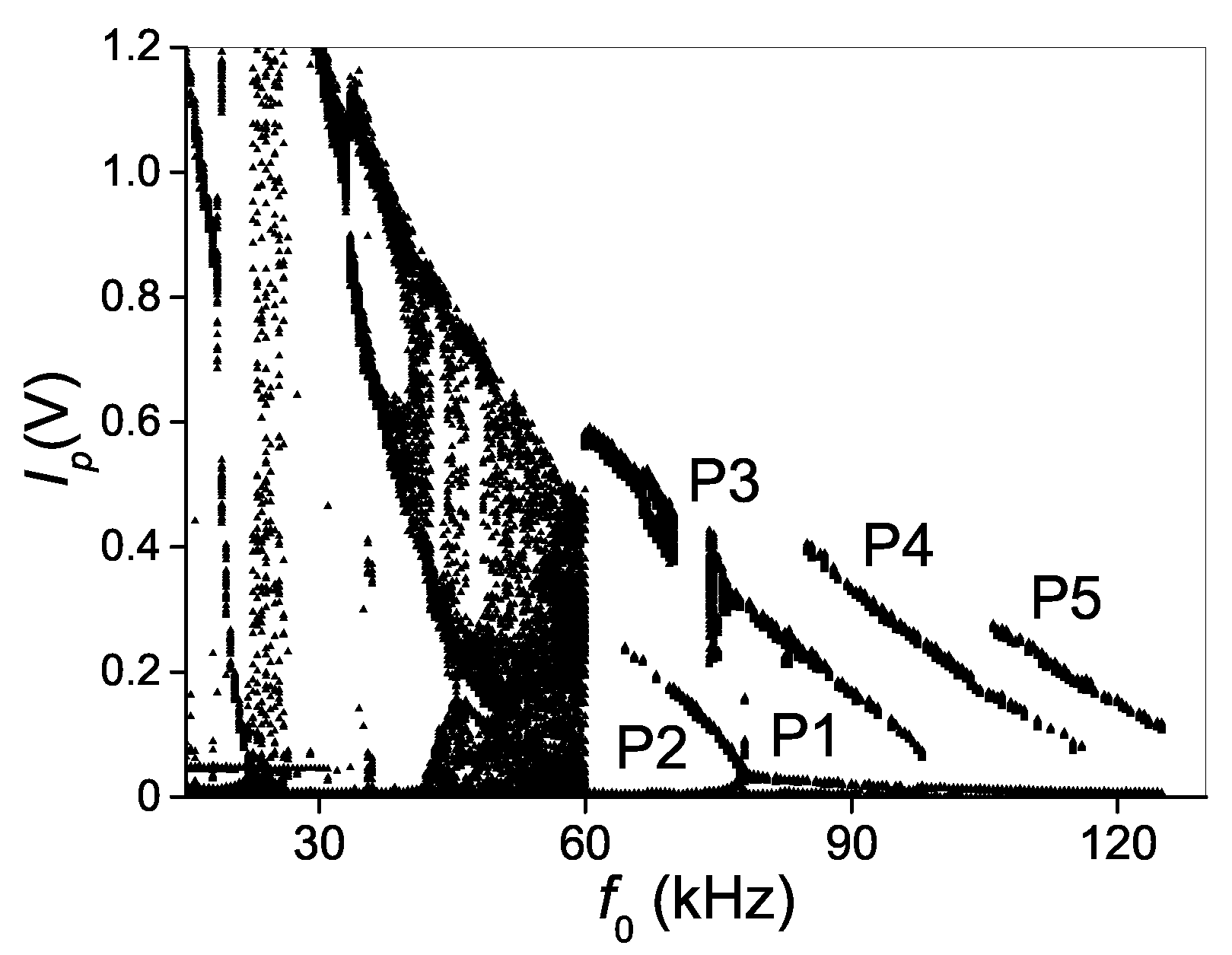
4.2. Experimental Bifurcation Diagram
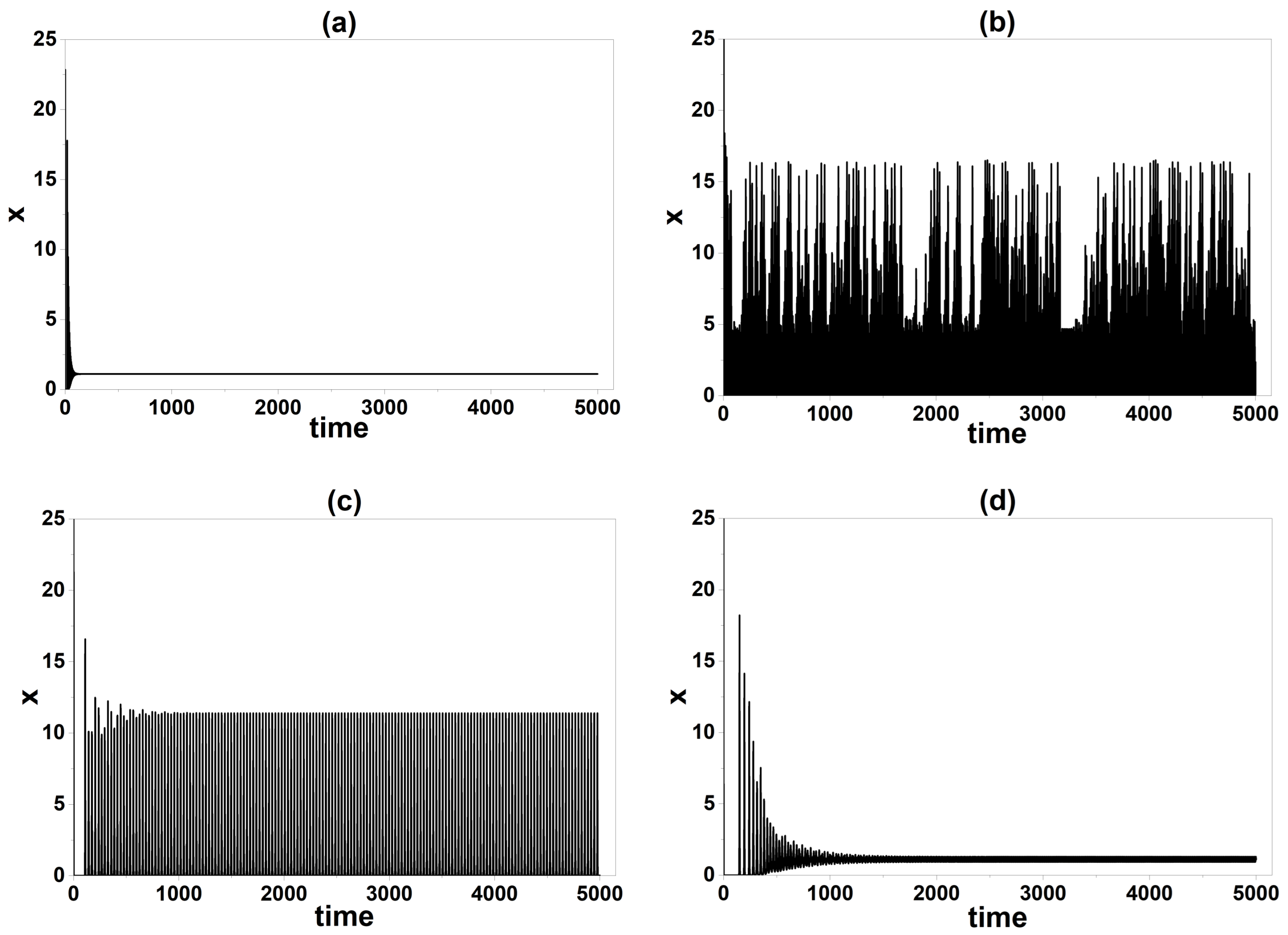
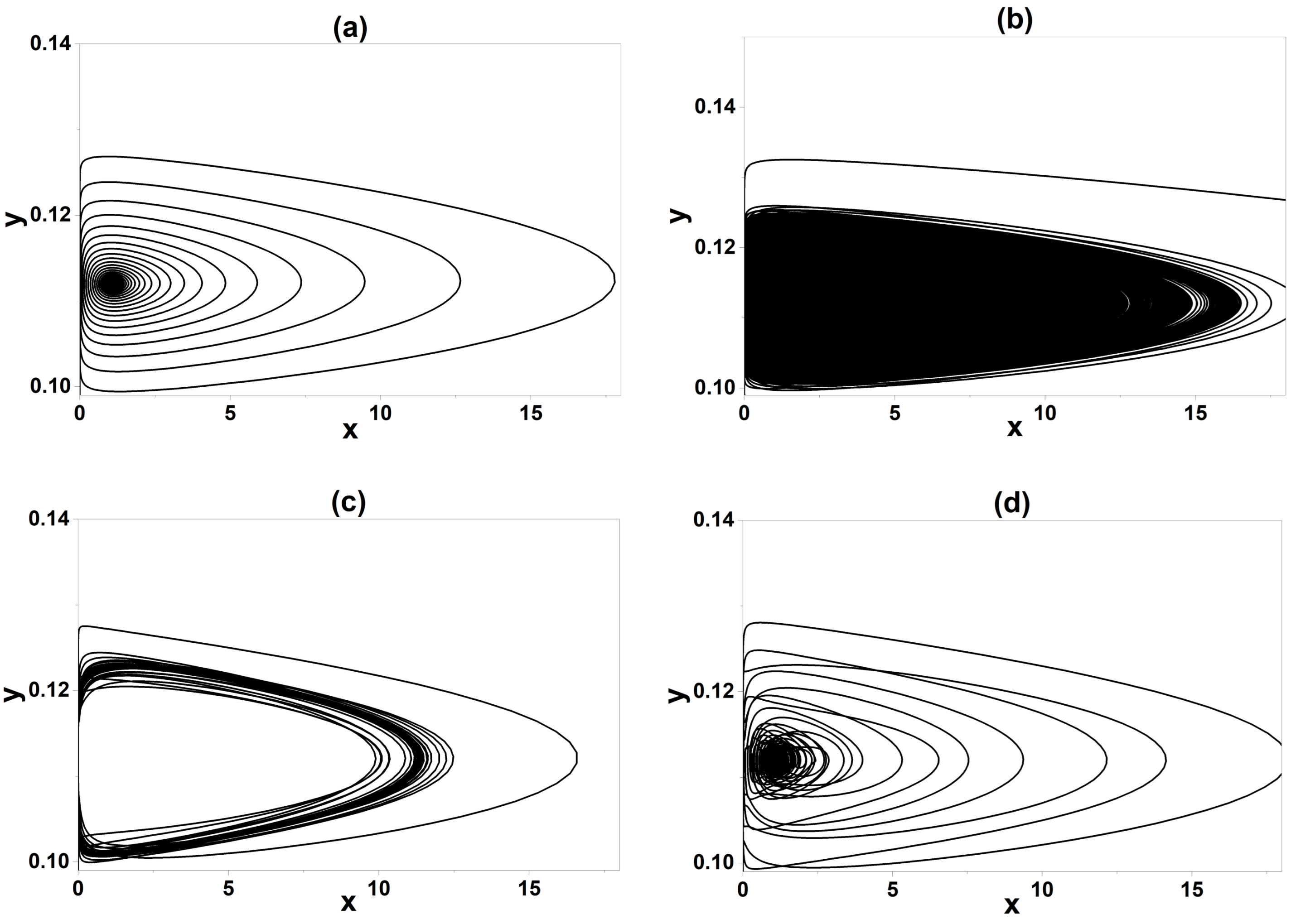
4.3. Comparison of Numerical and Experimental Results
5. Discussion
5.1. Physical Interpretation and Experimental Validation
5.2. The Fractional Order as a Control Parameter
5.3. Model Generality and Incorporation of External Factors
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Agrawal, G.P. Fiber-Optic Communication Systems, 4th ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Nilsson, J.; Eggleton, B.J. Erbium-doped fiber amplifiers and lasers. J. Light. Technol. 2000, 18, 1882–1892. [Google Scholar]
- Bellemare, A. Continuous-wave silica-based erbium-doped fibre lasers. Prog. Quantum Electron. 2003, 27, 211–266. [Google Scholar] [CrossRef]
- Tur, M.; Lembrikov, B.I.; Kip, D. Nonlinear dynamics of erbium-doped fiber lasers. IEEE J. Quantum Electron. 2004, 40, 1513–1522. [Google Scholar]
- Tamura, K.; Haus, H.A. Multistability in mode-locked fiber lasers. Appl. Phys. Lett. 1994, 64, 190–192. [Google Scholar] [CrossRef]
- Stewart, G.; Whitenett, G.; Vijayraghavan, K.; Sridaran, S. Investigation of the dynamic response of erbium fiber lasers with potential application for sensors. J. Light. Technol. 2007, 25, 1786–1796. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Jaimes-Reategui, R. Control of basins of attraction in a multistable fiber laser. Phys. Lett. A 2009, 374, 228–234. [Google Scholar] [CrossRef]
- Reategui, R.J.; Kir’yanov, A.V.; Pisarchik, A.N.; Barmenkov, Y.O.; Il’ichev, N.N. Experimental study and modeling of coexisting attractors and bifurcations in an erbium-doped fiber laser with diode-pump modulation. Laser Phys. 2004, 14, 1277–1281. [Google Scholar]
- Pisarchik, A.N.; Kir’yanov, A.V.; Barmenkov, Y.O.; Jaimes-Reátegui, R. Dynamics of an erbium-doped fiber laser with pump modulation: Theory and experiment. J. Opt. Soc. Am. B 2005, 22, 2107–2114. [Google Scholar] [CrossRef]
- Lacot, E.; Stoeckel, F.; Chenevier, M. Dynamics of an erbium-doped fiber laser. Phys. Rev. A 1994, 49, 3997. [Google Scholar] [CrossRef]
- Barba-Franco, J.J.; Romo-Muñoz, L.; Jaimes-Reátegui, R.; García-López, J.H.; Huerta-Cuéllar, G.; Pisarchik, A.N. Electronic equivalent of a pump-modulated erbium-doped fiber laser. Integration 2023, 89, 106–113. [Google Scholar] [CrossRef]
- Yanik, M.F.; Fan, S. Stopping light in a waveguide with an all-optical analogue of electromagnetically induced transparency. Phys. Rev. Lett. 2004, 92, 083901. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Afridi, M.I.; Islam, T.; Akbar, M.A.; Osman, M.S. The investigation of nonlinear time-fractional models in optical fibers and the impact analysis of fractional-order derivatives on solitary waves. Fractal Fract. 2024, 8, 627. [Google Scholar] [CrossRef]
- Fataf, N.A.A.; Rahim, M.F.A.; He, S.; Banerjee, S. A communication scheme based on fractional order chaotic laser for internet of things. Internet Things 2021, 15, 100425. [Google Scholar] [CrossRef]
- He, S.; Natiq, H.; Banerjee, S.; Sun, K. Complexity and chimera states in a network of fractional-order laser systems. Symmetry 2021, 13, 341. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Ma, C.; Cao, Y. Dynamic analysis of an improper fractional-order laser chaotic system and its image encryption application. Opt. Lasers Eng. 2020, 129, 106031. [Google Scholar] [CrossRef]
- Alzaid, S.S.; Chauhan, R.; Kumar, S.; Alkahtani, B.S.T. A high order numerical scheme for fractal-fractional laser system with chaos study. Fractals 2022, 30, 2240183. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. New Numerical Scheme with Newton Polynomial: Theory, Methods, and Applications; Academic Press: London, UK, 2021. [Google Scholar]
- Liu, Z. Bifurcation and control tactics in a fractional-order delayed single-model laser system. Eur. Phys. J. Plus 2022, 137, 576. [Google Scholar] [CrossRef]
- Khalaf, H.; Mahmoud, G.M.; Bountis, T.; AboElkher, A.M. A distributed-order fractional hyperchaotic detuned laser model: Dynamics, multistability and dual combination synchronization. Preprints 2025. [Google Scholar] [CrossRef]
- Ghoreishi, F.; Ghaffari, R.; Saad, N. Fractional order Runge–Kutta methods. Fractal Fract. 2023, 7, 245. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (Studies in Nonlinearity), 2nd ed.; Westview Press: Boulder, CO, USA, 2015. [Google Scholar]
- Gawade, S. The Newton–Raphson method: A detailed analysis. Int. J. Res. Appl. Sci. Eng. Technol. 2010, 12, 729–734. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Echenausía-Monroy, J.L.; Gilardi-Velázquez, H.E.; Jaimes-Reátegui, R.; Aboites, V.; Huerta-Cuéllar, G. A physical interpretation of fractional-order-derivatives in a jerk system: Electronic approach. Commun. Nonlin. Sci. Numer. Simul. 2020, 90, 105413. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Jaimes-Reátegui, R.; Sevilla-Escoboza, R.; Huerta-Cuellar, G. Multistate intermittency and extreme pulses in a fiber laser. Phys. Rev. E 2012, 86, 056219. [Google Scholar] [CrossRef]
- Afanador-Delgado, S.M.; Echenausía-Monroy, J.L.; Huerta-Cuellar, G.; García-López, J.H.; Lopez-Muñoz, E.E.; Jaimes-Reátegui, R. Logic gate generation in a monostable optical system: Improving the erbium-doped fiber laser reconfigurable logic operation. Photonics 2024, 11, 1103. [Google Scholar] [CrossRef]
- Jaimes-Reátegui, R.; De La Torre, J.O.E.; García-López, J.H.; Huerta-Cuellar, G.; Aboites, V.; Pisarchik, A.N. Generation of giant periodic pulses in the array of erbium-doped fiber lasers by controlling multistability. Opt. Commun. 2020, 477, 126355. [Google Scholar] [CrossRef]

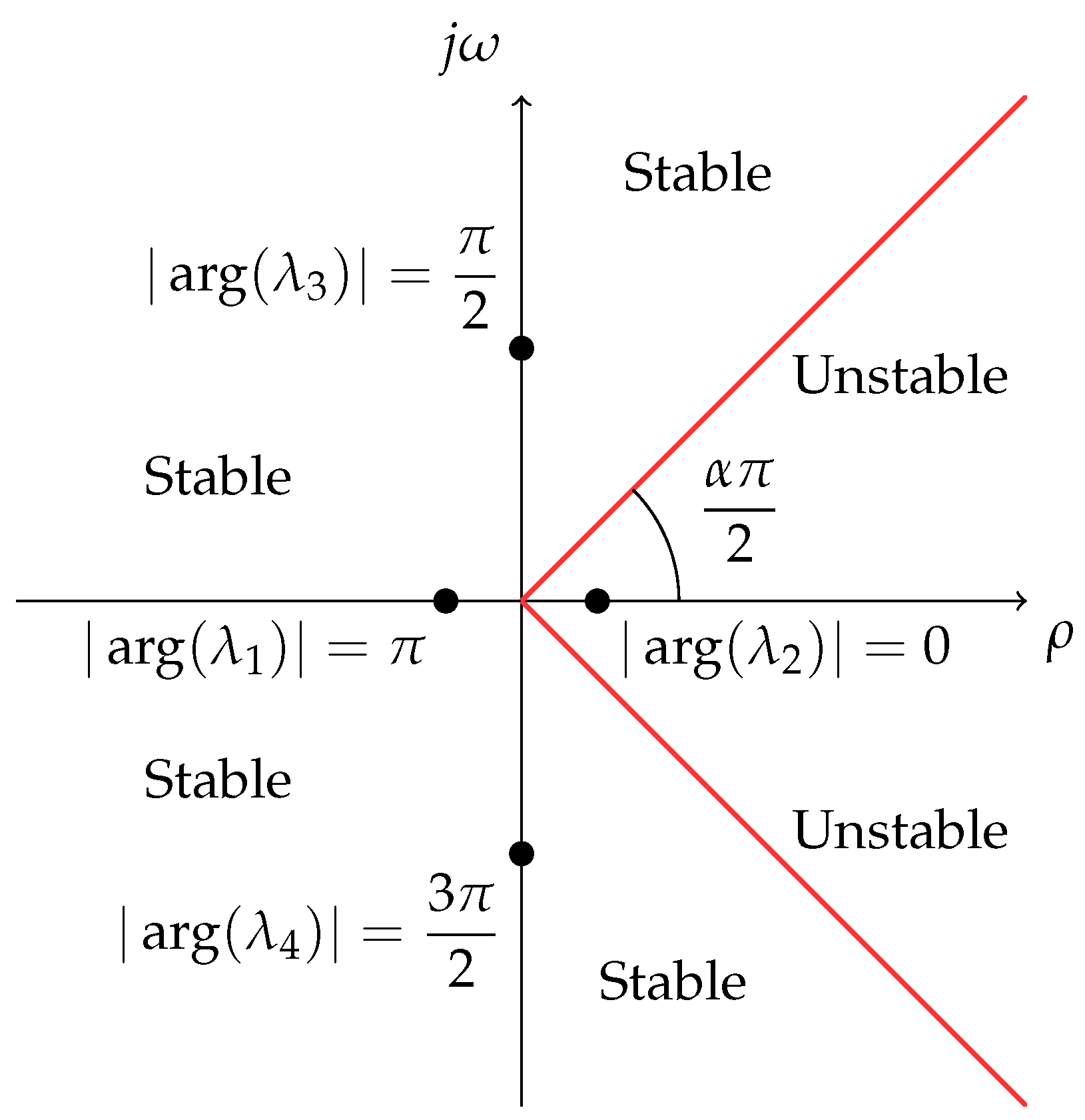

| Dimensionless Parameters | ||
|---|---|---|
| Symbol | Expression | Value |
| a | ||
| b | ||
| c | ||
| d | ||
| e | 506 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva Gómez, J.E.; Barba Franco, J.d.J.; Gallegos Infante, L.A.; García López, J.H.; Jaimes Reátegui, R.; Pisarchik, A.N. Fractional-Order Modeling of a Multistable Erbium-Doped Fiber Laser. Photonics 2025, 12, 1014. https://doi.org/10.3390/photonics12101014
Silva Gómez JE, Barba Franco JdJ, Gallegos Infante LA, García López JH, Jaimes Reátegui R, Pisarchik AN. Fractional-Order Modeling of a Multistable Erbium-Doped Fiber Laser. Photonics. 2025; 12(10):1014. https://doi.org/10.3390/photonics12101014
Chicago/Turabian StyleSilva Gómez, Jorge Eduardo, José de Jesús Barba Franco, Luís Armando Gallegos Infante, Juan Hugo García López, Rider Jaimes Reátegui, and Alexander N. Pisarchik. 2025. "Fractional-Order Modeling of a Multistable Erbium-Doped Fiber Laser" Photonics 12, no. 10: 1014. https://doi.org/10.3390/photonics12101014
APA StyleSilva Gómez, J. E., Barba Franco, J. d. J., Gallegos Infante, L. A., García López, J. H., Jaimes Reátegui, R., & Pisarchik, A. N. (2025). Fractional-Order Modeling of a Multistable Erbium-Doped Fiber Laser. Photonics, 12(10), 1014. https://doi.org/10.3390/photonics12101014







