Spectral Shaping of an Optical Frequency Comb to Control Atomic Dynamics
Abstract
1. Introduction
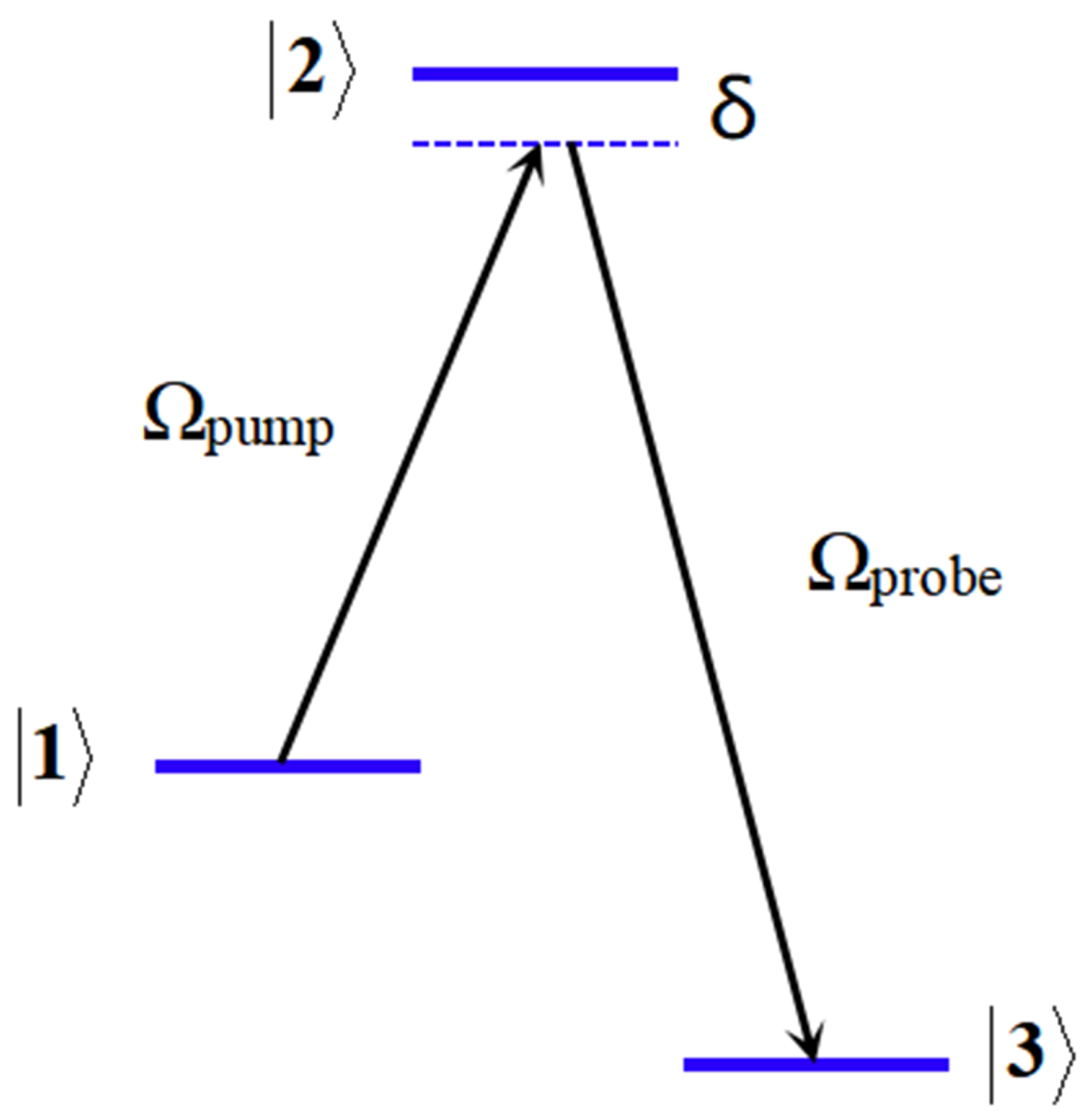
2. Theoretical Methods
3. Results and Discussion
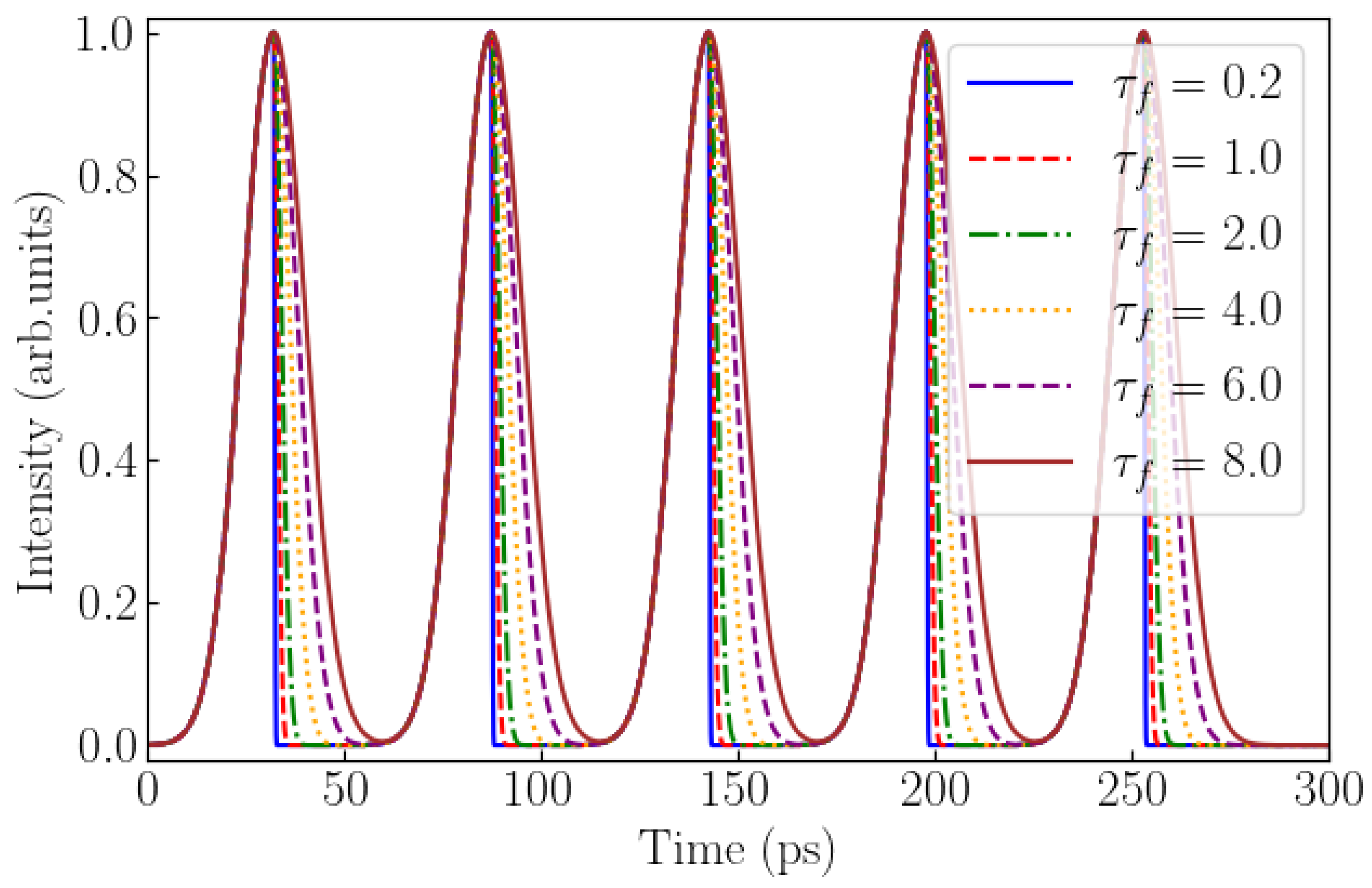
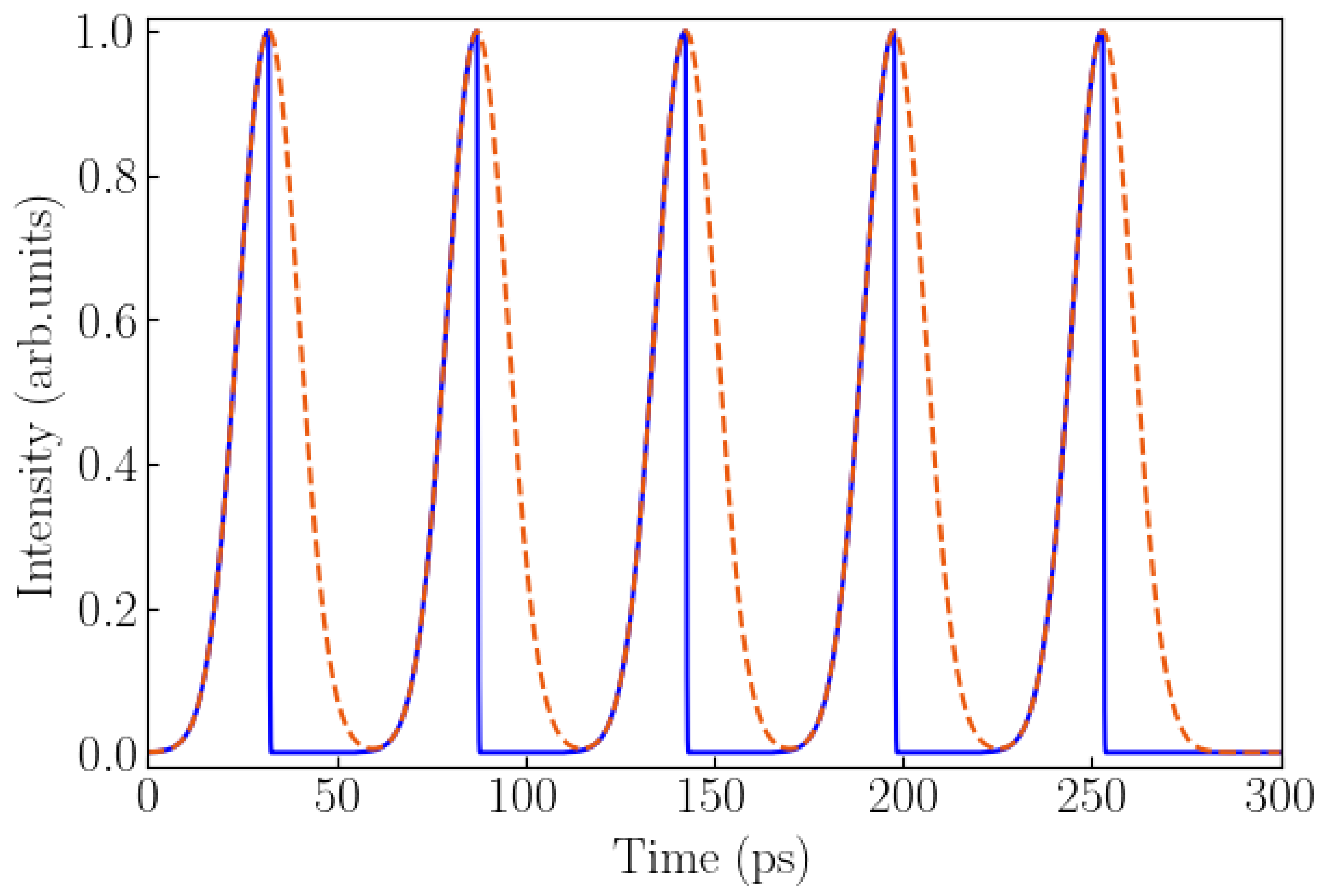
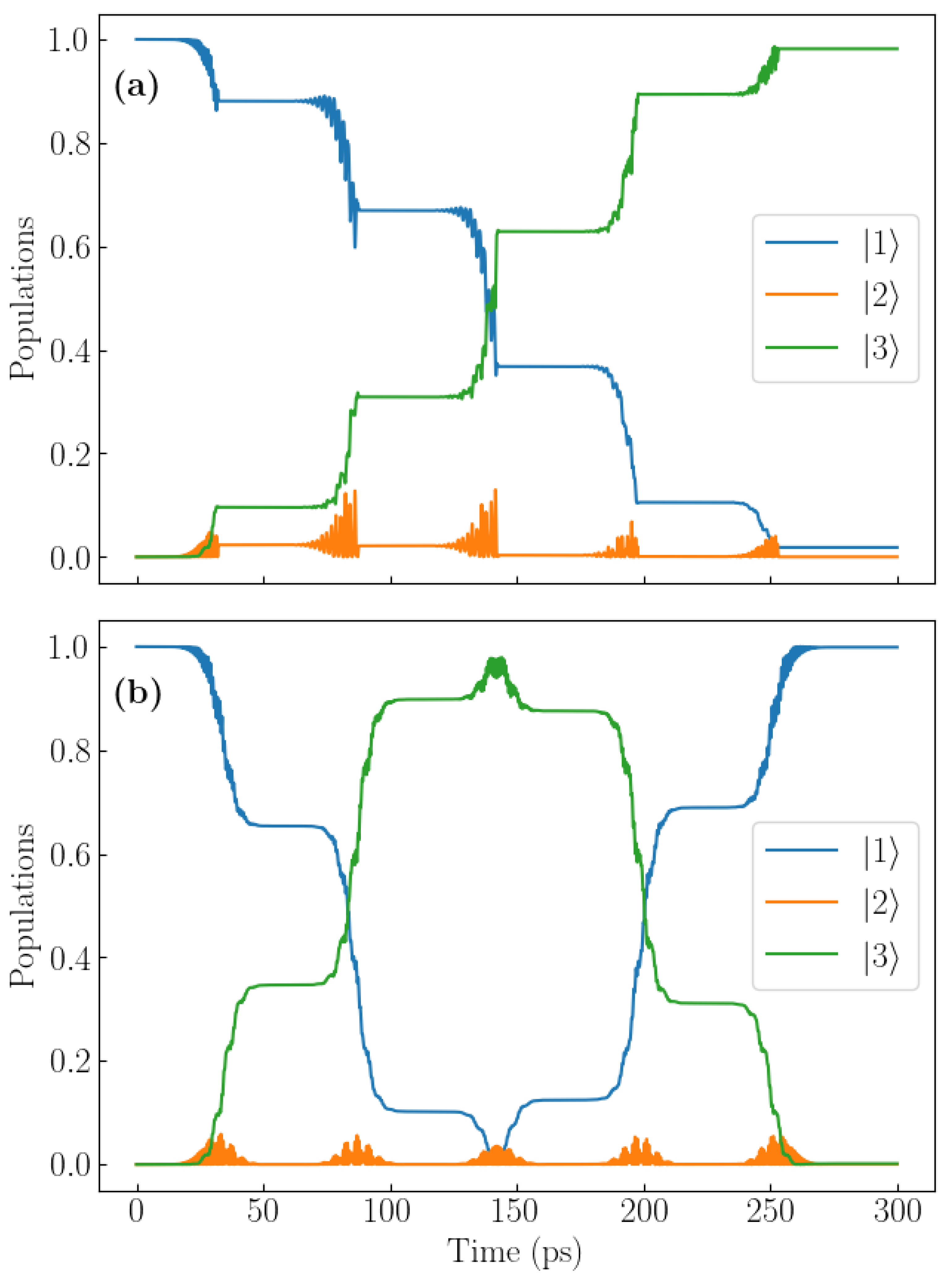
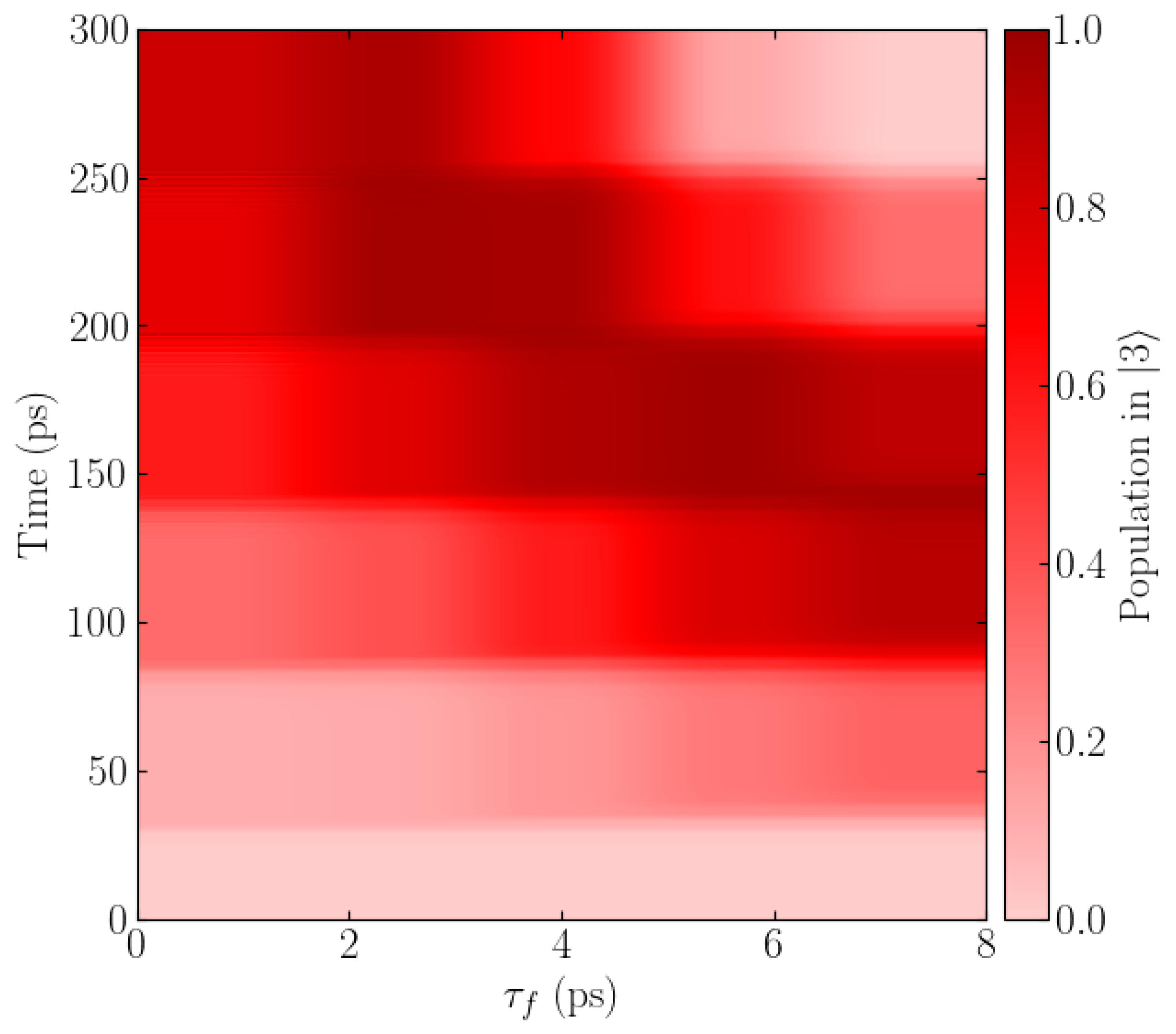
3.1. Different Fall Time
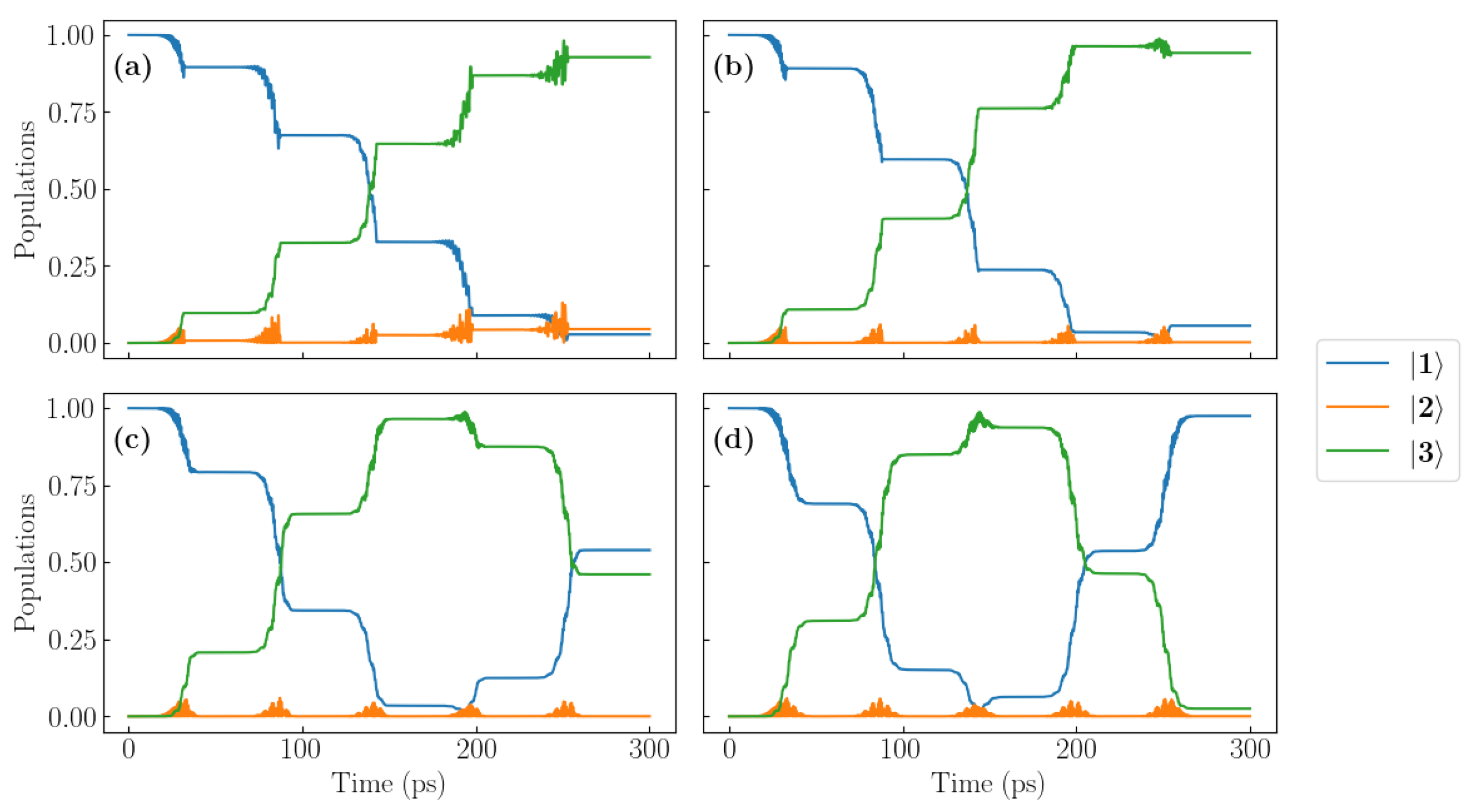
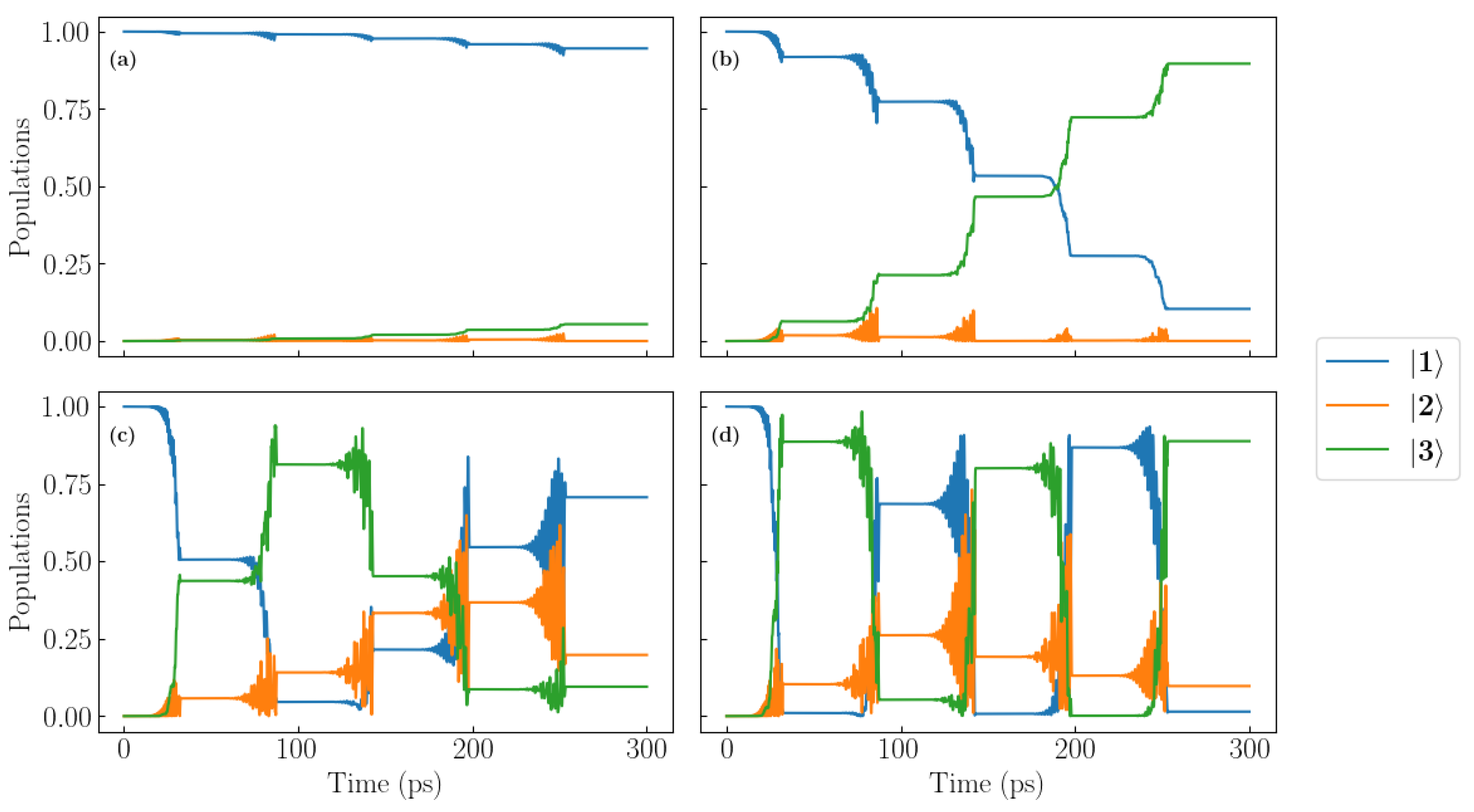
3.2. Number of Pulses
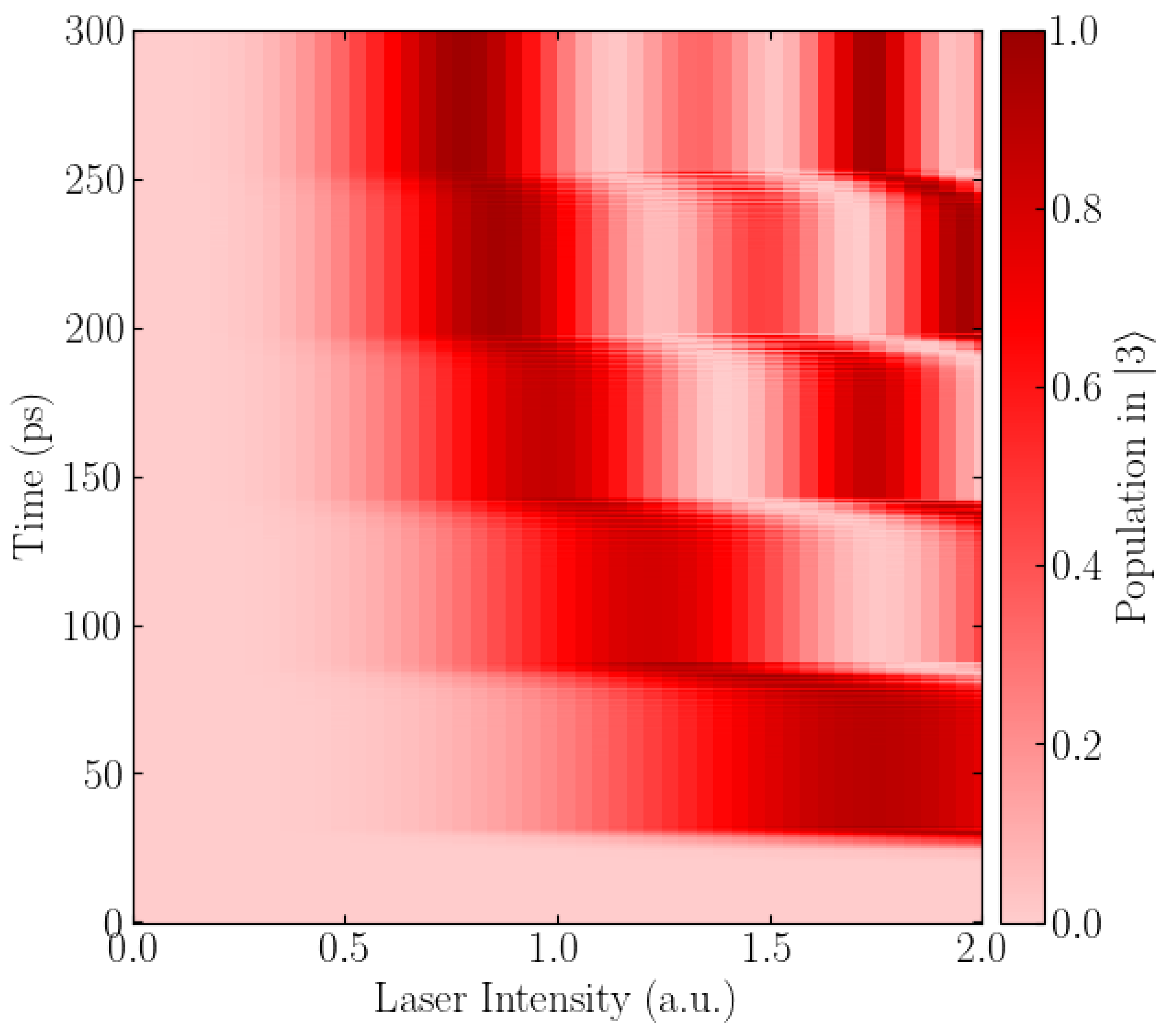
3.3. Laser Intensity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. [Google Scholar] [CrossRef]
- Thekkadath, G.; Bell, B.; Patel, R.; Kim, M.; Walmsley, I. Measuring the joint spectral mode of photon pairs using intensity interferometry. Phys. Rev. Lett. 2022, 128, 023601. [Google Scholar] [CrossRef]
- Marpaung, D.; Yao, J.; Capmany, J. Integrated microwave photonics. Nat. Photonics 2019, 13, 80–90. [Google Scholar] [CrossRef]
- Gu, Z.; Zhang, W.; Yu, Y.; Zhang, X. Disordered-guiding photonic chip enabled high-dimensional light field detection. Nat. Commun. 2025, 16, 7741. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Sua, Y.M.; Kumar, S.; Zhang, J.; Li, X.; Hu, Y.; Ghuman, P.; Huang, Y. Chip-integrated spectroscopy capable of temperature retrieval. Sci. Rep. 2025, 15, 30437. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, G.; Xu, L.; Fu, B. Polarization-multiplexed single-cavity dual combs and application in absorption spectroscopy. Sens. Actuators A Phys. 2023, 360, 114554. [Google Scholar] [CrossRef]
- Phillips, C.R.; Willenberg, B.; Nussbaum-Lapping, A.; Callegari, F.; Camenzind, S.L.; Pupeikis, J.; Keller, U. Coherently averaged dual-comb spectroscopy with a low-noise and high-power free-running gigahertz dual-comb laser. Opt. Express 2023, 31, 7103–7119. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.F.; Lesko, D.M.; Mashburn, C.; Chang, P.; Tsao, E.; Lind, A.J.; Diddams, S.A. Multi-harmonic near-infrared–ultraviolet dual-comb spectrometer. Opt. Lett. 2024, 49, 1684–1687. [Google Scholar] [CrossRef]
- Tian, H.; Sterczewski, L.A. Impact of optical frequency comb noise on free-running dual-comb spectroscopy. Opt. Express 2025, 33, 5075–5087. [Google Scholar] [CrossRef] [PubMed]
- Martin, E.P.; Ahmad, S.T.; Chandran, S.; Rosado, A.; Ruth, A.A.; Anandarajah, P.M. Stability Characterisation and Application of Mutually Injection Locked Gain Switched Optical Frequency Combs for Dual Comb Spectroscopy. J. Light. Technol. 2023, 41, 4516–4521. [Google Scholar] [CrossRef]
- Diao, Y.; Hu, H.; Li, X.; Li, Z.; Zeng, F.; Chen, Y.; You, S. Microwave-Controlled Spectroscopy Evolution for Different Rydberg States. Photonics 2025, 12, 715. [Google Scholar] [CrossRef]
- Magunia, A.; Rebholz, M.; Appi, E.; Papadopoulou, C.C.; Lindenblatt, H.; Trost, F.; Meister, S.; Ding, T.; Straub, M.; Borisova, G.D.; et al. Time-resolving state-specific molecular dissociation with XUV broadband absorption spectroscopy. Sci. Adv. 2023, 9, eadk1482. [Google Scholar] [CrossRef] [PubMed]
- Long, D.A.; Cich, M.J.; Mathurin, C.; Heiniger, A.T.; Mathews, G.C.; Frymire, A.; Rieker, G.B. Nanosecond time-resolved dual-comb absorption spectroscopy. Nat. Photonics 2024, 18, 127–131. [Google Scholar] [CrossRef]
- Chou, C.; Collopy, A.L.; Kurz, C.; Lin, Y.; Harding, M.E.; Plessow, P.N.; Fortier, T.; Diddams, S.; Leibfried, D.; Leibrandt, D.R. Frequency-comb spectroscopy on pure quantum states of a single molecular ion. Science 2020, 367, 1458–1461. [Google Scholar] [CrossRef]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Picqué, N.; Lipson, M.; Gaeta, A.L. Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat. Commun. 2018, 9, 1869. [Google Scholar] [CrossRef] [PubMed]
- Ycas, G.; Giorgetta, F.R.; Baumann, E.; Coddington, I.; Herman, D.; Diddams, S.A.; Newbury, N.R. High-coherence mid-infrared dual-comb spectroscopy spanning 2.6 to 5.2 μm. Nat. Photonics 2018, 12, 202–208. [Google Scholar] [CrossRef]
- Matselyukh, D.T.; Rott, F.; Schnappinger, T.; Zhang, P.; Li, Z.; Richardson, J.O.; de Vivie-Riedle, R.; Wörner, H.J. Attosecond spectroscopy of molecular charge transfer uncovers a 1.5-fs delay in population transfer. Nat. Commun. 2025, 16, 7211. [Google Scholar] [CrossRef]
- Maiuri, M.; Garavelli, M.; Cerullo, G. Ultrafast spectroscopy: State of the art and open challenges. J. Am. Chem. Soc. 2019, 142, 3–15. [Google Scholar] [CrossRef]
- Zanotto, S.; Conte, G.; Bellieres, L.C.; Griol, A.; Navarro-Urrios, D.; Tredicucci, A.; Martínez, A.; Pitanti, A. Optomechanical modulation spectroscopy of bound states in the continuum in a dielectric metasurface. Phys. Rev. Appl. 2022, 17, 044033. [Google Scholar] [CrossRef]
- Sielaff, L.; Kehl, A.; Aden, A.; Meyer, A.; Bennati, M. Pulsed dipolar hyperfine spectroscopy for molecular distance measurements in the angstrom to nanometer scale. Sci. Adv. 2025, 11, eady5665. [Google Scholar] [CrossRef]
- Silvestri, C.; Qi, X.; Taimre, T.; Rakić, A.D. Frequency combs induced by optical feedback and harmonic order tunability in quantum cascade lasers. APL Photonics 2023, 8, 116102. [Google Scholar] [CrossRef]
- Dan, L.; Xu, H.; Guo, P.; Zhao, J. Dynamics in direct two-photon transition by frequency combs. Europhys. Lett. 2022, 137, 25001. [Google Scholar] [CrossRef]
- Sekhar, P.; Fredrick, C.; Carlson, D.R.; Newman, Z.L.; Diddams, S.A. 20 GHz fiber-integrated femtosecond pulse and supercontinuum generation with a resonant electro-optic frequency comb. APL Photonics 2023, 8, 116111. [Google Scholar] [CrossRef]
- Wang, C.; Sun, Y.; Zhao, Q.; Yang, C.; Zeng, C.; Feng, Z.; Zhang, Y.; Li, L.; Zhou, K.; Wei, X.; et al. Ultrafine electro-optical frequency comb based on cascade phase modulation with cyclic frequency shifting. Opt. Lett. 2023, 48, 4665–4668. [Google Scholar] [CrossRef]
- Lambert, G.; Vodungbo, B.; Gautier, J.; Mahieu, B.; Malka, V.; Sebban, S.; Zeitoun, P.; Luning, J.; Perron, J.; Andreev, A.; et al. Towards enabling femtosecond helicity-dependent spectroscopy with high-harmonic sources. Nat. Commun. 2015, 6, 6167. [Google Scholar] [CrossRef]
- Peng, D.; Gu, C.; Zuo, Z.; Di, Y.; Zou, X.; Tang, L.; Deng, L.; Luo, D.; Liu, Y.; Li, W. Dual-comb optical activity spectroscopy for the analysis of vibrational optical activity induced by external magnetic field. Nat. Commun. 2023, 14, 883. [Google Scholar] [CrossRef]
- Bauer, C.P.; Bejm, Z.A.; Bollier, M.K.; Pupeikis, J.; Willenberg, B.; Keller, U.; Phillips, C.R. High-sensitivity dual-comb and cross-comb spectroscopy across the infrared using a widely tunable and free-running optical parametric oscillator. Nat. Commun. 2024, 15, 7211. [Google Scholar] [CrossRef] [PubMed]
- Han, J.J.; Zhong, W.; Zhao, R.C.; Zeng, T.; Li, M.; Lu, J.; Peng, X.X.; Shi, X.P.; Yin, Q.; Wang, Y.; et al. Dual-comb spectroscopy over a 100 km open-air path. Nat. Photonics 2024, 18, 1195–1202. [Google Scholar] [CrossRef]
- Villares, G.; Hugi, A.; Blaser, S.; Faist, J. Dual-comb spectroscopy based on quantum-cascade-laser frequency combs. Nat. Commun. 2014, 5, 5192. [Google Scholar] [CrossRef]
- Herman, D.I.; Walsh, M.; Genest, J. Mode-resolved optical frequency comb fixed point localization via dual-comb interferometry. Opt. Lett. 2024, 49, 7098–7101. [Google Scholar] [CrossRef]
- Zhang, C.; Qu, F.; Ou, P.; Sun, H.; He, S.; Fu, B. Recent advances and outlook in single-cavity dual comb lasers. Photonics 2023, 10, 221. [Google Scholar] [CrossRef]
- Nürnberg, J.; Willenberg, B.; Phillips, C.R.; Keller, U. Dual-comb ranging with frequency combs from single cavity free-running laser oscillators. Opt. Express 2021, 29, 24910–24918. [Google Scholar] [CrossRef] [PubMed]
- Bunel, T.; Chatterjee, D.; Lumeau, J.; Moreau, A.; Conforti, M.; Mussot, A. Dual-frequency comb in fiber Fabry–Perot resonator. APL Photonics 2025, 10, 036115. [Google Scholar] [CrossRef]
- Tsao, C.; Ling, H.; Hinkle, A.; Chen, Y.; Jha, K.K.; Yan, Z.L.; Utzat, H. Enhancing spectroscopy and microscopy with emerging methods in photon correlation and quantum illumination. Nat. Nanotechnol. 2025, 20, 1001–1016. [Google Scholar] [CrossRef]
- Sakurai, A.; Iwamoto, K.; Miwa, Y.; Hori, H.; Ishikawa, A.; Uchiyama, K.; Kobayashi, K.; Kishino, K.; Sakai, M. Scanning near-field optical spectroscopy and carrier transport based analysis in mesoscopic regions for two-dimensional semiconductors. Sci. Rep. 2022, 12, 10348. [Google Scholar] [CrossRef]
- Qi, Y.; Hu, D.; Jiang, Y.; Wu, Z.; Zheng, M.; Chen, E.X.; Liang, Y.; Sadi, M.A.; Zhang, K.; Chen, Y.P. Recent progresses in machine learning assisted Raman spectroscopy. Adv. Opt. Mater. 2023, 11, 2203104. [Google Scholar] [CrossRef]
- Chen, X.; Yao, Z.; Xu, S.; McLeod, A.S.; Gilbert Corder, S.N.; Zhao, Y.; Tsuneto, M.; Bechtel, H.A.; Martin, M.C.; Carr, G.L.; et al. Hybrid machine learning for scanning near-field optical spectroscopy. ACS Photonics 2021, 8, 2987–2996. [Google Scholar] [CrossRef]
- Saikia, D.; Dadhara, R.; Tanan, C.; Avati, P.; Verma, T.; Pandey, R.; Singh, S.P. Combating Antimicrobial Resistance: Spectroscopy Meets Machine Learning. Photonics 2025, 12, 672. [Google Scholar] [CrossRef]
- Stern, L.; Stone, J.R.; Kang, S.; Cole, D.C.; Suh, M.G.; Fredrick, C.; Newman, Z.; Vahala, K.; Kitching, J.; Diddams, S.A.; et al. Direct Kerr frequency comb atomic spectroscopy and stabilization. Sci. Adv. 2020, 6, eaax6230. [Google Scholar] [CrossRef]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef]
- Zhang, Z.; Peng, T.; Nie, X.; Agarwal, G.S.; Scully, M.O. Entangled photons enabled time-frequency-resolved coherent Raman spectroscopy and applications to electronic coherences at femtosecond scale. Light Sci. Appl. 2022, 11, 274. [Google Scholar] [CrossRef]
- Coppola, C.M.; De Carlo, M.; De Leonardis, F.; Passaro, V.M. High-Resolution On-Chip Digitally Tunable Spectrometer Based on Double-Cascaded Ring Resonators. Adv. Photonics Res. 2025, 6, 2500021. [Google Scholar] [CrossRef]
- Glier, T.E.; Tian, S.; Rerrer, M.; Westphal, L.; Lüllau, G.; Feng, L.; Dolgner, J.; Haenel, R.; Zonno, M.; Eisaki, H.; et al. Non-equilibrium anti-Stokes Raman spectroscopy for investigating Higgs modes in superconductors. Nat. Commun. 2025, 16, 7027. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Xiao, T.H.; Luo, Z.; Kitahama, Y.; Hiramatsu, K.; Kishimoto, N.; Itoh, T.; Cheng, Z.; Goda, K. Porous carbon nanowire array for surface-enhanced Raman spectroscopy. Nat. Commun. 2020, 11, 4772. [Google Scholar] [CrossRef]
- Wan, S.; Wang, P.Y.; Li, M.; Ma, R.; Niu, R.; Sun, F.W.; Bo, F.; Guo, G.C.; Dong, C.H. Self-locked broadband Raman-electro-optic microcomb. Nat. Commun. 2025, 16, 4829. [Google Scholar] [CrossRef]
- Engelhardt, G.; Bhoonah, A.; Liu, W.V. Detecting axion dark matter with Rydberg atoms via induced electric dipole transitions. Phys. Rev. Res. 2024, 6, 023017. [Google Scholar] [CrossRef]
- Chen, C.; Emperauger, G.; Bornet, G.; Caleca, F.; Gély, B.; Bintz, M.; Chatterjee, S.; Liu, V.; Barredo, D.; Yao, N.Y.; et al. Spectroscopy of elementary excitations from quench dynamics in a dipolar XY Rydberg simulator. Science 2025, 389, eadn0618. [Google Scholar] [CrossRef]
- Schlossberger, N.; Talashila, R.; Prajapati, N.; Holloway, C.L. Angle-of-arrival detection of radio-frequency waves via Rydberg-atom fluorescence imaging of standing waves in a glass vapor cell. Phys. Rev. Appl. 2025, 24, 024056. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.; Liu, Z.; Deng, Z.; Ding, D.; Shi, B.; Guo, G. Electric Field Measurement and Application Based on Rydberg Atoms. Electromagn. Sci. 2023, 1, 0020151. [Google Scholar] [CrossRef]
- Feng, Z.; Liu, X.; Song, Z.; Qu, J. Multi-parameter microwave quantum sensing with a single atomic probe. Sci. Rep. 2025, 15, 5379. [Google Scholar] [CrossRef] [PubMed]
- Jing, M.; Hu, Y.; Ma, J.; Zhang, H.; Zhang, L.; Xiao, L.; Jia, S. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat. Phys. 2020, 16, 911–915. [Google Scholar] [CrossRef]
- Torres-Company, V.; Weiner, A.M. Optical frequency comb technology for ultra-broadband radio-frequency photonics. Laser Photonics Rev. 2014, 8, 368–393. [Google Scholar] [CrossRef]
- Holzwarth, R.; Udem, T.; Hänsch, T.W.; Knight, J.; Wadsworth, W.; Russell, P.S.J. Optical frequency synthesizer for precision spectroscopy. Phys. Rev. Lett. 2000, 85, 2264. [Google Scholar] [CrossRef] [PubMed]
- Diddams, S.A.; Jones, D.J.; Ye, J.; Cundiff, S.T.; Hall, J.L.; Ranka, J.K.; Windeler, R.S.; Holzwarth, R.; Udem, T.; Hänsch, T.W. Direct link between microwave and optical frequencies with a 300 THz femtosecond laser comb. Phys. Rev. Lett. 2000, 84, 5102. [Google Scholar] [CrossRef]
- Davila-Rodriguez, J.; Ozawa, A.; Hänsch, T.W.; Udem, T. Doppler cooling trapped ions with a UV frequency comb. Phys. Rev. Lett. 2016, 116, 043002. [Google Scholar] [CrossRef]
- Stowe, M.C.; Cruz, F.C.; Marian, A.; Ye, J. High Resolution Atomic Coherent Control via Spectral Phase Manipulation of an Optical Frequency Comb. Phys. Rev. Lett. 2006, 96, 153001. [Google Scholar] [CrossRef]
- Picqué, N.; Hänsch, T.W. Frequency comb spectroscopy. Nat. Photonics 2019, 13, 146–157. [Google Scholar] [CrossRef]
- Lien, C.Y.; Seck, C.M.; Lin, Y.W.; Nguyen, J.H.; Tabor, D.A.; Odom, B.C. Broadband optical cooling of molecular rotors from room temperature to the ground state. Nat. Commun. 2014, 5, 4783. [Google Scholar] [CrossRef]
- Marin-Palomo, P.; Kemal, J.N.; Karpov, M.; Kordts, A.; Pfeifle, J.; Pfeiffer, M.H.; Trocha, P.; Wolf, S.; Brasch, V.; Anderson, M.H.; et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 2017, 546, 274–279. [Google Scholar] [CrossRef]
- Fortier, T.; Baumann, E. 20 years of developments in optical frequency comb technology and applications. Commun. Phys. 2019, 2, 153. [Google Scholar] [CrossRef]
- Malinovskaya, S.A.; Liu, G. Harmonic spectral modulation of an optical frequency comb to control the ultracold molecules formation. Chem. Phys. Lett. 2016, 664, 1–4. [Google Scholar] [CrossRef]
- Shi, W.; Malinovskaya, S. Implementation of a single femtosecond optical frequency comb for rovibrational cooling. Phys. Rev. A 2010, 82, 013407. [Google Scholar] [CrossRef]
- Mansourzadeh-Ashkani, N.; Saadati-Niari, M.; Zolfagharpour, F.; Nedaee-Shakarab, B. Nuclear-state population transfer using composite stimulated Raman adiabatic passage. Nucl. Phys. A 2021, 1007, 122119. [Google Scholar] [CrossRef]
- Muramatsu, M.; Hita, M.; Minemoto, S.; Sakai, H. Field-free molecular orientation by an intense nonresonant two-color laser field with a slow turn on and rapid turn off. Phys. Rev. A 2009, 79, 011403. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, G.R.; Cong, S.L. Efficient photoassociation with a train of asymmetric laser pulses. Phys. Rev. A 2011, 83, 045401. [Google Scholar] [CrossRef]
- Sussman, B.J.; Underwood, J.G.; Lausten, R.; Ivanov, M.Y.; Stolow, A. Quantum control via the dynamic Stark effect: Application to switched rotational wave packets and molecular axis alignment. Phys. Rev. A 2006, 73, 053403. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Bai, Z.; Fan, H.; Wang, X. Spectral Shaping of an Optical Frequency Comb to Control Atomic Dynamics. Photonics 2025, 12, 1015. https://doi.org/10.3390/photonics12101015
Zhang Y, Bai Z, Fan H, Wang X. Spectral Shaping of an Optical Frequency Comb to Control Atomic Dynamics. Photonics. 2025; 12(10):1015. https://doi.org/10.3390/photonics12101015
Chicago/Turabian StyleZhang, Yichi, Zhenqi Bai, Hongyan Fan, and Ximo Wang. 2025. "Spectral Shaping of an Optical Frequency Comb to Control Atomic Dynamics" Photonics 12, no. 10: 1015. https://doi.org/10.3390/photonics12101015
APA StyleZhang, Y., Bai, Z., Fan, H., & Wang, X. (2025). Spectral Shaping of an Optical Frequency Comb to Control Atomic Dynamics. Photonics, 12(10), 1015. https://doi.org/10.3390/photonics12101015





