Optical Fibers Use in On-Chip Fabry–Pérot Refractometry to Achieve High Q-Factor: Modeling and Experimental Assessment
Abstract
1. Introduction
2. Materials and Methods
2.1. Design and Theory
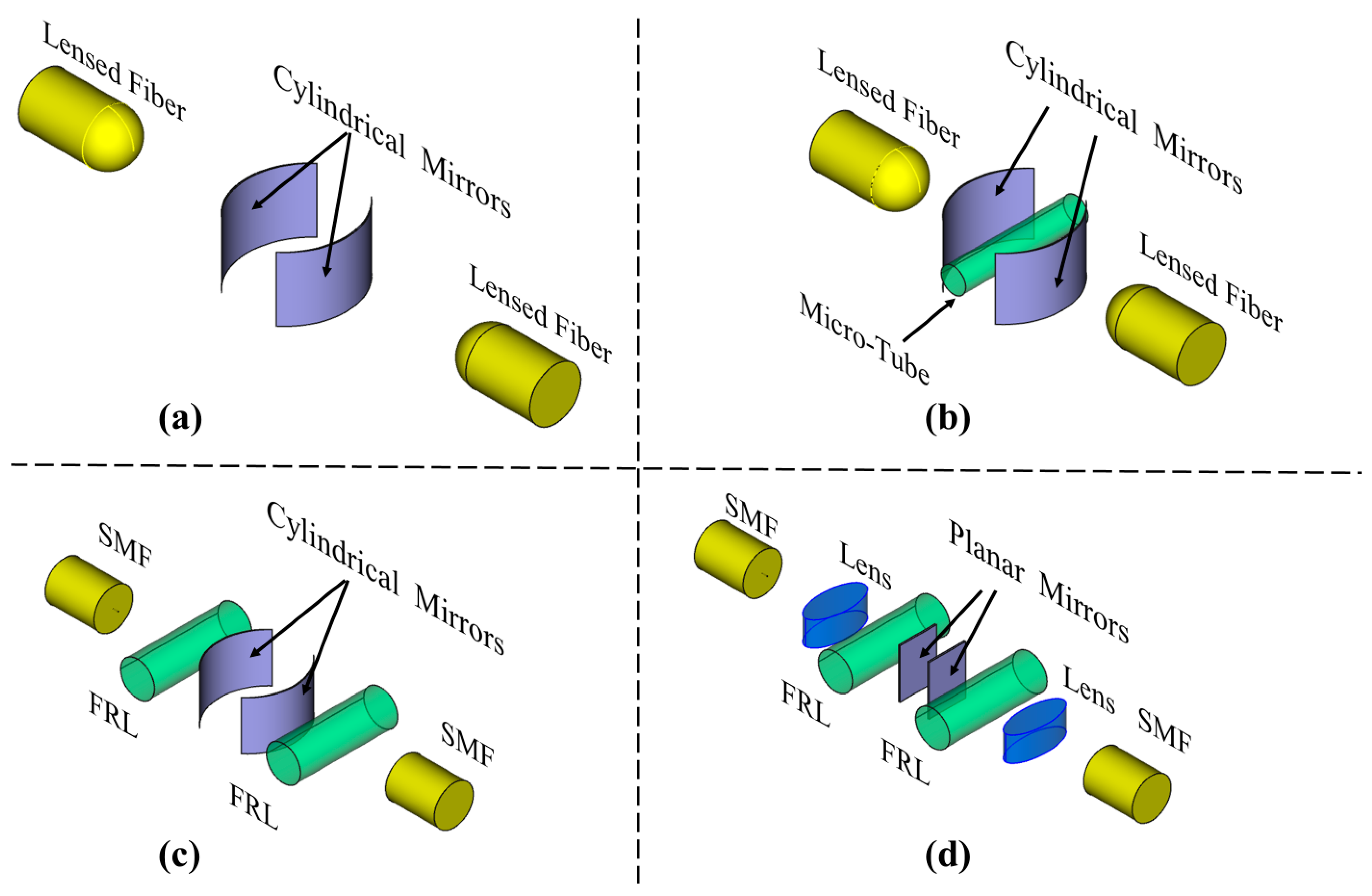
2.1.1. Optical FP Resonators’ Geometry and Performance Enhancement
2.1.2. Analytical Model and Coupling Efficiency
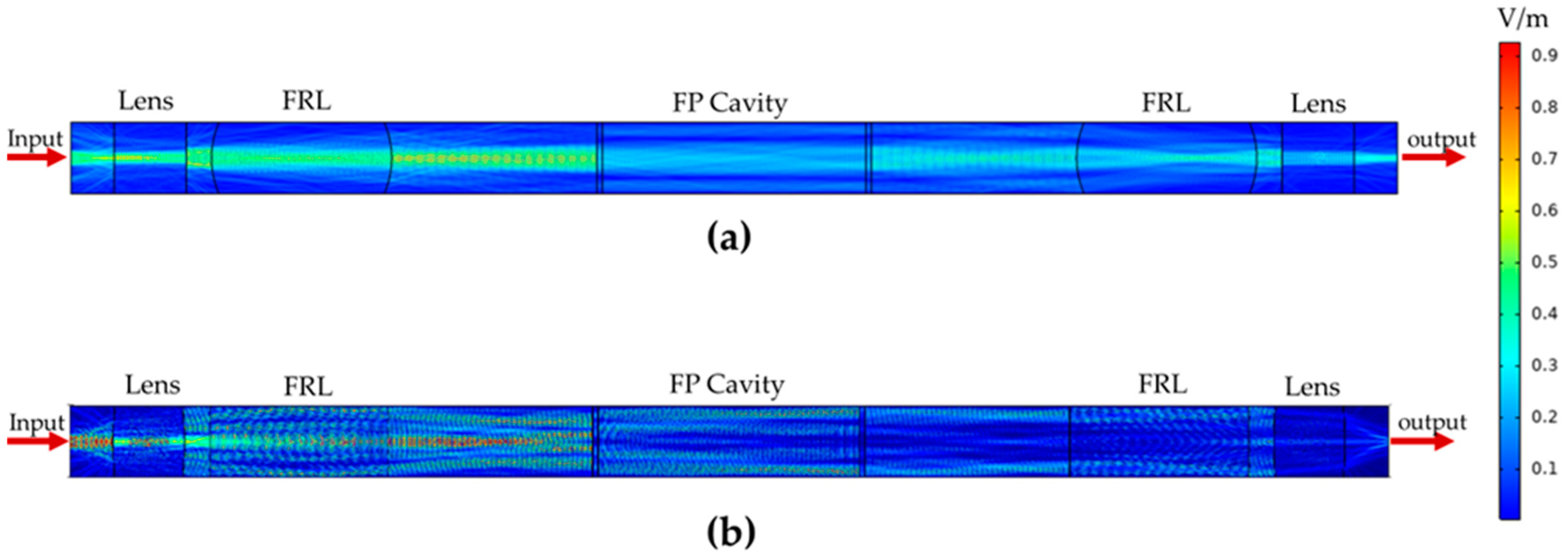
2.2. Simulation
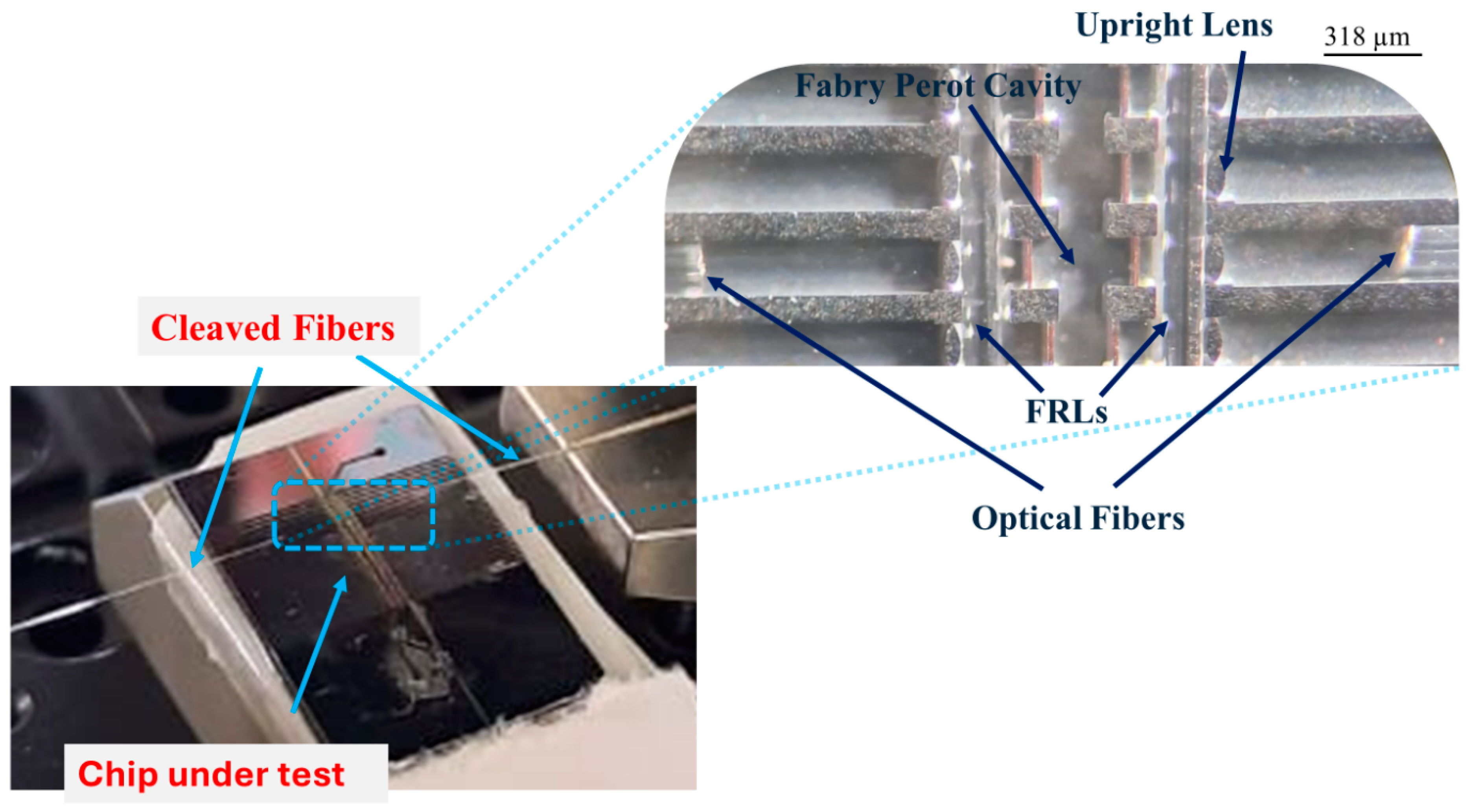
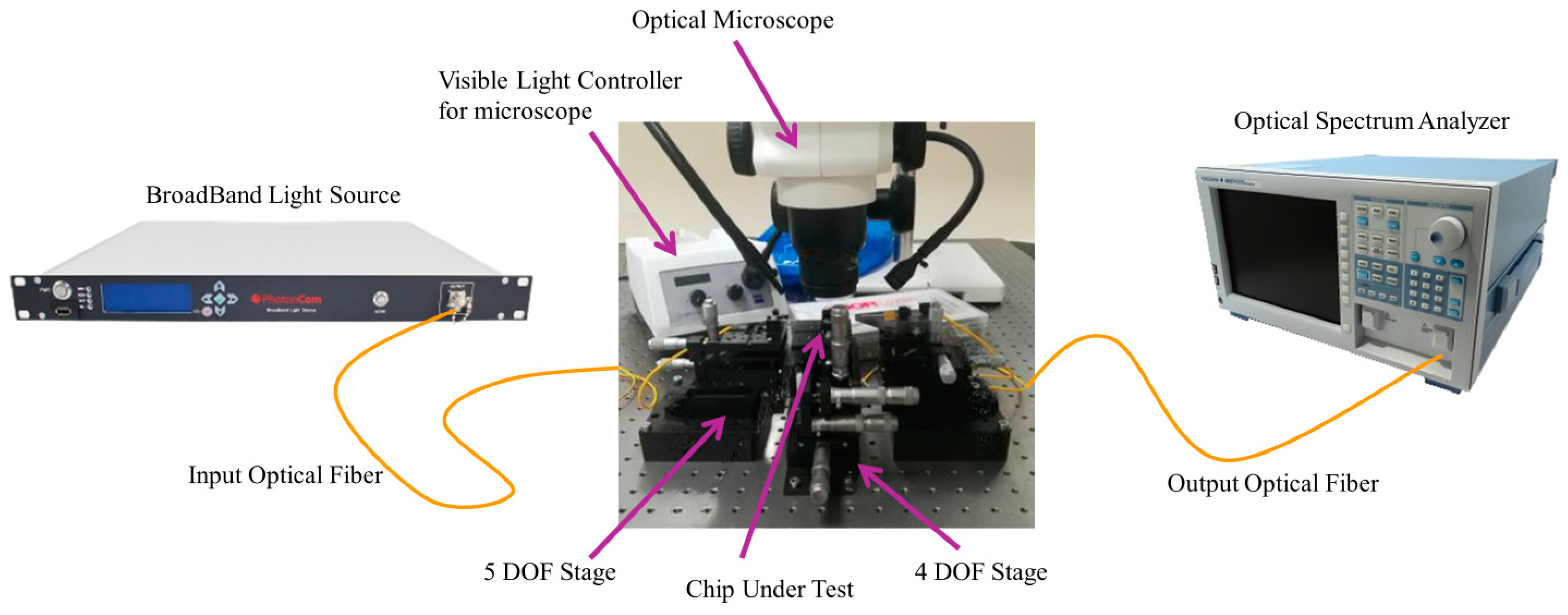
2.3. Experimental Methodology
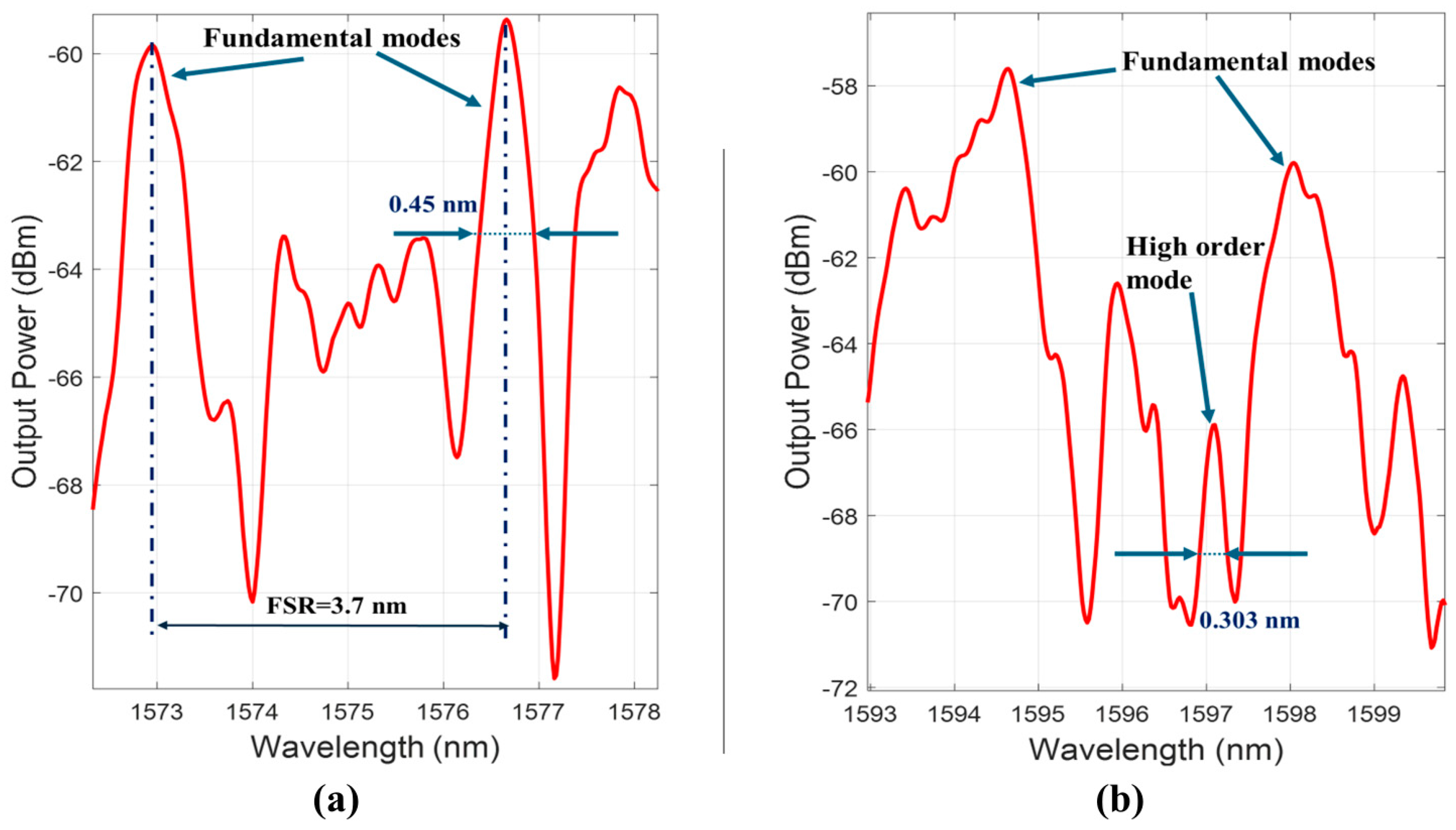
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jali, M.H.; Rahim, H.R.A.; Johari, A.M.; Baharom, M.F.; Ahmad, A.; Yusof, H.H.M.; Harun, S.W. Optical Microfiber Sensor: A Review. J. Physics Conf. Ser. 2021, 2075, 012021. [Google Scholar] [CrossRef]
- Floris, I.; Adam, J.M.; Calderón, P.A.; Sales, S. Fiber Optic Shape Sensors: A comprehensive review. Opt. Lasers Eng. 2021, 139, 106508. [Google Scholar] [CrossRef]
- Krohn, D.A.; MacDougall, T.; Mendez, A. Fiber Optic Sensor Fundamentals and Applications, 4th ed.; Society of Photo-Optical Instrumentation Engineers (SPIE): Washington, DC, USA, 2015. [Google Scholar] [CrossRef]
- Pendão, C.; Silva, I. Optical Fiber Sensors and Sensing Networks: Overview of the Main Principles and Applications. Sensors 2022, 22, 7554. [Google Scholar] [CrossRef]
- Bonopera, M. Fiber-Bragg-Grating-Based Displacement Sensors: Review of Recent Advances. Materials 2022, 15, 5561. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S. A review of distributed optical fiber sensors for civil engineering applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef] [PubMed]
- Mu, X.; Yang, Y.; Wang, J.; Bi, L. High sensitive Mach–Zehnder interferometer for seawater refractive index measurement. Ferroelectrics 2022, 595, 27–34. [Google Scholar] [CrossRef]
- Uniyal, A.; Srivastava, G.; Pal, A.; Taya, S.; Muduli, A. Recent Advances in Optical Biosensors for Sensing Applications: A Review. Plasmonics 2023, 18, 735–750. [Google Scholar] [CrossRef]
- Senthil, R.; Anand, U.; Krishnan, P. Hollow-core high-sensitive photonic crystal fiber for liquid-/gas-sensing applications. Appl. Phys. A 2021, 127, 282. [Google Scholar] [CrossRef]
- Bitarafan, M.H.; DeCorby, R.G. On-Chip High-Finesse Fabry-Perot Microcavities for Optical Sensing and Quantum Information. Sensors 2017, 17, 1748. [Google Scholar] [CrossRef]
- Syms, R.; Lohmann, A. MOEMS tuning element for a Littrow external cavity laser. J. Microelectromechan. Syst. 2003, 12, 921–928. [Google Scholar] [CrossRef]
- Gaber, N.; Sabry, Y.M.; Marty, F.; Bourouina, T. Optofluidic Fabry-Pérot Micro-Cavities Comprising Curved Surfaces for Homogeneous Liquid Refractometry—Design, Simulation, and Experimental Performance Assessment. Micromachines 2016, 7, 62. [Google Scholar] [CrossRef] [PubMed]
- Sabry, Y.; Bourouina, T.; Saadany, B.; Khalil, D. In-plane diffraction loss free optical cavity using coated optical fiber and silicon micromachined spherical mirror. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 25 August 2013. [Google Scholar] [CrossRef]
- Malak, M.; Gaber, N.; Marty, F.; Pavy, N.; Richalot, E.; Bourouina, T. Analysis of Fabry-Perot optical micro-cavities based on coating-free all-silicon cylindrical Bragg reflectors. Opt. Express 2013, 21, 2378–2392. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.M.; Mansour, M.A.; Ahmed, M.H.S.; Gaber, N.; Marty, F.; Bourouina, T. On-chip Optofluidic Structure for Hormonal Detection Using Stable Fabry-Pérot Resonator. In Proceedings of the 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET), Prague, Czech Republic, 20–22 July 2022. [Google Scholar] [CrossRef]
- Xu, H.; Qin, Y.; Hu, G.; Tsang, H.K. Million-Q integrated Fabry-Perot cavity using ultralow-loss multimode retroreflectors. Photon. Res. 2022, 10, 2549–2559. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Wang, K.; Li, H.; Skafidas, E. Ultra-broadband, compact, and high-reflectivity circular Bragg grating mirror based on 220 nm silicon-on-insulator platform. Opt. Express 2017, 25, 6653–6663. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, Q.; Xia, J. Traveling wave-like Fabry–Perot resonator-based add-drop filters. Opt. Lett. 2017, 42, 5158–5161. [Google Scholar] [CrossRef]
- ElZeiny, W.E.; Sabry, Y.M.; Khalil, D.A. Complex Kernel-based spectrum reconstruction algorithm for cascaded Fabry–Perot interferometric spectrometer. Appl. Opt. 2021, 60, 8999–9006. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, I.S.; Sabry, Y.M.; ElZeiny, W.E.; Badra, N.; Khalil, D.A. Transformation algorithm and analysis of the Fourier transform spectrometer based on cascaded Fabry-Perot interferometers. Appl. Opt. 2018, 57, 7225–7231. [Google Scholar] [CrossRef]
- Chin, L.K.; Liu, A.Q.; Lim, C.S.; Lin, C.L.; Ayi, T.C.; Yap, P.H. An optofluidic volume refractometer using Fabry–Pérot resonator with tunable liquid microlenses. Biomicrofluidics 2010, 4, 024107. [Google Scholar] [CrossRef]
- Gaber, N.; Sabry, Y.M.; Erfan, M.; Marty, F.; Bourouina, T. High-Q Fabry–Pérot Micro-Cavities for High-Sensitivity Volume Refractometry. Micromachines 2018, 9, 54. [Google Scholar] [CrossRef]
- Toraya, A.; Aboulela, N.G.A.; Marty, F.; Bourouina, T. On-chip structure for optofluidic sensing using stable Fabry-Pérot resonator. In MOEMS and Miniaturized Systems XX; SPIE: San Francisco, CA, USA, 2021. [Google Scholar] [CrossRef]
- Pal, B.P. Optical Fiber Sensors: A Versatile Technology Platform for Sensing. J. Indian Inst. Sci. 2014, 94, 283–310. [Google Scholar]
- Zheng, W. Optic lenses manufactured on fiber ends. In Proceedings of the 2015 Optoelectronics Global Conference (OGC), Shenzhen, China, 29 August 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 1991; ISBN 0-471-83965-5. [Google Scholar]
- Yariv, A. Quantum Electronics; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Liu, P.Y.; Chin, L.K.; Ser, W.; Chen, H.F.; Hsieh, C.-M.; Lee, C.-H.; Sung, K.-B.; Ayi, T.C.; Yap, P.H.; Liedberg, B.; et al. Cell refractive index for cell biology and disease diagnosis: Past, present and future. Lab Chip 2016, 16, 634–644. [Google Scholar] [CrossRef] [PubMed]
- Aly, A.H.; Awasthi, S.K.; Mohamed, A.M.; Matar, Z.S.; Mohaseb, M.A.; Al-Dossari, M.; Tammam, M.T.; Zaky, Z.A.; Amin, A.F.; Sabra, W. Detection of Reproductive Hormones in Females by Using 1D Photonic Crystal-Based Simple Reconfigurable Biosensing Design. Crystals 2021, 11, 1533. [Google Scholar] [CrossRef]
- Krupka, J.; Cwikla, A.; Mrozowski, M.; Clarke, R.N.; Tobar, M. High Q-factor microwave Fabry-Perot resonator with distributed Bragg reflectors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 1443–1451. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Ehteshami, N.; Liu, W.; Yao, J. Silicon-based on-chip electrically tunable sidewall Bragg grating Fabry–Perot filter. Opt. Lett. 2015, 40, 3153–3156. [Google Scholar] [CrossRef]
- Testa, G.; Persichetti, G.; Bernini, R. All-polymeric high-Q optofluidic Fabry–Perot resonator. Opt. Lett. 2021, 46, 352–355. [Google Scholar] [CrossRef]
- Guertin, R.; Lacasse, T.; Lemieux-Leduc, C.; Bianki, M.-A.; Peter, Y.-A. High-Performance, Low-Cost On-Chip Fabry-Perot Interferometer With Microfluidic Channel Using Single Anisotropic Wet Etching. J. Microelectromechan. Syst. 2023, 32, 347–351. [Google Scholar] [CrossRef]
- Leça, J.M.; Magalhães, Y.; Antunes, P.; Pereira, V.; Ferreira, M.S. Real-Time Measurement of Refractive Index Using 3D-Printed Optofluidic Fiber Sensor. Sensors 2022, 22, 9377. [Google Scholar] [CrossRef]
- You, K.E.; Uddin, N.; Kim, T.H.; Fan, Q.H.; Yoon, H.J. Highly sensitive detection of biological substances using microfluidic enhanced Fabry-Perot etalon-based optical biosensors. Sensors Actuators B Chem. 2018, 277, 62–68. [Google Scholar] [CrossRef]
- Tu, L.; Huang, L.; Wang, W. A novel micromachined Fabry-Perot interferometer integrating nano-holes and dielectrophoresis for enhanced biochemical sensing. Biosens. Bioelectron. 2019, 127, 19–24. [Google Scholar] [CrossRef]
- Jian, A.; Wu, Y.; Ji, J.; Li, D.; Zhang, Y.; Xue, X.; Sang, S. Low cell concentration detection by Fabry-Pérot resonator with sensitivity enhancement by dielectrophoresis. Sensors Actuators A Phys. 2021, 331, 112977. [Google Scholar] [CrossRef]
- Zhu, J.M.; Shi, Y.; Zhu, X.Q.; Yang, Y.; Jiang, F.H.; Sun, C.J.; Zhao, W.H.; Han, X.T. Optofluidic marine phosphate detection with enhanced absorption using a Fabry–Pérot resonator. Lab Chip 2017, 17, 4025–4030. [Google Scholar] [CrossRef] [PubMed]
- Guertin, R.; Bianki, M.-A.; Peter, Y.-A. Low-cost fabrication of an on-chip Fabry-Perot interferometer for dry environmental monitoring. In Proceedings of the 2023 International Conference on Optical MEMS and Nanophotonics (OMN) and SBFoton International Optics and Photonics Conference (SBFoton IOPC), Campinas, Brazil, 30 July–3 August 2023. [Google Scholar] [CrossRef]
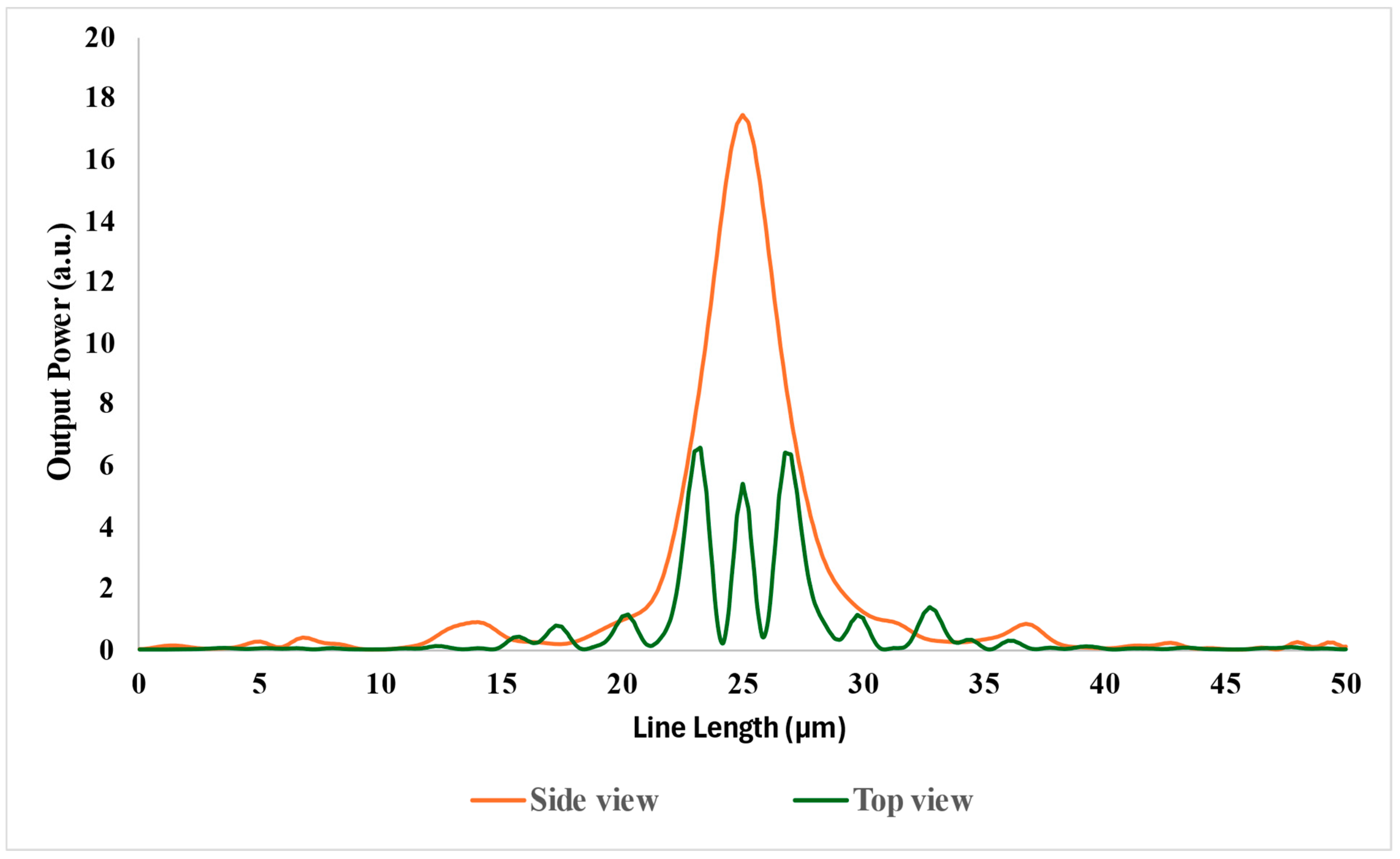


| Straight Mirrors (Figure 1d) | Cylindrical Mirrors (Figure 1c) | ||||
|---|---|---|---|---|---|
| Transverse mode order ) | Side view | Top view | Side view | Top view | |
| (0,0) | 99.55% | 48.19% | 91.99% | 73.2% | |
| (0,2) | 99.55% | 18.50% | 91.99% | 16.99% | |
| (2,0) | 0.45% | 48.19% | 7.07% | 73.2% | |
| (2,2) | 0.45% | 18.50% | 7.07% | 16.99% | |
| Ref. | Mirror Shape | Q-Factor | Analyte |
|---|---|---|---|
| [30] | Straight | >106 | Air |
| [31] | Straight | 3.35 × 104 | N/A |
| [32] | Straight | 3.03 × 104 | N/A |
| [33] | Straight | 2000 | N/A |
| [34] | Straight | 106 | Air |
| [35] | Straight | 260 | Air |
| [36] | Straight | 128.4 | Deionized Water |
| [37] | Straight | 3500 | Yeast Solution (3.65 × 105 cells/mL) |
| [38] | Straight | 270 | Deionized Water |
| [39] | Straight | 1150 | Air |
| [21] | Straight | 407 | n = 1.493 |
| [14] | Cylindrical | 1059 | Air |
| [12] | Cylindrical | 2896 | Toluene |
| [22] | Cylindrical | 9896 | Ethanol |
| Experimentally tested in this paper | Cylindrical | 3455 | Air |
| Experimentally tested in this paper | Straight | 5270 | Air |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansour, M.A.; Ali, A.M.; Marty, F.; Bourouina, T.; Gaber, N. Optical Fibers Use in On-Chip Fabry–Pérot Refractometry to Achieve High Q-Factor: Modeling and Experimental Assessment. Photonics 2024, 11, 852. https://doi.org/10.3390/photonics11090852
Mansour MA, Ali AM, Marty F, Bourouina T, Gaber N. Optical Fibers Use in On-Chip Fabry–Pérot Refractometry to Achieve High Q-Factor: Modeling and Experimental Assessment. Photonics. 2024; 11(9):852. https://doi.org/10.3390/photonics11090852
Chicago/Turabian StyleMansour, Mohamed Abdelsalam, Alaa M. Ali, Frédéric Marty, Tarik Bourouina, and Noha Gaber. 2024. "Optical Fibers Use in On-Chip Fabry–Pérot Refractometry to Achieve High Q-Factor: Modeling and Experimental Assessment" Photonics 11, no. 9: 852. https://doi.org/10.3390/photonics11090852
APA StyleMansour, M. A., Ali, A. M., Marty, F., Bourouina, T., & Gaber, N. (2024). Optical Fibers Use in On-Chip Fabry–Pérot Refractometry to Achieve High Q-Factor: Modeling and Experimental Assessment. Photonics, 11(9), 852. https://doi.org/10.3390/photonics11090852





