Digital Holographic Interferometry for Micro-Deformation Analysis of Morpho Butterfly Wing

Abstract

In this study, we present an analysis of deflections in a Morpho butterfly wing using digital holographic interferometry (DHI). Our methodology revolves around an off-axis lensless Fourier holographic setup, using laser excitation to induce deflections in the object. The implementation of a DHI setup, tailored for rapid monitoring of micro-deformation, is a central aspect of our research. We offer an overview of the theoretical foundations of this technique, complemented by both experimental and numerical results aimed at validating our findings. We designed an optical setup that enhanced both laser illumination and hologram reconstruction for the sample. The experimental findings decisively show that the proposed method is effective for rapid deformation analysis. The deformation of the wing can be measured with micro-meter accuracy thanks to numerical analysis.

1. Introduction

Engineered nanostructures often draw inspiration from the intricate nanoscale designs found in nature, which have evolved over billions of years to serve specific functions. In the realm of photonic applications, there is considerable fascination with the structural coloration exhibited by Morpho butterfly wings. Unlike traditional pigmentation, structural coloration relies on photonic resonances, resulting in the constructive interference of visible light. The small scales on Morpho butterfly wings possess ribbed lamellae layers with remarkable periodicity. This nanostructure selectively interacts with specific wavelengths of light, giving rise to the iconic blue iridescence synonymous with the Morpho butterfly. Beyond their aesthetic appeal, the hierarchical nanostructures present in butterfly wings offer compelling potential for functional applications. These wings have found utility in a wide array of fields, including optical gas sensors [1], solar cells [2], infrared detectors [3], photocatalysts [4], surface-enhanced Raman spectroscopy (SERS) substrates [5], and more recently in energy application [6]. Radiation detection attracts special attention as the need for low-cost imaging detectors with wide spectral ranges grows ever stronger [7].

In a previous study [7,8], the authors applied Euler–Bernoulli beam theory to describe wing deflection, simplifying the complex structure of a butterfly wing into a mathematical model of a cantilever beam. This approach provided valuable insights and a foundational understanding of the mechanical properties of butterfly wings. It effectively captured key aspects of wing behaviour and contributed to the field by offering a structured framework for analysis. However, it does not capture phase information on the whole object. Also, butterfly wings exhibit significant variations (inhomogeneity) in their structure and properties, which the cantilever beam model may not fully capture, potentially impacting the accuracy of the analysis. Furthermore, such analysis emphasizes static behaviour and does not account for the dynamic and fluid interactions that occur on the wing, which are essential for a comprehensive understanding of wing dynamics under external stimulation.

In contrast, DHI offers a superior approach for measuring deflection by providing direct, precise, and real-time measurements of deformation. Unlike the theoretical approximations of the Euler–Bernoulli beam theory, DHI delivers immediate and accurate insights into an object’s deformation. By capturing and analysing holograms of the object in both its initial (non-deformed) and deformed states, this method enables the creation of full-field deformation maps. It is suitable for analysing both small and large deformations, making it versatile and adaptable to various materials and structures. Additionally, as a non-contact and non-destructive measurement method, it ensures the integrity of the object remains intact throughout the analysis. DHI can capture real-time data, allowing for the observation of how the wing behaves under laser irradiation. This dynamic measurement capability is crucial for understanding the relaxation time and the viscoelastic properties of the wing material. In a recent study [9] on digital holography, a novel approach combining a free field-of-view scheme with infrared holographic detection was proposed to overcome the limitations of traditional optical microscopy and infrared spectroscopy. Additionally, DHI has demonstrated its effectiveness in measuring deformation on a variety of samples, including fiberglass plates, glass-reinforced plastics, metal plates [10], and chromium films [11].

In this manuscript, we describe an experiment for quantitatively measuring and monitoring dynamic deformations on butterfly wings. Our technique employs a DHI system equipped with a camera and a laser with high output power to capture rapid and unpredictable wing deformations with exceptional precision. Our study shows a series of phase maps illustrating wing deflection after laser excitation and engages in a discussion of the results. This non-destructive optical approach holds promise as an exceptional tool for analysing the response and dynamics of wing deformation under radiation. Additionally, our method stands out for its efficiency, requiring only a single Fourier transform, unlike other reconstruction techniques which need more computation time. This approach not only simplifies the process but also significantly speeds up the hologram reconstruction, making it more practical and effective for monitoring rapid changes in the object due to external stimuli.

2. Digital Hologram Reconstruction

The method involves capturing two digital holograms, representing the object in its original and deformed state. Employing the Fresnel method and a standard off-axis lensless digital Fourier holographic setup, each hologram is individually reconstructed using a single Fast Fourier Transform. In the Fresnel approximation (for both $x$- and $y$-values as well as for $\xi$- and $\eta$-values, which are small compared to the distance d between the reconstruction plane and the CCD), the complex amplitude is derived from the recorded hologram through a numerical reconstruction process, achieved by [12,13,14]:

$$\Gamma (\xi ,\eta )={\displaystyle \frac{i}{\lambda d}}\exp \left({\displaystyle \frac{-i2\pi d}{\lambda }}\right)\exp \left[-i{\displaystyle \frac{\pi }{\lambda d}}\left({\xi }^2+{\eta }^2\right)\right]\times {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{E}_R}}(x,y)h(x,y)\exp \left[-i{\displaystyle \frac{\pi }{\lambda d}}\left(x^2+y^2\right)\right]\exp \left[i{\displaystyle \frac{2\pi }{\lambda d}}\left(x\xi +y\eta \right)\right]dxdy$$

(1)

By applying the following substitutions to the Fresnel transform in Equation (1)

$$\nu ={\displaystyle \frac{\xi }{\lambda d}},\mu ={\displaystyle \frac{\eta }{\lambda d}}$$

(2)

We have for Equation (1):

$$\Gamma (\nu ,\mu )={\displaystyle \frac{i}{\lambda d}}\exp \left({\displaystyle \frac{-i2\pi d}{\lambda }}\right)\exp \left[-i\pi \lambda d\left({\nu }^2+{\mu }^2\right)\right]\times {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{E}_R}}(x,y)h(x,y)\exp \left[-i{\displaystyle \frac{\pi }{\lambda d}}\left(x^2+y^2\right)\right]\exp \left[i2\pi \left(x\nu +y\mu \right)\right]dxdy$$

(3)

A simplified formula for reconstructing the complex amplitude of the object wavefront is obtained and expressed through the reconstructed wavefront.

$$\Gamma (\nu ,\mu )={\displaystyle \frac{i}{\lambda d}}\exp \left({\displaystyle \frac{-i2\pi d}{\lambda }}\right)\exp \left[-i\pi \lambda d\left({\nu }^2+{\mu }^2\right)\right]\times {\Im }^{-1}\left\{E_R(x,y)h(x,y)\exp \left[-i{\displaystyle \frac{\pi }{\lambda d}}\left(x^2+y^2\right)\right]\right\}$$

(4)

where ${\Im }^{-1}$ is the inverse Fourier transform.

In the presented configuration of the holographic setup, both the object and the point source emitting a spherical wave are positioned within the same plane. Consequently, the spherical phase factor related to the Fresnel diffraction of the transmitted wave through the hologram is eliminated. This elimination is achieved through the utilization of a spherical reference wave, denoted as $E_R(x,y)$ possessing the identical average curvature as employed during the recording process, which can be expressed as follows:

$$E_R(x,y)=(const.)\exp \left(i{\displaystyle \frac{\pi }{\lambda d}}\left(x^2+y^2\right)\right)$$

(5)

By substituting $E_R(x,y)$ into Equation (4), we derive the formula for reconstructing the complex amplitude of the object wavefront, expressed as:

$$\Gamma (\nu ,\mu )={\displaystyle \frac{i}{\lambda d}}\exp \left({\displaystyle \frac{-i2\pi d}{\lambda }}\right)\exp \left[-i\pi \lambda d\left({\nu }^2+{\mu }^2\right)\right]{\Im }^{-1}\left\{h(x,y)\right\}$$

(6)

In Equation (6), inverse fast Fourier transform (IFFT) of only a single term, that is, recorded digital hologram is evaluated apart from some multiplicative constant. Thus, this method is simpler and faster as compared to other reconstruction methods such as Fresnel reconstruction and convolution method, in which a combination of several Fourier transforms and complex multiplications need to be evaluated.

For HI measurements, the phase can be calculated from the complex amplitude as:

$${\varphi }_1(\xi ,\eta )={\tan }^{-1}\left[{\displaystyle \frac{\mathrm{Im}[{\Gamma }_1(\xi ,\eta )]}{\mathrm{Re}[{\Gamma }_1(\xi ,\eta )]}}\right]$$

(7a)

$${\varphi }_2(\xi ,\eta )={\tan }^{-1}\left[{\displaystyle \frac{\mathrm{Im}[{\Gamma }_2(\xi ,\eta )]}{\mathrm{Re}[{\Gamma }_2(\xi ,\eta )]}}\right]$$

(7b)

where “Im” and “Re” represent the imaginary and real part of the reconstructed complex amplitude of the wave. The subscripts 1 and 2 indicate the undeformed and deformed states, respectively.

Considering that the calculation of (7a) and (7b) yields values in the range $[-\pi , \pi ],$ the wrapped interference phase map can be achieved by performing the following operation:

$$\Delta \varphi (\xi ,\eta )={\varphi }_2(\xi ,\eta )-{\varphi }_1(\xi ,\eta )$$

(8)

The subsequent unwrapping processes are generally needed to describe the actual object deformation or displacement with respect to its original state. The flowchart depicted in Figure 1 provides a visual representation of the sequential steps in the data processing and analysis procedure.

3. Experimental Setup and Discussion

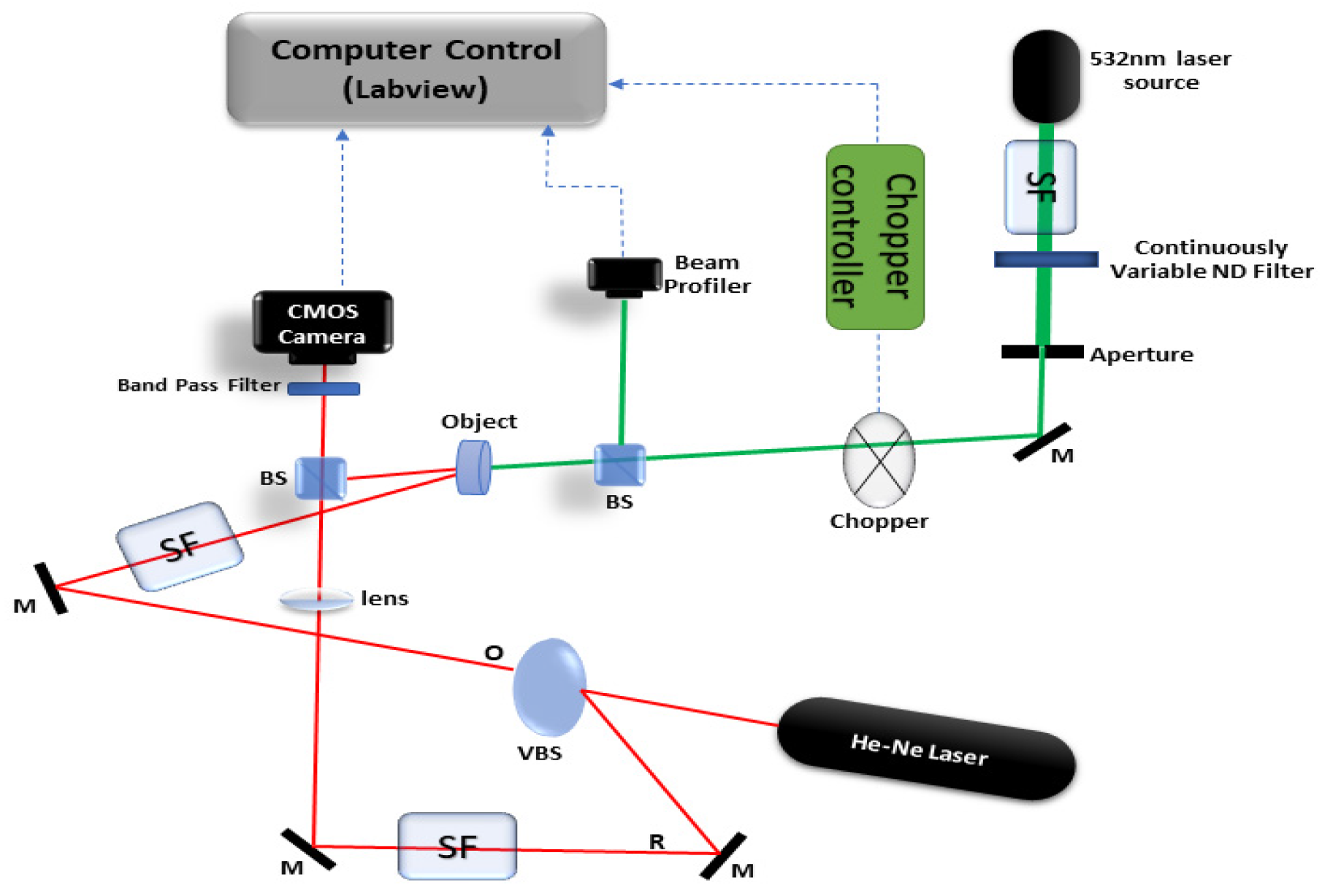
To analyse the deformation of a test object, we used a custom-built off-axis setup for digital holographic interferometry as shown in Figure 2. In this experimental setup, a coherent light source (LS) of wavelength 632.8 nm is used. A spatial filter (SP) is used in two arms to clean and expand the beam size to illuminate the full area of the object. The light from the beam expander is divided into two beams using a variable beamsplitter (VBS). The light wave that directly hits the camera is referred to as the reference wavefield. On the other hand, another light wave falls on the test object (OB), and the scattered wave from the morpho butterfly wing reaches the camera. This wave is referred to as the object wavefield (O). Mirrors (M) are used to steer the laser beams along the paths. The object is deformed using a green diode laser (532 nm) as the excitation laser as depicted in the schematic. Laser power values for excitation laser were in the range between 0.25 mw to 2 mw with a beam radius of about 2.5 mm. The interference between the scattered object wave and reference wave on the camera generates a hologram. The object is clamped between two aluminium rings with a diameter of 20 mm and a thickness of 2 mm. Corresponding to different deformation states, a series of holograms are recorded on the camera (Atlas10 20.4 MP Model) sequentially at 20 fps. The complex amplitude is obtained from a recorded hologram using a numerical reconstruction procedure as described before.

A selected part of the wing of a Morpho butterfly was cut with a laser and mounted around a circular ring as shown in Figure 3, with the non-iridescent side facing the excitation part. The wing itself is fragile and can easily be damaged during mechanical cutting. To overcome this issue, the samples were cut using a commercial CO₂ laser cutter without a protective air stream. The wing was cut to avoid veins which are stiffer than the membrane, and almost unresponsive due to a limited number of scales covering them. The diameter of the wing was about 25 mm and used as an object. Thanks to the large field of view of the designed system, the whole wing is adequately imaged. Since the wing exhibits a highly dispersive nature, we use an adjustable filter to channel more power onto the sample. This amplification enhances the quality of both the hologram and the subsequent reconstruction. In our DHI setup, we used a detector chip size of 17.5 mm, a resolution of 4504 × 4504 pixels, and a pixel size of 2.74 µm. The distance from the detector to the butterfly wing was 550 mm. The resolving power of our system, calculated with these parameters, is approximately 86.0 µm in both horizontal and vertical directions.

Numerical reconstruction is required to obtain the phase information of the object under study from each recorded experimental hologram. A small region in the recorded hologram, marked by red in Figure 3, was selected as a region of interest. The interference phase maps were obtained as the morpho butterfly wing was heated by the excitation laser at different powers. To calculate phase differences, which can be later related to micro-deformations of the object under study, a reference hologram of the object in a non-deformed state is reconstructed once, and then its phase is recovered. The pointwise $2\pi$-module subtraction between the phase information obtained from each hologram and the phase information recovered from the reference hologram yields the phase difference as shown in Figure 4.

4. Quantitative Measurement

In our research, we conducted a series of experiments and simulations to analyse and quantify the subtle deflections observed in a Morpho butterfly wing caused by the excitation laser. To achieve accurate measurements, we carefully arranged a holographic setup, ensuring that the object surface of the wing remained parallel to the image plane in its initial, undeformed state. This alignment allowed us to capture the wing’s deflection directly in the direction of the camera while we were inducing the excitation. Consequently, we were able to consider the deformation primarily as an out-of-plane displacement. We quantify the out-of-plane displacement, h of a Morpho butterfly wing when subjected to laser excitation:

$$h=\Delta \phi {\displaystyle \frac{\lambda }{4\pi }}$$

(9)

A phase variation of $2\pi$ corresponds to an out-of-plane deformation of $\lambda /2$.

The camera recorded off-axis digital holograms of the wing before, during and after the excitation process, at a frame rate of 20 fps. By subtracting the phase of the undeformed (reference) state from that of the deformed state, we obtained the wrapped phase differences of the wing at various time intervals. The laser excitation was applied for a duration of 150 milliseconds, followed by a period of 450 milliseconds without excitation.

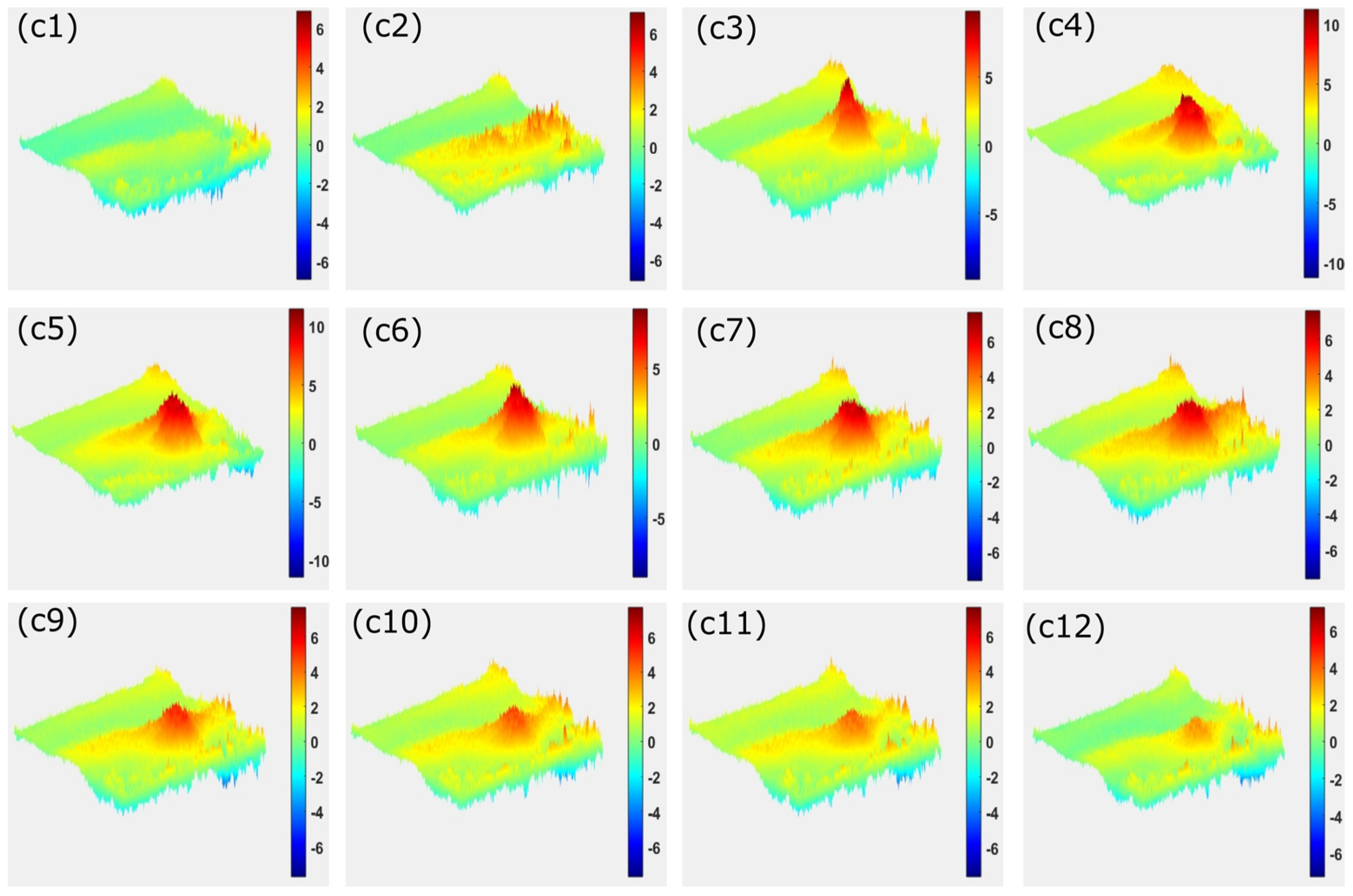
The interference phase maps depicted in Figure 4a–d were acquired for different laser excitation power on the wing. The phase jumps goes from −$\pi$ to $\pi$, Subsequent unwrapping procedures allowed us to derive the relative out-of-plane deformation of the wing. The interference phase maps in Figure 4 were obtained as the morpho wing was excited by an increasing intensity from 14.1 mW/cm² to 70.7 mW/cm². The rising density of fringes in Figure 4 indicates that the phase changes are increasingly related to the laser excitation intensity. Without the presence of excitation, no fringes were visible. Each fringe observed in the phase map corresponds to an out-of-plane deformation, equal to half the wavelength of the excitation laser light.

By employing Equation (9), we quantified the relative deflections, yielding values in the range of 1.50 µm to 2.90 µm for the maximum deflection amplitudes of the wing. We also recorded excitation laser power fluctuations with a power meter, showing a variation of approximately 10%, which has minimal impact on our experiment, making it negligible for the purposes of the study.

The average relaxation process observed in our study for the wing samples lasted approximately 350 milliseconds. This is distinctly evident in Figure 5, where recordings were made using a camera set at 20 frames per second, with a 150 ms exposure on the wing followed by a subsequent 450 ms off period.

To visualize the changes over time, we selected an excitation intensity (14.1 mW/cm²) and performed hologram reconstruction, Figure 5 shows the wrapped phase differences on the wing during excitation. In addition, the corresponding unwrapped phase maps are displayed in Figure 6. This visualisation allows us to observe the progression of the phase differences across the sample.

We would like to make a brief note that when using a low intensity of 7.0 mW/cm², we did not detect any fringes in the phase maps. This absence of fringes can be regarded as the method’s operational limit. We selected the laser power levels based on the butterfly wing’s response and the operational limits of our method. Experience shows that exceeding 70.7 mW/cm² could potentially damage the wing’s delicate microstructures, so we chose four different intensities to ensure reliable measurements while avoiding harm to the wing.

The amplitudes of the physical deflection were obtained from the unwrapped phase maps. We observed a linear deflection pattern with respect to the excitation power as shown in Figure 7.

As already mentioned, for the numerical simulations we took as inputs the phase values of the maximum out-of-plane deflections calculated from unwrapping the phase maps. The simulations proceeded in a rather simple way and were based on the determination of the phase value for each point of the object.

The method we introduce in this study has a broad range of applications for investigating minor deformations in sensitive objects. In this research, we deliberately selected a relatively complicated object for its unpredictable results. However, it is important to note that this method can be employed for analysing simpler objects. As the complexity of the object decrease, so does the challenge of analysing the collected data.

5. Conclusions

In conclusion, our analysis of small deflections using DHI reveals distinct advantages compared to the cantilever beam model. While the cantilever beam model is well-established for analysing deflections, especially in cases where material properties and deformation behaviours can be modelled mathematically, it primarily focuses on specific geometric configurations and often requires assumptions that may limit its applicability to complex or irregular structures. In contrast, our DHI-based method provides a more versatile approach, capable of analysing complex surfaces and capturing real-time data across a range of excitation conditions without the need for physical contact with the sample. Using our method, we effectively observed the deflection of a Morpho butterfly wing under laser excitation, capturing detailed phase-related information dynamically. This method enabled the generation of holograms that accurately imaged the wing’s displacement between its undeformed and deformed states, providing high-resolution measurements. Our approach demonstrates a high degree of versatility, making it suitable for analysing a wide range of samples, including different butterfly wings or similar artificial structures. While DHI has proven effective in capturing precise deflections, it is sensitive to environmental vibrations and requires careful setup to ensure accurate measurements. Additionally, the method’s resolution is limited by the optical setup, and while it works well for micrometer-scale deformations, it may not be suitable for analysing even finer nano-scale variations without further enhancements. The non-contact and optical nature of DHI allows it to capture phase information related to deformation independently of the specific sample material or geometry. While individual sample characteristics may affect measurement specifics, the fundamental ability of DHI to measure and analyse deformation remains consistent across various samples. This broad applicability shows the potential of DHI for use in diverse applications where precise, non-destructive measurement of deformation is required. This makes DHI particularly advantageous for studying delicate materials like the Morpho butterfly wing, where maintaining the sample’s integrity is critical. Integration of Artificial Intelligence (AI) in future studies could significantly enhance the speed and accuracy of interpreting complex data, as shown in [15] a new digital holographic technology that combines medical sensors and AI for visualization and depth perception of medical images, this can be beneficial in a wider range of materials, including synthetic and bio-inspired structures, to broaden the scope of the technique.