Refractive Index Evaluation in Active TDBC Layers for Photonics Applications

Abstract

Tetrachlorodiethyl Benzimidazo Carbocyanine (TDBC) layers are very interesting for photonics applications due to their huge oscillator strength, narrow absorption and low-cost fabrication. They are mainly used in strong coupling studies but also for wavelength selective grating fabrication, light concentration, absorption enhancement and so on. However, these intrinsic properties, particularly the refractive index, require further investigation. In this work, we first reviewed the values of the refractive index of TDBC layers reported in the literature. Using fitting with the Drude–Lorentz model, differences are highlighted. We then fabricated pure TDBC layers and measured their properties using ellipsometry and absorption spectroscopy. Finally, we also evaluated the refractive index as a function of the layer bleaching. This work shows that although the precise refractive index evaluation of pure TDBC layers is dependent on the measurement method, their oscillator strength force still remains very high without bleaching.

1. Introduction

Tetrachlorodiethyl Benzimidazo Carbocyanine (TDBC) is a cyanine dye within the polymethine class. TDBC dye layers typically form J-aggregates when the dye molecules pack closely together in a specific orientation, resulting in unique optical properties [1,2,3,4,5,6,7,8]. The strong absorption and fluorescence properties of TDBC J-aggregate enable a wide range of applications and techniques, such as fluorescence imaging, sensing [3,9], light concentration [10,11], strong coupling application [1,2,4,7,11,12,13], absorption enhancement [5,14], grating fabrication [15] and so on. Furthermore, TDBC layers are notable for their ability to be locally photo-bleached [15,16,17]. In optics, photo-bleaching is a photochemical alteration that permanently prevents a dye or a fluorophore molecule from fluorescing. For TDBC, photo-bleaching can induce significant changes in the refractive index with high contrast at the micro-scale, both spectrally and spatially [15,18]. However, intrinsic properties like the refractive index remain not fully understood, with variations reported in the literature [1,2,3,4,5,6,7].

In this work, we first present the main model used for the TDBC refractive index evaluation (i.e., the Drude–Lorentz model). We then review and fit the different reported values from the literature. Afterward, we measure the refractive index of pure TDBC layers deposited on SiO₂ by ellipsometry and absorption spectroscopy. Finally, we study the influence of photobleaching on the refractive index.

2. Refractive Index

2.1. Equations

The Equations below present the Drude–Lorentz model [7], which is commonly used to describe the refractive index of TDBC layers [1,2,3,4,5,6,7,8]. Note that a more sophisticated model was also reported [19]. The real and imaginary parts of the refractive index (n and k) can be derived from the dielectric constant ε presented in Equation (1), where E is the energy in eV, F_cv is what we will call the oscillator strength without unit, E_G is the energy of the HUMO-LUMO (Highest Occupied Molecular Orbital and Lowest Unoccupied Molecular Orbital) fundamental transition, ΔE is the absorption spectral width in eV and ${\epsilon }_{\infty }$ is the relative permittivity at infinite frequency without a unit.

$$\epsilon ={\epsilon }_{\infty }+F_{cv}·{\displaystyle \frac{{E_G}^2}{E_G^2-E^2-i.\mathsf{\Delta }E.E_G}}={\epsilon }_r+i.{\epsilon }_i={\left(n+i.k\right)}^2$$

(1)

$${\epsilon }_r=n^2-k^2 \mathrm{a}\mathrm{n}\mathrm{d} {\epsilon }_i=2nk$$

(2)

$$n=\sqrt{{\displaystyle \frac{\left|\epsilon \right|+{\epsilon }_r}{2}}}\mathrm{and}k=\sqrt{{\displaystyle \frac{\left|\epsilon \right|-{\epsilon }_r}{2}}}$$

(3)

The refractive index can be evaluated with two equivalent formalisms [19], using both the real and imaginary parts of the dielectric constant (ε_i and ε_r in Equation (2)) [5,6,7] or the n and k values [1,2,3,4] with usual Equation (3) when n >> k. To access the refractive index measurements, different experiments can be performed. For instance, using absorption measurement, the k value can be obtained (Equation (5)) for fitting F_cv, E_G and ΔE. A is the absorbance, λ is the wavelength, x is the layer thickness, I₀ is the optical intensity before the sample, and I after the sample.

$$\epsilon ={\epsilon }_{\infty }+{\displaystyle \frac{{E_G}^2.F_{cv}.({E_G}^2-E^2)}{{\left({E_G}^2-E^2\right)}^2+(\mathsf{\Delta }{E}^2.{E_G}^2)}}+i.{\displaystyle \frac{{E_G}^2.F_{cv}.(\mathsf{\Delta }E.E_G)}{{\left({E_G}^2-E^2\right)}^2+(\mathsf{\Delta }{E}^2.{E_G}^2)}}$$

(4)

$$A=Log{\displaystyle \frac{I_0}{I}} \mathrm{a}\mathrm{n}\mathrm{d} k={\displaystyle \frac{\lambda .\ln \left(10\right).A}{4\pi .x}}$$

(5)

2.2. Literature

To compare the different values used in the literature for the TDBC refractive index, we fitted the data reported in different articles [1,2,3,4,5,6,7] using WePlotDigitizer [20]. In Figure 1 are the extracted data using both the refractive index (top part of Figure 1) and dielectric constant (bottom part of Figure 1) formalisms. The extracted data are plotted with dots, and the corresponding fits with curves. We found a relatively good agreement between fit and data excepted for reference [3], which did not assume zero refractive index at around 2.2 eV [19] as pioneer work.

Table 1. Resume of the fitted parameter from the literature [1,2,3,4,5,6,7] and the methods used to make each sample.

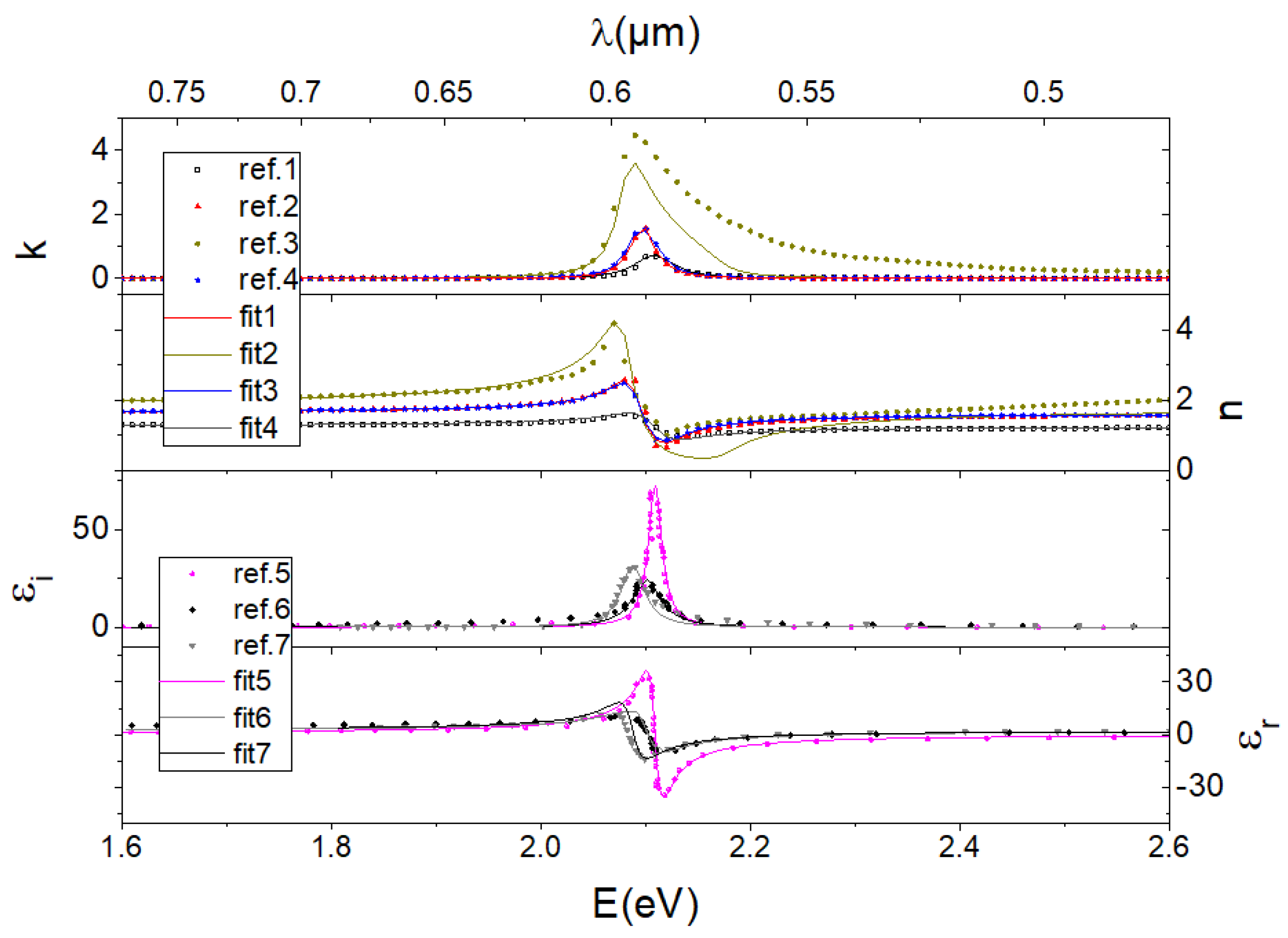
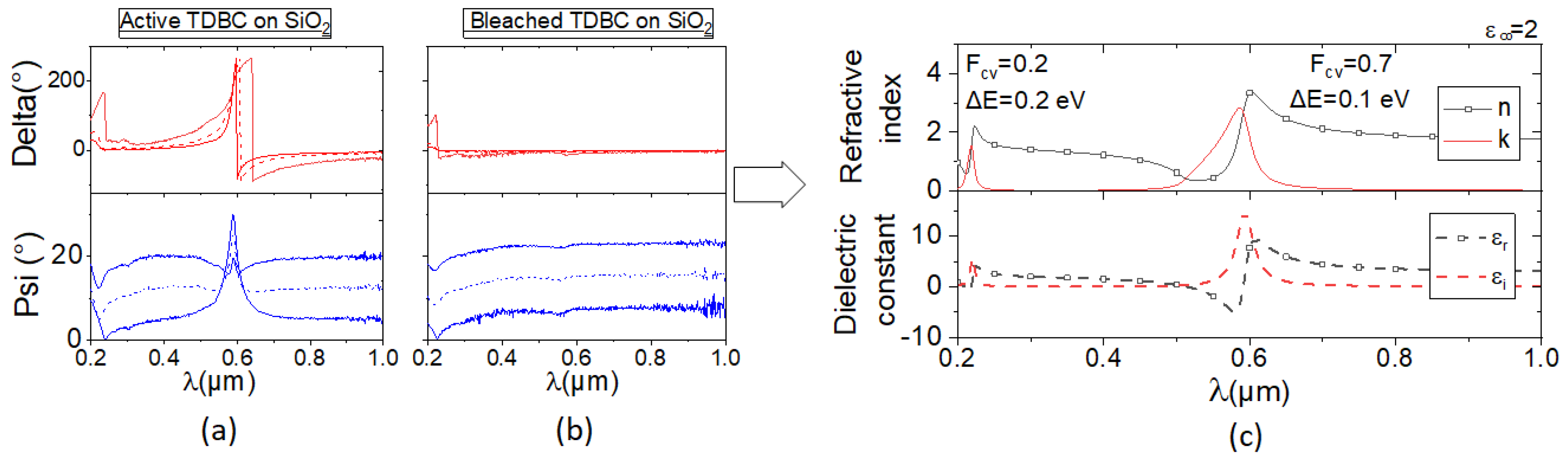
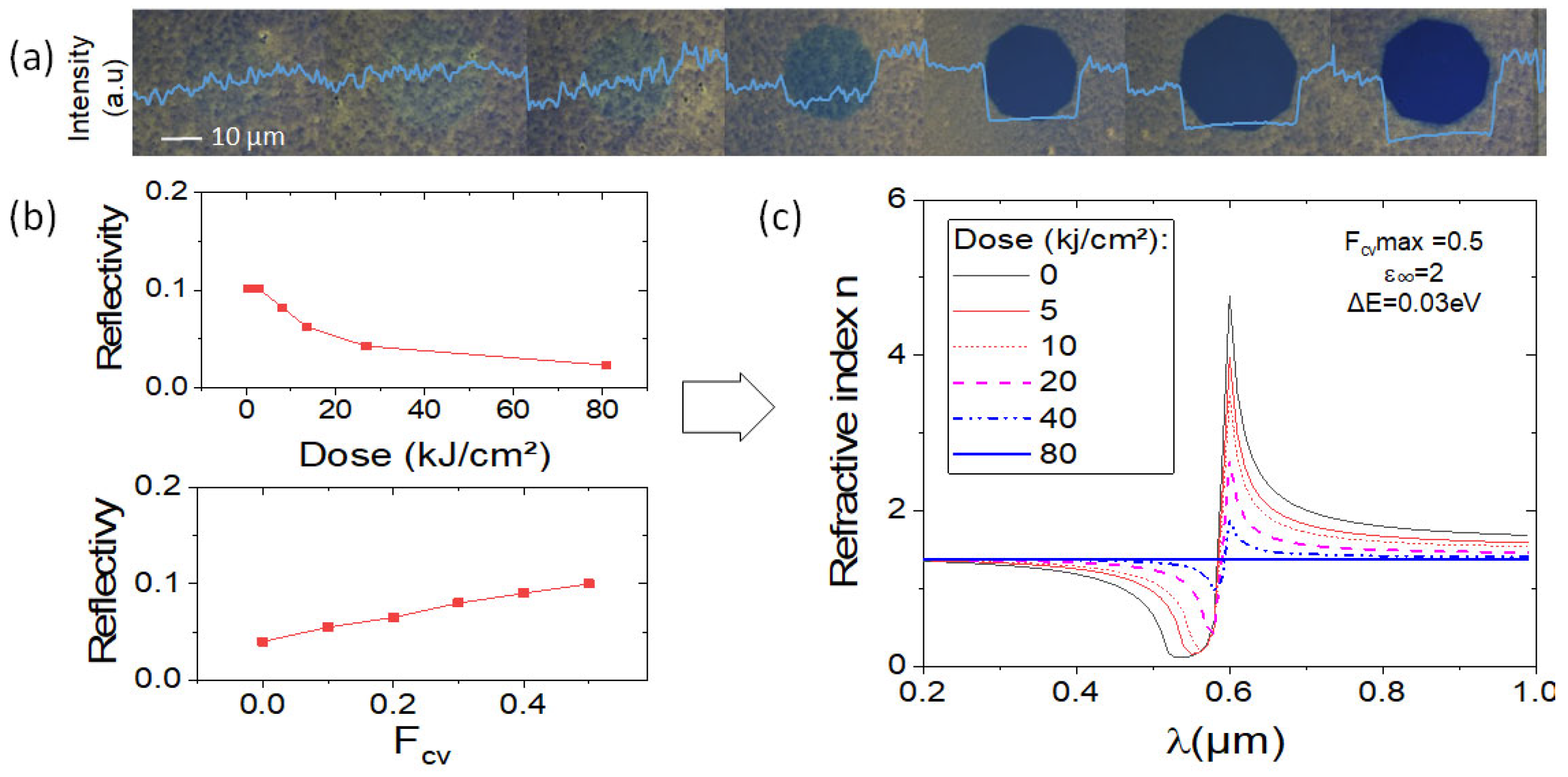
Article	Unit	[1]	[2]	[3]	[4]	[5]	[6]	[7]
${\epsilon }_{\infty }$		1.58	2.62	3.2	2.64	0.358	2.3	2.45
EG	eV	2.102	2.09	2.081	2.09	2.109	2.101	2.0878
Fcv		0.039	0.082	0.3	0.08	0.55	0.381	0.41
$∆$E	eV	0.041	0.025	0.026	0.027	0.016	0.033	0.027
Method		TDBC 0.5%/PVA 5%	TDBC doped PVA	TDBC	TDBC doped PVA	TDBC	TDBC	Theoretical [6]

contains ${\epsilon }_{\infty }$, F_cv, E_G and ΔE deduced from the fits calculated with the extracted data from these articles with Equations (1), (2) and (4). We observe variations in the reported values. A relatively good agreement is found for E_G and ΔE. However, F_CV values differ, likely due to the use of a PVA/TDBC mixture or differences in evaluation methods. Furthermore, different ${\epsilon }_{\infty }$ values are also observed but note that the fit uncertainty is high, especially when the data are plotted with the dielectric formalism [5,6,7] (i.e., using Equation (4)). Therefore, accurate measurements of the pure TDBC refractive are essential for a more detailed understanding of these interesting materials, as some differences remain in the literature.

3. Refractive Index Evaluation

3.1. Ellipsometry Measurements

The refractive index was determined in pure TDBC layer deposited on SiO₂ substrate (suprasil) by ellipsometry for active and bleached TDBC layers with similar fabrication steps indicated in [21]. The suprasil substrate was first immersed in a 2% PDAC (Poly-Diallyldimethyl-Ammonium-Chloride) solution for 5 min and rinsed 2 times for 5 min in deionized water. Prepared substrates were then dried with a usual blow gun. Then, TDBC layers were spin-coated at 2500 rpm using TDBC aqueous solution with 8.39 × 10⁻³ M concentration. Two samples were compared. The first one was kept in the dark to avoid any possible photo-bleaching for studying “active TDBC”, while the second one was exposed to light over several cm² using µPG101 365 nm continuous wave laser writer [15] for studying fully “bleached TDBC”. Refractive index measurements were performed in both samples with a J.A Woollam M-2000 spectroscopic Ellipsometer at different angles. Only 3 angles (60, 65 and 70°) were measured because it does not affect the fitting. The suprasil substrate was also measured separately, showing no signal change, which confirms that no confusion can occur with the studied layers; the measurements were solely due to the TDBC layers. In Figure 2 are the Psi and Delta parameters measured for active and bleached TDBC. Psi is the typical polarization change amplitude ratio and Delta is the phase difference, both accessed through the ellipsometry method. Fitting was computed with CompleteEASE (J.A Woolam) software with the Drude–Lorentz model incorporating two transitions [21].

First, we clearly see that the Psi and Delta measurements exhibit two main transitions at 590 and 220 nm, as expected [21]. The 590 nm energy corresponds to the HUMO-LOMO fundamental transition, which is well documented in the literature [1,2,3,4,5,6,7]. The 220 nm transition is identified as the second absorption transition of the molecule, detectable by ellipsometry due to its high oscillator strength. Such absorption bands have already been used for comparing Raman spectroscopy in active and bleached TDBC [21]. As expected, only the fundamental transition is removed by the bleaching, probably because the layers were bleached in the visible range, as studied in ref [21]. Figure 2c shows the extracted refractive index with the n and k formalism (Equation (1)) fitted with the ellipsometry data. We found an oscillator strength of around 0.7 for the 590 nm energy and 0.2 for the 220 nm transition. The oscillator strength of the fundamental transition is in good agreement with the literature for pure TDBC [3,5,6,7] (i.e., without PVA in Table 1). For the absorption spectral width (Table 1) ΔE, we found a larger value of 0.1 eV compared to the literature, probably due to the thickness variation evaluated at around 5 nm by the fit for a fixed thickness of 17 nm (as previously reported by Plasmon fitting [16]). Since the ellipsometry fitting is highly dependent on the thickness evaluation, it could be interesting to compare such results to other methods.

3.2. Absorption Measurements

Figure 3a shows the dispersive absorption measured in TDBC layers with different thicknesses. These layers were fabricated with the same recipe as described previously but with different spinning speeds at the last processing step, ranging from 1500 to 5000 rpm. As expected, the absorbance decreases with higher spinning speed according to the formation of thinner layers [22]. In order to evaluate the layer thickness, we assume a layer thickness at 17 nm (as previously reported by Plasmon fitting [16]) for the 2500 rpm speed. Thickness is indeed difficult to evaluate accurately since it is a soft material difficult to micro-pattern. Since the normalized absorption spectral width does not change between different speeds (bottom part of Figure 3a), we assume the same refractive index for all the layers. The other layers’ thicknesses were estimated by extrapolation based on the absorbance at 590 nm. The layer thickness as a function of the spinning speed showing a linear dependence is presented in Figure 3b. In Figure 3c is the calculated refractive index using both formalisms: n-k (Equations (2) and (3)) and ε (Equation (4)). These results show a better agreement with the literature compared to ellipsometry measurements, but the result remains highly sensitive to the thickness evaluation (Equation (5)), as presented in Figure 3b.

4. Bleaching Influence

Figure 4a presents different microstructures fabricated on SiO₂ with similar fabrication steps presented in Section 3.1, with different doses of insolation. For the insolation process, a Nikon microscope equipped with a white lamp focused on the layer with a 50x objective and a diaphragm were used with doses ranging from 0 to 80 kJ/cm². From such images, reflectivity was evaluated using grayscale extraction with ImageJ software. The average image intensities over 10 pixels in the center of each image are plotted in image 4a in blue color. By considering a theoretical averaged reflectivity R of 10% in the non-insolated part of the layer (calculated with Mathematica Wolfram software), R in the insolated region as a function of the dose (D) (used in Figure 4a) is plotted in Figure 4b. As previously reported, reflectivity decreases with the dose [15].

The theoretical R as a function of the oscillator strength F_cv is also plotted on the bottom panel of Figure 4b, as calculated with Mathematica Wolfram software. By combining R(D) and R(F_cv) in Figure 4b, we can conclude that the oscillator strength decreases with the dose reaching zero when the material is fully bleached. We have thus calculated the refractive index of the layer as a function of the dose (Figure 4c). Therefore, layer bleaching can significantly influence the refractive index evaluation since optical characterization can potentially bleach the layers.

5. Conclusions

In this work, we investigated the refractive index of TDBC layers by comparing the published data and our experimental results. Some discrepancies were first highlighted, especially when TDBC is mixed with PVA. We then measured the refractive index of the pure TDBC layer using ellipsometry. A very high oscillator strength is measured, as expected, though with an overestimated spectral width, probably due to the layer roughness. The absorption measurements were then performed for different layer thicknesses. Once again, we demonstrate a high oscillator strength but the exact values were highly dependent on layer thickness evaluation. Finally, local photo-bleaching was performed on the layer, showing that the oscillator strength evaluation can also be affected by the bleaching. Therefore, our work highlights that the precise refractive index evaluation can be strongly affected by both the measurement method and the fabrication process. Nevertheless, the pure active TDBC layers always exhibit a huge oscillator strength anyway, confirming their significant potential for photonics applications. Such work thus gives a better understanding of these promising layers and highlights the need for further investigations to accurately measure fundamental properties like the refractive index.