Research on High-Frequency PGC-EKF Demodulation Technology Based on EOM for Nonlinear Distortion Suppression
Abstract
1. Introduction
2. Principle of Demodulation Algorithm of PGC
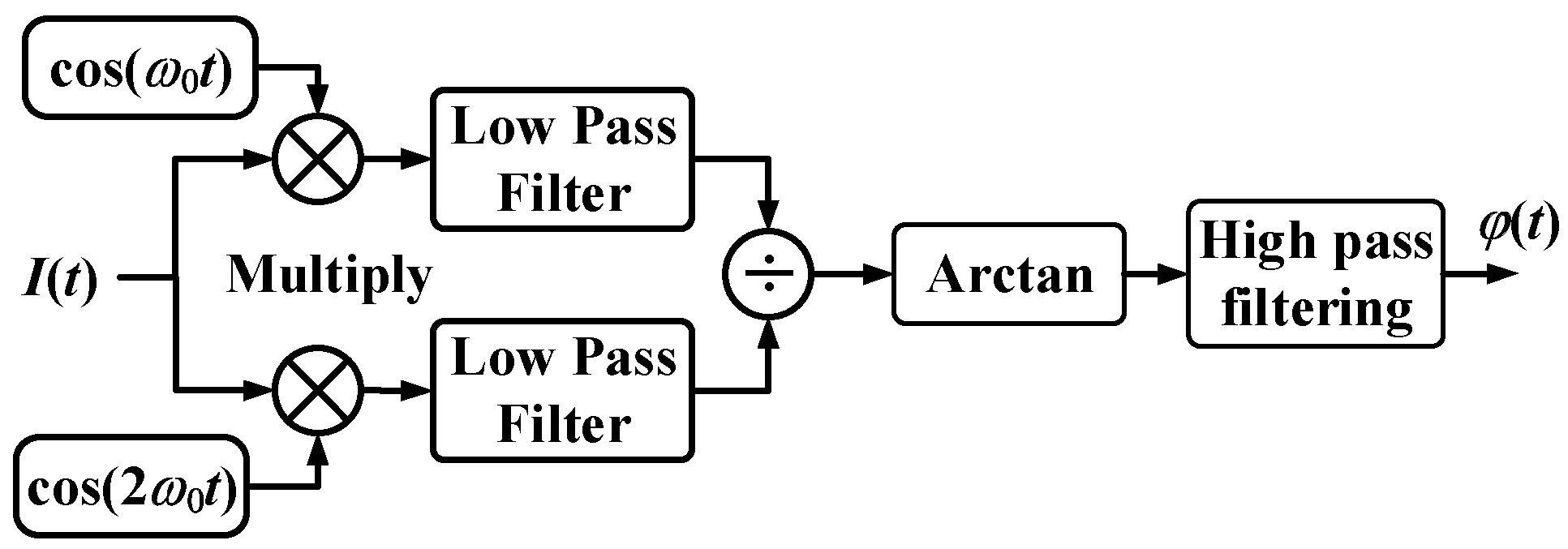
2.1. Principle of PGC-Arctan
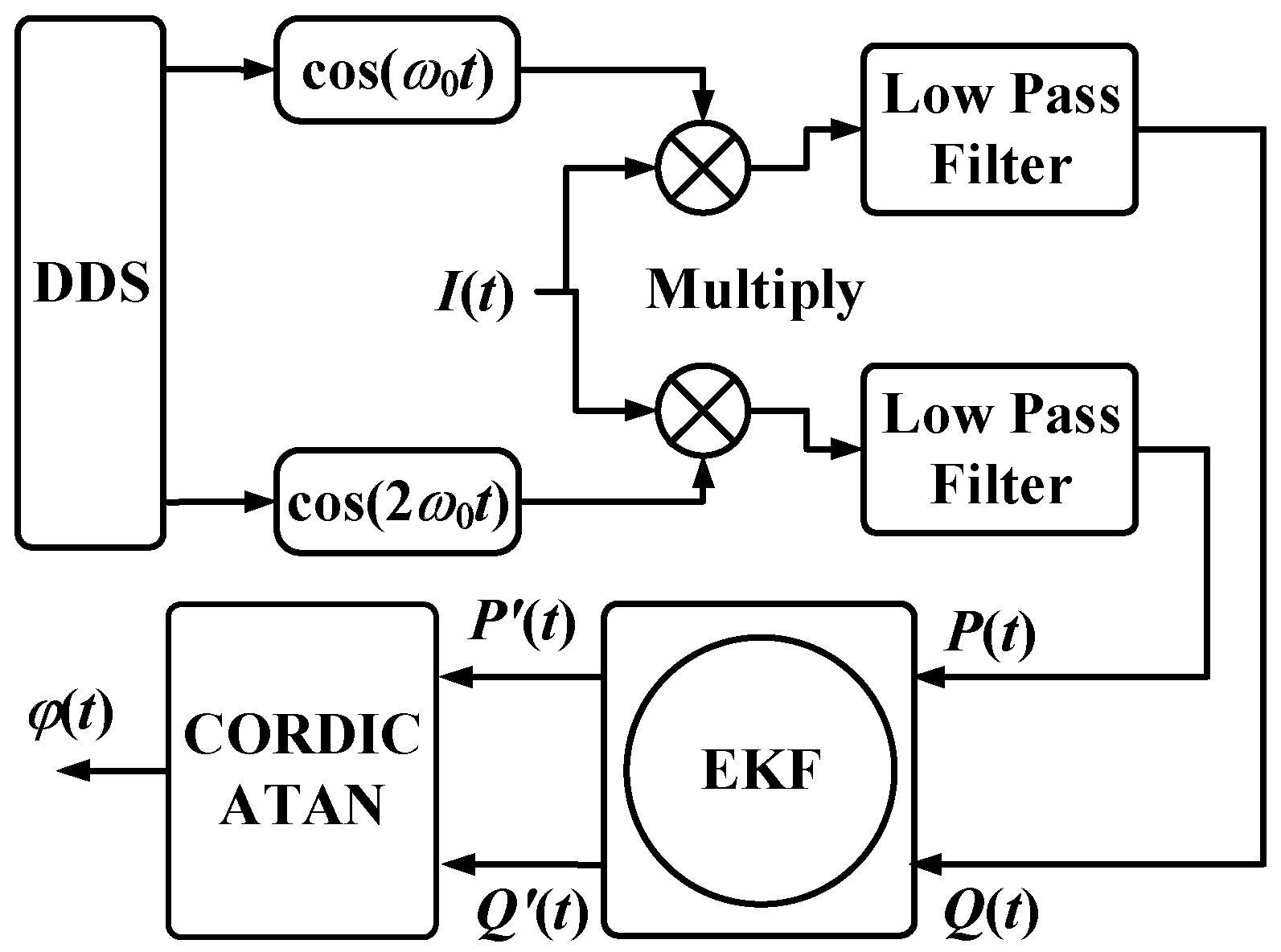
2.2. Principle of PGC-EKF
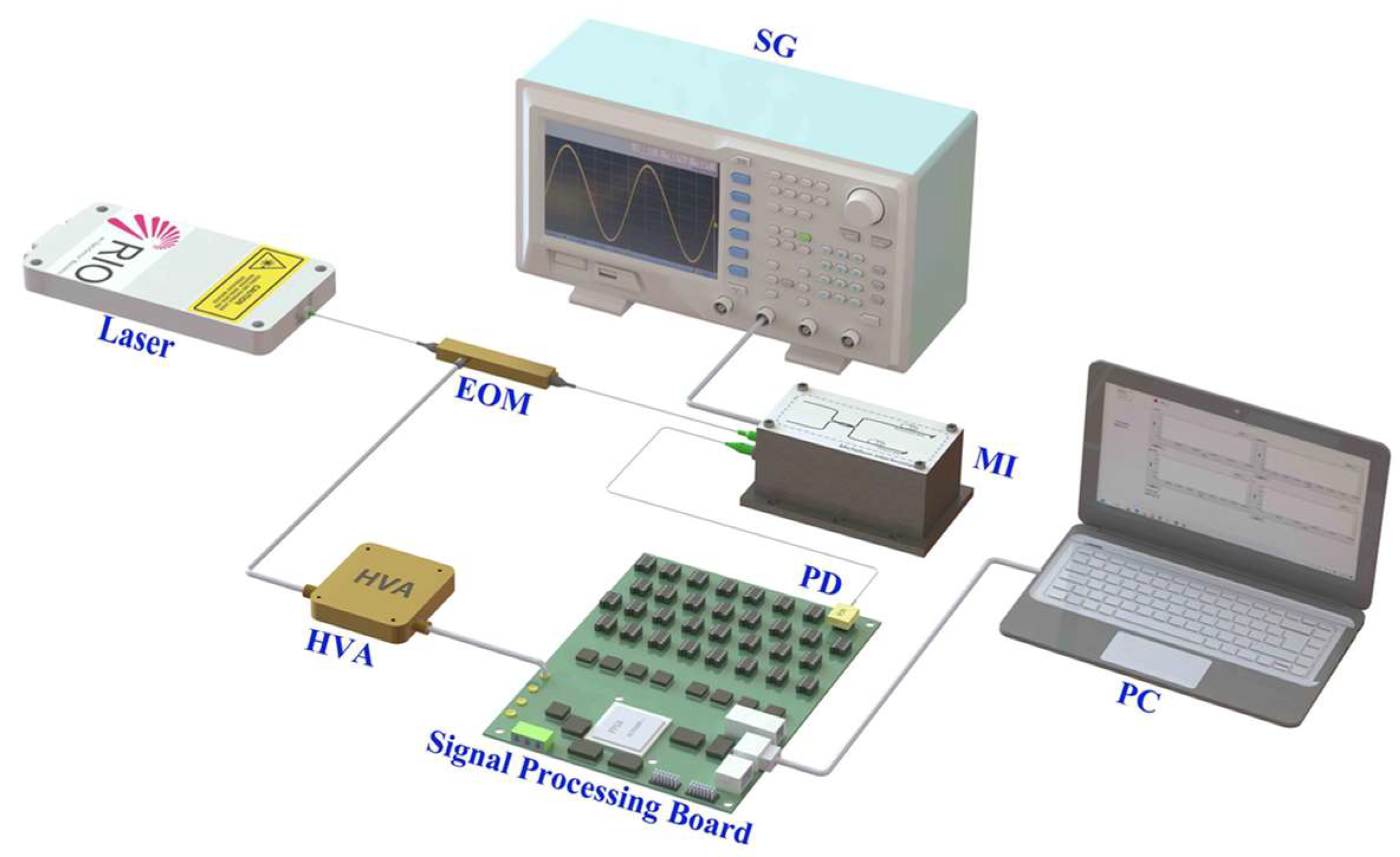
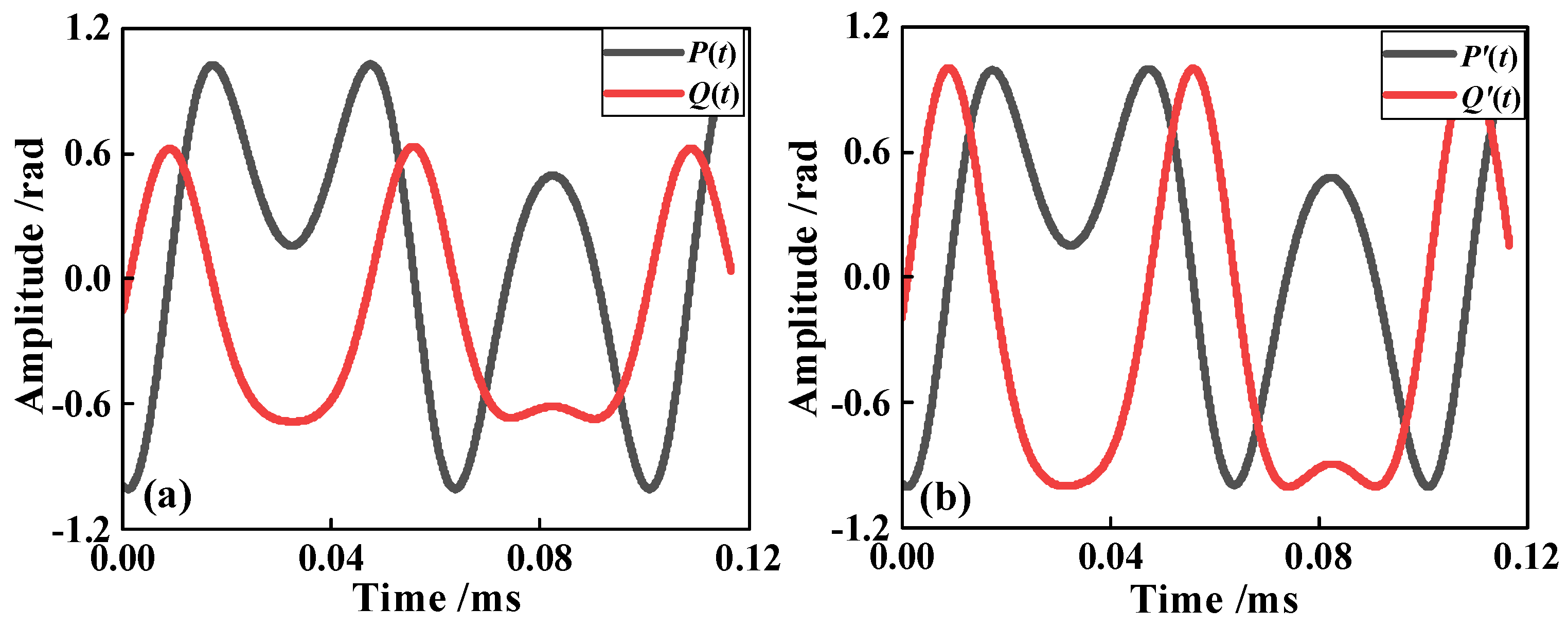
3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, J.; Li, D. Simulation and testing of a noise-limited demodulation system for a fiber-optic hydrophone system based on a Michelson interferometer. In Proceedings of the 2016 IEEE/OES China Ocean Acoustics (COA), Harbin, China, 9–11 January 2016; pp. 1–5. [Google Scholar]
- Wang, L.; Zhang, M.; Mao, X.; Liao, Y. The arctangent approach of digital pgc demodulation for optic interferometric sensors. In Interferometry XIII: Techniques and Analysis; SPIE: San Diego, CA, USA, 2006; Volume 6292, p. 62921E-10. [Google Scholar]
- Wang, T.; Cheng, Y.; Xu, C.; Li, H.; Cheng, J.; Peng, G.; Guo, Q. Spatial spectral characteristics of partial discharge with different electrode models. Photonics 2023, 10, 788. [Google Scholar] [CrossRef]
- Qiao, J.; Zhang, W.; Wang, Y.; Shao, Q.; Cai, J.; Zhao, H. Ultra-high SNR demodulation method for optical fiber sensors applied in power transformer partial discharge detection. Sensors 2022, 22, 2828. [Google Scholar] [CrossRef] [PubMed]
- Meng, Z.; Chen, W.; Wang, J.; Hu, X.; Chen, M.; Zhang, Y. Recent progress in fiber-optic hydrophones. Photonic Sens. 2021, 11, 109–122. [Google Scholar] [CrossRef]
- Kazimierski, W.; Zaniewicz, G. Determination of process noise for underwater target tracking with forward looking sonar. Remote Sens. 2021, 13, 1014. [Google Scholar] [CrossRef]
- Soman, R.; Wee, J.; Peters, K. Optical fiber sensors for ultrasonic structural health monitoring: A review. Sensors 2021, 21, 7345. [Google Scholar] [CrossRef]
- Li, H.; Li, D.; Xiong, C.; Si, W.; Fu, C.; Yuan, P.; Yu, Y. Low-Cost, High-Performance Fiber Optic Fabry–Perot Sensor for Ultrasonic Wave Detection. Sensors 2019, 19, 406. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, B.; Yan, L.; Xu, Z. Real-time normalization and nonlinearity evaluation methods of the PGC-arctan demodulation in an EOM-based sinusoidal phase modulating interferometer. Opt. Express 2018, 26, 605–616. [Google Scholar] [CrossRef]
- Hou, C.; Zhu, J.; Liu, B.; Shi, P.; Zhang, M.; Wang, H.; Luo, J.; Yu, B. Phase-shifted demodulation scheme for fiber-optic interferometric sensors with combined waveform phase modulation. Opt. Fiber Technol. 2023, 75, 103211. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, L.; Chen, B.; Xu, Z.; Xie, J. Real-time phase delay compensation of PGC demodulation in sinusoidal phase-modulation interferometer for nanometer displacement measurement. Opt. Express 2017, 25, 472–485. [Google Scholar] [CrossRef]
- Azmi, A.I.; Leung, I.; Chen, X.; Zhou, S.; Zhu, Q.; Gao, K.; Childs, P.; Peng, G. Fiber laser based hydrophone systems. Photonic Sens. 2011, 1, 210–221. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Tian, C.; Zhang, M.; Liao, Y. Analysis and optimization of the PGC method in all digital demodulation systems. J. Light. Technol. 2008, 26, 3225–3233. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, X.; Chang, J.; Zhou, H. Improved PGC demodulation algorithm for fiber optic interferometric sensors. Opt. Express 2024, 32, 2162–2178. [Google Scholar] [CrossRef]
- Gong, Y.; Yu, B.; Shi, J.; Guang, D.; Zhou, M.; Mu, S.; Fang, C.; Wu, X.; Zuo, C.; Li, S. Ameliorted algorithm for PGC to eliminate the influence of carrier phase delay with FFT. Opt. Fiber Technol. 2024, 82, 103554. [Google Scholar] [CrossRef]
- He, J.; Wang, L.; Li, F.; Liu, Y. An ameliorated phase generated carrier demodulation algorithm with low harmonic distortion and high stability. J. Light. Technol. 2010, 28, 3258–3265. [Google Scholar]
- Zhang, S.; Zhang, A.; Pan, H. Eliminating light intensity disturbance with reference compensation in interferometers. IEEE Photonics Technol. Lett. 2015, 27, 1888–1891. [Google Scholar] [CrossRef]
- Peng, F.; Hou, L.; Yang, J.; Yuan, Y.; Li, C.; Yan, D.; Yuan, L.; Zheng, H.; Chang, Z.; Ma, K.; et al. An improved fixed phased demodulation method combined with phase generated carrier (PGC) and ellipse fitting algorithm. In Proceedings of the 2015 International Conference on Optical Instruments and Technology: Optical Sensors and Application, Beijing, China, 8–10 May 2015; Volume 9620, p. 96200S. [Google Scholar]
- Wu, B.; Yuan, Y.; Yang, J.; Liang, S.; Yuan, L. Optimized phase generated carrier (PGC) demodulation algorithm insensitive to C value. In Proceedings of the Fifth Asia-Pacific Optical Sensors Conference, Jeju, Republic of Korea, 20–22 May 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9655, p. 96550C. [Google Scholar]
- Yu, Z.; Dai, H.; Zhang, M.; Zhang, J.; Liu, L.; Jin, X.; Luo, Y. High stability and low harmonic distortion PGC demodulation technique for interferometric optical fiber sensors. Opt. Laser Technol. 2019, 109, 8–13. [Google Scholar] [CrossRef]
- Volkov, A.V.; Plotnikov, M.Y.; Mekhrengin, M.V.; Miroshnichenko, G.P.; Aleynik, A.S. Phase modulation depth evaluation and correction technique for the PGC demodulation scheme in fiber-optic interferometric sensors. IEEE Sens. 2017, 17, 4143–4150. [Google Scholar] [CrossRef]
- Qu, Z.; Guo, S.; Hou, C.; Yang, J.; Yuan, L. Real-time self-calibration PGC-Arctan demodulation algorithm in fiber-optic interferometric sensors. Opt. Express 2019, 27, 23593–23609. [Google Scholar] [CrossRef] [PubMed]
- Hou, C.; Liu, G.; Guo, S.; Tian, S.; Yuan, Y. Large dynamic range and high sensitivity PGC demodulation technique for tri-component fiber optic seismometer. IEEE Access 2020, 8, 15085–15092. [Google Scholar] [CrossRef]
- Hou, C.; Zhang, J.; Yuan, Y.; Yang, J.; Yuan, L. Reliability demodulation algorithm design for phase generated carrier signal. IEEE Trans. Reliab. 2022, 71, 127–138. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, L.; Ge, Q.; Wu, X.; Yu, B. High precision and stabilization PGC demodulation scheme for fiber optic interferometric sensors. J. Light. Technol. 2023, 41, 6615–6620. [Google Scholar] [CrossRef]
- Jiang, Y.; Gu, S.; Zhang, G.; Ge, Q.; Xu, L.; Wu, X.; Yu, B. Highly robust PGC demodulation scheme for fiber optic interferometric sensors. IEEE Sens. J. 2023, 24, 1486–1493. [Google Scholar] [CrossRef]
- Xie, J.; Yan, L.; Chen, B.; Lou, Y. Extraction of carrier phase delay for nonlinear errors compensation of PGC demodulation in an SPM interferometer. J. Light. Technol. 2019, 37, 3422–3430. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Junaid Alvi, M.; Kim, H.J. Towards a smarter battery management system for electric vehicle applications: A critical review of lithium-lon battery state of charge estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- González-Cagigal, M.A.; Rosendo-Macías, J.A.; Gómez-Expósito, A. Estimation of equivalent model of photovoltaic array using unscented Kalman filters. J. Mod. Power Syst. Clean Energy 2024, 12, 819–827. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, B.; Liu, Y.; Chen, J. Application of adaptive EKF in real-time orbit determination. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 187. [Google Scholar] [CrossRef]
- Bogosyan, S.; Barut, M.; Gokasan, M. Sensorless-estimation of induction motors in wide speed range. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2007, 26, 1288–1303. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, W.; Meng, Z.; Sun, C. Phase noise characteristics of narrow-linewidth fiber laser and laser diode in unbalanced interferometers. Chin. Opt. Lett. 2013, 11, 021401. [Google Scholar] [CrossRef]
- Xiao, W.Z.; Cheng, J.; Zhang, D.W.; Kong, Y.; Ye, H.; He, J. High stability PGC demodulation technique for fiber-optic interferometric sensor. Opto-Electron. Eng. 2022, 49, 57–68. [Google Scholar]

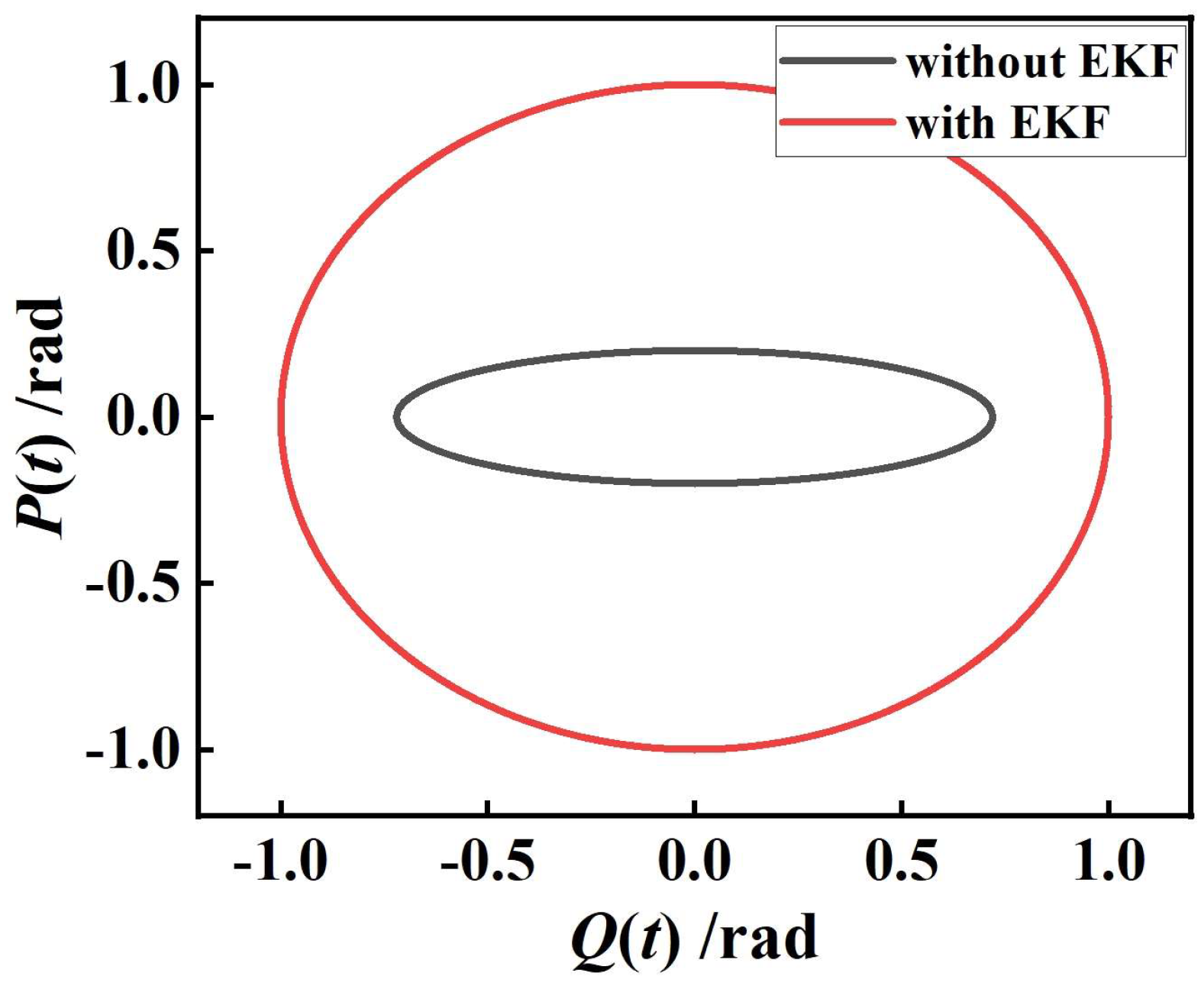
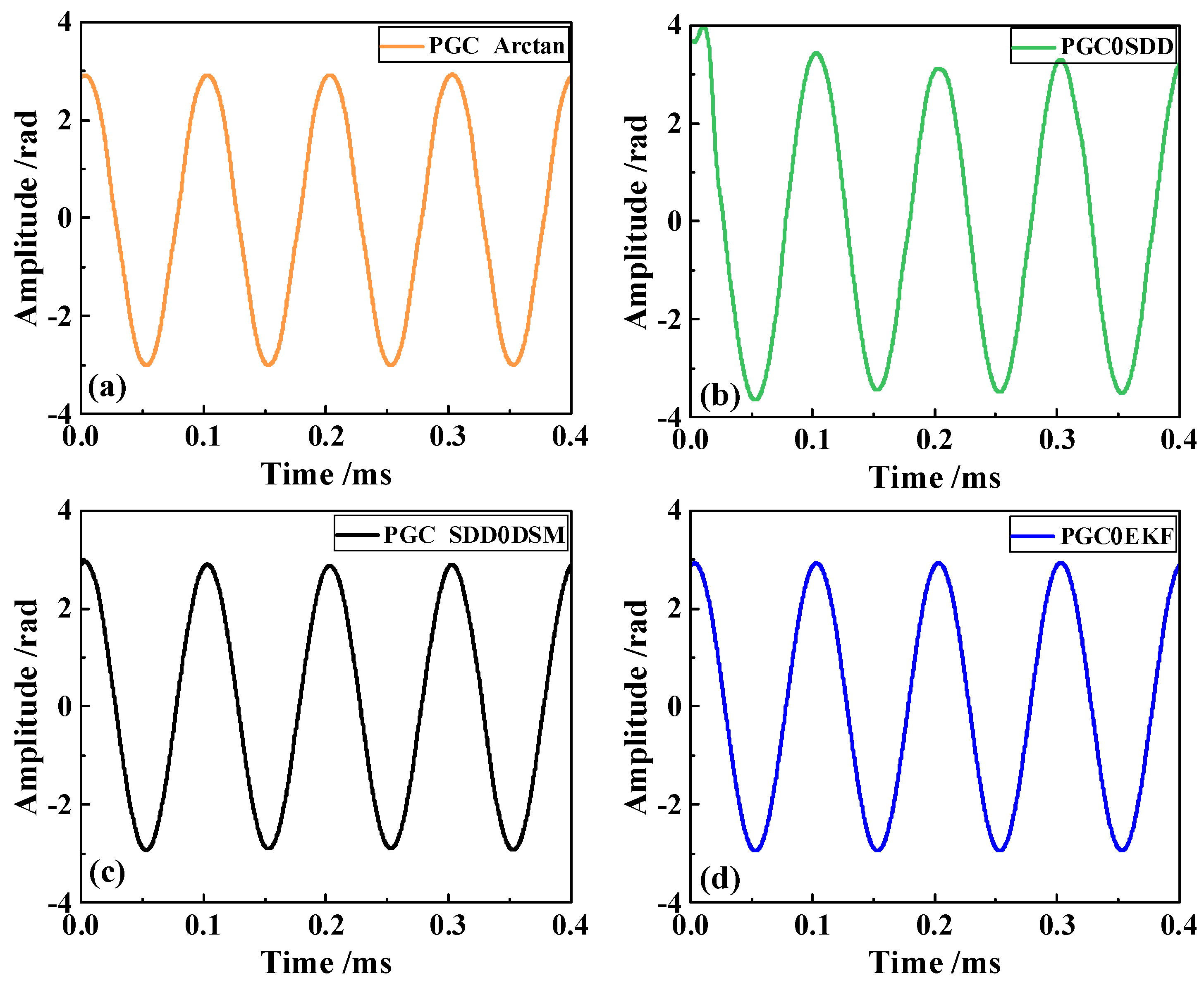
| C/rad | 1.5 | 2.0 | 2.5 | 2.63 | 3 |
|---|---|---|---|---|---|
| h | −7.85 × 104 | 8.69 × 102 | −2.32 × 104 | 3.81 × 104 | −4.47 × 104 |
| k | −1.53 × 105 | −4.64 × 104 | −2.72 × 105 | −1.92 × 105 | −1.71 × 105 |
| a | 5.58 × 107 | 5.79 × 107 | 5.14 × 107 | 5.04 × 107 | 3.82 × 107 |
| b | 2.40 × 107 | 3.59 × 107 | 4.57 × 107 | 4.82 × 107 | 5.29 × 107 |
| θ | −1.671 × 10−3 | 7.54 × 10−3 | −3.598 × 10−3 | −8.2 × 10−4 | 9.154 × 10−3 |
| h’ | −5.02 × 10−4 | −1.16 × 10−4 | 1.45 × 10−4 | −2.58 × 10−4 | 2.53 × 10−4 |
| k’ | −3.37 × 10−4 | −5.69 × 10−4 | −1.41 × 10−4 | −2.42 × 10−4 | 7.04 × 10−4 |
| a’ | 0.9895 | 1.003103 | 1.009126 | 1.000174 | 0.956017 |
| b’ | 0.9894 | 1.004748 | 1.008264 | 1.000287 | 0.955624 |
| θ’ | 1.701 × 10−3 | −1.97 × 10−4 | 8.08 × 10−4 | −7.3 × 10−4 | 1.983 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Li, Q.; Liang, J.; Shao, J.; Lu, Y.; Lin, Y.; Wang, T.; Li, X.; Zhao, Z.; Deng, C. Research on High-Frequency PGC-EKF Demodulation Technology Based on EOM for Nonlinear Distortion Suppression. Photonics 2024, 11, 801. https://doi.org/10.3390/photonics11090801
Wu P, Li Q, Liang J, Shao J, Lu Y, Lin Y, Wang T, Li X, Zhao Z, Deng C. Research on High-Frequency PGC-EKF Demodulation Technology Based on EOM for Nonlinear Distortion Suppression. Photonics. 2024; 11(9):801. https://doi.org/10.3390/photonics11090801
Chicago/Turabian StyleWu, Peng, Qun Li, Jiabi Liang, Jian Shao, Yuncai Lu, Yuandi Lin, Tonglei Wang, Xiaohan Li, Zongling Zhao, and Chuanlu Deng. 2024. "Research on High-Frequency PGC-EKF Demodulation Technology Based on EOM for Nonlinear Distortion Suppression" Photonics 11, no. 9: 801. https://doi.org/10.3390/photonics11090801
APA StyleWu, P., Li, Q., Liang, J., Shao, J., Lu, Y., Lin, Y., Wang, T., Li, X., Zhao, Z., & Deng, C. (2024). Research on High-Frequency PGC-EKF Demodulation Technology Based on EOM for Nonlinear Distortion Suppression. Photonics, 11(9), 801. https://doi.org/10.3390/photonics11090801





