1. Introduction
The world is three dimensional, but traditional imaging projects the 3D world into 2D images, which cannot easily reflect the real world because of the loss of depth information. Therefore, 3D measurement technology that can obtain the 3D coordinates of a measured surface is highly valued and developing rapidly [
1,
2,
3]. The structured light depth imager (SLDI) represents 3D visual measurement technology and obtains the surface 3D information in the form of a graphic or image, and it has the advantages of quickness, automation, non-contact, and high efficiency. Thus, it has been widely used in many production and life fields such as manufacturing, medical industry, entertainment industry, etc. [
4,
5,
6].
At the same time, structured light depth imaging technology has attracted much attention from the precision manufacturing industry because of its full field, high efficiency, high precision, and the ability to detect complex structural components. The quality and accuracy of precision workpieces depend to a large extent on the form, position, and dimensional tolerance of parts. However, traditional measurements cannot meet the requirements because of low efficiency. Therefore, SLDI has become an efficient detection tool due to its excellent performances. The quality of precision products is directly determined by the quality of precision molds, and the mold mechanism required by products has become more and more complex and precise, making it difficult for traditional inspection methods to meet new demands. Therefore, structured light depth imaging technology provides a powerful means to meet new demands. In the face of the continuous emergence of large-size and/or small-size complex precision workpieces, the traditional detection methods often face the issue that it is difficult or even impossible to measure. Structured light depth imaging technology can have efficient enough detection to solve this issue. Precision manufacturing products are being developed, from spot inspection to full-size inspection or full-batch inspection, and structured light depth imaging technology provides an effective method that is significantly different from traditional testing methods. Moreover, structured light depth imaging technology plays an important role in the forward and reverse design of precision products, digitization, and intelligence of precision manufacturing enterprises.
Greater requirements are put forward for the structured light depth imaging technology, which is prominently reflected in reducing the depth measurement error to meet the needs of precision manufacturing. The work of the depth imager includes two processes in principle, obtaining the phase through the fringe image and calculating the depth value according to the imaging model. Therefore, the depth error is caused by the phase measurement error and structure parameter error. Among them, the phase error is affected by many factors, such as the geometric and physical characteristics of the measured surface. The depth measurement error is also comprehensively affected by these factors, and its influence law is complex and difficult to determine. In order to avoid this problem, the existing depth imagers use the projective geometric model for imaging, and accurate imaging is achieved by adjusting the parameters of the projective geometric model [
7,
8]. However, each of the many projective geometric parameters is difficult to adjust due to the comprehensive influence of the structural parameter error and phase measurement error at the same time, which limits the depth measurement accuracy of the depth imager. There is still a certain gap in the requirements of precision measurement, and there are difficulties in it being widely used in the precision manufacturing industry [
9,
10,
11]. According to the working principle of SLDI, the depth image is obtained by the analytical imaging model. Therefore, the depth measurement error of the analytical imaging model caused by the structural parameter error and phase measurement error should be analyzed. The depth measurement error could be reduced by adjusting the structural parameters and phase measurement value, respectively, which is expected to be an effective way to improve the depth measurement accuracy of SLDI. Because the analytical imaging model of SLDI can directly express the influence of each structural parameter error on the depth measurement error, the structural parameters are expected to be adjusted more accurately. However, the obstacle lies in the complexity and coupling of the influence law of each structural parameter error on the depth error. The published works for reducing the measurement error caused by the assembly of the imager mainly focus on the analysis and compensation of the measurement error caused by the unsatisfactory device parameters in the imager [
12,
13,
14]. However, for the depth measurement error caused by structural parameters, the existing research results either stop at the optimal selection of structural parameters [
15,
16,
17] or stay at the level of qualitative error analysis [
18,
19]. It is rarely involved in using the analytical model and correcting structural parameters to reduce the error of depth measurement.
A structural parameter correction method of SLDI is proposed to reduce the depth measurement error caused by the structural parameter error (DMECSPE). Aiming at three structural parameters, an analytical imaging model and a model of the DMECSPE are established. The analytical imaging model quantitatively expresses the influence of structural parameters on the depth measurement value; the decoupling of the structural parameter error in the model of depth measurement error was achieved, and the depth error was found to be at a maximum at the maximal depth. Only one depth imaging of the standard plane is carried out at the maximum depth position, and the structural parameter correction is realized based on the analysis and processing of the experimental data of the depth measurement error. Moreover, the corrected analytical imaging model of SLDI is obtained, and the DMECSPE can be effectively reduced. The simulation results show that the proposed method is effective, and the actual measurement results show that the proposed method has a good depth imaging effect.
This paper is organized as follows:
Section 2 establishes an analytical imaging model of the SLDI;
Section 3 establishes a model of the DMECSPE and puts forward the correction method of structural parameters;
Section 4 carries out experiments and provides the experimental results;
Section 5 discusses the experimental results;
Section 6 summarizes the research work.
2. Analytical Imaging Model
The SLDI mainly consists of a pattern projector, a camera, and a computer [
20]. The coded patterns generated by the computer are projected onto the surface to be measured by the pattern projector. The camera acquires the surface images and then sends them to the computer for processing and decoding. Based on the decoding results, the computer calculates the 3D coordinate values
x,
y, and
z of the surface in the world coordinate system via trigonometry.
The spatial position of the camera in the SLDI is shown in
Figure 1. The point
is the surface point to be measured in the world coordinate system
, the point
is an image point of point
mapped to the imaging plane
in the imaging coordinate system
, and the coordinate plane
is coplanar with the coordinate plane
; the point
and the point
are the lens centers of the pattern projector and the camera, and
; the point
and point
are the projection points on the coordinate plane
and the coordinate plane
of the point
; the point
is the projection point on the coordinate plane
of the point
;
is the focal length of the camera lens, and
; the point
and the point
are the projection points on the axis
and the axis
of the image point
.
According to
Figure 1 and based on the triangulation method and the pinhole model, the analytical imaging model of the SLDI is derived as follows:
where
,
, and
are the structural parameters in this paper, they are the constant in the SLDI, and their errors lead to the measurement error of the SLDI;
and
are the pixel numbers of the camera image, which are directly read from the image during the imaging process; the coordinate of the origin
of the imaging coordinate system in the image coordinate system is
;
is pixel width along direction
;
and
are pixel counts, respectively, along directions
and
; the projection angle
is an unknown parameter, which needs to be obtained by coding and decoding images in the SLDI [
20]. It should be pointed out that there is no parameter
in the analytical imaging model, and Equation (1) can be established regardless of whether there is the symbol
on the left side of that. The left side of Equation (1) contains the symbol
, which can directly express the meaning for a single pixel. This is convenient for the following theoretical analysis and mathematical expression in experimental data processing.
3. Depth Error Model and Structural Parameter Correction
Firstly, the model of the DMECSPE is established. In the SLDI, the design values and the truth values of structural parameters are denoted as
,
, and
and
,
, and
. As a result, there are the structural parameter errors of
,
, and
. According to the analytical imaging model, the depth truth value
is obtained using the truth values of the structural parameters, while the depth measurement value
using the known design values because the truth values of the structural parameters are unknown. As a result, there is the depth measurement error
, which can be written as follows:
According to the analytical imaging model, the higher order terms of
can be ignored if
, and
can be described as follows:
Equation (3) is the model of the DMECSPE, where
It can be seen that the parameters , , , , and are constant, and increases as increases.
Next, the measurement error correction is discussed. The maximum depth to be measured is denoted as
, whose error is denoted as
, and according to Equations (3) and (4), we obtain
Then, the following method for correcting structural parameters is proposed.
Step 1: The standard reference plane is used as the surface to be measured and placed at , the depth true value of the plane is obtained through control or measurement, and the SLDI images the plane.
Step 2: The depth measurement value is calculated from Equation (1) when , , and are replaced with , , and ; , , and are additional errors of the structural parameters; , , and are designed constants and , , and ; .
Step 3: The depth measurement error
is calculated when there are additional errors of the structural parameters, and then its average value along the
direction is calculated as follows:
Step 4: Choose on one side of the camera imaging plane and on the other side, and calculate and from Equation (6).
Step 5: Let ; is obtained by linear fitting of data pairs according to using least squares regression analysis.
Step 6: Let ; and are obtained by linear fitting of data pairs and according to and using least squares regression analysis.
Step 7: Let ; and are obtained by linear fitting of data pairs and according to and using least squares regression analysis.
Step 8: Let
; the depth measurement value
without additional errors of the structure parameters is obtained; after that, calculate its average value along the
direction as follows:
and then calculate the average value of the depth measurement error without additional errors of the structure parameters from
.
Step 9: Substitute
and
, respectively, into the left and right sides of Equation (3) to form a linear system of
N equations as follows:
where
,
,
,
,
,
, and
are known quantities;
,
, and
are unknown quantities to be derived. Equation (8) is solved, and its least square solutions are denoted as
,
, and
.
Step 10: In Equation (1),
,
, and
are replaced with
,
, and
. This corrects the structural parameters, and then gives the corrected analytical imaging model and the corrected depth measurement value
as follows:
4. Experiment and Its Results
We used 3D Max and assembled a simulated SLDI to quantitatively verify the performance of our proposed method. Considering the existing commercially available devices, set
,
,
mm,
mm,
mm,
,
ranging from
to
, the depth to be measured ranging from 1000.0000 mm to 1365.0000 mm, and
. In a single imaging, the projector projected two sets with different frequencies of 10-step phase-shift cosine fringe patterns and 8-bit gray code stripe patterns; these fringe patterns were processed, and the wrapped phase, the absolute phase, and projection angle
were drawn successively [
20]; the depth measurement value was obtained from Equation (1).
In our quantitative simulation experiment, set mm, mm, , , , mm, mm, , , and mm. The experimental process and results were as follows.
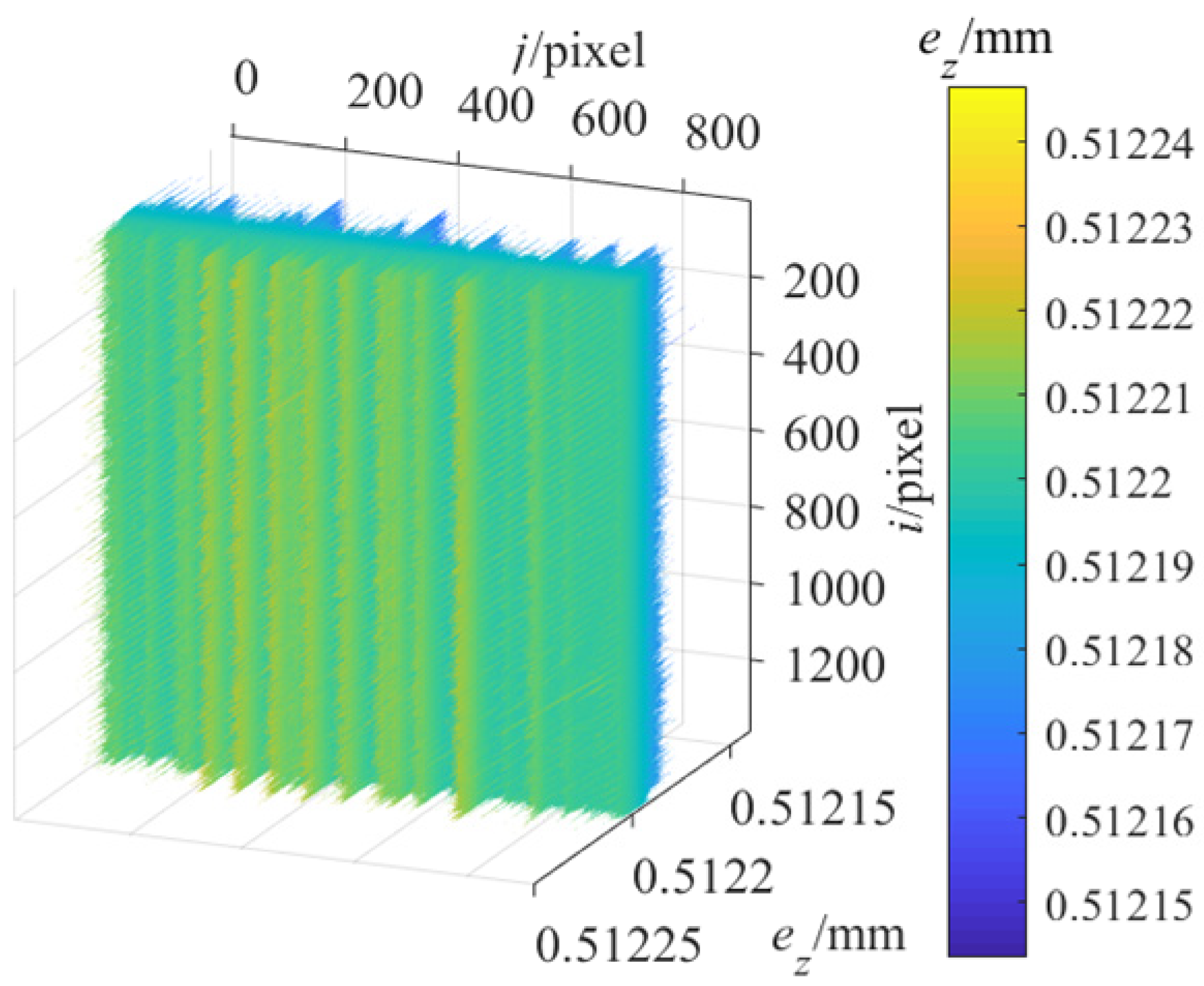
Performed steps 1 to 7. Let
, and
is shown in
Figure 2 where
,
, and
, respectively, stands for
,
, and
; obviously, the spatial distribution deviation of
is less than 1.0 × 10
−4 mm and can be negligible; then,
can be approximated as unchanged with
;
at
is tabulated in
Table 1,
was obtained by linear fitting of the experimental data in
Table 1 using least squares regression analysis.
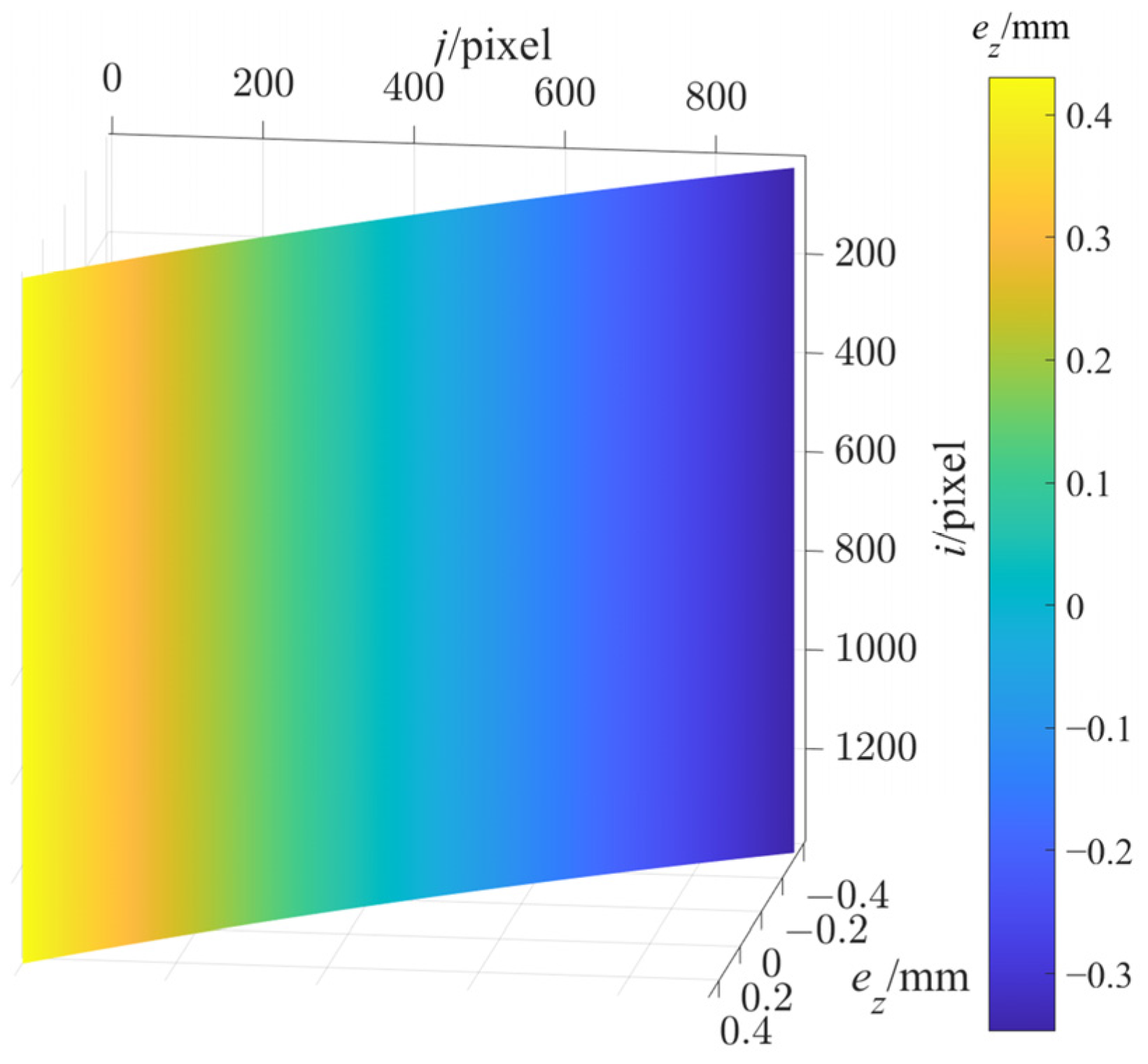
Let
, and
is shown in
Figure 3;
at
and
are tabulated in
Table 2. Let
, and
is shown in
Figure 4;
at
and
are tabulated in
Table 3. According to
Figure 3 and
Figure 4,
are independent of
, monotonically decrease with
, and can be approximated as linear.
,
,
, and
were obtained via linear fitting of the experimental data in
Table 2 and
Table 3 using least squares regression analysis, respectively.
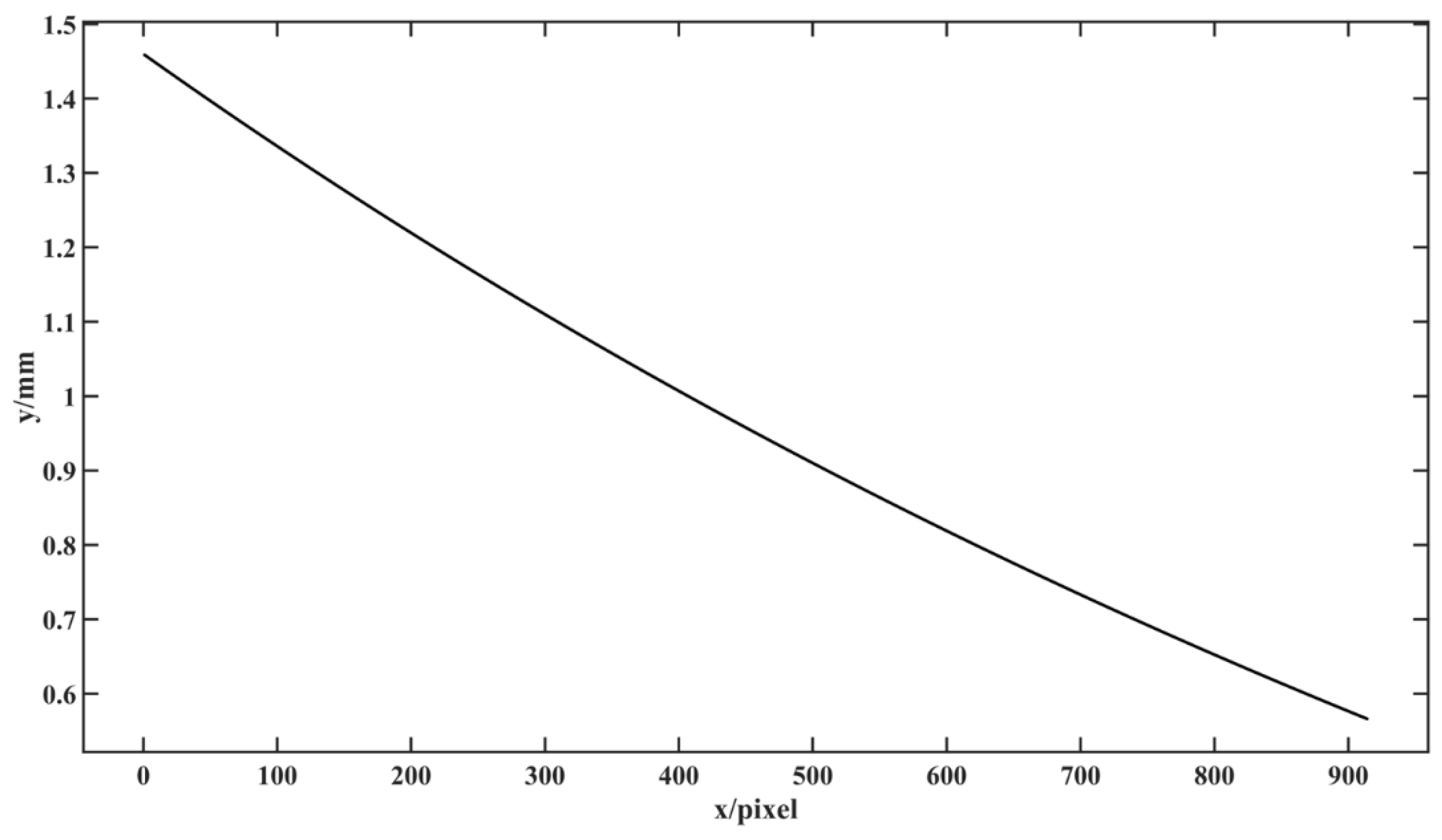
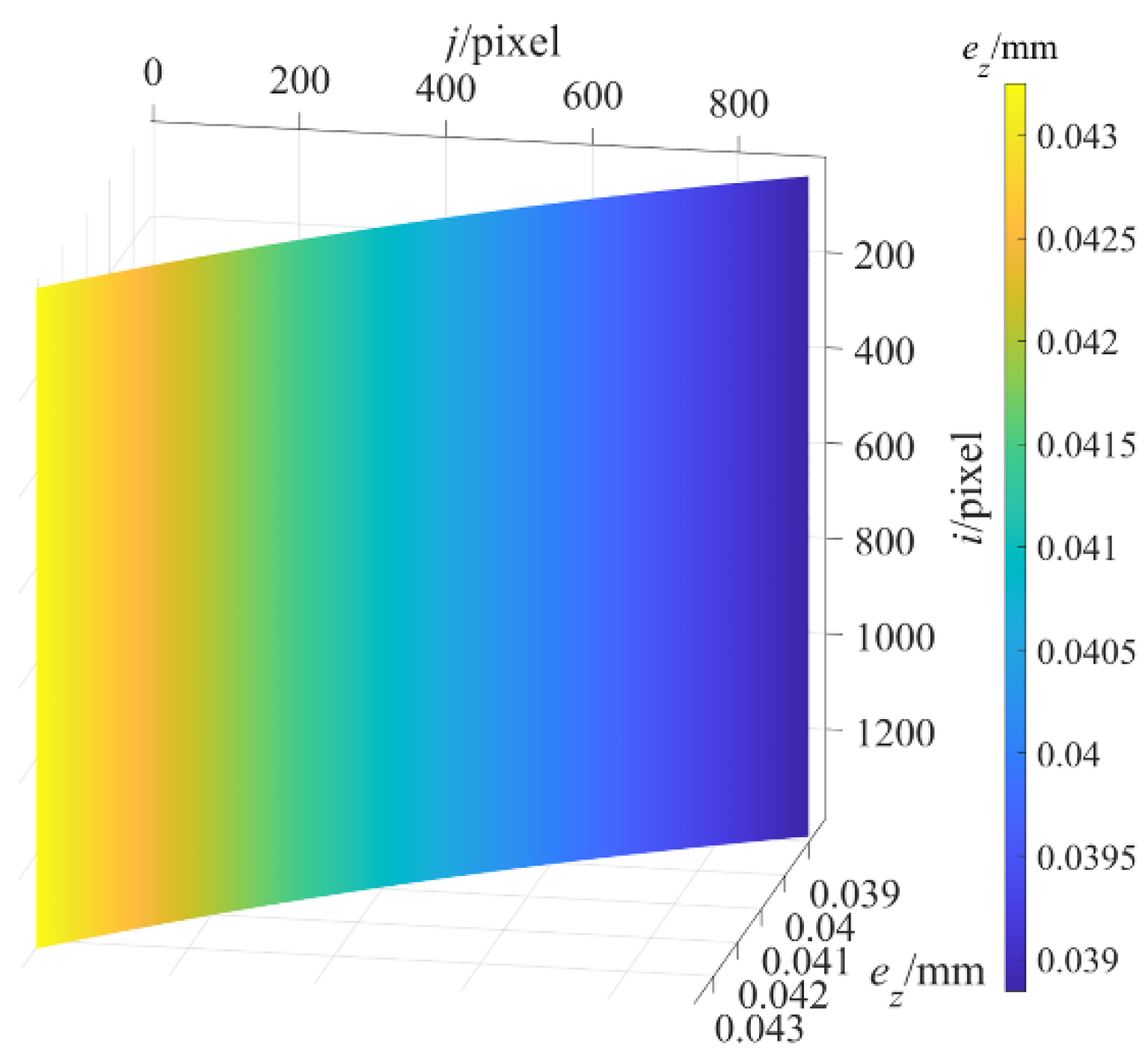
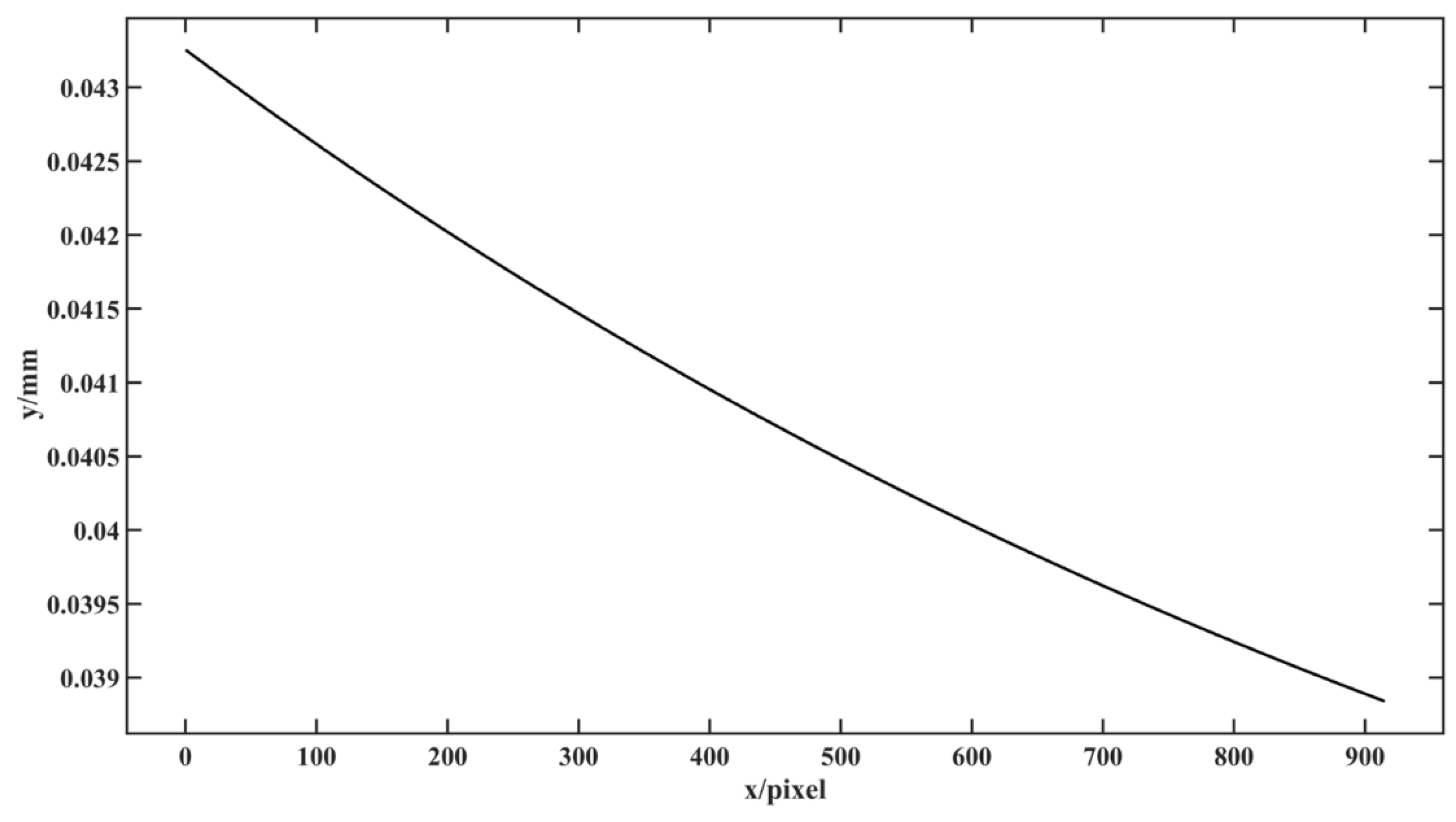
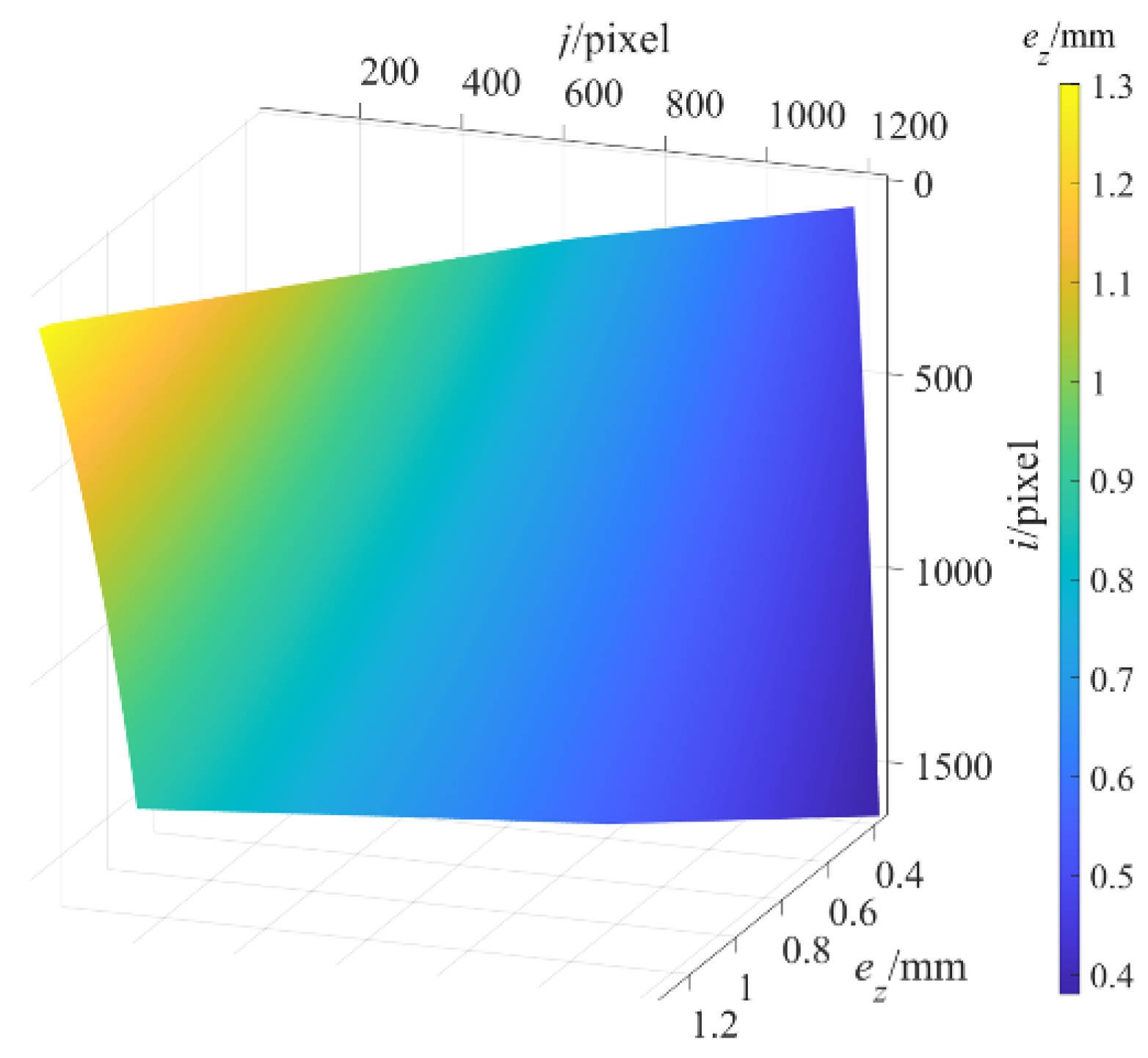
Performed Step 8. The depth measurement error image of the standard plane at the maximum measured depth of 1365.0000 mm before structural parameter correction is obtained as shown in
Figure 5, and further
at
are displayed as the black curve in
Figure 6, where y and x represent
and
, respectively, and then the maximum value of
is 1.4586 mm. Therefore, the depth measurement error
mm before structural parameter correction.
Performed Step 9. The result was that mm, mm, and .
Performed Step 10. The structural parameters were corrected, and then the analytical imaging model and the depth measurement value were obtained after structural parameter correction.
Continued data processing for
to verify the performance our proposed method. The experimental data processing of
followed exactly the same experimental data processing of
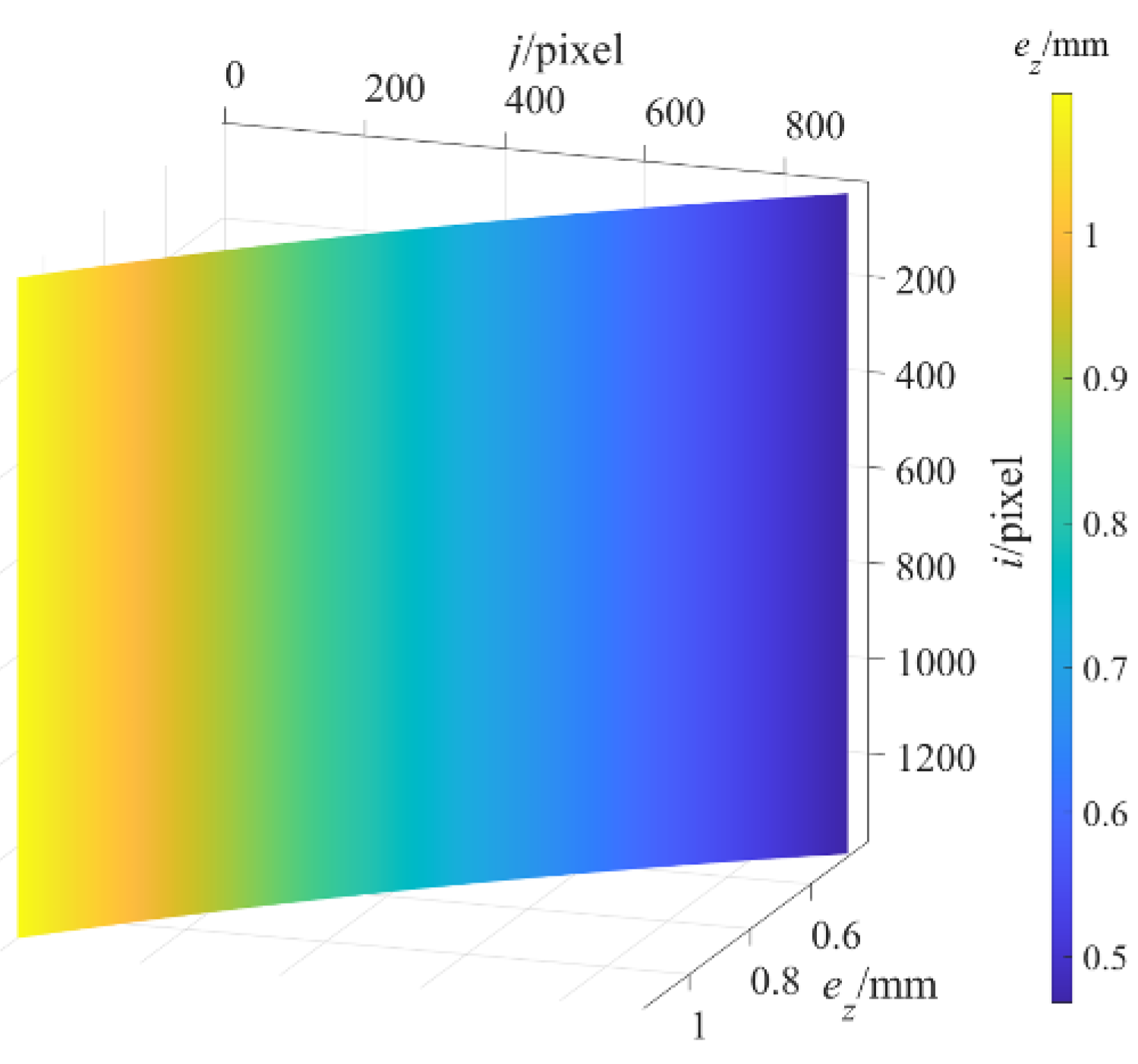
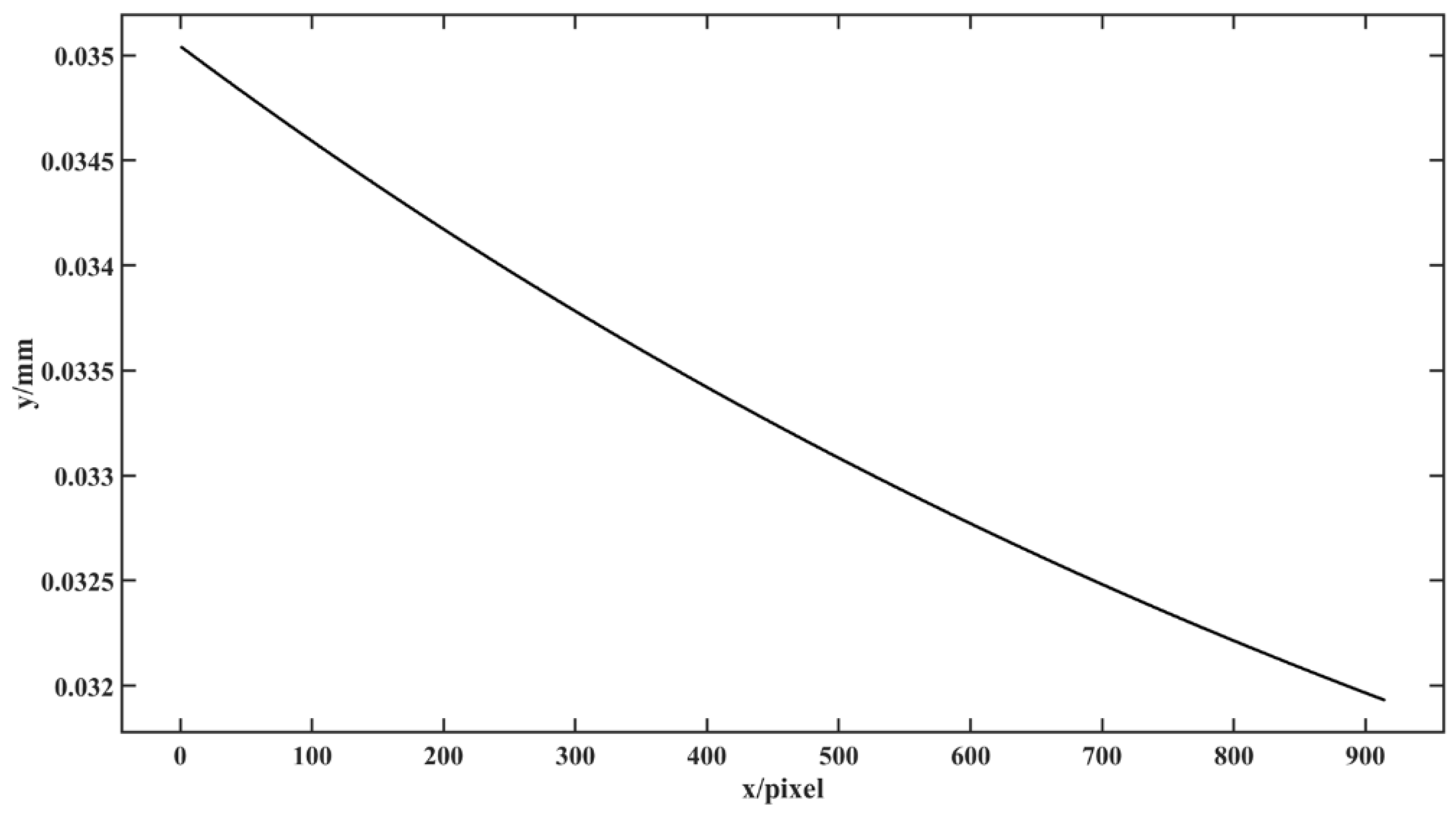
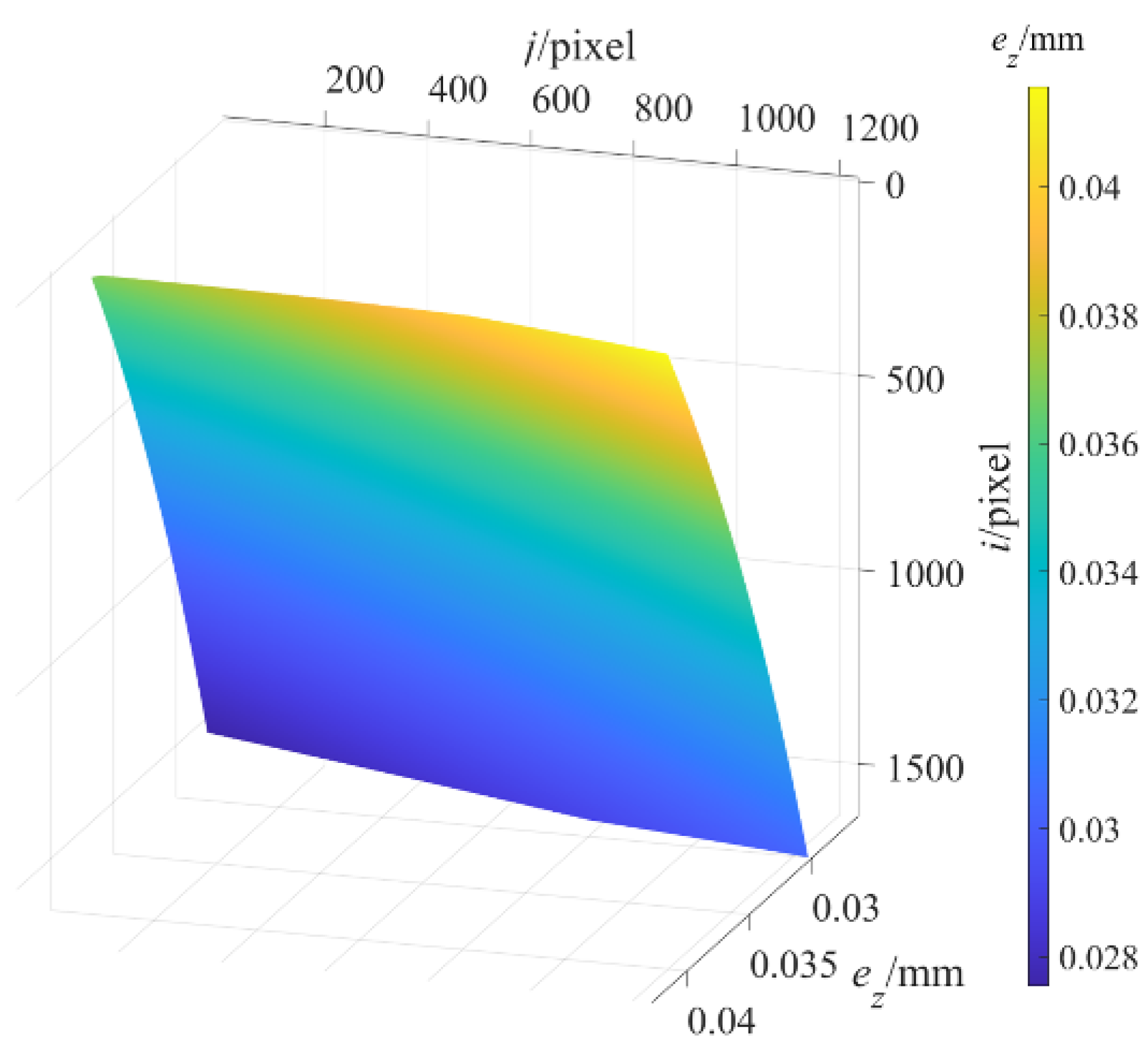
. The depth measurement error image of the standard plane at the maximum measured depth of 1365.0000 mm after structural parameter correction was obtained as shown in
Figure 7, and further,
of the average value of the depth measurement error after structural parameter correction are displayed as the black curve in
Figure 8, and then the maximum value of
is 0.0432 mm. Therefore, the depth measurement error is
mm after structural parameter correction. In contrast, the depth measurement error
after structural parameter correction is reduced to 3% of that before structural parameter correction. The results show that the proposed method significantly reduces the DMECSPE.
In order to verify the adaptability of the proposed correction method to different spatial positions and directions, quantitative comparative measurement experiments before and after structural parameter correction were carried out by using the SLDI for standard planes at different depths, standard inclined planes with different slopes, and standard hemispheres with different radii.
In the simulation measurement experiment of the standard plane, the comparative experimental measurement before and after structural parameter correction is carried out for the standard planes at each depth position with a spacing of 72.0000 mm in the depth measurement range from 1000.0000 mm to 1292.0000 mm. The maximum values of depth measurement error for the standard planes at different depths before and after structural parameter correction are shown in
Table 4.
Figure 9 and
Figure 10 are, respectively, the depth measurement error images of the standard plane at a depth of 1146.0000 mm before and after structural parameter correction.
Figure 11 and
Figure 12 are, respectively, the average curves of the depth measurement errors before and after structural parameter correction at the plane depth of 1146.0000 mm and
, where y represents the average value of the depth measurement errors and x represents
. By comparing
Figure 9 and
Figure 10, as well as
Figure 11 and
Figure 12, we can see that the proposed method significantly reduces the depth measurement error of the plane caused by structural parameter errors. It can be seen from
Table 4 that the depth measurement error of the plane after structural parameter correction is reduced to less than 3.5% of that before structural parameter correction.
In the simulation measurement experiment of the standard inclined plane, the standard plane at the depth of 1143.022 mm is rotated 15°, 30°, 45°, 60°, and 75° around the
x-axis and
y-axis of the world coordinate system
, respectively, to form standard inclined planes with different slopes, and then the comparative experimental measurement before and after structural parameter correction is carried out for each standard inclined plane. The maximum values of depth measurement error for the standard inclined planes with different slopes before and after structural parameter correction are shown in
Table 5.
Figure 13 and
Figure 14, respectively, show the depth measurement error images of the standard inclined plane formed by rotating the standard plane by 30° around the
x-axis and
y-axis before and after structural parameter correction. By comparing
Figure 13 and
Figure 14, we can see that the proposed method significantly reduces the depth measurement error of the inclined plane caused by structural parameter errors. It can be seen from
Table 5 that the depth measurement errors of the inclined plane after structural parameter correction is reduced to less than 5% of that before structural parameter correction.
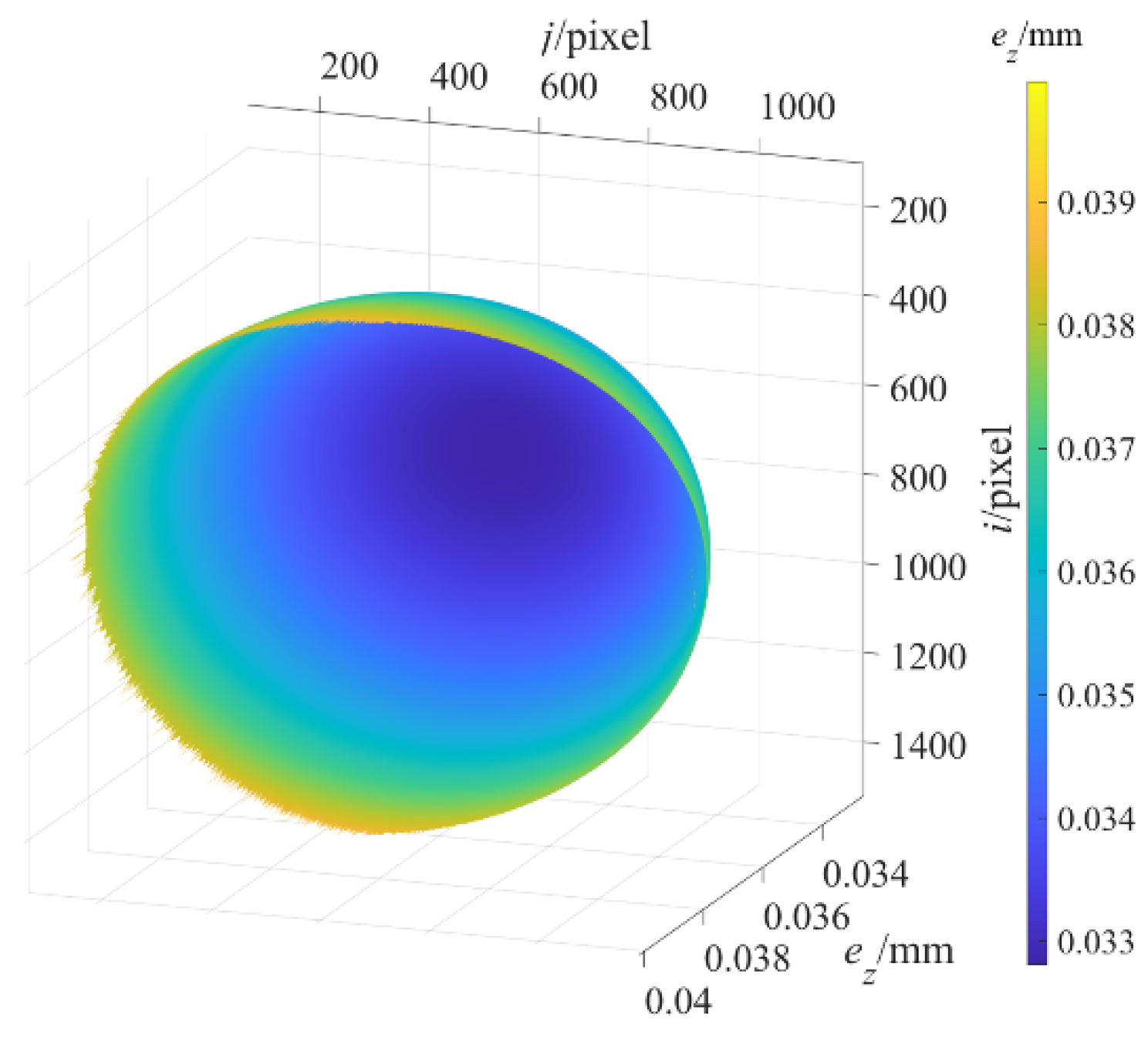
In the simulation measurement experiment of the standard hemispheres, the comparative experimental measurement before and after structural parameter correction is carried out for the standard hemispheres with spherical center coordinates (−92.4340 mm, 1365.0000 mm, 0 mm) and the radii of 90.0000 mm, 130.0000 mm, 170.0000 mm, 210.0000 mm, and 250.0000 mm, respectively. The maximum values of depth measurement error for the standard hemispheres with different radii before and after structural parameter correction are shown in
Table 6.
Figure 15 and
Figure 16, respectively, show the depth measurement error images of the standard hemisphere with a radius of 250.0000 mm before and after structural parameter correction. By comparing
Figure 15 and
Figure 16, we can see that the proposed method significantly reduces the depth measurement error of the hemisphere caused by structural parameter errors. It can be seen from
Table 6 that the depth measurement errors of the hemisphere after structural parameter correction is reduced to less than 4% of that before structural parameter correction.
We also assembled the experimental equipment of SLDI to qualitatively verify the performance of our proposed method. Our main equipment included a DLP projector (Texas Instruments, Dallas, Texas, USA, model: DLP4710EVM-LC) and a 3CCD camera (JAI, Miyazaki, Japan, model: AT-200GE) attached with a 20 mm lens (model: BV-L1020), and its parameters were exactly the same as those of our simulated SLDI except for the focal length of the camera lens, and the projection angle
is obtained using Gray code plus fringe method [
20]. The attitude position of the camera is adjusted according to the design value of the structural parameters in the process of device assembly, because the attitude position of the camera in the device is adjustable. However, it is difficult to accurately adjust the structural parameters to their design values in the assembly process because the central position and focal length of the camera lens are invisible. Therefore, the proposed method is used to correct the structural parameters.
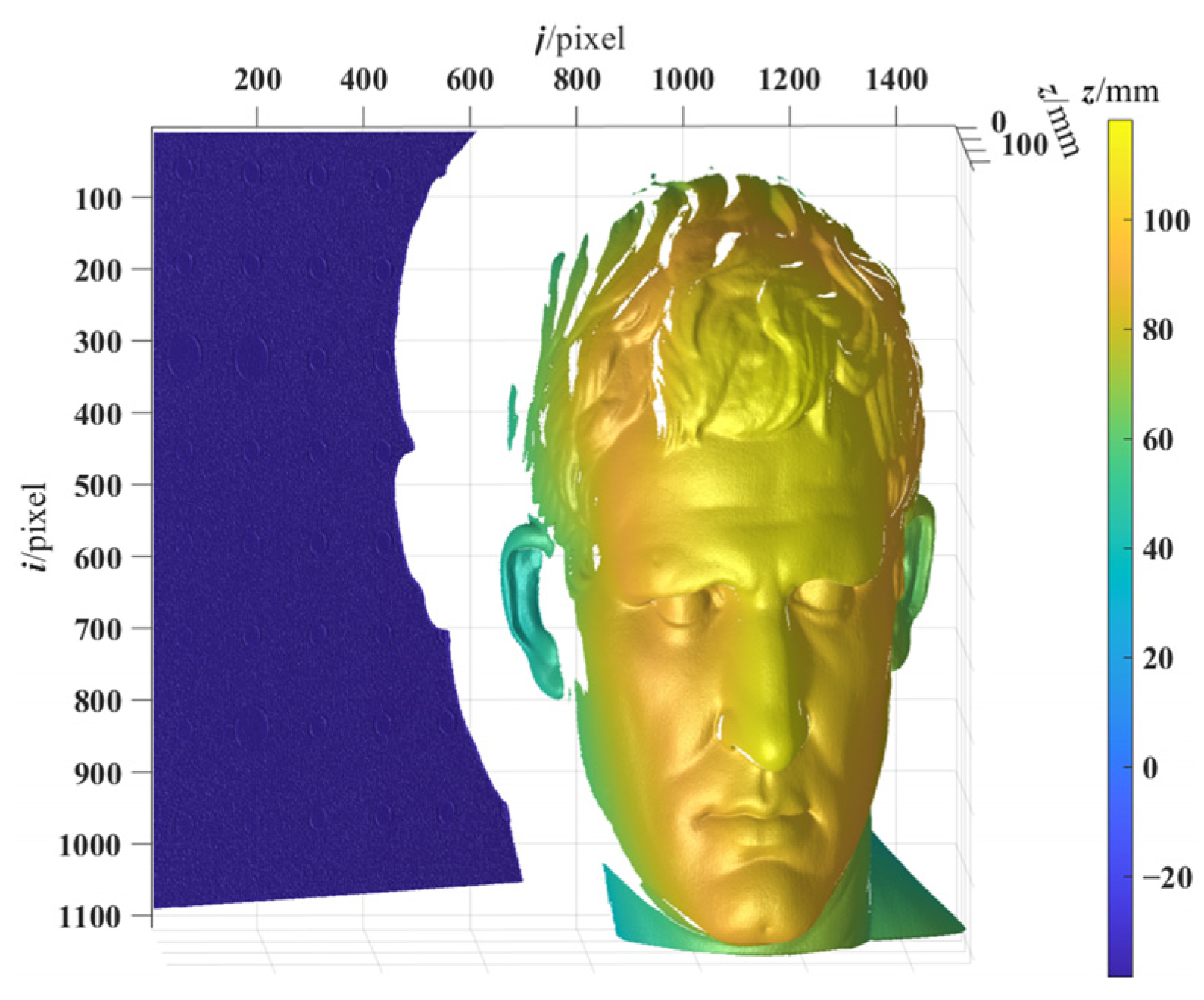
We measured a more complex scene to visually demonstrate the success of our proposed method.
Figure 17 shows the scene photograph, and the scene includes Statue A of Agrippa with complex morphology, Steel-plate B with bright feature points on dark surface, Shadow C, and Background D, and
Figure 18 shows the 3D reconstructed result of the scene. This experiment demonstrated that the proposed method can reconstruct complex 3D surfaces with fine details, isolated surfaces, and surfaces with a sharp contrast between light and dark. It is important to point out that the experimental result is only a qualitative result, as shown in
Figure 18, and a good depth imaging effect could be obtained by the method. The work does not provide the comparative analysis of the DMECSPE before and after correction. This is because in the actual measurement experiments, the depth measurement error of the SLDI includes the depth measurement error caused by both the phase measurement error and the structure parameter error. The depth measurement error caused by the latter is difficult to clearly observe because it is submerged by that caused by the former, and the former is complex and difficult to control in the actual measurement experiments. In addition, the depth measurement errors caused by the latter were only analyzed and corrected in this work, so it is difficult to quantitatively express the comparison of depth measurement errors before and after structural parameter correction.
5. Discussion
The projective geometric model was used in the existing SLDI to obtain the depth image, and all the parameters of the projective geometric model need to be adjusted to ensure the accuracy of the depth measurement. Each of these parameters is affected by many factors at the same time, such as structural parameter error and phase measurement error. Therefore, the influence law is complex. As a result, these parameters are difficult to adjust accurately. The depth measurement accuracy of the structured optical imager is limited, and it is difficult to be widely used in the field of precision manufacturing. The analytical imaging model is used to obtain the depth image, analyze the depth measurement error caused by the structure parameter error and phase measurement error, and reduce the depth measurement error by adjusting those errors, respectively. It is expected to be an effective way to improve the depth measurement accuracy of SLDI. Aiming at three structural parameters, an analytical imaging model and a model of DMECSPE are established. The adjustment method of structural parameters is proposed, which realizes the accurate adjustment of structural parameters and effectively reduces the depth measurement error caused by the error of structural parameters. Though many works were carried out about the depth measurement errors caused by structural parameters, the existing results either stop at the optimal selection of structural parameters [
15,
16,
17] or stay at the level of qualitative error analysis [
18,
19], and there is nearly no work to quantitatively analyze and correct the DMECSPE.
The simulation quantitative measurement experiments were carried out in this paper, and for the measured surfaces in different positions and different directions, the results proved that the proposed method can reduce the DMECSPE to less than 5% of that before the structural parameter correction. In addition, the actual qualitative measurement experiments were also carried out, and the results verified that the proposed method has a good depth imaging effect. The work does not provide the quantitative measurement experimental results for the etalon, so it is difficult to fully show the comparison of the changes of depth measurement errors before and after structural parameter correction. This is because in the actual measurement experiments, the depth measurement error of the SLDI includes the depth measurement error caused by both the phase measurement error and the structure parameter error. The depth measurement error caused by the latter is difficult to clearly observe because it is submerged by that caused by the former, and the former is complex and difficult to control in the actual measurement experiments.
In this work, the depth measurement error caused by structural parameter error was analyzed and corrected. Therefore, the analysis and correction of depth measurement errors caused by phase measurement errors will be an interesting work. Decouple those factors that affect the phase measurement error and obtain the influence law of a single factor on the phase measurement error, so as to independently correct the phase measurement error caused by each influence factor, and then higher accuracy depth measurement can be achieved. Moreover, the verification experiments show that the proposed method is simple and easy to implement.