Abstract
Photocathode laser pulse shaping is a crucial technology for enhancing the performance of X-ray free-electron lasers by optimizing the quality of electron beams generated from photocathodes within high-gradient radio frequency guns. By precisely shaping these laser pulses, it is possible to significantly reduce the transverse emittance of produced electron bunches. The optimal pulse shape is an ellipsoidal distribution, commonly referred to as the Kapchinskij–Vladimirskij profile. A pulse-shaping scheme utilizing a commercial Yb:KGW laser operating at 514 nm with a repetition rate of 1 MHz and duration of 260 fs has been developed for generating electron bunches with high peak and average power. This study presents the experimental realization of ellipsoidal pulses via three-dimensional amplitude shaping using spatial light modulators at 514 nm, followed by conversion to UV (257 nm) suitable for CsTe photocathodes. The preservation of pulse shape and a high conversion efficiency during this process are investigated and our experiments pave the way for future emittance minimization for X-ray free-electron lasers.
1. Introduction
Meeting the requirements of an X-ray free-electron laser with a photoinjector strongly benefits from shaping the photocathode laser pulses. One such advantageous shape is a transverse and longitudinal flat top, which homogenizes the charge distribution in the electron bunch. Using such flat-top pulses, low emittances of up to 2 nC bunch charge were demonstrated at the Photo Injector Test Facility at DESY in Zeuthen (PITZ) [1] via a pulse-stacking technique with birefringent filters [2,3] and a beam-shaping aperture (BSA) to generate a laser pulse distribution close to a homogeneously filled cylinder.
The optimization goal for pulse shaping is maximizing the single electron bunch brightness B:
where the generated charge Q should be maximized and the 6D phase-space volume, represented by normalized RMS emittances , should be minimized. The overall transverse emittance has contributions from the intrinsic cathode emittance , the RF-induced emittance , and contributions from the surrounding magnets such as the solenoid magnet as well as remaining magnetic field components at the surface of the cathode introduced by the solenoid magnet (cf. [4,5,6]):
To avoid nonlinear space charge forces and minimize emittance growth for high-bunch charges at a technologically maximized acceleration gradient, laser pulse shaping is a way to control the charge distribution in photoinjectors and reduce the space charge contribution .
For emphasizing the importance of photocathode laser pulse shaping, Table 1 summarizes ASTRA simulation results for PITZ [7,8,9] and shows the emittance and resulting 5D brightness for different pulse shapes of 20 ps full-bunch width and of charge 250 pC. The 5D brightness,
of an electron bunch can be used as a first approximation for the achievable undulator performance of an X-ray FEL.

Table 1.
Results of ASTRA simulations for different pulse shapes for the PITZ accelerator.
The ideal distribution for an electron bunch with minimized emittance is a uniformly filled 3D ellipsoid (also often called the 3D Kapchinskij–Vladimirskij distribution [10]) that has space charge fields that have a linear dependence on the position within the distribution [11,12] and is therefore immune to space-charge-induced phase-space dilution. The first scheme for generation of such a distribution using photoemission electron sources was proposed by Serafini [13] and subsequently refined by Luiten et al. [14] using an ultrashort laser impinging on a fast photoemitter in a strong accelerating electric field. The operating parameters of the electron source are chosen such that the distribution evolution is dominated by linear space charge force and is often referred to as the “blow-out regime”. High gradients at the cathode and laser pulses on the order of sub-100 femtoseconds are typical requirements to achieve this regime, which can be achieved by frequency-tripled titanium–sapphire lasers, being limited to a tens of kHz repetition rate. Improvements regarding this scheme are ongoing [15,16,17,18,19] for their potential to increase the peak brilliance of X-ray FELs and in ultrafast electron diffraction (UED) [20,21]. However, this scheme has drawbacks for high charges due to the formation of image charges close to the photocathode [22] or large contributions of intrinsic cathode emittance [17].
For driving photoinjectors of X-ray free-electron lasers to achieve high peak and average brightness, laser repetition rates on a multi-MHz level are necessary, which have been implemented by fourth-harmonic generation of Nd-doped, and later Yb-doped, solid-state lasers [23,24], or the recently developed fiber lasers [25,26]. Owing to their narrow spectral bandwidth, Yb-doped solid-state lasers exhibit a limited pulse duration, between 0.25 ps and 5 ps, making them less suitable for exploiting the blow-out regime. Implementing pulse-shaping schemes with these lasers is challenging due to their narrow spectral bandwidth and gain-narrowing in the amplifier stages, which hinder straightforward implementation of spatial light modulator-based 4-f configurations. The generation and characterization of the 3D ellipsoidal distribution are difficult because it is coupled both transversely and longitudinally. This challenge extends to commonly used pulse characterization methods that integrate one component of the distribution, as well as many diagnostic techniques employed in accelerator facilities.
Mironov et al. realized ellipsoidal distributions from these lasers using chirped pulses and an LCOS SLM (liquid crystal on silicon spatial light modulator) in a zero-dispersion grating stretcher setup [27]. The bandwidth-limited laser pulses are stretched to maintain a nearly linear relation between the frequency and temporal domains, enabling spectral shaping that directly translates into the temporal pulse structure. These pulses facilitate implementation of the slit-scan technique using a 2D spectrograph to assess their 3D shape. This scheme has been set up at PITZ and underwent recent upgrades [28]. Alternative approaches include employing profiled chirped volume Bragg gratings [29] or implementing an absorption mask for amplitude shaping [30], as well as utilizing oppositely chirped pulses for frequency conversion [31]. However, when realizing pulse shaping in the IR regime, a two-step frequency conversion, to green and then UV, is necessary, which can be prone to instabilities, while aiming for high conversion efficiencies. This can cause degradation of the quality of the shaped pulses that generate photoelectrons at the cathode [28].
We developed a scheme that uses the same pulse-shaping method as used for IR lasers and adapted it for the 514 nm wavelength [32], which has the advantage of being directly applicable to alkali antimonide photocathodes [33,34]. Utilizing laser systems at green wavelengths balances the demands for high peak and average power capabilities and the accessibility of efficient pulse-shaping devices, enabling continuous operation at a 1 MHz repetition rate with multiple watts of average power. Nevertheless, as alkali antimonide photocathodes are currently undergoing testing and not routinely employed at accelerator facilities, the pulse-shaping scheme is being investigated for CsTe photocathodes. In this context, the proposed shaping at the 514 nm wavelength offers an advantage due to its requirement of only one conversion step to UV, which decreases susceptibility to instabilities compared to a two-stage frequency conversion process for IR lasers. Although Gaussian or flat-top pulses are commonly employed to drive photoinjectors in X-ray FEL today, our research shows the potential benefits of using 3D ellipsoidal pulses for future upgrades, e.g., continuous-wave operation with reduced gun gradients [35,36,37]. Here, we present the first generation of 3D ellipsoidal pulses at a wavelength of 257 nm, achieved through our previously presented scheme, which has been characterized for spectral shaping with one amplitude-shaping unit [32]. Our experimental setup is extended with another pulse-shaping unit for 3D amplitude shaping.
The trend in photocathode laser development is shifting towards compact fiber-laser-based approaches with integrated pulse shapers for generating desired temporal pulse shapes, such as flat-top pulses, in the pre-amplification stages [25,26]. However, these lasers are limited to shaping in the spectral domain only and may suffer from reduced pulse quality due to subsequent amplification stages and two-stage frequency conversion to UV. Our approach offers greater flexibility in controlling the pulse shape, enabling optimization of photocathode laser systems for improved electron beam quality. We investigate pulse shape preservation for high conversion efficiency to UV for 3D amplitude shaping. Section 2 provides an overview of photocathode laser systems, the design of the pulse shaper, and the used characterization methods for shaped pulses. The pulse shaping results at 257 nm in Section 3 are followed by a discussion in Section 4.
2. Materials and Methods
The experimental setup can be viewed in Figure 1. Its four main components are the laser system and pulse stretching, 3D amplitude shaping with two sequential polarization-maintaining amplitude-shaping units, and UV conversion, as well as diagnostics for 3D characterization of the shaped pulses.
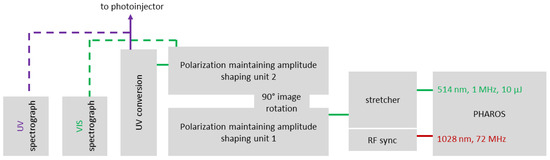
Figure 1.
Experimental setup for 3D amplitude shaping of chirped laser pulses at 515 nm and UV conversion.
2.1. Laser System and Pulse Stretching
The laser system for the 3D pulse-shaping experiments is a commercial Yb:KGW CPA system (Light Conversion PHAROS, Vilnius, Lithuania). The oscillator output is utilized for synchronization with a master oscillator, while high-power outputs are available at wavelengths of 1028 nm, 514 nm, and 257 nm, with a repetition rate of 1 MHz. The green output (260 fs pulse duration and pulse energies up to 10 µJ) is subsequently passed through a grating stretcher to generate linearly chirped pulses with a duration of 10 ps, which are then utilized for amplitude shaping within a 4-f zero-dispersion stretcher. Synchronization between the RF phases in the photoinjector and the laser pulse is achieved via a photodiode and piezoelectric translator, enabling adjustments to the oscillator’s cavity length with an RMS timing jitter of 35 fs [32,38]. The laser system’s pulse structure has been adapted to accommodate the accelerator facility’s requirements. Specifically, the macropulse repetition rate is set at 10 Hz, with each macropulse capable of being filled with micropulses featuring a repetition rate of 1 MHz.
The primary objective of the pulse-shaping and UV conversion scheme is to generate UV ellipsoidal pulses with a minimum pulse energy exceeding 50 nJ, sufficient for extracting a charge of approximately 500 pC from CsTe photocathodes within a high-gradient RF gun. To achieve this goal, each component in the presented scheme (stretcher, two pulse-shaping units, and UV conversion) must exhibit an efficiency greater than 27%. A 40% efficiency is achieved for stretching 10 µJ with 260 fs to 10 ps (transmission grating: Ibsen Photonics PCG-3039.5/450-810, roof prism mirrors: Thorlabs HRS1015-P01), which relaxes the efficiency goals of the subsequent units of the pulse-shaping scheme.
2.2. Three-Dimensional Shaping with Two Sequential Polarization-Maintaining Amplitude-Shaping Units
LCOS SLMs are a popular choice for pulse shaping due to their high dynamic range and damage threshold. Their versatility enables applications ranging from beam profile optimization in material processing [39] to manipulation of ultrashort laser pulses [40,41,42]. For photocathode lasers, typically Yb-doped systems, LCOS SLMs can be employed in amplitude shaping. Due to their narrow spectral bandwidth, these lasers are less favorable for phase shaping compared to titanium:sapphire lasers with their large spectral bandwidth. For amplitude shaping, the desired spectral profile is extracted from the initial laser pulse’s spectral distribution when it is temporally and spectrally linearly coupled. This coupling is achieved by stretching the bandwidth-limited pulses in a grating stretcher to approximately 10 ps. Notably, amplitude shaping introduces losses that reduce output energy depending on the desired pulse shape.
The setup for polarization-maintaining amplitude shaping is shown in Figure 2, it was previously described in [32]. A linearly polarized chirped beam, initially s-polarized, enters the pulse shaper module. For transmission through the polarizing beamsplitter (PBS101, Thorlabs Inc., Newton, NJ, USA), the polarization state is converted to p-polarization. A Faraday rotator (Electro-Optics Technology, Inc., Traverse City, MI, USA; 515 nm, +45°) and a half-wave plate subsequently rotate the beam back to its original s-polarized state, ensuring optimal diffraction efficiency from the transmission grating (PCG-3039.5/450-810, Ibsen Photonics, Farum, Denmark). A cylindrical lens compensates the angular dispersion of the grating and its focal length determines the 4-f geometry. The LCOS SLM (X10458 with HR coating for 1030 nm and 515 nm, Hamamatsu Photonics, Hamamatsu, Japan) can introduce controlled phase variations to spatial components. Amplitude shaping is achieved through the insertion of a quarter-wave plate in the shaper arm, allowing only s-polarized light that has undergone double passage through the quarter-wave plate and additional phase shift by the LCOS SLM to be transmitted by the grating. Following transmission through the half-wave plate and Faraday rotator (backward direction), the s-polarized beam component is coupled out by the polarizing beamsplitter. Prior to entering a second identical pulse shaper module, the beam is rotated 90° using a dove prism (PS992M-A, Thorlabs Inc., USA).
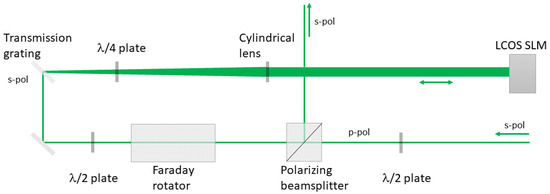
Figure 2.
Realization of polarization-maintaining amplitude shaping at 514 nm.
This approach enables amplitude shaping in the x- and y- planes. However, amplitude shaping in two planes can only approximate the shape of the desired 3D ellipsoid. The implemented scheme is therefore a compromise between overall transmission, alignment complexity, and 3D shape approximation.
2.3. UV Conversion
After 3D pulse shaping, a UV conversion section follows. The beam is focused with an f = +250 mm lens and close to the focal spot a 1 mm thick BBO crystal is placed for converting 514 nm wavelength beam into 257 nm wavelength at intensity levels of several . The crystal can be adjusted in its position and angle with respect to the laser beam and conversion efficiencies above 20% are routinely achieved for 10 ps to 15 ps pulse duration. Fine adjustment depends on the laser pulse shape that is introduced by the shapers. The UV beam is then collimated by another f = +250 mm lens after the crystal, and then, imaged in multiple steps to the photocathode [32] or to the diagnostics on the laser table.
To achieve UV pulses with high average and high peak powers, especially with shaped chirped pulses [43], special care has to be taken of the intensity in the BBO crystal to avoid color center formation, and achieve a good spatial pulse quality and high conversion efficiency. For the crystal thickness, group velocity mismatch and spatial walk-off have to be taken into account [44]. Working with heavily chirped pulses, in contrast to bandwidth-limited pulses, means the leading and falling edge usually do not reach the necessary intensity for UV conversion [32]. Other pulse-shaping schemes, like pulse stacking by birefringent filters [2,3,45], are not sensitive to these difficulties, since bandwidth-limited pulses are used. However, these schemes are limited to pulse shaping in the temporal dimension, e.g., the generation of flat-top pulse shapes. For UV conversion of chirped pulses special techniques can be applied to improve the beam quality of the UV signal, e.g., angular chirp matching [46,47,48]. For generation of 3D ellipsoidal pulses, oppositely chirped pulses can also be used for a sum frequency conversion scheme [31]. For our experiments we do not implement these advanced schemes, as we aim to investigate the influence of pulse shaping in a simple conversion setup that is less sensitive to alignment as a robust, simple setup for photocathode lasers. Further discussion of the frequency conversion of chirped pulses follows in Section 3.2.
2.4. Diagnostics
The 3D reconstruction of chirped pulses is achieved by the so-called slit-scan technique [27]. For such a measurement a high-resolution Czerny–Turner 2D imaging spectrograph is utilized and the chirped pulse is scanned over the slit by a movable mirror. For green and UV wavelengths, a slit-scan setup was realized [32] (Figure 3). The detectors in the 2D imaging spectrographs are a Prosilica GC 1350 (Allied Vision, Stadtroda, Germany, 1060 × 1024 pixel, 7.2 pm spectral resolution) for 514 nm and a CM-140-GE-UV (JAI, Copenhagen, Denmark, 1392 × 1040 pixel, 6.5 pm spectral resolution) for 257 nm.
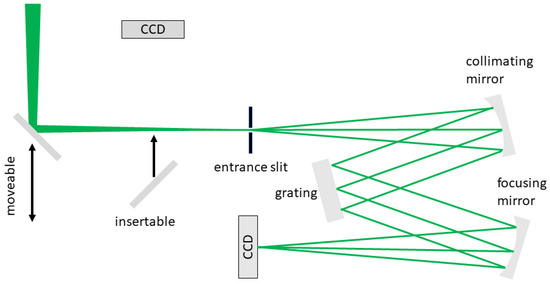
Figure 3.
Imaging Czerny–Turner spectrograph for 3D reconstruction of a chirped pulse. For optimization of the imaging conditions into the spectrograph, the beam profile can be measured at the plane of the entrance slit of the spectrograph by a CCD.
A simulated 3D ellipsoidal distribution is shown in Figure 4a. The projection in the x-y plane (Figure 4b) gives the beam profile. Figure 4c,d show 2D elliptic projections in the x- and y- planes. Slit-scan measurements with the 2D spectrographs for ellipsoidal pulses will give similar results. This type of measurement is also sensitive to typical alignment issues of pulse shapers and UV conversion in terms of spatial chirp.
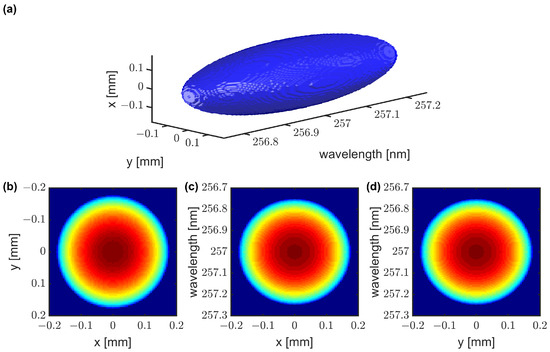
Figure 4.
Simulation of chirped 3D ellipsoid in spectral domain. (a) 3D volume. (b) Beam profile. (c,d) show the spectral projection along the spatial coordinates x and y.
In addition to spectral characterization of 3D shaped pulses, temporal characterization is possible for the generated electron bunch in the accelerator via a transverse deflecting structure [49] or cross-correlator measurements for the UV pulses. If the pulses are not 3D shaped and at 514 nm, much simpler pulse diagnostics can be used, e.g., commercial spectrometers (OceanOptics HR2000+, Orlando, FL, USA; 478.8 nm–555.3 nm, 38 pm spectral resolution). Also, temporal pulse shape characterization for 514 nm simplifies to intensity autocorrelation measurements with the SHG FROG option, where the UV spectrograph serves as a detector. However, deduction of a pulse shape for 257 nm is not always straightforward for measurements at 514 nm and vice versa and is further discussed in Section 3.2.
3. Results
3.1. Characterization of Unshaped Pulses
As a first experiment, stretched Gaussian pulses of 10 ps duration are characterized. These pass the two pulse shapers without applying any mask and bypass the UV conversion section. In Figure 5, a Gaussian pulse around 514 nm is shown. Projections in all the directions are shown (x-y is the beam profile, x- and y- are the 2D spectral distributions). Each projection shows a Gaussian distribution.
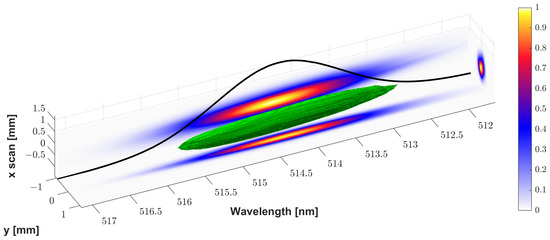
Figure 5.
A 3D reconstruction of a Gaussian pulse (green volume) with the slit-scan technique. Projections in x-y, x-, and y- planes are shown in false color. The integrated spectrum of Gaussian shape is shown as a black line.
When the pulse is converted to UV, it stays a Gaussian pulse in each projection and the 3D reconstruction (Figure 6). It should be noted that the rising and falling edges of the Gaussian distribution at 514 nm (Figure 5) are not properly converted into UV, which was previously observed in pulse-shaping experiments with chirped pulses [32]. Additionally, imaging conditions are slightly different compared to 514 nm for achieving proper imaging of the UV converted beam into the spectrograph. Details of frequency conversion are discussed in Section 3.2.
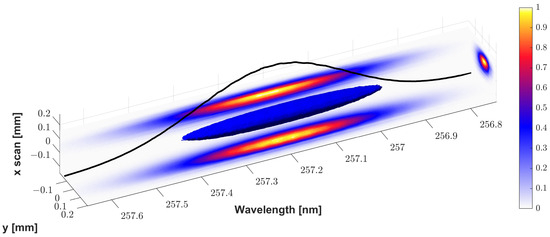
Figure 6.
A 3D reconstruction of a Gaussian pulse after UV conversion (blue volume) with the slit-scan technique. Projections in x-y, x-, and y- planes are shown in false color. The integrated spectrum of Gaussian shape is shown as a black line.
3.2. UV Conversion Efficiency and Pulse Shape Preservation
As stated in the previous section, using Gaussian pulse shapes without the usage of any amplitude shaping preserves the Gaussian pulse shape after UV conversion. However, this situation changes when amplitude shaping is involved. Here, it strongly depends on the desired wavelength for the photocathode (514 nm or 257 nm) to achieve a certain pulse shape, and the feedback signal for the pulse shapers has to be chosen accordingly. To analyze this, an experiment for pure temporal shaping of a parabolic shape is shown in Figure 7.
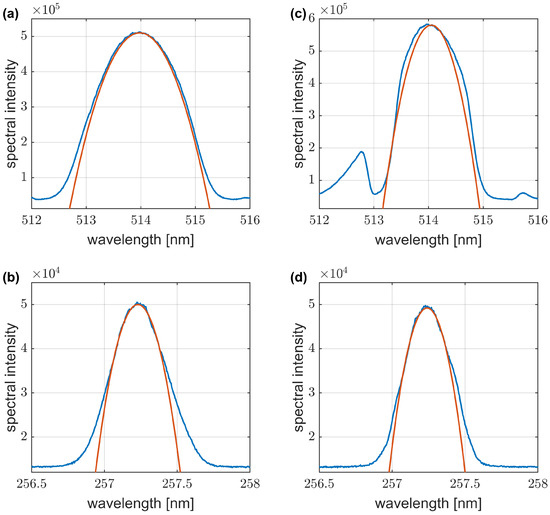
Figure 7.
Influence of the feedback system for pulse-shaping experiments with chirped pulses for a parabolic shape. Blue lines represent the measured spectra and parabolic fits are shown as red lines. (a) Optimization at 514 nm is close to parabolic shape (1.85 nm FWHM). (b) After UV conversion of the optimized pulse the parabolic pulse shape is not preserved (0.44 nm FWHM). (d) Optimization at 257 nm can improve the parabolic shape (0.40 nm FWHM) compared to (b). (c) Input pulse at 514 nm shows reduced spectral width (1.35 nm FWHM) compared to (a).
The spectrograph for 514 nm can be used to optimize the pulse shape. The agreement with a parabolic shape is shown by the red line fitted to the integrated spectrum of the 2D detector in Figure 7a. However, if this pulse shape is converted into UV, the parabolic shape is degraded and a more Gaussian shape is introduced by the conversion section (Figure 7b). To precompensate for this pulse shape degradation, the UV spectrograph can be used as a feedback system for pulse shaping and better agreement with the parabolic shape is achieved (Figure 7d). The input green pulse (Figure 7c) for achieving the parabolic shape in the UV shows several features. First, the central part of the spectrum shows the precompensation for the UV conversion by increasing the spectral shape above the level of the parabolic fit. Second, not all parts of the green spectrum contribute to the UV signal, because of the chirped pulse. The rising and falling edges of the pulse do not carry enough intensity to be efficiently converted into UV.
Our experimental findings support the neccessity to use UV feedback signals to optimize the resulting pulse shape after UV conversion. We have shown it here for spectral shaping, but it also holds true for shaping of the spatial profile.
3.3. Characterization of Ellipsoidal Pulses at 257 nm
For generation of 3D ellipsoidal shapes in the UV, the integrated projections should be parabolic in the spectral and each spatial domain (Figure 4). As feedback for the amplitude shaping the UV 2D spectrograph is used. The mirror for scanning the entrance slit of the spectrograph is therefore driven to a position where most of the signal is transmitted to the detector CCD. In this way, the spectrum and the y-profile can be optimized by the first amplitude-shaping unit. The x-profile is optimized with the beam profile that is detected with a CCD camera (Allied Vision Prosilica GC 1350, Stadtroda, Germany) at the position of the entrance slit of the 2D spectrograph (Figure 3). The resulting 3D distribution measured by the slit-scan technique is shown in Figure 8.
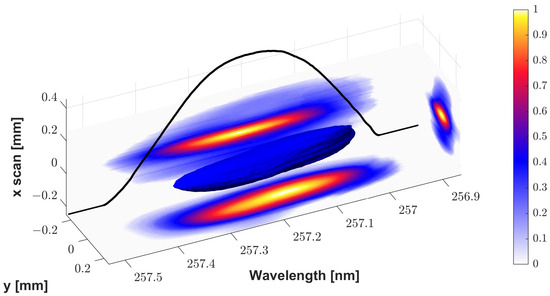
Figure 8.
A 3D reconstruction of a UV ellipsoidal pulse (blue volume) with the slit-scan technique. Projections in x-y, x-, and y- planes are shown in false color. The integrated spectrum of the parabolic shape is shown as a black line.
The projections in the x- and y- planes are close to elliptic. However, sidewings can be observed in the direction of scanning over the slit (x-direction). These can be attributed to spatial walk-off in the UV conversion section. Although the profile in the scanning direction has been optimized with a CCD, a serious amount of background is obtained in the more sensitive slit-scan measurement due to the better signal-to-noise ratio. Such sidewings cannot be observed in the y-direction, because the UV spectrograph was used as a feedback system where the y- plane was detected.
The achieved pulse energy for this shaped pulse is 35 nJ. Only 7% of the approximately 0.5 µJ after the two pulse-shaping units is converted to UV. Taking into account the UV design goal of 50 nJ excludes further beam profile improvement by use of apertures. Optimization of the phase-matching conditions in the UV conversion section achieved the highest conversion efficiency for the presented measurement.
4. Discussion
4.1. Total Efficiency for 3D Shaped UV Pulses
We have designed and implemented a pulse-shaping scheme to generate ellipsoidal pulses around 257 nm for photoelectron generation in a high-gradient RF gun. The process begins with commercial laser pulses featuring durations of approximately 260 fs and energies up to 10 µJ, which are then stretched to 10 ps using an efficiency of approximately 40%. Approximately 3.8 µJ enters the first polarization-maintaining amplitude shaper, and without applying a mask to the LCOS SLM 50% of the input pulse energy is transmitted to the second shaper, where a 90° rotation by a dove prism is realized to shape the other spatial plane. The output from this process (approximately 0.95 µJ without amplitude masking) then enters the UV conversion section, which exhibits an efficiency exceeding 20%. For Gaussian pulses lacking any amplitude shaping, we have achieved pulse energies of up to approximately 180 nJ in the UV regime.
The introduction of losses due to the LCOS SLMs within the pulse-shaping unit leads to a reduction in transmission. Specifically, when generating 3D ellipsoidal pulses, only approximately 0.5 µJ is transmitted to the UV conversion section, resulting in an efficiency decrease to around 7%. This ultimately yields a pulse energy of approximately 35 nJ.
4.2. Quality of UV Ellipsoidal Pulses
The use of a laser system operating at the 514 nm wavelength simplifies frequency conversion, requiring only one step compared to the two steps required for systems emitting at 1030 nm. This enables the implementation of a UV-based feedback loop using a 2D spectrograph, which can be employed to compensate for unwanted effects in the frequency conversion. Our results demonstrate that utilizing this UV spectrographic feedback yields a superior spectral parabolic shape compared to optimizing the profile at 514 nm. In contrast, when employing the same feedback mechanism at 514 nm, the parabolic shape is not preserved during frequency conversion.
Hence, to optimize the UV ellipsoid, we employed the UV diagnostics as feedback. The resulting 3D reconstruction shows good agreement with our desired pulse shape in the spectral domain. However, a constant background signal along the axis scanned over the entrance slit of the 2D spectrograph is observed (Figure 8). Two potential reasons for this deviation from the ideal ellipsoidal shape are identified. Firstly, the optimization process used to create the amplitude mask may not have been as precise due to limitations in measuring beam profiles at the entrance slit position using a CCD camera. In the other spatial dimension, which can be measured with the 2D spectrograph showing the y- plane, the background levels are less pronounced. This could be improved by rotating the beam profile 90° with a dove prism or mirror combination after the second pulse-shaping unit and before UV conversion. However, this would require careful alignment because of beam offsets. Another possibility would be a mirror combination to turn the beam 90°, which could be realized after UV conversion. Secondly, improving the quality of the UV beam through angular chirp matching may enhance the resulting pulse shape [48]. Further investigation is needed to determine if direct optimization with UV diagnostics remains possible for angular chirp matching.
4.3. Simplification for Alkali Antimonide Photocathodes
The key challenge in generating UV ellipsoidal pulses is maintaining high conversion efficiency while preserving the desired shape. Using alkali antimonide photocathodes significantly simplifies the experimental process, enabling direct shaping of 514 nm ellipsoidal pulses with our presented pulse-shaping scheme. This approach allows for a substantial increase in energy transmission to the photocathode, exceeding 500 nJ, due to the absence of conversion steps. Furthermore, the stretcher’s ability to independently vary pulse duration to several tens of picoseconds is also enabled, as intensity considerations can be neglected in the UV conversion section.
4.4. Towards Minimized Emittance from Photoinjectors for X-ray Free-Electron Lasers
Laser pulse shaping plays a crucial role for reducing the emittance of electron bunches from photoinjectors for high-brightness electron beams. With our pulse-shaping scheme, we aim for a 3D ellipsoidal distribution at 257 nm to be suitable for CsTe photocathodes. Minimizing the emittance for a given charge is a key aspect of improving the performance of an X-ray FEL in terms of a high photon flux and lasing at the shortest wavelength. To support future upgrades towards LP or CW operation [35,36], further emittance optimization beyond the current levels will be necessary. Our achieved UV ellipsoid requires additional spatial beam quality improvements, which we plan to achieve through the outlined methods. Ultimately, we will perform emittance measurements in our accelerator.
Author Contributions
Conceptualization, M.K. and F.S.; methodology, A.H., J.G. and M.G.; investigation, A.H.; formal analysis, A.H.; writing—original draft preparation, A.H.; writing—review and editing, A.H., M.G. and M.K.; project administration, M.G., M.K. and F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the European XFEL research and development program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data could be provided by the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ASTRA | A Space Charge Tracking Algorithm |
| BBO | Beta barium borate |
| BSA | Beam-shaping aperture |
| DESY | Deutsches Elektronen-Synchrotron |
| FEL | Free-electron laser |
| LCOS SLM | Liquid crystal on silicon spatial light modulator |
| PITZ | Photo Injector Test Facility at DESY in Zeuthen |
| RF | Radio frequency |
| RMS | Root mean square |
| UV | Ultraviolet |
| Yb:KGW | Ytterbium-doped potassium gadolinium tungstate |
References
- Krasilnikov, M.; Stephan, F.; Asova, G.; Grabosch, H.J.; Groß, M.; Hakobyan, L.; Isaev, I.; Ivanisenko, Y.; Jachmann, L.; Khojoyan, M.; et al. Experimentally minimized beam emittance from an L-band photoinjector. Phys. Rev. ST Accel. Beams 2012, 15, 100701. [Google Scholar] [CrossRef]
- Will, I. Generation of flat-top picosecond pulses by means of a two-stage birefringent filter. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2008, 594, 119–125. [Google Scholar] [CrossRef]
- Liu, F.; Huang, S.; Si, S.; Zhao, G.; Liu, K.; Zhang, S. Generation of picosecond pulses with variable temporal profiles and linear polarization by coherent pulse stacking in a birefringent crystal shaper. Opt. Express 2019, 27, 1467–1478. [Google Scholar] [CrossRef] [PubMed]
- Serafini, L.; Rosenzweig, J.B. Envelope analysis of intense relativistic quasilaminar beams in RF photoinjectors: A theory of emittance compensation. Phys. Rev. E 1997, 55, 7565–7590. [Google Scholar] [CrossRef]
- Limborg-Deprey, C.; Tomizawa, H. Maximizing brightness in photoinjectors. Int. J. Mod. Phys. 2007, 22, 3864–3881. [Google Scholar] [CrossRef]
- Sannibale, F. High-brightness electron injectors for high-duty cycle X-ray free electron lasers. Front. Phys. 2023, 11, 1187346. [Google Scholar] [CrossRef]
- Flöttmann, K. ASTRA—A Space Charge Tracking Algorithm. Available online: http://www.desy.de/mpyflo (accessed on 13 June 2024).
- Khojoyan, M.; Krasilnikov, M.; Stephan, F. 3D Ellipsoidal Beams for Ultimate Performance at the High Brightness Photoinjector PITZ; PITZ Internal Report; PITZ: Zeuthen, Germany, 2014. [Google Scholar]
- Khojoyan, M.; Krasilnikov, M.; Stephan, F.; Vashchenko, G. Beam dynamics optimization for the high brightness PITZ photo injector using 3D ellipsoidal cathode laser pulses. In Proceedings of the 35th International Free-Electron Laser Conference, FEL’13, New York, NY, USA, 26–30 August 2013; JACoW Publishing: Geneva, Switzerland, 2013; pp. 298–302. Available online: https://accelconf.web.cern.ch/FEL2013/papers/tupso36.pdf (accessed on 12 July 2024).
- Kapchinskij, I.M.; Vladimirskij, V.V. Limitations Of Proton Beam Current In A Strong Focusing Linear Accelerator Associated with The Beam Space Charge. In Proceedings of the 2nd International Conference on High-Energy Accelerators, Geneva, Switzerland, 14–19 September 1959; pp. 274–287. [Google Scholar]
- Reiser, M. Theory and Design of Charged Particle Beams; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Ha, G.; Kim, K.J.; Power, J.G.; Sun, Y.; Piot, P. Bunch shaping in electron linear accelerators. Rev. Mod. Phys. 2022, 94, 25006. [Google Scholar] [CrossRef]
- Serafini, L. Improving the beam quality of RF guns by correction of RF and space-charge effects. AIP Conf. Proc. 1992, 279, 645–674. [Google Scholar] [CrossRef]
- Luiten, O.J.; van der Geer, S.B.; de Loos, M.J.; Kiewiet, F.B.; van der Wiel, M.J. How to Realize Uniform Three-Dimensional Ellipsoidal Electron Bunches. Phys. Rev. Lett. 2004, 93, 094802. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Lewellen, J.W. Generating a Quasiellipsoidal Electron Beam by 3D Laser-Pulse Shaping. Phys. Rev. Lett. 2008, 100, 74801. [Google Scholar] [CrossRef]
- Musumeci, P.; Moody, J.T.; England, R.J.; Rosenzweig, J.B.; Tran, T. Experimental Generation and Characterization of Uniformly Filled Ellipsoidal Electron-Beam Distributions. Phys. Rev. Lett. 2008, 100, 244801. [Google Scholar] [CrossRef] [PubMed]
- Piot, P.; Sun, Y.E.; Maxwell, T.J.; Ruan, J.; Secchi, E.; Thangaraj, J.C.T. Formation and acceleration of uniformly filled ellipsoidal electron bunches obtained via space-charge-driven expansion from a cesium-telluride photocathode. Phys. Rev. ST Accel. Beams 2013, 16, 010102. [Google Scholar] [CrossRef]
- Xu, T.; Doran, D.S.; Liu, W.; Piot, P.; Power, J.G.; Whiteford, C.; Wisniewski, E. Demonstration of eigen-to-projected emittance mapping for an ellipsoidal electron bunch. Phys. Rev. Accel. Beams 2022, 25, 44001. [Google Scholar] [CrossRef]
- Faillace, L.; Agustsson, R.; Behtouei, M.; Bosco, F.; Bruhwiler, D.; Camacho, O.; Carillo, M.; Fukasawa, A.; Gadjev, I.; Giribono, A.; et al. High field hybrid photoinjector electron source for advanced light source applications. Phys. Rev. Accel. Beams 2022, 25, 63401. [Google Scholar] [CrossRef]
- Van Oudheusden, T.; de Jong, E.F.; van der Geer, S.B.; Op’t Root, W.P.E.M.; Luiten, O.J.; Siwick, B.J. Electron source concept for single-shot sub-100 fs electron diffraction in the 100 keV range. J. Appl. Phys. 2007, 102, 093501. [Google Scholar] [CrossRef]
- Filippetto, D.; Musumeci, P.; Li, R.K.; Siwick, B.J.; Otto, M.R.; Centurion, M.; Nunes, J.P.F. Ultrafast electron diffraction: Visualizing dynamic states of matter. Rev. Mod. Phys. 2022, 94, 045004. [Google Scholar] [CrossRef]
- Rosenzweig, J.; Cook, A.; England, R.; Dunning, M.; Anderson, S.; Ferrario, M. Emittance compensation with dynamically optimized photoelectron beam profiles. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2006, 557, 87–93. [Google Scholar] [CrossRef]
- Will, I.; Templin, H.I.; Schreiber, S.; Sandner, W. Photoinjector drive laser of the FLASH FEL. Opt. Express 2011, 19, 23770–23781. [Google Scholar] [CrossRef]
- Winkelmann, L.; Choudhuri, A.; Grosse-Wortmann, U.; Hartl, I.; Li, C.; Mohr, C.; Müller, J.; Peters, F.; Pfeiffer, S.; Salman, S. The European XFEL Photocathode Laser. In Proceedings of the 39th in Free Electron Laser Conference, FEL’19, Hamburg, Germany, 26–30 August 2019; JACoW Publishing: Geneva, Switzerland, 2019; pp. 423–426. [Google Scholar] [CrossRef]
- Gilevich, S.; Alverson, S.; Carbajo, S.; Droste, S.; Edstrom, S.; Fry, A.; Greenberg, M.; Lemons, R.; Miahnahri, A.; Polzin, W.; et al. The LCLS-II Photo-Injector Drive Laser System. In Proceedings of the Conference on Lasers and Electro-Optics, Virtual, 11–14 May 2020; Optica Publishing Group: Washington, DC, USA, 2020; p. SW3E.3. [Google Scholar] [CrossRef]
- Li, C.; Akcaalan, O.; Frede, M.; Grosse-Wortmann, U.; Hartl, I.; Mohr, C.; Puncken, O.; Seidel, M.; Tuennermann, H.; Vidoli, C.; et al. Photocathode Laser Development for Superconducting X-ray Free Electron Lasers at DESY. In Proceedings of the 12th in International Particle Accelerator Conference, IPAC’21, Virtual, 24–28 May 2021; JACoW Publishing: Geneva, Switzerland, 2021; pp. 3599–3601. [Google Scholar] [CrossRef]
- Mironov, S.Y.; Potemkin, A.K.; Gacheva, E.I.; Andrianov, A.V.; Zelenogorskii, V.V.; Krasilnikov, M.; Stephan, F.; Khazanov, E.A. Shaping of cylindrical and 3D ellipsoidal beams for electron photoinjector laser drivers. Appl. Opt. 2016, 55, 1630–1635. [Google Scholar] [CrossRef]
- Koschitzki, C.; Qian, H.; Aboulbanine, Z.; Adhikari, G.; Aftab, N.; Boonpornprasert, P.; Georgiev, G.; Good, J.; Gross, M.; Hoffmann, A.; et al. Chirped Pulse Laser Shaping for High Brightness Photoinjectors. In Proceedings of the 40th International Free Electron Laser Conference, FEL2022, Trieste, Italy, 22–26 August 2022; JACoW Publishing: Geneva, Switzerland, 2022; pp. 345–348. [Google Scholar] [CrossRef]
- Mironov, S.Y.; Poteomkin, A.K.; Gacheva, E.I.; Andrianov, A.V.; Zelenogorskii, V.V.; Vasiliev, R.; Smirnov, V.; Krasilnikov, M.; Stephan, F.; Khazanov, E.A. Generation of 3D ellipsoidal laser beams by means of a profiled volume chirped Bragg grating. Laser Phys. Lett. 2016, 13, 055003. [Google Scholar] [CrossRef]
- Gacheva, E.I.; Martyanov, M.A.; Poteomkin, A.K.; Kuzmin, I.V.; Mironov, S.Y. Shaping ellipsoidal laser pulses in the scheme with black analog masks for photoinjector applications. Laser Phys. Lett. 2023, 20, 125002. [Google Scholar] [CrossRef]
- Kuzmin, I.V.; Mironov, S.Y.; Martyanov, M.A.; Potemkin, A.K.; Khazanov, E.A. Highly efficient fourth harmonic generation of broadband laser pulses retaining 3D pulse shape. Appl. Opt. 2021, 60, 3128–3135. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, A.; Good, J.; Gross, M.; Krasilnikov, M.; Stephan, F. Towards Implementation of 3D Amplitude Shaping at 515 nm and First Pulseshaping Experiments at PITZ. Photonics 2024, 11, 6. [Google Scholar] [CrossRef]
- Galdi, A.; Balajka, J.; DeBenedetti, W.J.I.; Cultrera, L.; Bazarov, I.V.; Hines, M.; Maxson, J.M. Reduction of surface roughness emittance of Cs3Sb photocathodes grown via codeposition on single crystal substrates. Appl. Phys. Lett. 2021, 118, 244101. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Krasilnikov, M.; Oppelt, A.; Stephan, F.; Sertore, D.; Monaco, L.; Pagani, C.; Hillert, W. Development and Characterization of Multi-Alkali Antimonide Photocathodes for High-Brightness RF Photoinjectors. Micromachines 2023, 14, 1182. [Google Scholar] [CrossRef]
- Brinkmann, R.; Schneidmiller, E.; Sekutowicz, J.; Yurkov, M. Prospects for CW and LP operation of the European XFEL in hard X-ray regime. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2014, 768, 20–25. [Google Scholar] [CrossRef]
- Sekutowicz, J.; Ayvazyan, V.; Barlak, M.; Branlard, J.; Cichalewski, W.; Grabowski, W.; Kostin, D.; Lorkiewicz, J.; Merz, W.; Nietubyc, R.; et al. Research and development towards duty factor upgrade of the European X-ray Free Electron Laser linac. Phys. Rev. ST Accel. Beams 2015, 18, 50701. [Google Scholar] [CrossRef]
- Zhang, H.; Gilevich, S.; Miahnahri, A.; Alverson, S.; Brachmann, A.; Duris, J.; Franz, P.; Fry, A.; Hirschman, J.; Larsen, K.; et al. The LCLS-II Photoinjector Laser Infrastructure. arXiv 2023, arXiv:2307.12030. [Google Scholar] [CrossRef]
- Przygoda, K.; Rybaniec, R.; Butkowski, L.; Gerth, C.; Peier, P.; Schmidt, C.; Steffen, B.; Schlarb, H. MicroTCA.4-Based RF and Laser Cavities Regulation Including Piezocontrols. IEEE Trans. Nucl. Sci. 2017, 64, 1389–1394. [Google Scholar] [CrossRef]
- Häfner, T.; Strauß, J.; Roider, C.; Heberle, J.; Schmidt, M. Tailored laser beam shaping for efficient and accurate microstructuring. Appl. Phys. A 2018, 124, 111. [Google Scholar] [CrossRef]
- Wefers, M.M.; Nelson, K.A. Generation of high-fidelity programmable ultrafast optical waveforms. Opt. Lett. 1995, 20, 1047–1049. [Google Scholar] [CrossRef] [PubMed]
- Frumker, E.; Silberberg, Y. Phase and amplitude pulse shaping with two-dimensional phase-only spatial light modulators. J. Opt. Soc. Am. B 2007, 24, 2940–2947. [Google Scholar] [CrossRef]
- Weiner, A.M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 2000, 71, 1929–1960. [Google Scholar] [CrossRef]
- Dansette, P.-M.; Burokas, R.; Veselis, L.; Zaukevičius, A.; Michailovas, A.; Rusteika, N. Peculiarities of second harmonic generation with chirped femtosecond pulses at high conversion efficiency. Opt. Commun. 2020, 445, 124462. [Google Scholar] [CrossRef]
- Wang, H.; Weiner, A. Efficiency of short-pulse type-I second-harmonic generation with simultaneous spatial walk-off, temporal walk-off, and pump depletion. IEEE J. Quantum Electron. 2003, 39, 1600–1618. [Google Scholar] [CrossRef]
- Wang, T.; Xu, H.; Liu, Z.; Zhang, X.; Liu, J.; Xu, J.; Feng, L.; Li, J.; Liu, K.; Huang, S. Advanced drive laser system for a high-brightness continuous-wave photocathode electron gun. Opt. Express 2024, 32, 9699–9709. [Google Scholar] [CrossRef]
- Osvay, K.; Ross, I. Broadband sum-frequency generation by chirp-assisted group-velocity matching. J. Opt. Soc. Am. B 1996, 13, 1431–1438. [Google Scholar] [CrossRef]
- Willenberg, B.; Brunner, F.; Phillips, C.; Keller, U. High-power picosecond deep-UV source via group velocity matched frequency conversion. Optica 2020, 7, 485–491. [Google Scholar] [CrossRef]
- Kuzmin, I.; Mironov, S.; Gacheva, E.; Poteomkin, A.; Khazanov, E. Retaining 3D shape of picosecond laser pulses during optical harmonics generation. Appl. Opt. 2019, 58, 2678–2686. [Google Scholar] [CrossRef]
- Loisch, G.; Chen, Y.; Koschitzki, C.; Qian, H.; Gross, M.; Hannah, A.; Hoffmann, A.; Kalantaryan, D.; Krasilnikov, M.; Lederer, S.; et al. Direct measurement of photocathode time response in a high-brightness photoinjector. Appl. Phys. Lett. 2022, 120, 104102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).