Design of Diffractive Neural Networks for Solving Different Classification Problems at Different Wavelengths
Abstract
1. Introduction
2. Design of Spectral DNNs for Solving Several Classification Problems
3. Gradient Method for Designing Spectral DNNs
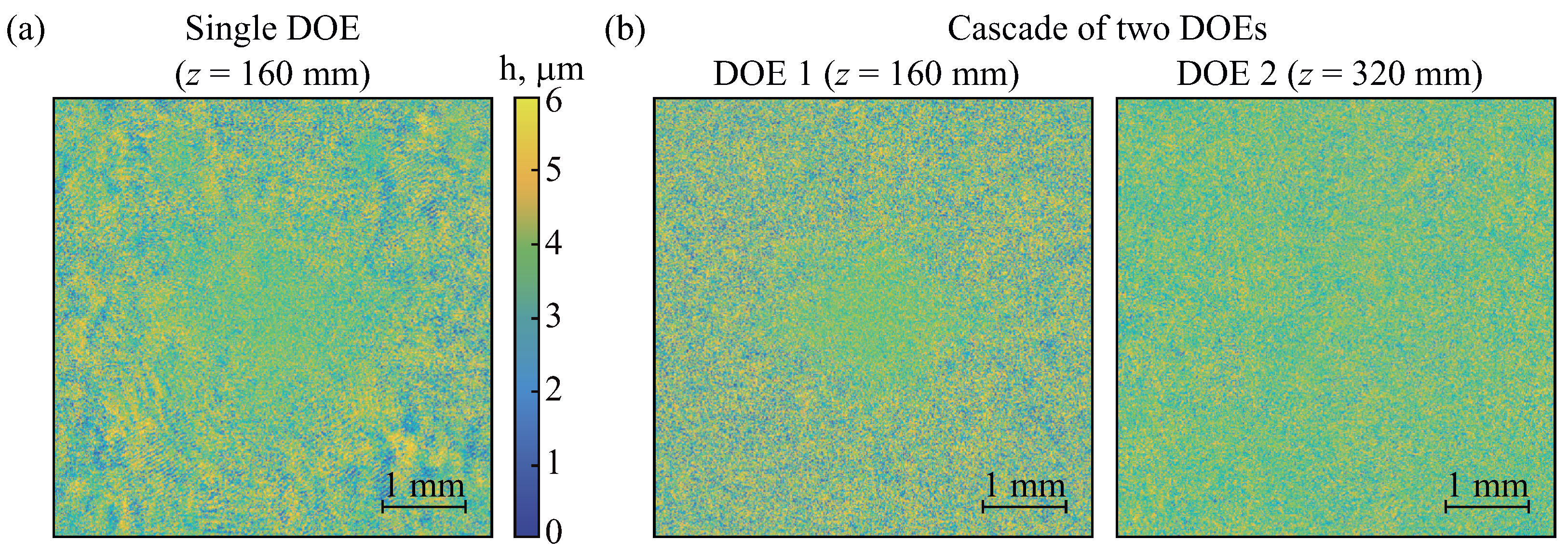
4. Design Examples of Spectral DNNs
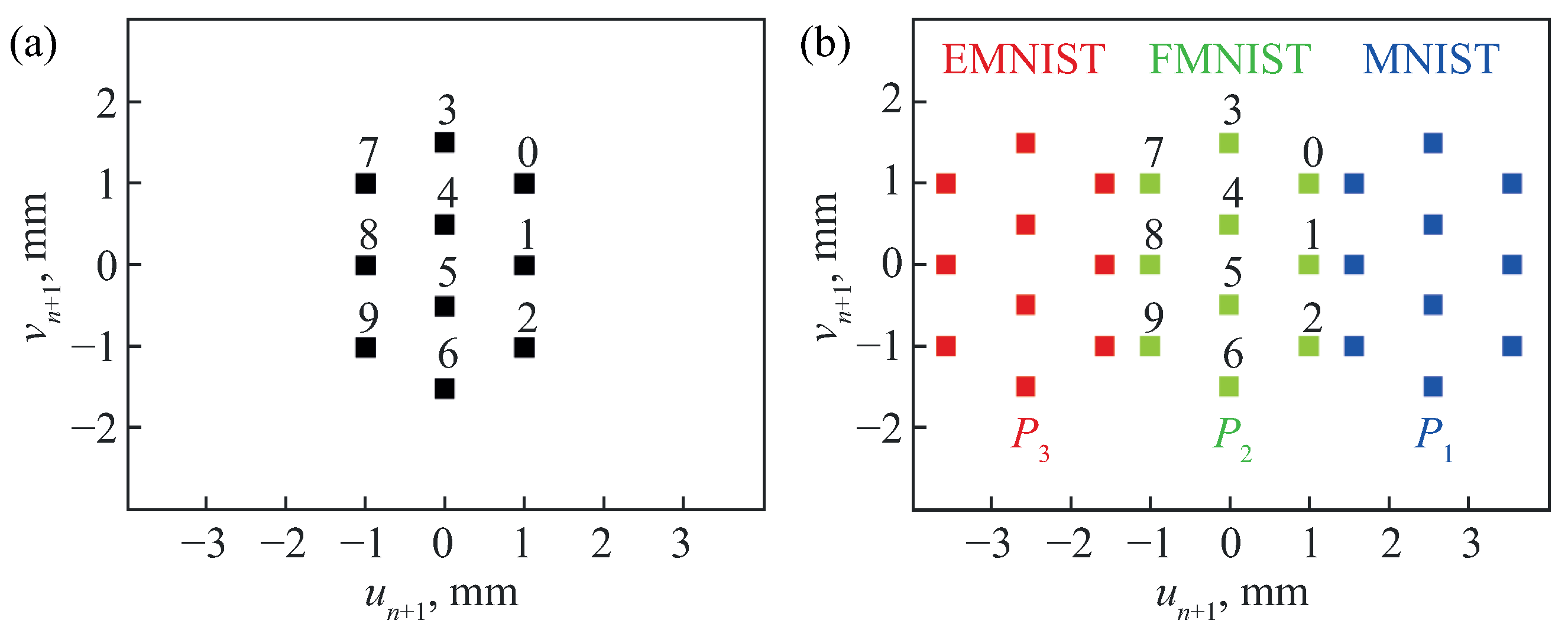
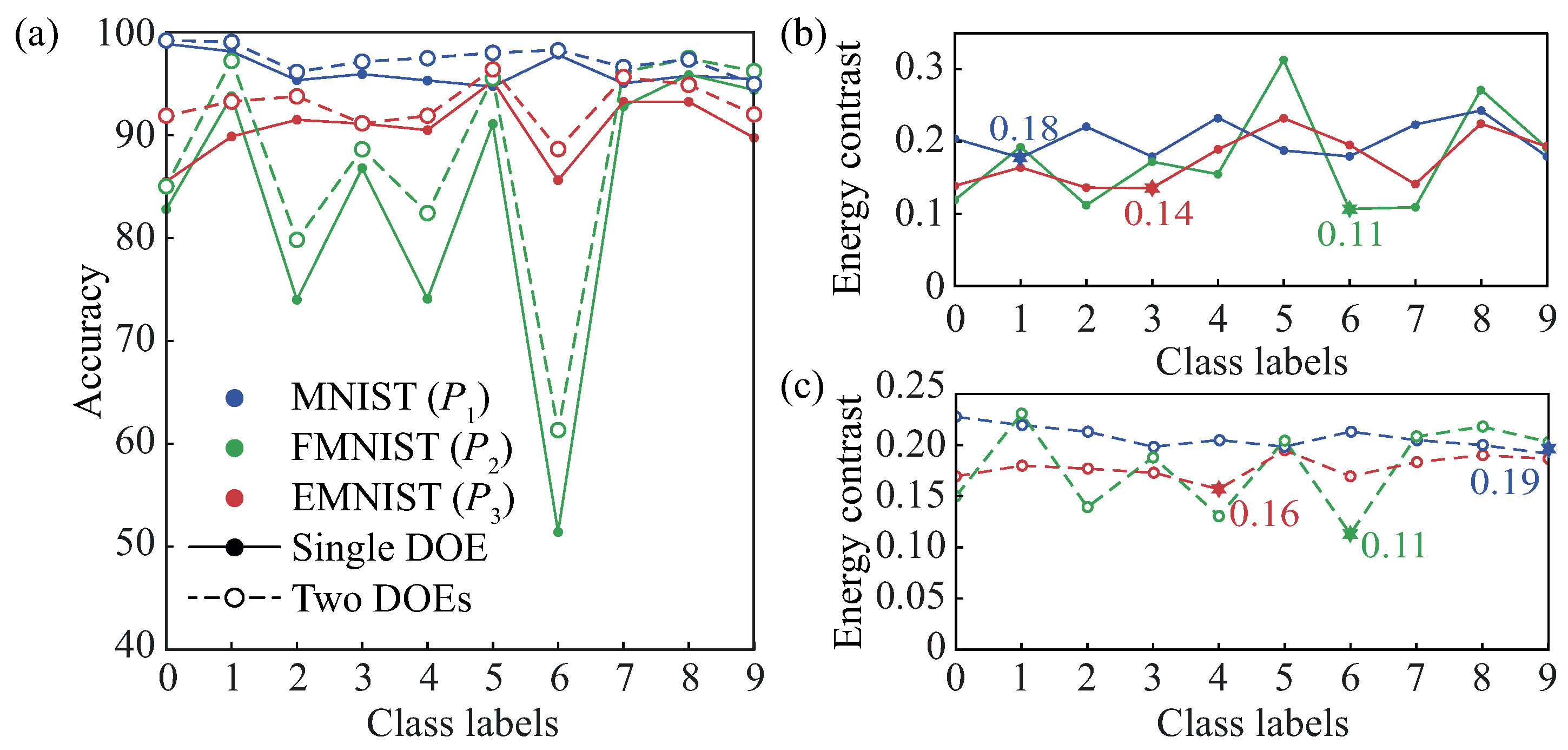
4.1. Sequential Solution of the Classification Problems
4.2. Parallel Solution of the Classification Problems
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Silva, A.; Monticone, F.; Castaldi, G.; Galdi, V.; Alù, A.; Engheta, N. Performing Mathematical Operations with Metamaterials. Science 2014, 343, 160–163. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zheng, H.; Kravchenko, I.I.; Valentine, J. Flat optics for image differentiation. Nat. Photonics 2020, 14, 316–323. [Google Scholar] [CrossRef]
- Estakhri, N.M.; Edwards, B.; Engheta, N. Inverse-designed metastructures that solve equations. Science 2019, 363, 1333–1338. [Google Scholar] [CrossRef]
- Kitayama, K.i.; Notomi, M.; Naruse, M.; Inoue, K.; Kawakami, S.; Uchida, A. Novel frontier of photonics for data processing—Photonic accelerator. APL Photonics 2019, 4, 090901. [Google Scholar] [CrossRef]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; Larochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Harris, N.C.; Carolan, J.; Bunandar, D.; Prabhu, M.; Hochberg, M.; Baehr-Jones, T.; Fanto, M.L.; Smith, A.M.; Tison, C.C.; Alsing, P.M.; et al. Linear programmable nanophotonic processors. Optica 2018, 5, 1623–1631. [Google Scholar] [CrossRef]
- Zhu, H.H.; Zou, J.; Zhang, H.; Shi, Y.Z.; Luo, S.B.; Wang, N.; Cai, H.; Wan, L.X.; Wang, B.; Jiang, X.D.; et al. Space-efficient optical computing with an integrated chip diffractive neural network. Nat. Commun. 2022, 13, 1044. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, M.; Jiang, X.D.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A.; Zhang, Y.; Yung, M.H.; et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 2021, 12, 457. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wu, B.; Cheng, J.; Dong, J.; Zhang, X. Compact, efficient, and scalable nanobeam core for photonic matrix-vector multiplication. Optica 2024, 11, 190–196. [Google Scholar] [CrossRef]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef]
- Yan, T.; Wu, J.; Zhou, T.; Xie, H.; Xu, F.; Fan, J.; Fang, L.; Lin, X.; Dai, Q. Fourier-space Diffractive Deep Neural Network. Phys. Rev. Lett. 2019, 123, 023901. [Google Scholar] [CrossRef]
- Zhou, T.; Fang, L.; Yan, T.; Wu, J.; Li, Y.; Fan, J.; Wu, H.; Lin, X.; Dai, Q. In situ optical backpropagation training of diffractive optical neural networks. Photon. Res. 2020, 8, 940–953. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, X.; Wu, J.; Chen, Y.; Xie, H.; Li, Y.; Fan, J.; Wu, H.; Fang, L.; Dai, Q. Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat. Photonics 2021, 15, 367–373. [Google Scholar] [CrossRef]
- Chen, H.; Feng, J.; Jiang, M.; Wang, Y.; Lin, J.; Tan, J.; Jin, P. Diffractive Deep Neural Networks at Visible Wavelengths. Engineering 2021, 7, 1483–1491. [Google Scholar] [CrossRef]
- Ferdman, B.; Saguy, A.; Xiao, D.; Shechtman, Y. Diffractive optical system design by cascaded propagation. Opt. Express 2022, 30, 27509–27530. [Google Scholar] [CrossRef]
- Zheng, S.; Xu, S.; Fan, D. Orthogonality of diffractive deep neural network. Opt. Lett. 2022, 47, 1798–1801. [Google Scholar] [CrossRef]
- Zheng, M.; Shi, L.; Zi, J. Optimize performance of a diffractive neural network by controlling the Fresnel number. Photon. Res. 2022, 10, 2667–2676. [Google Scholar]
- Wang, T.; Ma, S.Y.; Wright, L.G.; Onodera, T.; Richard, B.C.; McMahon, P.L. An optical neural network using less than 1 photon per multiplication. Nat. Commun. 2022, 13, 123. [Google Scholar] [CrossRef] [PubMed]
- Soshnikov, D.V.; Doskolovich, L.L.; Motz, G.A.; Byzov, E.V.; Bezus, E.A.; Bykov, D.A.; Mingazov, A.A. Design of cascaded diffractive optical elements for optical beam shaping and image classification using a gradient method. Photonics 2023, 10, 766. [Google Scholar] [CrossRef]
- Kulce, O.; Mengu, D.; Rivenson, Y.; Ozcan, A. All-optical synthesis of an arbitrary linear transformation using diffractive surfaces. Light. Sci. Appl. 2021, 10, 196. [Google Scholar] [CrossRef]
- Li, J.; Gan, T.; Bai, B.; Luo, Y.; Jarrahi, M.; Ozcan, A. Massively parallel universal linear transformations using a wavelength-multiplexed diffractive optical network. Adv. Photonics 2023, 5, 016003. [Google Scholar] [CrossRef]
- Mengu, D.; Tabassum, A.; Jarrahi, M.; Ozcan, A. Snapshot multispectral imaging using a diffractive optical network. Light. Sci. Appl. 2023, 12, 86. [Google Scholar] [CrossRef]
- Luo, Y.; Mengu, D.; Yardimci, N.T.; Rivenson, Y.; Veli, M.; Jarrahi, M.; Ozcan, A. Design of task-specific optical systems using broadband diffractive neural networks. Light. Sci. Appl. 2019, 8, 112. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, Y.; Negro, L.D. Design of ultracompact broadband focusing spectrometers based on diffractive optical networks. Opt. Lett. 2022, 47, 6309–6312. [Google Scholar] [CrossRef]
- Shi, J.; Chen, Y.; Zhang, X. Broad-spectrum diffractive network via ensemble learning. Opt. Lett. 2022, 47, 605–608. [Google Scholar] [CrossRef]
- Feng, J.; Chen, H.; Yang, D.; Hao, J.; Lin, J.; Jin, P. Multi-wavelength diffractive neural network with the weighting method. Opt. Express 2023, 31, 33113–33122. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef]
- Soifer, V.A.; Kotlyar, V.; Doskolovich, L. Iterative Methods for Diffractive Optical Elements Computation; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Ripoll, O.; Kettunen, V.; Herzig, H.P. Review of iterative Fourier-transform algorithms for beam shaping applications. Opt. Eng. 2004, 43, 2549–2556. [Google Scholar]
- Latychevskaia, T. Iterative phase retrieval in coherent diffractive imaging: Practical issues. Appl. Opt. 2018, 57, 7187–7197. [Google Scholar] [CrossRef]
- Deng, X.; Chen, R.T. Design of cascaded diffractive phase elements for three-dimensional multiwavelength optical interconnects. Opt. Lett. 2000, 25, 1046–1048. [Google Scholar] [CrossRef]
- Gülses, A.A.; Jenkins, B.K. Cascaded diffractive optical elements for improved multiplane image reconstruction. Appl. Opt. 2013, 52, 3608–3616. [Google Scholar] [CrossRef]
- Wang, H.; Piestun, R. Dynamic 2D implementation of 3D diffractive optics. Optica 2018, 5, 1220–1228. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Shi, J.; Wei, D.; Hu, C.; Chen, M.; Liu, K.; Luo, J.; Zhang, X. Robust light beam diffractive shaping based on a kind of compact all-optical neural network. Opt. Express 2021, 29, 7084–7099. [Google Scholar] [CrossRef] [PubMed]
- Buske, P.; Völl, A.; Eisebitt, M.; Stollenwerk, J.; Holly, C. Advanced beam shaping for laser materials processing based on diffractive neural networks. Opt. Express 2022, 30, 22798–22816. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Mingazov, A.A.; Byzov, E.V.; Skidanov, R.V.; Ganchevskaya, S.V.; Bykov, D.A.; Bezus, E.A.; Podlipnov, V.V.; Porfirev, A.P.; Kazanskiy, N.L. Hybrid design of diffractive optical elements for optical beam shaping. Opt. Express 2021, 29, 31875–31890. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Skidanov, R.V.; Bezus, E.A.; Ganchevskaya, S.V.; Bykov, D.A.; Kazanskiy, N.L. Design of diffractive lenses operating at several wavelengths. Opt. Express 2020, 28, 11705–11720. [Google Scholar] [CrossRef]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Cubillos, M.; Jimenez, E. Numerical simulation of optical propagation using sinc approximation. J. Opt. Soc. Am. A 2022, 39, 1403–1413. [Google Scholar] [CrossRef]




| Number of DOEs | Classification Problem | Wavelength (nm) | Sequential Regime | Parallel Regime | ||
|---|---|---|---|---|---|---|
| Overall Accuracy (%) | Minimum Contrast | Overall Accuracy (%) | Minimum Contrast | |||
| One | : MNIST | 457 | 96.41 | 0.17 | 96.25 | 0.18 |
| : FMNIST | 532 | 84.11 | 0.10 | 83.71 | 0.11 | |
| : EMNIST | 633 | 90.87 | 0.13 | 90.56 | 0.14 | |
| Two | : MNIST | 457 | 97.86 | 0.16 | 97.38 | 0.19 |
| : FMNIST | 532 | 86.93 | 0.11 | 87.96 | 0.11 | |
| : EMNIST | 633 | 93.07 | 0.12 | 92.93 | 0.16 | |
| Three | : MNIST | 457 | 97.89 | 0.20 | 97.41 | 0.21 |
| : FMNIST | 532 | 89.75 | 0.11 | 89.10 | 0.13 | |
| : EMNIST | 633 | 93.22 | 0.19 | 92.95 | 0.17 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Motz, G.A.; Doskolovich, L.L.; Soshnikov, D.V.; Byzov, E.V.; Bezus, E.A.; Golovastikov, N.V.; Bykov, D.A. Design of Diffractive Neural Networks for Solving Different Classification Problems at Different Wavelengths. Photonics 2024, 11, 780. https://doi.org/10.3390/photonics11080780
Motz GA, Doskolovich LL, Soshnikov DV, Byzov EV, Bezus EA, Golovastikov NV, Bykov DA. Design of Diffractive Neural Networks for Solving Different Classification Problems at Different Wavelengths. Photonics. 2024; 11(8):780. https://doi.org/10.3390/photonics11080780
Chicago/Turabian StyleMotz, Georgy A., Leonid L. Doskolovich, Daniil V. Soshnikov, Egor V. Byzov, Evgeni A. Bezus, Nikita V. Golovastikov, and Dmitry A. Bykov. 2024. "Design of Diffractive Neural Networks for Solving Different Classification Problems at Different Wavelengths" Photonics 11, no. 8: 780. https://doi.org/10.3390/photonics11080780
APA StyleMotz, G. A., Doskolovich, L. L., Soshnikov, D. V., Byzov, E. V., Bezus, E. A., Golovastikov, N. V., & Bykov, D. A. (2024). Design of Diffractive Neural Networks for Solving Different Classification Problems at Different Wavelengths. Photonics, 11(8), 780. https://doi.org/10.3390/photonics11080780






