Abstract
In this paper we present the principle of operation, fabrication and performance of a phosphorescent optical-fiber quasi-distributed sensor with contactless smartphone interrogation. An array of short strong corrugated long-period gratings (C-LPG) is used as a platform to spatially locate and to excite the phosphors whose time responses are temperature-dependent. The C-LPG array was fabricated using a pulsed CO2 laser. The quasi-distributed sensing array is excited by a UV LED and the normalized differential rise/decay time response measured by a smartphone is used as a measure of the temperature. The sensing spots have a volume smaller than 0.5 μL, can be separated by several millimeters to several meters and the interrogation can be simultaneous or in a sequence. The response and the sensitivity to temperature have been measured. The sensing array has been shown to measure abrupt and gradual temperature changes in space as well as time-dependent processes in the 0 °C to 100 °C range and with a measurement time of 1 s.
1. Introduction
The development and implementation of optical fiber-based luminescent temperature sensors has been developing for over two decades [1,2,3]. The use of optical fibers for the excitation of the sensing material and to lead-out the luminescence to a photo detector or spectrometer has definite advantages, such as the excitation of small-sized samples, construction of point dip sensors and isolation from electromagnetic interference. Both phosphorescent and fluorescent materials [4,5] have been proposed and tested as temperature-dependent luminescent probes. While luminescence caused by down conversion is typically used, materials with up-conversion excitation have also been proposed [6]. Both powders and polymers have been proposed and studied [7,8]. The characteristics of the luminescence that is used to retrieve the temperature can include the intensity [8], ratio of different peaks of the luminescent spectrum [5,9] and the decay time [10]. We have recently proposed [11,12] a fiber optic sensor based on the difference in the rise and decay time responses, and approach which increases the sensitivity and allows normalized signals to be used as a measure of temperature, which makes the sensor immune to power fluctuations of the source. Europium (Eu) and dysprosium (Dy)-doped strontium aluminates have been used as sensing materials since their rise and decay time responses have been studied in detail [13], especially the dependence on the excitation wavelength and on temperature [14,15]. In the above enumerated temperature sensors, either a spectrometer is used to measure the spectral changes or a photodetector to measure the total intensity changes. This means only one sensor at a time can be interrogated. In a number of cases, however, more than one sensor has to be interrogated, as is the case when we have to measure the spatial distribution of temperature and, consequently, thermal gradients and thermal flows. In such cases, the use of a smartphone as an interrogation unit that can detect both spectrally and time-dependent changes of luminescent materials is more appropriate [16]. As the smartphone can take 30 frames per second (fps), i.e., a measurement every 33.3 ms, it is perfectly suited to measure the rise and decay time responses of phosphorescent materials and perform time-gated measurements [17]. In case we need to excite more than one phosphorescent sensor for temperature measurements, the phosphor cannot be placed on the tip of a single fiber. Rather it should be deposited along the fiber which is not made to radiate light but to guide it. To solve the problem, corrugated fiber gratings can be used not as receivers of luminescence coming from outside the fiber [18] but as side-emitting excitation devices instead. Modification of the fiber surface and butt end using CO2 pulsed lasers, including the fabrication of corrugated gratings is well known and widely used [18,19,20] because of its simplicity and repeatability.
In this paper we propose a quasi-distributed optical-fiber phosphorescent temperature sensor, which is an array of corrugated long-period gratings (C-LPG) that side-radiate a portion of the UV light propagating along the fiber to excite phosphorescent sites deposited upon the corrugated sections. The rise and decay time responses of the phosphorescent light of the whole spatial array is simultaneously detected by a smartphone and the temperature of each sensing point is measured individually, thus revealing the spatial distribution of temperature and its evolution in time.
Section 2 is devoted to the principle of operation of the sensor array with more details on the rise/decay responses of the phosphor, the smartphone as an interrogation instrument and the fabrication of the CLPG array.
Section 3 presents the experimental set up and the results obtained on the characterization of the individual CLPGs and the performance of the sensing array in detecting abrupt and gradual spatial as well as time-dependent temperature changes.
Section 4 presents some comments and discussion based on the results obtained.
2. Principle of Operation
2.1. Temperature-Sensitive Phosphorescent Materials
2.1.1. Strontium Aluminates
There is a large variety [2,3,4,5,6,7] of temperature-dependent phosphors that have been proposed, tested and used for the development of temperature sensors. In this paper we prefer to use Eu2+ and Dy2+-doped strontium aluminate powder (SrAl2O4:Eu0.1,Dy0.2) synthesized by the combustion and solid-state reaction method [13]. Such powders have been extensively studied and their characteristics well-documented in our previous publications [12,14]. More particularly, we make use of sample #A from these previous studies because it has been found to be appropriate for temperature measurements in the 0 °C to 100 °C range [11,12,15]. Two properties of these materials are of interest: the temperature dependence of the luminescent intensity and the temperature dependence of their rise and decay time responses.
2.1.2. Temperature-Dependent Intensity Change
It is well known [4] that as temperature T increases, electrons release energy in non-radiative transitions rather than radiative recombinations thus reducing the intensity of luminescence which becomes temperature-dependent I(T). The normalized intensity ξ(T) over the whole spectrum is related to the absolute temperature T through the Arrhenius equation which, in its normalized form, reads as follows [15]:
where I(0) is the intensity at T = 0, A is the ratio of the attempt rate Γ0 and the radiative decay rate Γν of the 5d state [4] and k = 1.38 × 10−23 J/K is the Boltzmann constant, while ΔE is the activation energy of the transition corresponding to the band gap between the lowest energy of the Eu2+ 4f65d1 excited level and the bottom of the conduction band. The normalized intensity ξ(T) decreases slowly over a wide range of temperatures as shown elsewhere [4,15]. From the temperature dependence of the intensity I(T), the activation energy and the coefficient A for the sample used in our experiments were found as in [15]: ΔE ≈ −0.203 eV and A ≈ 395.
2.1.3. Rise and Decay Time Responses
The rise and decay time responses as well as the maximum intensity of the phosphorescence of Sr aluminates have been extensively studied and have been found to depend on the ambient temperature [13,14,15]. We consider here a phosphorescent sample excited by periodic rectangular pulses of a duty cycle
where Tp is the period and τp the duration of the ON (rise) response R(t), while Tp-τp is that of the OFF (decay) response D(t). For intensities RD = DD measured in the dark we use the following normalized quantities [11,12,13,14,15]:
In (3) and (4), R∞ is the total optical intensity for a sufficiently long illumination, D0 is the total optical intensity of the whole spectrum just before switching off the excitation, RD is the intensity measured in the dark, R(t) and D(t) are the emission intensities of the light emitted by the material after the excitation is switched ON (rise) and OFF (decay), t is the time in seconds, the amplitudes A, A0 and the powers α, α0 are constants, while τ and τ0 are time scaling parameters. These power law approximations have been found to hold after some initial instant t0 at which the ON response reaches the level a0 while the OFF response reaches b0. As shown in [14,15], the quantities b0 and 1 − a0 are a measure of the relative share of phosphorescence in luminescence.
The physical meaning of these power law parameters has been shown [15,16] to be the following. For the decay (OFF) response (Figure 1b), A stands for the level from which luminescence decays. A larger A′ > A stands for a stronger luminescence which shifts the response to a higher level (the upper A′, α dotted line in Figure 1b). The power α stands for the rate of decay. A larger α′ > α means a faster decay rate as illustrated by the A′, α′ dashed line in Figure 1b. For the rise (ON) response (Figure 1a), the physical meaning is reversed. A higher A′0 > A0 stands for a lower level from which luminescence starts increasing as shown by the dashed line in Figure 1a and is related to a larger share of phosphorescence while a lower level of A0 means a higher level of fluorescence. When a time-dependent measurement of the phosphorescence response is taken the intensity until the first measurement at t0 = Δt is missed, the exact time response is unknown and is noted by the red lines in Figure 1a,b. By that moment, the fluorescence process is over and what is measured afterwards is the slower phosphorescence afterglow [2,3,4]. Therefore, the level denoted by the solid circles from which the measurable response starts represents approximately the relative share of phosphorescence.
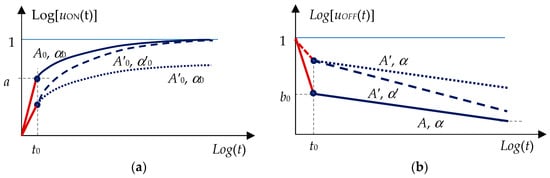
Figure 1.
Double log plot of normalized time responses: (a) rise (ON) time response; (b) decay (OFF) time response for different pairs of A, a and A0, a0.
All of the four power law parameters from (2) have been shown [14,15] to be dependent on the temperature T, the excitation duration τp and period Tp and hence on the duty cycle η so we can write the following:
As has been shown [15], the rise of temperature increases the relative share of phosphorescence and the rate of decay and the power parameters from (3) and (4) have been observed to increase with temperature until 60° and then slightly decrease. Figure 2 illustrates how the ON and OFF responses change as temperature increases form a lower T0 to a higher T. As seen, the increase in temperature causes a drop of the a0 level for the ON phase and a rise in the b0 level for the OFF phase.
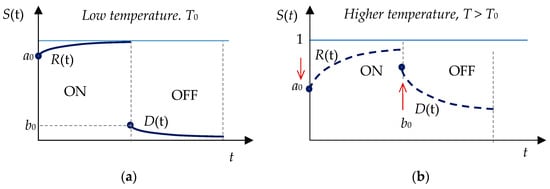
Figure 2.
Double log plot of normalized time responses for temperature changes: (a) rise (ON) time response; (b) decay (OFF) time response for different pairs of A, a and A0, a0.
Based on the above observation [15] as a measure of the temperature, we make use of the normalized differential signal defined as follows [11]:
where Ri and Di are the rise and decay intensities at the ith instant ti of the measurement after the start of, correspondingly, the rise and the decay time response [11]. This quantity can be negative depending on the phosphors used. To reduce fluctuations, we can calculate the ratio not at certain moments but over certain time intervals between instant tk and tm, in which case the quantity becomes the following:
As this quantity decreases with temperature, we shall make use of the quantity
which is in fact the decay normalized to ON + OFF intensity and which changes in the same direction as the temperature does and is immune to power fluctuations of the source.
2.2. Smartphone-Based Interrogation of Space-Multiplexed Temperature Sensors
The detection of the temperature-dependent time responses can be performed using either a spectrometer or a simple photodetector unit. The former can take a measurement about each 200 ms and measures the whole spectrum, while the latter in less than a millisecond but measures the integral intensity. Whichever method is used, only one sensor can be measured at a time.
2.2.1. The Smartphone as a Detection Unit
Should we need to take simultaneous measurements of several phosphorescence-based sensors in order to measure spatial temperature distributions, thermal gradients and associated thermal flows, we are in need of another interrogation approach. The natural solution is the use of the smartphone (or webcam) camera which offers the following advantages:
- It is sensitive in the 400 nm to 700 nm visible range where most of the phosphors emit;
- It can measure time-dependent light emissions at rates of 30 fps (33 ms) or 60 fps (16.7 ms) which allow typical phosphorescent time responses to be tracked;
- As the camera is based on 2D CCD arrays it can simultaneously measure a considerable number of independent spatially distributed luminescent point sensors;
- Touchless remote interrogation of spatially distributed sensors;
- Data processing capabilities;
- Connectivity to wireless sensing networks using Wi-Fi and Bluetooth technology.
We, therefore, explore the possibility of developing a spatially multiplexed quasi-distributed phosphorescent temperature sensor with smartphone interrogation.
2.2.2. Possible Interrogation Schemes
Figure 3 shows the two basic schemes for the excitation of a multitude of spatially distributed temperature-sensitive phosphorescent dots that can be interrogated simultaneously by a single smartphone camera if they are within its field of view.
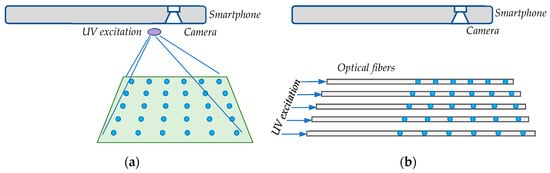
Figure 3.
Two basic schemes for simultaneous interrogation of spatially distributed phosphorescent dots: (a) with side illumination; (b) illumination using array of excitation fibers.
In the first scheme (Figure 3a), the sensing dots are illuminated from the side by a modulated UV LED whose emission wavelength is well outside the spectral range of the smartphone camera. The advantage of this approach is the simplicity of the construction, the disadvantage being the uneven illumination and need to place the sensing dots on a non-fluorescent surface.
In the second, the sensing phosphorescent dots are deposited upon the surface of an optical fiber with deliberately introduced deformations that cause parts of the guided excitation light to leave the fiber fore and excite the phosphors. The advantages of this approach are the controlled and stable excitation conditions, the freedom to attach the fibers to any type of surface and the possibility to integrate the excitation bus structure into a smart material. The disadvantage is the need to fabricate side-emitting deformations along the fiber and handling of the fiber. As the fiber can be up to tens of meters long, the fiber can be attached to large-scale structures whose surface temperatures can be monitored from a distance by a mobile phone.
2.3. Optical-Fiber Excitation Platform
As discussed in the introduction, a natural choice for an excitation and receiving medium is optical fiber. There are different approaches to produce a side-emitting fiber section, one of them being a taper usually produced with the help of a fusion splicer, and another being a partial chemical etching of the outer diameter. The third approach is to use a pulsed CO2 laser to produce predesigned and controllable corrugated fiber sections with desirable dimensions and depth of dips upon the outer fiber surface. The periods are as those of long-period gratings but since the fiber is heavily multimode, the specific spectral properties of LPGs in single-mode fibers are not observed. What is of interest is the side radiation, which in traditional LPGs is not of interest. We shall refer here to these undulated fiber structures as corrugated LPGs (C-LPG). The corrugated fiber grating was shown [7] to be appropriate to accept fluorescence from the surrounding medium, which implies it can be used for the reverse function—exciting luminescence in the area around the fiber.
2.3.1. CO2 Laser-Written Corrugated Long-Period Gratings (C-LPG)
To fabricate C-LPGs the radiation of a pulsed CO2 laser, emitting at 10.6 μm or 9.6 μm, is focused upon the fiber surface and the absorbed radiation melts the glass. Depending on the laser power and exposure duration, a valley is formed when the melted glass solidifies. Thus, corrugated gratings of N undulations of the fiber profile can be fabricated. The corrugated section of a fiber of outer diameter D is characterized by its period Λ, the undulation width w, its thickness of the waist d and inclination angle ψ as defined in Figure 4. The width w, the depth Δ = D − d and the angle ψ of the undulations are inter-related and depend on the laser power and number of laser scans needed to achieve the desired depth. The period Λ and the number of undulations m as well as the laser power and the laser beam scanning speed are preset.
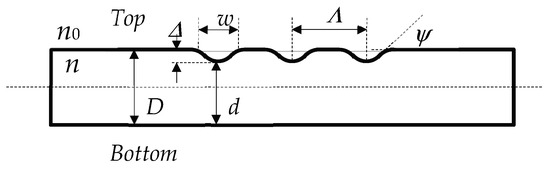
Figure 4.
Schematic representation of a corrugated optical fiber.
2.3.2. Radiation Diagram of a Corrugated LPG
A simple explanation of the radiation diagram is presented in Figure 5. For the sake of simplicity, a valley of the undulated profile is represented in a triangular shape whose inclination with respect to the fiber outer surface is α. Taking into account Snell’s law, we find that the rays in the fiber core propagate with respect to the axes through a maximum angle α such that
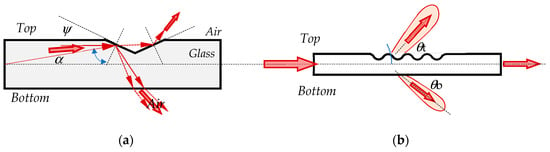
Figure 5.
Radiation pattern of the corrugated fiber structure in case the modulation angle ψ < 45°: (a) ray tracing; (b) resultant radiation diagram.
NA being the numerical aperture and n the core refractive index. Thus for a fiber of NA = 0.22 and n ≈ 1.46, α < 10°. In the case of ψ < 45°, the trajectory of a ray in the fiber which is almost parallel to the fiber axis is shown in Figure 5a, from which it is evident that part of the optical power will be reflected upward from the top side while the other part will be refracted and will be irradiated downward from the bottom side.
The resultant radiation diagram is illustrated in Figure 5b. Because the corrugated surface is on the top of the fiber the radiation pattern will be in the vertical plane as shown in the figure.
3. Experiments and Results
3.1. Inscription, Characterization and Functionalization of the Corrugated LPGs
The fabrication procedure of the sensing phosphorescent fiber optic arrays is as follows:
- (i)
- Inscription of the array of CLPGs;
- (ii)
- Measurement of the basic parameters of the corrugated structures;
- (iii)
- Deposition of the phosphorescent powder around the C-LPG.
We now proceed with the description of these steps.
3.1.1. Experimental Setup for C-LPG Inscription
The experimental setup to fabricate the corrugated fiber sections is shown in Figure 6a,b below. The corrugated long-period gratings were fabricated using a SYNRAD-pulsed CO2 laser (Synrad Inc., Mukilteo, WA, USA) emitting at λ = 10.6 μm, f = 20 kHz, and at 25% of maximum power; the focal length of the scanning head was 10 cm, and the spot size was about 100 μm. Arrays of varying numbers (5 to 10) of C-LPGs spaced at several millimeters (4 mm to 10 mm) were fabricated in a 105/125 μm multimode optical fiber. The fiber was stripped, wiped clean and installed under a 3 g tension. The writing process includes consecutive scans of the focused laser beam. During each scan all of the C-LPGs of the whole array are inscribed in a row. Each subsequent scan increases the depth Δ, the length l and the angle ψ of the dip which causes the power irradiated from the fiber to increase as well. As the number of scans per C-LPG of the array can be programmed, fine tuning of the parameters (Δ, l and ψ) can be realized.
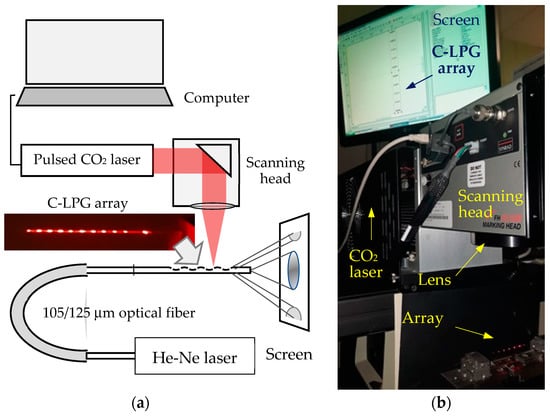
Figure 6.
Experimental set up. (a) The inset is a photo of the N = 10 corrugated gratings spaced at 4 mm and each containing 4 dips of Λ = 250 μm. (b) Photo of the experimental arrangement.
3.1.2. Characteristics of the Fabricated Corrugated Structures
The basic characteristics of interest are the dimensions of the C-LPG (dip depth Δ, length l and angle ψ) as well as the top and bottom radiation angles θt and θb. In Figure 7 we show examples of two C-LPGs of different strengths as a whole and of the individual dips, photos of their resultant radiation patterns and of the functionalized structures. We clearly see that a weaker C-LPG is characterized by lower values of Δ, l, ψ and top/bottom radiation angles θt and θb. To fix the phosphorescent power to the grating surface, a micro-drop of instant glue was deposited upon the corrugated surface and then minute quantities of the phosphorescent powder were added.

Figure 7.
Photos of two single C-LPGs each containing 4 dips of Λ = 250 μm of different depths with dimensions indicated: (a) a weaker C-LPG-#1; (b) a stronger C-LPG-#2, (c) radiation pattern with top and bottom radiation angles for the weaker C-LPG-#1; (d) same as (c) for the stronger C-LPG-#2; (e) C-LPG-#1 functionalized with Sr aluminate powder; (f) same as (e) but for the C-LPG-#2.
We next fabricated an array of 10 C-LPGs each of 4 dips with Λ = 250 μm and separated by 6 mm from one another. The photos of sections of the array and the side-radiation patterns are presented in Figure 8.

Figure 8.
Photos of arrays of C-LPGs each containing 4 dips of Λ = 250 μm of the same depths: (a) three C-LPGs in a row and two magnified; (b) one C-LPG of the array magnified with angle ψ indicated; (c) radiation pattern of the array of 10 C-LPGs with angles θt and θb indicated; (d) same as (c) magnified with only four C-LPGs visible.
As is seen, the side-irradiated power decreases with each subsequent C-LPG. If we assume that the transmission of each C-LPG is T0, then after the k-th grating, the resultant transmission will be
i.e., the optical power at the fiber output will decrease exponentially, which also means that the side-irradiated power will also decrease exponentially, which is visible in Figure 8c. There are three ways to equalize the side-irradiated power:
- To individually fine tune the dip depth and hence the radiation pattern and irradiated power;
- To excite the fiber from both ends;
- To deposit a reflector at the fiber output tip.
From the data in Figure 8a,b, we can find the experimental dependence of the dip angle ψ on the dip depth Δ, which is shown in Figure 9a. As should be expected, the dip angle increases with the depth but tends to saturate above 40 deg. On the other hand, the comparison with the side-radiation patterns shows that the radiation angled θt and θb increases with the dip angle. A more detailed study of the properties of C-LPGs in different types of fibers will be presented elsewhere.
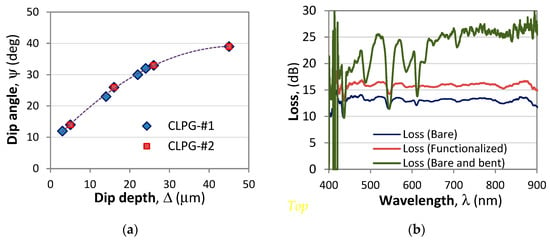
Figure 9.
Characteristics of the sensing array: (a) dependence of the dip angle ψ on the depth Δ; (b) spectral losses of a bare, a functionalized and a bent bare C-LPG sensing array.
Since the dips of the C-LPG introduce losses as demonstrated above, we present in Figure 9b their spectral dependences before and after functionalization with the phosphor. As is seen, the averaged losses of the bare C-LPG are around 13 dB and increase by about 3 dB after functionalization. The reason for this rise is the increased refractive index around the corrugated surface which causes more light to leave the fiber and is then additionally scattered. In both the bare and functionalized straight C-LPG arrays the loss ripples are of the same depth and same wavelengths. i.e., they do not depend on surrounding refractive index changes as in LPGs in single-mode fibers. When bent, the depths of the loss ripples increase to more than 10 dB, but do not shift spectrally. This indicates that the losses are from side radiation and not from wavelength-dependent intermodal coupling as in LPGs.
3.2. Performance of the Quasi-Distributed Sensor
3.2.1. Measurement Set-Up
In Figure 10 we present the setup for the contactless measurement of temperature by means of a mobile phone. It consists of two thermoelectric heaters/coolers TEC1 and TEC2 separated by a distance Δx that can vary their temperatures T1 and T2 from 5 °C to 75 °C and which is controlled by two thermistors. A thin (0.5 mm) metal plate was placed to thermally connect both TECs.
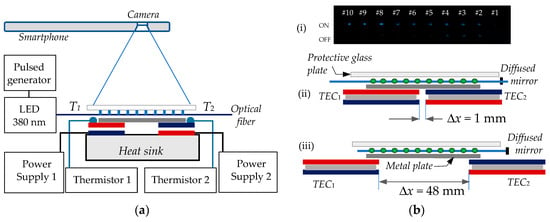
Figure 10.
Smartphone interrogation of the sensor array: (a) experimental setup; (b) the TEC and array arrangement: (i) photo of the ON/OFF luminescent array; (ii) arrangement for an abrupt temperature change (Δx = 1 mm); (iii) arrangement for a smooth temperature change Δx = 48 mm).
The array containing 10 sensing points was placed upon the metal plate. Since the volume of each sensor was less than 0.5 mm3, its temperature was strongly influenced by air currents. Therefore, a protective transparent glass plate was used to cover the sensing array. Since the optical power in the fiber decreases along the array (see Figure 8c), a diffused reflector created with 90% barium sulfate (BaSO4) and polyvinyl alcohol (PVA) was deposited at the fiber’s distal end which helped equalize the intensity of the luminescent sensors.
Three experiments were carried out. In the first, the array was placed entirely above one of the TECs and the responses of the ten sensors were taken at different temperatures in order to plot the N(T) dependence and the sensitivity ST = ΔN/ΔT.
In the second, the TECs were placed closed to each other with Δx = 1 mm. Sensing points #5 and #6 were placed exactly on either side of the separation (Figure 10b(i)).
In the third, the TECs were separated by Δx = 48 mm and sensors #1 and #10 were over the corresponding TECs (Figure 10b(ii)).
The UV LED (380 nm) was pulsed at a 1 Hz repetition rate (T = 1 s), a duty cycle of η = 50% and the mobile phone (Samsung A51) was placed at H = 15 cm above the sensing array. The frame rate of the smartphone was F = 30 fps, which translates into a sampling duration of Δt = 33.3 ms.
3.2.2. Results
Four consecutive experiments were performed to characterize the sensor array.
In the first experiment, the temperatures of the TEC were varied from 5 °C to 75 °C, during which a video clip was taken for at least ten ON/OFF cycles. The ON/OFF responses presenting the rise and decay curves averaged over 10 cycles for the 10th sensor is presented in Figure 11a. In this plot we clearly see the drop of phosphorescence with temperature as described by (1) and the slowing of the rise and decay responses in agreement with the comments in Section 2.1.3 and previous studies [11,15]. The red lines indicate the direction of change of the ON/OFF responses with temperature. Figure 11b presents the plots of the normalized decay NT as a function of the temperature for the 10th sensor as calculated from the plots in Figure 11a for three different summations in (7): i = 1 to 5, i = 1 to 8 and i = 1 to 15. The latter means integration (summation) over the whole ON and the whole OFF durations. We see that the temperature dependences ND(T) exhibit a change in slope and hence of the sensitivities for T > 45 °C. The calculated sensitivities in %/°C are listed to the right of the legend in Figure 11b.
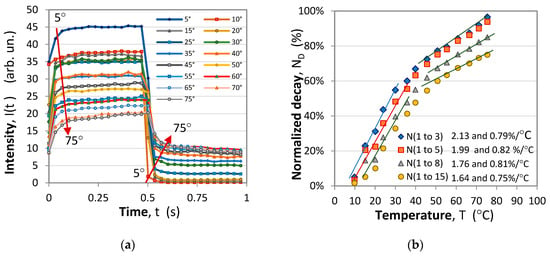
Figure 11.
Rise/Decay (ON/OFF) responses for temperatures from 5 °C to 75 °C: (a) ON/OFF time responses over a period T = 1 s and a duty factor η = 50%; (b) temperature dependence of the normalized decay NT(T).
Comparing the sensitivities we see that they drop by a factor of two above 45 °C and if the normalized difference is calculated over the initial moments of the ON/OFF responses the sensitivity is higher. This observation implies that the frequency of the LED modulation can be doubled and the period reduced to 0.5 s.
In the second experiment, several combinations of temperature pairs (T1, T2) of the two TECs were applied, as shown on each inset in Figure 12a, which is a photo of the array during ON and OFF durations. We calculate the normalized difference N of each sensor (k = 1 to 10) along the array and plot the dependence of N on the sensor number (the individual positions are shown in Figure 10b(i)) and the results are presented in Figure 12b. The plots show that the sensor array reproduces the abrupt change in temperature and the sensors #5 and #6 reflect the transition from the hot to the cold section.
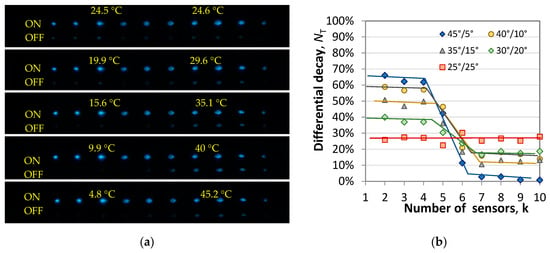
Figure 12.
Rise/decay (ON/OFF) responses for different pairs of temperatures at the two TECs separated by 1 mm: (a) photos of the sensor array during the ON and the OFF; (b) normalized differential signal N(T) for each sensor for an abrupt spatial change in the temperature.
In the third experiment, temperature pairs (T1, T2) were set with the TECs which were separated to a distance Δx = 48 mm (Figure 10b(iii)) so that sensor #1 was at the edge of the hot TEC while #10 was at the edge of the cold TEC. The responses were analogous to those from Figure 12b, but the transition was gradual in reproducing the temperature gradient along the metal plate connecting the TECs.
Figure 13 summarizes the typical response. Figure 13a compares the ON/OFF responses of sensors #10 (the coldest at 5 °C), #5 (in the middle at 40 °C) and #2 (the hottest at 75 °C), while Figure 13b presents the response of the whole array, i.e., the spatial distribution of the temperature along the metal plate. The dependence is almost linear as should be expected along a homogeneous thermally conductive medium. Figure 13c,d present the 1 − uON(t) = A0t−α0 and uOFF(t) = At−α expressions from (3) and (4) for sensor #1 at 75 °C and sensor #10 at the other end of the array at 5 °C. The power law fit yield A0 = 0.332, α0 = 0.16 for the ON and A = 0.2166, α = 0.199 for the OFF responses at 75 °C (hot end) versus A0 = 0.1044, α0 = 0.062 for the ON and A = 0.0188, α = 0.077 for the OFF responses at 5 °C (cold end) is in line with the reasoning in Section 2.1.3. Clearly, at high temperatures A, α, A0 and α0 are higher than at low temperatures, implying that at higher temperatures the relative share of phosphorescence in the overall luminescence process increases and the decay is faster as shown in [15].
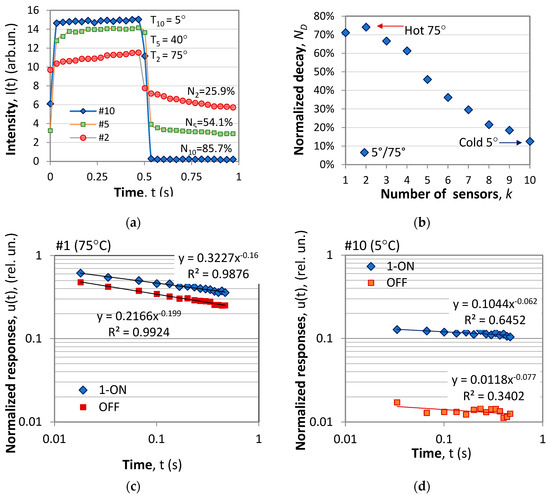
Figure 13.
Rise/decay (ON/OFF) responses at the extremities and the middle of the sensing array with 5 °C and 75 °C at the TECs: (a) ON/OFF time responses of the 2nd, 5th and 10th sensor with the corresponding temperatures and normalized differential signals; (b) normalized differential signal N(T) for each sensor which corresponds to the temperature gradient along the array; (c) 1 − uON(t) and uOFF(t) of sensor #10 at 75 °C; (d) same as (c) for sensor #1 at 5 °C.
In the fourth experiment, the time dependent response of the array was taken after the heaters/coolers were switched off at the end of the third experiment and the array returned to equilibrium. Figure 14a displays the evolution of the pulses of the sensor at the hot end detected by the mobile phone, and Figure 14b displays the normalized decay calculated for three different summations in (7): i = 1 to 5, i = 1 to 8 and i = 1 to 15. As is well seen, when summation is over a larger number of measurement points (i = 1 to 15) the ON and OFF phases fluctuations in the response from Figure 14b are weaker compared to the case of a smaller number of summation points (i = 1 to 5).
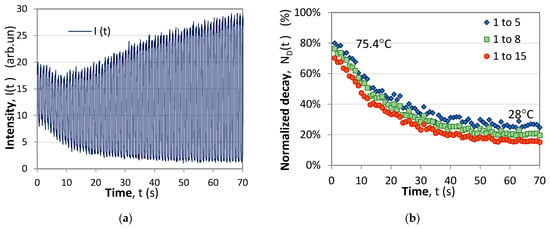
Figure 14.
Temperature relaxation process of the sensor at the hot end: (a) time response of the pulsed modulation during the process of reaching a thermal equilibrium; (b) normalized decay signals for three cases of summation.
4. Discussion
The presented quasi-distributed sensor principle of operation, construction and results require some comments and discussion.
In the first place, this is a further development of the optical-fiber (OF) temperature single-sensor arrangements presented elsewhere [12] and the application of mobile phones for the contactless interrogation of phosphorescent-based sensors.
Compared to previous phosphor sensors, the present structure is characterized by much smaller volumes of the used phosphor because of the efficient C-LPG-based excitation and a better time resolution because of the use of smartphones. The volume of the sensing region is an order of magnitude smaller than the one from [11] and can be further reduced to less than 0.1 μL with an improved phosphor deposition technology and more efficient luminescence. The time response resolution, which varies between 1 s for single pulse interrogation and 10 s for averaged measurements, can easily be reduced by a factor of two with a 30 fps frame rate and to about 0.2 s for a 60 fps frame rate, which would be an order of magnitude better compared to the sensor using spectrometer detection [11,16].
Second, the proposed scheme essentially is a spatially multiplexed sensor array and can be used because of the efficient side-excitation by means of the CLPG’s smaller diameter fibers. This generates two consequences. As the mass of the sensor decreases, the fiber endures a smaller bending diameter, which simplifies the handling and optical wiring of the fiber sensor. Next, since the fiber diameter is smaller, a bundle of up to 20 fibers can be powered with a single LED and hence a larger number of sensing arrays can be combined into a 2D sensing array. Such arrays can be simultaneously interrogated if the 2D sensing array is within the field of view of the smartphone camera. With an appropriate software and smartphone application, up to 20 × 10 individual points can be interrogated which implies the reconstruction of a temperature planar distribution. And hence the evaluation of heat flows and transfers. As the fiber platform can be up to tens of meters long, the individual sensors can be permanently attached to a control temperature at critical points over a fairly large area. In this case, the contactless interrogation is not simultaneous.
Third, the use of a smartphone offers the capability of contactless interrogation and the transfer of data to a larger Wi-Fi-compatible sensing network within the internet of things technology.
Fourth, the sensitivity of the sensor expressed in %/C depends on the following:
- (i)
- The phosphorescent material (also affects the range) as shown in [11,15];
- (ii)
- The duration over which rise and decay summation (integration) is carried out;
- (iii)
- The duty factor η.
- (iv)
- Fifth, the response time of the sensor essentially is affected by the following:
- (v)
- The rise/decay times of the phosphors; so to reduce it to the order of seconds, if needed, phosphors with similar decay times must be used;
- (vi)
- The modulation frequency (limited by the rise/decay times of the responses), whose increase will reduce the response time;
- (vii)
- The number of cycles over which the signal is averaged to reduce fluctuations, at the expense of response time;
- (viii)
- The frame rate of the smartphone whose increase (to 60 fps, for example) will reduce the response time.
Sixth, the temperature range of operation can be varied with a proper choice of phosphor. Phosphors having a short rise/decay time response at room temperature will have a longer response at higher temperatures and those with a long response at room temperature will have a shorter one at low temperatures. Although the principle of operation used for this sensor is the normalized differential rise/decay time response based on Equations (1) and (2), to increase the range at the expense of sensitivity and response time, only the intensity changes can be monitored. In this case the duty cycle should be closer to unity and the modulation frequency lower than 1 Hz to saturate the emission during the ON phase and monitor how the saturation level decreases with temperature following (1).
Compared to the variety of other types of temperature sensors [21,22,23], the quasi-distributed sensor demonstrated in this present paper has several basic features which define its specific niche:
- (i)
- It offers contactless simultaneous interrogation using smartphones or web cameras linked via Wi-Fi and Bluetooth to the internet as a part of a broader sensing network. None of the reported temperature sensors has this feature.
- (ii)
- It makes use of standard components of the lowest cost such as fibers and phosphorescent materials. It can also use polymer fiber. Interferometric sensors [21,22], be they Mach-Zender (MZI), Michelson (MI) or Fabry Perror (FP), require single-mode or specialty photonic crystal (PCF), holey (HOF) or microstructured (MOF) optical fibers.
- (iii)
- A single low-cost LED can excite and a single camera can interrogate several sensing arrays. Similar is the case of a quasi-distributed FBG sensing network using wavelength multiplexing whose temperature range is up to 100 °C. In contrast, all of the non-phosphorescent types of sensors are based on considerably more costly sources and detection equipment. The fluorescence-based sensors [21] require pulsed lasers and fast electronics or spectrometers to measure the intensity ratio of different fluorescence. Practically all of the interferometric and fiber Bragg grating (FBG) sensors function in the infrared communication band (1260 nm to 1630 nm) and employ orders of magnitude more costly sources and interrogation equipment and thus make practical sense mostly for multiplexed sensing networks.
- (iv)
- It is easy to fabricate by a high-productivity pulsed CO2 laser technique. In contrast, FBGs are made using an order of magnitude more costly excimer or femtosecond lasers [23]. The variety of interferometric sensors need more sophisticated splicers and for the micro-cavity-based MZI and FP interferometric sensors—a femtosecond laser [23].
- (v)
- The excitation fiber allows wiring of the sensing array along arbitrary paths to measure spatial distribution of temperature and thermal flows. This feature is similar to distributed temperature sensors (Raman, Brillouin [23] or Rayleigh type [22]) and quasi-distributed FBG sensors, which however need a special attachment in order to eliminate strain unless they measure both strain and temperature.
- (vi)
- Depending on the phosphor used, temperatures as high as several hundred degrees can be reached, which is what most of the silica-based fiber sensors offer. The sensor proposed here, however, offers no possibility for high temperature (above several hundred degrees) measurement.
- (vii)
- It can also be made from a polymer fiber [21], in which case the fabrication of the dips along the fiber would be even less costly. However, losses in the UV will be considerably higher so shorter fiber spans should be used.
Future research will be performed with other phosphors, types of fibers (such as 100 μm and 200 μm quartz polymer fibers) and smartphones having a 60 fps frame rate as well as the simultaneous interrogation of a larger number of arrays.
5. Conclusions
The results obtained allow the formulation of the following conclusions:
C1. An array of short and strong C-LPGs fabricated in a standard 105/125 μm multimode fiber has been proposed, developed and demonstrated as an excitation platform for a spatially quasi-distributed phosphorescent temperature sensor with contactless smartphone interrogation.
C2. The performance of the sensing array comprising 10 sensing points has been experimentally studied and has been demonstrated to correctly reproduce abrupt and gradual spatial changes in temperature caused by temperature gradients within the 5 °C to 75 °C range.
C3. Time dependent evolution of temperature with a 1 s measurement duration has been experimentally demonstrated for different integration ranges.
Author Contributions
Conceptualization, T.E.; methodology, T.E.; software, D.B. and K.N.; validation, S.F.; formal analysis, T.E.; investigation, S.F. and T.E.; resources, I.K.; data curation, K.N. and V.V.; writing—original draft preparation, T.E. and I.K.; writing—review and editing, T.E. and I.K.; visualization, T.E.; supervision, I.K.; project administration, T.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data can be provided upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aizawa, H.; Toba, E.; Katsumata, T.; Takahashi, J.; Matsunaga, K.; Komuro, S.; Morikawa, T. Long duration phosphor for a fiber-optic thermometer. In Proceedings of the 41st SICE Annual Conference, Osaka, Japan, 5–7 August 2002; pp. 2972–2975. [Google Scholar]
- McSherry, M.; Fitzpatrick, C.; Lewis, E. Review of luminescent based fibre optic temperature sensors. Sens. Rev. 2005, 25, 56–62. [Google Scholar] [CrossRef]
- Bao, Y.; Huang, Y.; Hoehler, M.; Chen, G. Review of fiber optic sensors for structural fire engineering. Sensors 2019, 19, 877. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Shang, Z.; Shi, M.; Cao, P.; Yang, B.; Zou, J. Preparing and testing the reliability of long afterglow SrAl2O4:Eu2+, Dy3+ phosphor flexible films for temperature sensing. RSC Adv. 2020, 10, 11418. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.; Wang, X.; Li, P.; Lv, M.; Hao, H.; Meng, L. An optical fiber temperature sensor based on fluorescence intensity ratio in Er3+/Yb3+ co-doped Gd2O3 phosphors. Ceram. Int. 2023, 49, 28913–28919. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, X.; Zhang, Y.; Li, Y.; Yao, X. Optical temperature sensing of up-conversion luminescent materials: Fundamentals and progress. J. Alloys Compd. 2020, 817, 152691. [Google Scholar] [CrossRef]
- Carrillo-Betancourt, R.A.; López-Camero, A.D.; Hernández-Cordero, J. Luminescent Polymer Composites for Optical Fiber Sensors. Polymers 2023, 15, 505. [Google Scholar] [CrossRef] [PubMed]
- Miluski, P.; Dorosz, D.; Mojda, J.; Kochanowicz, M.; Dorosz, J. Luminescent Polymer Optical Fibre Sensor for Temperature Measurement. Acta Phys. Pol. A 2015, 127, 730–733. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Shao, L.; Htwe, Z.; Yuan, P. Luminescence probe for temperature sensor based on fluorescence intensity ratio. Opt. Mater. Express 2017, 7, 1077. [Google Scholar] [CrossRef]
- Harun, S.W.; Yasin, M.; Hamzah, A.; Arof, H.; Ahmad, H. Temperature sensor based on lifetime measurement of Erbium fluorescence. J. Optoelectr. Adv. Mater. 2011, 13, 69–71. [Google Scholar]
- Fouzar, S.; Eftimov, T.; Kostova, I.; Dimitrova, T.L.; Benmounah, A.; Lakhssassi, A. A Simple Fiber Optic Temperature Sensor for Fire Detection In Hazardous Environment Based On Differential Time Rise/Decay Phosphorescence Response. IEEE Trans. Instr. Meas. 2022, 71, 9508908. [Google Scholar] [CrossRef]
- Fouzar, S.; Kostova, I.; Eftimov, T.A.; Nikolov, K. Phosphorescent Fibre Optic Tip Temperature Sensor. In Proceedings of the 4th International Conference on Phosphor Thermometry, Becici, Montenegro, 26–30 August 2024. Accepted. [Google Scholar]
- Eftimov, T.; Kostova, I.; Arapova, A.; Patronov, G. Rise and decay time responses of Sr aluminate phosphorescent materials. J. Lumin. 2021, 235, 117985. [Google Scholar] [CrossRef]
- Fouzar, S.; Kostova, I.; Eftimov, T.; Benmounah, A.; Ouchabane, M.; Lakhssassi, A. Excitation and spectral dependence of the rise and decay time responses of Eu2+ and Dy3+ doped strontium aluminates. J. Mater. Sci. Mater. Electron. 2022, 33, 20962–20980. [Google Scholar] [CrossRef]
- Fouzar, S.; Eftimov, T.; Kostova, I.; Benmounah, A.; Lakhssassi, A. Effects of temperature on the time responses of strontium aluminates. Opt. Mater. 2021, 122, 111619. [Google Scholar] [CrossRef]
- Eftimov, T.A.; Kostova, I.; Peltekov, A.; Hristova, K.; Brabant, D.; Fouzar, S.; Nikolov, K. A Study of Strontium Aluminates for All Optical Contactless Sensing Applications Using Smartphone Interrogation. Opt. Laser Technol. 2024, 176, 110965. [Google Scholar] [CrossRef]
- Fratto, B.E.; Culver, E.L.; Davis, G.; Deans, R.; Goods, J.B.; Hwang, S.; Keller, N.K.; Lawrence, J.A.; Petty, A.R.; Swager, T.M.; et al. Leveraging a smartphone to perform time-gated luminescence measurements. PLoS ONE 2023, 18, e0293740. [Google Scholar] [CrossRef] [PubMed]
- Chiniforooshan, Y.; Ma, J.; Bock, W.J.; Hao, W.; Wang, Z.Y. Corrugated Fiber Grating for Detection of Lead Ions in Water. J. Light. Technol. 2015, 33, 2549–2553. [Google Scholar] [CrossRef]
- Irawan, R.; Chuan, T.S.; Meng, T.C.; Ming, T.K. Rapid Constructions of Microstructures for Optical Fiber Sensors Using a Commercial CO2 Laser System. Open Biomed. Eng. J. 2008, 2, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Zhao, L.; Chen, M.; Cheng, J.; Yin, Z.; Liu, Q.; Yang, H.; Liao, W. Physical mechanism of pulsed laser interaction with fused silica optics during CO2 laser mitigation process. J. Non-Cryst. Solids 2021, 558, 120662. [Google Scholar] [CrossRef]
- Szczerska, M. Temperature Sensors Based on Polymer Fiber Optic Interferometer. Chemosensors 2022, 10, 228. [Google Scholar] [CrossRef]
- Yang, T.; Wang, X. Decoupling and Simultaneous Measurement of Nonuniform Strain and Temperature Using a Single Distributed Optical Fiber Ring. Exp. Mech. 2022, 62, 1531–1552. [Google Scholar] [CrossRef]
- Ma, S.; Xu, Y.; Pang, Y.; Zhao, X.; Li, Y.; Qin, Z.; Liu, Z.; Lu, P.; Bao, X. Optical Fiber Sensors for High-Temperature Monitoring: A Review. Sensors 2022, 22, 5722. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).