Improving the Two-Color Temperature Sensing Using Machine Learning Approach: GdVO4:Sm3+ Prepared by Solution Combustion Synthesis (SCS)
Abstract
1. Introduction
2. Materials and Methods
3. Results
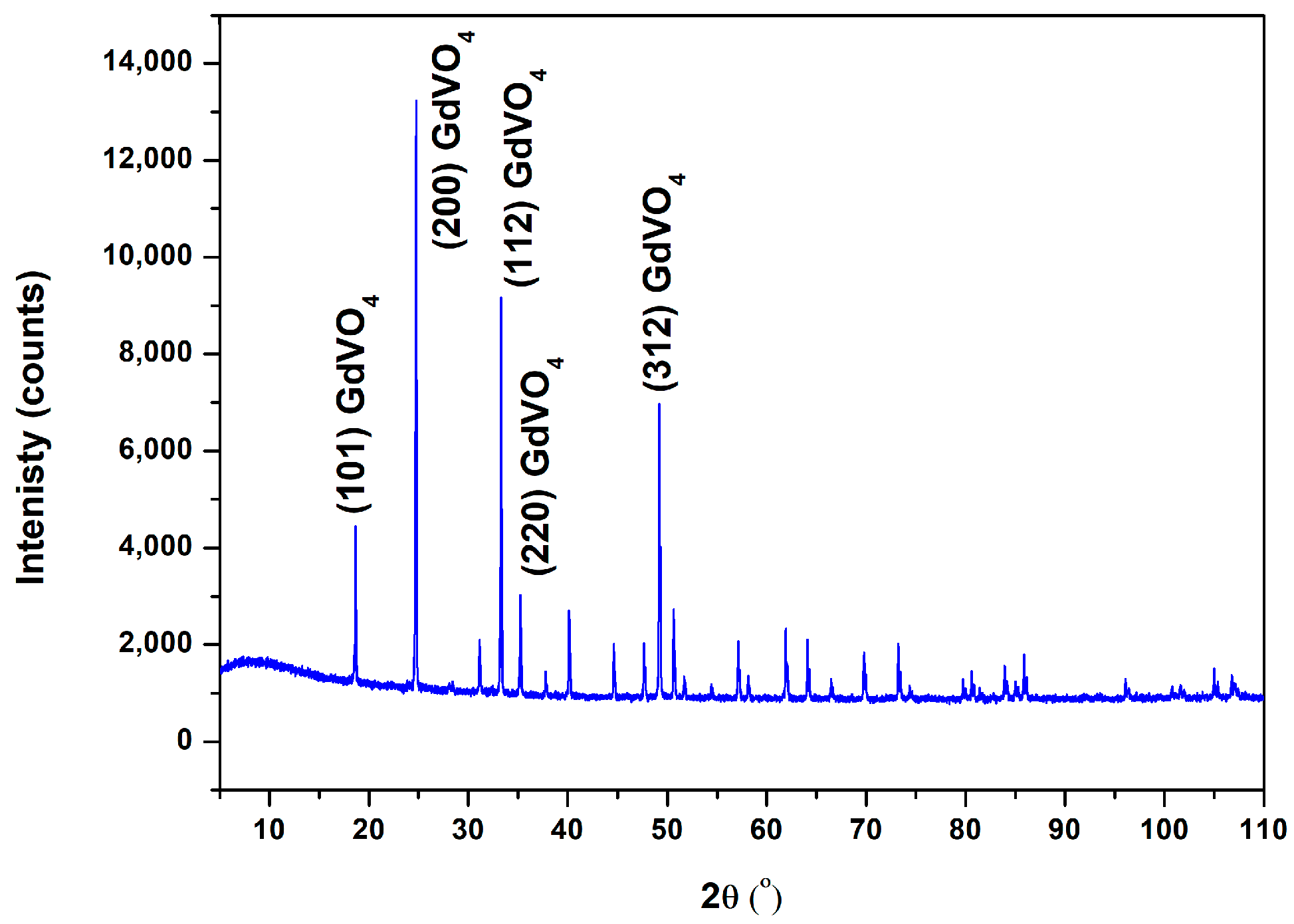
3.1. TEM, XRD, and SEM Study
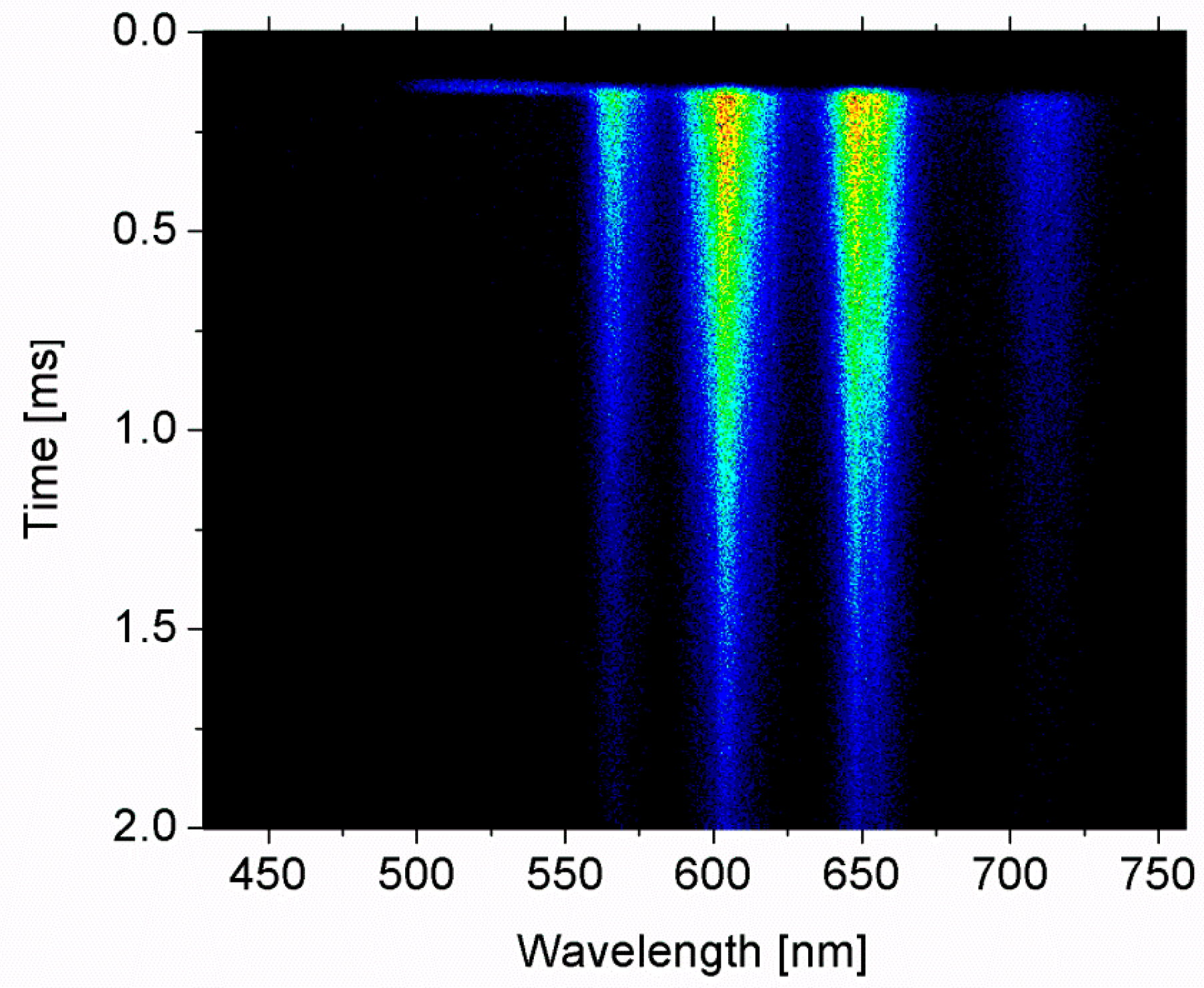
3.2. Photoluminescence and Lifetime Analysis
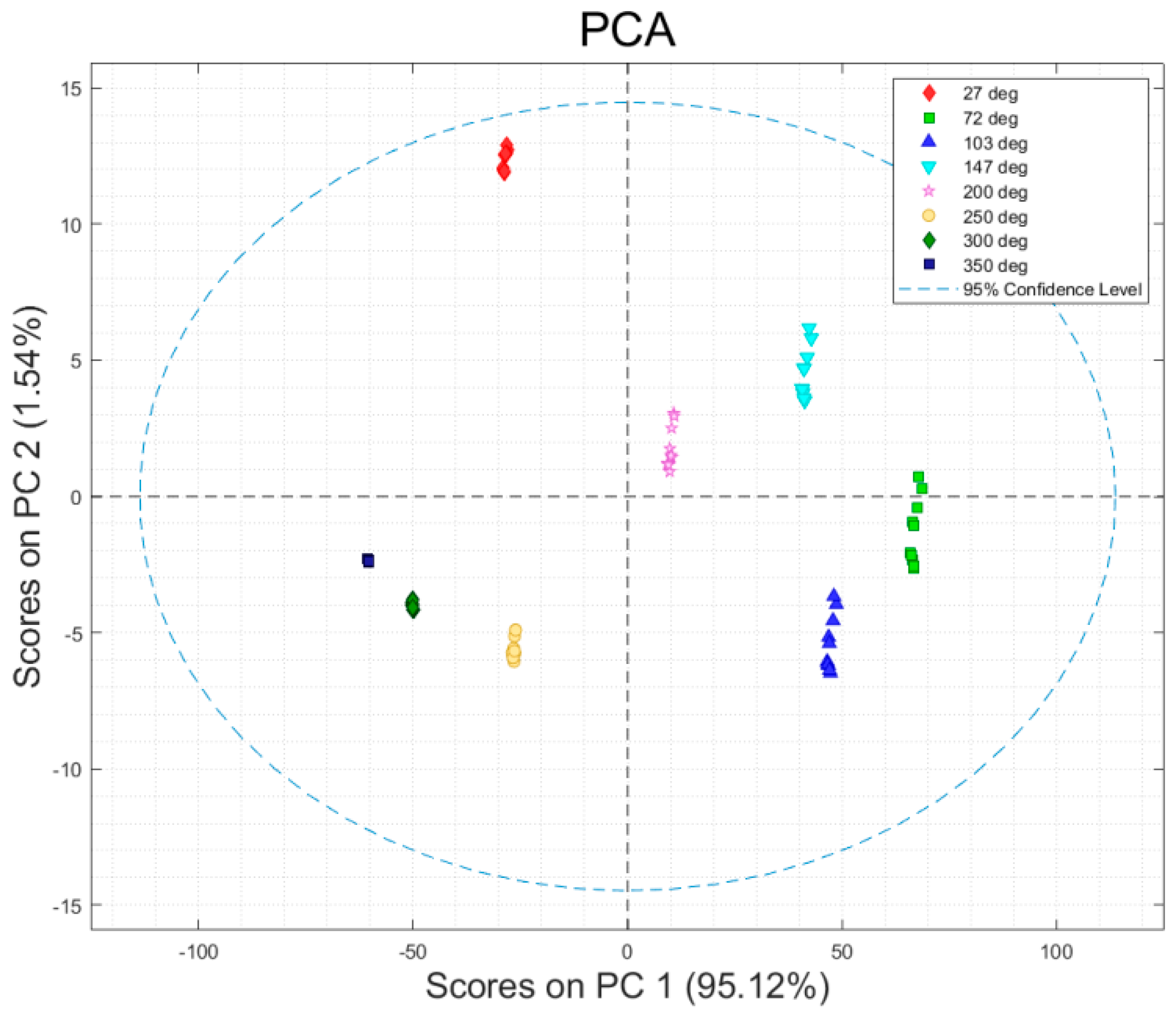
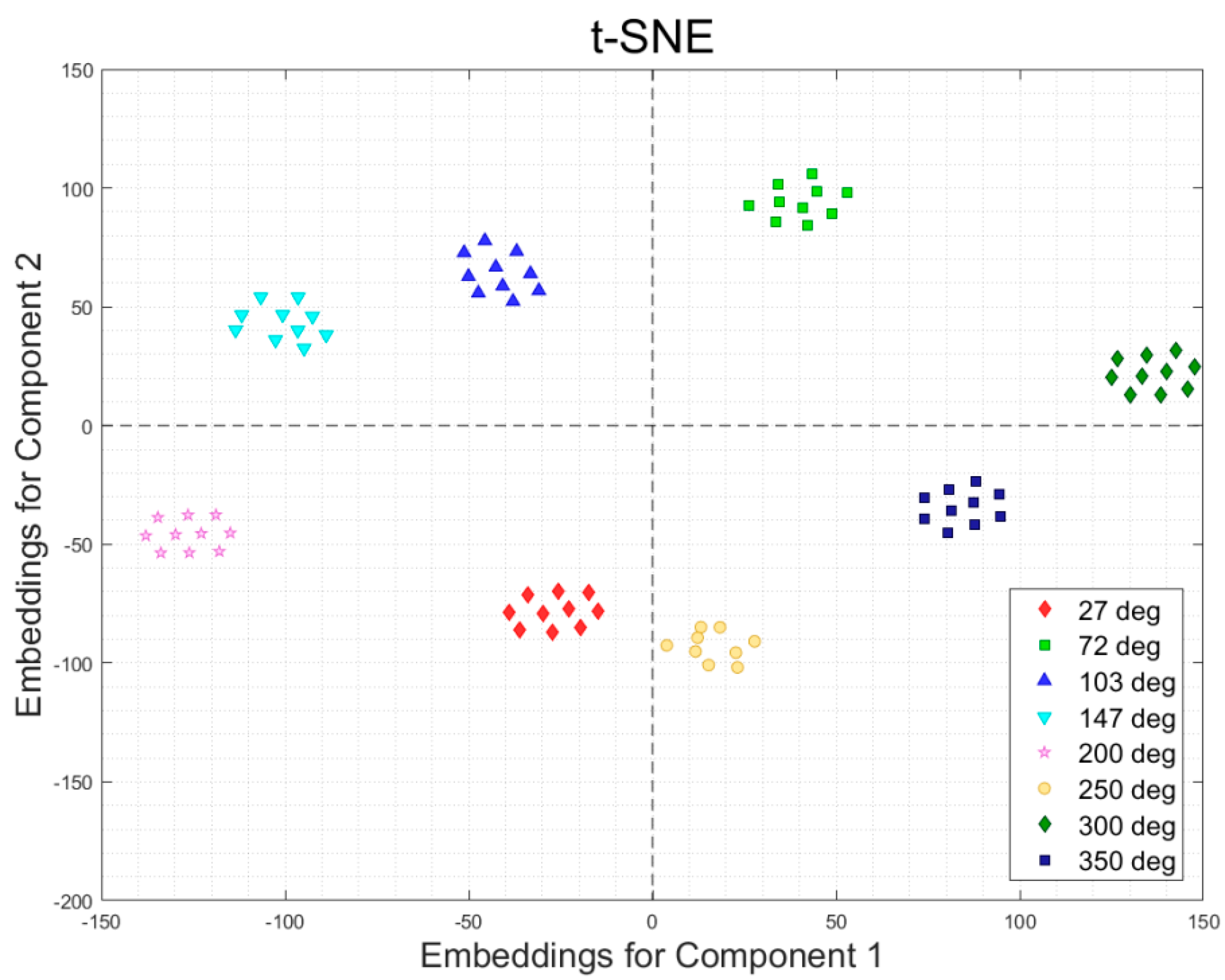
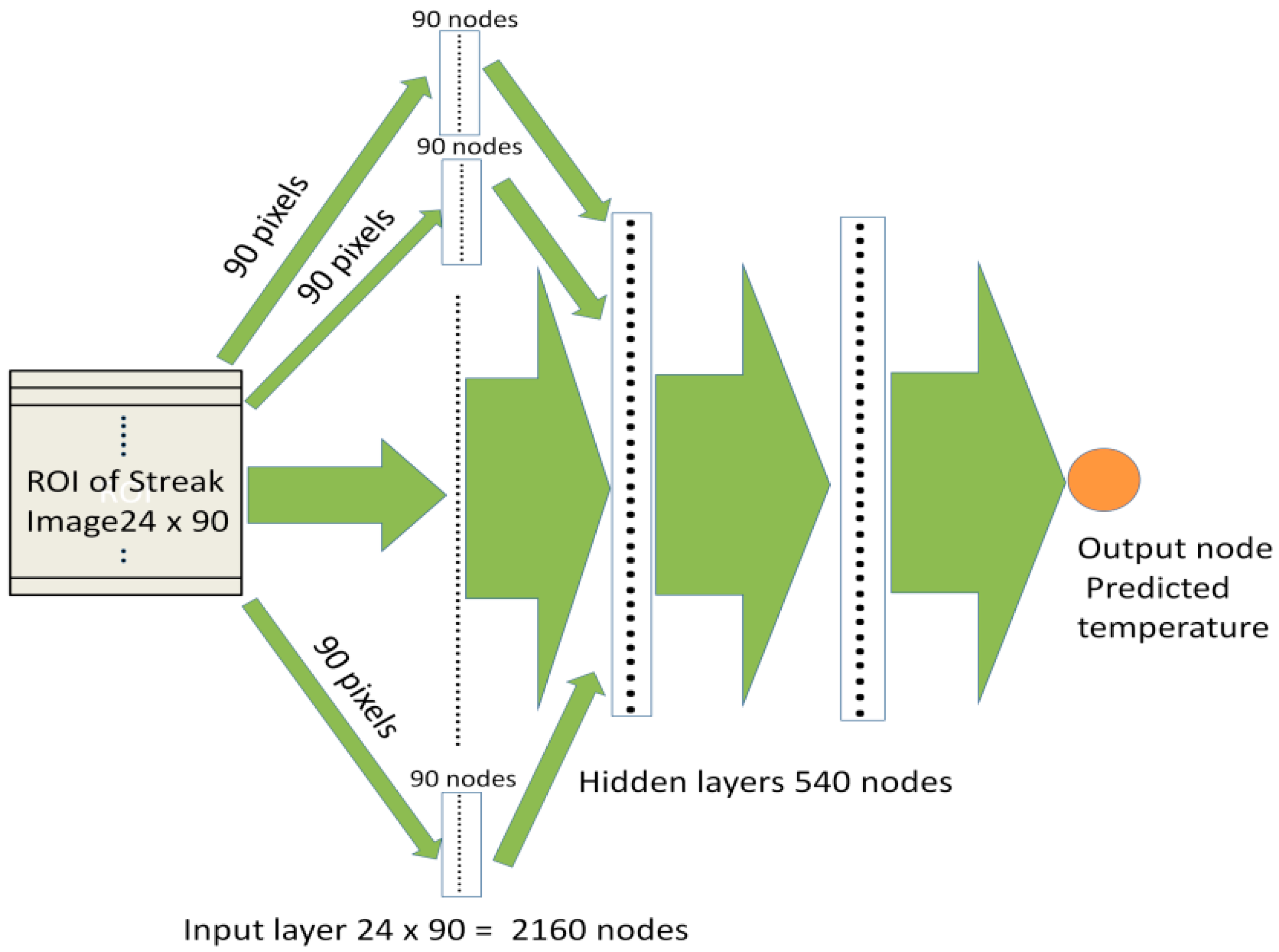
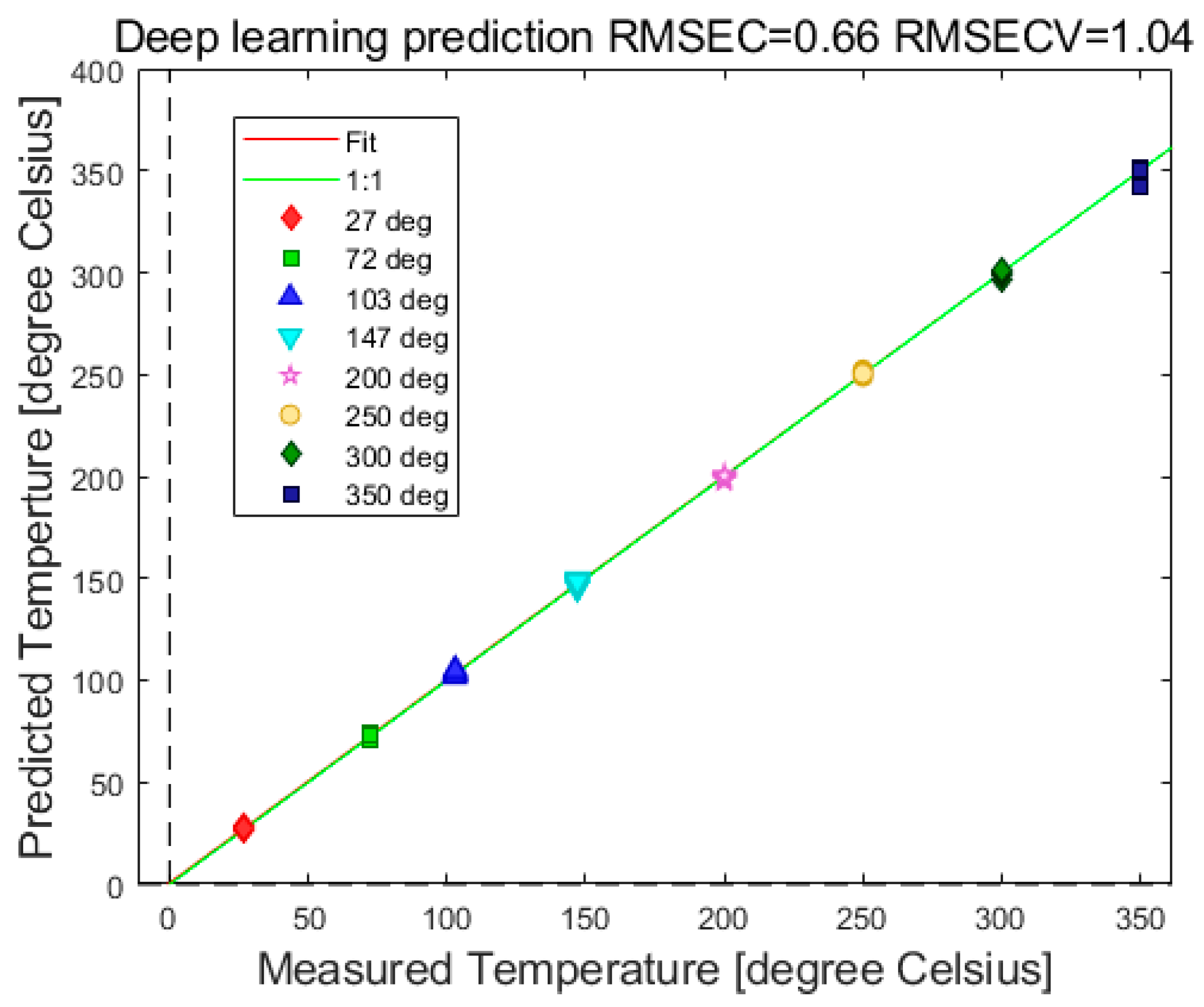
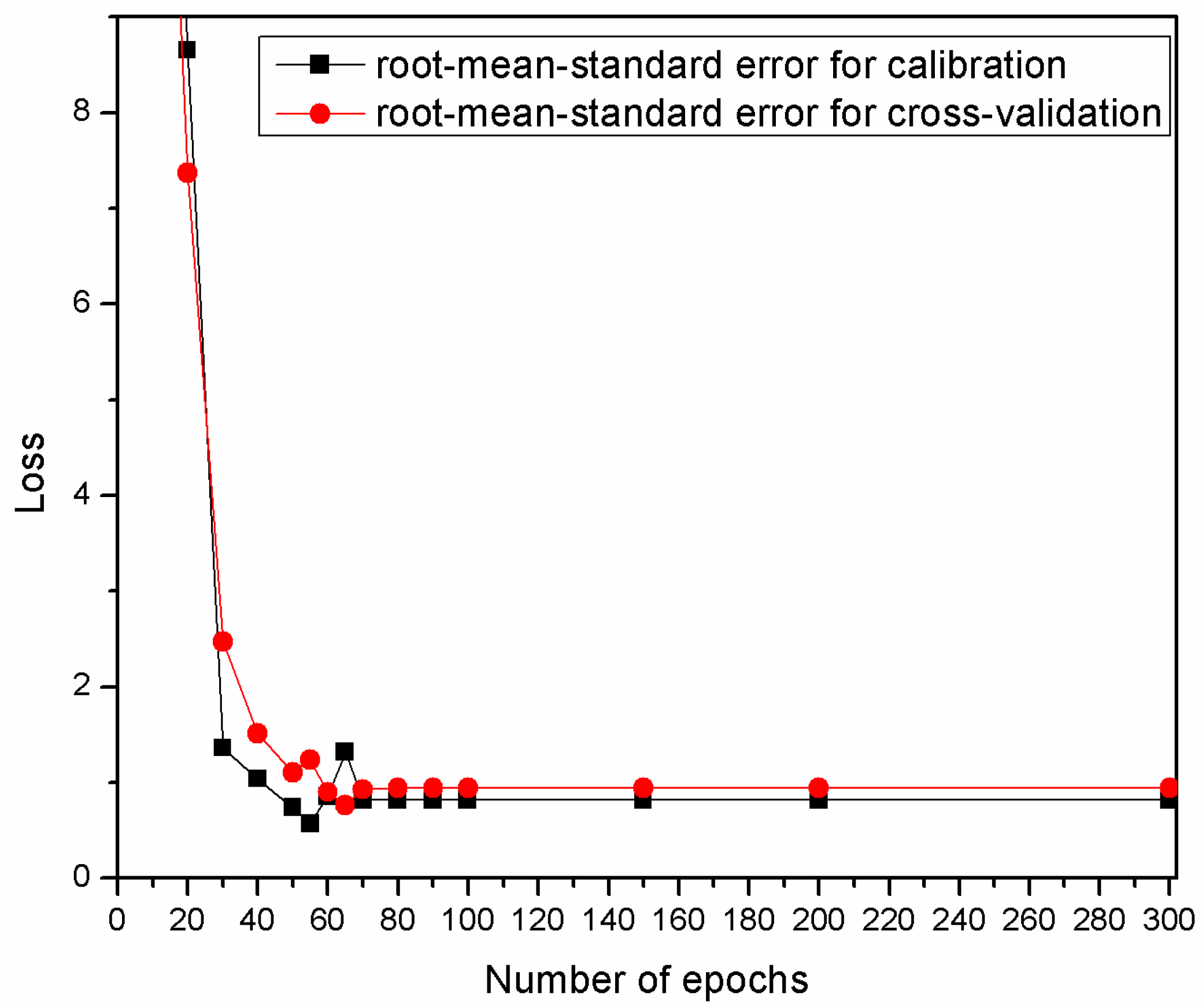
3.3. Photoluminescence and Lifetime Analysis Temperature Dependence of Photoluminescence
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rabasovic, M.S.; Krizan, J.; Savic-Sevic, S.; Mitric, M.; Rabasovic, M.D.; Marinkovic, B.P.; Sevic, D. Orange-Reddish Light Emitting Phosphor GdVO4:Sm3+ Prepared by Solution Combustion Synthesis. J. Spectrosc. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Nikolić, M.G.; Jovanović, D.J.; Đorđević, V.; Antić, Ž.; Krsmanović, R.M.; Dramićanin, M.D. Thermographic properties of Sm3+ -doped GdVO4 phosphor. Phys. Scr. 2012, T149, 014063. [Google Scholar] [CrossRef]
- Nikolić, M.G.; Antić, Ž.; Ćulubrk, S.; Nedeljković, J.M.; Dramićanin, M.D. Temperature sensing with Eu3+ doped TiO2 nanoparticles. Sens. Actuators B Chem. 2014, 201, 46–50. [Google Scholar] [CrossRef]
- Dramićanin, M.D.; Antić, Ž.; Ćulubrk, S.; Ahrenkiel, S.P.; Nedeljković, J.M. Self-referenced luminescence thermometry with Sm3+ doped TiO2 nanoparticles. Nanotechnology 2014, 25, 485501. [Google Scholar] [CrossRef] [PubMed]
- Lojpur, V.; Nikolić, M.G.; Jovanović, D.; Medić, M.; Antić, Ž.; Dramićanin, M.D. Luminescence thermometry with Zn2SiO4:Mn2+ powder. Appl. Phys. Lett. 2013, 103, 141912. [Google Scholar] [CrossRef]
- Lojpur, V.; Ćulubrk, S.; Dramićanin, M.D. Ratiometric luminescence thermometry with different combinations of emissions from Eu3+ doped Gd2Ti2O7 nanoparticles. J. Lumin. 2016, 169, 534–538. [Google Scholar] [CrossRef]
- Aldén, M.; Omrane, A.; Richter, M.; Särner, G. Thermographic phosphors for thermometry: A survey of combustion applications. Prog. Energy Combust. Sci. 2011, 37, 422–461. [Google Scholar] [CrossRef]
- Chatzidakis, M.; Botton, G.A. Towards calibration-invariant spectroscopy using deep learning. Sci. Rep. 2019, 9, 2126. [Google Scholar] [CrossRef]
- Dramićanin, T.; Zeković, I.; Periša, J.; Dramićanin, M.D. The Parallel Factor Analysis of Beer Fluorescence. J. Fluoresc. 2019, 29, 1103–1111. [Google Scholar] [CrossRef]
- Ranamukhaarachchi, S.A.; Peiris, R.H.; Moresoli, C. Fluorescence spectroscopy and principal component analysis of soy protein hydrolysate fractions and the potential to assess their antioxidant capacity characteristics. Food Chem. 2017, 217, 469–475. [Google Scholar] [CrossRef]
- Weng, S.; Yuan, H.; Zhang, X.; Li, P.; Zheng, L.; Zhao, J.; Huang, L. Deep learning networks for the recognition and quantitation of surface-enhanced Raman spectroscopy. Anal. 2020, 145, 4827–4835. [Google Scholar] [CrossRef]
- Cui, J.; Xu, W.; Yao, M.; Zheng, L.; Hu, C.; Zhang, Z.; Sun, Z. Convolutional neural networks open up horizons for luminescence thermometry. J. Lumin. 2023, 256, 119637. [Google Scholar] [CrossRef]
- Ximendes, E.; Marin, R.; Carlos, L.D.; Jaque, D. Less is more: Dimensionality reduction as a general strategy for more precise luminescence thermometry. Light Sci. Appl. 2022, 11, 237. [Google Scholar] [CrossRef]
- Barbon, S.; da Costa Barbon, A.P.A.; Mantovani, R.G.; Barbin, D.F. Machine Learning Applied to Near-Infrared Spectra for Chicken Meat Classification. J. Spectrosc. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Geronimo, B.C.; Mastelini, S.M.; Carvalho, R.H.; Barbon Júnior, S.; Barbin, D.F.; Shimokomaki, M.; Ida, E.I. Computer vision system and near-infrared spectroscopy for identification and classification of chicken with wooden breast, and physicochemical and technological characterization. Infrared Phys. Technol. 2019, 96, 303–310. [Google Scholar] [CrossRef]
- Junior, S.B.; Mastelini, S.M.; Barbon, A.P.A.; Barbin, D.F.; Calvini, R.; Lopes, J.F.; Ulrici, A. Multi-target prediction of wheat flour quality parameters with near infrared spectroscopy. Inf. Process. Agric. 2020, 7, 342–354. [Google Scholar] [CrossRef]
- Nolasco Perez, I.M.; Badaró, A.T.; Barbon, S.; Barbon, A.P.A.; Pollonio, M.A.R.; Barbin, D.F. Classification of Chicken Parts Using a Portable Near-Infrared (NIR) Spectrophotometer and Machine Learning. Appl. Spectrosc. 2018, 72, 1774–1780. [Google Scholar] [CrossRef] [PubMed]
- Rabasovic, M.S.; Savic-Sevic, S.; Križan, J.; Matovic, B.; Nikolic, M.; Sevic, D. Time resolved study of temperature sensing using Gd 2 O 3:Er,Yb: Deep learning approach. Phys. Scr. 2023, 98, 116003. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Rabasović, M.D.; Murić, B.D.; Čelebonović, V.; Mitrić, M.; Jelenković, B.M.; Nikolić, M.G. Luminescence thermometry via the two-dopant intensity ratio of Y2O3:Er3+, Eu3+. J. Phys. D Appl. Phys. 2016, 49, 485104. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Wise, B.M.; Gallagher, N.B.; Bro, R.; Shaver, J.M.; Windig, W.; Koch, R.S. Chemometrics Tutorial for PLS Toolbox and Solo; Eigenvector Research, Inc.: Wenatchee, WA, USA, 2006; ISBN 0-9761184-1-6. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579. [Google Scholar]
- McInnes, L.; Healy, J.; Saul, N.; Großberger, L. UMAP: Uniform Manifold Approximation and Projection. J. Open Source Softw. 2018, 3, 861. [Google Scholar] [CrossRef]
- Sevic, D.; Rabasovic, M.S.; Krizan, J.; Savic-Sevic, S.; Nikolic, M.G.; Marinkovic, B.P.; Rabasovic, M.D. YVO4:Eu3+ nanopowders: Multi-mode temperature sensing technique. J. Phys. D Appl. Phys. 2020, 53, 015106. [Google Scholar] [CrossRef]
- Lewis, C.; Erikson, J.W.; Sanchez, D.A.; McClure, C.E.; Nordin, G.P.; Munro, T.R.; Colton, J.S. Use of Machine Learning with Temporal Photoluminescence Signals from CdTe Quantum Dots for Temperature Measurement in Microfluidic Devices. ACS Appl. Nano Mater. 2020, 3, 4045–4053. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jelic, J.Z.; Dencevski, A.; Rabasovic, M.D.; Krizan, J.; Savic-Sevic, S.; Nikolic, M.G.; Aguirre, M.H.; Sevic, D.; Rabasovic, M.S. Improving the Two-Color Temperature Sensing Using Machine Learning Approach: GdVO4:Sm3+ Prepared by Solution Combustion Synthesis (SCS). Photonics 2024, 11, 642. https://doi.org/10.3390/photonics11070642
Jelic JZ, Dencevski A, Rabasovic MD, Krizan J, Savic-Sevic S, Nikolic MG, Aguirre MH, Sevic D, Rabasovic MS. Improving the Two-Color Temperature Sensing Using Machine Learning Approach: GdVO4:Sm3+ Prepared by Solution Combustion Synthesis (SCS). Photonics. 2024; 11(7):642. https://doi.org/10.3390/photonics11070642
Chicago/Turabian StyleJelic, Jovana Z., Aleksa Dencevski, Mihailo D. Rabasovic, Janez Krizan, Svetlana Savic-Sevic, Marko G. Nikolic, Myriam H. Aguirre, Dragutin Sevic, and Maja S. Rabasovic. 2024. "Improving the Two-Color Temperature Sensing Using Machine Learning Approach: GdVO4:Sm3+ Prepared by Solution Combustion Synthesis (SCS)" Photonics 11, no. 7: 642. https://doi.org/10.3390/photonics11070642
APA StyleJelic, J. Z., Dencevski, A., Rabasovic, M. D., Krizan, J., Savic-Sevic, S., Nikolic, M. G., Aguirre, M. H., Sevic, D., & Rabasovic, M. S. (2024). Improving the Two-Color Temperature Sensing Using Machine Learning Approach: GdVO4:Sm3+ Prepared by Solution Combustion Synthesis (SCS). Photonics, 11(7), 642. https://doi.org/10.3390/photonics11070642




