Impact of Grating Duty-Cycle Randomness on DFB Laser Performance
Abstract
1. Introduction
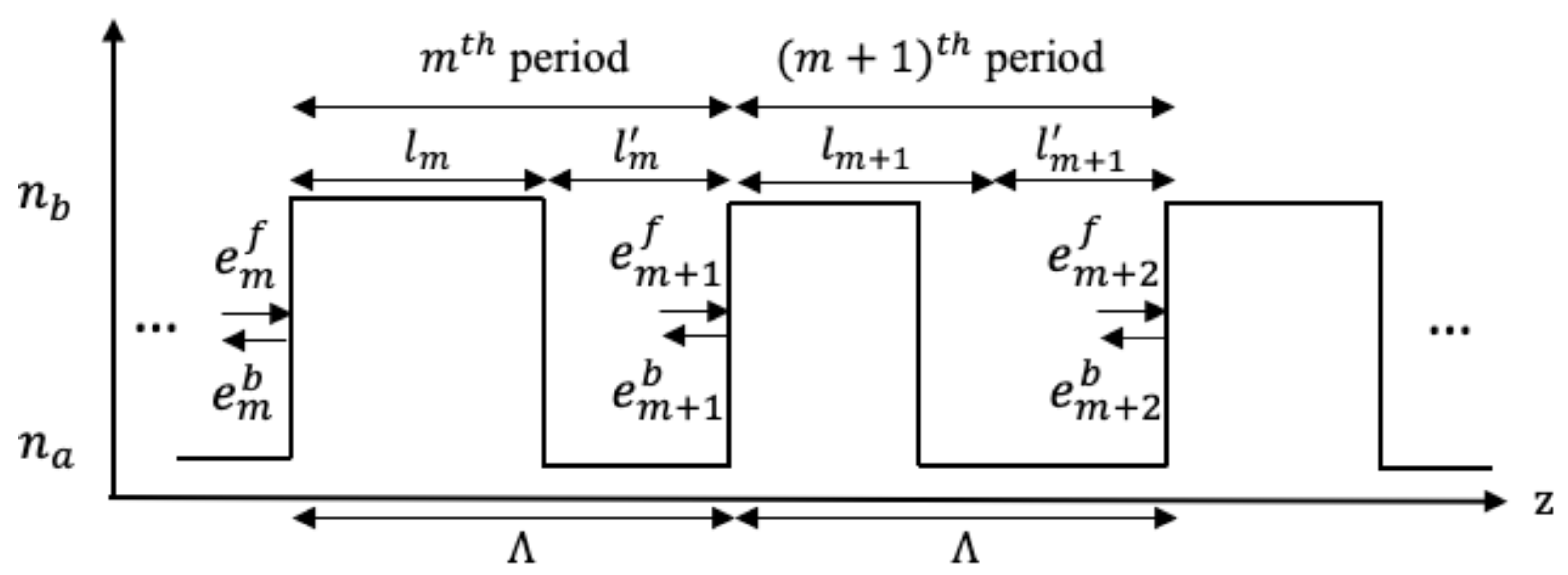
2. Theoretical Model for DFB Lasers with Grating DCR
2.1. The Modified TMM and Numerical Solution Technique
- E—electric field in [V/m];
- P—induced polarization of the host medium in [C/m2];
- —spontaneous emission source in [A/m2];
- —permittivity in a vacuum in [F/m];
- —permeability in a vacuum in [H/m];
- c—speed of light in vacuum in [m/s].
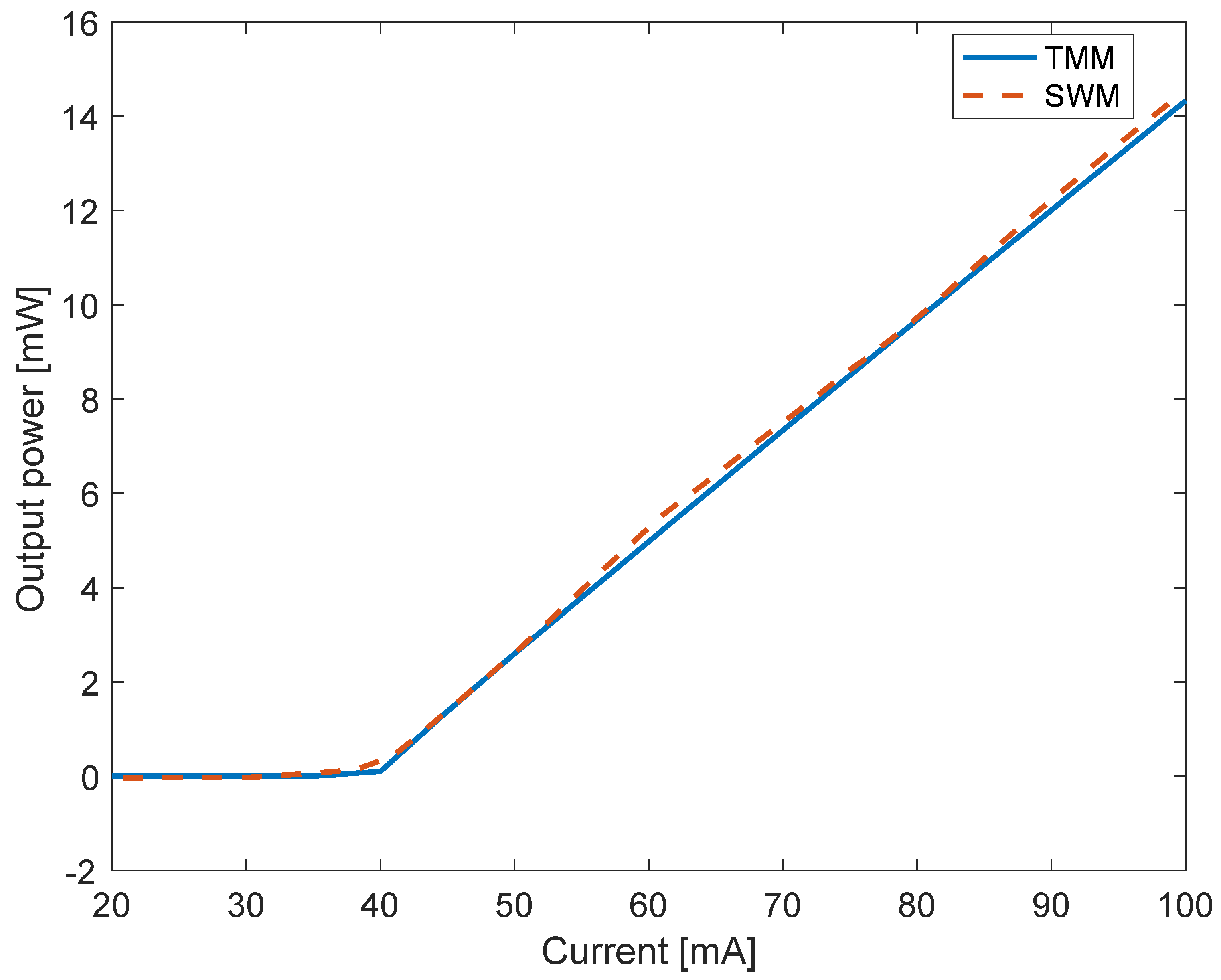
2.2. Model Validation
3. Simulation Result and Discussion
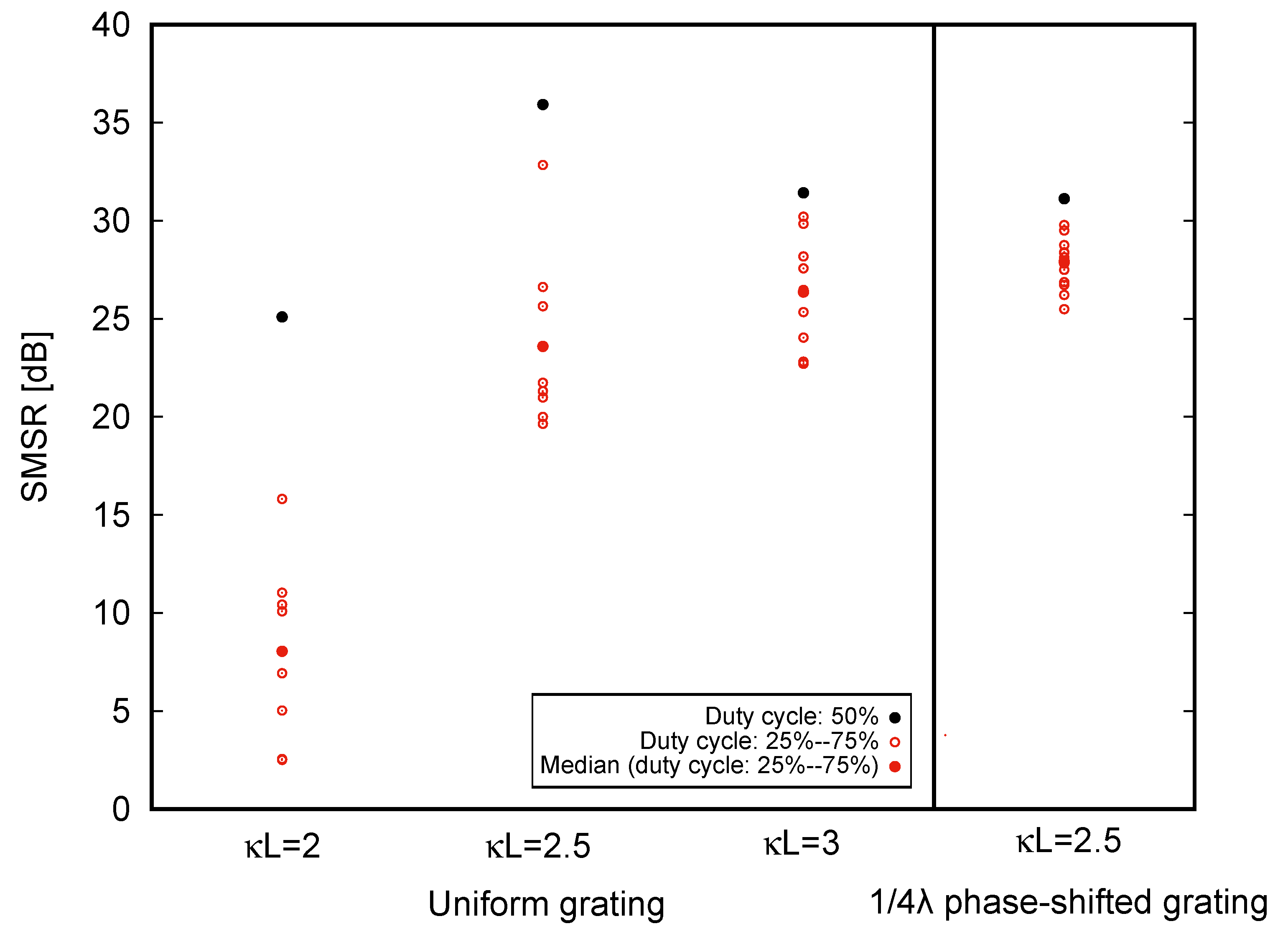
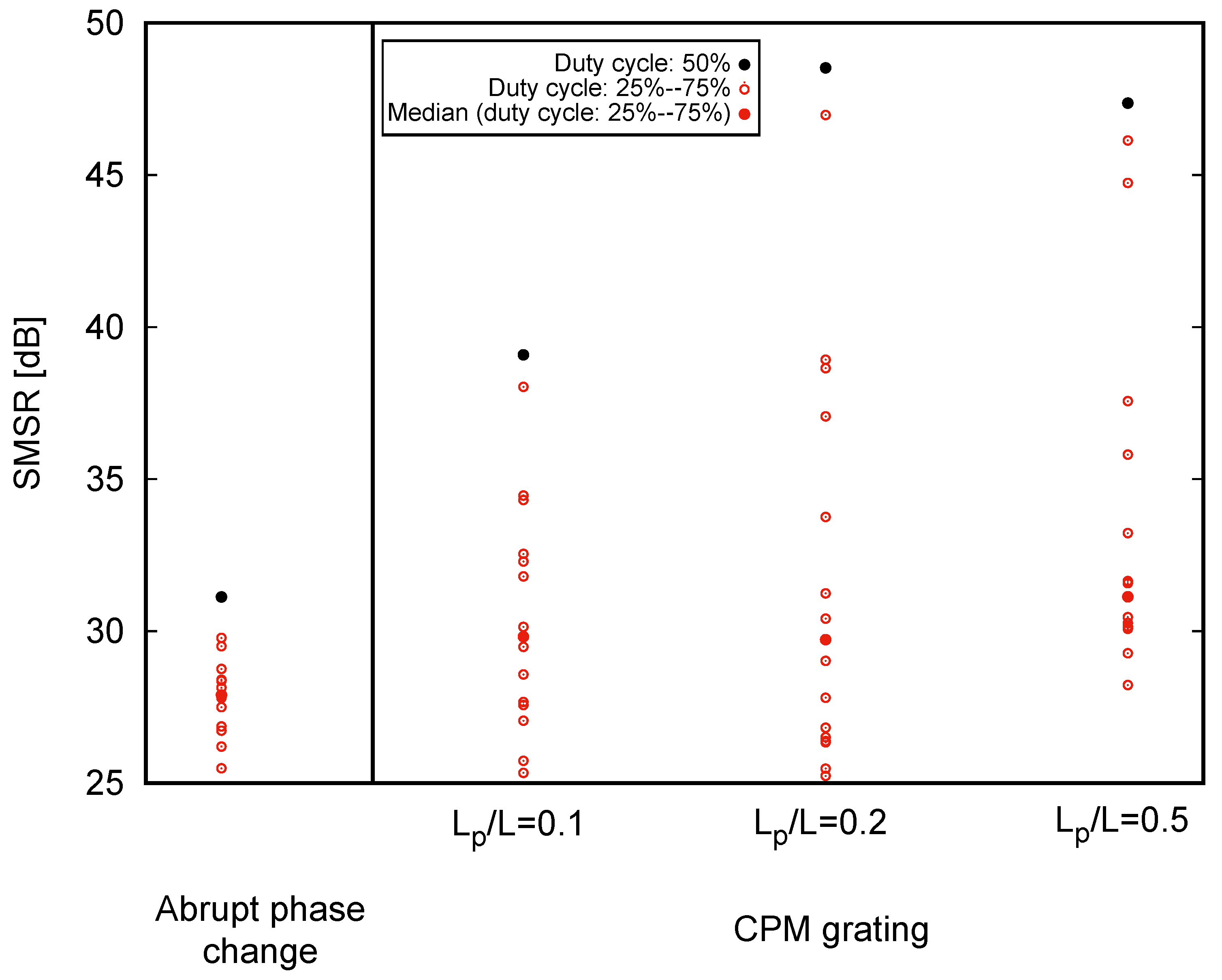
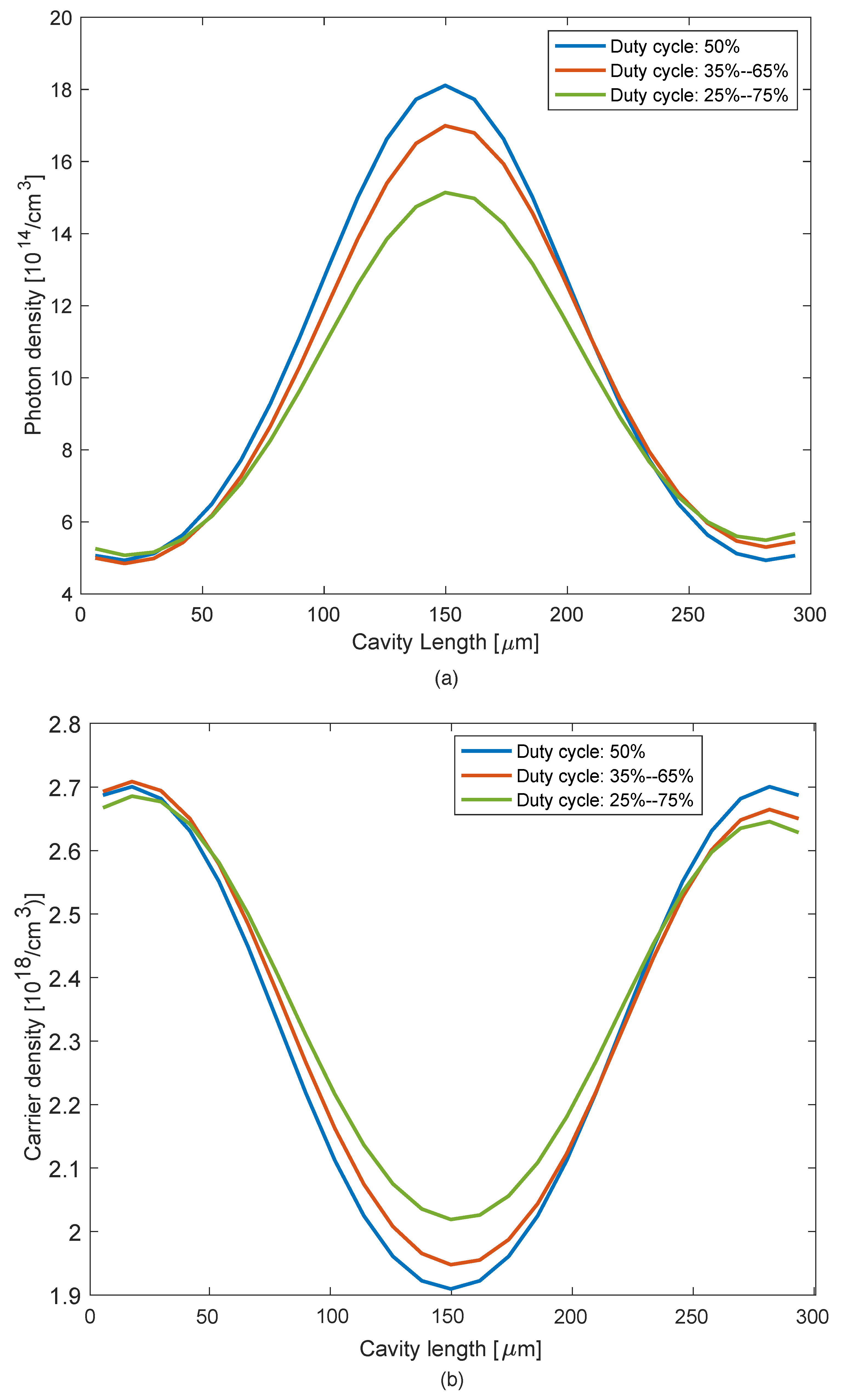
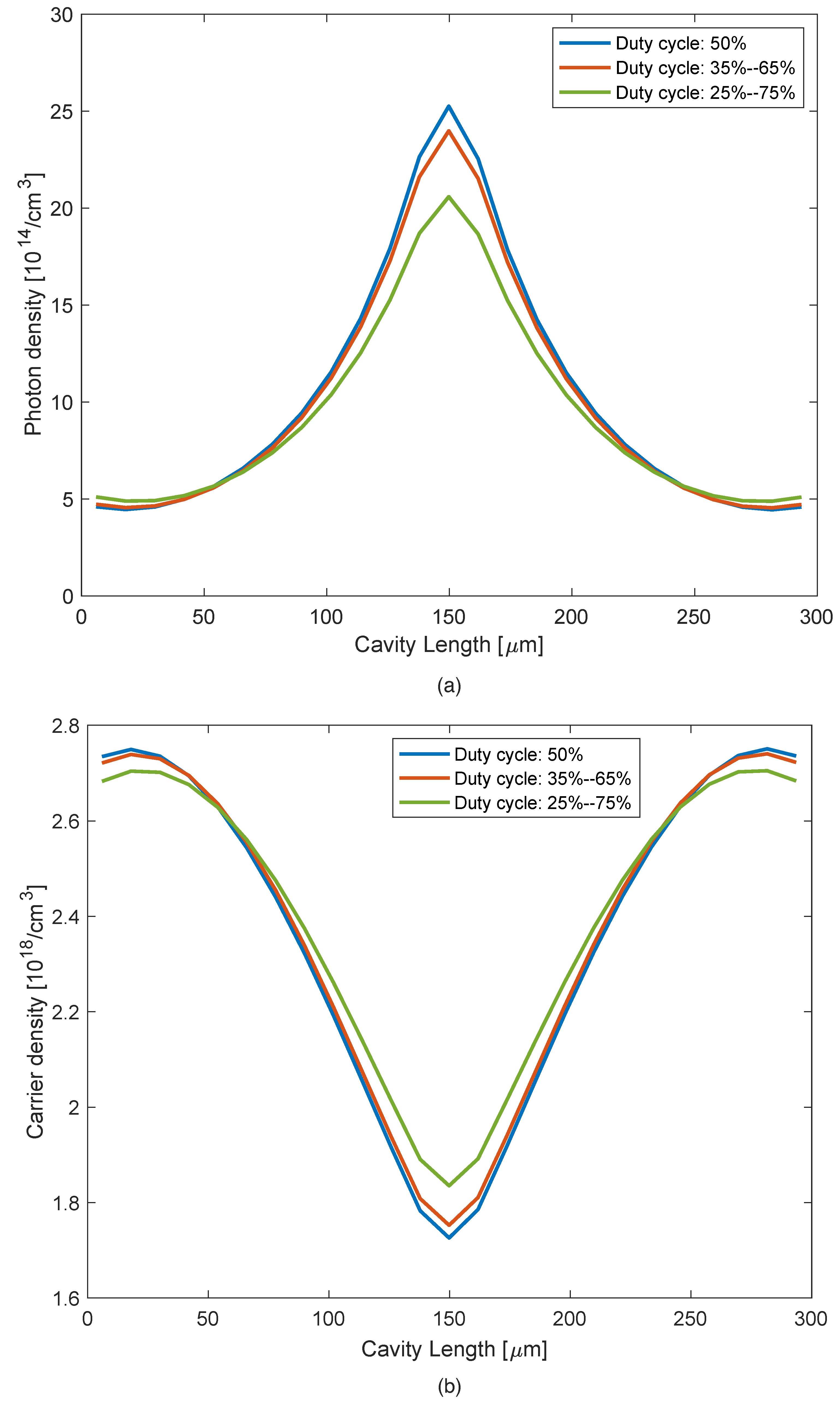
3.1. Effect of Grating DCR on SMSR
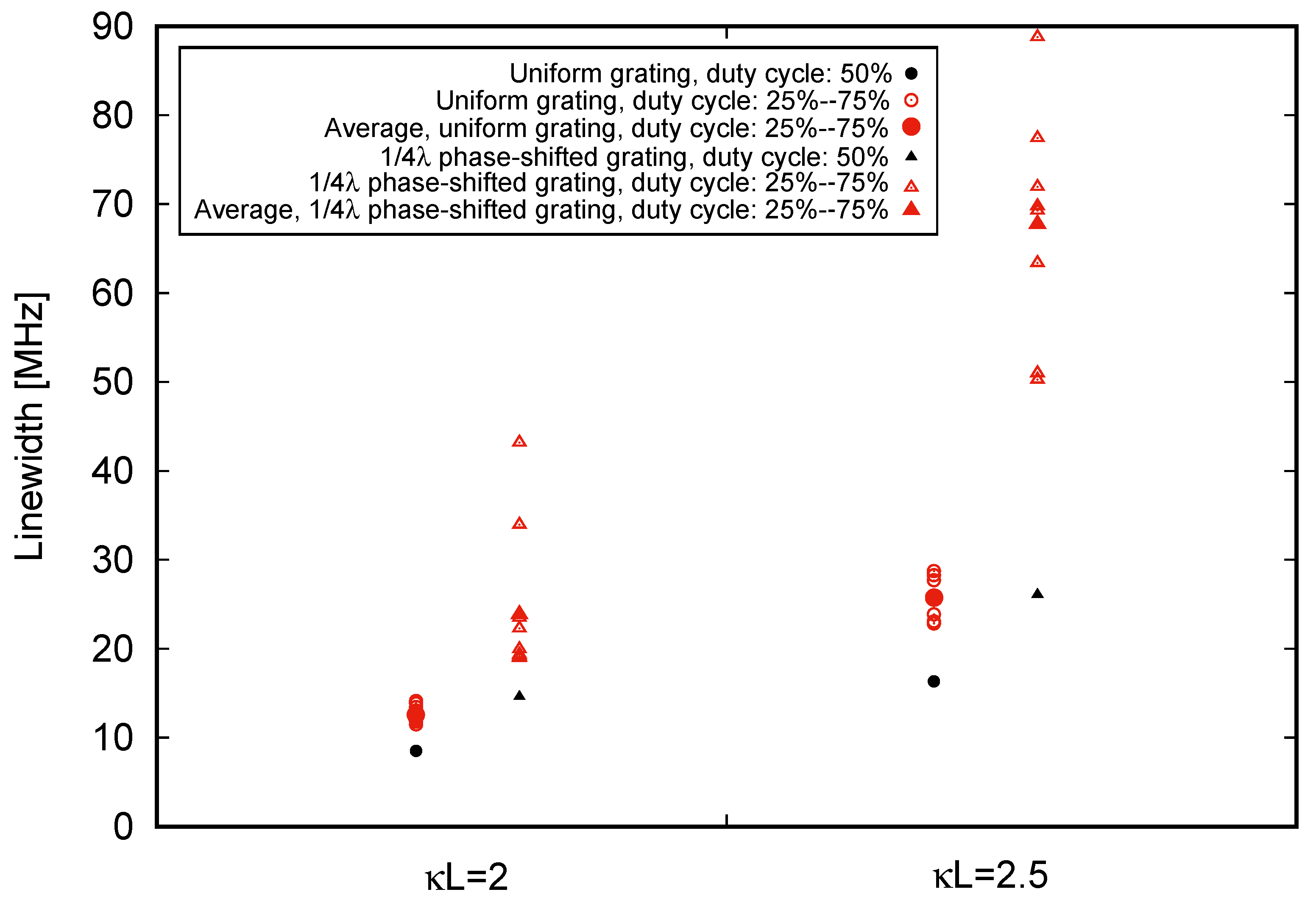
3.2. Effect of Grating DCR on Linewidth
3.3. Effect of Grating DCR on RIN
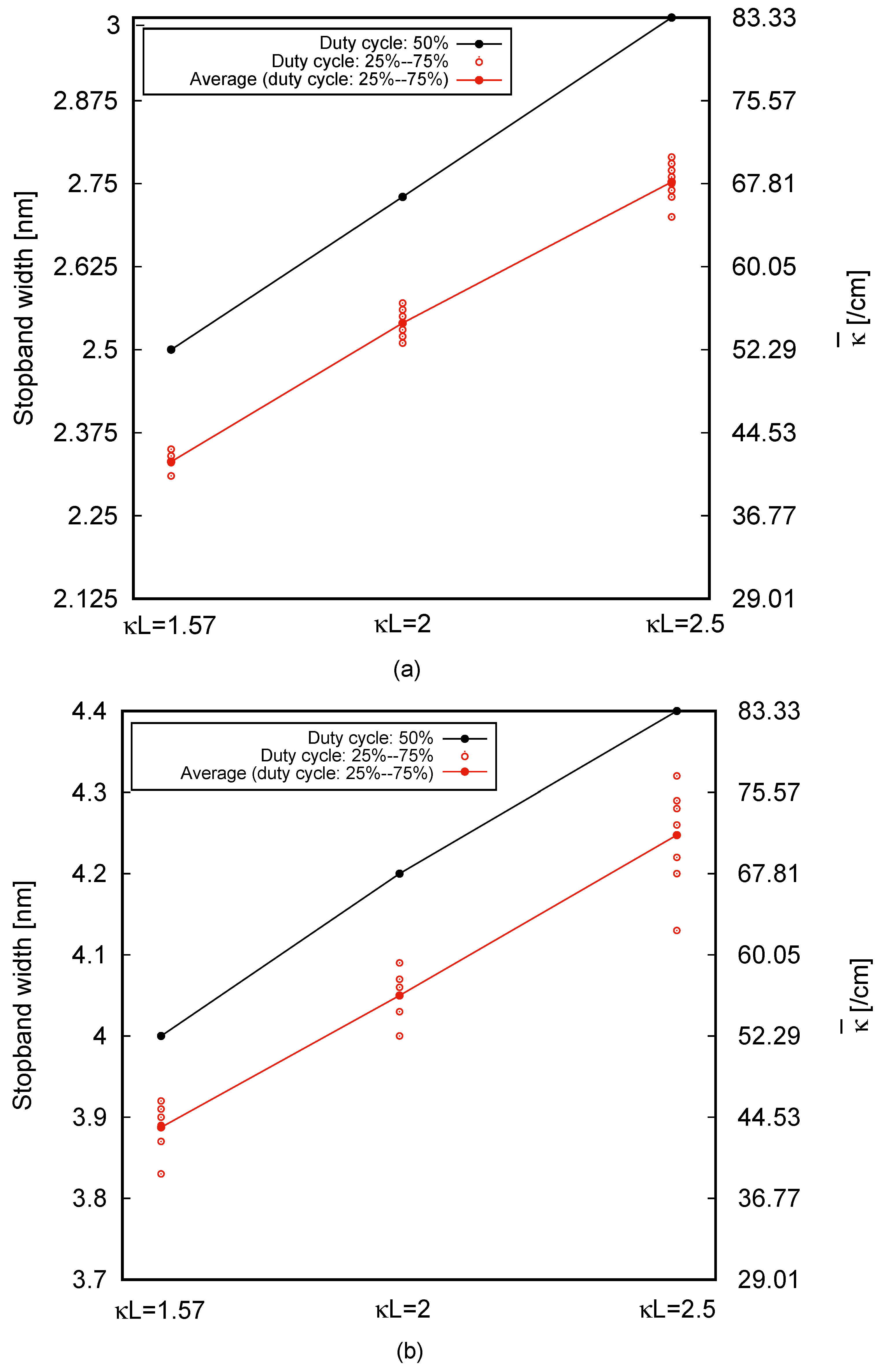
3.4. Effect of Grating DCR on Coupling Strength
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agrawal, G.P.; Dutta, N.K. Semiconductor Lasers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Li, X. Optoelectronic Devices: Design, Modeling, and Simulation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Tsang, C.F.; Marcenac, D.D.; Carroll, J.E.; Zhang, L.M. Comparison between power matrix model and time domain model in modelling large signal responses of DFB lasers. IEE Proc.-Optoelectron. 1994, 141, 89–96. [Google Scholar] [CrossRef]
- Zhang, L.M.; Yu, S.F.; Nowell, M.C.; Marcenac, D.D.; Carroll, J.E.; Plumb, R.G.S. Dynamic analysis of radiation and side-mode suppression in a second-order DFB laser using time-domain large-signal traveling wave model. IEEE J. Quantum Electron. 1994, 30, 1389–1395. [Google Scholar] [CrossRef]
- Kim, B.S.; Chung, Y.; Lee, J.S. An efficient split-step time-domain dynamic modeling of DFB/DBR laser diodes. IEEE J. Quantum Electron. 2000, 36, 787–794. [Google Scholar]
- Tromborg, B.; Lassen, H.E.; Olesen, H.; Pan, X. Traveling wave method for calculation of linewidth, frequency tuning, and stability of semiconductor lasers. IEEE Photonics Technol. Lett. 1992, 4, 985–988. [Google Scholar] [CrossRef]
- Gioannini, M.; Rossetti, M. Time-domain traveling wave model of quantum dot DFB lasers. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 1318–1326. [Google Scholar] [CrossRef]
- Li, W.; Huang, W.P.; Li, X.; Hong, J. Multiwavelength gain-coupled DFB laser cascade: Design modeling and simulation. IEEE J. Quantum Electron. 2000, 36, 1110–1116. [Google Scholar] [CrossRef]
- Xi, Y.; Li, X.; Huang, W. Time-domain standing-wave approach based on cold cavity modes for simulation of DFB lasers. IEEE J. Quantum Electron. 2008, 44, 931–937. [Google Scholar] [CrossRef]
- Xi, Y.; Huang, W.; Li, X. An efficient solution to the standing-wave approach based on cold cavity modes for simulation of DFB lasers. J. Light. Technol. 2009, 27, 3227–3234. [Google Scholar]
- Xi, Y.; Huang, W.; Li, X. A standing-wave model based on threshold hot-cavity modes for simulation of gain-coupled DFB lasers. J. Light. Technol. 2009, 27, 3853–3860. [Google Scholar]
- Kogelnik, H.; Vo Shank, C. Coupled-wave theory of distributed feedback lasers. J. Appl. Phys. 1972, 43, 2327–2335. [Google Scholar] [CrossRef]
- Streifer, W.; Scifres, D.; Burnham, R. Coupled wave analysis of DFB and DBR lasers. IEEE J. Quantum Electron. 1977, 13, 134–141. [Google Scholar] [CrossRef]
- Hong, J.; Huang, W.; Makino, T. On the transfer matrix method for distributed-feedback waveguide devices. J. Light. Technol. 1992, 10, 1860–1868. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Makino, T. Transfer matrix method with applications to distributed feedback optical devices. Prog. Electromagn. Res. 1995, 10, 271–319. [Google Scholar] [CrossRef]
- Zhao, S.Z. Numerical Simulation of a Combined Grating DFB Surface-Emitting Semiconductor Laser. Master’s Thesis, Huazhong University of Science & Technology, Wuhan, China, 2013. [Google Scholar]
- Davis, M.G.; O’Dowd, R.F. A new large-signal dynamic model for multielectrode DFB lasers based on the transfer matrix method. IEEE Photonics Technol. Lett. 1992, 4, 838–840. [Google Scholar] [CrossRef]
- Davis, M.G.; O’Dowd, R.F. A transfer matrix method based large-signal dynamic model for multielectrode DFB lasers. IEEE J. Quantum Electron. 1994, 30, 2458–2466. [Google Scholar] [CrossRef]
- Davis, M.G.; O’Dowd, R.F. A transfer matrix-based analysis of multielectrode DFB lasers. IEEE Photonics Technol. Lett. 1991, 3, 603–605. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Akiba, S.; Usami, M.; Utaka, K. 1.5-μm λ/4-shifted InGaAsP/InP DFB lasers. J. Light. Technol. 1987, 5, 1564–1573. [Google Scholar] [CrossRef]
- Li, X. Longitudinal spatial hole burning, its impact on laser operation, and suppression. Sci. Bull. 2015, 60, 1045–1046. [Google Scholar] [CrossRef][Green Version]
- Dai, Y.; Yao, J. Numerical study of a DFB semiconductor laser and laser array with chirped structure based on the equivalent chirp technology. IEEE J. Quantum Electron. 2018, 44, 938–945. [Google Scholar] [CrossRef]
- Okai, M. Spectral characteristics of distributed feedback semiconductor lasers and their improvements by corrugation-pitch-modulated structure. J. Appl. Phys. 1994, 75, 1–29. [Google Scholar] [CrossRef]
- Vankwikelberge, P.; Morthier, G.; Baets, R. CLADISS-a longitudinal multimode model for the analysis of the static, dynamic, and stochastic behavior of diode lasers with distributed feedback. IEEE J. Quantum Electron. 1990, 26, 1728–1741. [Google Scholar] [CrossRef]
- Tromborg, B.J.A.R.N.E.; Olesen, H.; Pan, X. Theory of linewidth for multielectrode laser diodes with spatially distributed noise sources. IEEE J. Quantum Electron. 1991, 27, 178–192. [Google Scholar] [CrossRef]
- Okuda, H.; Kinoshita, J.; Hirayama, Y.; Uematsu, Y. Longitudinal-mode characteristics for 1.3 μm GaInAsP/InP DFB lasers just below the threshold current. J. Appl. Phys. 1994, 75, 362–363. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Grating period [nm] | 244.5 |
| Active-region thickness d [μm] | 0.15 |
| Active-region cross-sectional area [μm2] | 0.3 |
| Facet reflectivity , | 0 |
| Laser cavity length L [μm] | 300 |
| Optical confinement factor | 0.3 |
| Effective index under zero injection | 3.2 |
| Group index | 3.6 |
| Optical modal loss [cm−1] | 50 |
| Differential gain [10−16 cm2] | 2.5 |
| Transparent carrier density [ cm−3] | 1.0 |
| Nonlinear gain saturation factor [ cm3] | 6.0 |
| Linewidth enhancement factor | 4.0 |
| Nonradiative carrier recombination rate through SRH process A [ s−1] | 0.1 |
| Carrier recombination coefficient through spontaneous emission and bimolecular processes B [10−10 cm3s−1] | 1.0 |
| Auger recombination coefficient C [10−29 cm6s−1] | 7.5 |
| Grating coupling coefficient [cm−1] | 50 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Kong, X.; Li, X. Impact of Grating Duty-Cycle Randomness on DFB Laser Performance. Photonics 2024, 11, 574. https://doi.org/10.3390/photonics11060574
Yang M, Kong X, Li X. Impact of Grating Duty-Cycle Randomness on DFB Laser Performance. Photonics. 2024; 11(6):574. https://doi.org/10.3390/photonics11060574
Chicago/Turabian StyleYang, Manpo, Xiangpeng Kong, and Xun Li. 2024. "Impact of Grating Duty-Cycle Randomness on DFB Laser Performance" Photonics 11, no. 6: 574. https://doi.org/10.3390/photonics11060574
APA StyleYang, M., Kong, X., & Li, X. (2024). Impact of Grating Duty-Cycle Randomness on DFB Laser Performance. Photonics, 11(6), 574. https://doi.org/10.3390/photonics11060574





