Angular Deviations, Lateral Displacements, and Transversal Symmetry Breaking: An Analytical Tutorial
Abstract
1. Introduction
2. The Integral Form of the Optical Beams
3. The Fresnel Coefficients and Their Derivatives
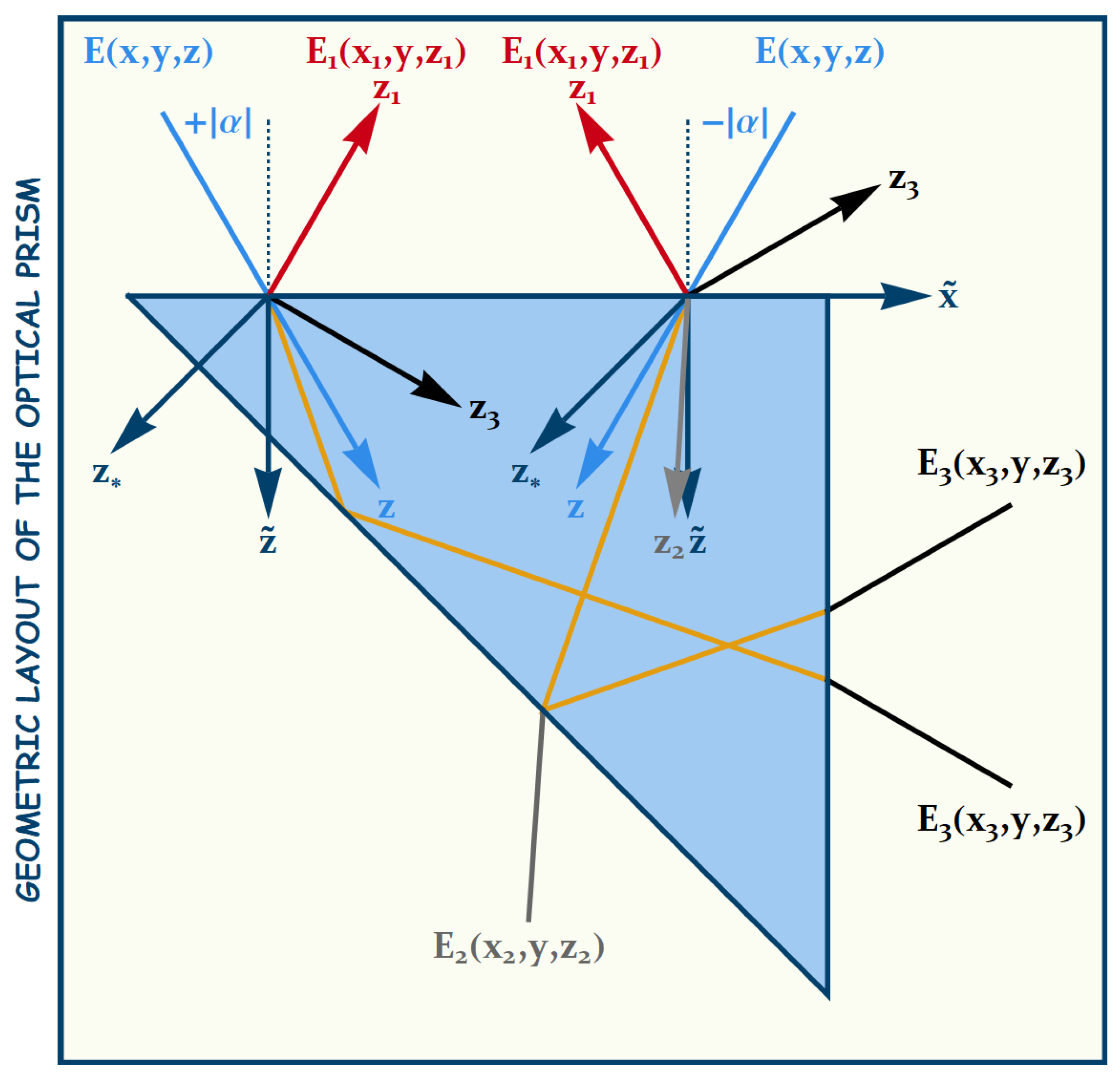
4. The Geometrical Phase Analysis
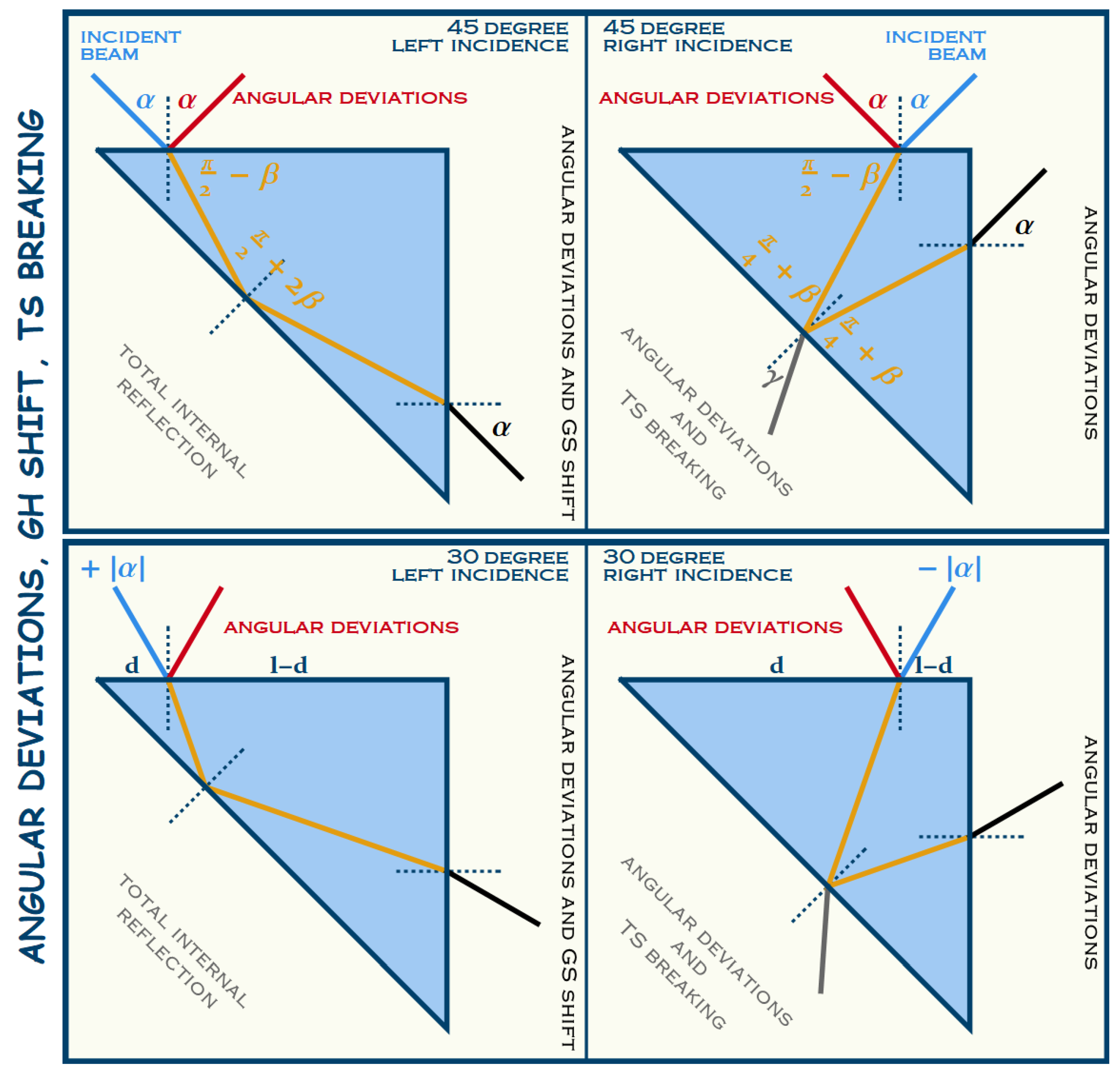
5. Optical Behavior of the Reflected and Transmitted Beams
5.1. Reflection by the Upper Interface
5.2. Transmitted by the Oblique Interface
5.3. Transmission by the Lateral Interface
6. Discussions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Born, A.M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Saleh, B.E.A.; Teich, M.C. Fundamental of Photonics; Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Svelto, O. Principles of Lasers; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Keiser, G. Optical Fiber Communications; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Ellerbroek, B.L. Laser Guide Star Adaptive Optics for Astronomy; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Birngruber, R.; Steiner, H. Lasers in Medicine; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- White, I.A.; Snyder, A.W.; Pask, C. Directional change of beams undergoing partial reflection. J. Opt. Soc. Am. 1977, 67, 703–705. [Google Scholar] [CrossRef]
- Chan, C.C.; Tamir, T. Angular shift of a Gaussian beam reflected near the Brewster angle. Opt. Lett. 1985, 10, 378–380. [Google Scholar] [CrossRef] [PubMed]
- Merano, M.; Aiello, A.; van Exter, M.P.; Woerdman, J.P. Observing angular deviations in the specular reflection of a light beam. Nat. Photonics 2009, 3, 337–340. [Google Scholar] [CrossRef]
- Araujo, M.; De Leo, S.; Maia, G. Optimizing weak measurements to detect angular deviations. Ann. Phys. 2017, 529, 1600357. [Google Scholar] [CrossRef]
- Horowitz, B.R.; Tamir, T. Lateral displacement of a light beam at a dielectric interface. J. Opt. Soc. Am. 1970, 61, 586–594. [Google Scholar] [CrossRef]
- Soboleva, I.V.; Moskalenko, V.V.; Fedyanin, A.A. Giant Goos-Hänchen effect and Fano resonance at photonic crystal surfaces. Phys. Rev. Lett. 2012, 108, 123901. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Aiello, A. Goos–Hänchen and Imbert–Fedorov beam shifts: An overview. J. Opt. 2013, 15, 014001. [Google Scholar] [CrossRef]
- Araujo, M.; De Leo, S.; Maia, G. Oscillatory behavior of light in the composite Goos-Hänchen shift. Phys. Rev. A 2017, 95, 053836. [Google Scholar] [CrossRef]
- Othman, A.; Asiri, S.; Al-Amri, M. Controllable large positive and negative Goos–Hänchen shifts with a double-Lambda atomic system. Sci. Rep. 2023, 13, 3789. [Google Scholar] [CrossRef]
- Goos, F.; Hänchen, H. Ein Neuer Und Fundamentaler Versuch Zur Totalreflexion. Ann. Phys. 1947, 436, 333–346. [Google Scholar]
- Artmann, K. BerechnungDer SeitenversetzungDes Totalreflektierten Strahles. Ann. Phys. 1948, 437, 87–102. [Google Scholar] [CrossRef]
- Goos, F.; Hänchen, H. Neumessung Des Strahlwersetzungseffektes Bei Totalreflexion. Ann. Phys. 1949, 440, 251–252. [Google Scholar] [CrossRef]
- Merano, M.; Aiello, A.; Hooft, G.W.M.; van Exter, P.; Eliel, E.R.; Woerdman, J.P. Observation of Goos-Hänchen shifts in metallic reflection. Opt. Lett. 2007, 15, 15928–15934. [Google Scholar] [CrossRef] [PubMed]
- Santana, O.; Carvalho, S.; De Leo, S.; de Araujo, L. Weak measurement of the composite Goos-Haenchen shift in the critical region. Opt. Lett. 2016, 41, 3884–3887. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Gao, B.; Zhang, J.; Wang, L.G. Experimental proof on the effect of beam width and spatial coherence on Goos-Hänchen shift. Opt. Laser Technol. 2023, 159, 109027. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F. Quantum Mechanics; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Hauge, E.H.; Stovneng, J.A. Tunneling times: A critical review. Rev. Mod. Phys. 1989, 61, 917–936. [Google Scholar] [CrossRef]
- Platero, G.; Aguado, R. Photon-assisted transport in semiconductor nanostructures. Phys. Rep. 2004, 395, 1–157. [Google Scholar] [CrossRef]
- Boev, M.V.; Kovalev, V.M.; Kibis, O.V. Optically induced resonant tunneling of electrons in nanostructures. Sci. Rep. 2023, 13, 19625. [Google Scholar] [CrossRef]
- Jayaswal, G.; Mistura, G.; Merano, M. Observing angular deviations in light-beam reflection via weak measurements. Opt. Exp. 2014, 39, 6257–6260. [Google Scholar]
- De Leo, S. Laser planar trapping. Laser Phys. Lett. 2020, 17, 116001. [Google Scholar] [CrossRef]
- Petrov, N.I.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Large positive and negative Goos-Hänchen shifts near the surface plasmon resonance in subwavelength grating. Opt. Exp. 2020, 28, 7552–7564. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Leo, S.; Mazzeo, M. Angular Deviations, Lateral Displacements, and Transversal Symmetry Breaking: An Analytical Tutorial. Photonics 2024, 11, 573. https://doi.org/10.3390/photonics11060573
De Leo S, Mazzeo M. Angular Deviations, Lateral Displacements, and Transversal Symmetry Breaking: An Analytical Tutorial. Photonics. 2024; 11(6):573. https://doi.org/10.3390/photonics11060573
Chicago/Turabian StyleDe Leo, Stefano, and Marco Mazzeo. 2024. "Angular Deviations, Lateral Displacements, and Transversal Symmetry Breaking: An Analytical Tutorial" Photonics 11, no. 6: 573. https://doi.org/10.3390/photonics11060573
APA StyleDe Leo, S., & Mazzeo, M. (2024). Angular Deviations, Lateral Displacements, and Transversal Symmetry Breaking: An Analytical Tutorial. Photonics, 11(6), 573. https://doi.org/10.3390/photonics11060573




