Abstract
In this paper, the coherent properties of partially coherent Bessel–Gaussian optical beams propagating through a uniform medium (free space) or a turbulent atmosphere are examined theoretically. The consideration is based on the analytical solution of the equation for the transverse second-order mutual coherence function of the field of partially coherent optical radiation in a turbulent atmosphere. For the partially coherent Bessel–Gaussian beam, the second-order mutual coherence function of the source field is taken as a Gaussian–Schell model. In this approximation, we analyze the behavior of the coherence degree and the integral coherence scale of these beams as a function of the propagation pathlength, propagation conditions, and beam parameters, such as the radius of the Gauss factor of the beam, parameter of the Bessel factor of the beam, topological charge, and correlation width of the source field of partially coherent radiation. It was found that, as a partially coherent vortex Bessel–Gaussian beam propagates through a turbulent atmosphere, there appear not two (as might be expected: one due to atmospheric turbulence and another due to the partial coherence of the source field), but only one ring dislocation of the coherence degree (due to the simultaneous effect of both these factors on the optical radiation). In addition, it is shown that the dislocation of the coherence degree that significantly affects the beam coherence level is formed only for beams, for which the coherence width of the source field is larger than the diameter of the first Fresnel zone.
1. Introduction
In singular optics, being one of the important fields of modern optics, much attention is paid to the study of vortex optical beams [1,2,3,4]. As it is well-known, vortex optical beams carry the orbital angular momentum. Therefore, they are suitable for solving the problem of compressing an information channel in telecommunication systems using different states for the orbital angular momentum of the carrier optical radiation [5]. The interest in beams with orbital angular momentum grew after the publication of [6]. It can be noted, however, that the study of optical beams with vortices began even earlier. For example, in [7,8], the structure of an optical field was studied in connection with the existence of points, at which the amplitude of this field is zero. At the places where the optical field has exactly zero value, the wave front of this field includes a spiral dislocation [9,10]. The issue of [6] was followed by numerous publications dealing with methods for the generation of vortex beams in the optical range [11,12]. Interest in this problem has existed recently [13,14] and still exists today [15,16,17].
The simplest optical elements that generate vortex optical fields are a spiral phase plate and a spiral axicon [18,19,20,21,22,23]. A feature of a vortex beam formed by such optical elements is an isolated intensity zero at the optical axis that appears just behind a spiral phase element. It was shown [24] that, as an optical beam propagates in a uniform medium, an optical vortex (a helical phase front) and the corresponding isolated intensity zero leads to the degradation of the quality of this beam. With the development of the theory of the propagation of partially coherent and polarized polychromatic optical radiation with the helical phase front in uniform and randomly inhomogeneous media, the study of coherence vortices has become urgent [25,26,27,28,29]. The phenomenon of diffraction is one of the manifestations of the wave nature of optical radiation [30]. Nevertheless, there exist optical structures capable of keeping their original intensity distribution of the optical field while propagating in a proper medium [1,2,3,4,22,23]. Bessel beams, for example, propagate without changing in a uniform medium (free space) [1,2,3,4].
The second-order mutual coherence function is widely used not only in the wave and singular optics, but also in other areas of physics [30,31,32,33]. Since the random diffraction reduces the coherence of optical radiation propagating along long randomly inhomogeneous paths, the study of this issue is of undoubted practical interest [34,35,36,37]. Specialists in adaptive optics have also turned their attention to Bessel and Bessel-like optical beams [38,39,40,41,42].
In this paper, the behavior of the coherence degree and the integral coherence scale of partially coherent vortex Bessel–Gaussian beams propagating through either a uniform medium (free space) or a randomly inhomogeneous turbulent atmosphere is analyzed theoretically. The consideration is based on the analytical solution of the equation for the transverse second-order mutual coherence function of the field of partially coherent optical radiation in a turbulent atmosphere [43]. For the partially coherent Bessel–Gaussian beam, the second-order mutual coherence function of the source field is set in the form of the Gaussian–Schell model. The behavior of the coherence degree and integral coherence scale of partially coherent vortex Bessel–Gaussian beams is analyzed as a function of the following parameters of optical radiation: the initial radius of the Gaussian factor of the beam field, parameter of the Bessel factor of the beam field, topological charge in the beam, and the coherence width of the source field of partially coherent radiation, as well as the propagation conditions and path length. The integral coherence scale of the partially coherent vortex Bessel–Gaussian beam is compared with the similar characteristic of the partially coherent non-vortex Gaussian beam.
2. Basic Definitions
For the partially coherent vortex Bessel–Gaussian optical beam propagating in the direction of the coordinate axis, the second-order mutual coherence function of the source field at is set as a product of the fields at the observation points by the Gauss-form correlator depending on the difference between the observation points (a Gaussian–Schell model source) [44,45,46,47,48,49]:
where the overbar means averaging over an ensemble of realizations of source fluctuations; is the initial amplitude of the beam at its optical axis; are spatial coordinates transverse to the direction of optical radiation propagation; and are the absolute values and arguments of these coordinates; ; is the Gaussian factor of the optical beam; is the Bessel factor of the beam; is the initial radius of the Gaussian factor of the beam field; is the curvature radius of the parabolic wavefront at the transmitting aperture; is the wave number of the optical radiation; is the wavelength of optical radiation in vacuum; is the wave vector component orthogonal to the axis of optical radiation propagation (parameter of the Bessel beam, a scalar parameter measured in ); is the wave vector component in the direction of the axis; is the topological charge of the vortex beam (dimensionless integer scalar parameter of vortex beam); is the mth-order first-kind Bessel function; and is the coherence width of the source field [48,49].
The coherent properties of partially coherent vortex Bessel–Gaussian beams propagating in a turbulent atmosphere are described with the transverse second-order mutual coherence function [43,44] of the beam field :
where the overbar, similarly to Equation (1), denotes the averaging over an ensemble of realizations of source fluctuations; is the ensemble of realizations of refractive index fluctuations in a turbulent atmosphere; and are observations points; and is the path length.
Let us consider the propagation of the partially coherent vortex Bessel–Gaussian beam in a turbulent atmosphere in the paraxial approximation [43], that is, near the optical axis of the beam. In this case, the following equation is true for the transverse second-order mutual coherence function (2) of the beam field () [43]:
where is the complex amplitude of the beam at the observation point ; and .
The equation for the transverse second-order mutual coherence function of the field of the partially coherent optical beam (3) in a turbulent atmosphere at an arbitrary form of the initial mutual coherence function (1) can be written asymptotically rigorously as [43]:
where is the function describing the effect of random inhomogeneities of the refractive index of a turbulent atmosphere on the optical radiation; is the spectrum of fluctuations of the refractive index of a turbulent atmosphere; and and are the sum and difference coordinates of observation points. We considered the Kolmogorov spectrum of refractive index fluctuations [43]: , where is the structure characteristic of refractive index fluctuations [43].
In this case, the integral of the function describing the effect of a randomly inhomogeneous medium on optical radiation from Equation (4) acquires the following form:
where is the coherence radius of a plane optical wave in a turbulent atmosphere [43,50]. As it was shown in [50,51], to facilitate the following analysis of Equation (4) with the initial condition (1), the effect of random inhomogeneities of a turbulent atmosphere can be taken into account in the square approximation for function :
3. Basic Relations
For a partially coherent vortex Bessel–Gaussian beam (1) propagating in a turbulent atmosphere (5) described with the square approximation (6), the integral equation for the transverse second-order mutual coherence function (4) of the field of the partially coherent Bessel–Gaussian beam (1) can be simplified. With allowance for Equation (6), the quadruple integral (4) with the initial distribution (1) can be converted using the following table relation [52]:
to a sixfold integral, which, after calculating the table integrals [52], can be transformed into a relation in the form of a double integral. In what follows, we analyze the integral equation obtained in this way (with the use of Equation (7)):
where is the transverse second-order mutual coherence function of the partially coherent non-vortex Gaussian beam propagating in a turbulent atmosphere [50]; and is the transverse second-order mutual coherence function of truncated (by the Gaussian beam) partially coherent vortex Bessel beam propagating in a turbulent atmosphere.
Particular equations for the functions and from Equation (8) are presented below. The first factor of Equation (8) that coincides with the transverse second-order mutual coherence function of the partially coherent Gaussian beam propagating in a turbulent atmosphere is independent of the Bessel beam parameters:
where and are polar coordinates of the sum and difference vectors of observation points and ; ; are the coordinates of the sum and difference vectors of observation points and upon normalization to the diameter of the first Fresnel zone ; is the current value of the radius of the partially coherent Gaussian beam [50]; , , and are geometric factors used when describing changes in the radius, wavefront curvature, and coherence of the partially coherent Gaussian beam in a turbulent atmosphere [50], respectively; is the beam-focusing parameter [50]; is the Fresnel number of the transmitting aperture [50]; is the parameter characterizing the propagation conditions for partially coherent optical radiation at a uniform path (optical thickness of a uniform medium for partially coherent radiation); and is the parameter characterizing the conditions of propagation of optical radiation in a turbulent atmosphere (optical thickness of the turbulent atmosphere) [50].
In Equation (8), the second factor is the transverse second-order mutual coherence function of the truncated (by the Gaussian beam) partially coherent vortex Bessel beam propagating in a turbulent atmosphere. This factor depends on the parameters of the Gaussian factor of the beam:
where is the normalized parameter of the Bessel beam; and and are geometric factors.
Thus, Equation (8) demonstrates not a complete, but only partial factorization of the contributions of the Gaussian and Bessel components of the beam. Equation (8) describes the transverse second-order mutual coherence function of the partially coherent vortex Bessel–Gaussian beam propagating in a turbulent atmosphere in the paraxial zone of the beam [43,50].
Correspondingly, at , Equation (8) describes the transverse second-order mutual coherence function of the partially coherent vortex Bessel–Gaussian beam in its paraxial zone for the propagation in a uniform medium (free space). Similarly, at , that is, for the propagation in a uniform medium (free space), the transverse second-order mutual coherence function of the truncated (by the Gaussian beam) partially coherent vortex Bessel beam in its paraxial zone is described by Equation (10).
Since the spatial coordinates are defined as in Equation (4), the normalized second-order mutual coherence function (complex coherence degree) of an optical beam has the following form [30,31,32,33,43,44,50]:
where is the mean intensity of the partially coherent optical beam in a turbulent atmosphere for the point . Knowing the complex coherence degree (11), we can write the equation for the absolute value of the complex coherence degree of the partially coherent optical beam at its optical axis ():
If the coherence degree described by Equation (12) has one maximum, then the coherence radius can be found from the condition: . At the same time, when describing the coherence of Bessel or Bessel–Gaussian optical beams (since the coherence degree has a more complex structure in these cases [29,35,51]), it is better determining the coherence degree scale through the integral equation [35,53,54]:
where is the integral coherence scale of an optical beam.
4. Coherence Degree of Bessel Beams
As it can be seen from Equation (8), the mathematical formula for the second-order mutual coherence function of the partially coherent vortex Bessel–Gaussian beam propagating in a turbulent atmosphere decomposes into two factors. One of them is the second-order mutual coherence function of the partially coherent non-vortex Gaussian beam in a turbulent atmosphere (9) [30], while another is the second-order mutual coherence function of the truncated (by the Gaussian beam) partially coherent vortex Bessel beam in a turbulent atmosphere (10). Since the second-order mutual coherence function of the partially coherent Gaussian optical beam propagating in a turbulent atmosphere has been studied thoroughly [50], we considered below the second-order mutual coherence function of the partially coherent truncated vortex Bessel–Gaussian beam in a turbulent atmosphere .
First, we considered the case of an unlimited (,) partially coherent vortex Bessel beam (1). In this case, the second-order mutual coherence function (10) takes the simpler form :
Correspondingly, at , Equation (14) describes the behavior of the second-order mutual coherence function of the unlimited partially coherent vortex Bessel beam propagating in a uniform medium.
4.1. Coherence Degree of Partially Coherent Bessel Beams in a Uniform Medium
As a fully coherent optical radiation with a helical phase profile propagates in a uniform medium, it keeps its coherence, that is, the coherence degree (12) of vortex optical radiation is equal to the unity at any point of the propagation path () [30,31,32], while the integral coherence scale (13) tends to infinity (). If a partially coherent vortex optical beam propagates in a uniform medium (free space), then its coherence decreases during the transfer of vortex radiation due to the presence of random diffraction at the transmitting aperture [25,26,27,28]: and .
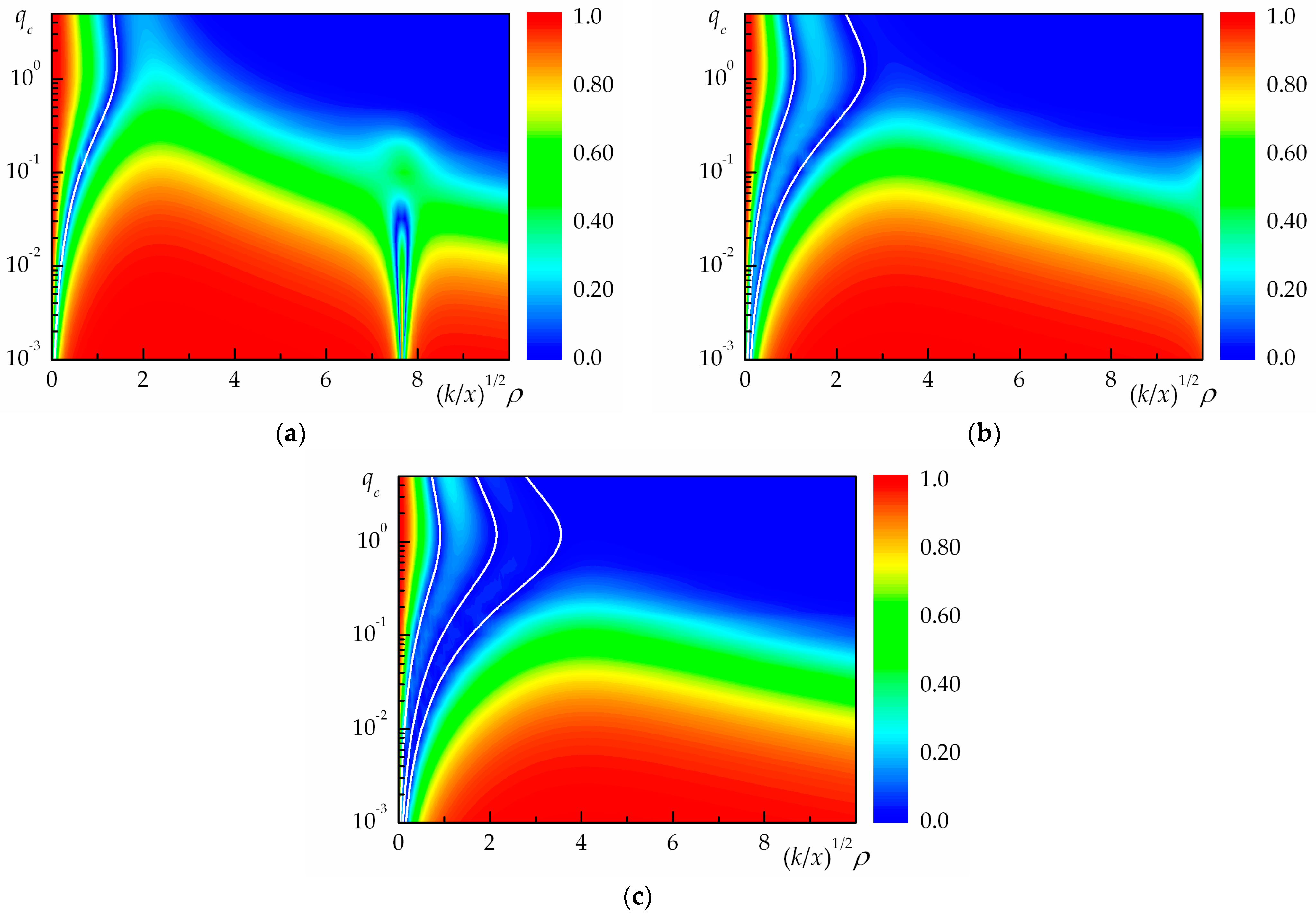
Figure 1a–c shows the coherence degree of partially coherent () vortex Bessel () beams for at the optical axes of the beams (), as calculated by Equations (11), (12) and (14) for the beams propagating along uniform paths (that is, at ). The coherence degree of vortex Bessel () beams as a function of the normalized radial coordinate and the optical thickness of a uniform medium for the partially coherent radiation is shown as color contour plots (100 pseudo-colors). In Figure 1a (), Figure 1b (), and Figure 1c (), we can see how the ring dislocation of coherence degree [26,29] appears and disappears in the paraxial zone () of partially coherent vortex Bessel beams propagating in a uniform medium. A ring dislocation is a zone of low coherence in the two-dimensional field of the coherence degree of optical radiation with the helical phase profile near the optical axis of the beam. A necessary condition for the existence of a ring dislocation of coherence degree for axially symmetric vortex beams (independent of the angular coordinate ) is that the coherence degree takes a zero value on at least one circle centered at the optical axis of the beam. The number of zeros in a ring dislocation of the coherence degree is equal to the topological charge of the vortex beam .
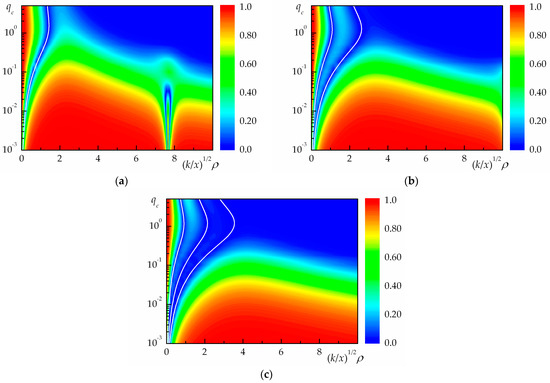
Figure 1.
Coherence degree of partially coherent vortex Bessel beams propagating in a uniform medium at for different values of the topological charge of the vortex beam : (a) ; (b) ; (c) . The white curves represent the coordinates of a ring dislocation.
It is worth recalling that the definition of a ring dislocation for an axially symmetric vortex Bessel beam (independent of the angular coordinate ) means the fulfillment of the condition that , where is the coordinate of a ring dislocation [29]. In fact, for the vortex beam with (see Figure 1a), we have one value of : at and at , while everywhere. As to the vortex beam with (see Figure 1b), in this case, we have two values of ( and ; let ): at , at , and at , while everywhere. As to the vortex beam with (see Figure 1c), in this case, we have three values of (, , and ; let ): at , at , at , and at , while everywhere. The data shown in Figure 1a–c suggest that, as the topological charge of the vortex beam increases, the coherence of vortex Bessel beams decreases due to an increase in the size of a ring dislocation.
As it can be seen in Figure 1a–c, the coherence degree of the Bessel beam at its optical axis, except for the zone of ring dislocation, generally decreases with an increase in the dimensionless variable . However, at , the coherence degree pattern periodically demonstrates twin regions of low coherence with an intermediate narrow subregion of high coherence. In particular, in Figure 1a for the Bessel optical beam with , we can see one such region in the range . The middle of this region of low coherence falls in the argument of , which corresponds to the doubled value of the first positive zero of the first-kind first-order Bessel function (). For the Bessel optical beam with in Figure 1b, such regions are practically invisible, since the middle of the first of them falls in (associated with the first positive zero of the first-kind second-order Bessel function equal to ). The existence of such regions of low coherence for the Bessel beam at can be explained by the effect of the beam regular structure [51], which still preserves at , on the beam coherence. It can be easily noticed (see Figure 1a–c) that the effect of the helical phase profile on the coherence of the partially coherent radiation preserves at the higher values of the optical thickness of a uniform medium (manifesting itself in the ring dislocation of coherence degree) than the effect of the regular structure of the Bessel beam (manifesting itself in the existence of secondary intensity minima of this beam).
4.2. Coherence Degree of Coherent Bessel Beams in a Turbulent Atmosphere
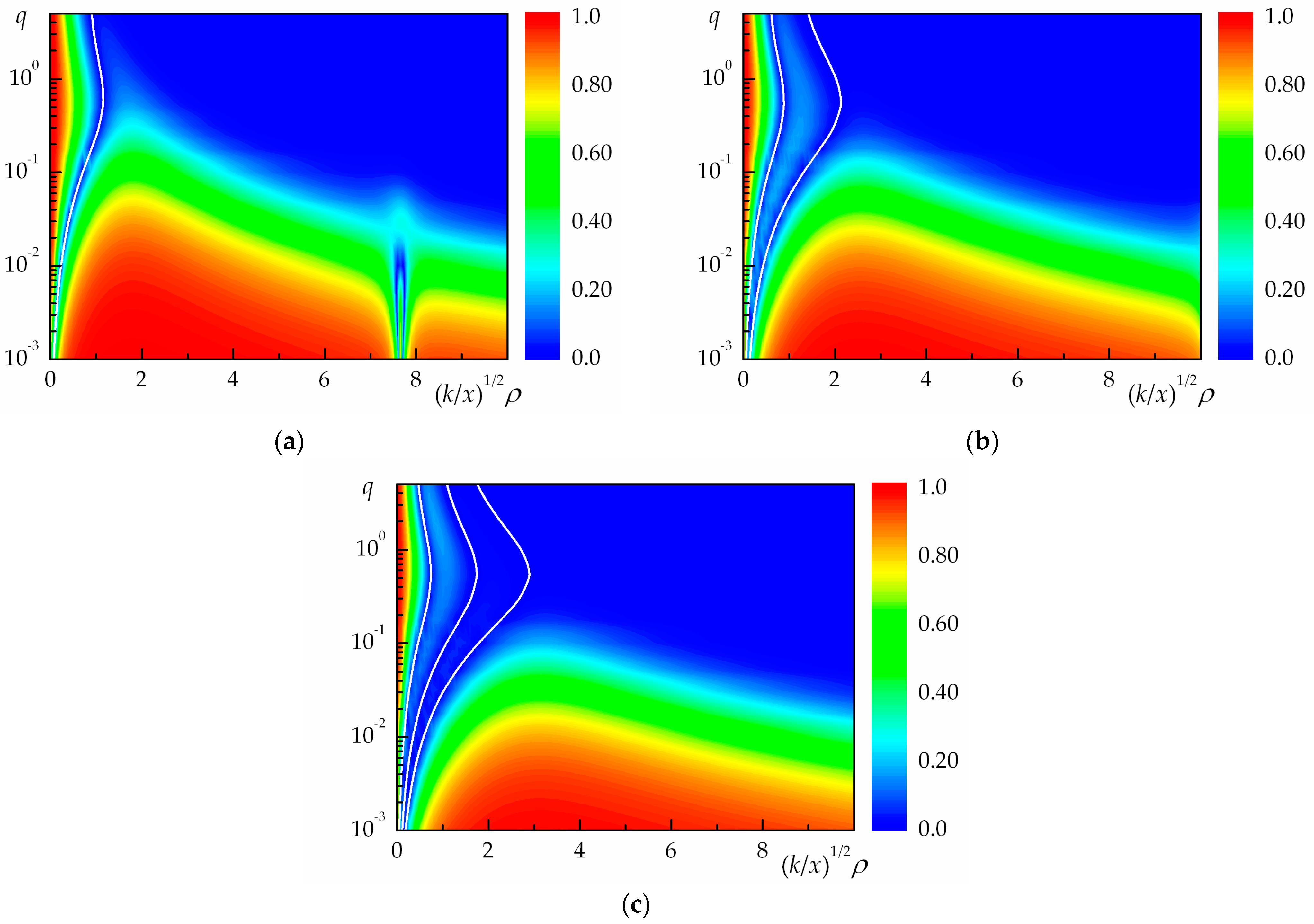
In this subsection, we consider the results concerning the propagation of fully coherent () optical radiation in a turbulent atmosphere (). The coherence degree of fully coherent vortex Bessel beams () propagating in a turbulent atmosphere for at the optical axis (), as calculated by Equations (11), (12) and (14), is shown in Figure 2a (for ), Figure 2b (for ), and Figure 2c (for ). Figure 2a–c is also the color contour plots (100 pseudo-colors) of the coherence degree of vortex Bessel beams: , as a function of the normalized radial coordinate , but with the optical thickness of a turbulent atmosphere as a dimensionless parameter. In this case, a ring dislocation of the coherence degree [29] is also formed in the paraxial zone () of the vortex Bessel beam.
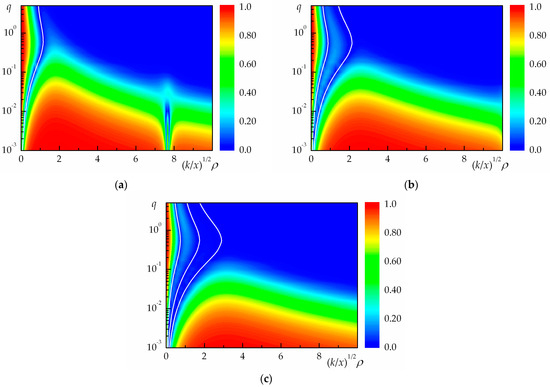
Figure 2.
Coherence degree of coherent vortex Bessel beams propagating in a turbulent atmosphere at for different values of the topological charge of the vortex beam : (a) ; (b) ; (c) . The white curves represent the coordinates of a ring dislocation.
The data shown in Figure 1 and Figure 2 allow us to conclude that the coherence transfer mechanisms for the partially coherent vortex Bessel beams in a uniform medium and fully coherent vortex Bessel beams in a turbulent atmosphere are nearly identical. The contour plots shown in these figures almost completely coincide in the main details, but some differences are observed only in their fine structure. However, these differences do exist, and they cannot be removed by the scaling of the plots. In this sense, the situation is fundamentally different from the case of the non-vortex Gaussian beam [50].
In connection with the aforementioned, we can conclude that the partially coherent optical radiation described by the Gaussian–Schell model is an optical wave with large phase distortions at the source. The turbulent atmosphere, in its turn, introduces large phase distortions to the optical wave during the propagation. This is the similarity and the difference between the two problems. The lower sensitivity of a non-vortex Gaussian beam to differences in these propagation schemes is associated with the ideal appodization of this beam to both a uniform medium and a turbulent atmosphere [50].
4.3. Coherence Degree of Partially Coherent Bessel Beams in a Turbulent Atmosphere
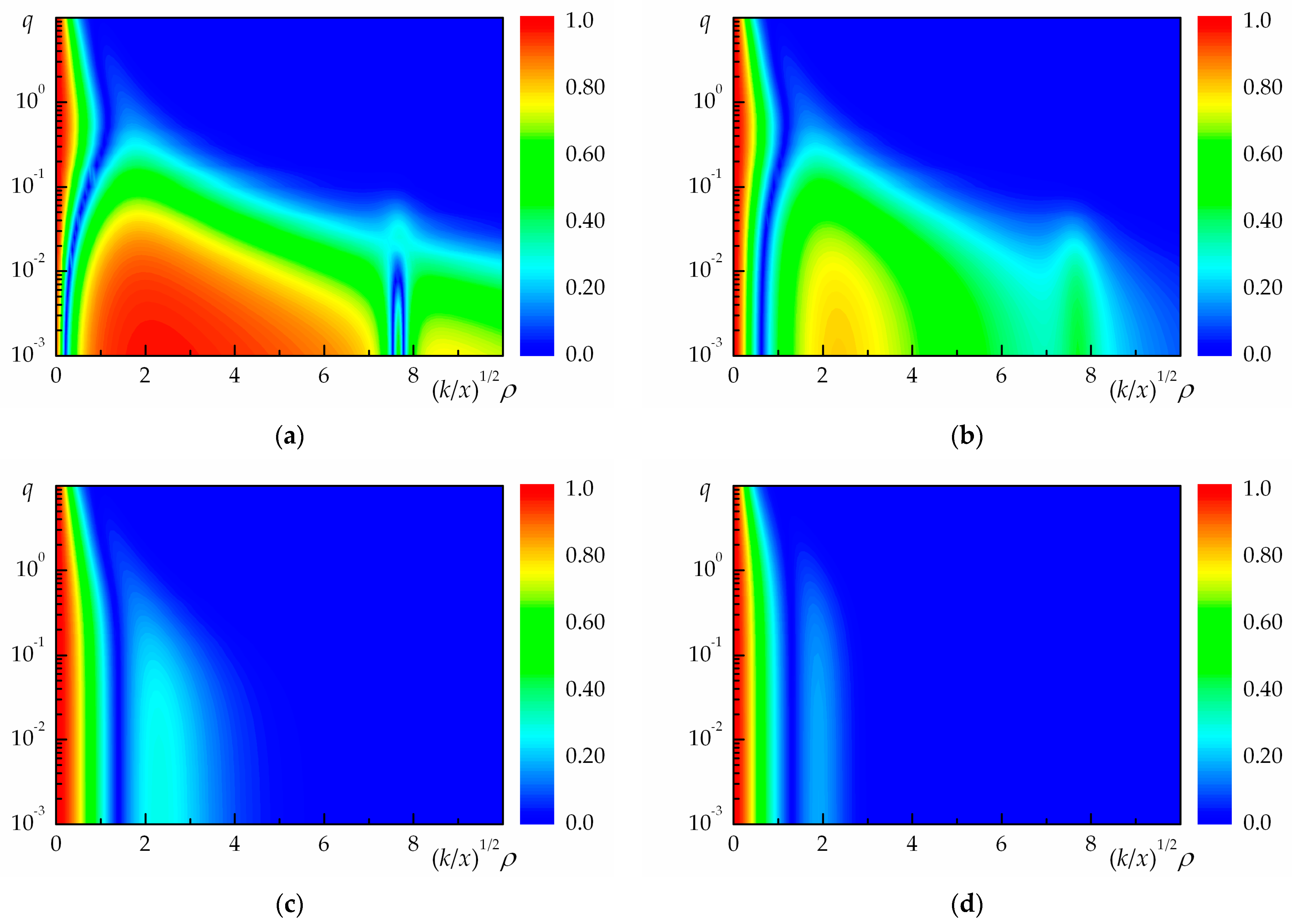
The process of transformation of the coherence degree of partially coherent vortex Bessel beams in a turbulent atmosphere is illustrated in Figure 3 (for beams with and ) at four values of the optical thickness of a uniform medium for the partially coherent radiation .
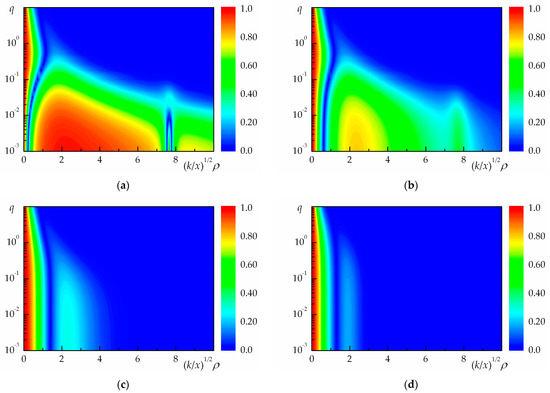
Figure 3.
Coherence degree of partially coherent vortex Bessel beams propagating in a turbulent atmosphere at and for different values of the dimensionless parameter : (a) ; (b) ; (c) ; (d) .
These figures show the color contour plots (100 pseudo-colors) of the coherence degree of partially coherent vortex Bessel beams as a function of the normalized coordinate and the normalized parameter (optical thickness of a turbulent atmosphere): . Regarding the coherence degree of partially coherent vortex Bessel beams propagating in a turbulent atmosphere, the following can be noted.
- (1)
- Factors affecting the coherence of the vortex Bessel beam, partial coherence of the optical radiation, and random inhomogeneities of a turbulent atmosphere exert not an additive, but a multiplicative distorting effect (see Equation (14) or Equation (10)).
- (2)
- As a partially coherent vortex Bessel beam propagates in a turbulent atmosphere, we could expect the formation of two ring dislocations: one due to atmospheric turbulence and another due to the partial coherence of the radiation source. However, only one ring dislocation of coherence degree of vortex Bessel beam is actually observed, because these factors affect optical radiation simultaneously.
- (3)
- A ring dislocation of the vortex Bessel beam is formed at any values of the optical thickness of a uniform medium for the partially coherent radiation .
- (4)
- As the optical thickness of a uniform medium for the partially coherent radiation increases, the ring dislocation of the partially coherent vortex Bessel beam grows in size, while its dependence on the optical thickness of a turbulent atmosphere reduces.
- (5)
- However, if the optical thickness of a uniform medium for the partially coherent radiation is greater than the unity (), a ring dislocation of the coherence degree is formed at low levels of the coherence degree and, thus, no longer exerts a significant effect on the coherence level of the partially coherent vortex Bessel beam as a whole.
- (6)
- (7)
- At a low level of the initial coherence of optical radiation (), the effect of atmospheric turbulence on the coherence degree manifests itself only in the area of strong radiation fluctuations due to turbulence () (see Figure 3c,d).
5. Integral Coherence Scale of Bessel Beams
If the data on the second-order mutual coherence function of the optical radiation field are available, we can assess the coherent properties of the field, in particular, the coherence scale of optical radiation [30,31,32,33,43,44,50]. It was shown in [35,53,54] that the integral coherence scale (13) of vortex Bessel and vortex Bessel–Gaussian beams, unlike the coherence radius of these beams, is almost uniquely related to the conditions of the propagation of optical radiation in a turbulent atmosphere. Thus, the integral coherence scale ( or ) (13) for vortex Bessel and vortex Bessel–Gaussian beams is a more representative and characteristic than their coherence radius ( or ).
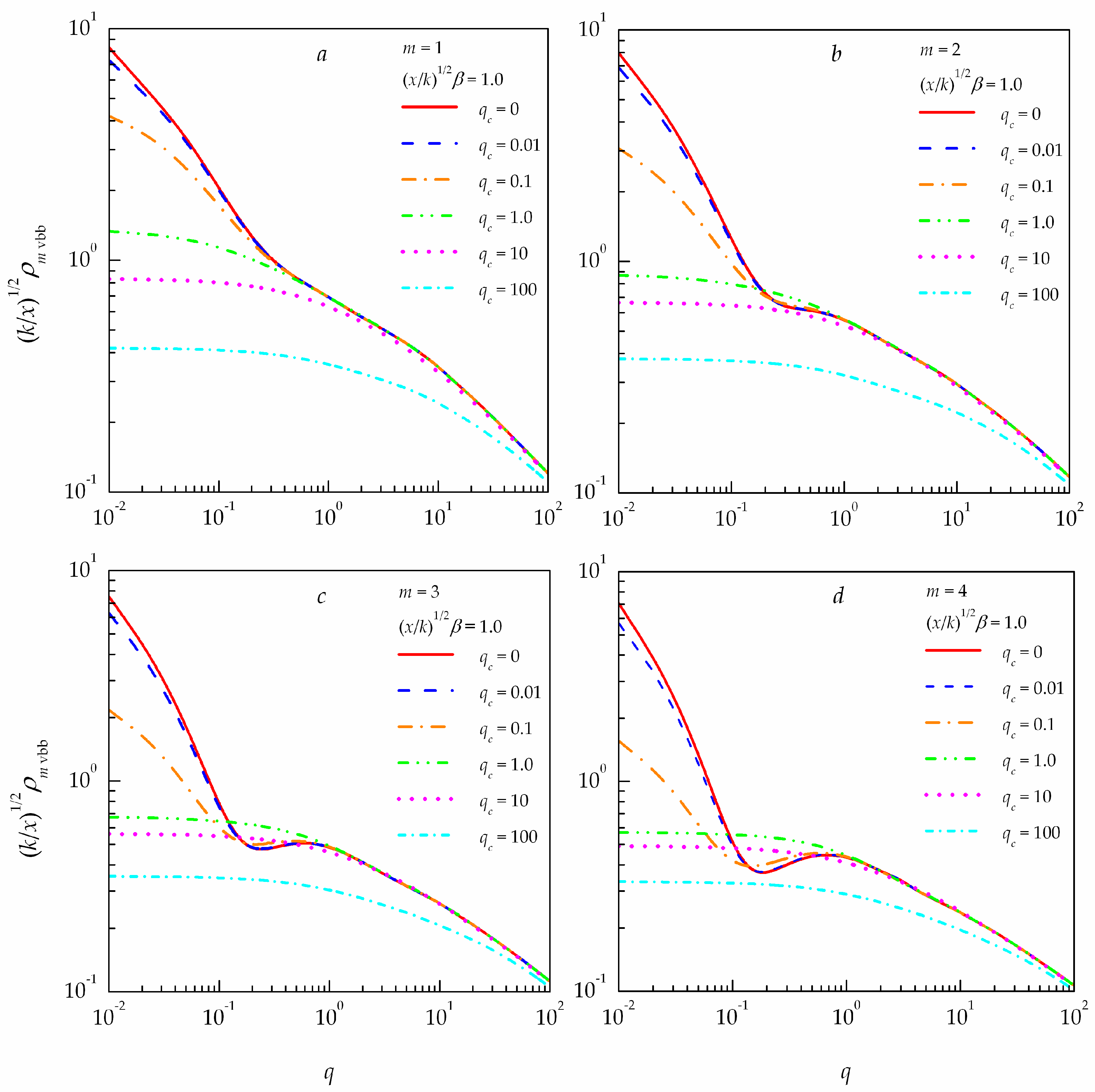
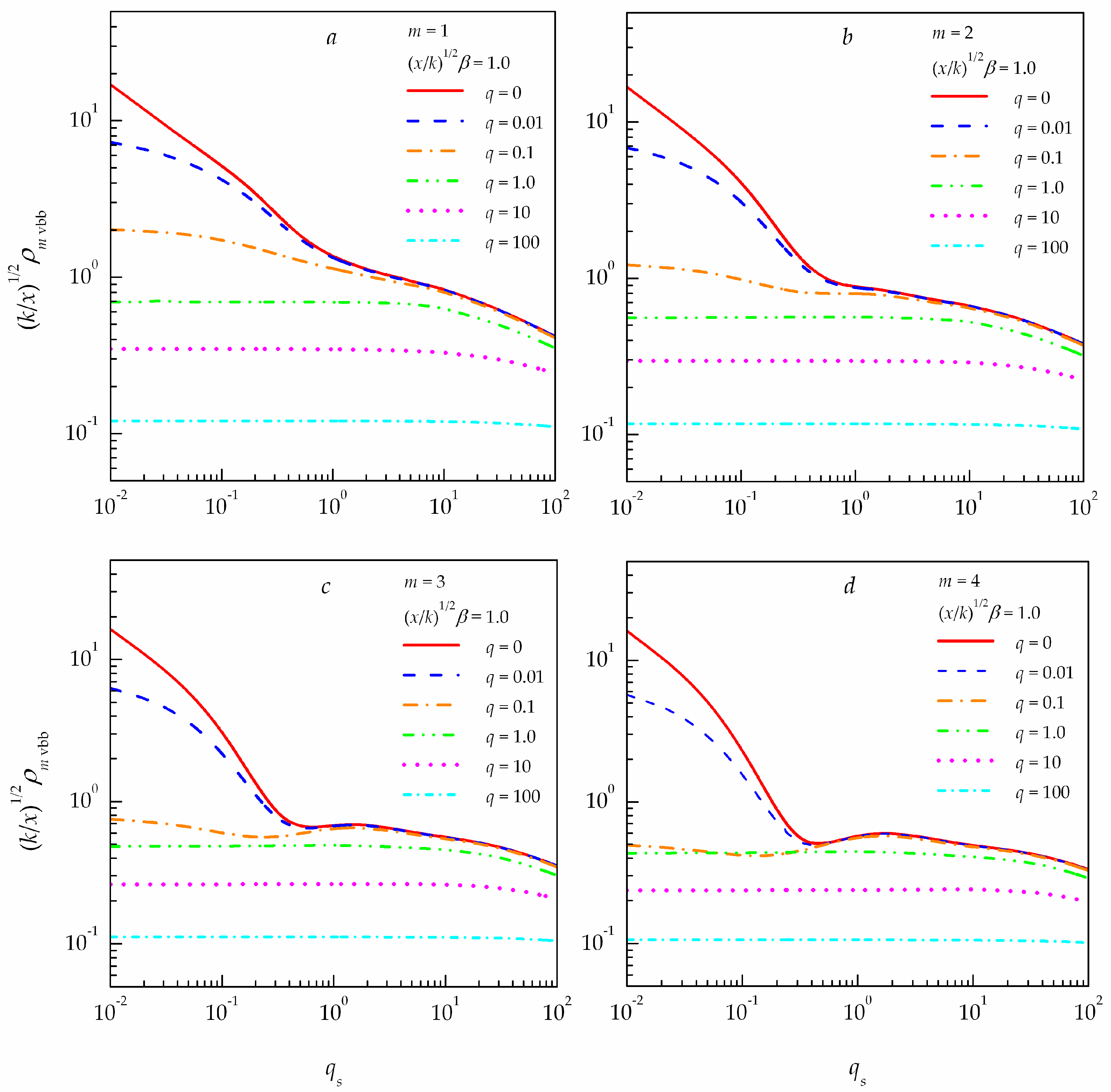
This section provides the integral coherence scale (13) of unlimited (,) partially coherent vortex Bessel beams (1) at the optical axis (), as calculated with Equations (11)–(14). Figure 4 depicts the integral coherence scale of partially coherent vortex Bessel beams with different values of the topological charge at the normalized parameter of the Bessel beam equal to the unity (). In Figure 4, the calculated results are shown to demonstrate the behavior of the integral coherence scale of partially coherent vortex Bessel beams in a turbulent atmosphere for several values of the normalized parameter (optical thickness of a uniform medium for partially coherent radiation).
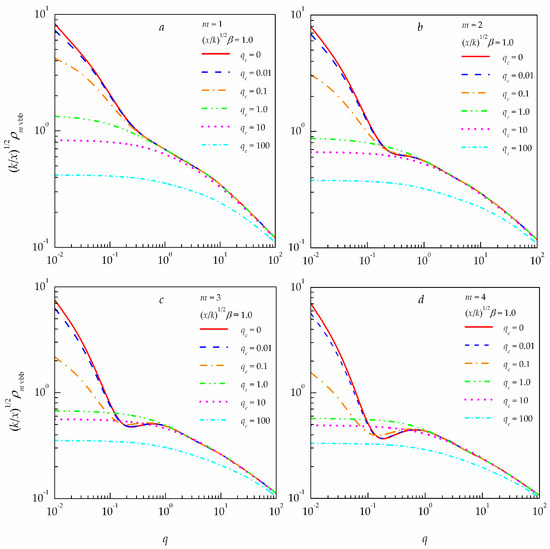
Figure 4.
Integral coherence scale of partially coherent vortex Bessel beams propagating in a turbulent atmosphere at different source coherence levels for four values of the topological charge of the vortex beam : (a) ; (b) ; (c) ; (d) .
One can see that, in the region of weak fluctuations of optical radiation due to atmospheric turbulence (), the integral coherence scale (13) of the partially coherent vortex Bessel beams (1) is significantly affected by the initial coherence of optical radiation. In the region of strong fluctuations of optical radiation due to atmospheric turbulence (), to the contrary, the decisive factor for the integral coherence scale (13) of the partially coherent vortex Bessel beams (1) is not the partial coherence of optical radiation, but the turbulence of the propagation medium.
The only exception is optical beams with very low initial coherence (). Turbulence has a minimal effect on them, because the decisive role in this case is played by the initial coherence of optical radiation. This is explained by the fact that, for these beams, the coherence is already at such a low level that atmospheric turbulence can almost completely suppress the process of coherence restoration when the incoherent optical radiation propagates along the path.
The results of these calculations are shown in Figure 5 to demonstrate the behavior of the integral coherence scale of partially coherent vortex Bessel beams for several values of the normalized parameter characterizing the conditions of radiation propagation in a turbulent atmosphere. It is easy to see (Figure 4) that significant changes in the integral coherence scale of partially coherent vortex Bessel beams are observed in the region of weak fluctuations of optical radiation due to turbulence () for optical beams with the high initial coherence ().
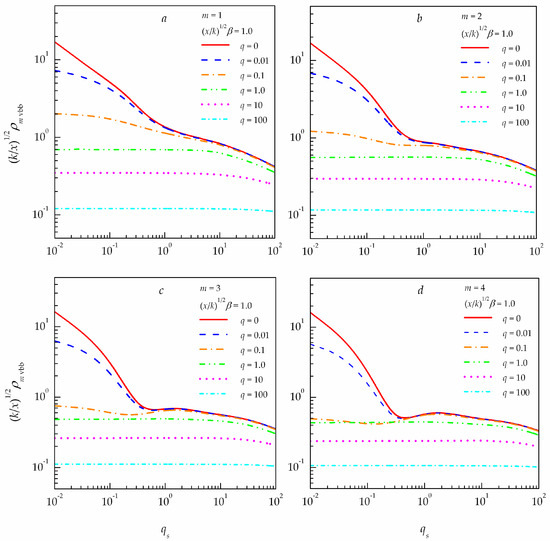
Figure 5.
Integral coherence scale of partially coherent vortex Bessel beams propagating in a turbulent atmosphere at different turbulence level in the propagation medium for four values of the topological charge of vortex beam : (a) ; (b) ; (c) ; (d) .
Thus, the data obtained for the integral coherence scale of partially coherent vortex Bessel beams for several values of the topological charge () at radiation propagation in a turbulent atmosphere (see Figure 4 and Figure 5) demonstrate that the integral coherence scale of partially coherent vortex Bessel beams changes significantly only the intermediate region of transition from weak to strong radiation fluctuations due to atmospheric turbulence only for optical beams with high initial coherence ().
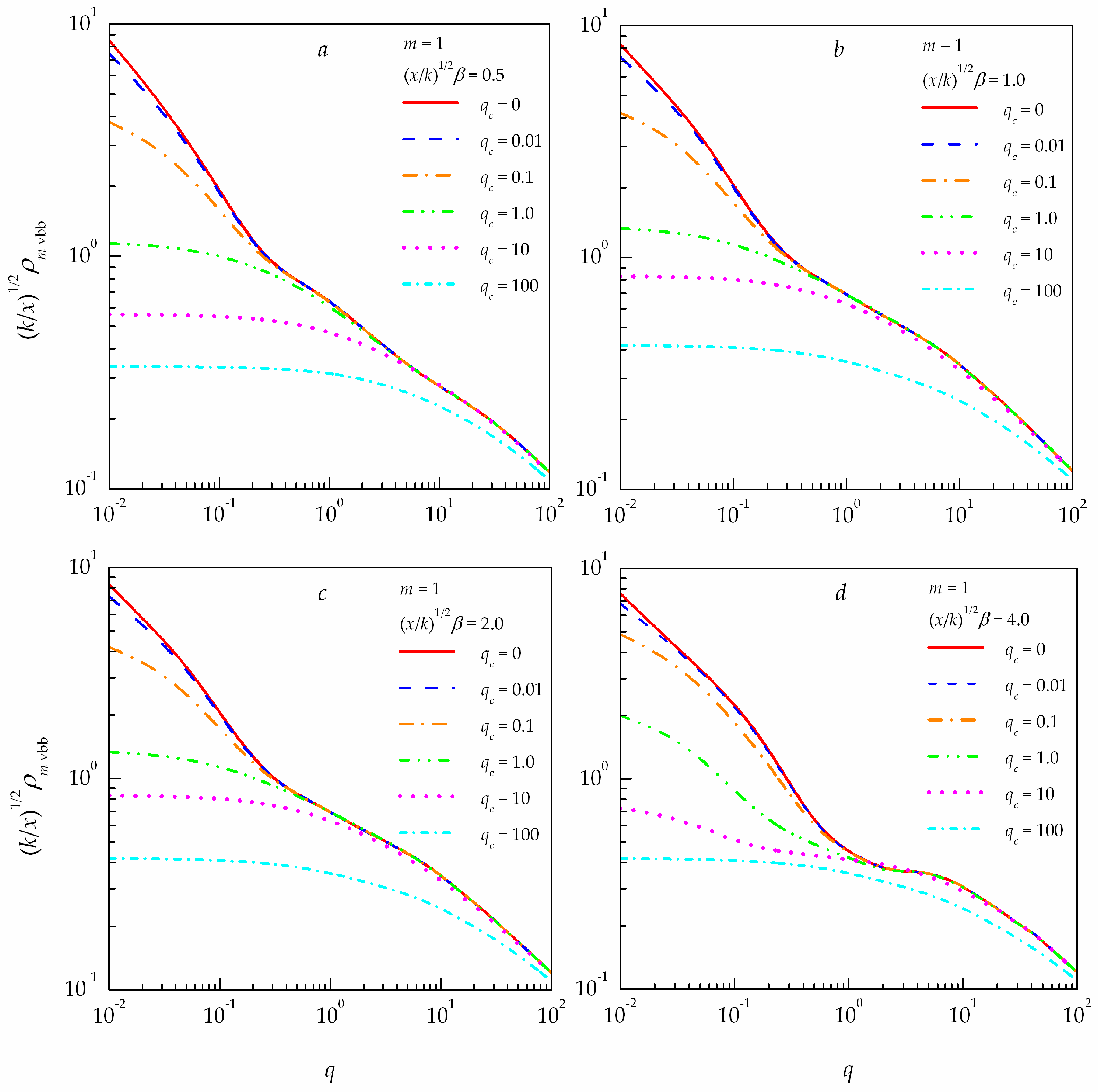
The data shown in Figure 6 are obtained for the integral coherence scale of partially coherent vortex Bessel at for different values of the Bessel beam parameter . These results demonstrate that the integral coherence scale of the partially coherent vortex Bessel beam depends rather weakly on the normalized Bessel parameter beam (in the range from 0.5 to 4.0).
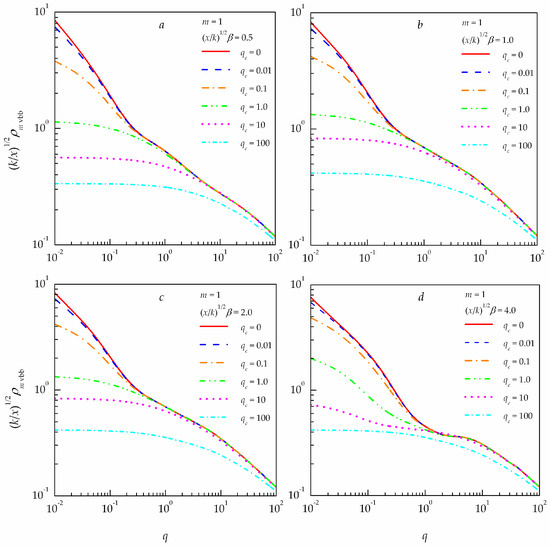
Figure 6.
Integral coherence scale of partially coherent vortex Bessel beams () propagating in a turbulent atmosphere at the different source coherence for four values of the Bessel beam parameter : (a) ; (b) ; (c) ; (d) .
The normalized Bessel beam parameter has the strongest effect on the integral coherence scale of the partially coherent vortex Bessel beam in the region of transition from weak to strong radiation fluctuations due to atmospheric turbulence. The only exception is partially coherent optical beams with the low initial coherence level , that is, partially coherent beams, for which the correlation width of the source field is smaller than the diameter of the first Fresnel zone.
It should be emphasized that the vortex character of the optical beam has a minimal effect on its coherence during the propagation. The vortex character influences only optical beams with high initial coherence () in the region and has practically no effect on the coherence behavior of beams with a low initial coherence level (). This phenomenon is associated with the ring dislocation of coherence degree of vortex Bessel beams [29] that forms at and disappears at (see Figure 3). All this happens in the region of transition from low to high fluctuations in a turbulent medium, i.e., when the diffraction-free beam still continues to keep (albeit partially) its invariant properties.
6. Integral Coherence Scale of Bessel–Gaussian Beams
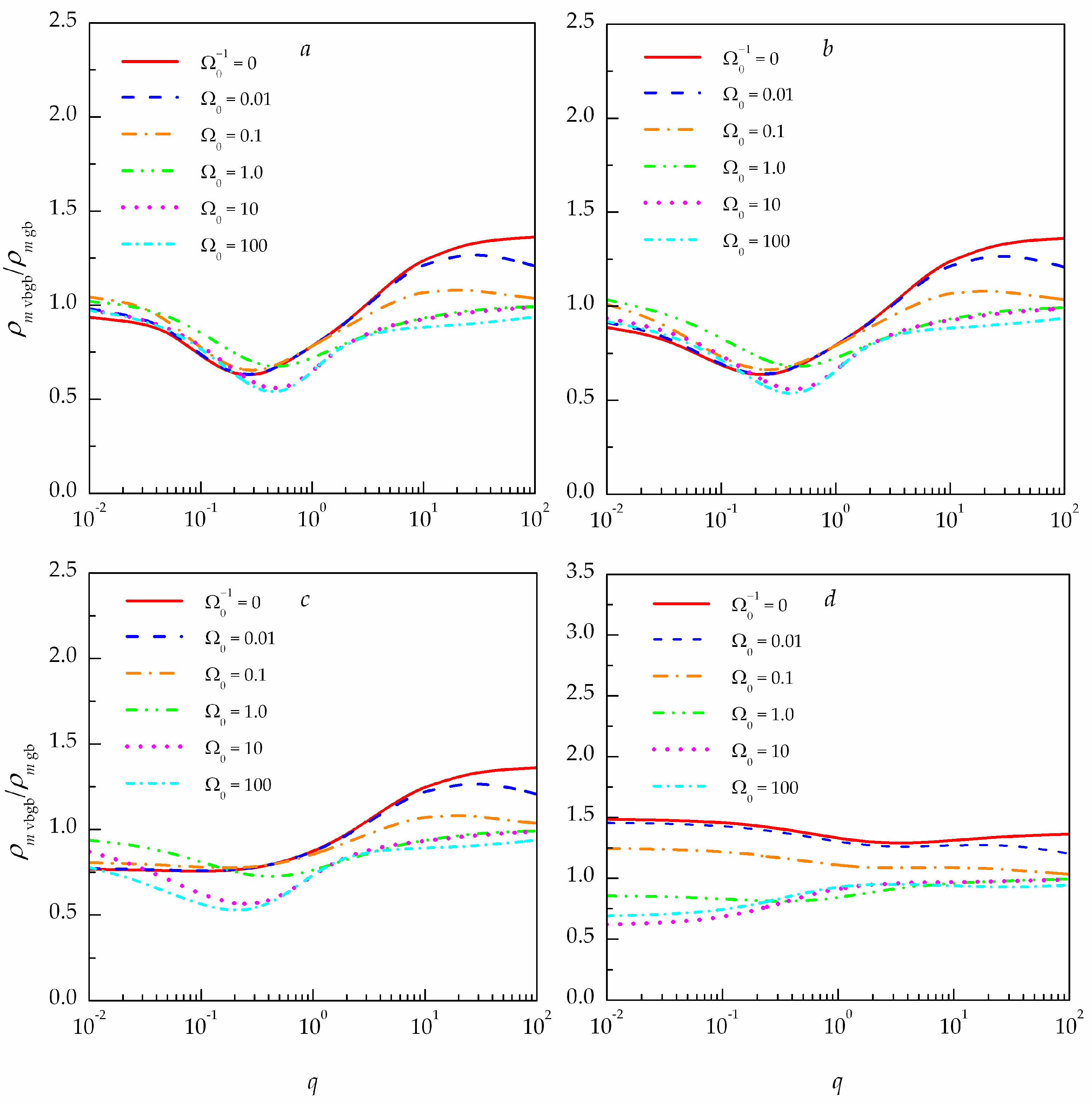
Figure 7 depicts the ratio of the integral scales of the collimated () partially coherent vortex Bessel–Gaussian beam () (1) and the collimated () partially coherent non-vortex Gaussian beam () propagating in a turbulent atmosphere. The data are obtained through numerical calculation by Equations (8) and (11)–(13) and Equations (9) and (11)–(13) for optical beams with and at the optical axis () for different values of the Fresnel number of the transmitting aperture .
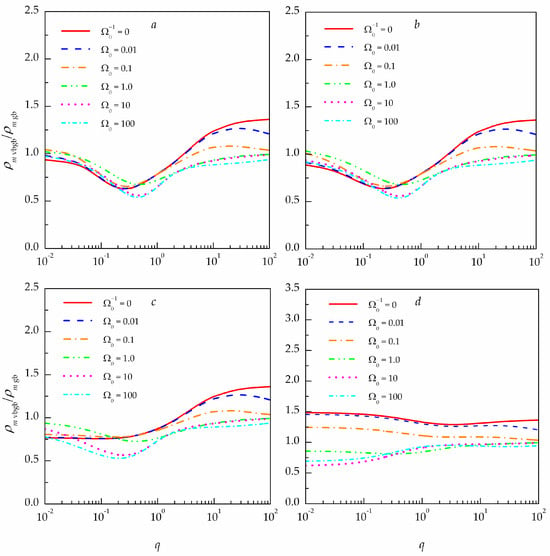
Figure 7.
Ratio of the integral coherence scales of partially coherent vortex Bessel–Gaussian and Gaussian beams with and at different values of the Fresnel number of the transmitting aperture for three source coherence levels : (a) ; (b) ; (c) ; (d) .
The comparison of the results (see Figure 7) obtained for the integral coherence scale of the collimated partially coherent Bessel–Gaussian beam in a turbulent atmosphere to that of the collimated non-vortex Gaussian beam demonstrates a weak dependence of the integral coherence scale of the collimated partially coherent Bessel–Gaussian beam in a turbulent atmosphere on the initial radius of the Gaussian factor of the beam field (1), that is, on the Fresnel number of the transmitting aperture .
Thus (see Figure 7), the integral coherence scale of the partially coherent vortex Bessel–Gaussian beam in a uniform medium or a turbulent atmosphere for optical beams with high initial coherence () differs only slightly from the integral coherence scale of the partially coherent non-vortex Gaussian beam in a uniform medium (see Figure 7) or a turbulent atmosphere, and their ratio (see Figure 7a–c) weakly depends on the Fresnel number of the transmitting aperture .
For optical beams with low initial coherence () (see Figure 7d), the situation is exactly the opposite: the ratio of the integral coherence scale of the partially coherent vortex Bessel–Gaussian beam to that of the partially coherent non-vortex Gaussian beam at the optical axes of the beams () depends significantly on the Fresnel number of the transmitting aperture , but only weakly on the level of fluctuations caused by atmospheric turbulence.
The described behavior of the integral coherence scale of vortex Bessel–Gaussian beam is associated with the fact that every ring of the Bessel beam carries approximately the same energy equal to the energy in the first ring of the Bessel beam, that is, the energy in the cross-section of the Bessel beam is distributed more uniformly than in the Gaussian beam.
7. Discussion
The results obtained for the statistical coherence characteristics of the partially coherent vortex Bessel–Gaussian beams propagating in a uniform medium or a turbulent atmosphere can be summarized in the form of the following statements.
- (1)
- The main factors affecting the coherence of partially coherent vortex Bessel–Gaussian beams propagating in turbulent atmosphere are atmospheric turbulence and the partial coherence of the source of optical radiation. These factors exert not an additive, but a multiplicative distorting effect on optical radiation.
- (2)
- The partial coherence of the source of optical radiation has a greater influence in the region of weak intensity fluctuations due to atmospheric turbulence than in the region of strong fluctuations.
- (3)
- An optical vortex (helical wavefront of the beam) plays a certain role in the transition region from weak to strong wave intensity fluctuations due to atmospheric turbulence.
- (4)
- Geometrical parameters of the Bessel and Gaussian components of partially coherent vortex Bessel–Gaussian beams propagating in a uniform medium or a turbulent atmosphere have a smaller effect on the coherence of these beams than the above factors do.
Author Contributions
Conceptualization, I.L. and V.L.; methodology, I.L. and V.L.; software, I.L.; validation, I.L.; formal analysis, I.L.; investigation, I.L.; resources, I.L.; writing—original draft preparation, I.L.; writing—review and editing, I.L.; visualization, I.L.; supervision, I.L.; project administration, I.L.; funding acquisition, I.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Allen, L.; Barnett, S.M.; Padgett, M.J. Optical Angular Momentum; Institute of Physics Publishing: Bristol, UK, 2003. [Google Scholar] [CrossRef]
- Abramochkin, E.G.; Volostnikov, V.G. Spiral light beams. Adv. Phys. Sci. 2004, 47, 1177–1203. [Google Scholar] [CrossRef]
- Andrews, D.L. Structured Light and Its Applications: An Introduction to Phase-Structured Beams and Nanoscale Optical Forces; Academic Press: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Abramochkin, E.G. Superpositions of Vortex Laser Beams; Fizmatlit: Moscow, Russia, 2023. (In Russian) [Google Scholar]
- Gibson, G.; Courtial, J.; Padgett, M.J.; Vasnetsov, M.; Pas’ko, V.; Barnett, S.M.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre—Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Baranova, N.B.; Zel’dovich, B.Y. Dislocations of the wave-front surface and zeros of the amplitude. J. Exp. Theor. Phys. 1981, 53, 925–929. [Google Scholar]
- Baranova, N.B.; Mamaev, A.V.; Pilipetsky, N.F.; Shkunov, V.V.; Zel’dovich, B.Y. Wave-front dislocations: Topological limitations for adaptive systems with phase conjugation. J. Opt. Soc. Am. 1983, 73, 525–528. [Google Scholar] [CrossRef]
- Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R. Soc. Lond. A 1974, 336, 165–190. [Google Scholar] [CrossRef]
- Berry, M.V.; Nye, J.F.; Wright, F.J. The elliptic umbilic diffraction catastrophe. Phil. Trans. R. Soc. Lond. A 1979, 291, 453–484. [Google Scholar] [CrossRef]
- Volyar, A.V.; Abramochkin, E.G.; Bretsko, M.V.; Khalilov, S.I.; Akimova, Y.E. General astigmatism of structured LG beams: Evolution and transformations of the OAM super-bursts. Photonics 2023, 10, 727. [Google Scholar] [CrossRef]
- Volyar, A.V.; Bretsko, M.V.; Khalilov, S.I.; Akimova, Y.E. Orbital angular momentum burst control in astigmatic structured beams in ABCD-matrix transforms. Comput. Opt. 2024, 48, 171–179. [Google Scholar] [CrossRef]
- Berry, M.V.; Jeffrey, M.R.; Mansuripur, M. Orbital and spin angular momentum in conical diffraction. J. Opt. A-Pure Appl. Opt. 2005, 7, 685–690. [Google Scholar] [CrossRef]
- Allen, L.; Padgett, M.J. Equivalent geometric transformations for spin and orbital angular momentum of light. J. Mod. Opt. 2007, 54, 487–491. [Google Scholar] [CrossRef]
- Volyar, A.V.; Abramochkin, E.G.; Akimova, Y.E.; Bretsko, M.V. Astigmatic-invariant structured singular beams. Photonics 2022, 9, 842. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A. Orbital angular momentum of paraxial propagation-invariant laser beams. J. Opt. Soc. Am. A 2022, 39, 1061–1065. [Google Scholar] [CrossRef]
- Volyar, A.V.; Bretsko, M.V.; Khalilov, S.I.; Akimova, Y.E. Structurally stable astigmatic vortex beams with super-high orbital angular momentum (ABCD matrix approach). Photonics 2023, 10, 1048. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Soifer, V.A. Rotor spatial filter for analysis and synthesis of coherent fields. Opt. Commun. 1992, 89, 159–163. [Google Scholar] [CrossRef]
- Soifer, V.A.; Golub, M.A. Laser Beam Mode Selection by Computer-Generated Holograms; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Pyatnitskii, L.N. Optical discharge in the field of a Bessel laser beam. Adv. Phys. Sci. 2010, 53, 159–177. [Google Scholar] [CrossRef]
- Pyatnitskii, L.N. Wave Bessel Beams; Fizmatlit: Moscow, Russia, 2012. (In Russian) [Google Scholar]
- Kotlyar, V.V.; Kovalev, A.A.; Kozlova, E.S.; Savelyeva, A.A.; Stafeev, S.S. New type of vortex laser beams: Squared Laguerre—Gaussian beam. Optik 2022, 270, 169916. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Kozlova, E.S.; Savelyeva, A.A.; Stafeev, S.S. Geometric progression of optical vortices. Photonics 2022, 9, 407. [Google Scholar] [CrossRef]
- Ramee, S.; Simon, R. Effect of holes and vortices on beam quality. J. Opt. Soc. Am. A 2000, 17, 84–94. [Google Scholar] [CrossRef] [PubMed]
- Gbur, G.; Visser, T.D. Coherence vortices in partially coherent beams. Opt. Commun. 2003, 222, 117–125. [Google Scholar] [CrossRef]
- Maleev, I.D.; Palacios, D.M.; Marathay, A.S.; Swartzlander, G.A. Spatial correlation vortices in partially coherent light: Theory. J. Opt. Soc. Am. B 2004, 21, 1895–1900. [Google Scholar] [CrossRef]
- Gbur, G.; Swartzlander, G.A. Complete transverse representation of a correlation singularity of a partially coherent field. J. Opt. Soc. Am. B 2008, 25, 1422–1429. [Google Scholar] [CrossRef]
- Ding, C.; Pan, L.; Lu, B. Phase singularities and spectral changes of spectrally partially coherent higher-order Bessel—Gauss pulsed beams. J. Opt. Soc. Am. A 2009, 26, 2654–2661. [Google Scholar] [CrossRef] [PubMed]
- Lukin, I.P. Ring dislocation of the coherence degree of a vortex Bessel beam in a turbulent atmosphere. Atmos. Ocean. Opt. 2015, 28, 415–425. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 4th ed.; Pergamon Press: New York, NY, USA, 1968. [Google Scholar]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Gbur, G.; Visser, T.D. The structure of partially coherent fields. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2010; Volume 55, pp. 285–341. [Google Scholar] [CrossRef]
- Lukin, I.P. Mean intensity of vortex Bessel beams propagating in turbulent atmosphere. Appl. Opt. 2014, 53, 3287–3293. [Google Scholar] [CrossRef] [PubMed]
- Lukin, I.P. Coherence of a Bessel beam and a conic wave in turbulent atmosphere. J. Appl. Remote Sens. 2018, 12, 042405. [Google Scholar] [CrossRef]
- Nelson, W.; Palastro, J.P.; Davis, C.C.; Sprangle, P. Propagation of Bessel and Airy beams through atmospheric turbulence. J. Opt. Soc. Am. A 2014, 31, 603–609. [Google Scholar] [CrossRef]
- Liu, X.; Liu, L.; Chen, Y.; Cai, Y. Partially coherent vortex beam: From theory to experiment. In Vortex Dynamics and Optical Vortices; Perez-De-Tejada, H., Ed.; InTech: Houston, TX, USA, 2017; pp. 275–296. [Google Scholar] [CrossRef]
- Chen, S.; Li, S.; Zhao, Y.; Liu, J.; Zhu, L.; Wang, A.; Du, J.; Shen, L.; Wang, J. Demonstration of 20-Gbit/s high-speed Bessel beam encoding/decoding link with adaptive turbulence compensation. Opt. Lett. 2016, 41, 4680–4683. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, H.; Zhang, X.; Li, H.; Xi, L. Transmission characteristics of adaptive compensation for joint atmospheric turbulence effects on the OAM-based wireless communication system. Appl. Sci. 2019, 9, 901. [Google Scholar] [CrossRef]
- Dedo, M.I.; Wang, Z.; Guo, K.; Sun, Y.; Shen, F.; Zhou, H.; Gao, J.; Sun, R.; Ding, Z.; Guo, Z. Retrieving performances of vortex beams with GS algorithm after transmitting in different types of turbulences. Appl. Sci. 2019, 9, 2269. [Google Scholar] [CrossRef]
- Li, J.; Xie, C.; Qiu, Y.; Xiao, N.; Hu, M. The aberration correction of high-order Bessel—Gaussian beams. Optik 2020, 221, 163968. [Google Scholar] [CrossRef]
- Lukin, V.P.; Lukin, I.P. Overview of modern technologies for measuring, predicting and correcting turbulent distortions in optical waves. Comput. Opt. 2024, 48, 68–80. (In Russian) [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar] [CrossRef]
- Beran, M.J.; Parrent, G.B. Theory of Partial Coherence; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar] [CrossRef]
- Schell, A.C. A technique for the determination of the radiation pattern of a partially coherent aperture. IEEE Trans. Antennas Propag. 1967, 15, 187–188. [Google Scholar] [CrossRef]
- Kon, A.I.; Tatarskii, V.I. On the theory of the propagation of partially coherent light beams in a turbulent atmosphere. Radiophys. Quantum Electron. 1972, 15, 1187–1192. [Google Scholar] [CrossRef]
- Arutyunyan, A.G.; Akhmanov, S.A.; Golyaev, Y.D.; Tunkin, V.G.; Chirkin, A.S. Spatial field and intensity correlation functions of laser radiation. J. Exp. Theor. Phys. 1973, 37, 764–771. [Google Scholar]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef] [PubMed]
- Ricklin, J.C.; Davidson, F.M. Atmospheric optical communication with a Gaussian Schell beam. J. Opt. Soc. Am. A 2003, 20, 856–866. [Google Scholar] [CrossRef] [PubMed]
- Belen’kii, M.S.; Lukin, V.P.; Mironov, V.L.; Pokasov, V.V. Coherence of Laser Radiation in the Atmosphere; Nauka: Novosibirsk, Russia, 1985. (In Russian) [Google Scholar]
- Lukin, I.P. Coherence of a Bessel beam in a turbulent atmosphere. Atmos. Ocean. Opt. 2012, 25, 328–337. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Lukin, I.P. Coherence of vortex pseudo-Bessel beams in turbulent atmosphere. Comput. Opt. 2019, 43, 926–935. (In Russian) [Google Scholar] [CrossRef]
- Lukin, I.P. Coherence of vortex Bessel-like beams in a turbulent atmosphere. Appl. Opt. 2020, 50, 3833–3841. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).