Design of Photonic Molecule-Based Multiway Beam Splitter/Coupler with Variable Division Ratio
Abstract
1. Introduction
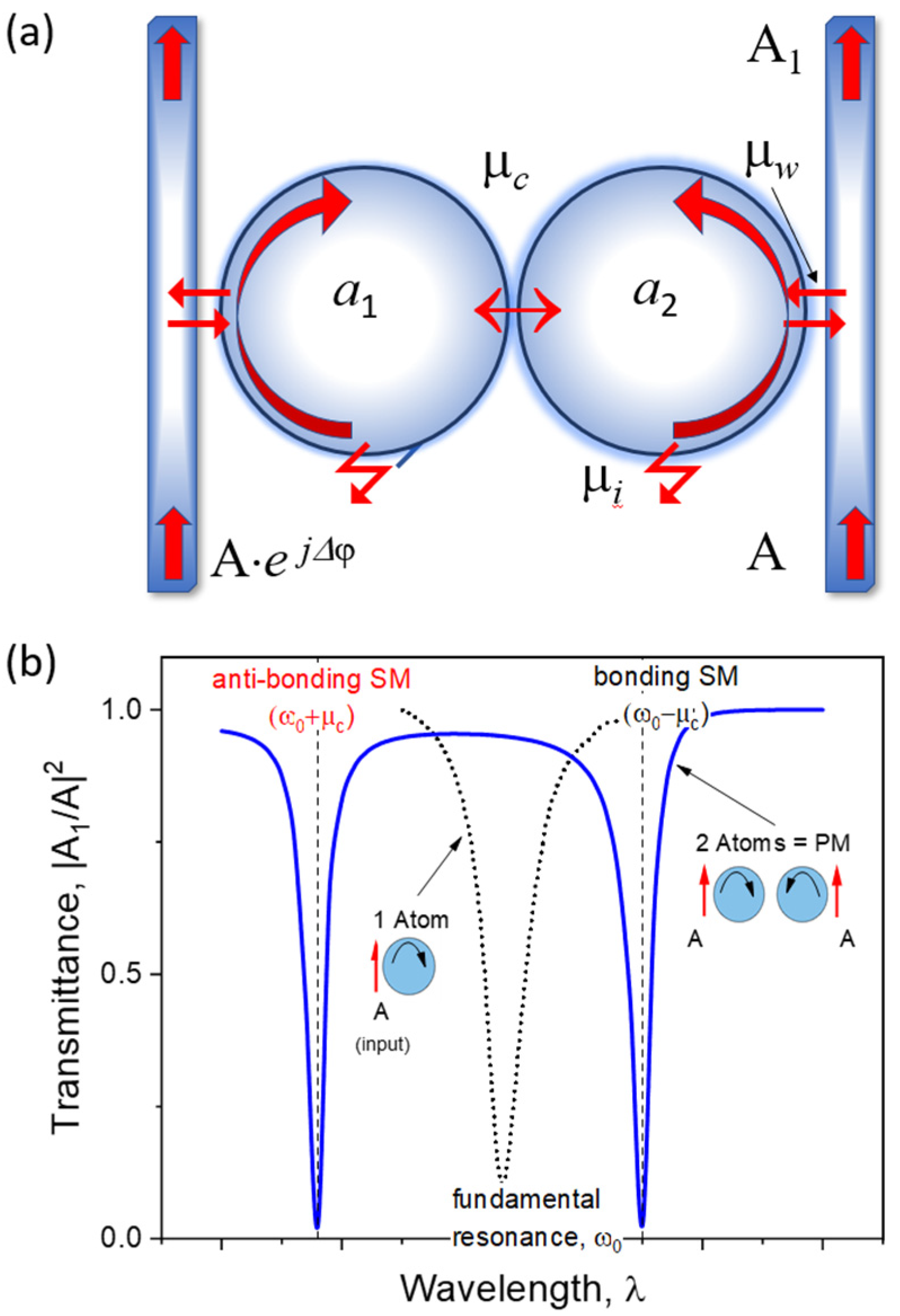
2. PM-BS Structural Model and Working Principle
3. Discussion
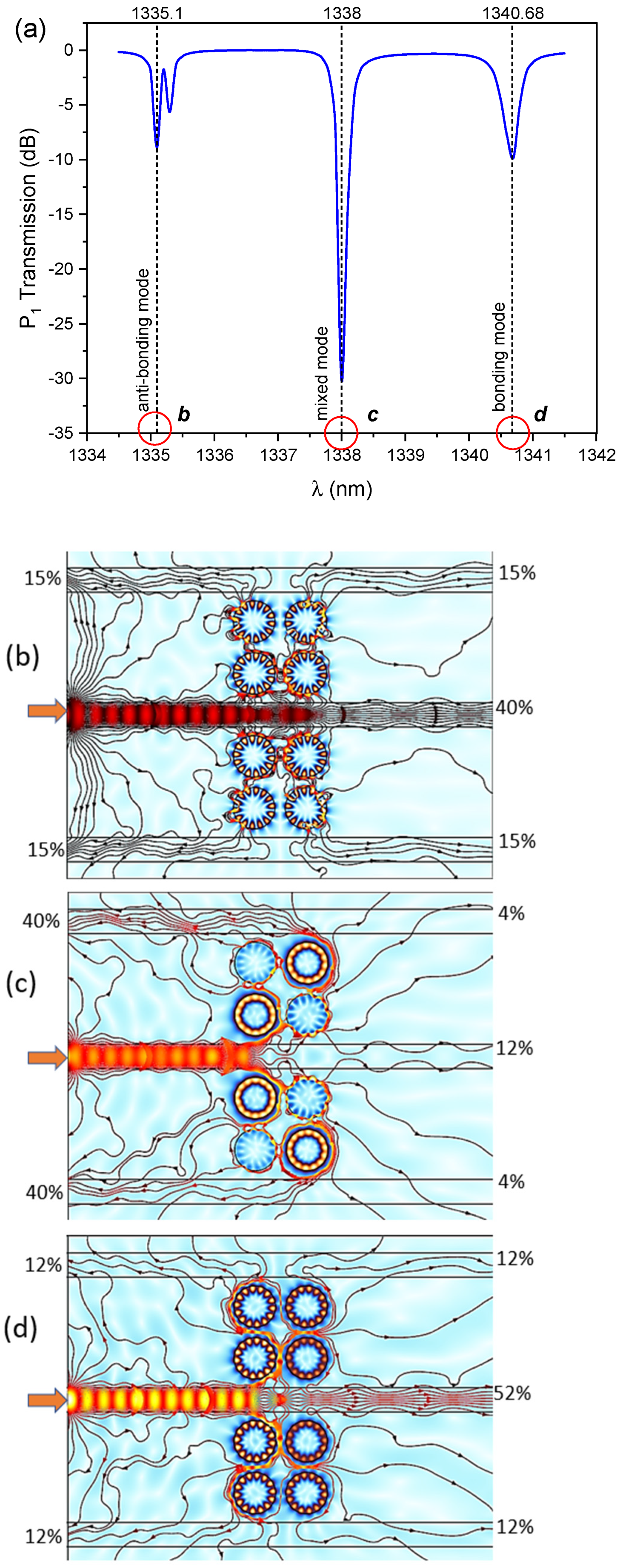
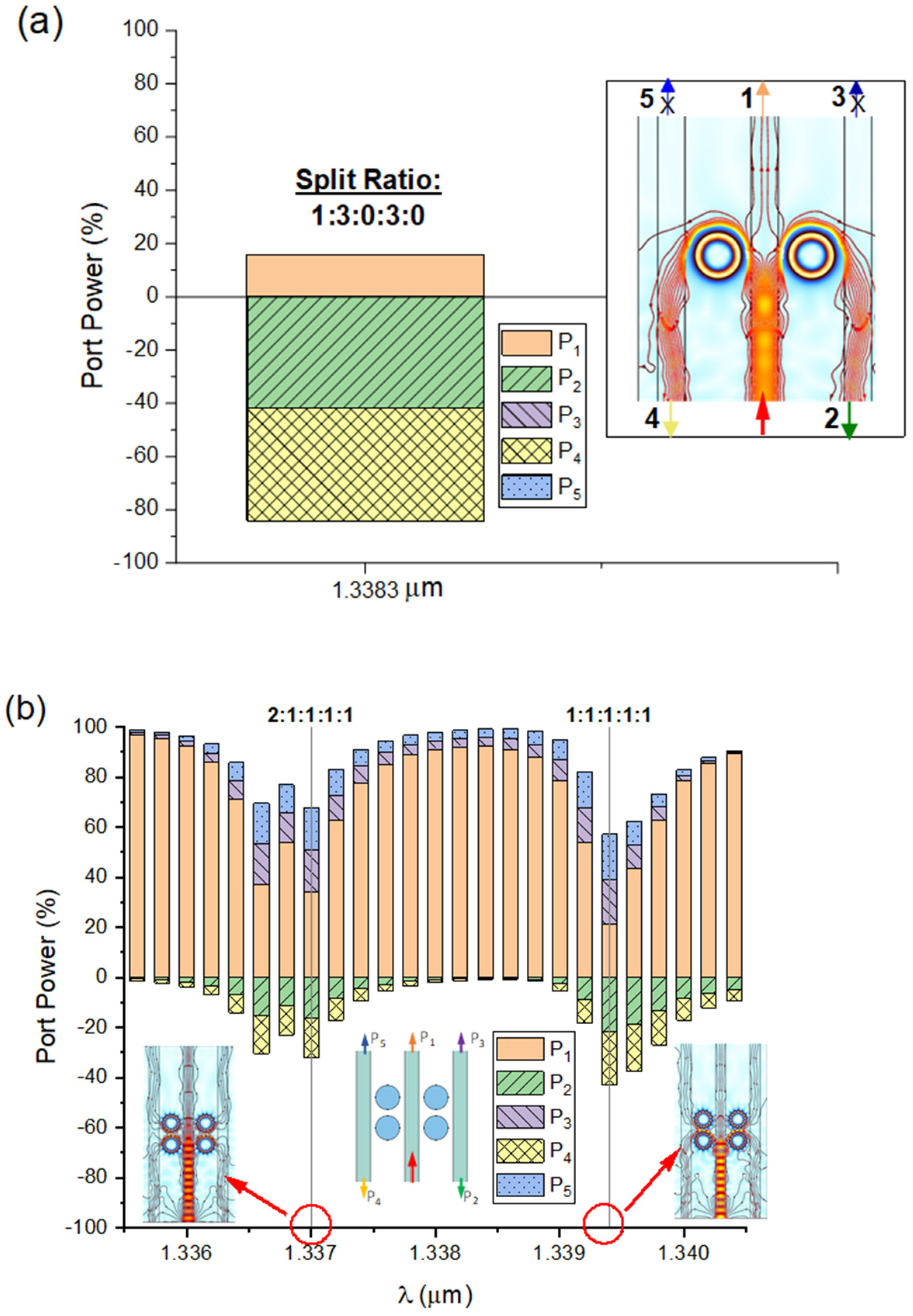
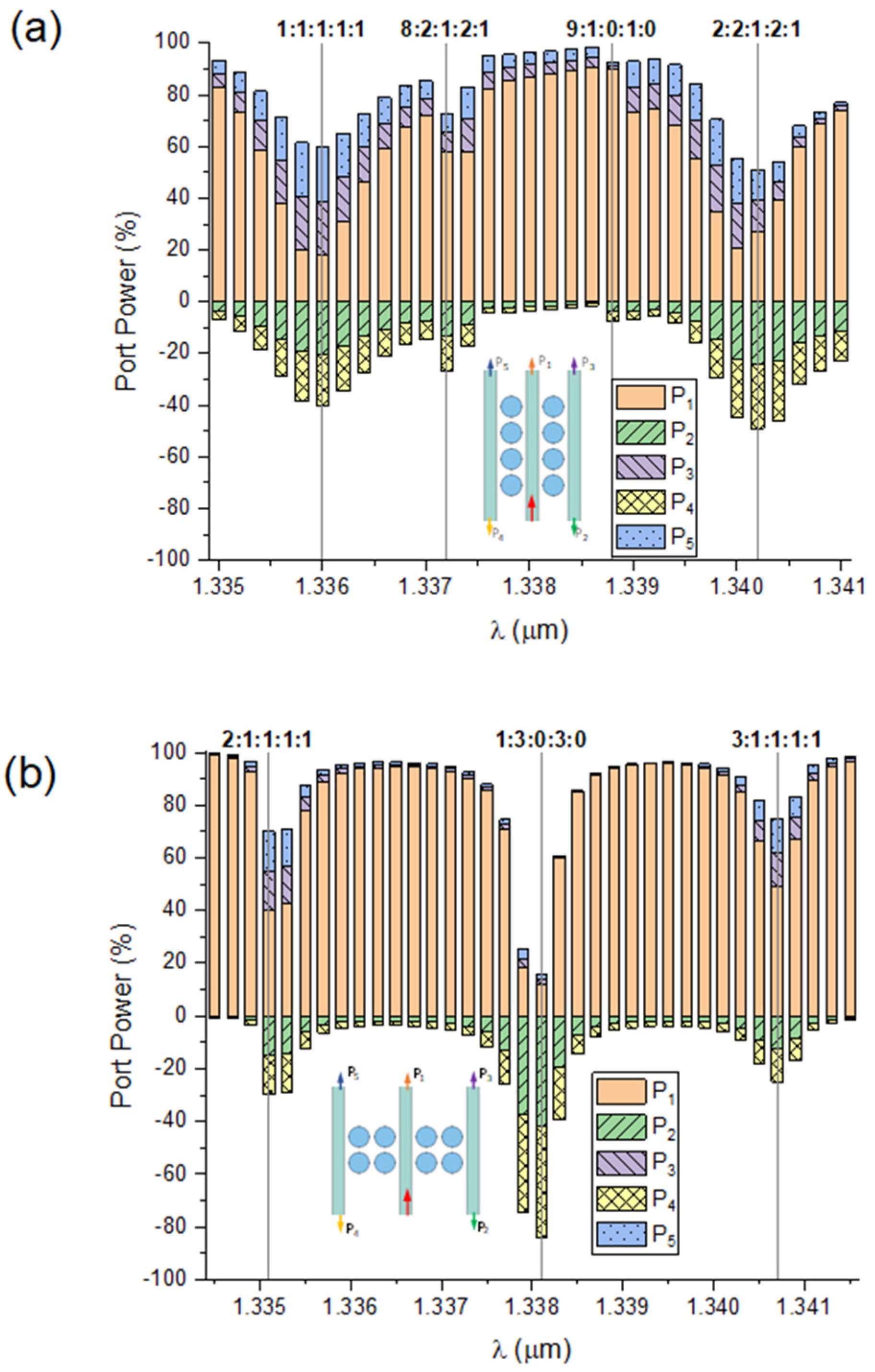
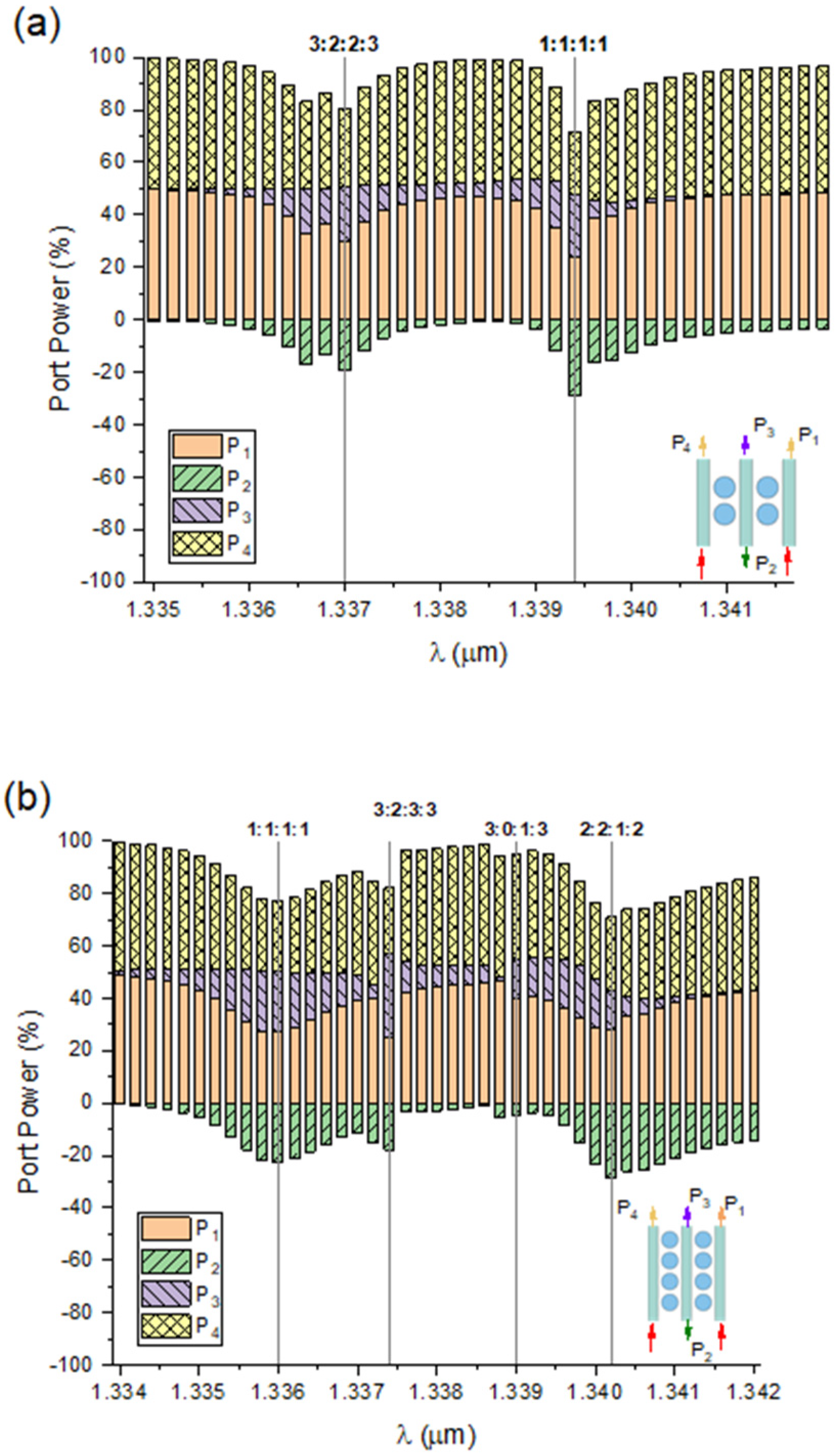
3.1. Structural Types of PM-Based Beam Splitter
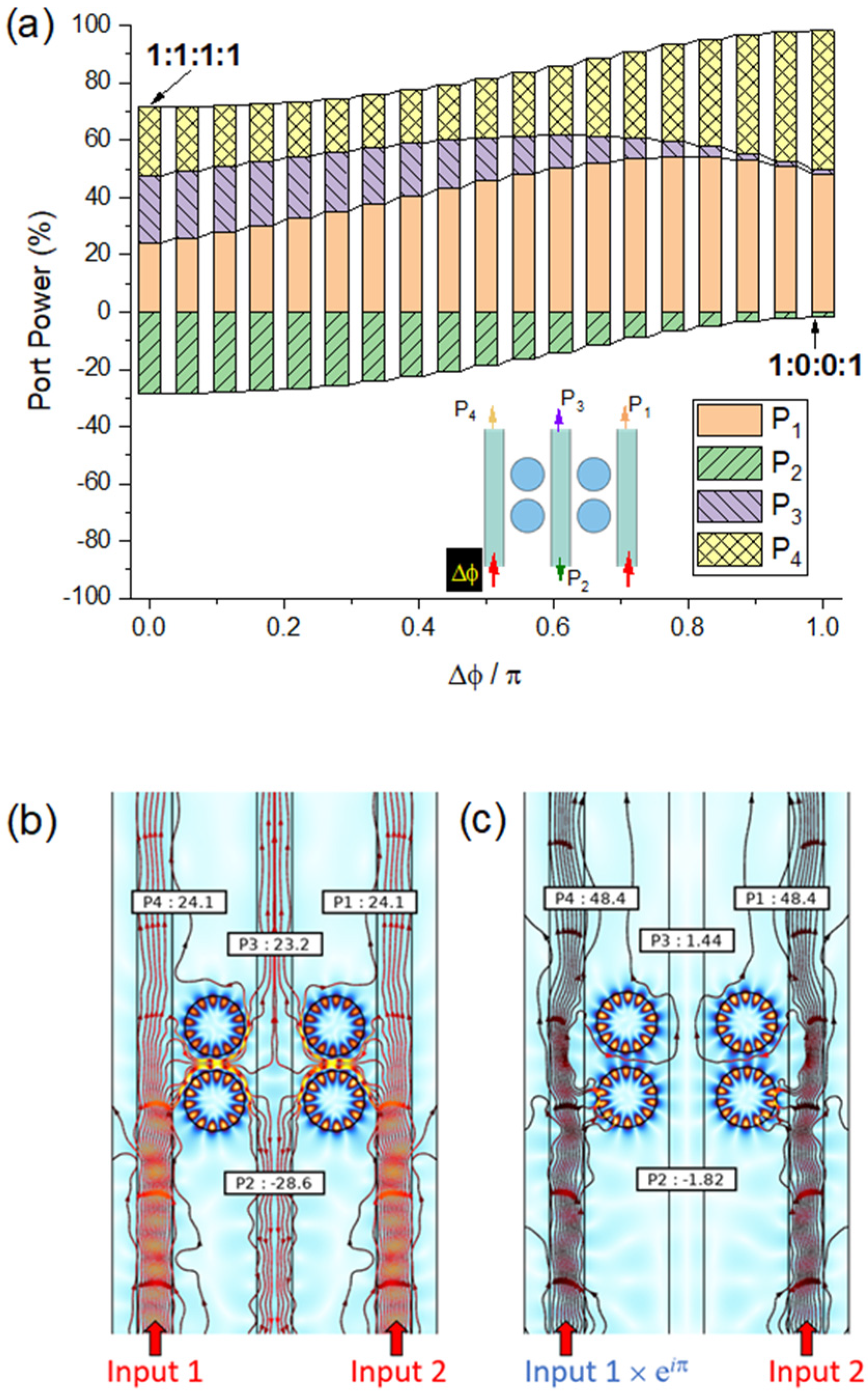
3.2. Design of PM-Based Optical Coupler
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pasquazi, A.; Razzari, L.; Moss, D.J.; Coen, S.; Erkintalo, M.; Chembo, Y.K.; Hansson, T.; Wabnitz, S.; Del’Haye, P.; Xue, X.; et al. Micro-combs: A novel generation of optical sources. Phys. Rep. 2018, 729, 1–81. [Google Scholar] [CrossRef]
- Xia, Z.; Eftekhar, A.A.; Soltani, M.; Momeni, B.; Li, Q.; Chamanzar, M.; Yegnanarayanan, S.; Adibi, A. High resolution on-chip spectroscopy based on miniaturized microdonut resonators. Opt. Express 2011, 19, 12356–12364. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Velichansky, V.L.; Ilchenko, V.S.; Gorodetsky, M.L.; Hollberg, L.; Yarovitsky, A.V. Narrow-line-width diode laser with a high-Q microsphere resonator. Opt. Commun. 1998, 158, 305–312. [Google Scholar] [CrossRef]
- Popovic, M.A.; Barwicz, T.; Dahlem, M.S.; Gan, F.; Holzwarth, C.W.; Rakich, P.T.; Smith, H.I.; Ippen, E.P.; Kartner, F.X. Tunable, fourth-order silicon microring-resonator add-drop filters. In Proceedings of the 33rd European Conference and Exhibition of Optical Communication, Berlin, Germany, 16–20 September 2007; pp. 1–2. [Google Scholar] [CrossRef]
- Bagheri, A.; Nazari, F.; Moravvej-Farshi, M.K. Bidirectional switchable beam splitter/filter based graphene loaded Si ring resonators. Phys. Scr. 2021, 96, 125536. [Google Scholar] [CrossRef]
- Madsen, C.K.; Lenz, G. Optical all-pass filters for phase response design with applications for dispersion compensation. IEEE Photon. Technol. Lett. 1998, 10, 994–996. [Google Scholar] [CrossRef]
- Heebner, J.E.; Boyd, R.W. Enhanced all-optical switching by use of a nonlinear fiber ring resonator. Opt. Lett. 1999, 24, 847–849. [Google Scholar] [CrossRef]
- Chhipa, M.K.; Madhav, B.T.P.; Suthar, B. An all-optical ultracompact microring-resonator-based optical switch. J. Comput. Electron. 2021, 20, 419–425. [Google Scholar] [CrossRef]
- Grassani, D.; Azzini, S.; Liscidini, M.; Galli, M.; Strain, M.J.; Sorel, M.; Sipe, J.E.; Bajoni, D. Micrometer-scale integrated silicon source of time-energy entangled photons. Optica 2015, 2, 88–94. [Google Scholar] [CrossRef]
- Kumar, V.S.P.; Sunita, P.; Kumar, M.; Kumari, N.; Karar, V.; Sharma, A.L. Design and fabrication of multilayer dichroic beam splitter. Adv. Mater. Proc. 2017, 2, 398. [Google Scholar] [CrossRef][Green Version]
- Chen, X.; Zou, H.; Su, M.; Tang, L.; Wang, C.; Chen, S.; Su, C.; Li, Y. All-Dielectric Metasurface-Based Beam Splitter with Arbitrary Splitting Ratio. Nanomaterials 2021, 11, 1137. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, L.; Yun, H.; Ma, M.; Kumar, A.; El-Fiky, E.; Li, R.; Abadíacalvo, N.; Chrostowski, L.; Jaeger, N.A.F.; et al. Polarization-independent mode-evolution-based coupler for the silicon-on-insulator platform. IEEE Photon. J. 2018, 10, 4900410. [Google Scholar] [CrossRef]
- Pérez-Armenta, C.; Ortega-Moñux, A.; Luque-González, J.M.; Halir, R.; Reyes-Iglesias, P.J.; Schmid, J.; Cheben, P.; Molina-Fernández, Í.; Wangüemert-Pérez, J.G. Polarization-independent multimode interference coupler with anisotropy-engineered bricked metamaterial. Photon. Res. 2022, 10, A57–A65. [Google Scholar] [CrossRef]
- Moniem, T.A. All-optical digital 4 × 2 encoder based on 2D photonic crystal ring resonators. J. Mod. Opt. 2016, 63, 735–741. [Google Scholar] [CrossRef]
- Rahmi, B.; Badaoui, H.; Abri, M.; Imam, A. High-performance all-optical 3×8 photonic crystal decoder using nonlinear micro-ring resonators. App. Phys. B 2023, 129, 35. [Google Scholar] [CrossRef]
- Xu, W.; Hu, L.; Shao, K.; Liang, H.; He, T.; Dong, S.; Zhu, J.; Wei, Z.; Wang, Z.; Cheng, X. Design of arbitrary energy distribution beam splitters base on multilayer metagratings by a hybrid evolutionary particle swarm optimization. Opt. Express 2023, 31, 41339–41350. [Google Scholar] [CrossRef]
- Ren, Y.; Liang, Z.; Shi, X.; Yang, F.; Zhang, X.; Dai, R.; Zhang, S.; Liu, W. Infrared All-Dielectric Metasurface Beam Splitter Based on Transflective Structures. Appl. Sci. 2023, 13, 5207. [Google Scholar] [CrossRef]
- Xu, Y.; Tian, Z.; Meng, X.; Chai, Z. Methods and applications of on-chip beam splitting: A review. Front. Phys. 2022, 10, 985208. [Google Scholar] [CrossRef]
- Little, B.E.; Chu, S.T.; Absil, P.P.; Hryniewicz, J.V.; Johnson, F.G.; Seiferth, F.; Gill, D.; Van, V.; King, O.; Trakalo, M. Very high-order microring resonator filters for WDM applications. IEEE Photonics Technol. Lett. 2004, 16, 2263–2265. [Google Scholar] [CrossRef]
- Peng, Z.; Arakawa, T. Tunable Vernier Series-Coupled Microring Resonator Filters Based on InGaAs/InAlAs Multiple Quantum-Well Waveguide. Photonics 2023, 10, 1256. [Google Scholar] [CrossRef]
- Selim, M.A.; Anwar, M. Enhanced Q-factor and effective length silicon photonics filter utilizing nested ring resonators. J. Opt. 2023, 25, 115801. [Google Scholar] [CrossRef]
- Jin, L.; Li, M.; He, J.-J. Highly-sensitive silicon-on-insulator sensor based on two cascaded micro-ring resonators with vernier effect. Opt. Commun. 2011, 284, 156–159. [Google Scholar] [CrossRef]
- Rakovich, Y.P.; Donegan, J.F. Photonic atoms and molecules. Laser Photon. Rev. 2010, 4, 179–191. [Google Scholar] [CrossRef]
- Liao, K.; Hu, X.; Gan, T.; Liu, Q.; Wu, Z.; Fan, C.; Feng, X.; Lu, C.; Liu, Y.; Gong, Q. Photonic molecule quantum optics. Adv. Opt. Photon. 2020, 12, 60–134. [Google Scholar] [CrossRef]
- Boriskina, S.V. Theoretical prediction of a dramatic Q-factor enhancement and degeneracy removal of whispering gallery modes in symmetrical photonic molecules. Opt. Lett. 2006, 31, 338. [Google Scholar] [CrossRef]
- Li, Y.; Abolmaali, F.; Allen, K.W.; Limberopoulos, N.I.; Urbas, A.; Rakovich, Y.; Maslov, A.V.; Astratov, V.N. Whispering gallery mode hybridization in photonic molecules. Laser Photonics Rev. 2017, 11, 1600278. [Google Scholar] [CrossRef]
- Geints, Y.E. Manipulating the supermodes in photonic molecules: Prospects for all-optical switching and sensing. J. Opt. Soc. Am. B 2023, 40, 1875–1881. [Google Scholar] [CrossRef]
- Chremmos, I.; Schwelb, O.; Uzunoglu, N. (Eds.) Photonic Microresonator Research and Applications; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Evans, P.W.; Holonyak, N. Room temperature photopumped laser operation of native-oxide-defined coupled GaAs-AlAs superlattice microrings. Appl. Phys. Lett. 1996, 69, 2391–2393. [Google Scholar] [CrossRef]
- Bayer, M.; Gutbrod, T.; Reithmaier, J.P.; Forchel, A.; Reinecke, T.L.; Knipp, P.A.; Dremin, A.A.; Kulakovskii, V.D. Optical modes in photonic molecules. Phys. Rev. Lett. 1998, 81, 2582–2585. [Google Scholar] [CrossRef]
- Geints, Y.E. Phase-controlled supermodes in symmetric photonic molecules. J. Quant. Spectrosc. Radiat. Transf. 2023, 302, 108524. [Google Scholar] [CrossRef]
- Hoang, T.X.; Chu, H.-S.; García-Vidal, F.J.; Png, C.E. High-performance dielectric nano-cavities for near- and mid-infrared frequency applications. J. Opt. 2022, 24, 094006. [Google Scholar] [CrossRef]
- Tian, T.; Liao, Y.; Feng, X.; Cui, K.; Liu, F.; Zhang, W.; Huang, Y. Metasurface-Based Free-Space Multi-Port Beam Splitter with Arbitrary Power Ratio. Adv. Optical Mater. 2023, 11, 2300664. [Google Scholar] [CrossRef]
- Long, J.; Jia, H.; Zhang, J.; Chen, C. Low-loss and compact, dual-mode, 3-dB power splitter combining a directional coupler, a multimode interferometer, and a Y-junction. Appl. Opt. 2024, 63, 2030–2035. [Google Scholar] [CrossRef] [PubMed]
- Manolatou, C.; Khan, M.J.; Fan, S.; Villeneuve, P.R.; Haus, H.A.; Joannopoulos, J.D. Coupling of modes analysis of resonance channel add-drop filters. IEEE J. Quantum Electron. 1999, 35, 1322–1331. [Google Scholar] [CrossRef]
- Schinke, C.; Peest, P.C.; Schmidt, J.; Brendel, R.; Bothe, K.; Vogt, M.R.; Kröger, I.; Winter, S.; Schirmacher, A.; Lim, S.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv. 2015, 5, 67168. [Google Scholar] [CrossRef]
- Matsko, A.B.; Ilchenko, V.S. Optical resonators with whispering-gallery modes Part I: Basics. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 3–14. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley: New York, NY, USA, 1983. [Google Scholar]
- Mishchenko, M.I.; Videen, G.; Babenko, V.A.; Khlebtsov, N.G.; Wriedt, T. T-matrix theory of electromagnetic scattering by particles and its applications: A comprehensive reference database. J. Quant. Spectrosc. Radiat. Transf. 2004, 88, 357–406. [Google Scholar] [CrossRef]
- Xu, Y.-L. Electromagnetic scattering by an aggregate of spheres. Appl. Opt. 1995, 34, 4573–4588. [Google Scholar] [CrossRef] [PubMed]
- Draine, B.T.; Goodman, J. Beyond Clausius-Mossotti: Wave propagation on a polarizable point lattice and the discrete dipole approximation. Astrophys. J. 1993, 405, 685. [Google Scholar] [CrossRef]
- Kanaev, A.V.; Astratov, V.N.; Cai, W. Optical coupling at a distance between detuned spherical cavities. Appl. Phys. Lett. 2006, 88, 111111. [Google Scholar] [CrossRef]
- Geints, Y.E.; Minin, I.V.; Minin, O.V. Coupled Optical Resonances in a Dielectric Microsphere: Physical Concept of a Miniature Optical Pressure Sensor. Atmos. Ocean. Opt. 2022, 6, 802–810. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geints, Y.E. Design of Photonic Molecule-Based Multiway Beam Splitter/Coupler with Variable Division Ratio. Photonics 2024, 11, 600. https://doi.org/10.3390/photonics11070600
Geints YE. Design of Photonic Molecule-Based Multiway Beam Splitter/Coupler with Variable Division Ratio. Photonics. 2024; 11(7):600. https://doi.org/10.3390/photonics11070600
Chicago/Turabian StyleGeints, Yury E. 2024. "Design of Photonic Molecule-Based Multiway Beam Splitter/Coupler with Variable Division Ratio" Photonics 11, no. 7: 600. https://doi.org/10.3390/photonics11070600
APA StyleGeints, Y. E. (2024). Design of Photonic Molecule-Based Multiway Beam Splitter/Coupler with Variable Division Ratio. Photonics, 11(7), 600. https://doi.org/10.3390/photonics11070600




