Generalized-Mode Averaging Technique for Wrapped Phase
Abstract
1. Introduction
2. Principles
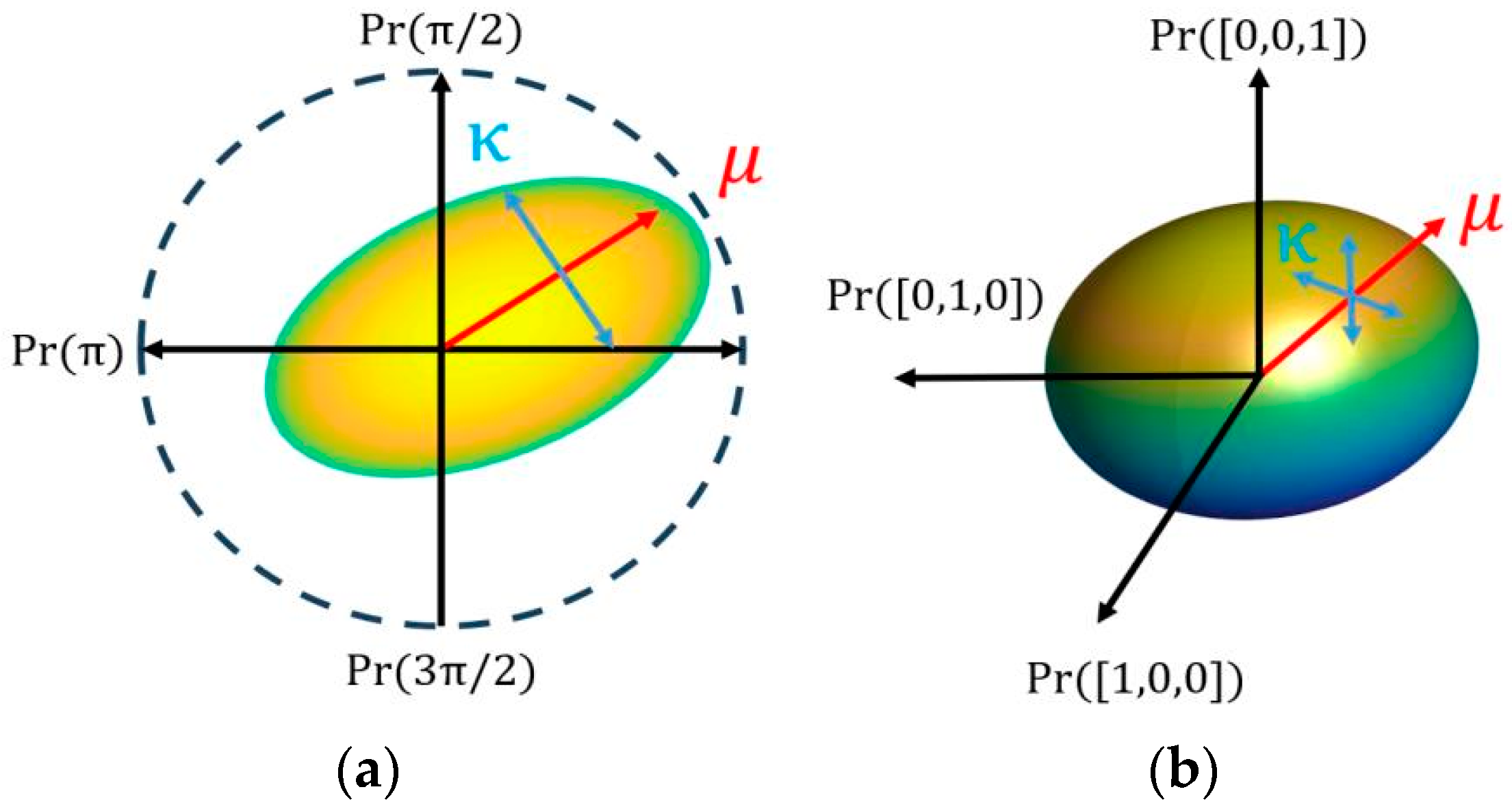
2.1. Von Mises (Circular Normal) Distribution
2.2. Generalized-Mode Averaging Technique
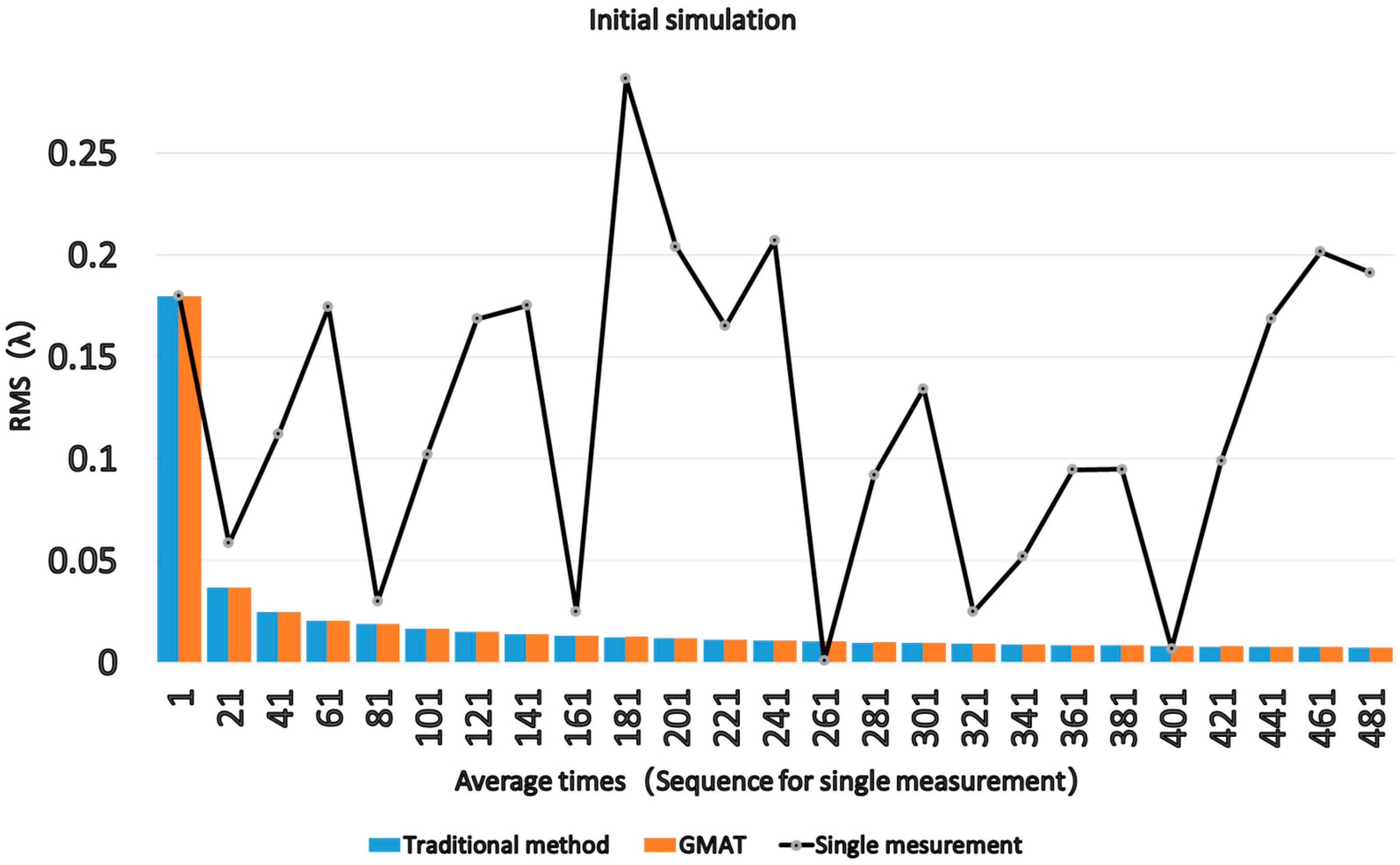
3. Simulation and Discussion
3.1. Analysis of Simple Models
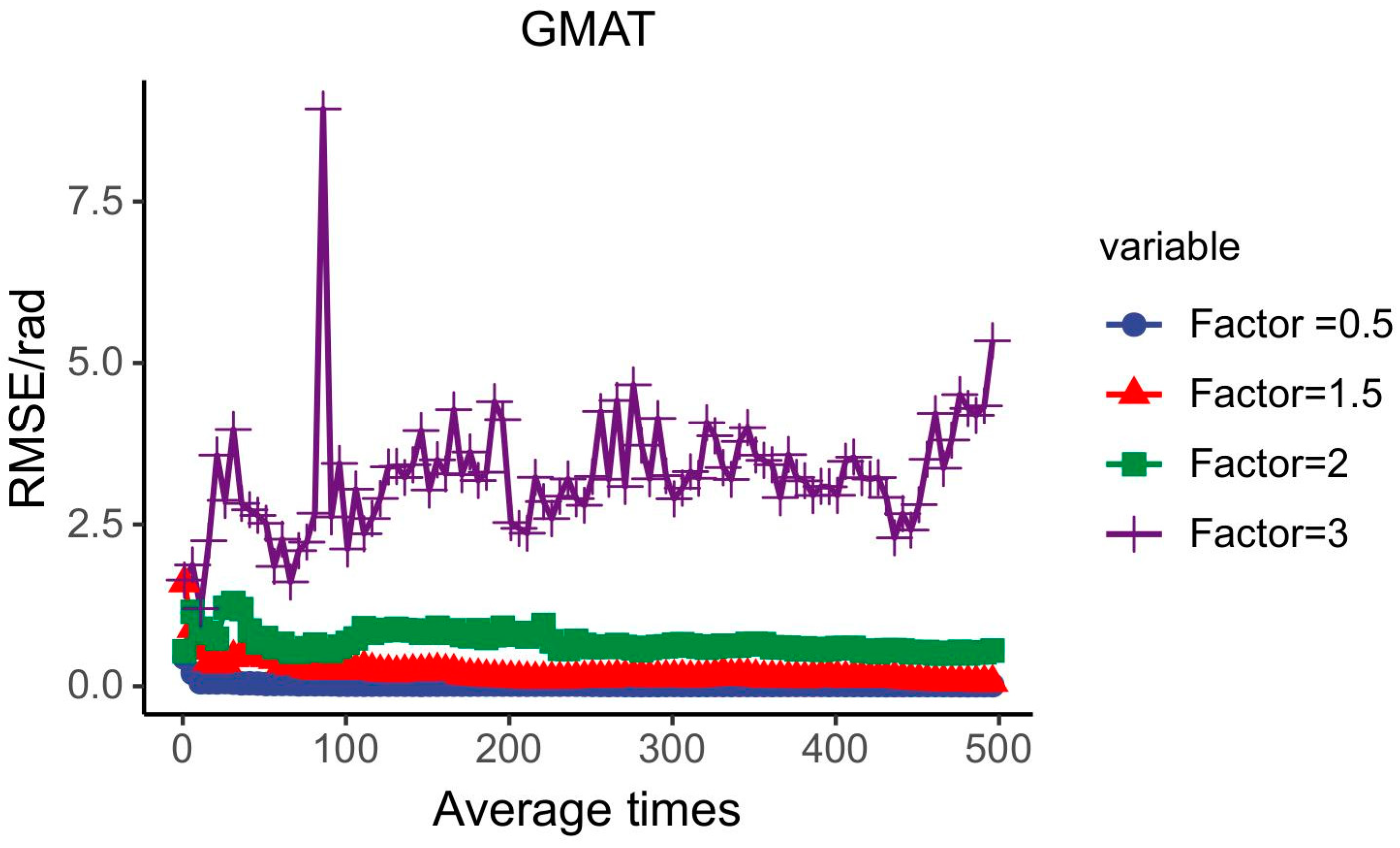
3.2. Analysis of Atmospheric Turbulence
3.3. Judgment of Whether We Can Use the GMAT
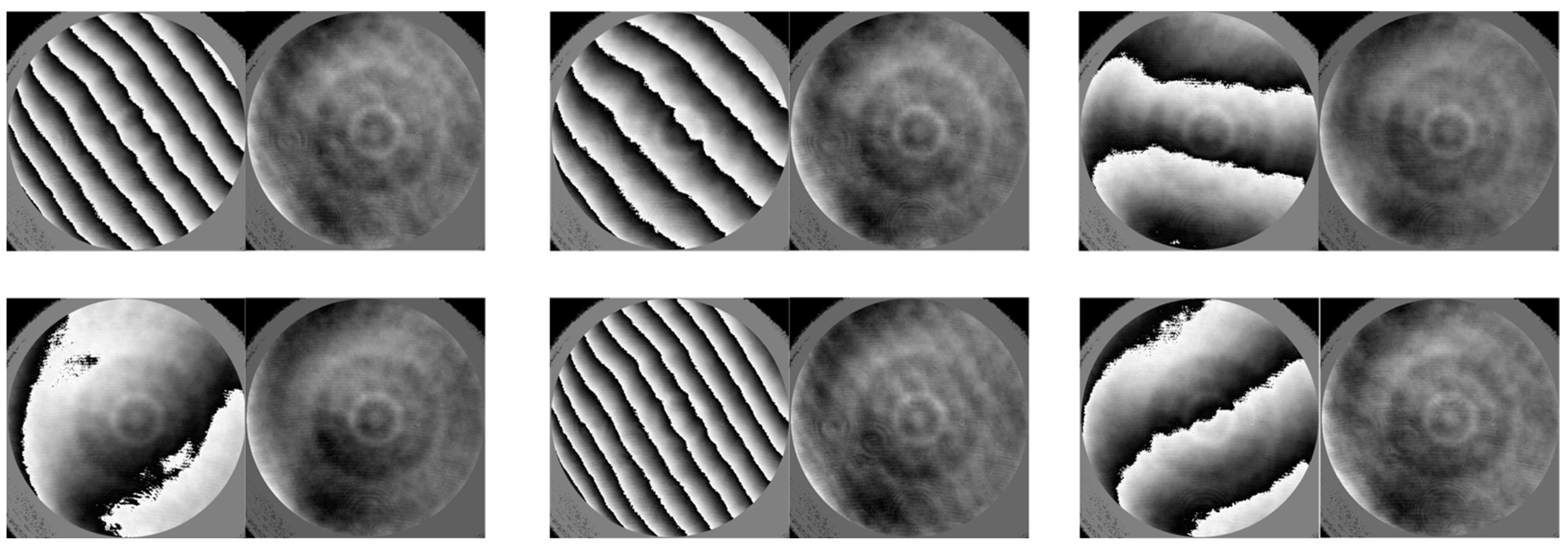
4. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, F.; Wu, Y.; Chen, Q.; Liu, H.; Yan, F.; Zhang, S.; Wan, Y.; Fan, W. Overview of advanced manufacturing technology of large-aperture aspheric mirror. Opto-Electron. Eng. 2020, 47, 200203. [Google Scholar]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Smythe, R.; Moore, R. Instantaneous phase measuring interferometry. Opt. Eng. 1984, 23, 361–364. [Google Scholar] [CrossRef]
- Kujawinska, M.; Wojciak, J. Spatial-carrier phase-shifting technique of fringe pattern analysis. In Proceedings of the Industrial Applications of Holographic and Speckle Measuring Techniques, Hague, The Netherlands, 11–15 March 1991. [Google Scholar]
- Malacara, D. (Ed.) Optical Shop Testing; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 59. [Google Scholar]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software, 1st ed.; Wiely-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Aebischer, H.A.; Waldner, S. A simple and effective method for filtering speckle-interferometric phase fringe patterns. Opt. Commun. 1999, 162, 205–210. [Google Scholar] [CrossRef]
- Kemao, Q. Two-dimensional windowed Fourier transform for fringe pattern analysis: Principles, applications and implementations. Opt. Lasers Eng. 2007, 45, 304–317. [Google Scholar] [CrossRef]
- Agarwal, N.; Chenxing, W.; Qian, K. Windowed Fourier ridges for demodulation of carrier fringe patterns with nonlinearity: A theoretical analysis. Appl. Opt. 2018, 57, 6198–6206. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Ma, Y.; Su, Z.; Dai, M.; Yang, F.; He, X. Speckle-interferometric phase fringe patterns de-noising by using fringes’ direction and curvature. Opt. Lasers Eng. 2019, 119, 30–36. [Google Scholar] [CrossRef]
- Yan, K.; Yu, Y.; Huang, C.; Sui, L.; Qian, K.; Asundi, A. Fringe pattern denoising based on deep learning. Opt. Commun. 2019, 437, 148–152. [Google Scholar] [CrossRef]
- Kim, O.; Rhee, H.; Lee, Y. Dual-path Phase Unwrapping Algorithm Based on Geodesic Curvature for Interferometric Fringe Analysis. J. Korean Phys. Soc. 2020, 76, 202–209. [Google Scholar] [CrossRef]
- Baharmast, A.; Kostamovaara, J.T. High-speed wide dynamic range linear mode time-of-flight receiver based on zero-crossing timing detection. Opt. Eng. 2016, 55, 104102. [Google Scholar] [CrossRef]
- Liu, B.; Ruan, Y.; Yu, Y. All-Fiber Laser-Self-Mixing Sensor for Acoustic Emission Measurement. J. Light. Technol. 2021, 39, 4062–4068. [Google Scholar] [CrossRef]
- Sun, X.; Wang, H.; Liu, B. Measurement of microsurface topography using a self-mixing optical configuration. Opt. Eng. 2018, 57, 051503. [Google Scholar] [CrossRef]
- Malacara, Z.; Manuel, S. Interferogram Analysis for Optical Testing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kim, O.; Bong, J.L.; Lee, Y.W.; Yang, H.S. Phase retrieval by pattern classification and circular mean for robust optical testing. Opt. Lasers Eng. 2021, 137, 106304. [Google Scholar] [CrossRef]
- Watson, G.S. Distributions on the circle and sphere. J. Appl. Probab. 1982, 19, 265–280. [Google Scholar] [CrossRef]
- Fisher, R.A. Dispersion on a sphere. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1953, 217, 295–305. [Google Scholar] [CrossRef]
- Fisher, N.I.; Toby, L.; Embleton, B.J.J. Statistical Analysis of Spherical Data; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Vargas, J.; Quiroga, J.A.; Álvarez-Herrero, A.; Belenguer, T. Phase shifting interferometry based on induced vibrations. Opt. Express 2011, 19, 584–596. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Liu, J.; Liu, S.; Zheng, Z.; Zhang, H.; Zhang, G. New method for detecting air turbulence. J. Appl. Opt. 2007, 28, 406–411. [Google Scholar] [CrossRef]










| Averaging Times | 20 | 50 | 100 | 150 | 200 |
|---|---|---|---|---|---|
| GMAT (SNR) | RMS (wave length) | ||||
| 1.579 dB | 0.022 | 0.015 | 0.011 | 0.009 | 0.007 |
| −1.732 dB | 0.185 | 0.129 | 0.095 | 0.083 | 0.078 |
| −3.841 dB | 1.706 | 2.321 | 0.255 | 0.201 | 0.187 |
| Traditional method (SNR) | RMS (wave length) | ||||
| 1.579 dB | 0.073 | 0.049 | 0.032 | 0.026 | 0.023 |
| −1.732 dB | 2.036 | 1.355 | 0.919 | 0.797 | 0.765 |
| −3.841 dB | 3.546 | 2.664 | 1.992 | 1.732 | 1.722 |
| Averaging Times | 1 | 2 | 5 | 10 | 15 |
|---|---|---|---|---|---|
| Time cost (s) | |||||
| GMAT | 2.384 | 2.387 | 2.402 | 2.474 | 2.655 |
| Traditional method | 2.372 | 4.84 | 11.755 | 22.034 | 34.640 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.; Liu, F.; Wu, Y. Generalized-Mode Averaging Technique for Wrapped Phase. Photonics 2024, 11, 561. https://doi.org/10.3390/photonics11060561
Tang Z, Liu F, Wu Y. Generalized-Mode Averaging Technique for Wrapped Phase. Photonics. 2024; 11(6):561. https://doi.org/10.3390/photonics11060561
Chicago/Turabian StyleTang, Zhan, Fengwei Liu, and Yongqian Wu. 2024. "Generalized-Mode Averaging Technique for Wrapped Phase" Photonics 11, no. 6: 561. https://doi.org/10.3390/photonics11060561
APA StyleTang, Z., Liu, F., & Wu, Y. (2024). Generalized-Mode Averaging Technique for Wrapped Phase. Photonics, 11(6), 561. https://doi.org/10.3390/photonics11060561




