Abstract
This study presents an efficient and practical intra-cavity approach for selectively generating vortex array laser beams employing a dual-phase modulation digital laser system, which has not yet been completed in single-phase modulation digital laser. The stable optical vortex array laser beams were formed by superimposing cavity Hermite–Gaussian (HG) eigenmodes. In particular, when the selected cavity HG modes shared the same Gouy phase, the resulting optical vortex beam could preserve its light field pattern, thereby maintaining the optical vortex properties in the near and far fields. Numerical results demonstrated that employing dual-phase modulation could establish optimal boundary conditions for the selection of HG modes within the cavity, successfully generating various vortex array laser beams. The experimental validation of the proposed method confirmed the ability to select optical vortex array lasers solely by controlling the loaded phase of the dual-phase modulation digital laser. These results demonstrate the ability of digital lasers to generate and dynamically control optical vortex array lasers.
1. Introduction
In 1992, Allen et al. demonstrated that a vortex beam with a helical wavefront , where denotes the topological charge, carries the orbital angular momentum (OAM) of magnitude [1]. These vortex beams feature a helical phase distribution, resulting in a phase singularity at the center of the beam and a doughnut-shaped intensity pattern. Another type of optical vortex, known as vector beams, characterizes polarization singularity, distinguishing it from the vortex beam. Owing to their amazing properties related to OAM, vortex beams have become one of the most intriguing and practical structured beams with rapid advancements in their generation methods, applications, and future developments, which are frequently reviewed and updated in the literature [2,3,4,5,6,7].
Various methods have been explored to generate vortex beams to meet the demand for vortex beam applications [5,8], which can be categorized into extra- and intra-cavity methods. Extra-cavity methods involve the use of diffractive optical elements such as spiral phase plates [9] and astigmatic mode converters [10], or computer-generated holograms on rewritable devices such as spatial light modulator (SLM) [11] and digital micromirror device [12], or more modern optical element such as metasurfaces [13,14]. Intra-cavity methods refer to laser resonators equipped with specialized optical elements such as spot defects [15], ring-shape pumping [16], a quarter-wave plate and q-plate [17], metasurface J-plates [18], spiral phase modulation [19,20], and integrated micro laser [21] that can directly generate vortex beam. Digital lasers, which are laser resonators with one or two intra-SLM panels that can mimic spot defects [22] or spiral phase modulations [23,24], offer the flexible generation and control of the topological charge of the output vortex beam.
As research into optical vortex beams continues to expand, some attention has shifted towards investigating optical vortex arrays, also known as optical vortex crystals or lattices [25,26]. These beam structures comprise arrays of zero-intensity holes, each corresponding to a phase singularity with a distinct topological charge. The evolution of single vortex beams to the arrays of multiple vortex beams has facilitated the advancement of high-efficiency laser nanofabrication techniques and automultiscopic 3D displays [27]. This progress has also significantly enhanced the performance of contemporary optical communication systems [28,29], sorting microscale objects [30], and optical tweezers [31,32].
Similar to single vortex beams, optical vortex arrays can be produced directly by extra-cavity methods, such as the following: astigmatic mode converters [33,34], SLM [35,36,37,38], Dammam gratings [28,39], and metasurface [40,41,42,43,44]. However, astigmatic mode converters require an input beam, a specific combination of structured beams, to convert into a vortex array; other methods often reduce efficiency by carving out a portion of the input beam to form a vortex beam profile. Optical vortices can also be generated directly in the laser system through in-cavity methods. However, compared to a single vortex beam, the laser configuration for generating vortex arrays is rare, including the superimposing of frequency-degenerate cavity modes [45,46,47,48,49,50,51,52], metasurfaces [53], and multiple microring lasers [54,55]. Although metasurfaces and multiple microring lasers can form many discrete singularities, and their topological charge can be tuned at will, these approaches require the manufacturing of optical elements through nano-technology. In traditional laser systems, by utilizing a nonlinear process in the gain medium, the transverse mode locking of the same or different frequency-degenerated cavity modes such as Hermite–Gaussian (HG), Laguerre–Gaussian (LG) or Ince–Gaussian (IG) modes with phase shift forms an array of vortices with topological charge 1 in laser resonator [45,46,47,48,49,50,51,52]. These laser cavities with different schemes, such as off-axis pumping [45], shaped pumping [48,49,50], cavity elements misalignment [51], or cavity length [52] to select multi-modes simultaneously lasing, leading the change in the intensity distribution of the output vortex array. However, these approaches require mechanical adjustments, potentially limiting applications and necessitating fast and flexible control. Furthermore, the transverse mode locking approach may be constrained by the effect of transverse mode spacing on the stability of the pattern with increasing pump power above the lasing threshold [52].
In this work, we present the production of vortex laser arrays formed by superimposing HG modes with the dual-phase modulation digital laser, achieving a flexible selection of vortex laser arrays within the cavity. The conventional digital laser cavity [22], limited by the controlled freedom of single-phase modulation in one round-trip path, can only support a single cavity mode or a superposition of multi-mode without phase singularities [22]. This problem can be addressed by introducing an additional phase control into the conventional digital laser resonator, which has been used to generate vortex beams [24]. With the dual-phase modulation digital laser, stable and optimal boundary conditions are established for selecting multiple HG modes with the phase shift within the cavity. Numerical simulations demonstrate that employing dual-phase modulation enabled the successful generation of various vortex array laser beams. The experimental validation of this approach confirms the capability to generate an optical vortex array solely through controlling the loaded phase in the dual-phase modulation digital laser.
2. Approach and Simulation Verification
2.1. Forming Vortex Array with Generating Superimposing Degenerated Hermite–Gaussian Modes
Various vortex array laser beams can be directly generated from the laser cavity by producing and superimposing degenerate HG beams with a specific phase shift. The expressions of HG modes can be expressed as
where is the normalization constant, is the Hermite polynomial of th order, and represent, respectively, the beam waist and the radius of wavefront curvature of the fundamental mode at position , and is the Gouy phase. The Gouy phase of the mode is where and is the Rayleigh length. Figure 1 shows the beam profile and phase distribution of five vortex arrays formed by five groups of frequency-degenerated HG modes, i.e., HG modes have the same . The red dots in Figure 1b mark the position of optical vortices in phase diagrams. Because of sharing the same Gouy phase, the resulting optical vortex array can maintain its beam pattern as it propagates, preserving its optical vortex property in both the near and far field; this distinguishes it from vortex arrays formed by embedded vortex HG modes [56].

Figure 1.
Some vortex arrays formed by different combinations of the degenerated family of Hermite–Gaussian (HG) modes. Theoretical results for the (a) amplitude and (b) phase of the vortex array at beam waist positions are presented.
2.2. Laser Model and Simulation Verification
The laser light measurement setup and the setup of the digital laser with dual-phase modulations are presented in Figure 2a, where one SLM panel is separated into two sections to achieve dual-phase modulation during a single round-trip of intra-cavity oscillation [24]. The plot inside the red dotted box of Figure 2a shows the proposed digital laser system, and the others illustrate the experimental setup for measuring the laser light. The black dotted box in Figure 2a is an example of the loaded phase diagram to produce the superimposing modes. This digital laser resonator, shown in the red dotted box, comprised a single SLM panel, a right-angle prism, and a dichroic mirror (DM), and the pumping beam was focused on the laser crystal through the DM. The components of the laser system were as follows: the SLM used was a reflective type of pure phase-controlled (LCOS-SLM X13138-03WR) from Hamamatsu Photonics (Hamamatsu, Japan), with the working area being 16.0 × 12.8 and pixel dimensions being 12.5 × 12.5 , totaling 1280 × 1024 pixels. The SLM provides 216 steps for describing 0 to 2π phase change, 96% fill factor, and 97% light-adopting efficiency. The effective length of the cavity was 44 cm. At the center of the cavity, the beam waist of fundamental Gaussian mode was set as , accounting for the pump area of the present laser setup.
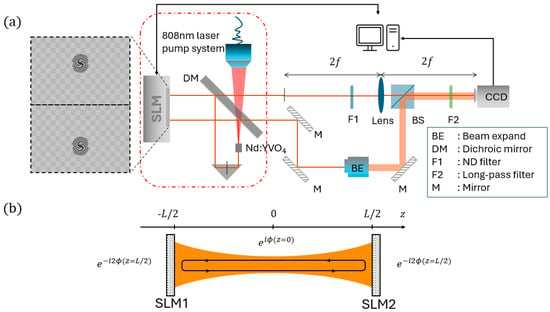
Figure 2.
(a) The laser light measurement and the digital laser setup with an example SLM loaded phase diagram for generating vortex array formed by . The red dotted box shows the dual-SLM digital cavity. (b) A schematic diagram of an equivalent SLM-SLM laser resonator simplified from the experiment laser resonator.
Figure 2b shows an equivalent SLM-SLM resonator of the experiment digital laser setup utilized in simulations. The target light field to be generated was denoted as , where and respectively, describe the beam amplitude and phase of the light field, oscillating within the cavity. The oscillation light field in the resonator was selected and maintained successfully by simultaneously controlling the conditions of both end-phase boundaries provided by the SLMs. The loaded phase diagram on the SLM was calculated in detail as follows: Initially, the lasing beam characteristics, such as the beam waist , the specific group of HG modes, the phase difference among these modes, and the wavenumber , were determined. Next, the Fresnel–Kirchhoff integration [57] was employed to calculate the beam profile of the vortex array at the SLM plane, denoted by where L is the effective cavity length, and and are the beam amplitude and phase at the SLM, respectively. By introducing suitable end-phase conditions, i.e., a phase modulation through the SLM, , the desired oscillating light pattern was effectively maintained within the dual-SLM resonator. Particularly, the output phase of the beam from the SLM panel was , the minus value was from the reflection of coordinates when the beam reflects from the SLM panel [58]. The checkerboard pattern of and was applied to the low amplitude region ( of the brightest spot peak amplitude) of the vortex array beam at the SLM to diffract out unwanted modes.
In this study, the method proposed by Endo et al. was employed to determine the convergent lasing mode in diode-pumped solid-state lasers [59,60,61]. The simulation mimicked the actual lasing process from the initial spontaneous random field, a light field with the same amplitude and random phase distribution ranging from 0 to 2π. The simulations assumed that the gain medium receives a homogeneous pump; the gain process of the light field in the crystal is described in detail in a previous study [60]. During the simulation, the light field oscillating back and forth was continuously modulated by the loaded phase each time it was reflected by the SLM and gradually formed a stable light field. The simulation results for generating a vortex array of the beam with the cavity having a dual-phase modulation are mentioned in Figure 3. The simulation parameters referred to the real values of the experimental setup, mentioned in Section 3, and included the following: SLM pixel size, SLM phase step, SLM diffraction loss, laser cavity length, crystal material, and crystal thickness.
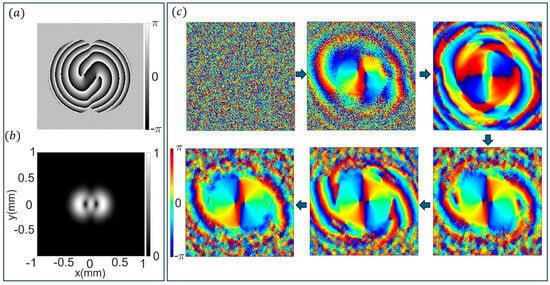
Figure 3.
Simulation results of the mode generation via SLM-SLM cavity. (a) The phase diagram on the SLM for generating the mode. (b) The amplitude of a convergent optical vortex array comprising the mode. (c) The phase development of the intra-cavity light field from a random phase beam to the mode while propagating inside the cavity with dual-phase modulation.
Figure 3a and Figure 3b, respectively, present the phase diagram used in the simulation and the simulation amplitude of a selected vortex array formed by . Figure 3c shows the six sampled phase distributions at the specified beam waist position, illustrating the progress of the lasing pattern from an initial random phase to the final vortex array of the superimposing modes. The phase diagrams in Figure 3c were collected after every three round trips from the initial random field. The simulation results demonstrate that the dual-phase modulation digital laser can generate superimposing degenerating family HG modes with a specific phase shift to obtain stable vortex array beams.
3. Experiment Setup
The experimental parameters are presented as follows: According to Figure 2a, a quasi-continuous wave (QCW) 808 nm pumping light source was used to pump the , 3%-doped, a-cut uncoated crystal. The a-cut crystal provided the polarization of the intra-cavity light field, matching the working polarization of the SLM. The laser crystal dissipated heat by being mounted onto a copper sheet. By employing QCW pumping, a duty cycle of 3%, and a frequency of 100 Hz, thermal effects are decreased, and the crystal is protected from potential damage caused by intense pumping. In the normal cavity, the beam waist of the cavity is at the prism position instead of the crystal. The 45-degree-tilted plate DM—a 25 diameter short-pass filter—served as an output coupler with reflectance >97% at 1064 and transmittance >85% at 808 . The prism in the experimental setup is the right-angle prism of Thorlab (Newton, NJ, USA) with a right-angle production error range of . Tilt and displacement corrections are integrated into the SLM-loaded phases to compensate for the production tilt error of the right-angle prism and minor misalignment issues. Detailed descriptions are mentioned in our previous work [24]. Referring to Figure 2a, two intra-cavity light beams are shown reflecting from two distinct lateral positions (left side and right side) of the SLM. Subsequently, these two light beams transmit through the DM at separate positions, resulting in the generation of two output laser beams. One output beam was captured by a camera through a lens while the other was expanded to interfere with the first through a beam splitter. A long-pass filter was used to prevent the pumping light from reaching the camera to ensure better quality result images.
4. Results and Discussion
Figure 4a presents the experimental results for the generation of the five vortex arrays of different HG mode groups, i.e., the five ideal vortex arrays presented in Figure 1. The intensity profiles and the position of the singularity points display slight asymmetry, attributable to the slight misalignment of pump schemes with the optical axis. Additionally, implementing an end-pump scheme within a crystal resulted in a non-uniform gain profile. Consequently, certain modes gained higher energy, leading to a non-uniform distribution of intensity in the output. This problem could be overcome by adopting a broader side-pump scheme, ensuring a uniform gain profile throughout the laser cavity. The vortices within these holes were determined by examining the interference pattern between the optical lattices comprising HG modes and a plane wave, as shown in Figure 4b. The theoretical results of the interference pattern with a plane wave for the vortex array in a coherent state reveal bifurcations in all holes, as depicted in Figure 4c. Despite the asymmetry in the intensity profiles, the quantity and orientation of vortices agreed well with the theoretical predictions. Figure 4b also confirms that the generated optical vortex beam was produced by the coherent superposition of the HG modes rather than the incoherent superposition of the HG modes [51].
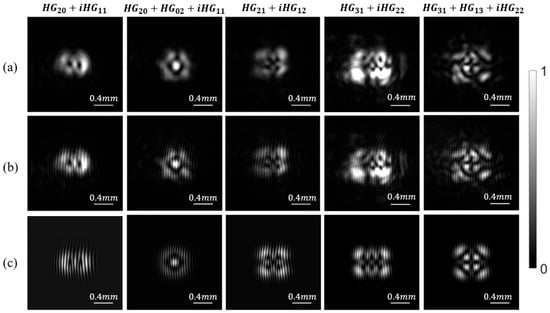
Figure 4.
The experimental results for the vortex array beam formed by superimposing degenerated family Hermite–Gaussian (HG) modes shown in Figure 1. (a,b) are the intensity profile and their corresponding interference pattern with plane wave, respectively. (c) are the numerical results of the interference pattern of the five ideal vortex arrays with plane waves.
During propagation, the vortex array and superposition of the degenerated family of the modes of the same value retain an unchanged intensity profile. In the experiment, a lens with a focus length of was used to observe the far field of the resulting vortex arrays. Figure 5 demonstrates the experimental observations of the far-field beam profiles and their corresponding interference pattern, and the plane wave for the vortex array is shown in Figure 4. The results confirm the stable propagation of these kinds of vortex arrays produced by the dual-SLM cavity through free space.
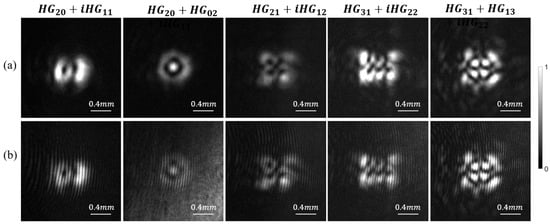
Figure 5.
The experimental results for the far-field beam profile of the vortex array of the five degenerated families of the Hermite–Gaussian (HG) modes. The intensity profile (a) and their corresponding interference pattern (b) with plane wave, respectively.
Moreover, the dual-SLM cavity can generate vortex arrays from different HG families with different values. For instance, Figure 6 illustrates a vortex array created by . The theoretical intensity distribution and phase profile of near-field and far-field beam profiles are presented in Figure 6a, while the corresponding experimental results are shown in Figure 6b. However, owing to the phase mismatch in the Gouy phase among different frequency-degenerate HG families, such kinds of vortex arrays are unstable during propagation, causing the difference in vortex characteristics in the far-field laser field. More examples of the lasing of the light beams from non-frequency-degenerate family modes, and , are shown in Figure 7. Figure 6 and Figure 7 highlight the versatility and convenience offered by the dual-SLM resonator in selecting lasing modes from different-family HG modes, compared to the microchip cavities utilizing the nonlinear process and cavity misalignment to cause and control the spontaneous phase and frequency locking of transverse modes from non-frequency-degenerate families [47].

Figure 6.
The beam profile at the far field and near field of vortex array from a different family of Hermite–Gaussian (HG) modes, . The numerical (a) and experimental (b) results, respectively.

Figure 7.
More results on the superposition of the Hermite–Gaussian (HG) modes from different families. The theoretical results for the near and far field intensity pattern of and (a) and the corresponding experimental results (b).
The current dual-SLM resonator setup has a low Fresnel number, an important criterion for evaluating the capability of the laser cavity in supporting high-order transverse modes [52,62]. A small Fresnel number implies significant diffraction losses, particularly for higher-order modes. In an end-pumped laser, the order of transverse modes was limited by the pump across the section. The Fresnel number can be given by , where is the radius of the pump section and is the beam waist of the cavity fundamental mode [52]. As the crystal was not located at the center of the cavity, the value was replaced by the beam waist of the fundamental mode at the crystal position, with . At and , the Fresnel number, , was 5, i.e., representing a relatively low Fresnel number condition of the cavity. The Fresnel number indicates how large the resonator aperture is compared to the confocal mode size of that resonator. Employing the equation for the beam waist of the mode in dimension, [63], the largest-order of , , that will fit within the pump cross section was determined by [62]. The experimental results were close to the values indicating the best performance of the cavity. To approach higher order modes in the future, a new resonator design supporting large number of transverse modes, such as degenerated laser cavity in a self-imaging (4f) configuration can be used [53,64].
The trade-off between power and operational flexibility is the disadvantage of digital laser. The output power of the dual-phase modulation digital laser is normally lower than that of traditional laser cavities [22]. Referring to the five vortex array laser shown in Figure 4a, at an average input power of 1.5 W and a pump section radius of 0.9 mm, the average output power of vortex arrays formed by , , , , and were, respectively, 0.239 mW, 0.225 mW, 0.269 mW, 0.133 mW, and 0.143 mW. This laser system exhibited a lower laser output efficiency compared to the output efficiencies of other solid-state lasers [48], which can be attributed to two major factors. The first factor is the energy loss caused by the beam passing through multiple components multiple times in the cavity, e.g., the loss in transmission of DM, the double diffraction loss, and the imperfect fill factor of the SLM panel [22]. Another factor is that the laser excitation mechanism used resulted in more optical pumping energy loss and lower energy usage efficiency. The loss in transmission of the pumping energy at DM, accounting for 15% of the input power, could be mitigated by employing a side-pump scheme. However, the beam pattern of the dual-phase modulation digital laser remained well-maintained under high pump conditions. Figure 8 shows the intensity and interference patterns of the vortex array formed by the modes at threshold power (i.e., W), , and The position and directions of the bifurcation fringes remained unchanged as the pump power increased, unlike the cavity utilizing the transverse mode locking approach, where cavity modes are sensitive to pump power [48,50,52].

Figure 8.
The intensity (a) and interference pattern (b) vortex array formed by the modes at different pump powers.
5. Conclusions
In conclusion, the successful generation of stable and efficient vortex array laser beams was demonstrated in this study, with the implementation of a dual-phase modulation technique within a digital laser system. The numerical outcomes prove that the dual-phase modulation can provide optimal boundary conditions for selecting the HG mode family, thereby facilitating the direct formation of a vortex array in the cavity. This approach is not limited to HG modes but can apply to the superposition of cavity modes such as LG modes, IG modes, or even the combination of HG and LG modes [65]. The experiments of this study confirmed the approach for generating vortex arrays formed by a group of degenerated family HG modes with the value up to four. The proposed method can be expanded to generate vortex arrays with a higher count of optical vortices in digital lasers by elevating the Fresnel numbers of the cavity. The findings of this study highlight the novelty in the capability of the digital laser in the field of optical vortex array lasers, paving the way for advanced applications of vortex array laser beams.
Author Contributions
Conceptualization, K.-F.T. and S.-C.C.; methodology, K.-F.T. and S.-C.C.; software, K.-F.T.; validation, L.L.N.T.; writing—original draft preparation, L.L.N.T.; writing—review and editing, L.L.N.T. and S.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
National Science and Technology Council, Taiwan (NSTC 112-2112-M-006-018).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, [Shu-Chun Chu, scchu@mail.ncku.edu.tw], upon reasonable request.
Acknowledgments
The authors wish to acknowledge the help of research assistant Kuo-Chih Chang in developing ideas for the experiment process.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T. Roadmap on structured light. J. Opt. 2016, 19, 013001. [Google Scholar] [CrossRef]
- He, C.; Shen, Y.; Forbes, A. Towards higher-dimensional structured light. Light Sci. Appl. 2022, 11, 205. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Wang, Y.; Yuan, Y.; Burokur, S.N. A Review of Orbital Angular Momentum Vortex Beams Generation: From Traditional Methods to Metasurfaces. Appl. Sci. 2020, 10, 1015. [Google Scholar] [CrossRef]
- Lian, Y.; Qi, X.; Wang, Y.; Bai, Z.; Wang, Y.; Lu, Z. OAM beam generation in space and its applications: A review. Opt. Lasers Eng. 2022, 151, 106923. [Google Scholar] [CrossRef]
- Forbes, A. Advances in Orbital Angular Momentum Lasers. J. Light. Technol. 2023, 41, 2079–2086. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; van der Veen, H.E.L.O.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Kumar, A.; Vaity, P.; Banerji, J.; Singh, R.P. Making an optical vortex and its copies using a single spatial light modulator. Phys. Lett. A 2011, 375, 3634–3640. [Google Scholar] [CrossRef]
- Gong, L.; Ren, Y.; Liu, W.; Wang, M.; Zhong, M.; Wang, Z.; Li, Y. Generation of cylindrically polarized vector vortex beams with digital micromirror device. J. Appl. Phys. 2014, 116, 183105. [Google Scholar] [CrossRef]
- Yi, J.; Li, D.; Feng, R.; Ratni, B.; Jiang, Z.H.; De Lustrac, A.; Werner, D.H.; Burokur, S.N. Design and validation of a metasurface lens for converging vortex beams. Appl. Phys. Express 2019, 12, 084501. [Google Scholar] [CrossRef]
- Chen, Q.; Qu, G.; Yin, J.; Wang, Y.; Ji, Z.; Yang, W.; Wang, Y.; Yin, Z.; Song, Q.; Kivshar, Y.; et al. Highly efficient vortex generation at the nanoscale. Nat. Nanotechnol. 2024. [Google Scholar] [CrossRef] [PubMed]
- Ito, A.; Kozawa, Y.; Sato, S. Generation of hollow scalar and vector beams using a spot-defect mirror. J. Opt. Soc. Am. A 2010, 27, 2072–2077. [Google Scholar] [CrossRef]
- Kim, D.J.; Kim, J.W. Direct generation of an optical vortex beam in a single-frequency Nd:YVO4 laser. Opt. Lett. 2015, 40, 399–402. [Google Scholar] [CrossRef]
- Naidoo, D.; Roux, F.S.; Dudley, A.; Litvin, I.; Piccirillo, B.; Marrucci, L.; Forbes, A. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photonics 2016, 10, 327–332. [Google Scholar] [CrossRef]
- Sroor, H.; Huang, Y.-W.; Sephton, B.; Naidoo, D.; Vallés, A.; Ginis, V.; Qiu, C.-W.; Ambrosio, A.; Capasso, F.; Forbes, A. High-purity orbital angular momentum states from a visible metasurface laser. Nat. Photonics 2020, 14, 498–503. [Google Scholar] [CrossRef]
- Oron, R.; Danziger, Y.; Davidson, N.; Friesem, A.A.; Hasman, E. Laser mode discrimination with intra-cavity spiral phase elements. Opt. Commun. 1999, 169, 115–121. [Google Scholar] [CrossRef]
- Eggleston, M.; Godat, T.; Munro, E.; Alonso, M.A.; Shi, H.; Bhattacharya, M. Ray transfer matrix for a spiral phase plate. J. Opt. Soc. Am. A 2013, 30, 2526–2530. [Google Scholar] [CrossRef]
- Miao, P.; Zhang, Z.; Sun, J.; Walasik, W.; Longhi, S.; Litchinitser, N.M.; Feng, L. Orbital angular momentum microlaser. Science 2016, 353, 464–467. [Google Scholar] [CrossRef] [PubMed]
- Ngcobo, S.; Litvin, I.; Burger, L.; Forbes, A. A digital laser for on-demand laser modes. Nat. Commun. 2013, 4, 2289. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.Y.; Li, Y.W. Spiral-Phase-Defect Resonator and Its Application in Vortex Laser of Controllable Topological Charges. IEEE Photonics J. 2022, 14, 1548307. [Google Scholar] [CrossRef]
- Thi, L.L.N.; Chang, K.-C.; Shu, S.-C. Dual modulation digital laser for generating vortex beams with tunable orbital angular momentum. Opt. Laser Technol. 2024, 176, 110928. [Google Scholar] [CrossRef]
- Du, J.; Quan, Z.; Li, K.; Wang, J. Optical vortex array: Generation and applications. Chin. Opt. Lett. 2024, 22, 020011. [Google Scholar]
- Zhu, L.; Tang, M.; Li, H.; Tai, Y.; Li, X. Optical vortex lattice: An exploitation of orbital angular momentum. Nanophotonics 2021, 10, 2487–2496. [Google Scholar] [CrossRef]
- Li, X.; Chu, J.; Smithwick, Q.; Chu, D. Automultiscopic displays based on orbital angular momentum of light. J. Opt. 2016, 18, 085608. [Google Scholar] [CrossRef]
- Lei, T.; Zhang, M.; Li, Y.; Jia, P.; Liu, G.N.; Xu, X.; Li, Z.; Min, C.; Lin, J.; Yu, C.; et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 2015, 4, e257. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photon. Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Guo, C.-S.; Yu, Y.-N.; Hong, Z. Optical sorting using an array of optical vortices with fractional topological charge. Opt. Commun. 2010, 283, 1889–1893. [Google Scholar] [CrossRef]
- Curtis, J.E.; Koss, B.A.; Grier, D.G. Dynamic holographic optical tweezers. Opt. Commun. 2002, 207, 169–175. [Google Scholar] [CrossRef]
- Ladavac, K.; Grier, D.G. Microoptomechanical pumps assembled and driven by holographic optical vortex arrays. Opt. Express 2004, 12, 1144–1149. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.C.; Lu, T.H.; Huang, K.F.; Chen, Y.F. Generation of optical vortex array with transformation of standing-wave Laguerre-Gaussian mode. Opt. Express 2011, 19, 10293–10303. [Google Scholar] [CrossRef]
- Abramochkin, E.; Razueva, E.; Volostnikov, V. General astigmatic transform of Hermite–Laguerre–Gaussian beams. J. Opt. Soc. Am. A 2010, 27, 2506–2513. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.; Wang, T.; Gao, C. Perfect optical vortex array with controllable diffraction order and topological charge. J. Opt. Soc. Am. A 2016, 33, 1836–1842. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, B.; Lü, S.; Liu, Y.; Li, S.; Cao, Z.; Qi, X. Arrays of Gaussian vortex, Bessel and Airy beams by computer-generated hologram. Opt. Commun. 2016, 363, 85–90. [Google Scholar] [CrossRef]
- Kapoor, A.; Kumar, M.; Senthilkumaran, P.; Joseph, J. Optical vortex array in spatially varying lattice. Opt. Commun. 2016, 365, 99–102. [Google Scholar] [CrossRef]
- Ma, H.; Li, X.; Tai, Y.; Li, H.; Wang, J.; Tang, M.; Tang, J.; Wang, Y.; Nie, Z. Generation of Circular Optical Vortex Array. Ann. Phys. 2017, 529, 1700285. [Google Scholar] [CrossRef]
- García-Martínez, P.; Sánchez-López, M.M.; Davis, J.A.; Cottrell, D.M.; Sand, D.; Moreno, I. Generation of Bessel beam arrays through Dammann gratings. Appl. Opt. 2012, 51, 1375–1381. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar Photonics with Metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Maguid, E.; Chriki, R.; Yannai, M.; Kleiner, V.; Hasman, E.; Friesem, A.A.; Davidson, N. Topologically Controlled Intracavity Laser Modes Based on Pancharatnam-Berry Phase. ACS Photonics 2018, 5, 1817–1821. [Google Scholar] [CrossRef]
- Jin, J.; Pu, M.; Wang, Y.; Li, X.; Ma, X.; Luo, J.; Zhao, Z.; Gao, P.; Luo, X. Multi-Channel Vortex Beam Generation by Simultaneous Amplitude and Phase Modulation with Two-Dimensional Metamaterial. Adv. Mater. Technol. 2017, 2, 1600201. [Google Scholar] [CrossRef]
- Piccardo, M.; Ambrosio, A. Recent twists in twisted light: A Perspective on optical vortices from dielectric metasurfaces. Appl. Phys. Lett. 2020, 117, 140501. [Google Scholar] [CrossRef]
- Shen, Y.; Wan, Z.; Fu, X.; Liu, Q.; Gong, M. Vortex lattices with transverse-mode-locking states switching in a large-aperture off-axis-pumped solid-state laser. J. Opt. Soc. Am. B 2018, 35, 2940–2944. [Google Scholar] [CrossRef]
- Huyet, G.; Martinoni, M.C.; Tredicce, J.R.; Rica, S. Spatiotemporal Dynamics of Lasers with a Large Fresnel Number. Phys. Rev. Lett. 1995, 75, 4027–4030. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhao, C. Spontaneous phase and frequency locking of transverse modes in different orders. Phys. Rev. Appl. 2020, 13, 024010. [Google Scholar] [CrossRef]
- Zhang, S.; Fu, Z.; Lai, L.; Jia, F.; Qiao, D.; Fan, Y.; Li, K.; Copner, N. Transverse mode locking of different frequency-degenerate families based on annular beam pumping. Opt. Lett. 2021, 46, 3195–3198. [Google Scholar] [CrossRef]
- Chen, K.; Xu, L.; Ni, A.; Tang, J.; Yi, K.; Jia, F.; Qiao, D.; Li, K.; Copner, N. Generation of a vortex point adjustable vortex array based on decentered annular beam pumping. Opt. Lett. 2023, 48, 2599–2602. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, Y.; Wang, X.; Zhao, S.; Jie, Y.; Zhao, C. Selective Generation of Laser Transverse Modes by Gain Regulation with a Digital Micromirror Device. IEEE Photonics Technol. Lett. 2022, 34, 420–423. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Z.; Gao, Y.; Zhao, S.; Jie, Y.; Zhao, C. Investigation on the Formation of Laser Transverse Pattern Possessing Optical Lattices. Front. Phys. 2022, 9, 801916. [Google Scholar] [CrossRef]
- Chen, Y.F.; Lan, Y.P. Transverse pattern formation of optical vortices in a microchip laser with a large Fresnel number. Phys. Rev. A 2001, 65, 013802. [Google Scholar] [CrossRef]
- Piccardo, M.; de Oliveira, M.; Toma, A.; Aglieri, V.; Forbes, A.; Ambrosio, A. Vortex laser arrays with topological charge control and self-healing of defects. Nat. Photonics 2022, 16, 359–365. [Google Scholar] [CrossRef]
- Qiao, X.; Midya, B.; Gao, Z.; Zhang, Z.; Zhao, H.; Wu, T.; Yim, J.; Agarwal, R.; Litchinitser, N.M.; Feng, L. Higher-dimensional supersymmetric microlaser arrays. Science 2021, 372, 403–408. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Wang, J.; Strain, M.J.; Johnson-Morris, B.; Zhu, J.; Sorel, M.; O’Brien, J.L.; Thompson, M.G.; Yu, S. Integrated Compact Optical Vortex Beam Emitters. Science 2012, 338, 363–366. [Google Scholar] [CrossRef] [PubMed]
- Porfirev, A.P.; Khonina, S.N. Simple method for efficient reconfigurable optical vortex beam splitting. Opt. Express 2017, 25, 18722–18735. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Fu, S.; Wang, T.; Gao, C. Generating perfect polarization vortices through encoding liquid-crystal display devices. Appl. Opt. 2016, 55, 6501–6505. [Google Scholar] [CrossRef]
- Chu, S.-C.; Otsuka, K. Numerical study for selective excitation of Ince-Gaussian modes in end-pumped solid-state lasers. Opt. Express 2007, 15, 16506–16519. [Google Scholar] [CrossRef] [PubMed]
- Endo, M.; Kawakami, M.; Nanri, K.; Takeda, S.; Fujioka, T. Two-dimensional simulation of an unstable resonator with a stable core. Appl. Opt. 1999, 38, 3298–3307. [Google Scholar] [CrossRef]
- Hu, A.; Lei, J.; Chen, P.; Wang, Y.; Li, S. Numerical investigation on the generation of high-order Laguerre-Gaussian beams in end-pumped solid-state lasers by introducing loss control. Appl. Opt. 2014, 53, 7845–7853. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Sausalito, CA, USA, 1986. [Google Scholar]
- Carter, W.H. Spot size and divergence for Hermite Gaussian beams of any order. Appl. Opt. 1980, 19, 1027–1029. [Google Scholar] [CrossRef] [PubMed]
- Tradonsky, C.; Mahler, S.; Cai, G.; Pal, V.; Chriki, R.; Friesem, A.A.; Davidson, N. High-resolution digital spatial control of a highly multimode laser. Optica 2021, 8, 880–884. [Google Scholar] [CrossRef]
- Song, L.-M.; Yang, Z.-J.; Li, X.-L.; Zhang, S.-M. Coherent superposition propagation of Laguerre–Gaussian and Hermite–Gaussian solitons. Appl. Math. Lett. 2020, 102, 106114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).