Temporal Analysis of Speckle Images in Full-Field Interferometric and Camera-Based Optical Dynamic Measurement
Abstract
1. Introduction
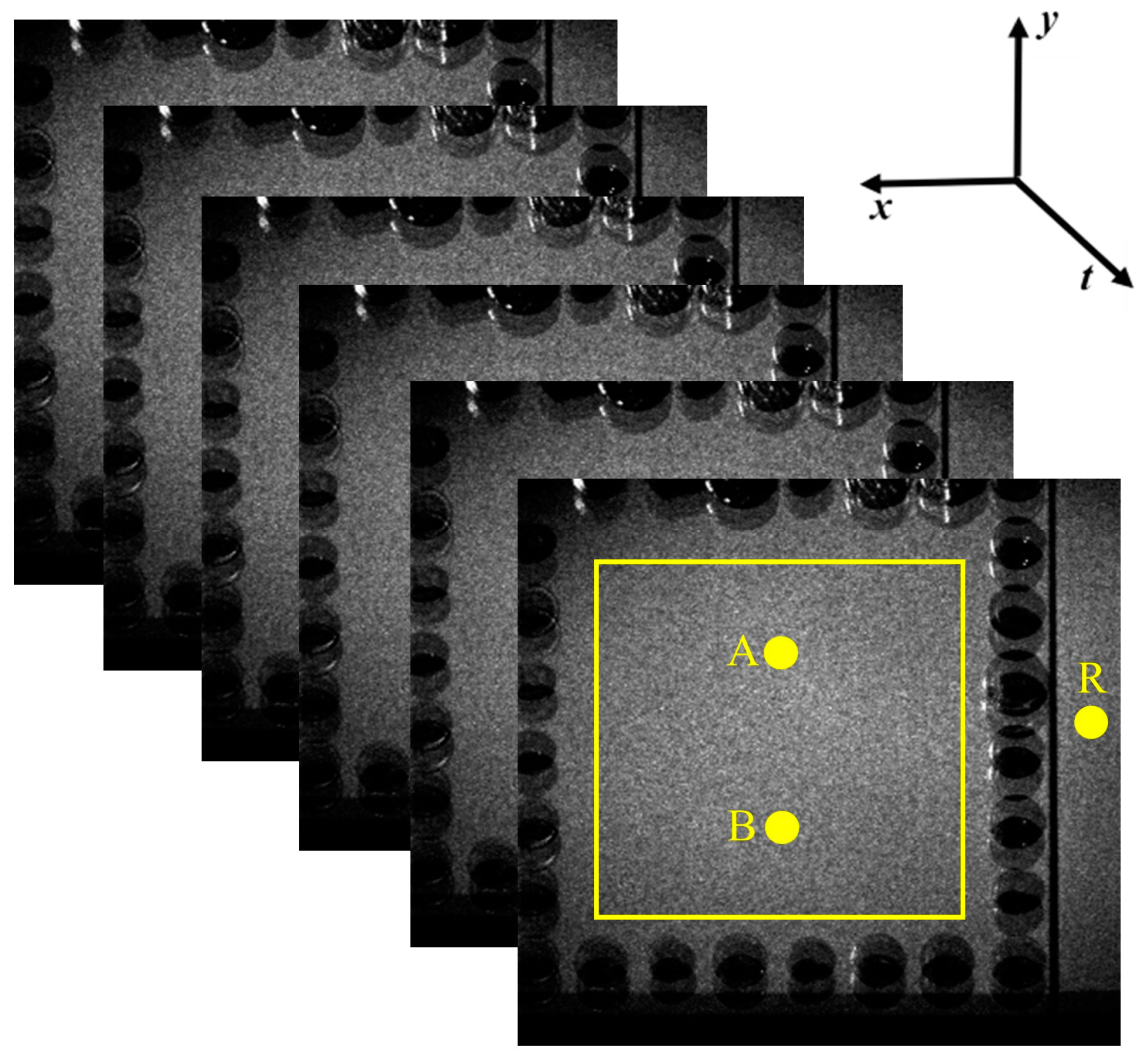
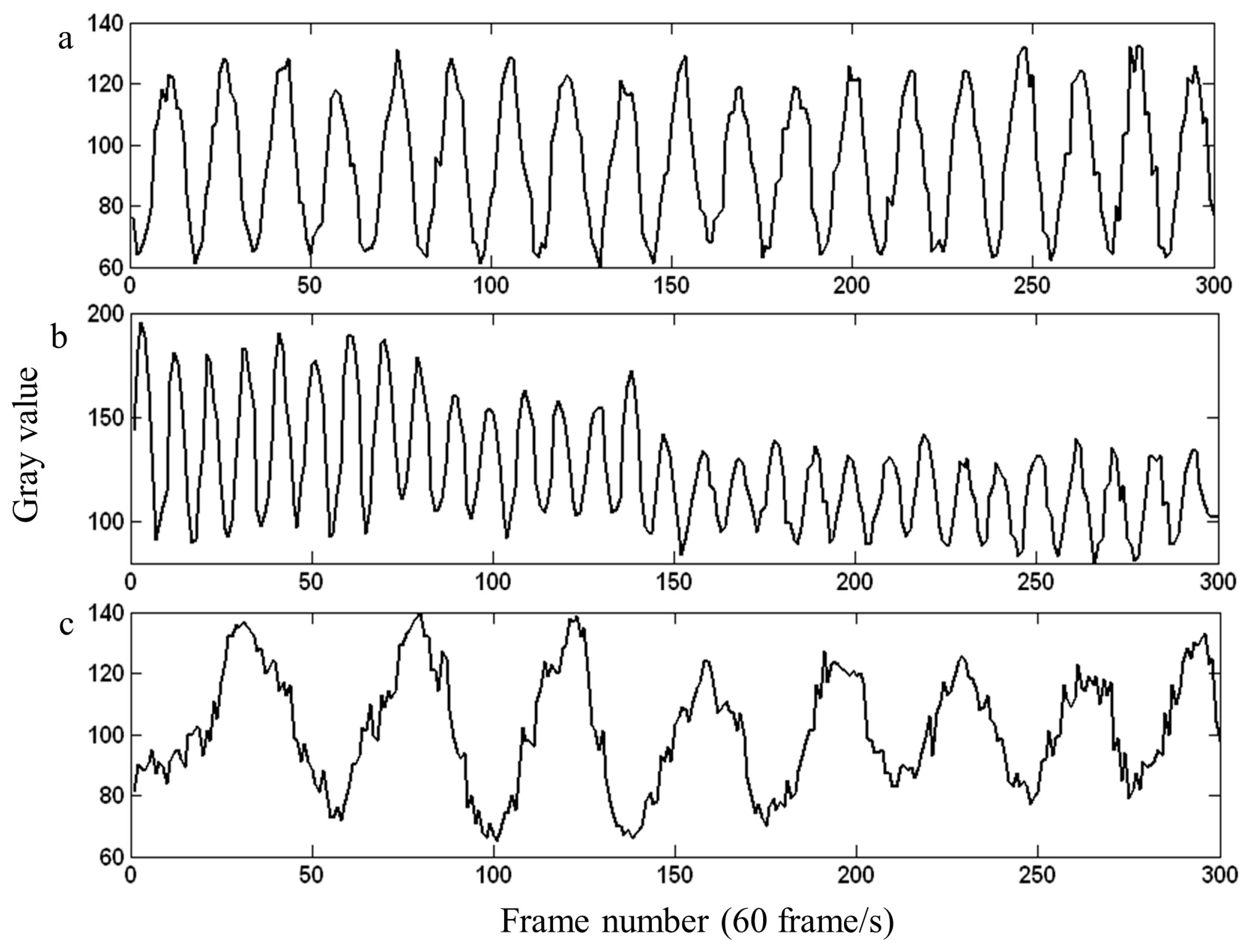
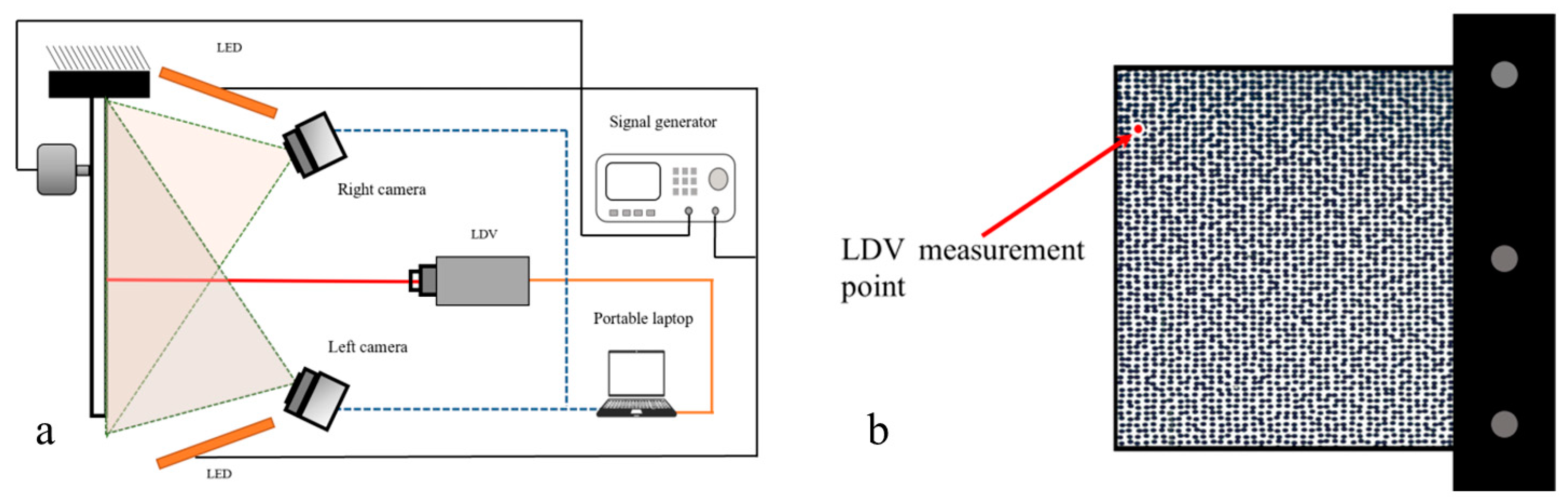
2. Temporal Analysis in Dynamic Digital Shearography
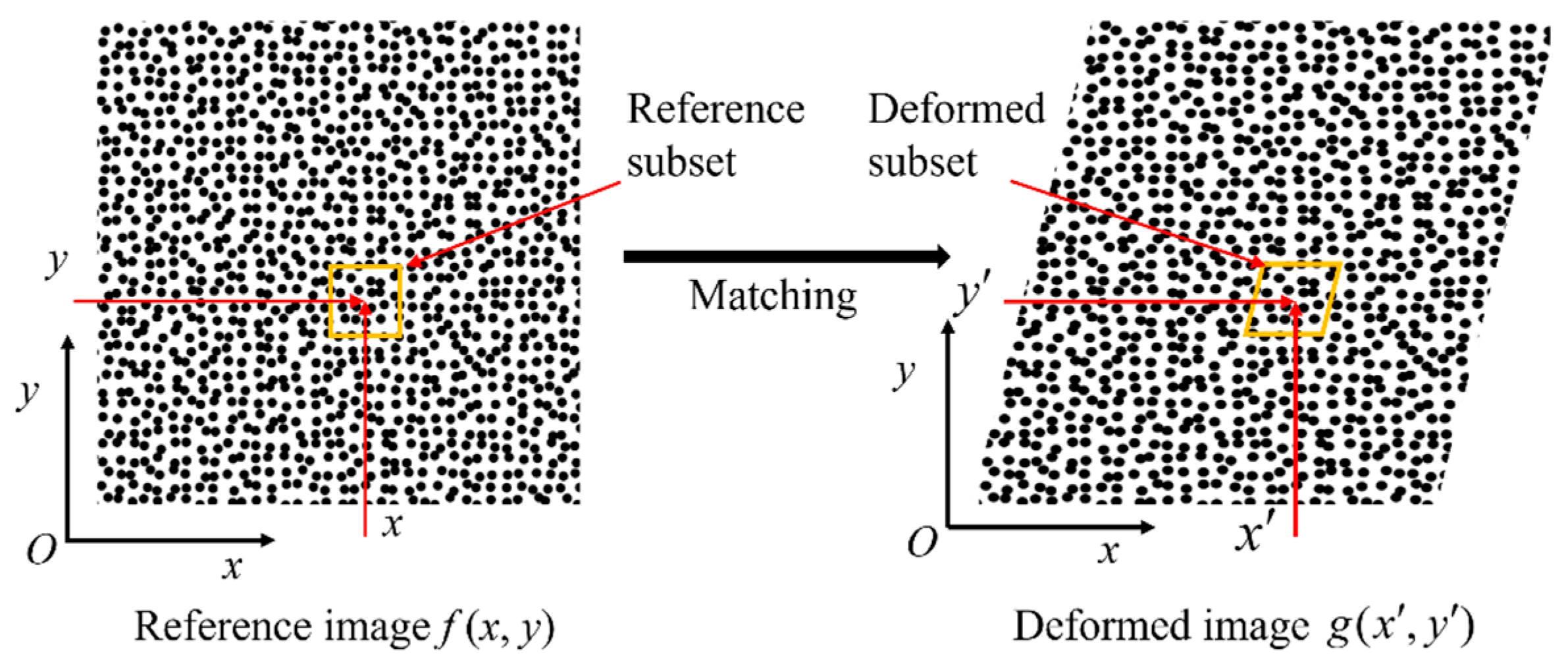
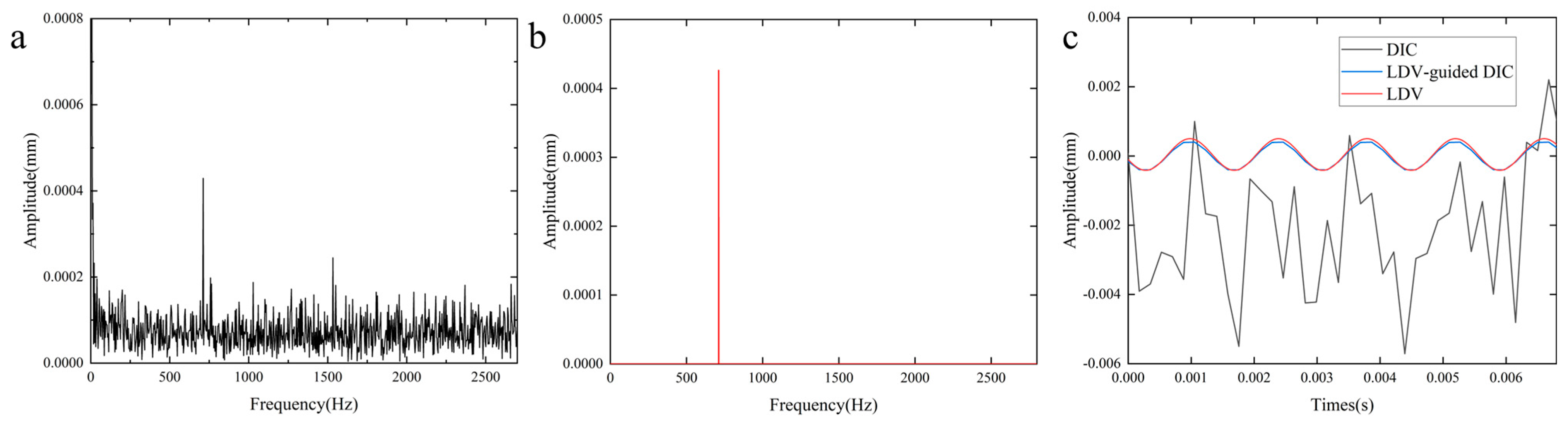
3. Temporal Analysis in Dynamic Digital Image Correlation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vest, C.M. Holographic Interferometry; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Hung, Y.Y. Shearography: A new optical method for strain measurement and nondestructive testing. Opt. Eng. 1982, 21, 213391. [Google Scholar] [CrossRef]
- Partovi Shabestari, N.; Rashidian Vaziri, M.R.; Bakhshandeh, M.; Alidokht, I.; Alizadeh, Y. Fabrication of a simple and easy-to-make piezoelectric actuator and its use as phase shifter in digital speckle pattern interferometry. J. Opt. 2019, 48, 272–282. [Google Scholar] [CrossRef]
- Hung, Y.Y.; Shang, H.M.; Yang, L. Unified approach for holography and shearography in surface deformation measurement and nondestructive testing. Opt. Eng. 2003, 42, 1197–1207. [Google Scholar] [CrossRef]
- Huang, H.; Yuan, E.; Zhang, D.; Sun, D.; Yang, M.; Zheng, Z.; Zhang, Z.; Gao, L.; Panezai, S.; Qiu, K. Free Field of View Infrared Digital Holography for Mineral Crystallization. Cryst. Growth Des. 2023, 23, 7992–8008. [Google Scholar] [CrossRef]
- Post, D.; Han, B.; Ifju, P. High Sensitivity Moiré: Experimental Analysis for Mechanics and Materials; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. Opt. Lett. 1997, 22, 1268–1270. [Google Scholar] [CrossRef] [PubMed]
- Shan, M.; Hao, B.; Zhong, Z.; Diao, M.; Zhang, Y. Parallel two-step spatial carrier phase-shifting common-path interferometer with a Ronchi grating outside the Fourier plane. Opt. Express 2013, 21, 2126–2132. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Yao, J.; Zhou, Y.; Sun, C.; Yang, P.; Miao, H.; Chen, J. Calibration of an arbitrarily arranged projection moiré system for 3D shape measurement. Opt. Lasers Eng. 2018, 104, 135–140. [Google Scholar] [CrossRef]
- Seif, M.A.; Khashaba, U.A.; Rojas-Oviedo, R. Measuring delamination in carbon/epoxy composites using a shadow moiré laser based imaging technique. Compos. Struct. 2007, 79, 113–118. [Google Scholar] [CrossRef]
- Zhang, S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques. Opt. Lasers Eng. 2010, 48, 149–158. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.-J.; Schreier, H.W. Image Correlation for Shape, Motion and Deformation Measurements; Springer: Boston, MA, USA, 2009; ISBN 978-0-387-78746-6. [Google Scholar]
- Tay, C.; Quan, C.; Huang, Y.; Fu, Y. Digital image correlation for whole field out-of-plane displacement measurement using a single camera. Opt. Commun. 2005, 251, 23–36. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, W.; Zhang, Q. High-speed three-dimensional shape measurement based on shifting Gray-code light. Optis Express 2019, 27, 22631–22844. [Google Scholar] [CrossRef] [PubMed]
- Pedrini, G.; Osten, W.; Gusev, M.E. High-speed digital holographic interferometry for vibration measurement. Appl. Opt. 2006, 45, 3456–3462. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Guo, M.; Liu, H.; Yan, K.; Xu, Y.J.; Miao, H.; Fu, Y. A multi-point laser Doppler vibrometer with fiber-based configuration. Rev. Sci. Instrum. 2013, 84, 121702. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Luo, W.D.; Dale, M.; Petniunas, A. High-speed ESPI and related techniques: Overview and its application in the automotive industry. Opitcs Lasers Eng. 2003, 40, 459–485. [Google Scholar] [CrossRef]
- Qian, K.; Fu, Y.; Liu, Q.; Seah, H.S.; Asundi, A. Generalized three-dimensional windowed Fourier transform for fringe analysis. Opt. Lett. 2006, 31, 2121–2123. [Google Scholar] [CrossRef] [PubMed]
- Joenathan, C.; Franze, B.; Haible, P.; Tiziani, H.J. Large in-plane displacement measurement in dual-beam speckle interferometry using temporal phase measurement. J. Mod. Opt. 1998, 45, 1975–1984. [Google Scholar] [CrossRef]
- Kemao, Q. Applications of windowed Fourier fringe analysis in optical measurement: A review. Opt. Lasers Eng. 2015, 66, 67–73. [Google Scholar] [CrossRef]
- Goudemand, N. Application of dynamic phase shifting wavelet analysis to electronic speckle contouring. Appl. Opt. 2006, 25, 3704–3711. [Google Scholar] [CrossRef] [PubMed]
- Shiraishi, T.; Toyooca, S.; Kadono, H.; Saito, T. Dynamic ESPI system for spatio-temporal strain analysis of a deforming solid object. Key Eng. Mater. 2006, 326–328, 95–98. [Google Scholar] [CrossRef]
- Pan, B. Bias error reduction of digital image correlation using Gaussian pre-filtering. Opt. Lasers Eng. 2013, 51, 1161–1167. [Google Scholar] [CrossRef]
- Gao, Z.; Xu, X.; Su, Y.; Zhang, Q. Experimental analysis of image noise and interpolation bias in digital image correlation. Opt. Lasers Eng. 2016, 81, 46–53. [Google Scholar] [CrossRef]
- Fu, Y.; Guo, M.; Liu, H. Determination of instantaneous curvature and twist by digital shearography. Opt. Eng. 2012, 51, 083602. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, G.; Wei, Y.; Chen, B.; Fu, Y. Temporal Analysis of Speckle Images in Full-Field Interferometric and Camera-Based Optical Dynamic Measurement. Photonics 2024, 11, 548. https://doi.org/10.3390/photonics11060548
Bai G, Wei Y, Chen B, Fu Y. Temporal Analysis of Speckle Images in Full-Field Interferometric and Camera-Based Optical Dynamic Measurement. Photonics. 2024; 11(6):548. https://doi.org/10.3390/photonics11060548
Chicago/Turabian StyleBai, Guojun, Yuchen Wei, Bing Chen, and Yu Fu. 2024. "Temporal Analysis of Speckle Images in Full-Field Interferometric and Camera-Based Optical Dynamic Measurement" Photonics 11, no. 6: 548. https://doi.org/10.3390/photonics11060548
APA StyleBai, G., Wei, Y., Chen, B., & Fu, Y. (2024). Temporal Analysis of Speckle Images in Full-Field Interferometric and Camera-Based Optical Dynamic Measurement. Photonics, 11(6), 548. https://doi.org/10.3390/photonics11060548



