Abstract
In this paper, an innovative approach is introduced to address the noise issues associated with micro–cantilever array deflection measurement systems employing multiple lasers. Conventional systems are affected by laser mode hopping during switching, resulting in wavelength instability and beam spot fluctuations that take several hundred milliseconds to stabilize. To mitigate these limitations, a high–speed laser modulation technique is utilized, leveraging the averaging effect over multiple modulation cycles within the sampling window. By driving the lasers with a high–frequency carrier signal, a low–noise and stable output suitable for micro–cantilever beam deflection measurement is achieved. The effectiveness of this approach is demonstrated by simultaneously modulating the lasers and rapidly observing the spectral and centroid variations during high–speed switching using a custom–built high–speed spectrometer. The centroid fluctuations are also analyzed under different modulation frequencies. The experimental results confirm that the high–speed modulation method can reduce the standard deviation of beam spot fluctuations by more than 90%, leading to significant improvements in noise reduction compared to traditional laser switching methods. The proposed high–speed laser modulation approach offers a promising solution for enhancing the precision and stability of multi–laser micro–cantilever array deflection measurement systems.
1. Introduction
Micro–cantilever beam deflection measurement has emerged as a valuable tool in various fields, particularly in biological and chemical sensing applications [1,2,3,4,5,6]. This technique has been widely employed in the detection and analysis of biochemical species, as well as in the realm of physical measurements [7,8,9,10]. As illustrated in Figure 1, the most common optical readout method for micro–cantilever deflection is the optical beam deflection (OBD) technique. In this simple optical setup, a laser beam is reflected off the surface of the micro–cantilever, and the position of the reflected spot is tracked using a position–sensitive detector.

Figure 1.
An illustration of the laser spot centroid position variation in a microcantilever beam system. The left diagram shows a schematic of the microcantilever array and laser optical path, with the microcantilever array drawn to scale. The right side shows the centroid position variation curve over time after laser activation, along with snapshots of the laser spot at different moments.
The angular deflection of the microcantilever has a direct proportional relationship with the displacement of the laser spot on the detector. By monitoring the change in the position of the reflected beam, the bending of the microcantilever can be precisely measured.
Multi–channel systems, which employ an array of micro–cantilevers, offer enhanced sensitivity and throughput compared to single–cantilever setups [11,12,13,14]. These systems rely on detecting the deflection of individual cantilevers by reflecting laser beams off their surfaces and tracking the position of the reflected spots using position–sensitive detectors [10,11,15].
In multi–channel micro–cantilever systems, a common approach is to use multiple lasers and switch between them to interrogate individual cantilevers sequentially. However, this laser switching process often introduces noise and instability [16]. When a laser is turned on or off, it undergoes a transient period where its output power and wavelength fluctuate due to current variations and mode hopping [17]. This instability leads to variations in the reflected beam spot pattern and calculated centroid, as illustrated in Figure 1, compromising the accuracy and precision of the deflection measurement. Stabilizing the laser output after each switch typically requires several hundred milliseconds, limiting the overall measurement speed and throughput [16,18].
To address the challenges associated with laser switching noise and instability, we explore the application of high–speed laser modulation techniques. Instead of completely turning the lasers on and off, we drive them with a high–frequency carrier signal, effectively modulating their output intensity within short periods. By carefully selecting the modulation frequency and duty cycle, we aim to induce rapid mode hopping, resulting in an averaging effect on the laser spectrum and centroid position.
Similar techniques have been employed in commercial applications such as DVD and CD systems [19,20], where high–speed laser modulation, often exceeding 200 MHz, is used to achieve stable and low–noise operation. However, these systems typically utilize compact, integrated components with a single laser source and receiver, and their direct application to multi–cantilever beam deflection measurements, which require multiple lasers to interrogate individual cantilevers simultaneously, has not been extensively explored.
The primary objective of this study is to investigate the feasibility and effectiveness of high–speed laser modulation in reducing noise and improving the stability of micro–cantilever beam array deflection measurement systems. By addressing the challenges associated with laser switching, we aim to enhance the accuracy, precision, and throughput of these systems, thereby expanding their potential for practical applications in fields such as environmental monitoring, drug discovery, and medical diagnostics.
In the following sections, we will present the design and implementation of our high–speed laser modulation technique, along with the experimental results demonstrating its performance in reducing noise and improving stability.
2. Principle and Method
2.1. High–Speed Modulation
2.1.1. Laser Mode Hopping and Its Impact on Wavelength Stability
The laser beam deflection technique is widely employed for measuring micro–cantilever deflection due to its high–speed operation, ability to work in free space, and capability to detect deflection even in liquid environments. Semiconductor lasers are commonly used in micro–cantilever beam systems because of their high–speed switching capability and relatively low cost [21,22,23]. However, semiconductor lasers are susceptible to mode hopping and changes in their primary operating mode, especially in applications that require frequent switching, which can affect the precision of deflection measurements.
This effect is particularly pronounced during the switching process, where a frequent on/off operation can lead to temperature and driving current variations. While wavelength stability is not typically a critical requirement for these systems, as the primary focus is on maintaining a stable beam spot, the interaction of the laser beam with non–single–mode fibers, reflective surfaces, or micro–cantilever cavity windows can lead to speckle patterns and other effects [24]. Even with a well–collimated single–mode laser beam, reflected or refracted light from the micro–cantilever or the reaction cell’s window forms a speckle field. Slight wavelength changes, especially after the laser is turned on, can significantly alter the reflected speckle pattern due to the complex coherent superposition. These changes in the speckle pattern affect the centroid distribution and calculated position used for micro–cantilever deflection measurements.
2.1.2. Averaging Effect of High–Speed Modulation within the Sampling Window
To mitigate the noise induced by laser switching and mode hopping, we propose a method that employs high–speed modulation to perform multiple mode hops within a short time window. By rapidly modulating the laser, wavelength fluctuations can be averaged out over multiple sampling windows, significantly reducing the beam spot jitter. This approach is particularly effective when coupled with devices such as cameras or position–sensitive detectors (PSDs) with relatively low sampling bandwidths.
Our experimental setup utilizes cameras as the primary detection devices, offering the advantage of well–defined and adjustable sampling time windows. By synchronizing the camera’s exposure time with the modulation period, we can effectively capture and average the rapid beam spot movement, resulting in a stable centroid position. This technique can also be applied to PSD–based systems, provided that the switching frequency is significantly higher than the PSD’s sampling frequency.
2.2. System Design and Implementation
2.2.1. Microcantilever Detection System
The microcantilever detection system, as illustrated in Figure 2a, comprises a temperature–controlled cell, optical detection components, and a fluid control system. The cell houses the OCTO–500S microcantilever array (MICROMOTIVE, Germany), which features eight cantilevers (500 μm long, 90 μm wide, and 1 μm thick) with a 250 μm spacing. The cantilevers feature a gold layer on the top surface and a titanium bonding layer on the bottom, providing stability and the desired reactivity. The cantilevers feature a gold layer on the top surface, which enhances their reflectivity, improving the signal–to–noise ratio of the optical readout, and allows for potential functionalization through the formation of strong thiol bonds. A titanium bonding layer on the bottom provides stability during reactions.
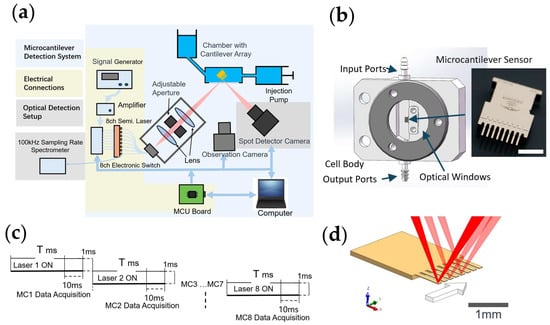
Figure 2.
(a) A schematic of the microcantilever system. (b) A 3D model of the cell body and a photograph of the microcantilever array with a 1 mm scale bar. (c) A laser switching strategy and timing diagram. (d) A schematic of lasers sequentially illuminating different tips of the microcantilever array.
The cell, designed to perform measurements in a liquid environment, is made of a non–reactive metal and features an embedded heating plate and a temperature sensor with a resolution of 0.01 °C, controlled by a commercial controller (Shafan TCB–NE, China) and monitored via a serial port for data logging and analysis. The window is angled at 6 degrees relative to the microcantilevers to ensure that reflections from the window do not enter the sensor simultaneously with the reflections from the microcantilevers, allowing for only the microcantilever reflections to be detected. The window is also coated with an anti–reflection film to minimize optical interference, as shown in the schematic representation in Figure 2a. Barbed connectors allow for the cell to be connected to an external injection pump via silicone tubes for fluid control.
A customized V–groove fiber array with 8 FC/PC ports and precisely embedded bare fibers is used at the laser emission point. The 250 μm fiber output spacing matches the microcantilever array pitch, and a 1:1 lens focuses the beams onto the microcantilevers, simplifying the alignment.
Figure 2d illustrates the sequential scanning of the laser spots across the microcantilever array, and Figure 2c shows the laser switching strategy and timing diagram. In this scheme, each channel is illuminated for T ms, followed by a 10 ms exposure and then a 1 ms pause before switching to the next channel. The T time is crucial as it provides the necessary duration for the laser to stabilize after switching. In subsequent experiments, we demonstrate that conventional non–modulated laser switching strategies may require a longer stabilization time, potentially up to 300 ms, to allow for the system to reach a stable state. Consequently, scanning all 8 cantilevers using a non–modulated approach might take 2–3 s.
Optical detection is achieved using a CMOS camera (Hikvision MV–CA016, China) equipped with a IMX296 image sensor (Sony, Tokyo, Japan), which serves as the spot detection camera in Figure 2a, capturing the position of the reflected laser spots to determine the microcantilever deflection. The camera’s adjustable exposure time (1/100 s or 1/120 s) helps reduce signal disturbances. A custom Python script calculates the centroid of each spot for the deflection measurements.
2.2.2. Electrical Connections and Circuit Design
To facilitate the experimental testing of various waveforms, we implemented an electrical connection scheme (Figure 3a) that combines a BUF634 buffer amplifier and an 8–channel N–channel MOSFET (NMOS) switch array. The input waveform, generated by a Rigol DG822 signal generator, produces voltage signals within the 2–3 volt range. These signals are then buffered by the BUF634, which acts as a voltage follower, providing a low–impedance output signal capable of driving the laser diodes effectively.
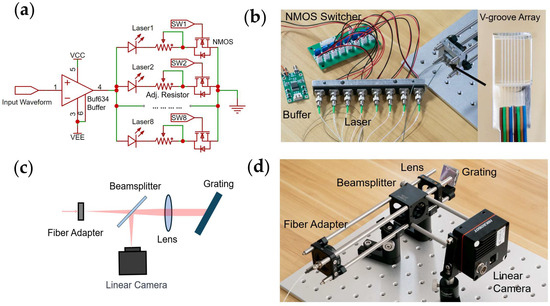
Figure 3.
The electrical connections, circuit design, and optical detection setup. (a) A schematic of the electrical connection. (b) A photograph of the circuit boards, multiple lasers, and V–groove array. (c) A schematic of the custom–built 100 kHz spectrometer. (d) A photograph of the custom–built spectrometer.
The amplified signals are fed into the 8–channel NMOS switch array, where the gate terminals (SW1 to SW8 in Figure 3a) are connected to the ESP32 microcontroller’s digital output pins. The microcontroller, programmed using PlatformIO, generates switching signals to selectively enable or disable individual laser diodes (Laser1 to Laser8 in Figure 3a), allowing for only one laser to be active at a time. This design allows for a single signal source and high–speed waveform circuit to drive multiple lasers, with the ESP32 controlling the active laser and handling the light source control and camera synchronization.
Adjustable current–limiting resistors between the BUF634 and NMOS switches ensure the laser diodes operate within the desired range, allowing for fine–tuning of the optical output power, set to approximately 3 mW per laser diode.
By combining the high–speed switching capabilities of the NMOS controller with the waveform generation and amplification provided by the signal generator and BUF634, our circuit enables the exploration of various modulation techniques to optimize the laser output stability and reduce noise in the multi–cantilever beam deflection measurement system.
2.2.3. Optical Detection Setup
To evaluate the average wavelength and positioning performance of the beam spot under high–speed modulation, we conducted tests on various waveforms and frequencies. As common commercial spectrometers have low speeds below a few hundred hertz, we built a custom 100 kHz spectrometer (Figure 3c,d), designed to achieve high–speed data acquisition and a sufficient sampling rate.
Our custom–built spectrometer consists of an FC/PC fiber input, a 200 mm achromatic lens, a half–mirror, 1200 lines/mm reflective diffraction grating, and a MV–CL022–91GM camera (Hikvision, China) with a pixel size of 14 μm and a sampling rate of up to 100 kHz. Each pixel corresponds to a spectral resolution of 0.047 nm, resulting in an overall system resolution of approximately 0.14 nm. The grating is configured in a Littrow configuration, with the first–order diffracted light focused onto the linear camera using a 200 mm focal length lens. The system is calibrated using a known wavelength of 633 nm from a helium–neon laser. This setup allows us to record and analyze the rapid variations in the laser spectrum during the switching process.
For the beam spot centroid testing, the camera is positioned 150 mm away from the micro–cantilever beam, with the focus point located at the rigid base of the cantilever to exclude the influence of the cantilever’s own deflection. This arrangement ensures that the observed changes in the beam spot position are solely attributed to the laser’s performance under high–speed modulation rather than the mechanical response of the micro–cantilever.
3. Experimental Results and Analysis
To evaluate the performance of the high–frequency modulation technique, we conducted experiments comparing it with traditional laser switching methods.
We simultaneously observed the changes in the system’s centroid spot position and laser spectrum before and after implementing the high–frequency modulation. Additionally, we investigated the system’s response to a 1 kHz square wave modulation, recording the corresponding changes in the centroid spot position and laser spectrum. We then explored the effects of different modulation waveforms and frequencies on the system’s stability by measuring the standard deviation of the centroid position over multiple measurement cycles, using both square and sine waves at various frequencies. This analysis revealed that an optimal frequency value could be obtained. Finally, we conducted temperature step detection experiments on microcantilevers using both optimized modulation and direct switching methods, demonstrating the improved signal–to–noise ratio achieved by our proposed technique.
3.1. Centroid Spot Position and Laser Spectrum Analysis
To investigate the system’s response to high–frequency modulation, we conducted experiments comparing the laser spectrum and centroid spot position under both modulated and non–modulated conditions. Initially, we captured the laser spectrum and centroid spot position using a 10 ms sampling window at a frame rate of 100 Hz, corresponding to Figure 4a–e. During this 10 ms exposure time, the camera integrates the light from the laser, which is modulated at a higher frequency.
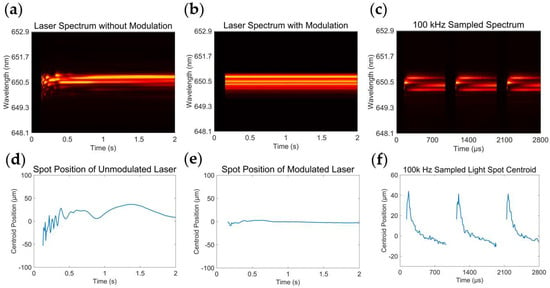
Figure 4.
The laser spectra and centroid spot position measurements with and without modulation. (a) An unmodulated laser spectrum over 2 s, captured at 100 Hz with a 10 ms exposure time. (b) A 1 kHz square wave modulated laser spectrum over 2 s, captured at 100 Hz. (c) A 1 kHz modulated laser spectrum observed at 100 kHz with a 10 μs exposure time, showing periodic behavior within the individual modulation periods. The laser is operated with an 80% duty cycle. (d) The unmodulated laser centroid position variation, captured with a 10 ms sampling window for improved accuracy and noise reduction. (e) A 1 kHz modulated laser centroid position variation, captured with a 10 ms sampling window, integrating multiple modulation periods. (f) A 1 kHz modulated laser centroid position observed at 100 kHz, revealing the high–speed dynamics within each on/–off cycle.
Under non–modulated conditions (Figure 4a,d), significant spectral jumps and changes in the beam spot centroid were observed, particularly during the initial stages of the switching process. In contrast, when the laser was modulated at a frequency of 1 kHz and the sampling window was set to 10 ms, encompassing 10 modulation cycles (Figure 4b,e), the magnitude of the spectral jumps and centroid position fluctuations was significantly reduced compared to the non–modulated conditions.
To gain a more detailed understanding of the high–frequency modulation effects, we employed a line array camera, the same model used in the spectrometer, to measure the laser spectrum and beam spot position with a consistent 100 kHz sampling rate. Figure 4c shows the high–speed measurement of the laser spectrum under 1 kHz high–frequency modulation, captured using a 10 μs sampling window at a 100 kHz frame rate, revealing the rapid changes within each modulation cycle. Similarly, Figure 4f illustrates the high–speed measurement of the centroid position under the same modulation conditions.
During the 1 kHz high–frequency modulation, the laser spectrum (Figure 4c) and centroid position (Figure 4f) underwent rapid changes within each modulation cycle. However, when averaged over a wider time scale sampling window, such as the 10 ms window used in Figure 4b,e, both the laser spectrum and centroid position reached stable values. This averaging effect explains the reduced fluctuations observed in the 10 ms exposure time measurements compared to the non–modulated state, as the integration of multiple modulation periods effectively smooths out the high–frequency variations. Although some fluctuations persisted, likely due to the overall temperature variations during the initial startup, their magnitude was significantly reduced compared to the non–modulated state.
These experimental results demonstrate that high–frequency modulation effectively reduces the magnitude of spectral jumps and centroid position fluctuations, leading to a more stable system performance compared to non–modulated conditions.
3.2. Centroid Stability under Different Modulation Waveforms and Frequencies
To further investigate the impact of modulation parameters on centroid stability, the beam spot position was measured under various modulation frequencies and waveforms. Figure 5a shows approximately 20 beam spot position curves each under 1 kHz and 100 kHz sine wave modulation. The system’s sampling rate is 100 Hz.

Figure 5.
(a) Comparison of spot position curves under 1 kHz and 100 kHz sinusoidal modulation. (b) Standard deviation of spot position fluctuations over time for different frequencies and waveforms, including direct switching without any modulation (Direct SW), sinusoidal modulation (Sin), and square wave modulation (SQR). (c) Average standard deviation of the first 30 elements (0–300 ms) for different modulation conditions.
In practical applications, the consistency of the beam spot position under specific conditions is of utmost importance. This is because our cantilever array light source employs a scanning approach, where the beam sequentially illuminates each cantilever for a short duration before moving to the next one and repeating the cycle. For any given cantilever, there is a relatively long–time gap between each occasion that it is probed by the beam. If the beam spot position on that cantilever differs too much between successive scans, it will introduce noise and instability into the signal obtained from that cantilever. Therefore, achieving high beam position consistency over time is crucial for obtaining reliable data from the cantilever sensor array without signal fluctuations caused by variation in the illumination conditions.
Although noticeable fluctuations in the curves over time may be observed, the primary concern is the consistency of the beam spot under the same conditions at different moments. If the sampled beam spot at a specific instant has a fixed bias, the noise introduced by the laser can be considered negligible, making the standard deviation a more critical metric.
To quantitatively evaluate the variation in the beam spot position dispersion over time, the standard deviation was calculated for multiple data sets under different modulation conditions. The modulation frequencies ranged from 1 kHz to 10 MHz for both sine wave and square wave modulation. For each modulation configuration, approximately 20 curves were measured and aligned by their mean values. The standard deviation of these curves over time was then determined for each configuration.
Figure 5b displays the standard deviation curves over time for the sine wave and square wave modulation at various frequencies. From the figure, it can be observed that even within the first 10 ms of laser onset (the first frame of sampling), the 100 kHz sine wave modulation already achieves a very small standard deviation.
Figure 5c illustrates the relationship between the average standard deviation of the first 30 sampling points (0 to 300 ms) and the modulation frequency. Interestingly, the standard deviation does not exhibit a monotonic relationship with frequency, suggesting the existence of an optimal modulation frequency that minimizes the system’s standard deviation. Under the experimental conditions, the optimal frequency for sine wave modulation is around 100 kHz, while for square wave modulation, it is around 1 MHz. Near the optimal frequency, the system’s standard deviation remains at a low level. Taking 100 kHz sine wave modulation as an example, the standard deviation of the beam spot position remains consistently low throughout the initial 10 ms of sampling, without significant fluctuations (Figure 5b). Consequently, by operating at an appropriate frequency, the waiting time associated with system channel switching can be substantially reduced, thereby enhancing the system bandwidth by several folds.
The experimental results clearly demonstrate the advantages of frequency modulation while also revealing the existence of an optimal working range. The specific optimal frequency may depend on factors such as the laser model, maximum driving current, square wave duty cycle, and ambient temperature.
3.3. Temperature Step Measurement Performance
To further validate the effectiveness of the high–frequency modulation technique, tests were conducted in real–world measurement scenarios. Temperature variations were measured using a microcantilever beam system, and the results were compared with the previous data obtained by the research group using direct switching methods.
The microcantilever beam was subjected to temperature gradients between 25.0 °C and 25.2 °C, while the ambient temperature was maintained at approximately 20 °C. The cell was filled with a PBS solution, and the microcantilever beam deflection was monitored as the temperature changed. In the conventional switching method, a waiting time of 312.5 ms was introduced after each switching event, and the sampling was performed at a moment when the system standard deviation was relatively small. The overall sampling rate of the system was 0.4 Hz. In contrast, based on the optimization results observed in previous experiments, we employed a 100 kHz sine wave modulation and sampled the system 5 ms after each laser switching event. The single sampling cycle time of the entire system was 20 ms, resulting in an overall sampling rate of 6.25 Hz.
In contrast, Figure 6b presents the step response after implementing the high–speed laser modulation technique. A notable reduction in noise levels is observed, resulting in a smoother and more stable response.
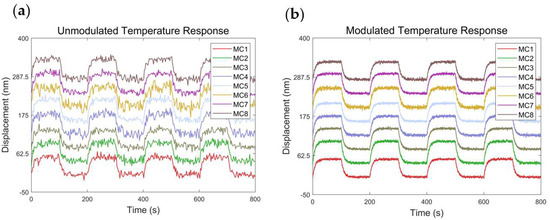
Figure 6.
(a) Unmodulated temperature response: The temperature gradient ranges from 25.0 °C to 25.2 °C, with substantial noise present due to the laser switching instability. The sampling rate is 0.4 Hz. (b) Modulated temperature response with 100 kHz high–frequency laser modulation: A significant reduction in noise is observed, resulting in a smoother and more stable response. The sampling rate is increased to 6.25 Hz.
To quantitatively assess the improvement, we calculated the signal–to–noise ratio (SNR) for both scenarios. In Figure 6a, without high–speed laser modulation, the SNR values ranged from approximately 13.4 dB to 16.3dB. These relatively low SNR values confirm the presence of significant noise in the measurements. On the other hand, Figure 6b, which employs high–speed laser modulation, exhibits substantially higher SNR values, ranging from 26.6 dB to 29.3 dB. This remarkable improvement in the SNR, with an increase of over 12 dB, clearly demonstrates the effectiveness of the proposed technique in enhancing the signal quality and reducing noise.
In summary, the temperature step measurement performance tests validate the efficacy of the high–frequency modulation technique in real–world applications. Employing a 100 kHz sine wave modulation led to a significant improvement in the signal–to–noise ratio compared to the conventional direct switching method.
In summary, the temperature step measurement performance tests validate the efficacy of the high–frequency modulation technique in real–world applications. By implementing a 100 kHz sine wave modulation, which enables the rapid stabilization of the laser output and laser spot, we were able to significantly reduce the switching wait time. This reduction in wait time led to a notable improvement in the system’s bandwidth, increasing it from 0.4 Hz to 6.25 Hz. Simultaneously, the high–frequency modulation technique resulted in a substantial enhancement of the signal–to–noise ratio compared to the conventional direct switching method.
4. Discussion and Conclusions
In this study, we have demonstrated the effectiveness of high–frequency modulation in improving the stability and accuracy of microcantilever beam–based sensing systems. Our experimental results show that by employing a 100 kHz sine wave modulation and optimizing the sampling timing, we can significantly reduce noise levels and enhance the signal–to–noise ratio by over 12 dB compared to the conventional direct switching method.
The detailed observations of the centroid stability and beam spot position under high–frequency modulation reveal that the dispersion between different curves is significantly smaller, indicating improved measurement repeatability. Furthermore, we have identified the existence of an optimal modulation frequency range that minimizes the system’s standard deviation, ensuring that the system maintains a low standard deviation and reduces the waiting time associated with system channel switching.
The real–world temperature step measurement tests further validate the efficacy of the high–frequency modulation technique, demonstrating an improved measurement accuracy, stability, and signal–to–noise ratio. It is worth noting that the specific optimal modulation frequency can be determined automatically by the system itself. The system can easily calculate its own standard deviation and identify the optimal modulation frequency. This self–calibration process can be performed before the measurement starts, ensuring the best possible performance for different system configurations and applications.
In conclusion, this study introduces a novel approach for enhancing the stability and accuracy of multi–laser, multi–microcantilever beam–based sensing systems via high–frequency modulation. The experimental results and real–world tests demonstrate the effectiveness of this technique in suppressing noise, enhancing the signal quality. The findings of this study may provide valuable insights and guidance for similar systems utilizing the optical beam deflection (OBD) method and contribute to the advancement of sensor technologies in related fields.
Author Contributions
W.X.: Conceptualization, Methodology, Software, Validation, Formal Analysis, Investigation, Visualization, Writing—Original Draft, Resources; Y.S.: Writing—Review and Editing, Resources; Q.Z.: Writing—Review and Editing, Funding Acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (Grant No. 32061160475).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 32061160475) and the experimental assistance provided by Qiubo Chen.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Meyer, G.; Amer, N.M. Novel optical approach to atomic force microscopy. Appl. Phys. Lett. 1988, 53, 1045–1047. [Google Scholar] [CrossRef]
- Berger, R.; Delamarche, E.; Lang, H.P.; Gerber, C.; Gimzewski, J.K.; Meyer, E.; Güntherodt, H.-J. Surface Stress in the Self-Assembly of Alkanethiols on Gold. Science 1997, 276, 2021–2024. [Google Scholar] [CrossRef]
- Lee, G.U.; Chrisey, L.A.; Colton, R.J. Direct Measurement of the Forces Between Complementary Strands of DNA. Science 1994, 266, 771–773. [Google Scholar] [CrossRef]
- Zhang, J.; Lang, H.P.; Huber, F.; Bietsch, A.; Grange, W.; Certa, U.; Mckendry, R.; Güntherodt, H.-J.; Hegner, M.; Gerber, C. Rapid and label-free nanomechanical detection of biomarker transcripts in human RNA. Nat. Nanotechnol. 2006, 1, 214–220. [Google Scholar] [CrossRef] [PubMed]
- Biswal, S.L.; Raorane, D.; Chaiken, A.; Birecki, H.; Majumdar, A. Nanomechanical Detection of DNA Melting on Microcantilever Surfaces. Anal. Chem. 2006, 78, 7104–7109. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Lang, H.P.; Yoshikawa, G.; Gerber, C. Optimization of DNA Hybridization Efficiency by pH-Driven Nanomechanical Bending. Langmuir 2012, 28, 6494–6501. [Google Scholar] [CrossRef] [PubMed]
- Ji, H.-F.; Hansen, K.; Hu, Z.; Thundat, T. Detection of pH Variation Using Modified Microcantilever Sensors. Sens. Actuators B Chem. 2001, 72, 233–238. [Google Scholar] [CrossRef]
- Tabard-Cossa, V.; Godin, M.; Beaulieu, L.Y.; Grütter, P. A differential microcantilever-based system for measuring surface stress changes induced by electrochemical reactions. Sens. Actuators B Chem. 2005, 107, 233–241. [Google Scholar] [CrossRef]
- Vashist, S.K.; Holthöfer, H. Microcantilevers for Sensing Applications. Meas. Control 2010, 43, 84–88. [Google Scholar] [CrossRef]
- Boisen, A.; Dohn, S.; Keller, S.S.; Schmid, S.; Tenje, M. Cantilever-like micromechanical sensors. Rep. Prog. Phys. 2011, 74, 036101. [Google Scholar] [CrossRef]
- Battiston, F.M.; Ramseyer, J.-P.; Lang, H.P.; Baller, M.K.; Gerber, C.; Gimzewski, J.K.; Meyer, E.; Güntherodt, H.-J. A chemical sensor based on a microfabricated cantilever array with simultaneous resonance-frequency and bending readout. Sens. Actuators B Chem. 2001, 77, 122–131. [Google Scholar] [CrossRef]
- Mertens, J.; Alvarez, M.; Tamayo, J. Real-time profile of microcantilevers for sensing applications. Appl. Phys. Lett. 2005, 87, 234102. [Google Scholar] [CrossRef]
- Yue, M.; Stachowiak, J.C.; Lin, H.; Datar, R.; Cote, R.; Majumdar, A. Label-Free Protein Recognition Two-Dimensional Array Using Nanomechanical Sensors. Nano Lett. 2008, 8, 520–524. [Google Scholar] [CrossRef] [PubMed]
- Yue, M.; Lin, H.; Dedrick, D.E.; Satyanarayana, S.; Majumdar, A.; Bedekar, A.S.; Sundaram, S. A 2-D microcantilever array for multiplexed biomolecular analysis. J. Microelectromechanical Syst. 2004, 13, 290–299. [Google Scholar] [CrossRef]
- Álvarez, M.; Tamayo, J. Optical sequential readout of microcantilever arrays for biological detection. Sens. Actuators B Chem. 2005, 106, 687–690. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, L.; Li, C.; Wu, S.; Zhang, Q. Microcantilever array instrument based on optical fiber and performance analysis. Rev. Sci. Instrum. 2017, 88, 075007. [Google Scholar] [CrossRef] [PubMed]
- Yılmazlar, I.; Sabuncu, M. Speckle noise reduction based on induced mode Hopping in a semiconductor laser diode by drive current modulation. Opt. Laser Technol. 2015, 73, 19–22. [Google Scholar] [CrossRef]
- Nieradka, K.; Małozięć, G.; Kopiec, D.; Grabiec, P.; Janus, P.; Sierakowski, A.; Gotszalk, T. Expanded beam deflection method for simultaneous measurement of displacement and vibrations of multiple microcantilevers. Rev. Sci. Instrum. 2011, 82, 105112. [Google Scholar] [CrossRef] [PubMed]
- Hwu, E.E.-T.; Boisen, A. Hacking CD/DVD/Blu-ray for Biosensing. ACS Sens. 2018, 3, 1222–1232. [Google Scholar] [CrossRef]
- Bosco, F.G.; Hwu, E.-T.; Chen, C.-H.; Keller, S.; Bache, M.; Jakobsen, M.H.; Hwang, I.-S.; Boisen, A. High throughput label-free platform for statistical bio-molecular sensing. Lab Chip 2011, 11, 2411–2416. [Google Scholar] [CrossRef]
- Petermann, K. External Optical Feedback Phenomena in Semiconductor Lasers. IEEE J. Sel. Top. Quantum Electron. 1995, 1, 480–489. [Google Scholar] [CrossRef]
- Fukuma, T.; Kimura, M.; Kobayashi, K.; Matsushige, K.; Yamada, H. Development of Low Noise Cantilever Deflection Sensor for Multienvironment Frequency-Modulation Atomic Force Microscopy. Rev. Sci. Instrum. 2005, 76, 053704. [Google Scholar] [CrossRef]
- Herfst, R.W.; Klop, W.A.; Eschen, M.; Van Den Dool, T.C.; Koster, N.B.; Sadeghian, H. Systematic Characterization of Optical Beam Deflection Measurement System for Micro and Nanomechanical Systems. Measurement 2014, 56, 104–116. [Google Scholar] [CrossRef]
- Murray, M.; Davis, A.; Kirkendall, C.; Redding, B. Speckle-Based Strain Sensing in Multimode Fiber. Opt. Express 2019, 27, 28494. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).