The Impact of Pulse Shaping on Coherent Dynamics near a Conical Intersection
Abstract
1. Introduction
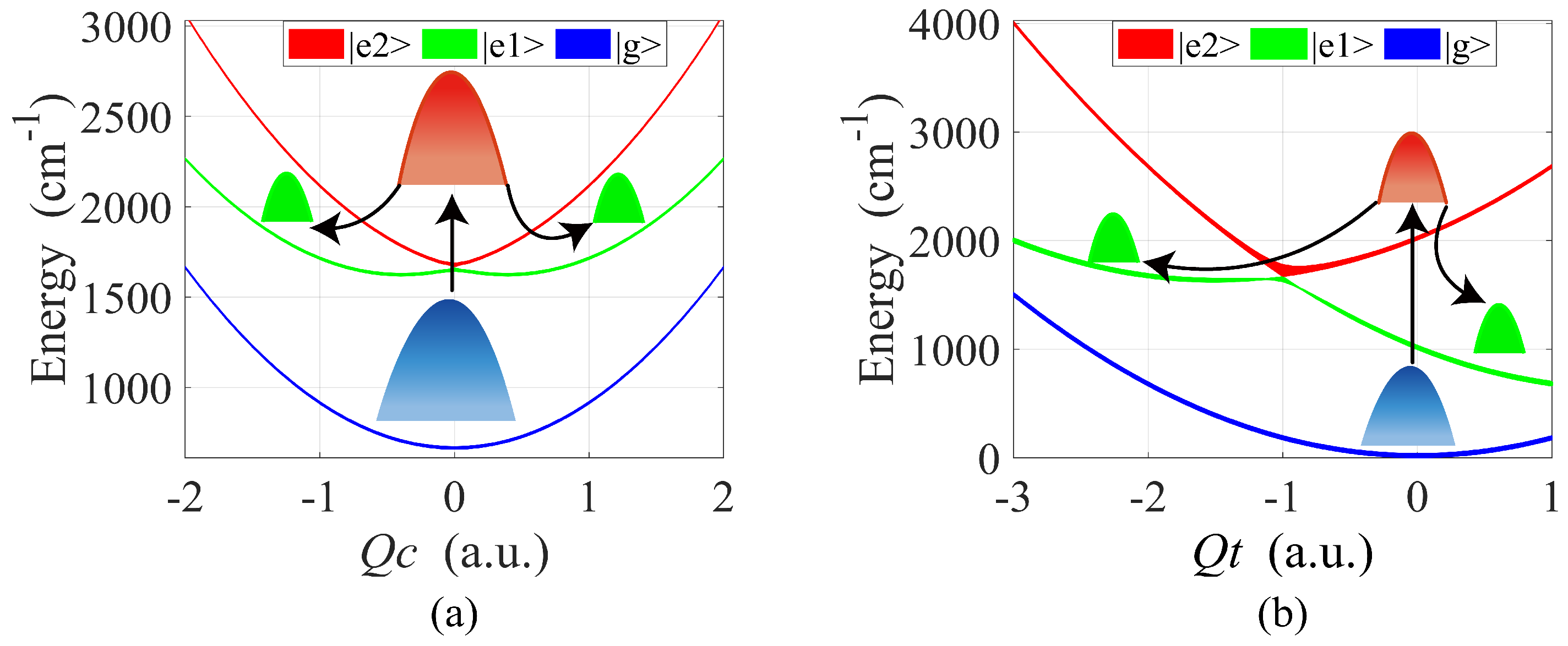
2. Theoretical Model
3. Results
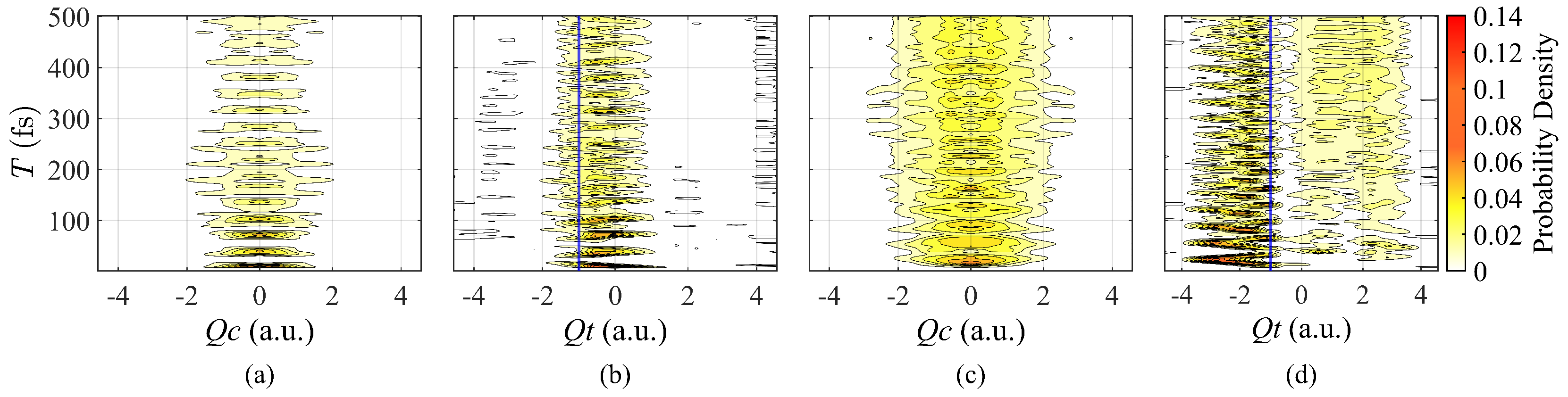
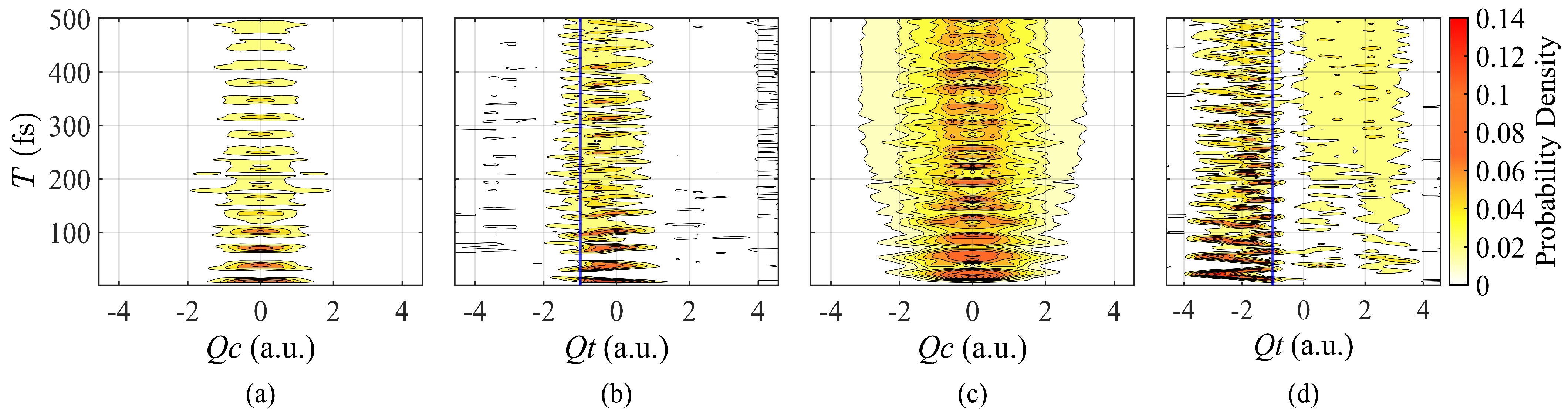
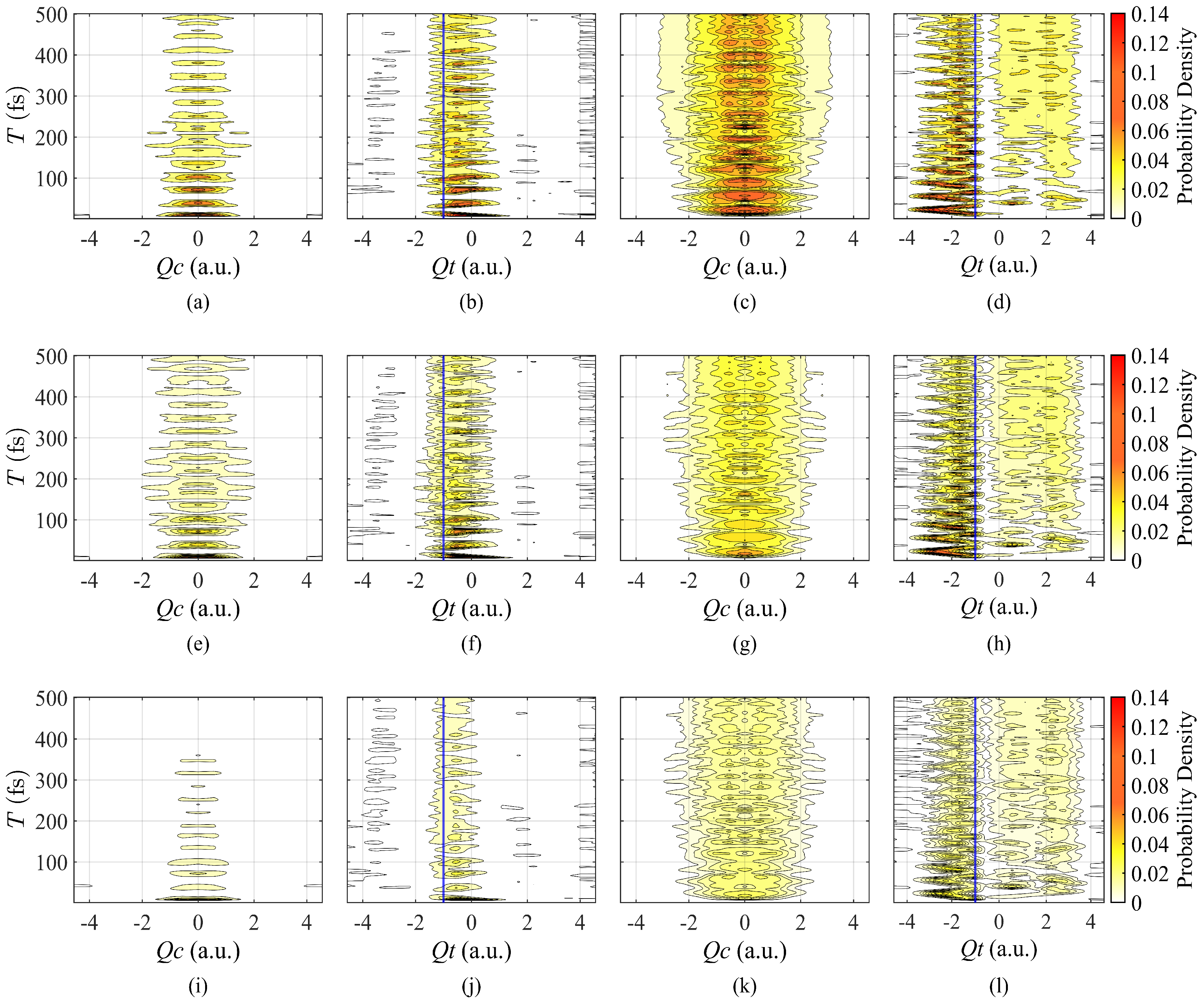
3.1. Synthesis of Artificial Pulse with Modulation of Amplitudes
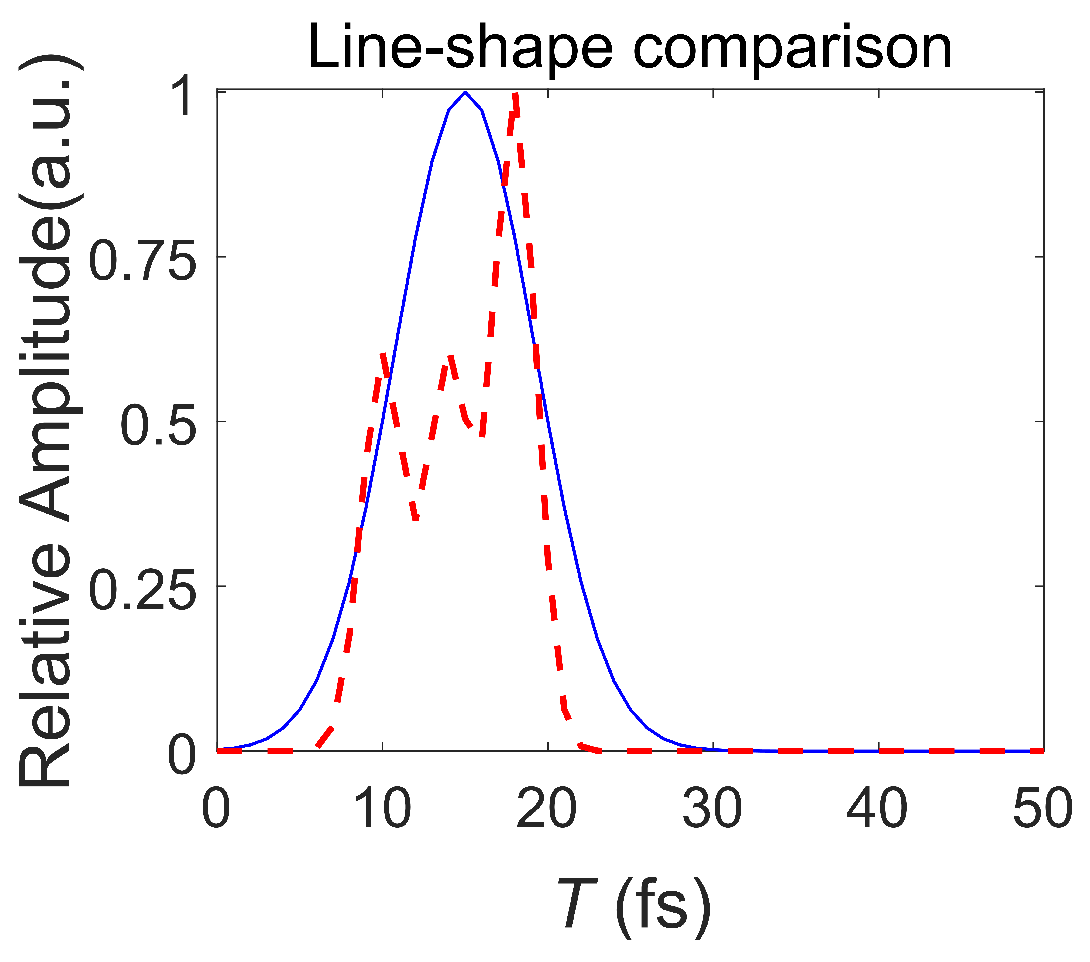
3.2. Pulse with Different Durations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. The Description of TNL
Appendix A.2. Supplementary Information on Model Parameter Settings

References
- Domcke, W.; Yarkony, D.R.; Koppel, H. Conical Intersection: Electronic Structure, Dynamics and Spectroscopy. In World Scientific; Domcke, W., Yarkony, D.R., Koppel, H., Eds.; World Scientific: Singapore, 2004. [Google Scholar]
- Domcke, W.; Yarkony, D.R.; Koppthe, H. Conical intersections: Theory, computation and experiment In World Scientific; Domcke, W., Yarkony, D.R., Koppel, H., Eds.; World Scientific: Singapore, 2011. [Google Scholar]
- Kowalewski, M.; Fingerhut, B.P.; Dorfman, K.E.; Bennett, K.; Mukamel, S. Simulating Coherent Multidimensional Spectroscopy of Nonadiabatic Molecular Processes. Infrared X-ray Regime Chem. Rev. 2017, 117, 12165–12226. [Google Scholar] [PubMed]
- Hoffman, D.P.; Mathies, R.A. Femtosecond Stimulated Raman Exposes the Role of Vibrational Coherence in Condensed-Phase Photoreactivity. Acc. Chem. Res. 2016, 49, 616–625. [Google Scholar] [CrossRef] [PubMed]
- Arimondo, E.; Orriols, G. Nonabsorbing atomic coherences by coherent two-photon transitions in a three-level optical pumping. Nuovo Cimento Lett. 1976, 17, 333–338. [Google Scholar] [CrossRef]
- Kowalewski, M.; Bennett, K.; Dorfman, K.E.; Mukamel, S. Catching conical intersections in the act: Monitoring transient electronic coherences by attosecond stimulated X-ray Raman signals. Phys. Rev. Lett. 2015, 115, 193003. [Google Scholar] [CrossRef] [PubMed]
- Jadoun, D.; Zhang, Z.; Kowalewski, M. Raman Spectroscopy of Conical Intersections Using Entangled Photons. J. Phys. Chem. Lett. 2024, 15, 2023–2030. [Google Scholar] [CrossRef] [PubMed]
- Polli, D.; Altoè, P.; Weingart, O.; Spillane, K.M.; Manzoni, C.; Brida, D.; Tomasello, G.; Orlandi, G.; Kukura, P.; Mathies, R.A.; et al. Conical intersection dynamics of the primary photoisomerization event in vision. Nature 2010, 467, 440–443. [Google Scholar] [CrossRef]
- Schnedermann, C.; Liebel, M.; Kukura, P. Mode-Specificity of Vibrationally Coherent Internal Conversion in Rhodopsin during the Primary Visual Event. Am. Chem. Soc. 2015, 137, 2886–2891. [Google Scholar] [CrossRef] [PubMed]
- Zinchenko, K.S.; Ardana-Lamas, F.; Seidu, I.; Neville, S.P.; van der Veen, J.; Lanfaloni, V.U.; Schuurman, M.S.; Wörner, H.J. Sub-7-femtosecond conical-intersection dynamics probed at the carbon K-edge. Science 2021, 371, 489–494. [Google Scholar] [CrossRef]
- Johnson, P.J.M.; Farag, M.H.; Halpin, A.; Morizumi, T.; Prokhorenko, V.I.; Knoester, J.; Jansen, T.L.; Ernst, O.P.; Miller, R.D. The Primary Photochemistry of Vision Occurs at the Molecular Speed Limit. J. Phys. Chem. B 2017, 121, 4040–4047. [Google Scholar] [CrossRef]
- Johnson, P.J.M.; Halpin, A.; Morizumi, T.; Prokhorenko, V.I.; Ernst, O.P.; Miller, R.D. Local vibrational coherences drive the primary photochemistry of vision. Nat. Chem. 2015, 7, 980–986. [Google Scholar] [CrossRef]
- Musser, A.J.; Liebel, M.; Schnedermann, C.; Wende, T.; Kehoe, T.B.; Rao, A.; Kukura, P. Evidence for conical intersection dynamics mediating ultrafast singlet exciton fission. Nat. Phys. 2015, 11, 352–357. [Google Scholar] [CrossRef]
- Duan, H.-G.; Jha, A.; Li, X.; Tiwari, V.; Ye, H.; Nayak, P.K.; Zhu, X.L.; Li, Z.; Martinez, T.J.; Thorwart, M.; et al. Intermolecular vibrations mediate ultrafast singlet fission. Sci. Adv. 2008, 6, abb0052. [Google Scholar] [CrossRef]
- Kukura, P.; McCamant, D.W.; Yoon, S.; Wandschneider, D.B.; Mathies, R.A. Structural Observation of the Primary Isomerization in Vision with Femtosecond-Stimulated Raman. Science 2005, 310, 1006–1009. [Google Scholar] [CrossRef] [PubMed]
- Kuramochi, H.; Tsutsumi, T.; Saita, K.; Wei, Z.; Osawa, M.; Kumar, P.; Liu, L.; Takeuchi, S.; Taketsugu, T.; Tahara, T. Ultrafast Raman observation of the perpendicular intermediate phantom state of stilbene photoisomerization. Nat. Chem. 2024, 16, 22–27. [Google Scholar] [CrossRef] [PubMed]
- Mandal, A.; Ziegler, L.D. Vibrational line shape effects in plasmon-enhanced stimulated Raman spectroscopies. J. Chem. Phys. 2021, 155, 194701. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, S.; Ruhman, S.; Tsuneda, T.; Chiba, M.; Taketsugu, T.; Tahara, T. Spectroscopic Tracking of Structural Evolution in Ultrafast Stilbene Photoisomerization. Science 2008, 322, 1073–1077. [Google Scholar] [CrossRef]
- Frontiera, R.R.; Mathies, R.A. Femtosecond stimulated Raman spectroscopy. Laser Photonics Rev. 2011, 5, 102–113. [Google Scholar] [CrossRef]
- Batignani, G.; Ferrante, C.; Scopigno, T. Accessing excited state molecular vibrations by femtosecond stimulated Raman spectroscopy. J. Phys. Chem. Lett. 2020, 11, 7805–7813. [Google Scholar] [CrossRef]
- Lynch, P.G.; Das, A.; Alam, S.; Rich, C.C.; Frontiera, R.R. Mastering Femtosecond Stimulated Raman Spectroscopy: A Practical Guide. ACS Phys. Chem. Au 2023, 4, 1–18. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, X.; Wolf, T.J.; Li, Z.; Nunes, J.P.F.; Coffee, R.; Cryan, J.P.; Gühr, M.; Hegazy, K.; Heinz, T.F.; et al. Imaging CF3I conical intersection and photodissociation dynamics with ultrafast electron diffraction. Science 2018, 361, 64–67. [Google Scholar] [CrossRef]
- Chen, L.; Gelin, M.F.; Chernyak, V.Y.; Domcke, W.; Zhao, Y. Dissipative dynamics at conical intersections: Simulations with the hierarchy equations of motion method. Faraday Discuss. 2016, 194, 61–80. [Google Scholar] [CrossRef] [PubMed]
- González-Luque, R.; Garavelli, M.; Bernardi, F.; Merchán, M.; Robb, M.A.; Olivucci, M. Computational evidence in favor of a two-state, two-mode model of the retinal chromophore photoisomerization. Proc. Natl. Acad. Sci. USA 2000, 97, 9379–9384. [Google Scholar] [CrossRef]
- Krčmȧř, J.; Gelin, M.F.; Egorova, D.; Domcke, W. Signatures of conical intersections in two-dimensional electronic spectra. J. Phys. B 2014, 47, 124019. [Google Scholar] [CrossRef]
- Chen, L.; Gelin, M.F.; Zhao, Y.; Domcke, W. Mapping of Wave Packet Dynamics at Conical Intersections by Time- and Frequency-Resolved Fluorescence Spectroscopy: A Computational Study. J. Phys. Chem. Lett. 2019, 10, 5873–5880. [Google Scholar] [CrossRef] [PubMed]
- Qi, D.L.; Duan, H.G.; Sun, Z.R.; Miller, R.J.; Thorwart, M. Tracking an electronic wave packet in the vicinity of a conical intersection. J. Chem. Phys. 2017, 147, 074101. [Google Scholar] [CrossRef]
- Duan, H.G.; Qi, D.L.; Sun, Z.R.; Miller, R.D.; Thorwart, M. Signature of the geometric phase in the wave packet dynamics on hypersurfaces. Chem. Phys. 2018, 515, 21–27. [Google Scholar] [CrossRef]
- Duan, H.-G.; Thorwart, M. Quantum Mechanical Wave Packet Dynamics at a Conical Intersection with Strong Vibrational Dissipation. J. Phys. Chem. Lett. 2016, 7, 382–386. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.-G.; Miller, R.J.D.; Thorwart, M. Impact of Vibrational Coherence on the Quantum Yield at a Conical Intersection. J. Phys. Chem. Lett. 2016, 7, 3491–3496. [Google Scholar] [CrossRef]
- Timmers, H.; Zhu, X.; Li, Z.; Kobayashi, Y.; Sabbar, M.; Hollstein, M.; Reduzzi, M.; Martínez, T.J.; Neumark, D.M.; Leone, S.R. Disentangling conical intersection and coherent molecular dynamics in methyl bromide with attosecond transient absorption spectroscopy. Nat. Commun. 2019, 10, 3133. [Google Scholar] [CrossRef]
- Keefer, D.; Freixas, V.M.; Song, H.; Tretiak, S.; Fernandez-Alberti, S.; Mukamel, S. Monitoring molecular vibronic coherences in a bichromophoric molecule by ultrafast X-ray spectroscopy. Chem. Sci. 2021, 12, 5286–5294. [Google Scholar] [CrossRef]
- Hosseinizadeh, A.; Breckwoldt, N.; Fung, R.; Sepehr, R.; Schmidt, M.; Schwander, P.; Santra, R.; Ourmazd, A. Few-fs resolution of a photoactive protein traversing a conical intersection. Nature 2021, 599, 697–701. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, X.F.; Nunes, J.P.; Yu, J.K.; Parrish, R.M.; Wolf, T.J.; Centurion, M.; Gühr, M.; Li, R.; Liu, Y.; et al. Simultaneous observation of nuclear and electronic dynamics by ultrafast electron diffraction. Science 2020, 368, 885–889. [Google Scholar] [CrossRef]
- Nam, Y.; Keefer, D.; Nenov, A.; Conti, I.; Aleotti, F.; Segatta, F.; Lee, J.Y.; Garavelli, M.; Mukamel, S. Conical Intersection Passages of Molecules Probed by X-ray Diffraction and Stimulated Raman Spectroscopy. J. Phys. Chem. Lett. 2021, 12, 12300–12309. [Google Scholar] [CrossRef] [PubMed]
- von Conta, A.; Tehlar, A.; Schletter, A.; Arasaki, Y.; Takatsuka, K.; Wörner, H.J. Conical-intersection dynamics and ground-state chemistry probed by extreme-ultraviolet time-resolved photoelectron spectroscopy. Nat. Commun. 2018, 9, 3162. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenko, V.I.; Nagy, A.M.; Waschuk, S.A.; Brown, L.S.; Birge, R.R.; Miller, R.D. Coherent control of retinal isomerization in bacteriorhodopsin. Science 2006, 313, 1257–1261. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Doblhoff-Dier, K.; Roither, S.; Schöffler, M.S.; Kartashov, D.; Xu, H.; Rathje, T.; Paulus, G.G.; Baltuška, A.; Gräfe, S.; et al. Attosecond-recollision-controlled selective fragmentation of polyatomic molecules. Phys. Rev. Lett. 2012, 109, 243001. [Google Scholar] [CrossRef] [PubMed]
- Levin, L.; Skomorowski, W.; Rybak, L.; Kosloff, R.; Koch, C.P.; Amitay, Z. Coherent control of bond making. Phys. Rev. Lett. 2015, 114, 233003. [Google Scholar] [CrossRef]
- Cerullo, G.; Bardeen, C.J.; Wang, Q.; Shank, C.V. High-power femtosecond chirped pulse excitation of molecules in solution. Chem. Phys. Lett. 1996, 262, 362–368. [Google Scholar] [CrossRef]
- Batignani, G.; Sansone, C.; Ferrante, C.; Fumero, G.; Mukamel, S.; Scopigno, T. Excited-state energy surfaces in molecules revealed by impulsive stimulated Raman excitation profiles. J. Phys. Chem. Lett. 2021, 12, 9239–9247. [Google Scholar] [CrossRef]
- Batignani, G.; Mai, E.; Fumero, G.; Mukamel, S.; Scopigno, T. Absolute excited state molecular geometries revealed by resonance Raman signals. Nat. Commun. 2022, 13, 7770. [Google Scholar] [CrossRef]
- May, V.; Kühn, O. Charge and Energy Transfer Dynamics in Molecular Systems; John Wiley and Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Gelin, M.F.; Egorova, D.; Domcke, W. Efficient method for the calculation of time- and frequency-resolved four-wave mixing signals and its application to photon-echo spectroscopy. J. Chem. Phys. 2005, 123, 164112. [Google Scholar] [CrossRef] [PubMed]
- Gelin, M.F.; Egorova, D.; Domcke, W. Optical N-Wave-Mixing Spectroscopy with Strong and Temporally Well-Separated Pulses: The Doorway-Window Representation. J. Phys. Chem. B 2011, 115, 5648–5658. [Google Scholar] [CrossRef] [PubMed]
- Kleinekathöfer, U. Non-Markovian theories based on a decomposition of the spectral density. J. Chem. Phys. 2004, 121, 2505–2514. [Google Scholar] [CrossRef] [PubMed]
- Meier, C.; Tannor, D.J. Non-Markovian evolution of the density operator in the presence of strong laser fields. J. Chem. Phys. 1999, 111, 3365–3376. [Google Scholar] [CrossRef]


| DQY | Duration | 2 fs | 3 fs | 4 fs |
|---|---|---|---|---|
| Pulse Shape | ||||
| Line type 1 | 2.43% | 5.03% | 6.83% | |
| Line type 2 | 3.38% | 6.88% | 3.92% | |
| Line type 3 | 2.15% | 4.46% | 6.77% | |
| Line type 4 | 2.80% | 5.63% | 5.96% | |
| Line type 5 | 3.80% | 6.98% | 2.41% | |
| Line type 6 | 1.55% | 2.30% | 1.26% | |
| Line type 7 | 1.09% | 2.06% | 3.00% | |
| Line type 8 | 1.82% | 3.44% | 4.68% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Q.; Yu, J.; Duan, H.; He, H. The Impact of Pulse Shaping on Coherent Dynamics near a Conical Intersection. Photonics 2024, 11, 511. https://doi.org/10.3390/photonics11060511
Deng Q, Yu J, Duan H, He H. The Impact of Pulse Shaping on Coherent Dynamics near a Conical Intersection. Photonics. 2024; 11(6):511. https://doi.org/10.3390/photonics11060511
Chicago/Turabian StyleDeng, Qici, Junjie Yu, Hongguang Duan, and Hongxing He. 2024. "The Impact of Pulse Shaping on Coherent Dynamics near a Conical Intersection" Photonics 11, no. 6: 511. https://doi.org/10.3390/photonics11060511
APA StyleDeng, Q., Yu, J., Duan, H., & He, H. (2024). The Impact of Pulse Shaping on Coherent Dynamics near a Conical Intersection. Photonics, 11(6), 511. https://doi.org/10.3390/photonics11060511






