An Effective Model for Capturing the Role of Excitonic Interactions in the Wave-Packet Dynamics of DNA Nucleobases
Abstract
1. Introduction
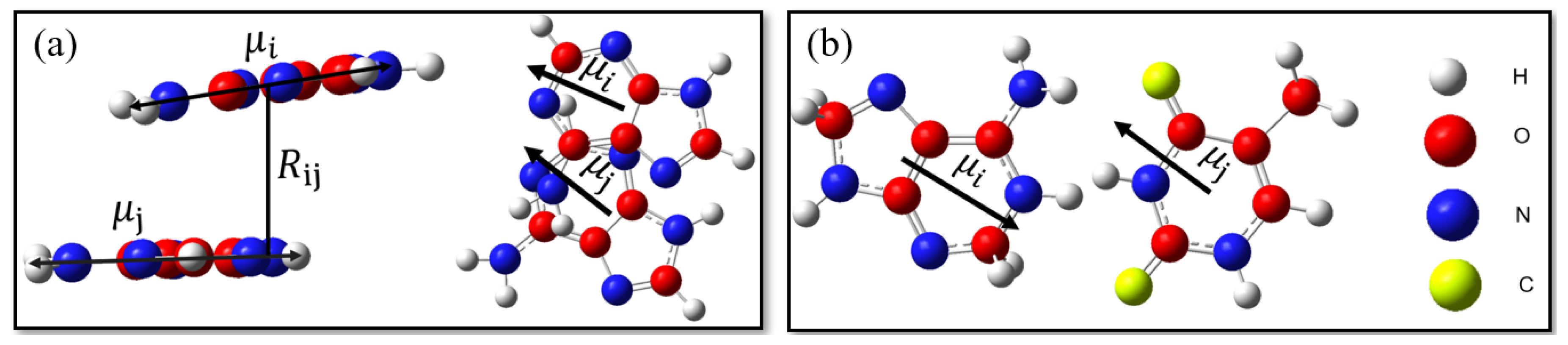
2. Materials and Methods
3. Results
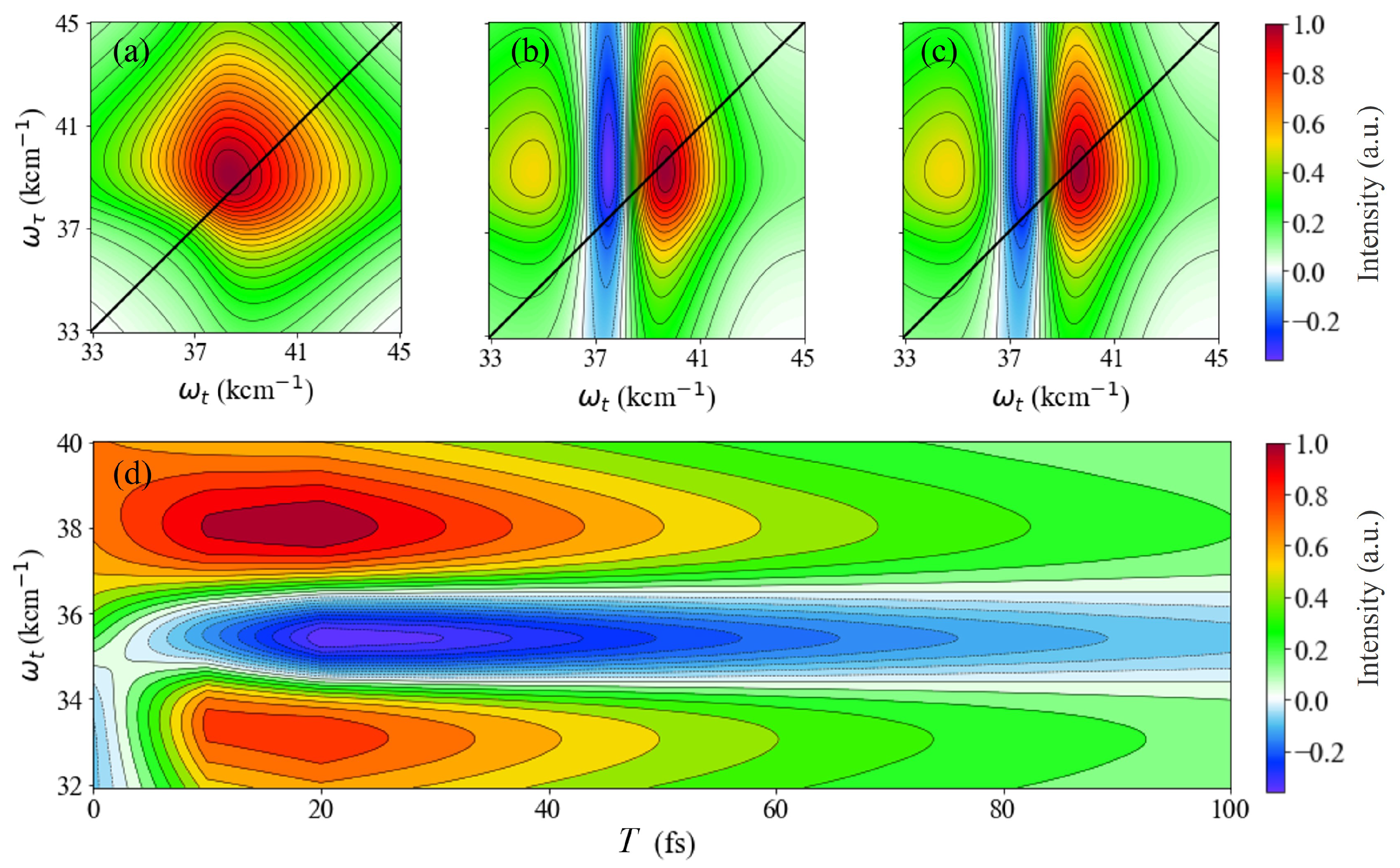
3.1. The 2D Electron Spectra of DNA Bases
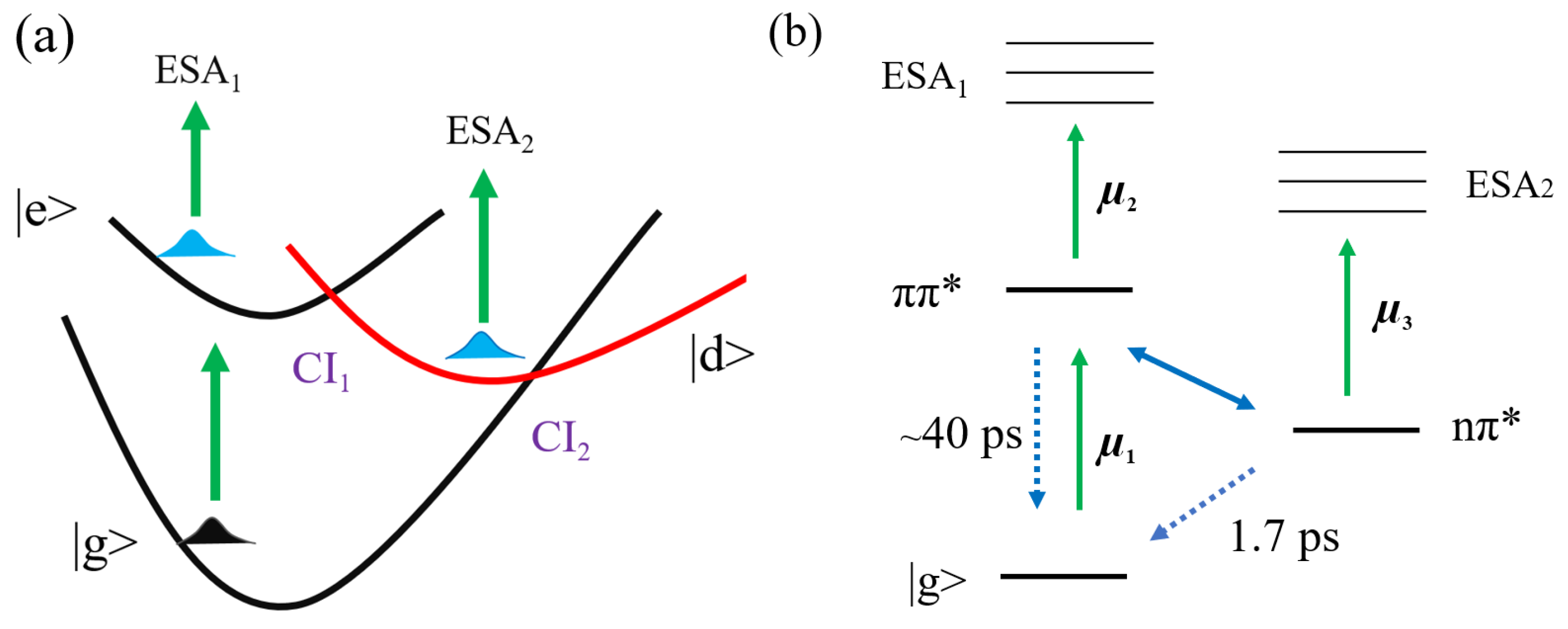
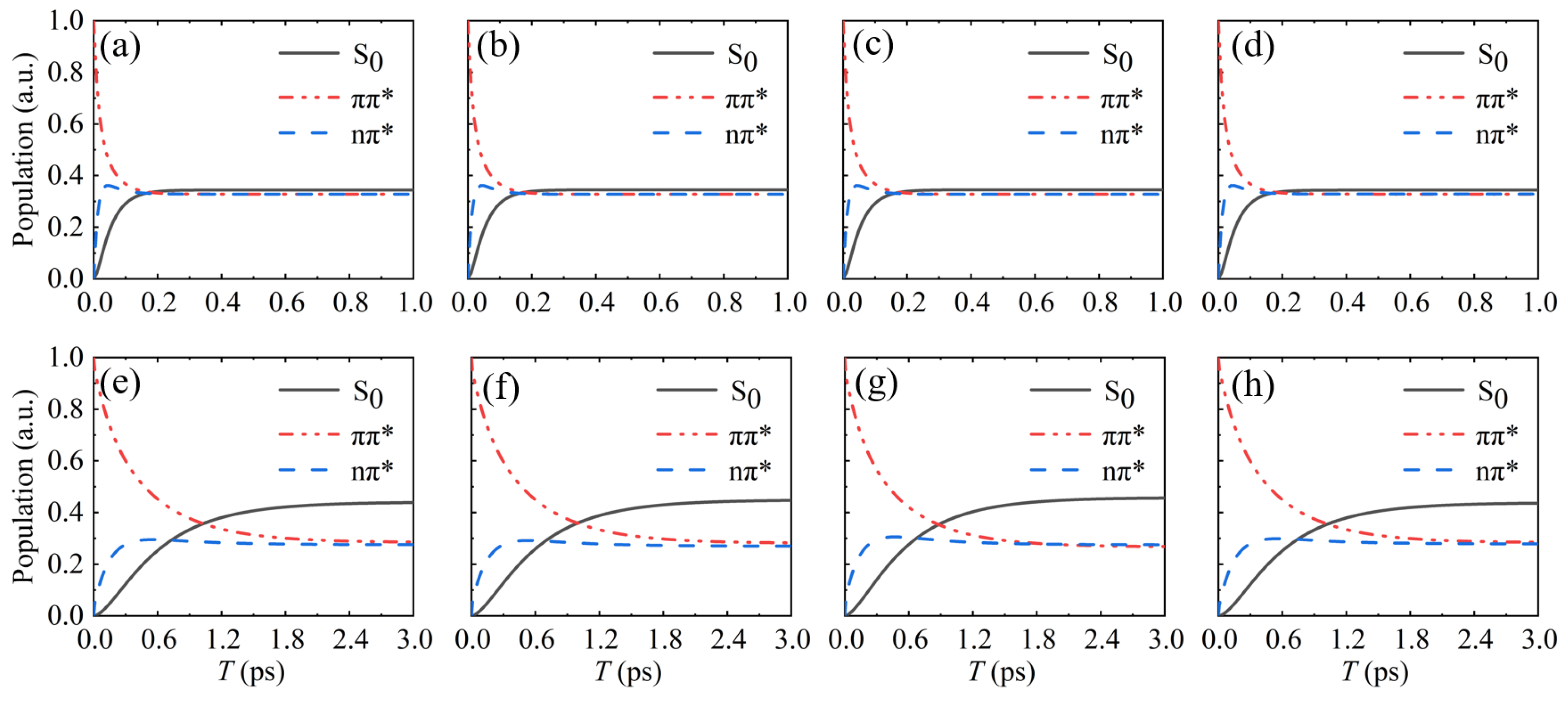
3.2. Impact of Base Stacking on Population Transfer in Nucleobases
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Phase Matching Approach
Appendix B. The Hierarchy Equations of Motion
References
- Crespo-Hernández, C.E.; Cohen, B.; Hare, P.M.; Kohler, B. Ultrafast excited-state dynamics in nucleic acids. Chem. Rev. 2004, 104, 1977–2019. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Lan, Z.; Thiel, W. Computational modeling of photoexcitation in DNA single and double strands. In Photoinduced Phenomena in Nucleic Acids II; DNA Fragments and Phenomenological Aspects; Springer: Cham, Switzerland, 2015; pp. 89–122. [Google Scholar]
- Barbatti, M.; Borin, A.C. Photoinduced Phenomena in Nucleic Acids II: DNA Fragments and Phenomenological Aspects; Springer: Cham, Switzerland, 2015; ISBN 9783319132723. [Google Scholar]
- Gray, H.B. Charge Transfer in DNA: From Mechanism to Application; John Wiley Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Middleton, C.T.; de La Harpe, K.; Su, C.; Law, Y.K.; Crespo-Hernández, C.E.; Kohler, B. DNA excited-state dynamics: From single bases to the double helix. Annu. Rev. Phys. Chem. 2009, 60, 217–239. [Google Scholar] [CrossRef] [PubMed]
- Keefer, D.; Schnappinger, T.; de Vivie-Riedle, R.; Mukamel, S. Visualizing conical intersection passages via vibronic coherence maps generated by stimulated ultrafast X-ray Raman signals. Proc. Natl. Acad. Sci. USA 2020, 117, 24069–24075. [Google Scholar] [CrossRef] [PubMed]
- Barbatti, M.; Aquino, A.J.A.; Szymczak, J.J.; Nachtigallová, D.; Hobza, P.; Lischka, H. Relaxation mechanisms of UV-photoexcited DNA and RNA nucleobases. Proc. Natl. Acad. Sci. USA 2010, 107, 21453–21458. [Google Scholar] [CrossRef] [PubMed]
- Domcke, W.; Yarkony, D.R. Role of conical intersections in molecular spectroscopy and photoinduced chemical dynamics. Annu. Rev. Phys. Chem. 2012, 63, 325–352. [Google Scholar] [CrossRef] [PubMed]
- Domcke, W.; Yarkony, D.R. Köppel, H. Conical Intersections: Theory, Computation and Experiment; World Scientific: Singapore, 2011; Volume 17. [Google Scholar]
- Domcke, W.; Yarkony, D.R.; Köppel, H. Electronic Structure, Dynamics and Spectroscopy; World Scientific: Singapore, 2004. [Google Scholar]
- Crespo-Otero, R.; Barbatti, M. Recent Advances and Perspectives on Nonadiabatic Mixed Quantum-Classical Dynamics. Chem. Rev. 2018, 118, 7026–7068. [Google Scholar] [CrossRef] [PubMed]
- Crespo-Hernández, C.E.; Cohen, B.; Kohler, B. Base stacking controls excited-state dynamics in A.T DNA. Nature 2005, 436, 1141–1144. [Google Scholar] [CrossRef] [PubMed]
- Markovitsi, D.; Talbot, F.; Gustavsson, T.; Onidas, D.; Lazzarotto, E.; Marguet, S. Molecular spectroscopy: Complexity of excited-state dynamics in DNA. Nature 2006, 441, E7; discussion E8. [Google Scholar] [CrossRef] [PubMed]
- Fujitsuka, M.; Majima, T. Charge transfer dynamics in DNA revealed by time-resolved spectroscopy. Chem. Sci. 2017, 8, 1752–1762. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenko, V.I.; Picchiotti, A.; Pola, M.; Dijkstra, A.G.; Miller, R.J.D. New Insights into the Photophysics of DNA Nucleobases. J. Phys. Chem. Lett. 2016, 7, 4445–4450. [Google Scholar] [CrossRef] [PubMed]
- Picchiotti, A.; Nenov, A.; Giussani, A.; Prokhorenko, V.I.; Miller, R.J.D.; Mukamel, S.; Garavelli, M. Pyrene, a Test Case for Deep-Ultraviolet Molecular Photophysics. J. Phys. Chem. Lett. 2019, 10, 3481–3487. [Google Scholar] [CrossRef] [PubMed]
- Kleinermanns, K.; Nachtigallová, D.; de Vries, M.S. Excited state dynamics of DNA bases. Int. Rev. Phys. Chem. 2013, 32, 308–342. [Google Scholar] [CrossRef]
- Conti, I.; Nenov, A.; Höfinger, S. Excited state evolution of DNA stacked adenines resolved at the CASPT2//CASSCF/Amber level: From the bright to the excimer state and back. Phys. Chem. Chem. Phys. 2015, 17, 7291–7302. [Google Scholar] [CrossRef] [PubMed]
- Borrego-Varillas, R.; Nenov, A.; Kabaciński, P.; Conti, I.; Ganzer, L.; Oriana, A.; Jaiswal, V.K.; Delfino, I.; Weingart, O.; Manzoni, C.; et al. Tracking excited state decay mechanisms of pyrimidine nucleosides in real time. Nat. Commun. 2021, 12, 7285. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, A.G.; Prokhorenko, V.I. Simulation of photo-excited adenine in water with a hierarchy of equations of motion approach. J. Chem. Phys. 2017, 147, 64102. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, A.; Tanimura, Y. Quantum Dynamics of System Strongly Coupled to Low-Temperature Colored Noise Bath: Reduced Hierarchy Equations Approach. J. Phys. Soc. Jpn. 2005, 74, 3131–3134. [Google Scholar] [CrossRef]
- Tanimura, Y. Reduced hierarchy equations of motion approach with Drude plus brownian spectral distribution: Probing electron transfer processes by means of two-dimensional correlation spectroscopy. J. Chem. Phys. 2012, 137, 22A550. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.-G.; Thorwart, M. Quantum Mechanical Wave Packet Dynamics at a Conical Intersection with Strong Vibrational Dissipation. J. Phys. Chem. Lett. 2016, 7, 382–386. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.-G.; Miller, R.J.D.; Thorwart, M. Impact of Vibrational Coherence on the Quantum Yield at a Conical Intersection. J. Phys. Chem. Lett. 2016, 7, 3491–3496. [Google Scholar] [CrossRef]
- Qi, D.-L.; Duan, H.-G.; Sun, Z.-R.; Miller, R.J.D.; Thorwart, M. Tracking an electronic wave packet in the vicinity of a conical intersection. J. Chem. Phys. 2017, 147, 74101. [Google Scholar] [CrossRef]
- Tuna, D.; Sobolewski, A.L.; Domcke, W. Mechanisms of ultrafast excited-state deactivation in adenosine. J. Phys. Chem. A 2014, 118, 122–127. [Google Scholar] [CrossRef] [PubMed]
- Perun, S.; Sobolewski, A.L.; Domcke, W. Ab initio studies on the radiationless decay mechanisms of the lowest excited singlet states of 9H-adenine. J. Am. Chem. Soc. 2005, 127, 6257–6265. [Google Scholar] [CrossRef] [PubMed]
- Rozenman, G.G.; Peisakhov, A.; Zadok, N. Dispersion of organic exciton polaritons—A novel undergraduate experiment. Eur. J. Phys. 2022, 43, 35301. [Google Scholar] [CrossRef]
- Roller, E.-M.; Argyropoulos, C.; Högele, A.; Liedl, T.; Pilo-Pais, M. Plasmon-Exciton Coupling Using DNA Templates. Nano Lett. 2016, 16, 5962–5966. [Google Scholar] [CrossRef] [PubMed]
- Khalil, M.; Tokmakoff, A. Signatures of vibrational interactions in coherent two-dimensional infrared spectroscopy. Chem. Phys. 2001, 266, 213–230. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Jha, A.; Liang, X.-T.; Thorwart, M.; Dwayne Miller, R.J.; Duan, H.-G. Disentangling the complexity of coupled vibrations by two-dimensional electronic-vibrational spectroscopy. J. Phys. B At. Mol. Opt. Phys. 2023, 56, 145001. [Google Scholar] [CrossRef]
- Kistler, K.A.; Spano, F.C.; Matsika, S. A benchmark of excitonic couplings derived from atomic transition charges. J. Phys. Chem. B 2013, 117, 2032–2044. [Google Scholar] [CrossRef] [PubMed]
- Tsuchimoto, M.; Tanimura, Y. Spins Dynamics in a Dissipative Environment: Hierarchal Equations of Motion Approach Using a Graphics Processing Unit (GPU). J. Chem. Theory Comput. 2015, 11, 3859–3865. [Google Scholar] [CrossRef]
- Kramer, T.; Noack, M.; Reinefeld, A.; Rodríguez, M.; Zelinskyy, Y. Efficient calculation of open quantum system dynamics and time-resolved spectroscopy with distributed memory HEOM (DM-HEOM). J. Comput. Chem. 2018, 39, 1779–1794. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, T.; Jha, A.; Zhang, P.-P.; Duan, H.-G. An Effective Model for Capturing the Role of Excitonic Interactions in the Wave-Packet Dynamics of DNA Nucleobases. Photonics 2024, 11, 566. https://doi.org/10.3390/photonics11060566
Guan T, Jha A, Zhang P-P, Duan H-G. An Effective Model for Capturing the Role of Excitonic Interactions in the Wave-Packet Dynamics of DNA Nucleobases. Photonics. 2024; 11(6):566. https://doi.org/10.3390/photonics11060566
Chicago/Turabian StyleGuan, Tong, Ajay Jha, Pan-Pan Zhang, and Hong-Guang Duan. 2024. "An Effective Model for Capturing the Role of Excitonic Interactions in the Wave-Packet Dynamics of DNA Nucleobases" Photonics 11, no. 6: 566. https://doi.org/10.3390/photonics11060566
APA StyleGuan, T., Jha, A., Zhang, P.-P., & Duan, H.-G. (2024). An Effective Model for Capturing the Role of Excitonic Interactions in the Wave-Packet Dynamics of DNA Nucleobases. Photonics, 11(6), 566. https://doi.org/10.3390/photonics11060566




