Integrated Photonic Passive Building Blocks on Silicon-on-Insulator Platform
Abstract
1. Introduction
- Coupling with external fibers.
- Splitting devices.
- Filtering and phase shifting during transmission.
2. Coupling with External Fiber
- Edge Coupling: Referred to as “in-plane”, “end-fire”, or “butt” coupling. Involves directing the light beam in/out of the waveguide through the lateral sides, ensuring propagation in the same plane. It requires high-quality optical facets on the chip sides to achieve efficient coupling (typically exceeding 80%) with minimal polarization dependence.
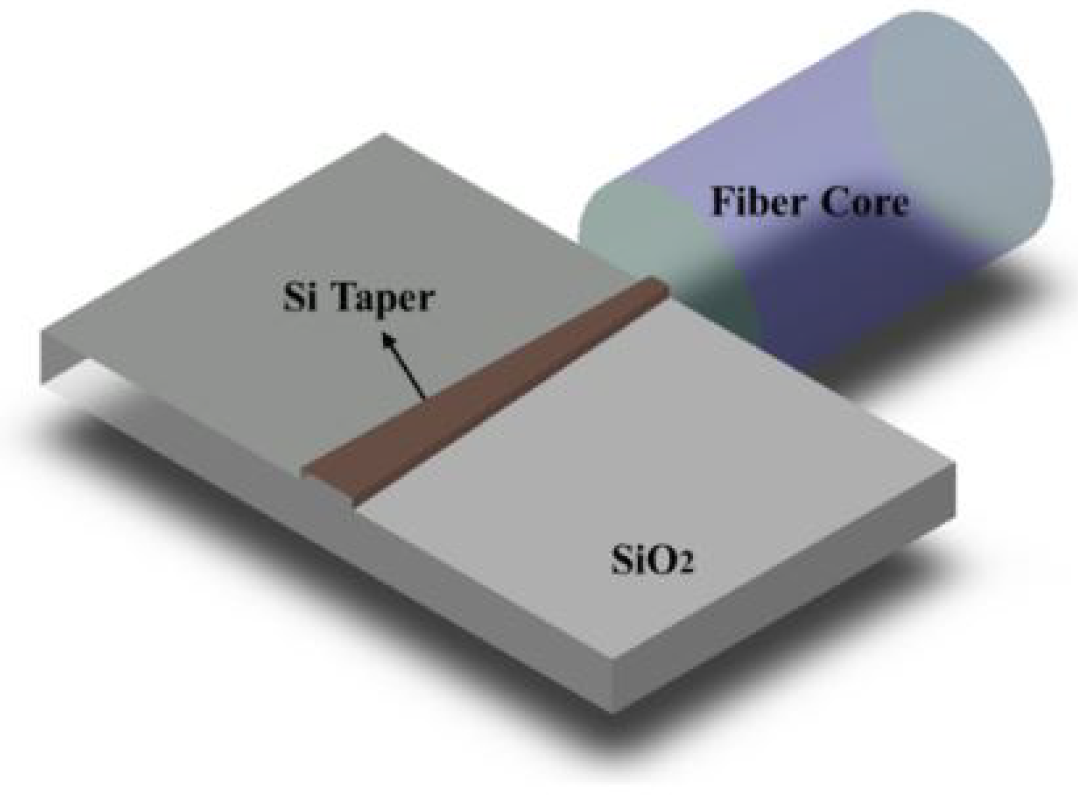
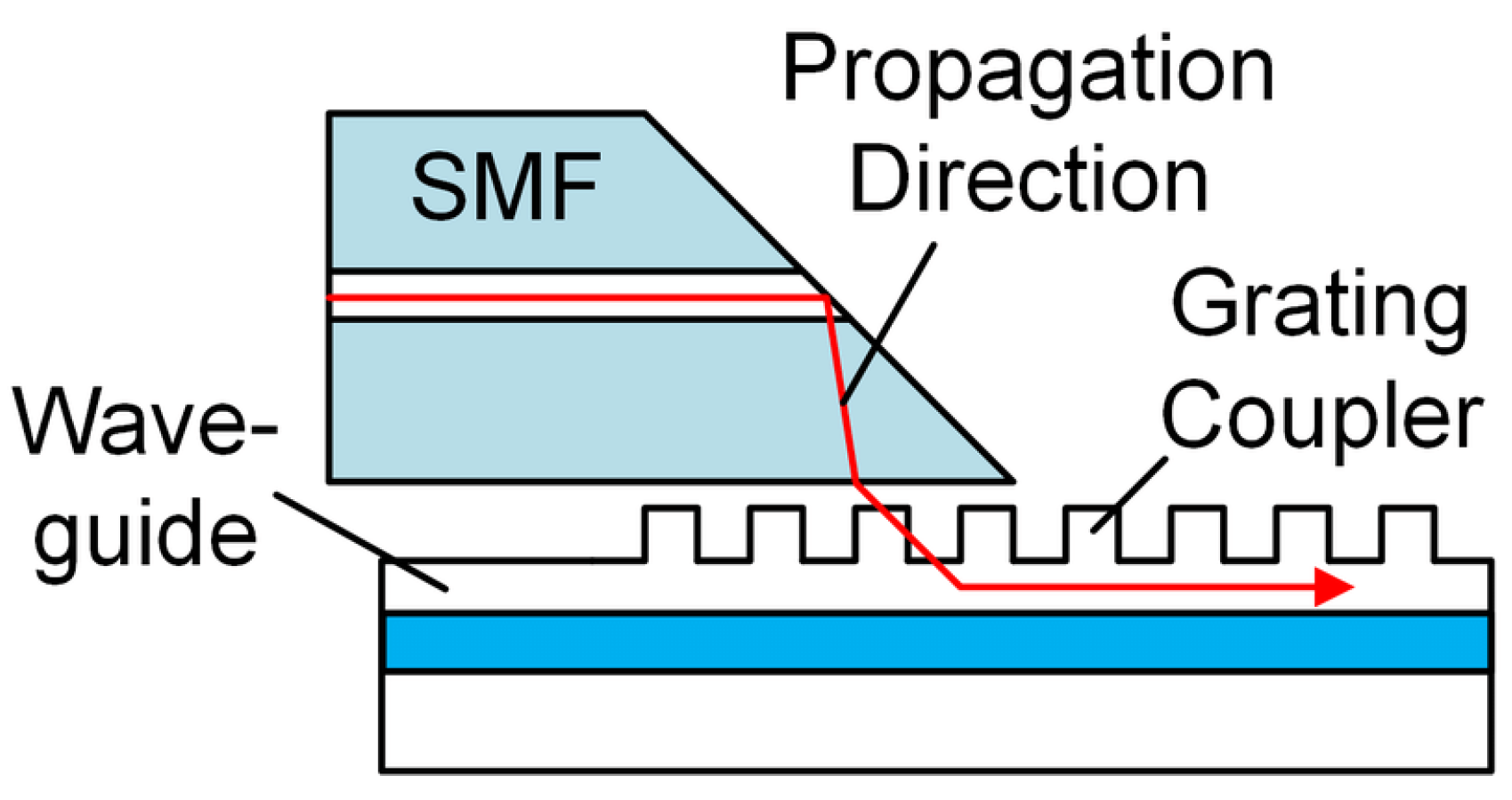
- Vertical Coupling: In this approach, the light beam is directed onto the top surface of the silicon chip (or the bottom if necessary). A specially designed coupling structure alters the k-vector direction, facilitating the coupling of light into the integrated waveguide. The widely adopted vertical coupling solution relies on diffractive gratings, which are known for their relaxed positioning tolerances, ease of lithographic fabrication, and suitability for multi-point wafer characterizations. However, the simplest forms of these structures inherently exhibit sensitivity to polarization and wavelength, necessitating careful design and optimization to mitigate these limitations. Vertical coupling ensures greater positioning independence at the cost of higher losses. It also enables coupling on the chip surface, facilitating coupling at any point without the need to enter and exit from the edges.
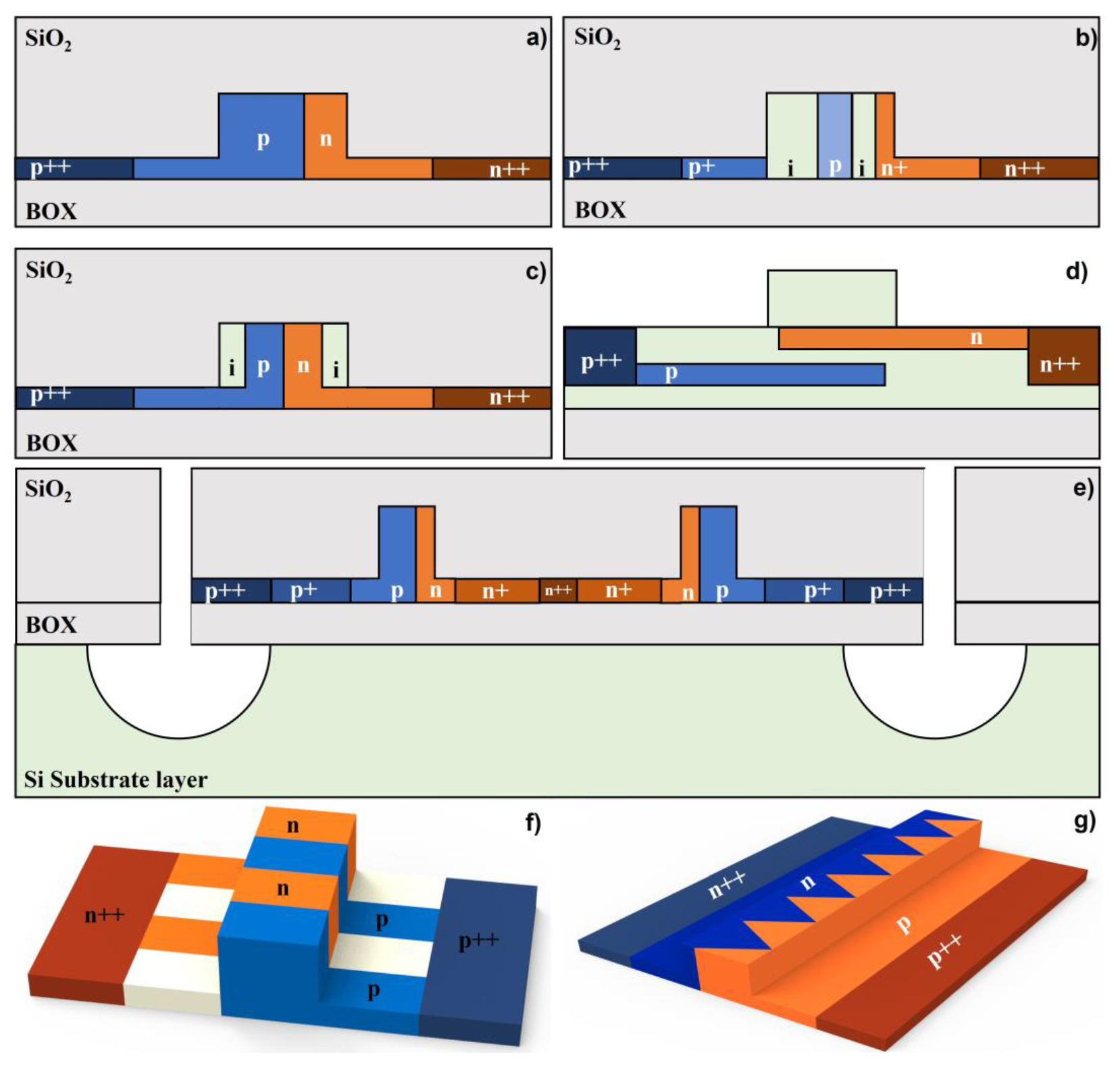
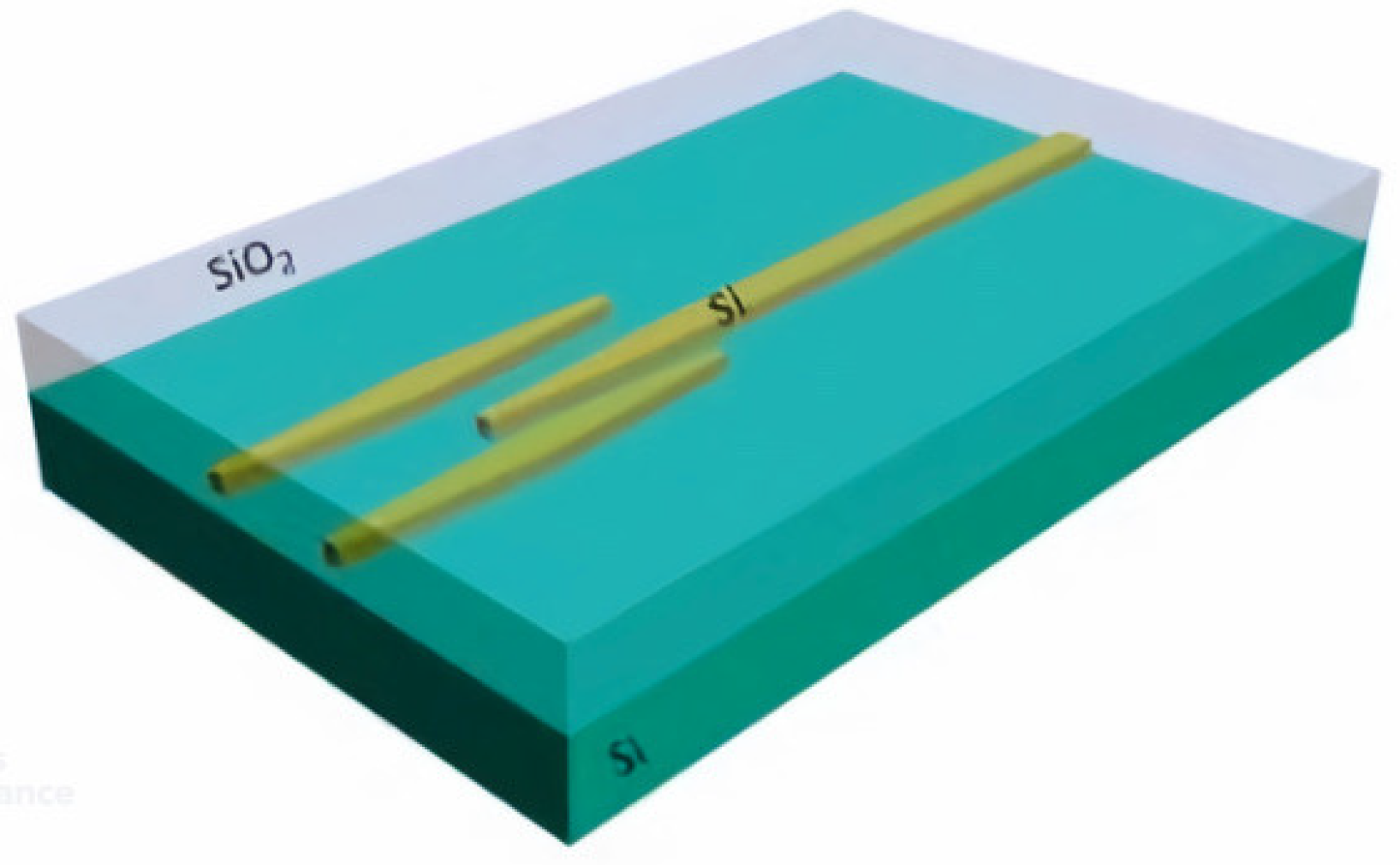
2.1. Edge Coupling
2.1.1. Structural Profiles of Inverse Tapers
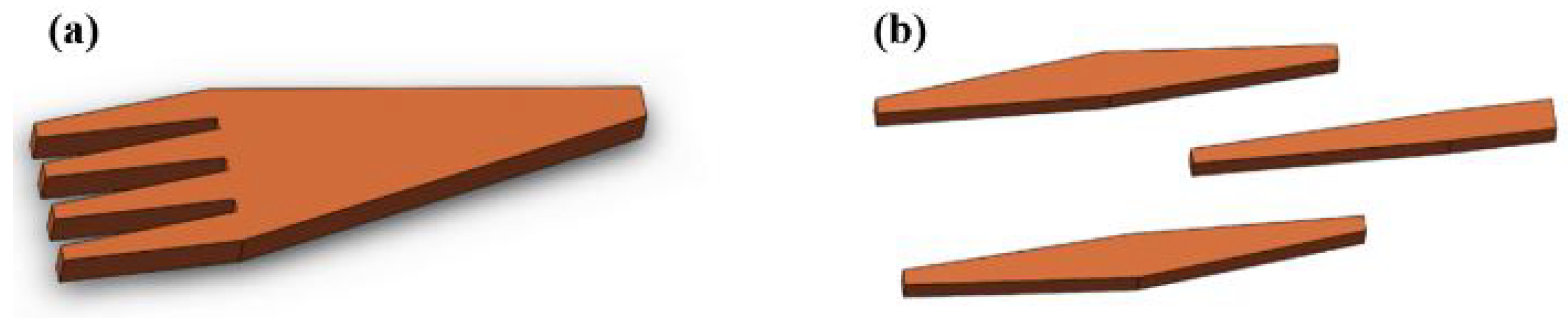
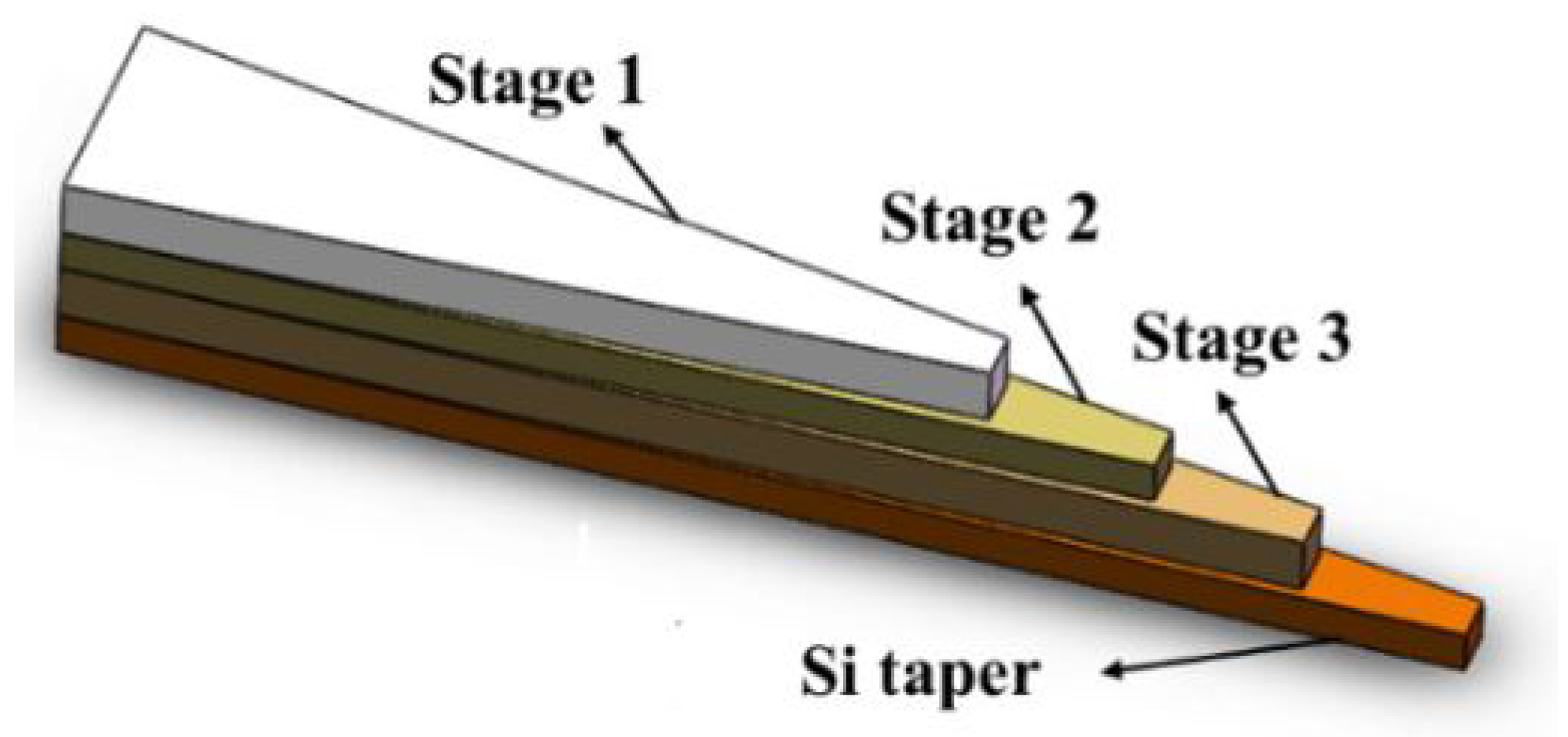
2.1.2. Multi-Tip Tapers and Multiple Tapers
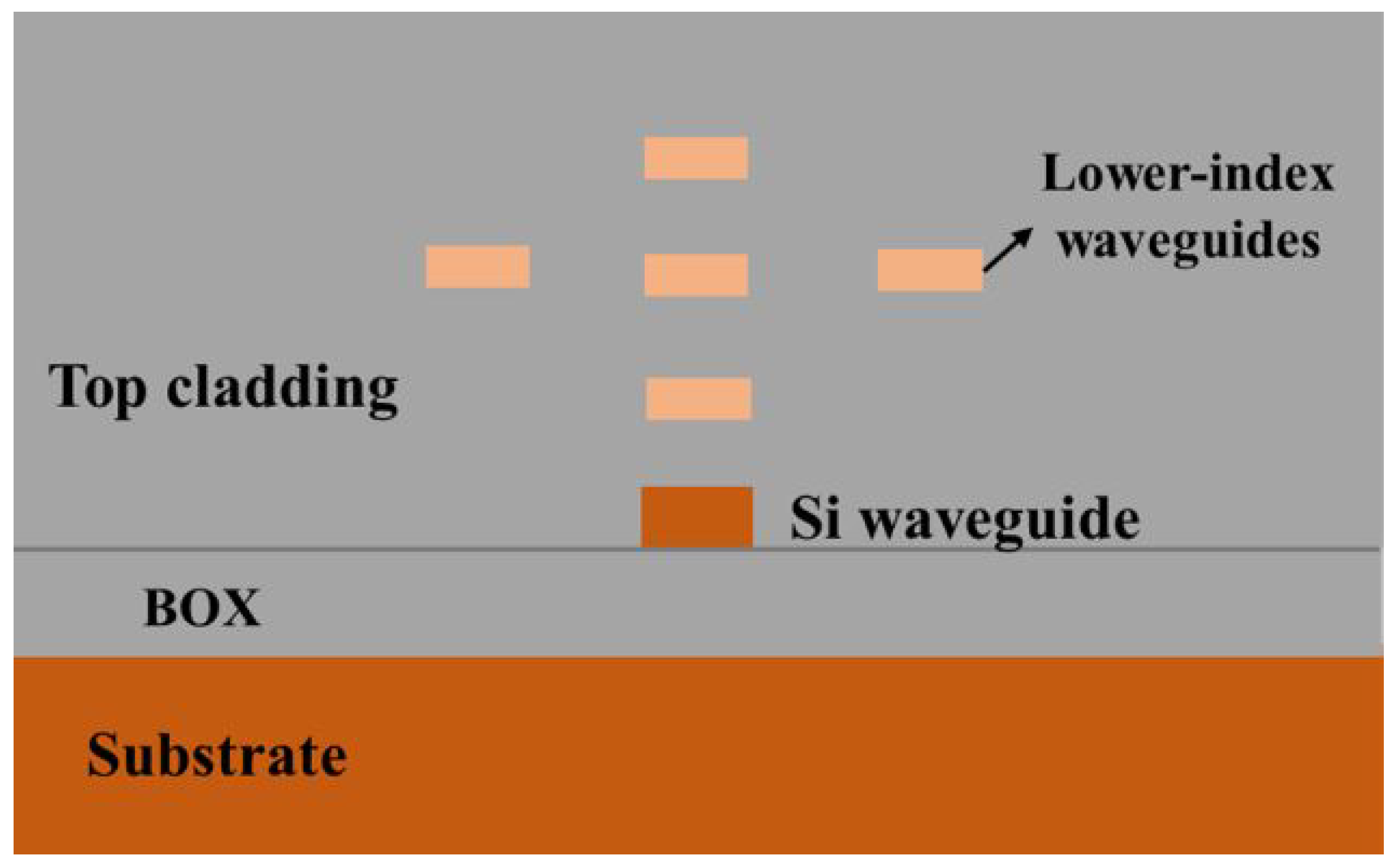
2.1.3. Vertical Multi-Layer Edge Couplers
| Edge C. Configuration | Coupling Loss (dB) | Polarization | Size (µm) | Manufacturing Process |
|---|---|---|---|---|
| Taper with linear profile [25] | 1.37/2.13 | TE/TM | 250/200 | simple |
| Taper with exponential | ||||
| profile [25] | 1.37/2.12 | TE/TM | 170/140 | simple |
| Taper with quadratic profile [25] | 1.39/1.87 | TE/TM | 170/150 | simple |
| Edge double-tip inverse | ||||
| taper [31] | 1.10/1.52 | TE/TM | 40 | intermediate |
| Trident edge coupler [34] | <1.5/<1.7 | TE/TM | 300 | intermediate |
| Trident edge coupler [34] | <1.5/<1.7 | TE/TM | 300 | intermediate |
| GRIN waveguide with a 2D inverse taper [59] | 0.29/0.27 | TE/TM | 300 | very hard |
| Silicon nitride spot size converter [60] | 0.18 | TE | 600 | medium |
| Nano-taper coupler cladded with SU8 cladding [50] | 0.5/0.9 | TE/TM | 300 | simple but expensive |
| Compact cantilever | ||||
| coupler [62] | 0.62/0.50 | TE/TM | 7 | very hard |
| Sustainable 3D edge couplers [58] | 0.70/1.34 | TE/TM | 55 | hard |
| 0.80/1.60 | ||||
| 1.00/1.14 | ||||
| Buried 3D spot size | ||||
| converter [57] | 0.54 | TE | 100 | very hard |
2.2. Vertical Coupling
2.2.1. Parameters of Grating Couplers’ Structures
2.2.2. Coupling Strategies
2.2.3. Multi-Layer Grating Coupler
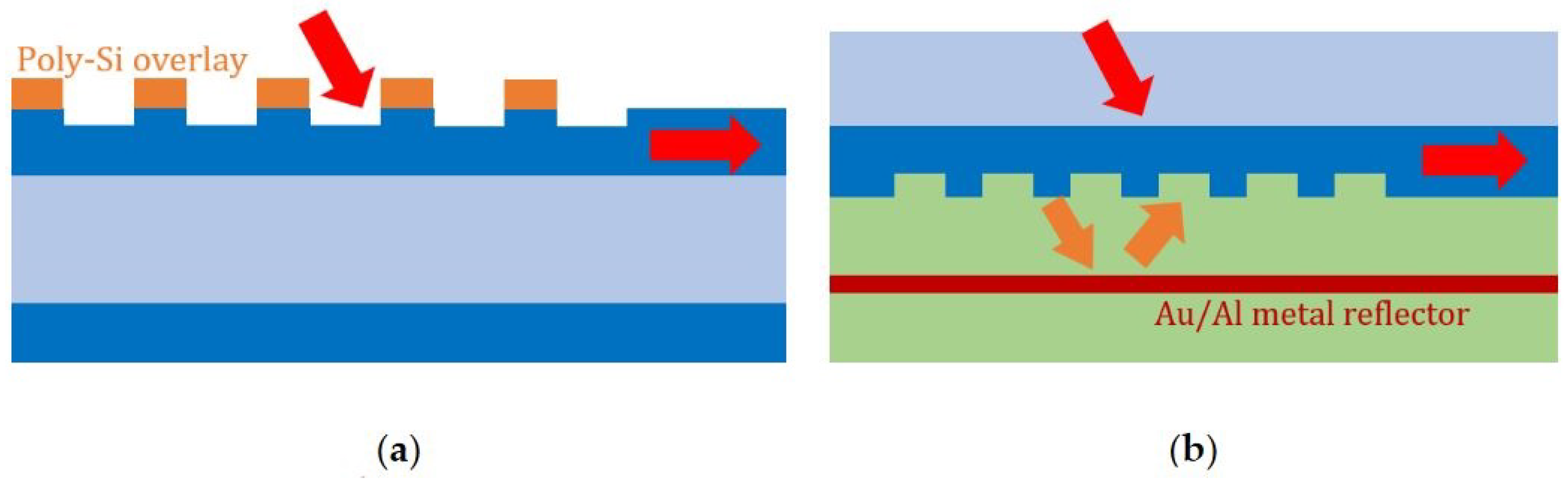
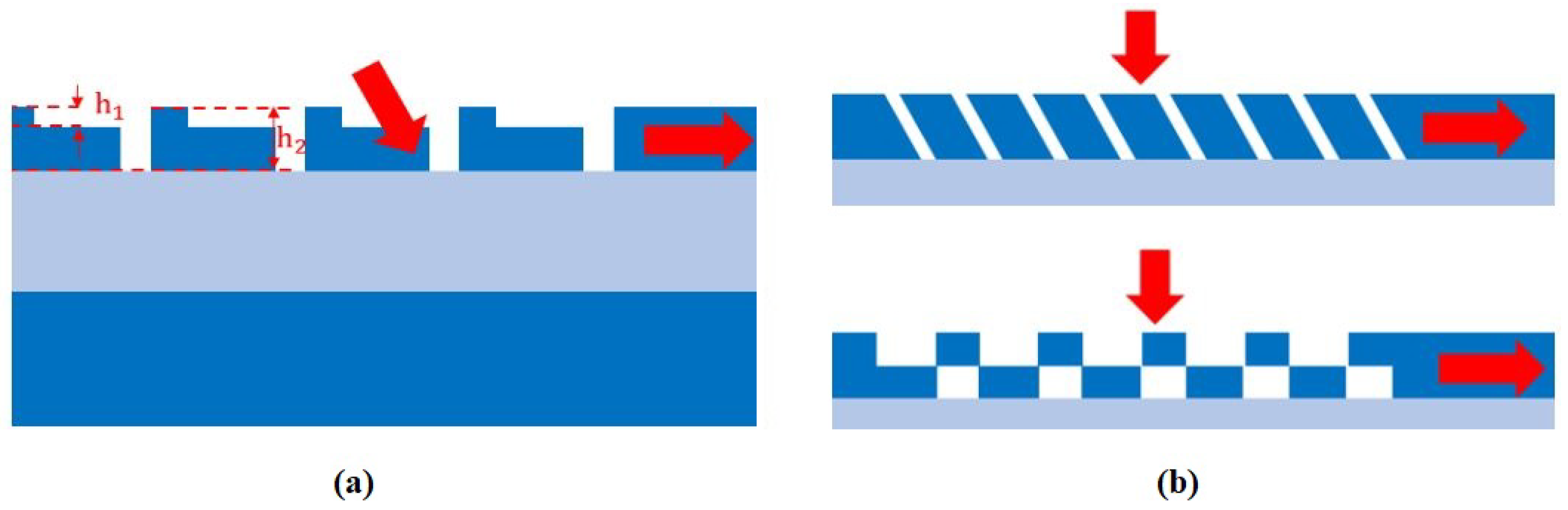
2.2.4. Grating Structural Innovations
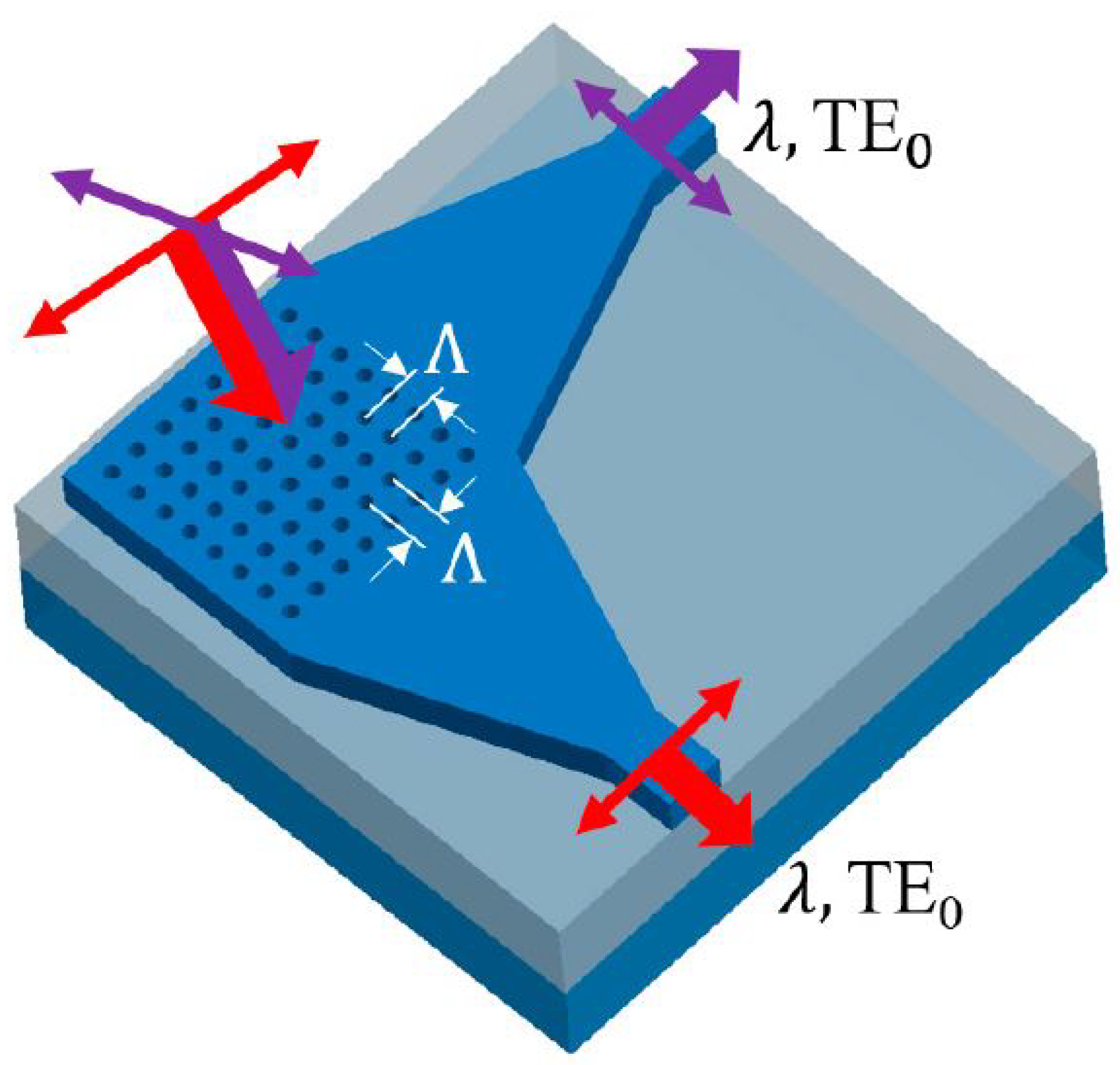
2.2.5. Two-Dimensional Grating Couplers
| Grating C. Configuration | Experimental C. Loss (dB) | Polarization | Bandwidth | To Be Modified |
|---|---|---|---|---|
| Shallow etched grating coupler [73] | 3.1 | TE | 44 nm 1 dB | simple |
| Poly-Si overlay [69] | 1.6 | TE | 33 nm 1 dB | simple |
| Non-uniform shallow etch depth 70 nm [82] | 0.8 | TE | 75 nm 3 dB | simple |
| GC dual band // demultiplexer [83] | 4.9 | TE | 81 nm 3 dB | intermediate |
| Slanted grating couplers fabricated by FIB [79] | 3.32 | TE | 80 nm 3 dB | intermediate |
| Grating couplers with backside metal mirrors [72] | 0.5 | TE | 40 nm 1 dB | very hard |
| Double etch L-shaped grating [75] | 2.7 | TE | 62 nm 3 dB | simple but expensive |
| Apodized shallow grating coupler [74] | 2.7 | TE | 41 nm 1 dB | very hard |
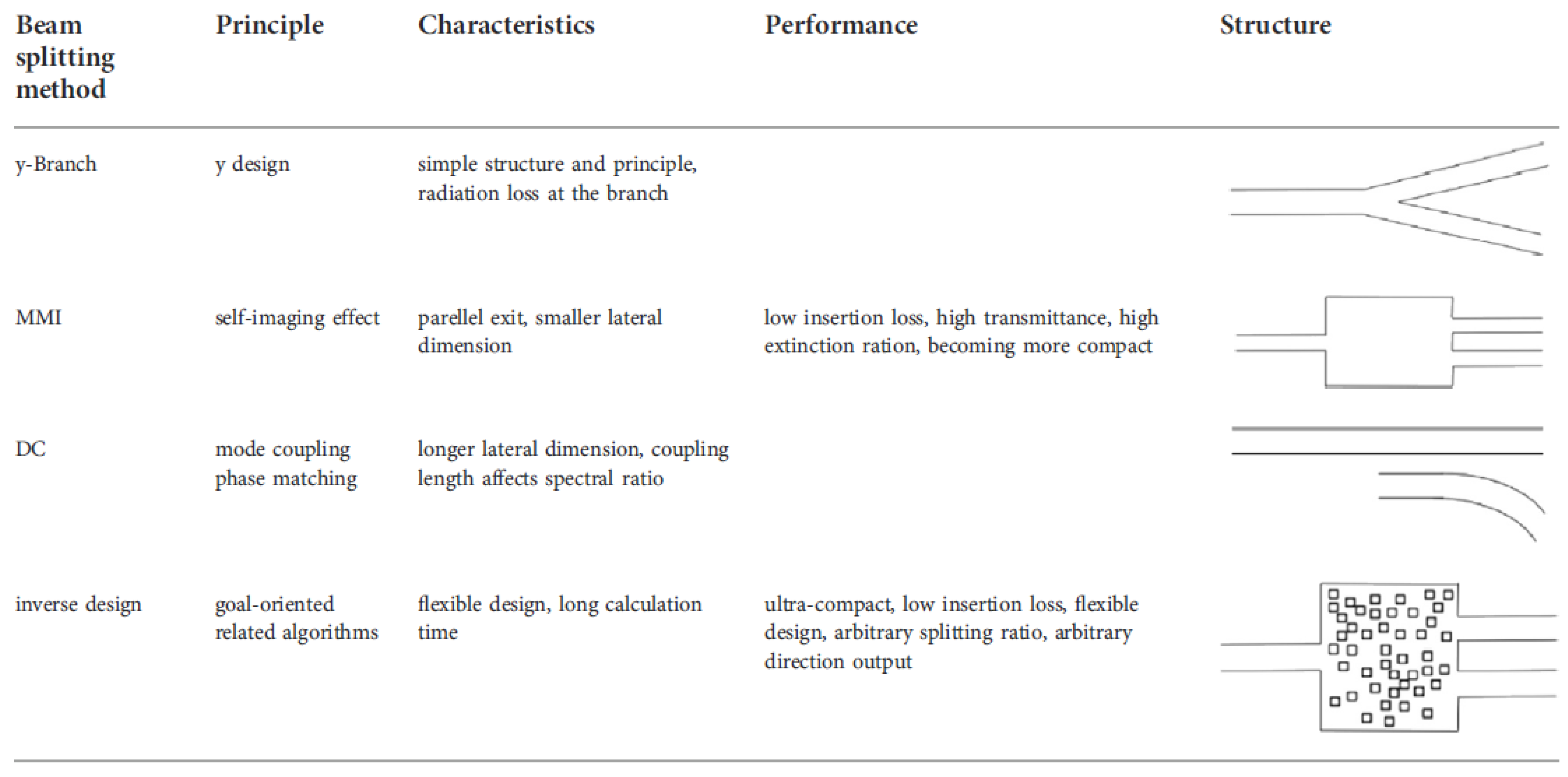
3. Splitting Devices
- Y-branches.
- Directional couplers.
- Multimode interferometer and inverse design devices.
3.1. Y-Branch
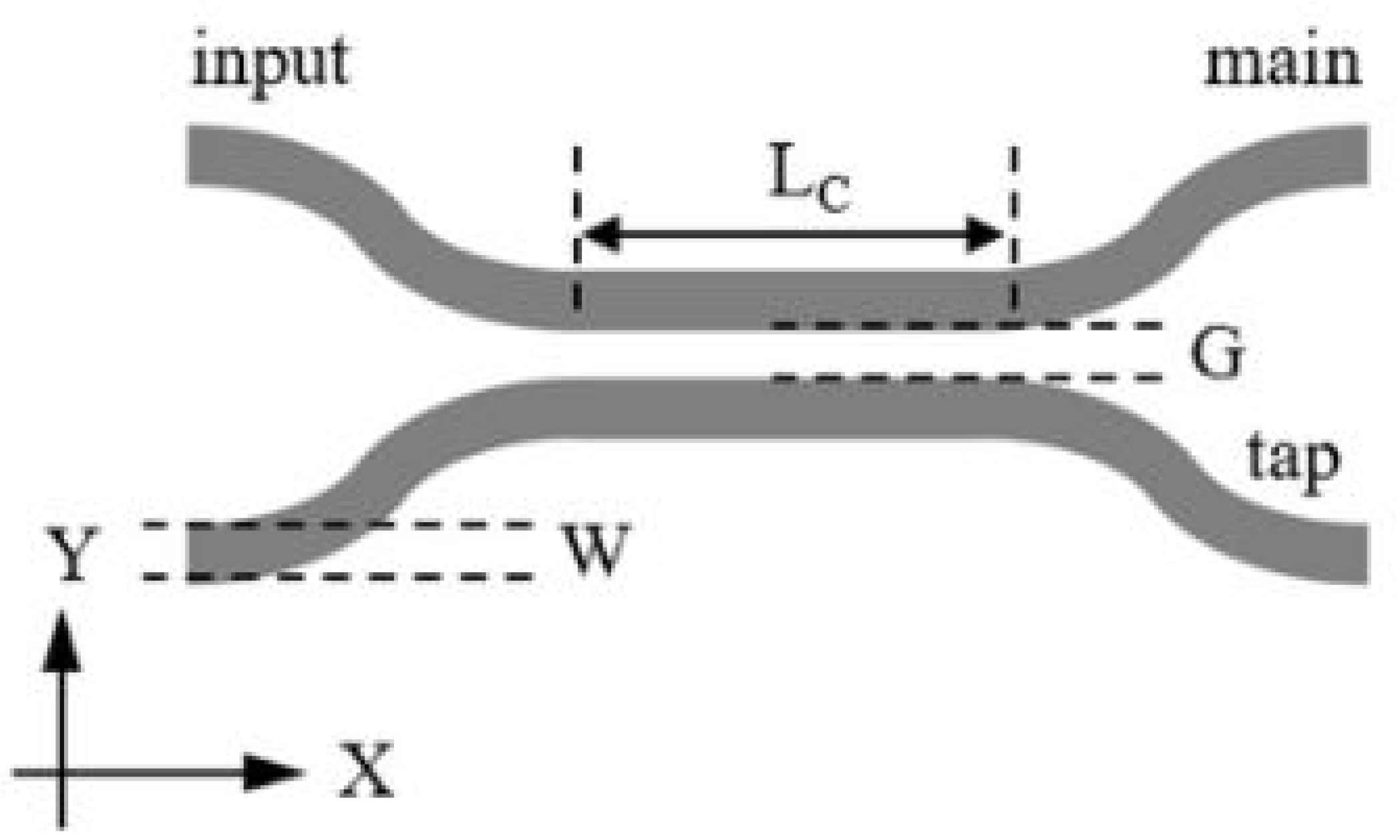
3.2. Directional Coupler
3.3. Multimode Interferometer (MMI) and Inverse Design Devices
4. Transmission and Signal Perturbation
4.1. Waveguide Technology
4.1.1. Bending Losses
4.1.2. Waveguide Crossings
4.2. Phase Shifter
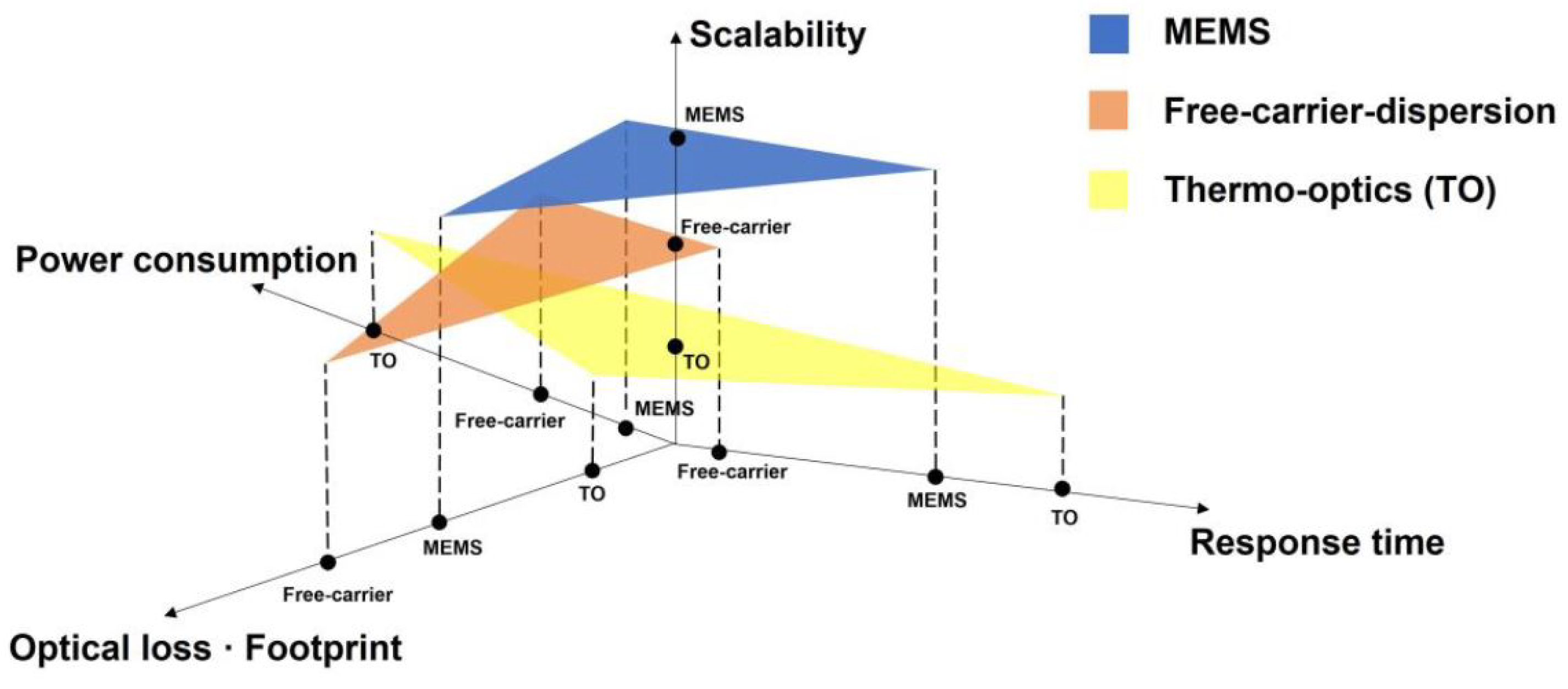
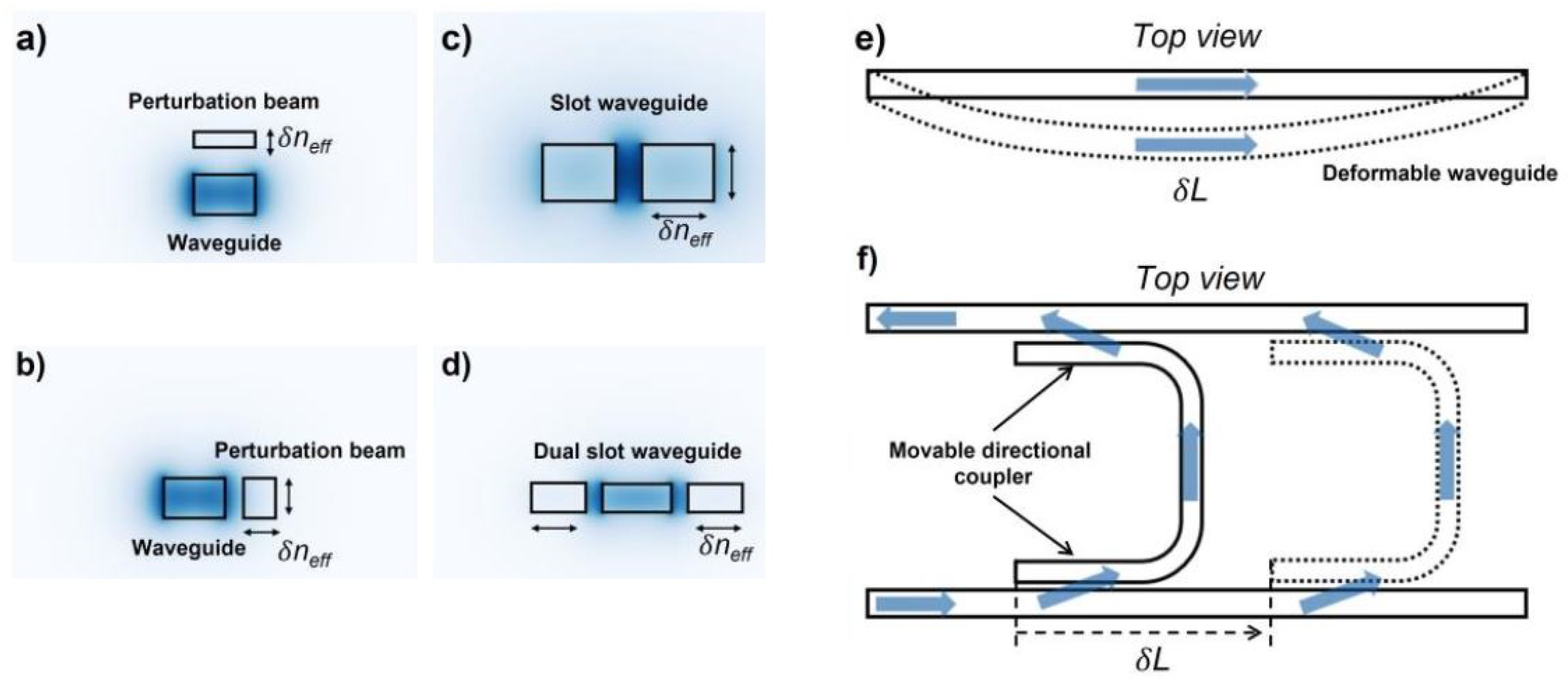
4.2.1. MEMS-Based Phase Shifter
4.2.2. Thermo-Optical Phase Shifter
4.2.3. Free-Carrier-Depletion-Based Phase Shifter
| Shifter Type | Efficiency * (V mm) and Consumption * (mW) | Modulation Speed (MHz) | Insertion Loss (dB) |
|---|---|---|---|
| MEMS evanescent field perturbation [133] | 0.535 | 0.503 | 0.33 dB |
| MEMS optical mode | |||
| modification [135] | 0.02 | 0.04 | 0.26 dB |
| MEMS opt. path length adjustment [137] | 75 | 0.139 | 0.1 dB |
| TPS conventional TiN heater [147] | 21.4 mW | 0.18 | <0.01 dB |
| TPS Doped Silicon [147] | 22.8 mW | 0.45 | <0.01 dB |
| TPS 2D layer ITO [146] | 10 mW | 0.19 | <0.01 dB |
| Conventional TPS with air trench [143] | 1.7 mW | 0.010 | 0.1 dB |
| TPS spiral waveguide [149] | 3 mW | 0.039 | 0.9 dB |
| Standard PN junction [153] | ∼0.8 V · mm (3 V) | 12 × 103 | 1.2 dB |
| Junction PIPIN [154] | 35 V mm (0 V) | 42 × 103 | 2.5 dB |
| Corner doping | |||
| concentration [155] | 26.7 V mm (−6 V) | 8.9 × 103 | 4.5 dB |
| Grown vertical junction diodes [156] | 7.4 V mm (1 V) | 48 × 103 | 3.8 dB |
| Interleaved PN [159] | 1.9 V mm (1 V) | 6.8 × 103 | ∼2 dB |
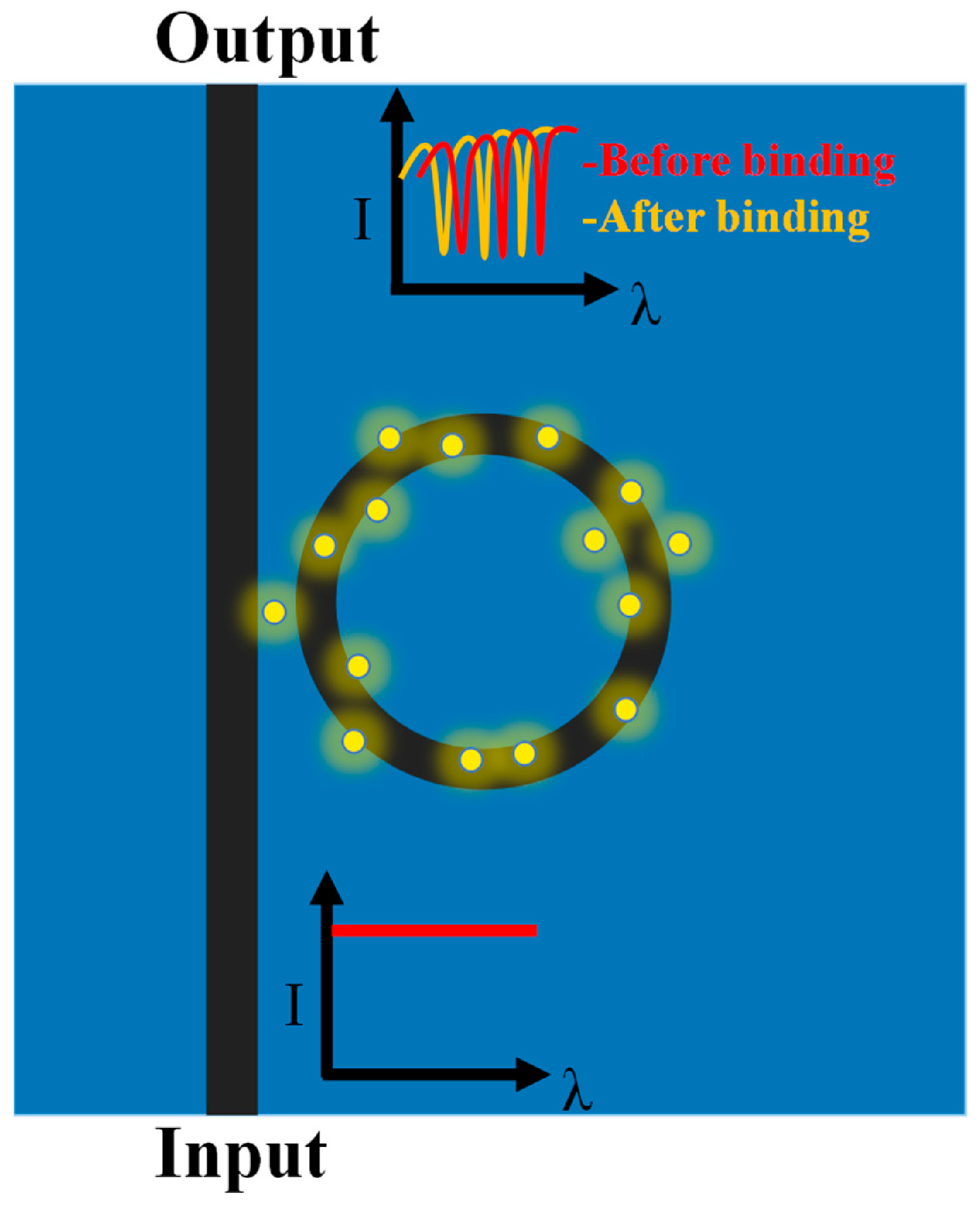
4.3. Ring Resonators
5. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lipson, M. The revolution of silicon photonics. Nat. Mater. 2022, 21, 974–975. [Google Scholar] [CrossRef]
- Shahbaz, M.; Butt, M.A.; Piramidowicz, R. A Concise Review of the Progress in Photonic Sensing Devices. Photonics 2023, 10, 698. [Google Scholar] [CrossRef]
- Shekhar, S.; Bogaerts, W.; Chrostowski, L.; Bowers, J.E.; Hochberg, M.; Soref, R.; Shastri, B.J. Roadmapping the next generation of silicon photonics. Nat. Commun. 2024, 15, 751. [Google Scholar] [CrossRef]
- Pelucchi, E.; Fagas, G.; Aharonovich, I.; Englund, D.; Figueroa, E.; Gong, Q.; Hannes, H.; Liu, J.; Lu, C.Y.; Matsuda, N.; et al. The potential and global outlook of integrated photonics for quantum technologies. Nat. Rev. Phys. 2022, 4, 194–208. [Google Scholar] [CrossRef]
- Piergentili, P.; Amanti, F.; Andrini, G.; Armani, F.; Bellani, V.; Bonaiuto, V.; Cammarata, S.; Campostrini, M.; Cornia, S.; Dao, T.H.; et al. Quantum Information with Integrated Photonics. Appl. Sci. 2023, 14, 387. [Google Scholar] [CrossRef]
- Siew, S.Y.; Li, B.; Gao, F.; Zheng, H.Y.; Zhang, W.; Guo, P.; Xie, S.W.; Song, A.; Dong, B.; Luo, L.W.; et al. Review of silicon photonics technology and platform development. J. Light. Technol. 2021, 39, 4374–4389. [Google Scholar] [CrossRef]
- Andrini, G.; Amanti, F.; Armani, F.; Bellani, V.; Bonaiuto, V.; Cammarata, S.; Campostrini, M.; Dao, T.H.; De Matteis, F.; Demontis, V.; et al. Solid-State Color Centers for Single-Photon Generation. Photonics 2024, 11, 188. [Google Scholar] [CrossRef]
- Ceccarelli, F.; Acconcia, G.; Gulinatti, A.; Ghioni, M.; Rech, I.; Osellame, R. Recent advances and future perspectives of single-photon avalanche diodes for quantum photonics applications. Adv. Quantum Technol. 2021, 4, 2000102. [Google Scholar] [CrossRef]
- Xiang, C.; Bowers, S.M.; Bjorlin, A.; Blum, R.; Bowers, J.E. Perspective on the future of silicon photonics and electronics. Appl. Phys. Lett. 2021, 118, 220501. [Google Scholar]
- Mu, X.; Wu, S.; Cheng, L.; Fu, H. Edge couplers in silicon photonic integrated circuits: A review. Appl. Sci. 2020, 10, 1538. [Google Scholar] [CrossRef]
- Cheng, L.; Mao, S.; Li, Z.; Han, Y.; Fu, H. Grating couplers on silicon photonics: Design principles, emerging trends and practical issues. Micromachines 2020, 11, 666. [Google Scholar] [CrossRef]
- Marchetti, R.; Lacava, C.; Carroll, L.; Gradkowski, K.; Minzioni, P. Coupling strategies for silicon photonics integrated chips. Photonics Res. 2019, 7, 201–239. [Google Scholar] [CrossRef]
- Carroll, L.; Lee, J.S.; Scarcella, C.; Gradkowski, K.; Duperron, M.; Lu, H.; Zhao, Y.; Eason, C.; Morrissey, P.; Rensing, M.; et al. Photonic packaging: Transforming silicon photonic integrated circuits into photonic devices. Appl. Sci. 2016, 6, 426. [Google Scholar] [CrossRef]
- Cardenas, J.; Luke, K.; Luo, L.; Poitras, C.; Morton, P.; Lipson, M. High coupling efficiency etched facet tapers in silicon. In Proceedings of the 2012 Conference on Lasers and Electro-Optics, San Jose, CA, USA, 6–11 May 2012. [Google Scholar]
- Chuang, S. Physics of Photonic Devices, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 273–279. [Google Scholar]
- Chrostowski, L.; Hochberg, M. Silicon Photonics Design: From Devices to Systems, 1st ed.; Cambridge University Press: Cambridge, UK, 2015; pp. 10–14. [Google Scholar]
- Dong, P.; Preble, S.F.; Robinson, J.T.; Manipatruni, S.; Lipson, M. Inducing photonic transitions between discrete modes in a silicon optical microcavity. Phys. Rev. Lett. 2008, 100, 033904. [Google Scholar] [CrossRef]
- Stern, B.; Zhu, X.; Chen, C.P.; Tzuang, L.D.; Cardenas, J.; Bergman, K.; Lipson, M. On-chip mode-division multiplexing switch. Optica 2015, 2, 530–535. [Google Scholar] [CrossRef]
- He, Y.; Zhang, Y.; Zhu, Q.; An, S.; Cao, R.; Guo, X.; Qiu, C.; Su, Y. Silicon high-order mode (de) multiplexer on single polarization. J. Light. Technol. 2018, 36, 5746–5753. [Google Scholar] [CrossRef]
- Fu, Y.; Ye, T.; Tang, W.; Chu, T. Efficient adiabatic silicon-on-insulator waveguide taper. Photonics Res. 2014, 2, 41–44. [Google Scholar] [CrossRef]
- Seok, T.; Quack, N.; Han, S.; Muller, R.; Wu, M. Large-scale broadband digital silicon photonic switches with vertical adiabatic couplers. Optica 2016, 3, 64–70. [Google Scholar] [CrossRef]
- Suchoski, P.; Ramaswamy, R. Design of single-mode step-tapered waveguide sections. IEEE J. Sel. Top. Quant. 1987, 23, 205–211. [Google Scholar] [CrossRef]
- Wang, J.; Qi, M.; Xuan, Y.; Huang, H.; Li, Y.; Li, M.; Chen, X.; Jia, Q.; Sheng, Z.; Wu, A.; et al. Proposal for fabrication-tolerant SOI polarization splitter-rotator based on cascaded MMI couplers and an assisted bi-level taper. Opt. Express 2014, 22, 27869–27879. [Google Scholar] [CrossRef]
- Hettrick, S.; Wang, J.; Li, C.; Wilkinson, J.; Shepherd, D. An experimental comparison of linear and parabolic tapered waveguide lasers and a demonstration of broad-stripe diode pumping. J. Light. Technol. 2004, 22, 845–849. [Google Scholar] [CrossRef]
- Ren, G.; Chen, S.; Cheng, Y.; Zhai, Y. Study on inverse taper based mode transformer for low loss coupling between silicon wire waveguide and lensed fiber. Opt. Commun. 2011, 284, 4782–4788. [Google Scholar] [CrossRef]
- Snyder, A.; Love, J. Optical Waveguide Theory; Springer Science & Business Media: New York, NY, USA, 2012; pp. 238–280. [Google Scholar]
- Liu, Y.; Yu, J. Low-loss coupler between fiber and waveguide based on silicon-on-insulator slot waveguides. Appl. Opt. 2007, 46, 7858–7861. [Google Scholar] [CrossRef]
- Tu, X.; Fu, H.; Geng, D. Y-branch edge coupler between cleaved single mode fiber and nano-scale waveguide on silicon-on-insulator platform. In Proceedings of the 2014 Asia Communications and Photonics Conference, Shanghai, China, 11–14 November 2014. [Google Scholar]
- Mu, X.; Wu, S.; Cheng, L.; Tu, X.; Fu, H. High-performance silicon nitride fork-shape edge coupler. In Proceedings of the 2019 Frontiers in Optics, Washington, DC, USA, 15–19 September 2019. [Google Scholar]
- Tu, Y.; Fu, P.; Huang, D. High-efficiency ultra-broadband multi-tip edge couplers for integration of distributed feedback laser with silicon-on-insulator waveguide. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Wang, J.; Xuan, Y.; Lee, C.; Niu, B.; Liu, L.; Liu, G.; Qi, M. Low-loss and misalignment-tolerant fiber-to-chip edge coupler based on double-tip inverse tapers. In Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- Hatori, N.; Urino, Y.; Shimizu, T.; Okano, M.; Yamamoto, T.; Mori, M.; Nakamura, T.; Arakawa, Y. Quantum dot laser for a light source of an athermal silicon optical interposer. Photonics 2015, 2, 355–364. [Google Scholar] [CrossRef]
- Itoh, K.; Kuno, Y.; Hayashi, Y.; Suzuki, J.; Hojo, N.; Amemiya, T.; Nishiyama, N.; Arai, S. Crystalline/Amorphous Si Integrated Optical Couplers for 2D/3D Interconnection. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 255–263. [Google Scholar] [CrossRef]
- Tu, X.; Dumais, P.; Li, M.; Goodwill, D.; Fu, H.; Geng, D.; Bernier, E. Low polarization-dependent-loss silicon photonic trident edge coupler fabricated by 248 nm optical lithography. In Proceedings of the Asia Communications and Photonics Conference, Hong Kong, 19–23 November 2015; Optica Publishing Group: Washington, DC, USA; p. AS4B-3. [Google Scholar]
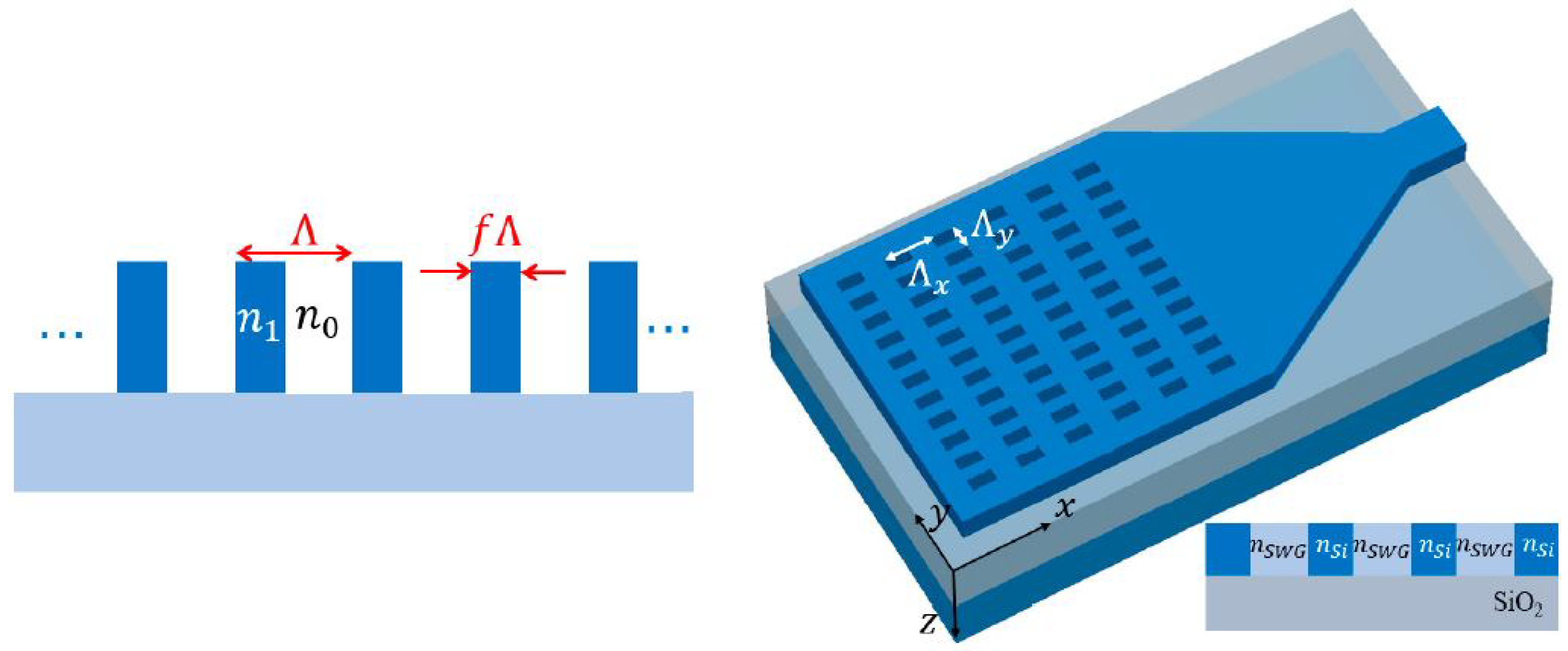
- Cheben, P.; Bock, P.J.; Schmid, J.H.; Lapointe, J.; Janz, S.; Xu, D.X.; Densmore, A.; Delâge, A.; Lamontagne, B.; Hall, T.J. Refractive index engineering with subwavelength gratings for efficient microphotonic couplers and planar waveguide multiplexers. Opt. Lett. 2010, 35, 2526–2528. [Google Scholar] [CrossRef]
- Cheben, P.; Schmid, J.H.; Wang, S.; Xu, D.X.; Vachon, M.; Janz, S.; Lapointe, J.; Painchaud, Y.; Picard, M.J. Broadband polarization independent nanophotonic coupler for silicon waveguides with ultra-high efficiency. Opt. Express 2015, 23, 22553–22563. [Google Scholar] [CrossRef]
- Donzella, V.; Sherwali, A.; Flueckiger, J.; Fard, S.T.; Grist, S.M.; Chrostowski, L. Sub-wavelength grating components for integrated optics applications on SOI chips. Opt. Express 2014, 22, 21037–21050. [Google Scholar] [CrossRef]
- Cheben, P.; Xu, D.; Janz, S.; Densmore, A. Subwavelength waveguide grating for mode conversion and light coupling in integrated optics. Opt. Express 2006, 14, 4695–4702. [Google Scholar] [CrossRef]
- Voigt, K.; Brulis, V.; Petermann, K.; Zimmermann, L. Study of backend waveguide arrays for adiabatic coupling to Si waveguides. In Proceedings of the 2017 IEEE 14th International Conference on Group IV Photonics (GFP), Berlin, Germany, 23–25 August 2017; IEEE: New York, NY, USA, 2017; pp. 143–144. [Google Scholar]
- Picard, M.J.; Latrasse, C.; Larouche, C.; Painchaud, Y.; Poulin, M.; Pelletier, F.; Guy, M. CMOS-compatible spot-size converter for optical fiber to sub-um silicon waveguide coupling with low-loss low-wavelength dependence and high tolerance to misalignment. In Proceedings of the Silicon Photonics XI. SPIE, San Francisco, CA, USA, 14 March 2016; Volume 9752, pp. 132–138. [Google Scholar]
- Sisto, M.M.; Fisette, B.; Paultre, J.E.; Paquet, A.; Desroches, Y. Novel spot size converter for coupling standard single mode fibers to SOI waveguides. In Proceedings of the Silicon Photonics XI. SPIE, San Francisco, CA, USA, 14 March 2016; Volume 9752, pp. 199–213. [Google Scholar]
- Doylend, J.K.; Knights, A.P. Design and Simulation of an Integrated Fiber-to-Chip Coupler for Silicon-on-Insulator Waveguides. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1363–1370. [Google Scholar] [CrossRef]
- Kruse, K.; Middlebrook, C.T. Polymer taper bridge for silicon waveguide to single mode waveguide coupling. Opt. Commun. 2016, 362, 87–95. [Google Scholar] [CrossRef]
- Dewanjee, A.; Caspers, J.N.; Aitchison, J.S.; Mojahedi, M. Demonstration of a compact bilayer inverse taper coupler for Si-photonics with enhanced polarization insensitivity. Opt. Express 2016, 24, 28194–28203. [Google Scholar] [CrossRef]
- Khilo, A.; Popović, M.A.; Araghchini, M.; Kärtner, F.X. Efficient planar fiber-to-chip coupler based on two-stage adiabatic evolution. Opt. Express 2010, 18, 15790–15806. [Google Scholar] [CrossRef]
- Park, H.; Kim, S.; Park, J.; Joo, J.; Kim, G. A fiber-to-chip coupler based on Si/SiON cascaded tapers for Si photonic chips. Opt. Express 2013, 21, 29313–29319. [Google Scholar] [CrossRef]
- Fang, Q.; Song, J.; Luo, X.; Tu, X.; Jia, L.; Yu, M.; Lo, G. Low Loss Fiber-to-Waveguide Converter With a 3-D Functional Taper for Silicon Photonics. IEEE Photonics Technol. Lett. 2016, 28, 2533–2536. [Google Scholar] [CrossRef]
- Lee, J.M.; Kim, D.J.; Ahn, H.; Park, S.H.; Kim, G. Temperature Dependence of Silicon Nanophotonic Ring Resonator With a Polymeric Overlayer. J. Light. Technol. 2007, 25, 2236–2243. [Google Scholar] [CrossRef]
- Raghunathan, V.; Yagüe, J.L.; Xu, J.; Michel, J.; Gleason, K.K.; Kimerling, L.C. Co-polymer clad design for high performance athermal photonic circuits. Opt. Express 2012, 20, 20808–20813. [Google Scholar] [CrossRef]
- Pu, M.; Liu, L.; Ou, H.; Yvind, K.; Hvam, J.M. Ultra-low-loss inverted taper coupler for silicon-on-insulator ridge waveguide. Opt. Commun. 2010, 283, 3678–3682. [Google Scholar] [CrossRef]
- Ku, K.N.; Lee, M.C.M. Wide-band optical mode converters for coupling between fibers and silicon photonic wires with large misalignment tolerance. J. Light. Technol. 2013, 31, 1616–1620. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Chang, C.J.; Lee, M.C.; Tseng, F.G. SU8 3D prisms with ultra small inclined angle for low-insertion-loss fiber/waveguide interconnection. Opt. Express 2011, 19, 18956–18964. [Google Scholar] [CrossRef] [PubMed]
- Harke, A.; Lipka, T.; Amthor, J.; Horn, O.; Krause, M.; Muller, J. Amorphous Silicon 3-D Tapers for Si Photonic Wires Fabricated With Shadow Masks. IEEE Photonics Technol. Lett. 2008, 20, 1452–1454. [Google Scholar] [CrossRef]
- Jia, L.; Song, J.; Liow, T.Y.; Luo, X.; Tu, X.; Fang, Q.; Koh, S.C.; Yu, M.; Lo, G. Mode size converter between high-index-contrast waveguide and cleaved single mode fiber using SiON as intermediate material. Opt. Express 2014, 22, 23652–23660. [Google Scholar] [CrossRef] [PubMed]
- Maegami, Y.; Takei, R.; Omoda, E.; Amano, T.; Okano, M.; Mori, M.; Kamei, T.; Sakakibara, Y. Spot-size converter with a SiO2 spacer layer between tapered Si and SiON waveguides for fiber-to-chip coupling. Opt. Express 2015, 23, 21287–21295. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ling, Y.C.; Zhang, Y.; Shang, K.; Yoo, S.J.B. High-Density Wafer-Scale 3-D Silicon-Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–10. [Google Scholar] [CrossRef]
- Zhang, W.; Ebert, M.; Reynolds, J.; Chen, B.; Yan, X.; Du, H.; Banakar, M.; Tran, D.; Littlejohns, C.; Reed, G.; et al. Buried 3D spot-size converters for silicon photonics. Optica 2021, 8, 1102–1108. [Google Scholar] [CrossRef]
- Li, X.; Yu, S.; Gui, C. Fiber-to-Chip Three-Dimensional Silicon-on-Insulator Edge Couplers with High Efficiency and Tolerance. Micromachines 2023, 14, 1500. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wang, Z.; Ye, N.; Pang, F.; Song, Y. The low-loss spot size converter for alignment with cleaved single mode fiber. Appl. Sci. 2023, 13, 8157. [Google Scholar] [CrossRef]
- Brunetti, G.; Heuvink, R.; Schreuder, E.; Armenise, M.; Ciminelli, C. Silicon Nitride Spot Size Converter With Very Low-Loss over the C-Band. IEEE Photonics Technol. Lett. 2023, 35, 1215–1218. [Google Scholar] [CrossRef]
- Fang, Q.; Liow, T.Y.; Song, J.F.; Tan, C.W.; Yu, M.B.; Lo, G.Q.; Kwong, D.L. Suspended optical fiber-to-waveguide mode size converter for silicon photonics. Opt. Express 2010, 18, 7763–7769. [Google Scholar] [CrossRef]
- Wood, M.; Sun, P.; Reano, R.M. Compact cantilever couplers for low-loss fiber coupling to silicon photonic integrated circuits. Opt. Express 2012, 20, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Nambiar, S.; Sethi, P.; Selvaraja, S.K. Grating-assisted fiber to chip coupling for SOI photonic circuits. Appl. Sci. 2018, 8, 1142. [Google Scholar] [CrossRef]
- Mahajan, R.; Li, X.; Fryman, J.; Zhang, Z.; Nekkanty, S.; Tadayon, P.; Jaussi, J.; Shumarayev, S.; Agrawal, A.; Jadhav, S.; et al. Co-packaged photonics for high performance computing: Status, challenges and opportunities. J. Light. Technol. 2021, 40, 379–392. [Google Scholar] [CrossRef]
- Subbaraman, H.; Xu, X.; Hosseini, A.; Zhang, X.; Zhang, Y.; Kwong, D.; Chen, R.T. Recent advances in silicon-based passive and active optical interconnects. Opt. Express 2015, 23, 2487–2511. [Google Scholar] [CrossRef]
- Kopp, C.; Bernabe, S.; Bakir, B.B.; Fedeli, J.M.; Orobtchouk, R.; Schrank, F.; Porte, H.; Zimmermann, L.; Tekin, T. Silicon photonic circuits: On-CMOS integration, fiber optical coupling, and packaging. IEEE J. Sel. Top. Quantum Electron. 2010, 17, 498–509. [Google Scholar] [CrossRef]
- Snyder, B.; O’Brien, P. Packaging process for grating-coupled silicon photonic waveguides using angle-polished fibers. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 954–959. [Google Scholar] [CrossRef]
- Karnick, D.; Skwierawski, P.; Schneider, M.; Eisenblätter, L.; Weber, M. Optical links for detector instrumentation: On-detector multi-wavelength silicon photonic transmitters. J. Instrum. 2017, 12, C03078. [Google Scholar] [CrossRef]
- Zhou, X.; Tsang, H.K. High efficiency multimode waveguide grating coupler for few-mode fibers. IEEE Photonics J. 2022, 14, 1–5. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, Y.; Xu, J.; Wang, X.; Wu, Y.; Chen, Y.; Li, J.; Xu, K. An Efficient Silicon Grating Coupler for a 2 μm Waveband Based on a Polysilicon Overlay. Photonics 2023, 10, 952. [Google Scholar] [CrossRef]
- Vermeer, M.L.; Alhareeb, N.K.; Trieu, H.K.; Lipka, T. Fabrication of distributed Bragg reflectors to reduce coupling losses of photonic circuits. In Proceedings of the Mikro-Nano-Integration; 9. GMM-Workshop, Aachen, Germany, 21–22 November 2022; pp. 1–4. [Google Scholar]
- Hoppe, N.; Zaoui, W.S.; Rathgeber, L.; Wang, Y.; Klenk, R.H.; Vogel, W.; Kaschel, M.; Portalupi, S.L.; Burghartz, J.; Berroth, M. Ultra-efficient silicon-on-insulator grating couplers with backside metal mirrors. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–6. [Google Scholar] [CrossRef]
- Sharma, T.; Kwon, H.; Park, J.; Han, S.; Son, G.; Jung, Y.; Yu, K. Coupling performance enhancement using SOI grating coupler design. Opt. Commun. 2018, 427, 452–456. [Google Scholar] [CrossRef]
- He, L.; Liu, Y.; Galland, C.; Lim, A.E.J.; Lo, G.Q.; Baehr-Jones, T.; Hochberg, M. A High-Efficiency Nonuniform Grating Coupler Realized With 248-nm Optical Lithography. IEEE Photonics Technol. Lett. 2013, 25, 1358–1361. [Google Scholar] [CrossRef]
- Benedikovic, D.; Alonso-Ramos, C.; Pérez-Galacho, D.; Guerber, S.; Vakarin, V.; Marcaud, G.; Le Roux, X.; Cassan, E.; Marris-Morini, D.; Cheben, P.; et al. L-shaped fiber-chip grating couplers with high directionality and low reflectivity fabricated with deep-UV lithography. Opt. Lett. 2017, 42, 3439–3442. [Google Scholar] [CrossRef]
- Zhao, Z.; Fan, S. Design Principles of Apodized Grating Couplers. J. Light. Technol. 2020, 38, 4435–4446. [Google Scholar] [CrossRef]
- Hansen, S.E.; Arregui, G.; Babar, A.N.; Albrechtsen, M.; Lahijani, B.V.; Christiansen, R.E.; Stobbe, S. Efficient low-reflection fully etched vertical free-space grating couplers for suspended silicon photonics. Opt. Express 2023, 31, 17424–17436. [Google Scholar] [CrossRef]
- Li, S.; Zhou, C.; Cao, H.; Wu, J. Simple design of slanted grating with simplified modal method. Opt. Lett. 2014, 39, 781–784. [Google Scholar] [CrossRef]
- Schrauwen, J.; Van Laere, F.; Van Thourhout, D.; Baets, R. Focused-Ion-Beam Fabrication of Slanted Grating Couplers in Silicon-on-Insulator Waveguides. IEEE Photonics Technol. Lett. 2007, 19, 816–818. [Google Scholar] [CrossRef]
- Watanabe, T.; Fedoryshyn, Y.; Leuthold, J. 2-D Grating Couplers for Vertical Fiber Coupling in Two Polarizations. IEEE Photonics J. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Lin, C.C.; Lu, Y.C.; Liu, Y.H.; Wang, L.; Na, N. Design of a Completely Vertical, Polarization-Independent Two-Dimensional Grating Coupler with High Coupling Efficiency. Sensors 2023, 23, 4662. [Google Scholar] [CrossRef]
- Kumar, P.; Mishra, A.; Shivaleela, E.; Srinivas, T. Inverse Design of SOI based broadband Grating Coupler. In Proceedings of the 2022 IEEE Research and Applications of Photonics in Defense Conference (RAPID), Miramar Beach, FL, USA, 12–14 September 2022; IEEE: New York, NY, USA, 2022; pp. 1–2. [Google Scholar]
- Cheng, G.; Yi, Q.; Xu, F.; Yang, M.; Yan, Z.; Li, Q.; Zou, Y.; Yu, Y.; Shen, L. Efficient 1.55 and 2 μm Dual-Band SOI Grating Coupler for Light Coupling and On-Chip Wavelength Division (De) multiplexing. Adv. Photonics Res. 2023, 4, 2200149. [Google Scholar] [CrossRef]
- Xu, Y.; Tian, Z.; Meng, X.; Chai, Z. Methods and applications of on-chip beam splitting: A review. Front. Phys. 2022, 10, 985208. [Google Scholar] [CrossRef]
- Yang, N.; Xiao, J. A compact silicon-based polarization-independent power splitter using a three-guide directional coupler with subwavelength gratings. Opt. Commun. 2020, 459, 125095. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, S.; Lim, A.E.J.; Lo, G.Q.; Galland, C.; Baehr-Jones, T.; Hochberg, M. A compact and low loss Y-junction for submicron silicon waveguide. Opt. Express 2013, 21, 1310–1316. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Hu, X.; Chen, D.; Wang, L.; Li, M.; Feng, P.; Xiao, X.; Yu, S. Ultra-broadband, Low Loss and Ultra-Compact 3dB Power Splitter Based On Y-Branch With Step Waveguide. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; IEEE: New York, NY, USA, 2019; pp. 1–3. [Google Scholar]
- Han, L.; Kuo, B.P.P.; Alic, N.; Radic, S. Ultra-broadband multimode 3dB optical power splitter using an adiabatic coupler and a Y-branch. Opt. Express 2018, 26, 14800–14809. [Google Scholar] [CrossRef] [PubMed]
- Pendam, N.; Vardhani, C. Design, simulation & optimization of 3D low-loss asymmetrical Y-branch optical power splitter on SOI platform. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; IEEE: New York, NY, USA, 2016; pp. 755–757. [Google Scholar]
- Ozcan, C.; Mojahedi, M.; Aitchison, J.S. Short, broadband, and polarization-insensitive adiabatic Y-junction power splitters. Opt. Lett. 2023, 48, 4901–4904. [Google Scholar] [CrossRef] [PubMed]
- Ni, B.; Xiao, J. Ultracompact and broadband silicon-based TE-pass 1 × 2 power splitter using subwavelength grating couplers and hybrid plasmonic gratings. Opt. Express 2018, 26, 33942–33955. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Park, T.H.; Oh, M.C. Broadband integrated optic polarization splitters by incorporating polarization mode extracting waveguide. Sci. Rep. 2017, 7, 4789. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, L.; Xia, H.; Cao, S.; Wang, L.; Yang, S.; Wu, Y.; Tai, R. Integrated silicon metasurface polarization beam splitter on a standard SOI substrate. Optik 2021, 227, 166096. [Google Scholar] [CrossRef]
- Liao, J.; Tian, Y.; Yang, Z.; Xu, H.; Tang, C.; Wang, Y.; Zhang, X.; Kang, Z. Inverse design of highly efficient and broadband mode splitter on SOI platform. Chin. Opt. Lett. 2024, 22, 011302. [Google Scholar] [CrossRef]
- Lv, D.; Wu, L.; Liu, C.; Li, A.; Wang, R.; Wu, A. Broadband and Low-Loss Silicon Photonic Directional Coupler for Signal Power Tapping on the 3 μm SOI Waveguide Platform. Photonics 2023, 10, 776. [Google Scholar] [CrossRef]
- Paredes, B.; Mohammed, Z.; Villegas, J.; Rasras, M. Dual-band (O & C-bands) two-mode multiplexer on the SOI platform. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar]
- Wang, J.; Liang, D.; Tang, Y.; Dai, D.; Bowers, J.E. Realization of an ultra-short silicon polarization beam splitter with an asymmetrical bent directional coupler. Opt. Lett. 2013, 38, 4–6. [Google Scholar] [CrossRef]
- Dai, D.; Bowers, J.E. Novel ultra-short and ultra-broadband polarization beam splitter based on a bent directional coupler. Opt. Express 2011, 19, 18614–18620. [Google Scholar] [CrossRef]
- Wu, H.; Dai, D. High-Performance Polarizing Beam Splitters Based on Cascaded Bent Directional Couplers. IEEE Photonics Technol. Lett. 2017, 29, 474–477. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, M.H.; Kim, Y.; Kim, K.H. High-extinction-ratio directional-coupler-type polarization beam splitter with a bridged silicon wire waveguide. Opt. Lett. 2018, 43, 3241–3244. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zou, X.; Xie, C.; Zhang, Y. Ultrahigh extinction ratio and ultralow insertion loss for polarization beam splitter based on two folded asymmetrical directional couplers with dual-stage etching. Appl. Opt. 2023, 62, 965–971. [Google Scholar] [CrossRef] [PubMed]
- Teo, T.Y.; Krbal, M.; Mistrik, J.; Prikryl, J.; Lu, L.; Simpson, R.E. Comparison and analysis of phase change materials-based reconfigurable silicon photonic directional couplers. Opt. Mater. Express 2022, 12, 606–621. [Google Scholar] [CrossRef]
- Chen, Y.; Xiao, J. Compact and broadband silicon-based transverse electric-pass power splitter using triple-guide directional couplers with hybrid plasmonic waveguides and subwavelength gratings. J. Nanophotonics 2020, 14, 036013. [Google Scholar] [CrossRef]
- Meng, Y.; Chen, Y.; Lu, L.; Ding, Y.; Cusano, A.; Fan, J.A.; Hu, Q.; Wang, K.; Xie, Z.; Liu, Z.; et al. Optical meta-waveguides for integrated photonics and beyond. Light. Sci. Appl. 2021, 10, 235. [Google Scholar] [CrossRef]
- Cheben, P.; Halir, R.; Schmid, J.H.; Atwater, H.A.; Smith, D.R. Subwavelength integrated photonics. Nature 2018, 560, 565–572. [Google Scholar] [CrossRef]
- Sattari, H.; Takabayashi, A.Y.; Zhang, Y.; Verheyen, P.; Bogaerts, W.; Quack, N. Compact broadband suspended silicon photonic directional coupler. Opt. Lett. 2020, 45, 2997–3000. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Zhang, G.; Mojaver, K.H.R.; Liboiron-Ladouceur, O. Broadband polarization/mode insensitive 3-dB optical coupler for silicon photonic switches. Opt. Express 2023, 31, 14068–14080. [Google Scholar] [CrossRef] [PubMed]
- Grabulosa, A.; Porte, X.; Jung, E.; Moughames, J.; Kadic, M.; Brunner, D. (3+ 1) D printed adiabatic 1-to-M broadband couplers and fractal splitter networks. Opt. Express 2023, 31, 20256–20264. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, G.; Marocco, G.; Di Benedetto, A.; Giorgio, A.; Armenise, M.N.; Ciminelli, C. Design of a large bandwidth 2 × 2 interferometric switching cell based on a sub-wavelength grating. J. Opt. 2021, 23, 085801. [Google Scholar] [CrossRef]
- Cooney, K.; Peters, F.H. Analysis of multimode interferometers. Opt. Express 2016, 24, 22481–22515. [Google Scholar] [CrossRef]
- Zhang, Y.; Schneider, M.; Eisenblätter, L.; Karnick, D.; Kühner, T.; Weber, M. Multimode interferometers for integrated transceivers on 250 nm SOI platform. J. Instrum. 2020, 15, P02022. [Google Scholar] [CrossRef]
- Yi, Q.; Cheng, G.; Yan, Z.; Li, Q.; Xu, F.; Zou, Y.; Li, T.; Sun, Y.; Zou, Y.; Yu, Y.; et al. Silicon MMI-based power splitter for multi-band operation at the 1.55 and 2 μm wave bands. Opt. Lett. 2023, 48, 1335–1338. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Soref, R.; Mu, J. Compact polarization splitter based on a silicon angled multimode interferometer structure. Appl. Opt. 2019, 58, 4070–4074. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.; Huang, Y.W.; Yi, H.X.; Wang, X.J.; Li, Y.P.; Li, L.; Hu, W.W. A compact SOI polarization beam splitter based on multimode interference coupler. In Proceedings of the 2011 Asia Communications and Photonics Conference and Exhibition (ACP), Shanghai, China, 13–16 November 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Hassan, S.; Chack, D.; Mahajan, V. High extinction ratio and low loss polarization beam splitter based on multimode interference for PICs. Appl. Opt. 2020, 59, 3369–3375. [Google Scholar] [CrossRef]
- Ren, F.; Chen, W.; Zhangsun, T.; Zhang, Y.; Fan, X.; Wang, J. Variable-ratio mode-insensitive 1× 2 power splitter based on MMI couplers and phase shifters. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Rahbardar Mojaver, K.; Liboiron-Ladouceur, O. Multi-Transverse-Mode Silicon Photonics for Quantum Computing. In Proceedings of the Great Lakes Symposium on VLSI 2023, Knoxville, TN, USA, 5–7 June 2023; pp. 551–556. [Google Scholar]
- Moskalev, D.; Kozlov, A.; Salgaeva, U.; Krishtop, V.; Perminov, A.V.; Venediktov, V. A Semi-Analytical Method for the S-Parameter Calculations of an N× M Multimode Interference Coupler. Photonics 2023, 10, 1260. [Google Scholar] [CrossRef]
- Loonen, R.C.; de Vries, S.; Goia, F. Inverse design for advanced building envelope materials, systems and operation. In Rethinking Building Skins; Elsevier: Amsterdam, The Netherlands, 2022; pp. 377–402. [Google Scholar]
- Piggott, A.Y.; Petykiewicz, J.; Su, L.; Vučković, J. Fabrication-constrained nanophotonic inverse design. Sci. Rep. 2017, 7, 1786. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kim, J.Y.; Yoon, J.; Yoon, H.; Park, H.H.; Kurt, H. Experimental demonstration of inverse-designed silicon integrated photonic power splitters. Nanophotonics 2022, 11, 4581–4590. [Google Scholar] [CrossRef]
- Qiu, C.; Sheng, Z.; Li, H.; Liu, W.; Li, L.; Pang, A.; Wu, A.; Wang, X.; Zou, S.; Gan, F. Fabrication, Characterization and Loss Analysis of Silicon Nanowaveguides. J. Light. Technol. 2014, 32, 2303–2307. [Google Scholar] [CrossRef]
- Sheng, Z.; Dai, D.; He, S. Comparative study of losses in ultrasharp silicon-on-insulator nanowire bends. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1406–1412. [Google Scholar] [CrossRef]
- Vlasov, Y.A.; McNab, S.J. Losses in single-mode silicon-on-insulator strip waveguides and bends. Opt. Express 2004, 12, 1622–1631. [Google Scholar] [CrossRef]
- Mashanovich, G.Z.; Gardes, F.Y.; Thomson, D.J.; Hu, Y.; Li, K.; Nedeljkovic, M.; Soler Penades, J.; Khokhar, A.Z.; Mitchell, C.J.; Stankovic, S.; et al. Silicon Photonic Waveguides and Devices for Near- and Mid-IR Applications. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 407–418. [Google Scholar] [CrossRef]
- Selvaraja, S.K.; Sethi, P. Review on optical waveguides. Emerg. Waveguide Technol. 2018, 95, 458. [Google Scholar]
- Hong, S.; Zhang, L.; Wang, Y.; Zhang, M.; Xie, Y.; Dai, D. Ultralow-loss compact silicon photonic waveguide spirals and delay lines. Photonics Res. 2022, 10, 1–7. [Google Scholar] [CrossRef]
- Wu, S.; Mu, X.; Cheng, L.; Mao, S.; Fu, H. State-of-the-art and perspectives on silicon waveguide crossings: A review. Micromachines 2020, 11, 326. [Google Scholar] [CrossRef]
- Tsarev, A.V. Efficient silicon wire waveguide crossing with negligible loss and crosstalk. Opt. Express 2011, 19, 13732–13737. [Google Scholar] [CrossRef]
- Bogaerts, W.; Dumon, P.; Van Thourhout, D.; Baets, R. Low-loss, low-cross-talk crossings for silicon-on-insulator nanophotonic waveguides. Opt. Lett. 2007, 32, 2801–2803. [Google Scholar] [CrossRef]
- Sun, H.; Qiao, Q.; Guan, Q.; Zhou, G. Silicon photonic phase shifters and their applications: A review. Micromachines 2022, 13, 1509. [Google Scholar] [CrossRef]
- Quack, N.; Takabayashi, A.Y.; Sattari, H.; Edinger, P.; Jo, G.; Bleiker, S.J.; Errando-Herranz, C.; Gylfason, K.B.; Niklaus, F.; Khan, U.; et al. Integrated silicon photonic MEMS. Microsystems Nanoeng. 2023, 9, 27. [Google Scholar] [CrossRef] [PubMed]
- Edinger, P.; Takabayashi, A.Y.; Errando-Herranz, C.; Khan, U.; Sattari, H.; Verheyen, P.; Bogaerts, W.; Quack, N.; Gylfason, K.B. Silicon photonic microelectromechanical phase shifters for scalable programmable photonics. Opt. Lett. 2021, 46, 5671–5674. [Google Scholar] [CrossRef] [PubMed]
- Sattari, H.; Graziosi, T.; Kiss, M.; Seok, T.J.; Han, S.; Wu, M.C.; Quack, N. Silicon photonic MEMS phase-shifter. Opt. Express 2019, 27, 18959–18969. [Google Scholar] [CrossRef] [PubMed]
- Baghdadi, R.; Gould, M.; Gupta, S.; Tymchenko, M.; Bunandar, D.; Ramey, C.; Harris, N.C. Dual slot-mode NOEM phase shifter. Opt. Express 2021, 29, 19113–19119. [Google Scholar] [CrossRef] [PubMed]
- Xin, C.; Zhang, Z.; Wang, X.; Fan, C.; Li, M. Ultracompact single-layer optical MEMS accelerometer based on evanescent coupling through silicon nanowaveguides. Sci. Rep. 2022, 12, 21697. [Google Scholar] [CrossRef] [PubMed]
- Chiu, W.C.; Chang, C.C.; Wu, J.M.; Lee, M.C.M.; Shieh, J.M. Optical phase modulators using deformable waveguides actuated by micro-electro-mechanical systems. Opt. Lett. 2011, 36, 1089–1091. [Google Scholar] [CrossRef]
- Song, L.; Li, H.; Dai, D. Mach–Zehnder silicon-photonic switch with low random phase errors. Opt. Lett. 2021, 46, 78–81. [Google Scholar] [CrossRef]
- Sabouri, S.; Mendoza Velasco, L.A.; Catuneanu, M.; Namdari, M.; Jamshidi, K. Thermo Optical Phase Shifter With Low Thermal Crosstalk for SOI Strip Waveguide. IEEE Photonics J. 2021, 13, 1–12. [Google Scholar] [CrossRef]
- Singh, T.; Khaira, N.K.; Mansour, R.R. Thermally Actuated SOI RF MEMS-Based Fully Integrated Passive Reflective-Type Analog Phase Shifter for mmWave Applications. IEEE Trans. Microw. Theory Tech. 2021, 69, 119–131. [Google Scholar] [CrossRef]
- Gao, W.; Li, X.; Lu, L.; Liu, C.; Chen, J.; Zhou, L. Broadband 32× 32 Strictly-Nonblocking Optical Switch on a Multi-Layer Si3N4-on-SOI Platform. Laser Photonics Rev. 2023, 17, 2300275. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, W.; Zhu, W.; Lu, M.; Chen, Y.; Shi, S.; Guo, C.; Hu, G.; Cui, Y.; Yun, B. Optimization and comprehensive comparison of thermo-optic phase shifter with folded waveguide on SiN and SOI platforms. Opt. Commun. 2024, 555, 130242. [Google Scholar] [CrossRef]
- Gao, F.; Xie, W.; Tan, J.Y.S.; Leong, C.; Li, C.; Luo, X.; Lo, G.Q. Comprehensive Investigation of Thermo-Optic Phase Shifters on a Multi-Layered SiN-on-SOI Platform. J. Light. Technol. 2023, 41, 3108–3114. [Google Scholar] [CrossRef]
- Zhong, C.; Zhang, Z.; Ma, H.; Wei, M.; Ye, Y.; Wu, J.; Tang, B.; Zhang, P.; Liu, R.; Li, J.; et al. Silicon thermo-optic switches with graphene heaters operating at mid-infrared waveband. Nanomaterials 2022, 12, 1083. [Google Scholar] [CrossRef]
- Yan, S.; Zhu, X.; Frandsen, L.H.; Xiao, S.; Mortensen, N.A.; Dong, J.; Ding, Y. Slow-light-enhanced energy efficiency for graphene microheaters on silicon photonic crystal waveguides. Nat. Commun. 2017, 8, 14411. [Google Scholar] [CrossRef] [PubMed]
- Parra, J.; Hurtado, J.; Griol, A.; Sanchis, P. Ultra-low loss hybrid ITO/Si thermo-optic phase shifter with optimized power consumption. Opt. Express 2020, 28, 9393–9404. [Google Scholar] [CrossRef]
- Jacques, M.; Samani, A.; El-Fiky, E.; Patel, D.; Xing, Z.; Plant, D.V. Optimization of thermo-optic phase-shifter design and mitigation of thermal crosstalk on the SOI platform. Opt. Express 2019, 27, 10456–10471. [Google Scholar] [CrossRef]
- Harris, N.C.; Ma, Y.; Mower, J.; Baehr-Jones, T.; Englund, D.; Hochberg, M.; Galland, C. Efficient, compact and low loss thermo-optic phase shifter in silicon. Opt. Express 2014, 22, 10487–10493. [Google Scholar] [CrossRef]
- Qiu, H.; Liu, Y.; Luan, C.; Kong, D.; Guan, X.; Ding, Y.; Hu, H. Energy-efficient thermo-optic silicon phase shifter with well-balanced overall performance. Opt. Lett. 2020, 45, 4806–4809. [Google Scholar] [CrossRef]
- Miller, S.A.; Chang, Y.C.; Phare, C.T.; Shin, M.C.; Zadka, M.; Roberts, S.P.; Stern, B.; Ji, X.; Mohanty, A.; Gordillo, O.A.J.; et al. Large-scale optical phased array using a low-power multi-pass silicon photonic platform. Optica 2020, 7, 3–6. [Google Scholar] [CrossRef]
- Fang, Z.; Chen, R.; Zheng, J.; Khan, A.I.; Neilson, K.M.; Geiger, S.J.; Callahan, D.M.; Moebius, M.G.; Saxena, A.; Chen, M.E.; et al. Ultra-low-energy programmable non-volatile silicon photonics based on phase-change materials with graphene heaters. Nat. Nanotechnol. 2022, 17, 842–848. [Google Scholar] [CrossRef] [PubMed]
- Sobu, Y.; Simoyama, T.; Tanaka, S.; Tanaka, Y.; Morito, K. 70 Gbaud Operation of All-Silicon Mach–Zehnder Modulator based on Forward-Biased PIN Diodes and Passive Equalizer. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Li, X.; Xiao, X.; Xu, H.; Li, Z.; Chu, T.; Yu, J.; Yu, Y. Highly Efficient Silicon Michelson Interferometer Modulators. IEEE Photonics Technol. Lett. 2013, 25, 407–409. [Google Scholar] [CrossRef]
- Ziebell, M.; Marris-Morini, D.; Rasigade, G.; Fédéli, J.M.; Crozat, P.; Cassan, E.; Bouville, D.; Vivien, L. 40 Gbit/s low-loss silicon optical modulator based on a pipin diode. Opt. Express 2012, 20, 10591–10596. [Google Scholar] [CrossRef] [PubMed]
- Tu, X.; Liow, T.Y.; Song, J.; Luo, X.; Fang, Q.; Yu, M.; Lo, G.Q. 50-Gb/s silicon optical modulator with traveling-wave electrodes. Opt. Express 2013, 21, 12776–12782. [Google Scholar] [CrossRef]
- Azadeh, S.S.; Merget, F.; Romero-García, S.; Moscoso-Mártir, A.; von den Driesch, N.; Müller, J.; Mantl, S.; Buca, D.; Witzens, J. Low V π Silicon photonics modulators with highly linear epitaxially grown phase shifters. Opt. Express 2015, 23, 23526–23550. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Li, X.; Xiao, X.; Yu, S. Silicon intensity Mach–Zehnder modulator for single lane 100 Gb/s applications. Photonics Res. 2018, 6, 109–116. [Google Scholar] [CrossRef]
- Begović, A.; Kim, Y.H.; Jiang, L.; Anderson, S.; Huang, Z.R. Low VπLπ and Driving Voltage Interleaved Silicon Phase Shifter for Modulation Applications. IEEE Photonics J. 2022, 14, 1–6. [Google Scholar] [CrossRef]
- Cai, H.; Fu, S.; Yu, Y.; Zhang, X. Lateral-Zigzag PN Junction Enabled High-Efficiency Silicon Micro-Ring Modulator Working at 100Gb/s. IEEE Photonics Technol. Lett. 2022, 34, 525–528. [Google Scholar] [CrossRef]
- Nivethitha, V.; Sivasubramanian, A. Design and simulate the demultiplexer using photonic crystal ring resonator for DWDM system. Opt. Quantum Electron. 2024, 56, 98. [Google Scholar] [CrossRef]
- Westerveld, W.J.; Mahmud-Ul-Hasan, M.; Shnaiderman, R.; Ntziachristos, V.; Rottenberg, X.; Severi, S.; Rochus, V. Sensitive, small, broadband and scalable optomechanical ultrasound sensor in silicon photonics. Nat. Photonics 2021, 15, 341–345. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. A Review of Photonic Sensors Based on Ring Resonator Structures: Three Widely Used Platforms and Implications of Sensing Applications. Micromachines 2023, 14, 1080. [Google Scholar] [CrossRef]
- Paschotta, R. Q Factor. RP Photonics Encyclopedia. 2006. Available online: https://www.rp-photonics.com/q_factor.html (accessed on 13 May 2024).
- Kumari, S.; Prince, S. Photonic Beamforming Incorporating Ring Resonator Based on Silicon-on-Insulator Waveguide Technology. Silicon 2022, 14, 8869–8879. [Google Scholar] [CrossRef]
- Robinson, J.T.; Chen, L.; Lipson, M. On-chip gas detection in silicon optical microcavities. Opt. Express 2008, 16, 4296–4301. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, G.A.; Hu, S.; Weiss, S.M. Porous silicon ring resonator for compact, high sensitivity biosensing applications. Opt. Express 2015, 23, 7111–7119. [Google Scholar] [CrossRef]
- Kundal, S.; Khandelwal, A. Improving the performance of ring resonator refractive index sensor through structural modifications. Optik 2024, 296, 171555. [Google Scholar] [CrossRef]
- Saha, N.; Brunetti, G.; di Toma, A.; Armenise, M.N.; Ciminelli, C. Silicon Photonic Filters: A Pathway from Basics to Applications. Adv. Photonics Res. 2024, 2300343. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amanti, F.; Andrini, G.; Armani, F.; Barbato, F.; Bellani, V.; Bonaiuto, V.; Cammarata, S.; Campostrini, M.; Dao, T.H.; De Matteis, F.; et al. Integrated Photonic Passive Building Blocks on Silicon-on-Insulator Platform. Photonics 2024, 11, 494. https://doi.org/10.3390/photonics11060494
Amanti F, Andrini G, Armani F, Barbato F, Bellani V, Bonaiuto V, Cammarata S, Campostrini M, Dao TH, De Matteis F, et al. Integrated Photonic Passive Building Blocks on Silicon-on-Insulator Platform. Photonics. 2024; 11(6):494. https://doi.org/10.3390/photonics11060494
Chicago/Turabian StyleAmanti, Francesco, Greta Andrini, Fabrizio Armani, Fabrizio Barbato, Vittorio Bellani, Vincenzo Bonaiuto, Simone Cammarata, Matteo Campostrini, Thu Ha Dao, Fabio De Matteis, and et al. 2024. "Integrated Photonic Passive Building Blocks on Silicon-on-Insulator Platform" Photonics 11, no. 6: 494. https://doi.org/10.3390/photonics11060494
APA StyleAmanti, F., Andrini, G., Armani, F., Barbato, F., Bellani, V., Bonaiuto, V., Cammarata, S., Campostrini, M., Dao, T. H., De Matteis, F., Demontis, V., Donati, S., Di Giuseppe, G., Ditalia Tchernij, S., Fontana, A., Forneris, J., Frontini, L., Gunnella, R., Iadanza, S., ... Vitali, V. (2024). Integrated Photonic Passive Building Blocks on Silicon-on-Insulator Platform. Photonics, 11(6), 494. https://doi.org/10.3390/photonics11060494









