Cryogenic Thermo-Optical Coefficient of SU-8 Measured Using a Racetrack Resonator at 850 nm
Abstract
1. Introduction
2. Materials and Methods
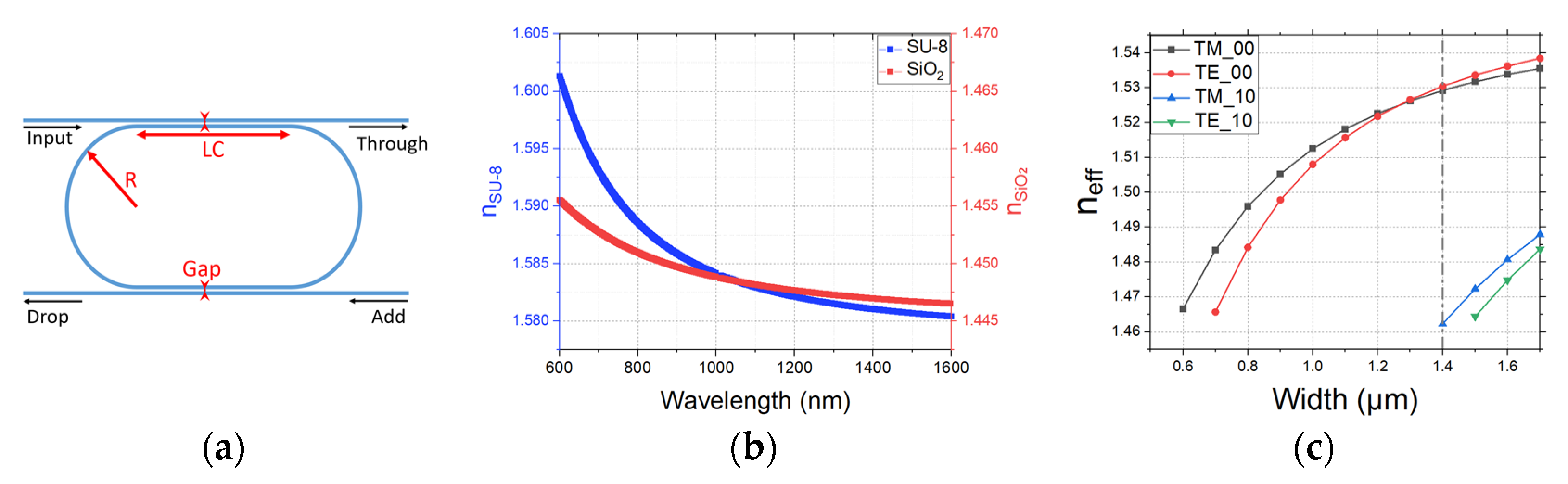
2.1. Racetrack Design and Modelling
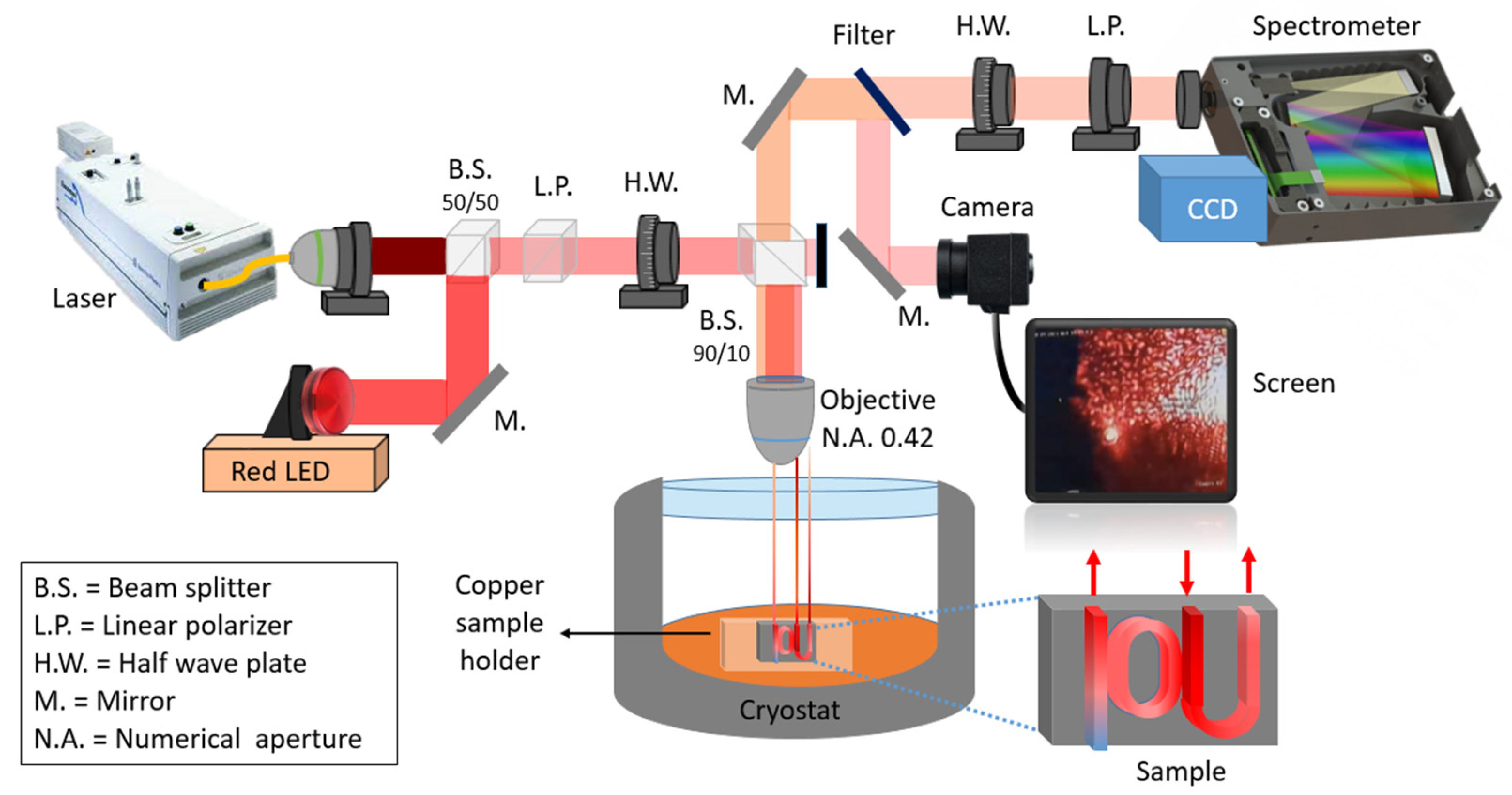
2.2. Racetrack Fabrication and Characterization Setup
3. Results
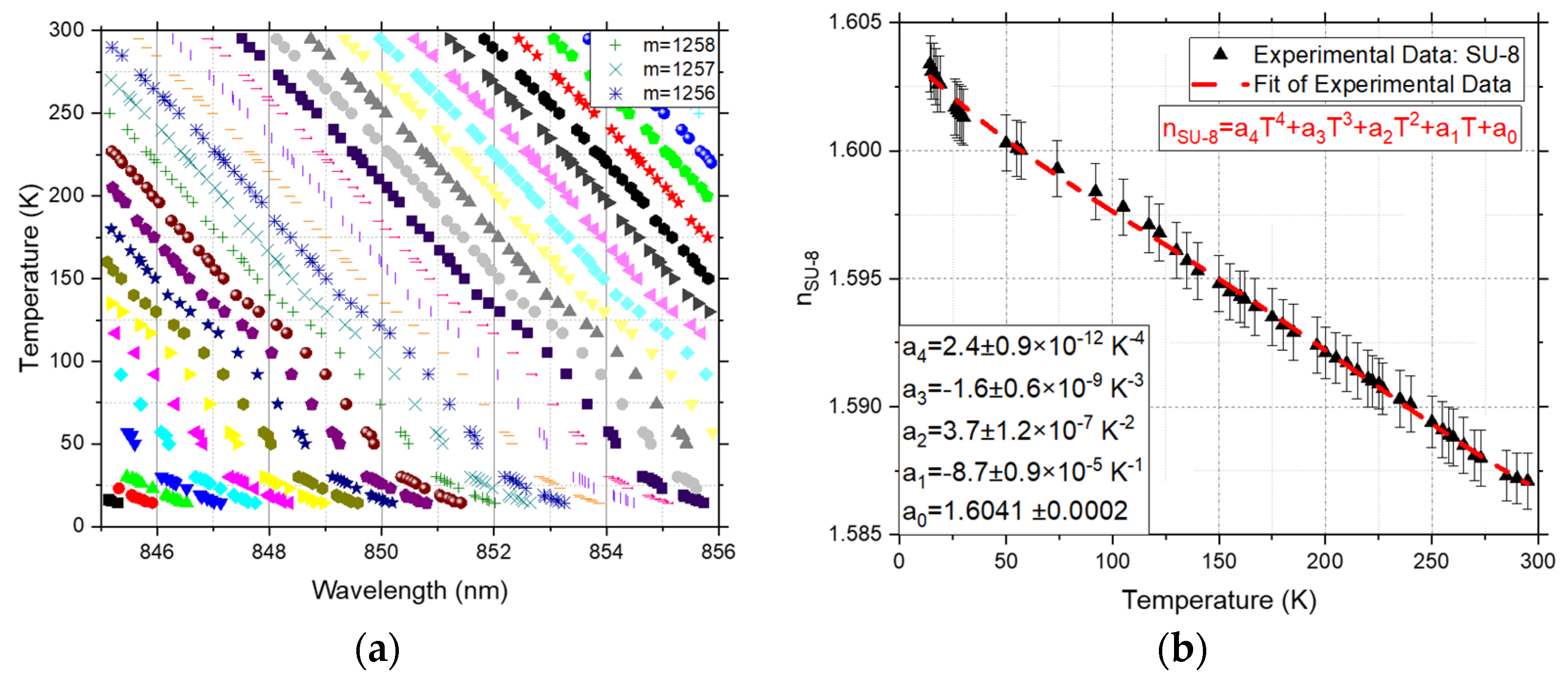
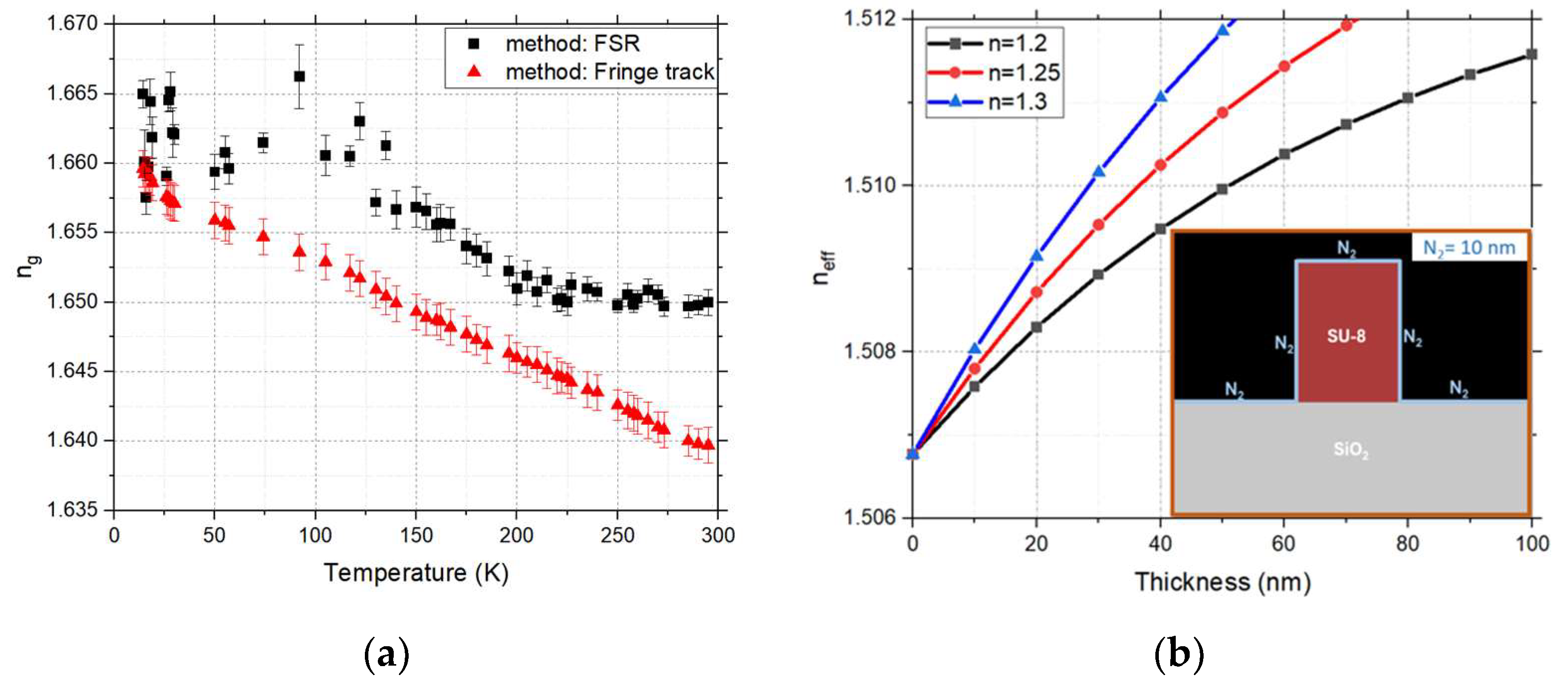
3.1. Q-Factor and Tracking of neff for Multiple Resonance: Fringe Tracking
3.2. Measurement of
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Osgood, R., Jr.; Meng, X. Chapter 1 Integrated Optics: An Overview. In Principles of Photonic Integrated Circuits—Materials, Device Physics, Guided Wave Design, 1st ed.; Springer Nature: Berlin, Germany, 2021; pp. 1–9. [Google Scholar]
- Xin, Y.; Pandraud, G.; Zhang, Y.; French, P. Single-mode tapered vertical SU-8waveguide fabricated by E-beam lithography for analyte sensing. Sensors 2019, 19, 3383. [Google Scholar] [CrossRef]
- Hwang, Y.; Phillips, N.; Otten, D.E.; Riesen, N.; Lancaster, D.G. Efficient coupling between single mode fibers and glass chip waveguides via graded refractive index fiber tips. Opt. Express 2022, 30, 12294–12307. [Google Scholar] [CrossRef] [PubMed]
- Zuo, H.; Yu, S.; Gu, T.; Hu, J. Low loss, flexible single-mode polymer photonics. Opt. Express 2019, 27, 11152. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xu, H.; Zhang, G.; Chen, Y.; Wang, H.; Tan, K.H.; Wicaksono, S.; Sun, C.; Kong, Q.; Wang, C.; et al. Hybrid and heterogeneous photonic integrated near-infrared InGaAs/InAlAs single-photon avalanche diode. Quantum Sci. Technol. 2023, 8, 025009. [Google Scholar] [CrossRef]
- Pelucchi, E.; Fagas, G.; Aharonovich, I.; Englund, D.; Figueroa, E.; Gong, Q.; Hannes, H.; Liu, J.; Lu, C.Y.; Matsuda, N.; et al. The potential and global outlook of integrated photonics for quantum technologies. Nat. Rev. Phys. 2022, 4, 194–208. [Google Scholar] [CrossRef]
- Baranov, A.I.; Kudyashov, D.A.; Morozov, I.A.; Shugurov, K.Y.; Uvarov, A.V.; Maximova, A.A.; Vyacheslavova, E.A.; Gudovskikh, A.S. The SU-8 spin-coating on silicon nanowires formed by cryogenic dry etching. J. Phys. Conf. Ser. 2021, 2086, 012078. [Google Scholar] [CrossRef]
- Kim, Y.K.; Yi, S.H.; Kim, S.W.; Ju, B.K. A novel low-temperature microcap packaging using SU-8 bonding. In Proceedings of the TRANSDUCERS 2007–2007 International Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 2107–2110. [Google Scholar]
- Lima, R.S.; Leão, P.A.; Piazzetta, M.H.; Monteiro, A.M.; Shiroma, L.Y.; Gobbi, A.L.; Carrilho, E. Sacrificial adhesive bonding: A powerful method for fabrication of glass microchips. Sci. Rep. 2015, 5, 13276. [Google Scholar] [CrossRef] [PubMed]
- Gangnaik, A.S.; Georgiev, Y.M.; Holmes, J.D. New Generation Electron Beam Resists: A Review. Chem. Mater. 2017, 29, 1898–1917. [Google Scholar] [CrossRef]
- Tu, X.; Chen, S.L.; Song, C.; Huang, T.; Guo, L.J. Ultrahigh Q Polymer Microring Resonators for Biosensing Applications. IEEE Photonics J. 2019, 11, 4200110. [Google Scholar] [CrossRef]
- Ng, K.B.; Chong, W.Y.; Lim, C.S.; Ahmad, H. Single-mode SU-8 waveguide fabricated using ultrafast direct laser writing. Optik 2022, 270, 170068. [Google Scholar] [CrossRef]
- Leviton, D.B.; Frey, B.J. Temperature-dependent absolute refractive index measurements of synthetic fused silica. In Optomechanical Technologies for Astronomy; SPIE: Bellingham, WA, USA, 2006; p. 62732K. [Google Scholar] [CrossRef]
- Borreman, A.; Musa, S.; Kok, A.A.M.; Diemeer, M.; Driessen, A. Fabrication of polymeric multimode waveguides and devices in SU-8 photoresist using selective polymerization. In Proceedings of the 7th IEEE/LEOS Benelux Chapter Annual Symposium, Amsterdam, The Netherlands, 9 December 2002; Vrije Universiteit: Amsterdam, Netherlands, 2002. [Google Scholar]
- Schimpf, C.; Manna, S.; da Silva, S.F.C.; Aigner, M.; Rastelli, A. Entanglement-based quantum key distribution with a blinking-free quantum dot operated at a temperature up to 20 K. Adv. Photonics 2021, 3, 065001. [Google Scholar] [CrossRef]
- Liao, S.K.; Cai, W.Q.; Liu, W.Y.; Zhang, L.; Li, Y.; Ren, J.G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Yano, O.; Yamaokat, H. Cryogenic properties of polymers. Prog. Polym. Sci. 1995, 20, 585–613. [Google Scholar] [CrossRef]
- Chen, D.; Li, J.; Yuan, Y.; Gao, C.; Cui, Y.; Li, S.; Liu, X.; Wang, H.; Peng, C.; Wu, Z. A review of the polymer for cryogenic application: Methods, mechanisms and perspectives. Polymers 2021, 13, 320. [Google Scholar] [CrossRef]
- Lee, K.H.; Green, A.M.; Taylor, R.A.; Sharp, D.N.; Turberfield, A.J.; Brossard, F.S.; Williams, D.A.; Briggs, G.A.D. Cryogenic two-photon laser photolithography with SU-8. Appl. Phys. Lett. 2006, 88, 6–9. [Google Scholar] [CrossRef]
- Rego, G. Temperature Dependence of the Thermo-Optic Coefficient of SiO2 Glass. Sensors 2023, 23, 6023. [Google Scholar] [CrossRef]
- Elshaari, A.W.; Zadeh, I.E.; Jöns, K.D.; Zwiller, V. Thermo-Optic Characterization of Silicon Nitride Resonators for Cryogenic Photonic Circuits. IEEE Photonics J. 2016, 8, 2701009. [Google Scholar] [CrossRef]
- Cariou, J.M.; Dugas, J.; Martin, L.; Michel, P. Refractive-index variations with temperature of PMMA and polycarbonate. Appl. Opt. 1986, 25, 334. [Google Scholar] [CrossRef]
- Leviton, D.B.; Frey, B.J. Cryogenic High-Accuracy Refraction Measuring System (CHARMS): A new facility for cryogenic infrared through far-ultraviolet refractive index measurements. Opt. Fabr. Metrol. Mater. Adv. Telesc. 2004, 5494, 492. [Google Scholar] [CrossRef]
- Liao, S.; Ni, L.; Ren, Q.F. Design of a cryogenic absolute prism refractometer for infrared optical materials. In Seventh International Symposium on Precision Engineering Measurements and Instrumentation; SPIE: Bellingham, WA, USA, 2011; Volume 8321. [Google Scholar] [CrossRef]
- Mendoza-Castro, J.H.; Vorobev, A.S.; Iadanza, S.; Lendl, B.; Grande, M.; O’Faolain, L. Enhanced Fano resonances in a Silicon Nitride Photonic Crystal Nanobeam-assisted Micro Ring Resonator for dual telecom band operation. In Proceedings of the 2023 Conference on Lasers and Electro-Optics Europe and European Quantum Electronics Conference, CLEO/Europe-EQEC 2023, Munich, Germany, 26–30 June 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Yang, L.; Dai, D.; He, J.J.; He, S. Observation of the thermal nonlinear optical effect in a microring resonator based on a small SU-8 polymer ridge optical waveguide. In Proceedings of the 2009 Asia Communications and Photonics Conference and Exhibition, ACP 2009, Shanghai, China, 2–6 December 2009. [Google Scholar] [CrossRef]
- Dai, D.; Yang, B.; Yang, L.; Sheng, Z. Design and fabrication of SU-8 polymer-based micro-racetrack resonators. Passiv. Compon. Fiber-Based Devices V 2008, 7134, 713414. [Google Scholar] [CrossRef]
- Samanta, S.; Dey, P.K.; Banerji, P.; Ganguly, P. Development of micro-ring resonator-based optical bandpass filter using SU-8 polymer and optical lithography. Opt. Mater. 2018, 77, 122–126. [Google Scholar] [CrossRef]
- Ariannejad, M.M.; Amiri, I.S.; Azzuhri, S.R.B.; Zakaria, R.; Yupapin, P. Polarization dependence of SU-8 micro ring resonator. Results Phys. 2018, 11, 515–522. [Google Scholar] [CrossRef]
- Huang, Y.; Paloczi, G.T.; Yariv, A.; Zhang, C.; Dalton, L.R. Fabrication and replication of polymer integrated optical devices using electron-beam lithography and soft lithography. J. Phys. Chem. B 2004, 108, 8606–8613. [Google Scholar] [CrossRef]
- Lee, Y.; Zhang, H.F.; Sun, C. Highly sensitive ultrasound detection using nanofabricated polymer micro-ring resonators. Nano Converg. 2023, 10, 30. [Google Scholar] [CrossRef] [PubMed]
- Finardi, C.A.; Carvalho, W., Jr.; Zoldan, V.C.; Panepucci, R.R.; Malheiros-Silveira, G.N. Foundry produced SU-8 inverted-rib waveguide-based components. In Optical Manufacturing and Testing XIII; SPIE: Bellingham, WA, USA, 2020; Volume 11487. [Google Scholar]
- Malheiros-Silveira, G.N.; Finardi, C.A.; Bürger, T.S.; Van Etten, E.A.; Da Silva, R.C.; Coelho, A.V.; Daltrini, A.M.; Panepucci, R.R. High-resolution notch filters and diplexers based on SU-8 inverted rib waveguides. Appl. Opt. 2019, 58, 7331–7335. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Li, Y.; Yao, M.; Lv, X.; Liang, J.; Wu, Y.; Zhang, D. Low power consumption polymer/silica hybrid thermo-optic switch based on racetrack resonator. IEEE Photonics J. 2022, 14, 6634006. [Google Scholar] [CrossRef]
- Chakraborty, T.; Gordillo, O.A.J.; Barrow, M.; Lipson, M.; Murphy, T.E.; Grutter, K.E. Thermo-Optic Characterization of SU-8 at Cryogenic Temperature. Opt. Mater. Express 2024, 14, 435–444. [Google Scholar] [CrossRef]
- Material Properties: Silicon. Available online: https://trc.nist.gov/cryogenics/materials/Silicon/Silicon.htm (accessed on 14 August 2024).
- Carrasco, E.; Castillo, J.M.; Escribano, R.; Herrero, V.J.; Moreno, M.A.; Rodrıguez, J. A cryostat for low-temperature spectroscopy of condensable species. Rev. Sci. Instrum. 2002, 73, 3469–3473. [Google Scholar] [CrossRef]
- Öberg, K.I.; van Dishoeck, E.F.; Linnartz, H. Photodesorption of ices I: CO2 and N2. Astron. Astrophys. 2009, 496, 281–293. [Google Scholar] [CrossRef]
- Fray, N.; Schmitt, B. Sublimation of ices of astrophysical interest: A bibliographic review. Planet. Space Sci. 2009, 57, 2053–2080. [Google Scholar] [CrossRef]
- Rocha, W.R.M.; Pilling, S.; Domaracka, A.; Rothard, H.; Boduch, P. Infrared complex refractive index of N-containing astrophysical ices free of water processed by cosmic-ray simulated in laboratory. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 228, 117826. [Google Scholar] [CrossRef] [PubMed]

| Temperature (λ = 850 nm) | nSU-8 | neff | ng | FSR (nm) |
|---|---|---|---|---|
| 295 K | 1.587 | 1.496 | 1.639 | 0.620 |
| 14 K | 1.600 | 1.508 | 1.655 | 0.614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina-Rangel, S.A.; Maraviglia, N.; O’Hara, J.; Vorobev, A.S.; Iadanza, S.; Pelucchi, E.; O’Faolain, L. Cryogenic Thermo-Optical Coefficient of SU-8 Measured Using a Racetrack Resonator at 850 nm. Photonics 2024, 11, 800. https://doi.org/10.3390/photonics11090800
Medina-Rangel SA, Maraviglia N, O’Hara J, Vorobev AS, Iadanza S, Pelucchi E, O’Faolain L. Cryogenic Thermo-Optical Coefficient of SU-8 Measured Using a Racetrack Resonator at 850 nm. Photonics. 2024; 11(9):800. https://doi.org/10.3390/photonics11090800
Chicago/Turabian StyleMedina-Rangel, Salvador A., Nicola Maraviglia, John O’Hara, Artem S. Vorobev, Simone Iadanza, Emanuele Pelucchi, and Liam O’Faolain. 2024. "Cryogenic Thermo-Optical Coefficient of SU-8 Measured Using a Racetrack Resonator at 850 nm" Photonics 11, no. 9: 800. https://doi.org/10.3390/photonics11090800
APA StyleMedina-Rangel, S. A., Maraviglia, N., O’Hara, J., Vorobev, A. S., Iadanza, S., Pelucchi, E., & O’Faolain, L. (2024). Cryogenic Thermo-Optical Coefficient of SU-8 Measured Using a Racetrack Resonator at 850 nm. Photonics, 11(9), 800. https://doi.org/10.3390/photonics11090800







