Study of Reducing Atmospheric Turbulence-Induced Beam Wander of a Twisted Electromagnetic Elliptical Vortex Beam
Abstract
1. Introduction
2. BW of a TPCEV Beam in Non-Kolmogorov Atmospheric Turbulence
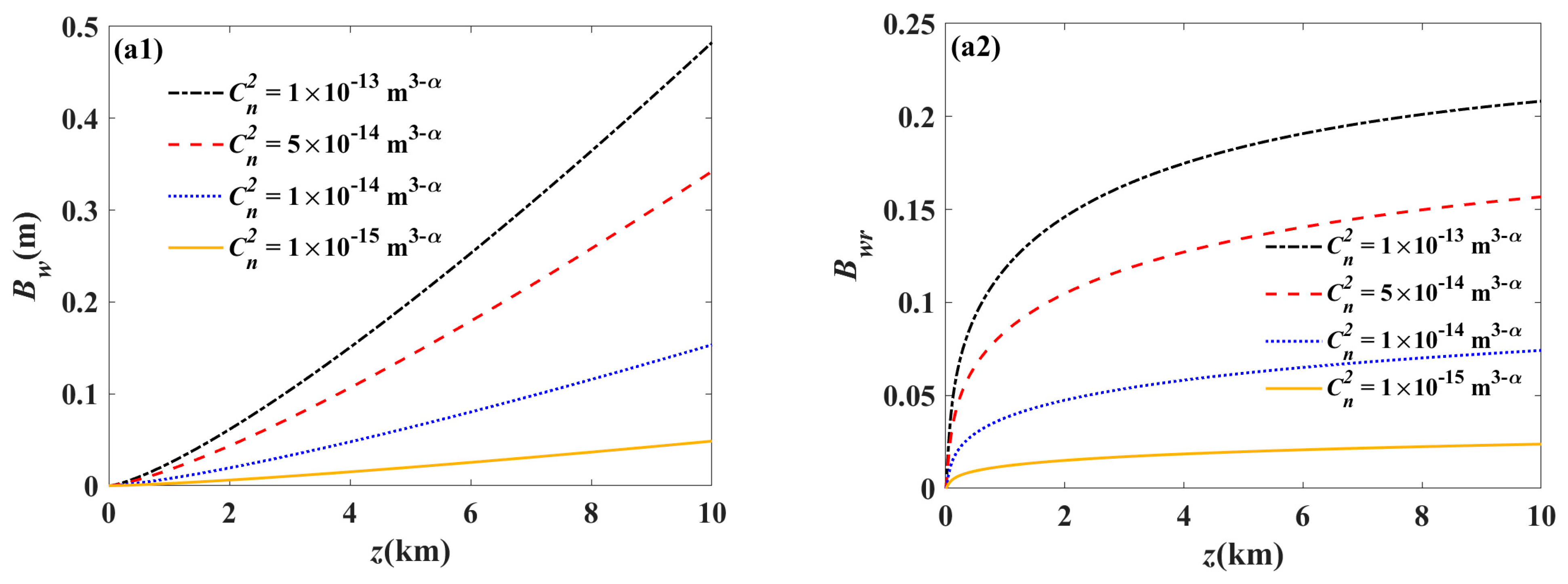
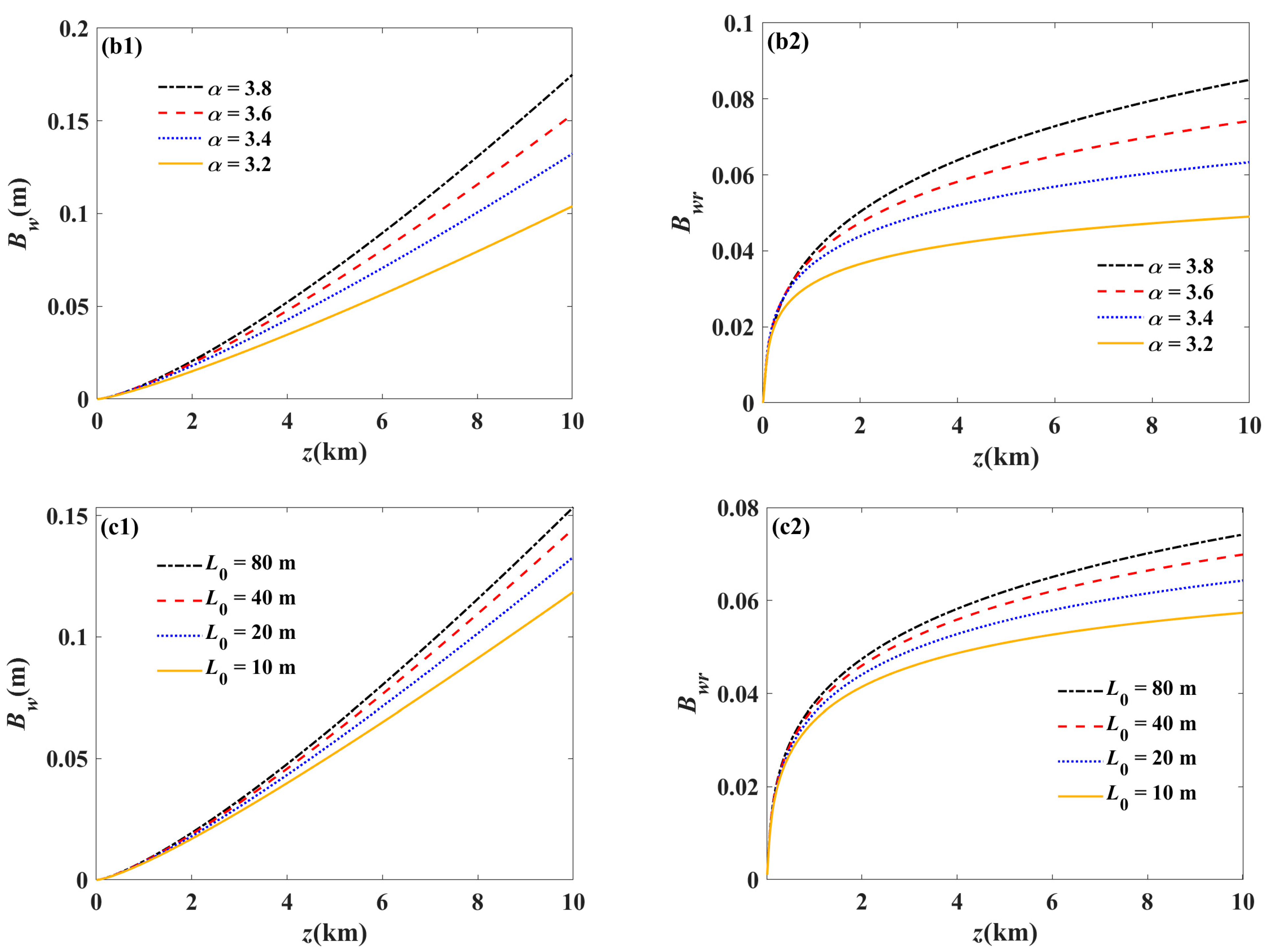
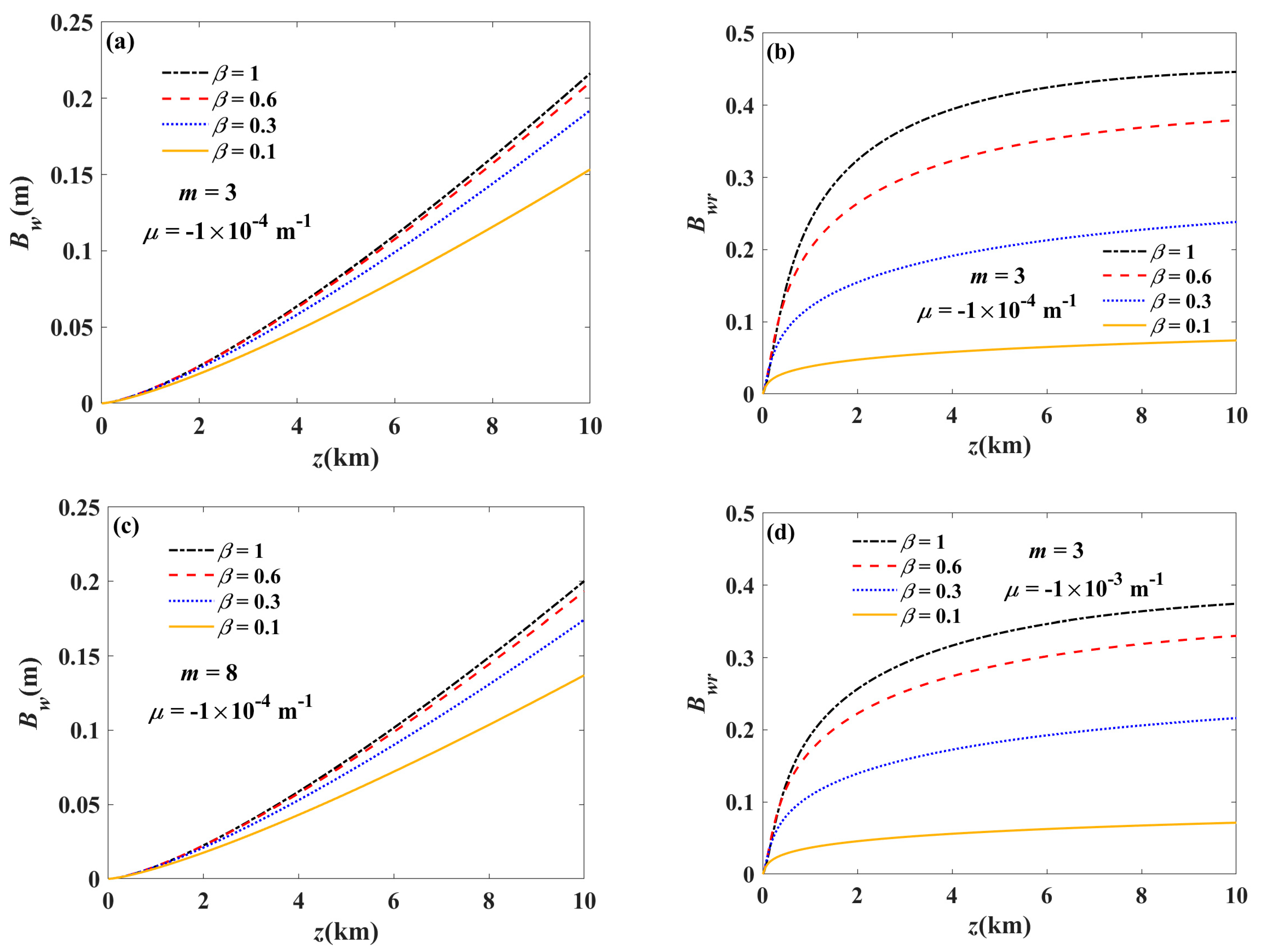
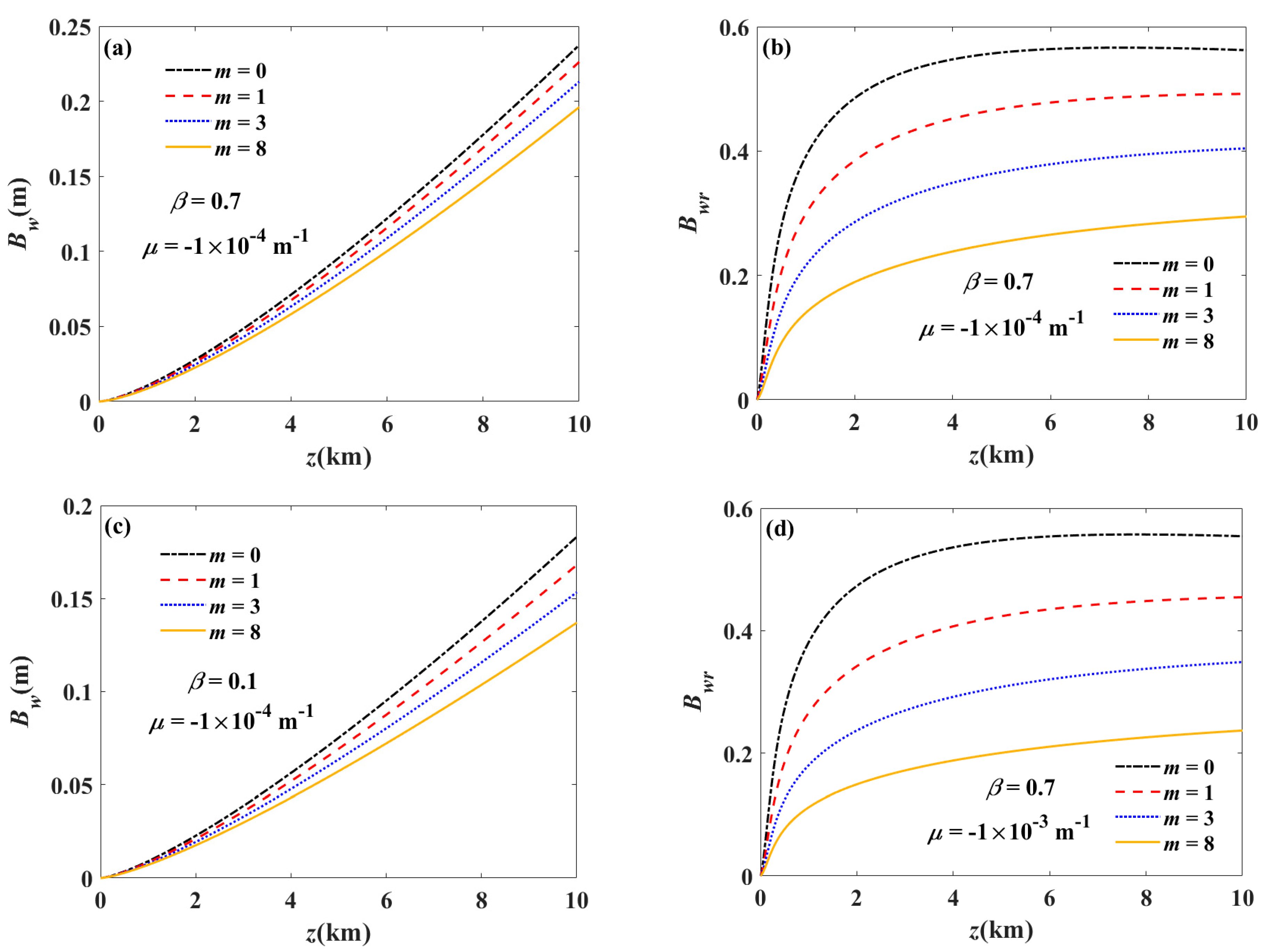
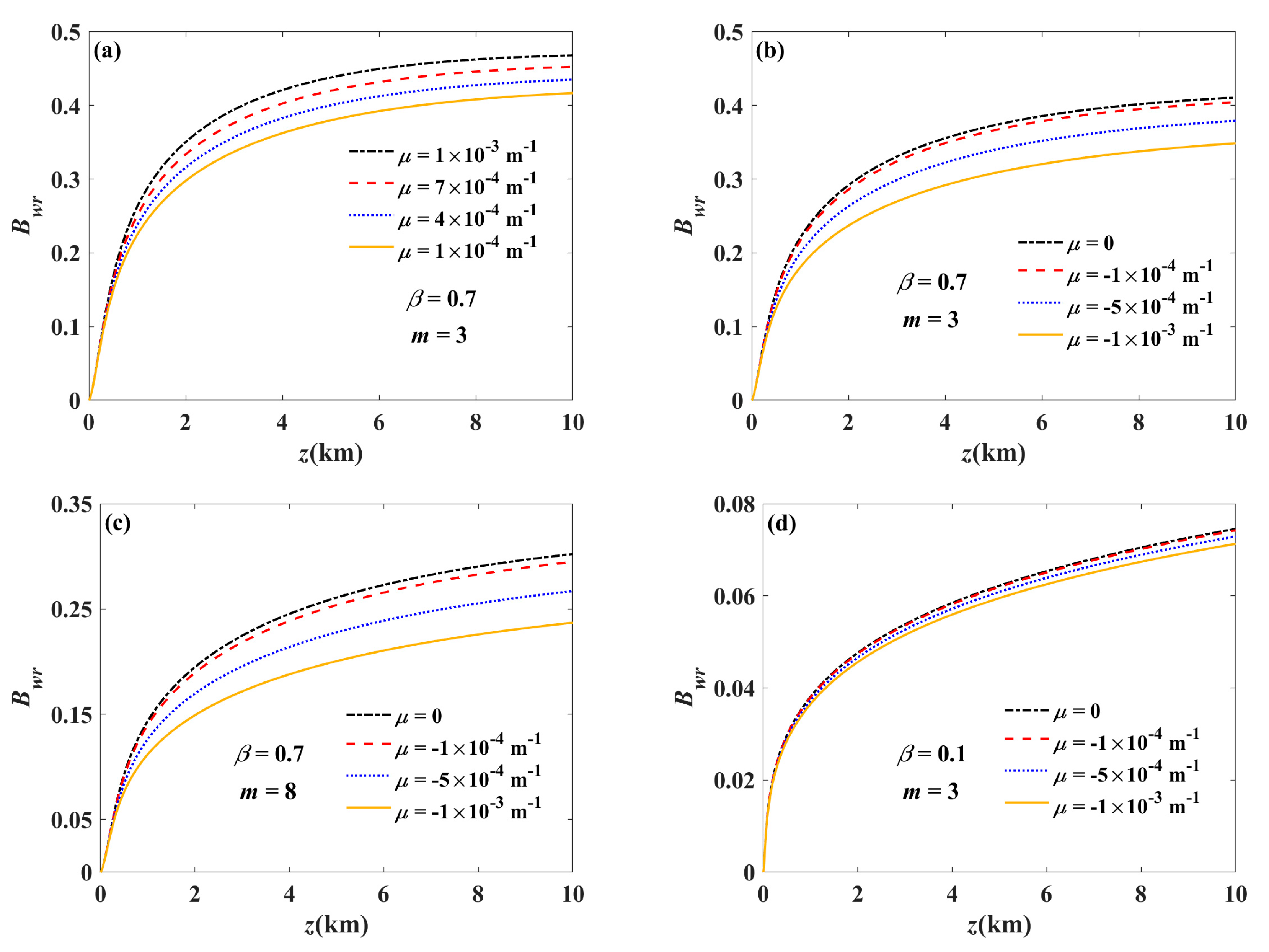
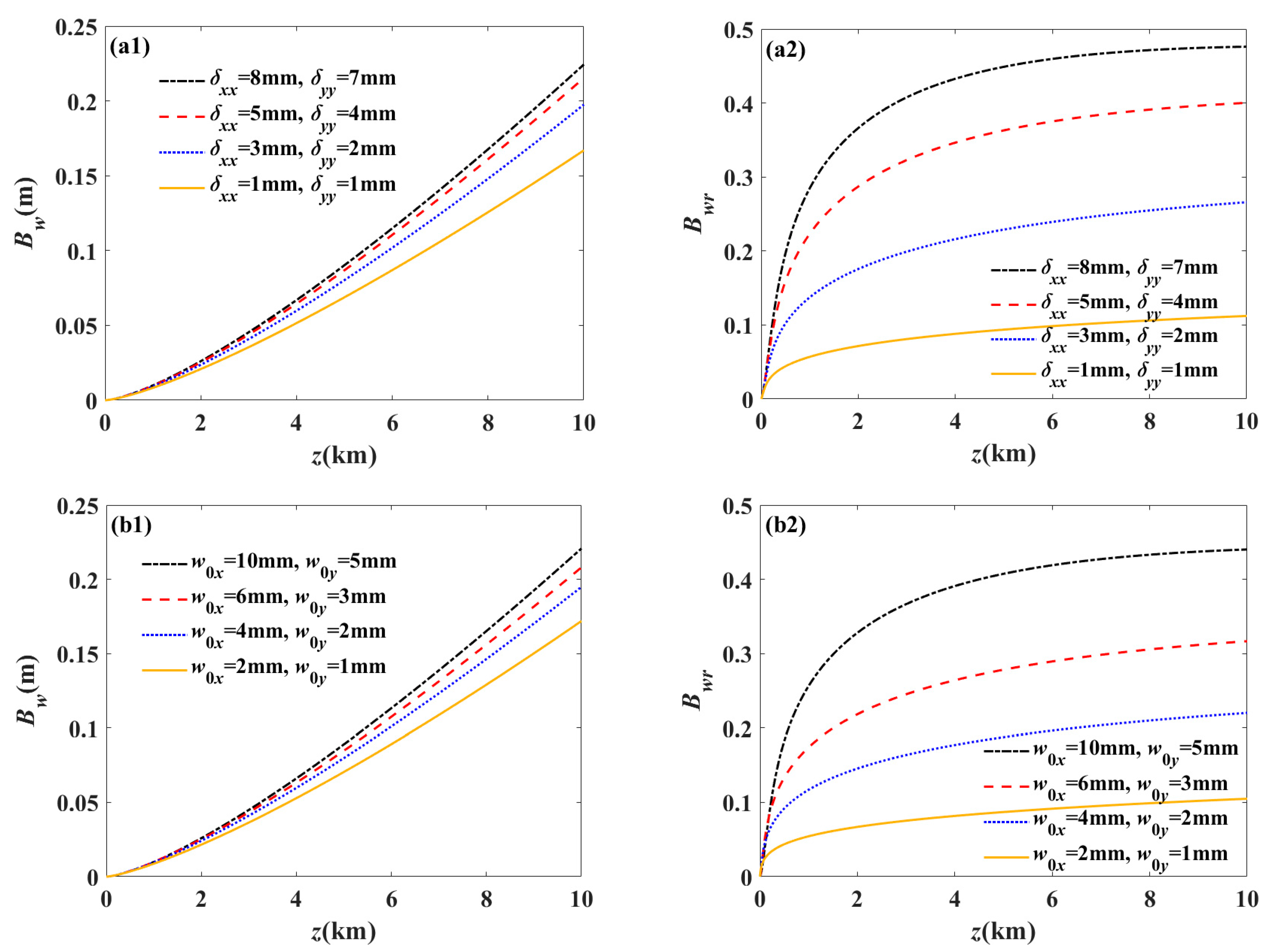
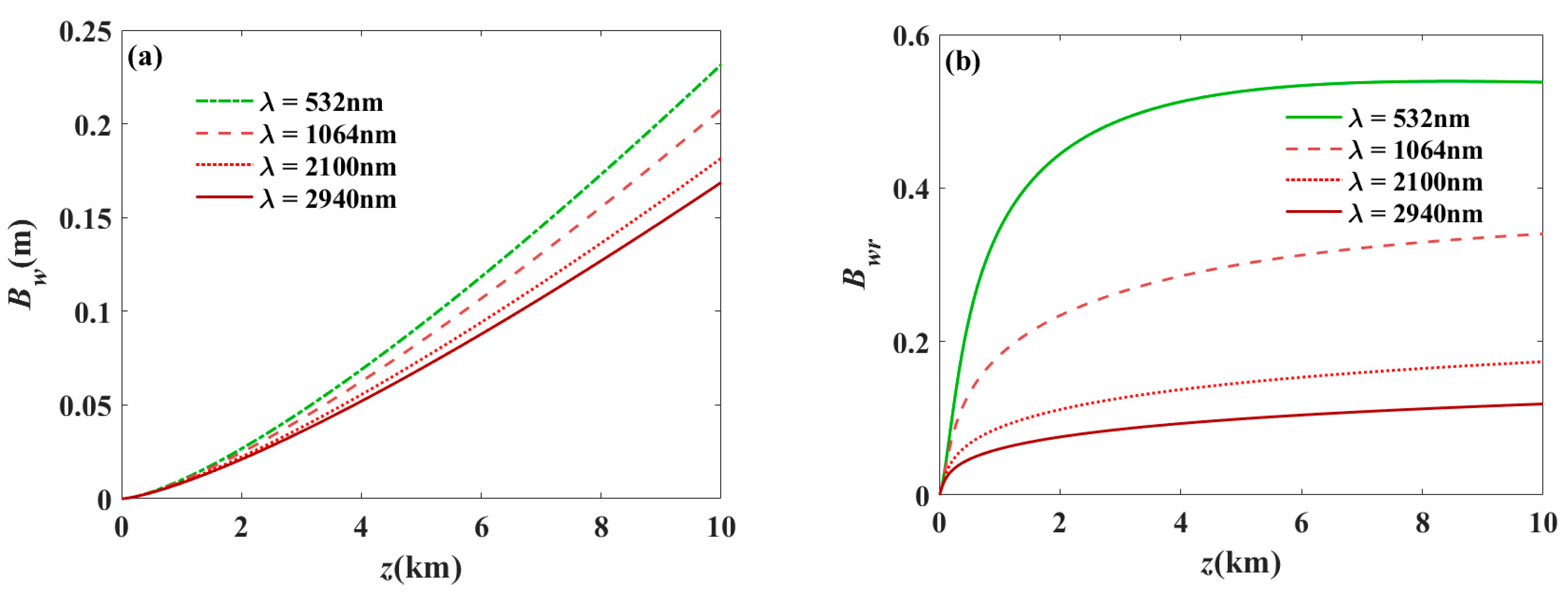
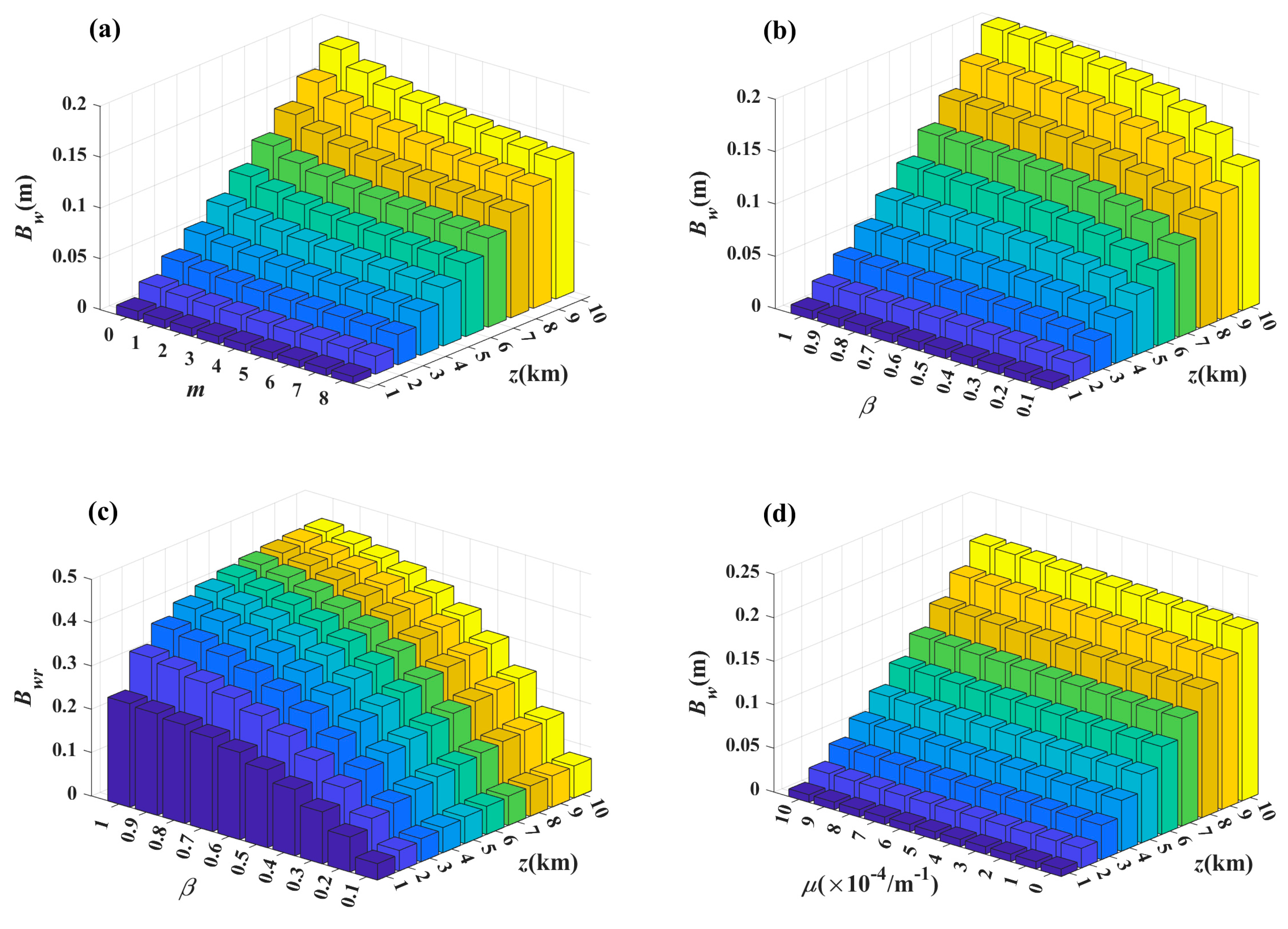
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kolmogorov, A.N. The local structure of turbulence in an incompressible viscous fluid for very large Reynolds numbers. C. R. Acad. Sci. URSS 1941, 30, 301–305. [Google Scholar]
- Kolmogorov, A.N. Dissipation of energy in the locally isotropic turbulence. C. R. Acad. Sci. URSS 1941, 32, 16–18. [Google Scholar]
- Ho, T.L. Coherence degration of Gaussian beams in a turbulent atmosphere. J. Opt. Soc. Am. 1970, 60, 667–673. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Dan, Y.; Zhang, B. Second moments of partially coherent beams in atmospheric turbulence. Opt. Lett. 2009, 34, 563–565. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Li, Y.; Zhao, X. Intensity and effective beam width of partially coherent Laguerre-Gaussian beams through a turbulent atmosphere. J. Opt. Soc. Am. A 2015, 32, 1623–1630. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Dai, W.; Tang, H.; Guo, H. Beam wander of random electromagnetic Gaussian-shell model vortex beams propagating through a Kolmogorov turbulence. Opt. Commun. 2015, 336, 55–58. [Google Scholar] [CrossRef]
- Wen, W.; Chu, X.; Cai, Y. Dependence of the beam wander of an airy beam on its kurtosis parameter in a turbulent atmosphere. Opt. Laser Technol. 2015, 68, 6–10. [Google Scholar] [CrossRef]
- Xu, Y.; Dan, Y.; Zhang, B. Spreading and M2-factor based on second-order moments for partially-coherent anomalous hollow beam in turbulent atmosphere. Optik 2016, 127, 4590–4595. [Google Scholar] [CrossRef]
- Huang, K.; Xu, Y.; Li, Y. Average intensity of a Laguerre-Gaussian vector vortex beam through inhomogeneous atmospheric turbulence. Photonics 2023, 10, 1189. [Google Scholar] [CrossRef]
- Shchepakina, E.; Korotkova, O. Second-order statistics of stochastic electromagnetic beams propagating through non-Kolmogorov turbulence. Opt. Express 2010, 18, 10650–10658. [Google Scholar] [CrossRef]
- Toselli, I.; Andrews, L.C.; Phillips, R.L.; Ferrero, V. Angle of arrival fluctuations for free space laser beam propagation through non-Kolmogorov turbulence. Proc. SPIE 2007, 6551, 149–160. [Google Scholar]
- Wang, Y.; Bai, L.; Xie, J.; Zhang, D.; Lv, Q.; Guo, L. Spiral spectrum of high-order elliptic Gaussian vortex beams in a non-Kolmogorov turbulent atmosphere. Opt. Express 2021, 29, 16056–16072. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, J.; Deng, D. Second-order statistics of a partially coherent electromagnetic rotating elliptical Gaussian vortex beam through non-Kolmogorov turbulence. Opt. Express 2018, 26, 21249–21257. [Google Scholar] [CrossRef]
- Xu, Y.; Dan, Y.; Yu, J.; Cai, Y. Kurtosis parameter K of arbitrary electromagnetic beams propagating through non-Kolmogorov turbulence. J. Mod. Opt. 2017, 64, 1976–1987. [Google Scholar] [CrossRef]
- Huang, Y.; Zeng, A.; Gao, Z.; Zhang, B. Beam wander of partially coherent array beams through non-Kolmogorov turbulence. Opt. Lett. 2015, 40, 1619–1622. [Google Scholar] [CrossRef]
- Xu, Y.; Tian, H.; Dan, Y.; Feng, H.; Wang, S. Beam wander and M2-factor of partially coherent electromagnetic hollow Gaussian beam propagating through non-Kolmogorov turbulence. J. Mod. Opt. 2017, 64, 844–854. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, X.; Wang, F.; Wei, D.; Gbur, G.; Cai, Y. Experimental study of reducing beam wander by modulating the coherence structure of structured light beams. Opt. Lett. 2019, 44, 4371–4374. [Google Scholar] [CrossRef]
- Zeng, T.; Gui, Y.; Guo, J.; Guo, L. Suppressing turbulence-induced laser beam wandering by using an axicon. Opt. Lett. 2023, 48, 5077–5080. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Yuan, C.; Zheng, G.; Chen, Y. Beam wander of partially coherent twisted elliptical vortex beam in turbulence. Optik 2020, 218, 165037. [Google Scholar] [CrossRef]
- Khan, S.; Joshia, S.; Kanseri, B.; Senthilkumaran, P. Detection of partially coherent polarization singular vector beams using Stokes polarimetry. Appl. Phys. Lett. 2021, 118, 051104. [Google Scholar] [CrossRef]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]
- Dan, Y.; Zhang, B. Beam propagation factor of partially coherent flat-topped beams in a turbulent atmosphere. Opt. Express 2008, 16, 15563–15575. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Cai, Y.; Qu, J.; Eyyuboğlu, H.T.; Baykal, Y.; Korotkova, O. M2-factor of coherent and partially coherent dark hollow beams propagating in turbulent atmosphere. Opt. Express 2009, 17, 17344–17356. [Google Scholar] [CrossRef]
- Wu, Z.; Feng, Z.; Ye, S.; Song, B.; Wei, R.; Yu, C. Beam properties of a partially coherent beam propagating horizontally in atmospheric turbulence. Photonics 2023, 10, 477. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Ma, Z.; Pan, Y.; Dou, J.; Zhao, J.; Li, B.; Hu, Y. Statistical properties of partially coherent higher-order Laguerre-Gaussian power-exponent phase vortex beams. Photonics 2023, 10, 461. [Google Scholar] [CrossRef]
- Bai, Y.; Lv, H.; Fu, X.; Yang, Y. Vortex beam: Generation and detection of orbital angular momentum [Invited]. Chin. Opt. Lett. 2022, 20, 012601. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 69. [Google Scholar] [CrossRef]
- Yao, J.; Qin, Y.; Bai, Y.; Gao, M.; Zhou, L.; Li, J.; Jiang, Y.; Yang, Y. Generation of Optical Vortices by Diffraction from Circular Apertures. ACS Photonics 2023, 10, 4267–4272. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Elliptic Gaussian optical vortex. Phys. Rev. A 2017, 95, 053805. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A. Controlling orbital angular momentum of an optical vortex by varying its ellipticity. Opt. Commun. 2018, 410, 202–205. [Google Scholar] [CrossRef]
- Wu, K.; Huai, Y.; Zhao, T.; Jin, Y. Propagation of partially coherent four-petal elliptic Gaussian vortex beams in atmospheric turbulence. Opt. Express 2018, 26, 30061–30075. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Liu, L.; Yu, J.; Liu, X.; Cai, Y.; Baykal, Y.; Li, W. Propagation of a radially polarized twisted Gaussian Schell-model beam in turbulent atmosphere. J. Opt. 2016, 18, 125601. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Guo, Y.; Qian, X.; Zhu, W.; Li, J. Changes in orbital angular momentum distribution of a twisted partially coherent array beam in anisotropic turbulence. Opt. Express 2022, 30, 36665–36677. [Google Scholar] [CrossRef]
- Mays, J.; Gbur, G. Angular momentum of vector-twisted-vortex Gaussian Schell-model beams. J. Opt. Soc. Am. A 2023, 40, 1417–1424. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Qi, G.; Wu, Y.; Shi, Y.; Zhao, C.; Jin, S. Partially coherent twisted vector vortex beam enabling manipulation of high-dimensional classical entanglement. Opt. Express 2023, 31, 38305–38317. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, H.; Liu, L.; Chen, Y.; Wang, F.; Cai, Y. Experimental synthesis and demonstration of the twisted Laguerre-Gaussian Schell-mode beam. Photonics 2023, 10, 314. [Google Scholar] [CrossRef]
- Liu, L.; Wang, H.; Liu; Ye, Y.; Wang, F.; Cai, Y.; Peng, X. Radially polarized twisted partially coherent vortex beams. Opt. Express 2022, 30, 7511–7525. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Z.; Liu, L.; Chen, Y.; Wang, F.; Cai, Y. Orbital angular momentum spectra of twisted Laguerre-Gaussian Schell-model beams propagating in weak-to-strong Kolmogorov atmospheric turbulence. Opt. Express 2023, 31, 916–928. [Google Scholar] [CrossRef]
- Tong, Z.; Korotkova, O. Beyond the classical Rayleigh limit with twisted light. Opt. Lett. 2012, 37, 2595–2597. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, X.; Zhao, C.; Wang, F.; Gbur; Greg; Cai, Y. Spiral spectrum of a Laguerre-Gaussian beam propagating in anisotropic non-Kolmogorov turbulent atmosphere along horizontal path. Opt. Express 2019, 27, 25342–25356. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Xu, Y.; An, B. Coherent properties of partially coherent vortex beam with nonuniform polarization propagating in turbulent atmosphere. Results Phys. 2024, 56, 107227. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, G.; Liu, Y.; Wang, H.; Hoenders, B.J.; Liang, C.; Cai, Y.; Zeng, J. Robust measurement of orbital angular momentum of a partially coherent vortex beam under amplitude and phase perturbations. Opto-Electron. Sci. 2024, 3, 240001. [Google Scholar] [CrossRef]
- Peng, X.; Liu, L.; Wang, F.; Popov, S.; Cai, Y. Twisted Laguerre-Gaussian Schell-model beam and its orbital angular moment. Opt. Express 2018, 26, 33956. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Xu, Y.; Li, Y.; Cao, J. Study of Reducing Atmospheric Turbulence-Induced Beam Wander of a Twisted Electromagnetic Elliptical Vortex Beam. Photonics 2024, 11, 492. https://doi.org/10.3390/photonics11060492
Huang K, Xu Y, Li Y, Cao J. Study of Reducing Atmospheric Turbulence-Induced Beam Wander of a Twisted Electromagnetic Elliptical Vortex Beam. Photonics. 2024; 11(6):492. https://doi.org/10.3390/photonics11060492
Chicago/Turabian StyleHuang, Kai, Yonggen Xu, Yuqiang Li, and Jin Cao. 2024. "Study of Reducing Atmospheric Turbulence-Induced Beam Wander of a Twisted Electromagnetic Elliptical Vortex Beam" Photonics 11, no. 6: 492. https://doi.org/10.3390/photonics11060492
APA StyleHuang, K., Xu, Y., Li, Y., & Cao, J. (2024). Study of Reducing Atmospheric Turbulence-Induced Beam Wander of a Twisted Electromagnetic Elliptical Vortex Beam. Photonics, 11(6), 492. https://doi.org/10.3390/photonics11060492





