Improved Optics for Super-Resolution Time-Lapse Observations of Biological Phenomenon Using Speckle Interferometry
Abstract
1. Introduction
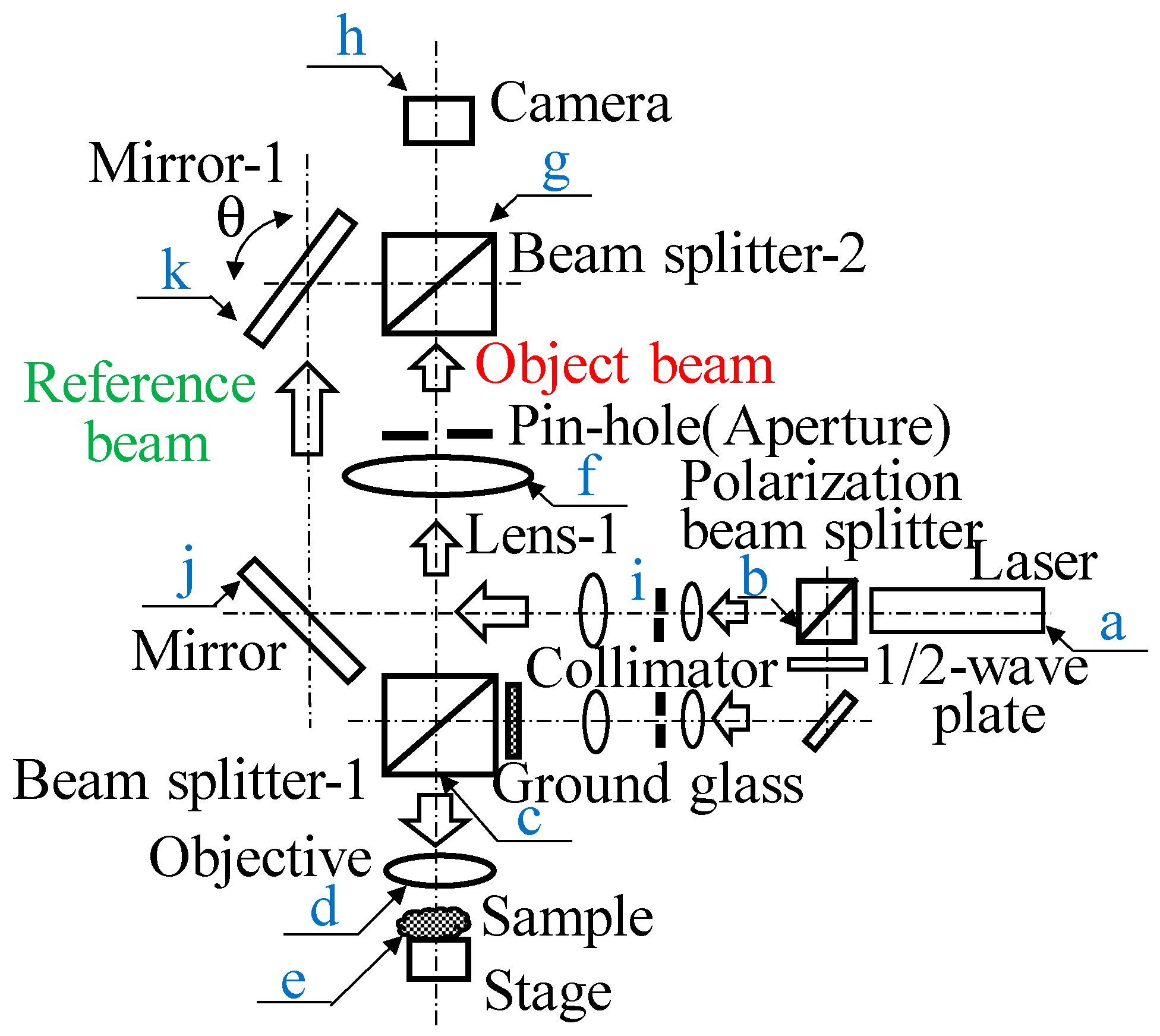
2. Super-Resolution Optics Based on Speckle Interferometry with the Object Placed Horizontally
3. Results and Discussion
3.1. Verification of the Super-Resolution Function of the Newly Constructed Optical System
3.2. Investigation of the Case Where the Objective Lens Was out of Focus on the Measured Surface
3.3. Investigation of Spatial Resolution of the Proposed Optical System
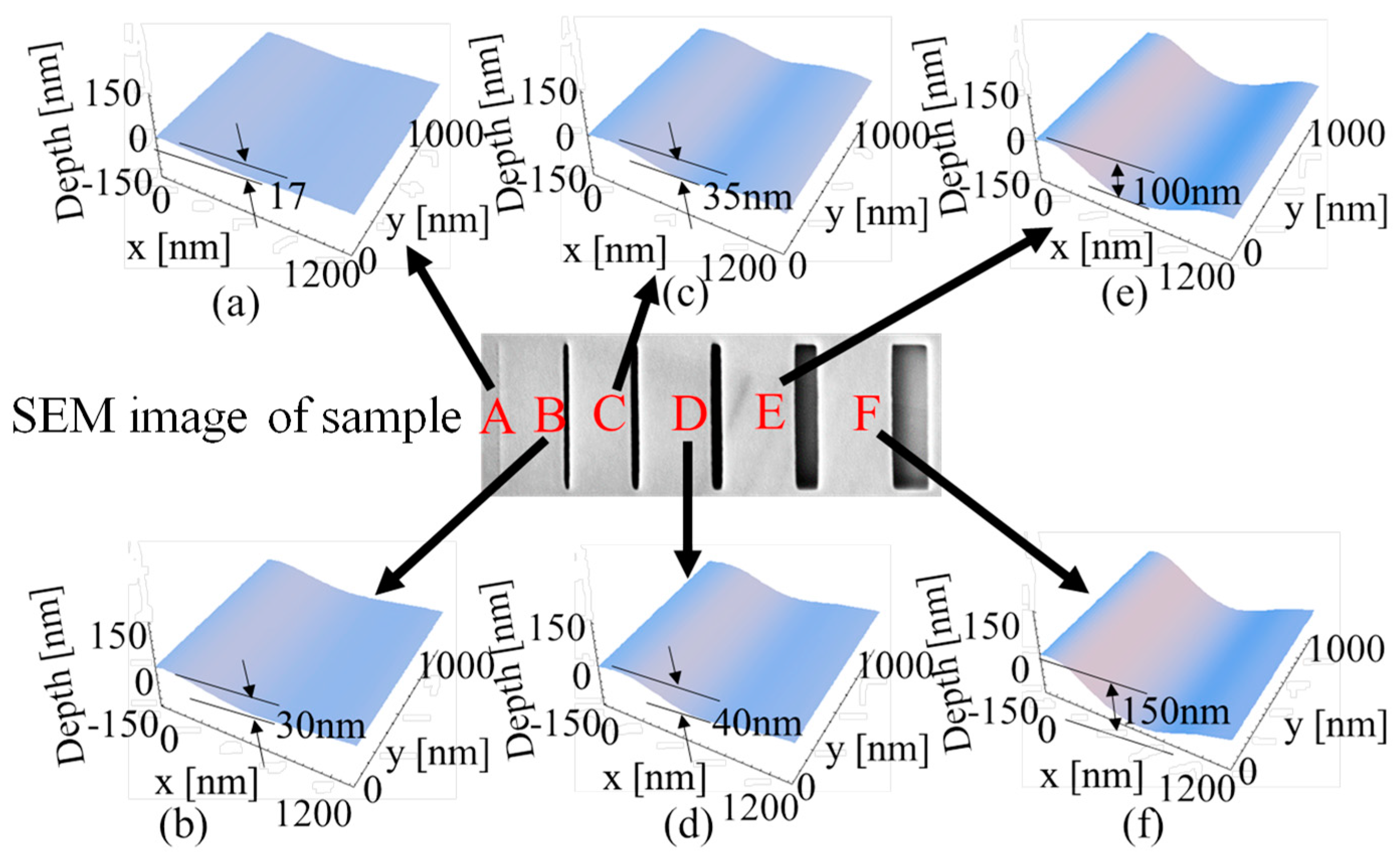
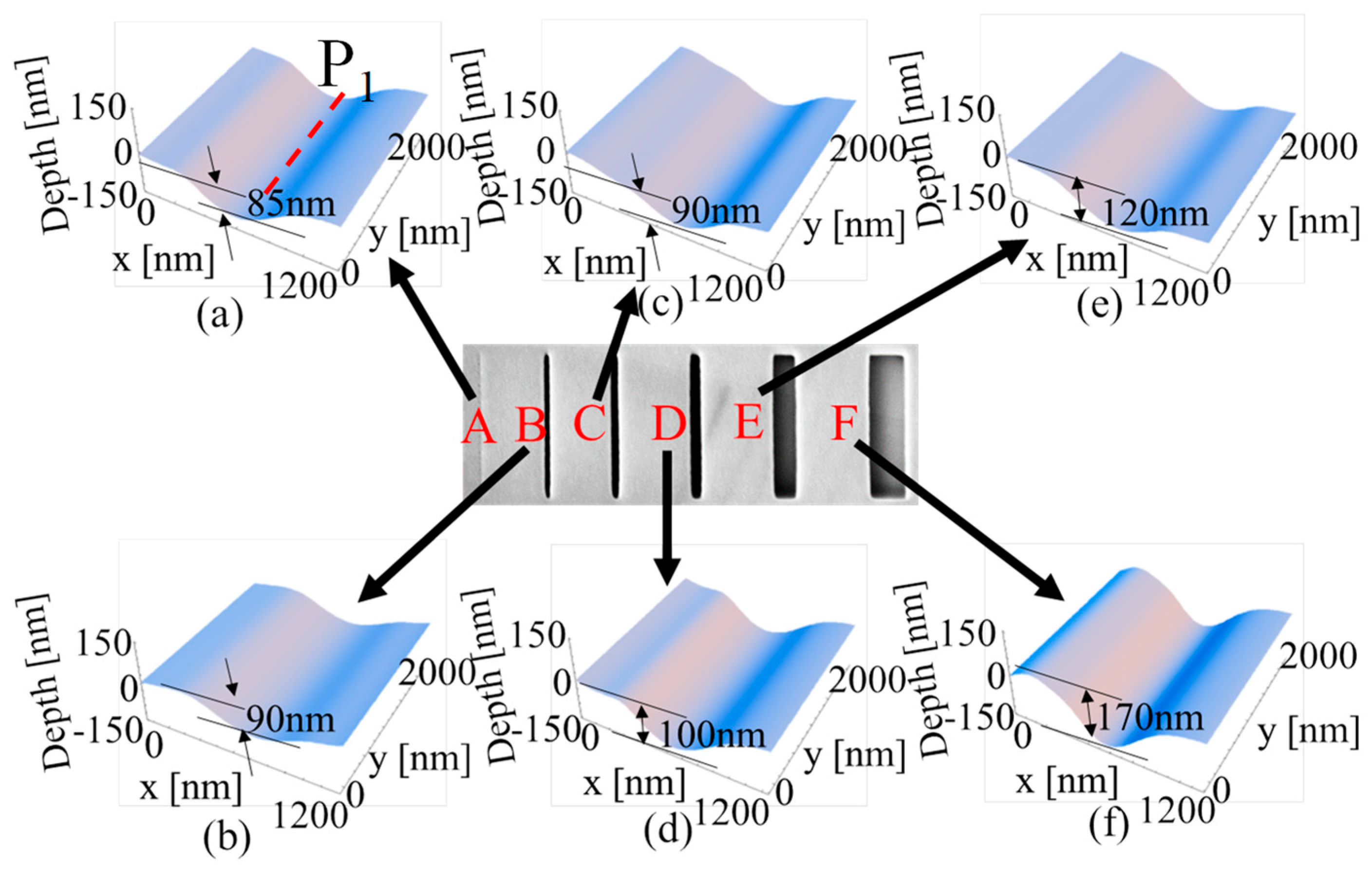
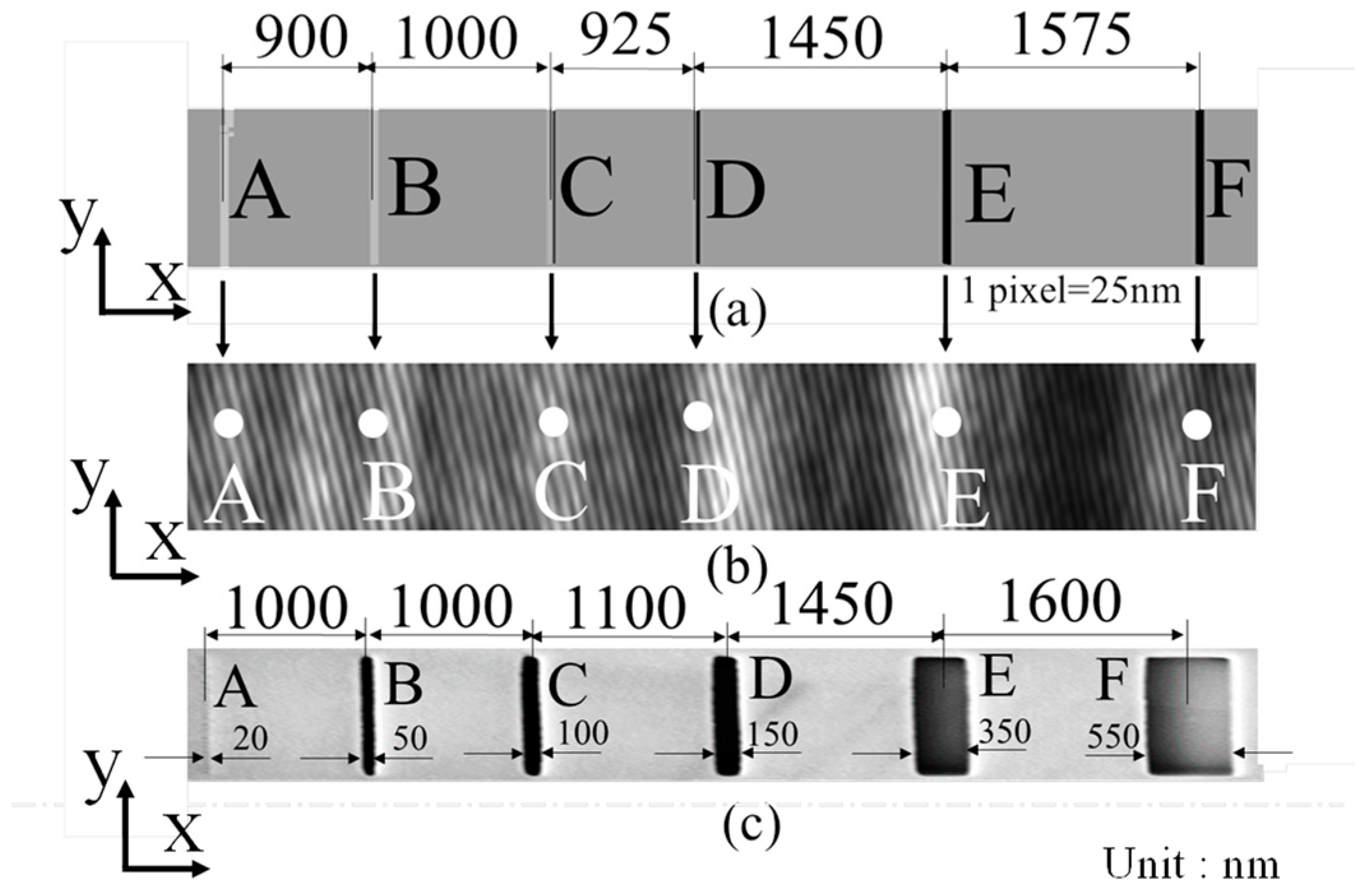
3.3.1. Investigation of Measurement Resolution of the Proposed Optical System with Objects of Different Line Widths
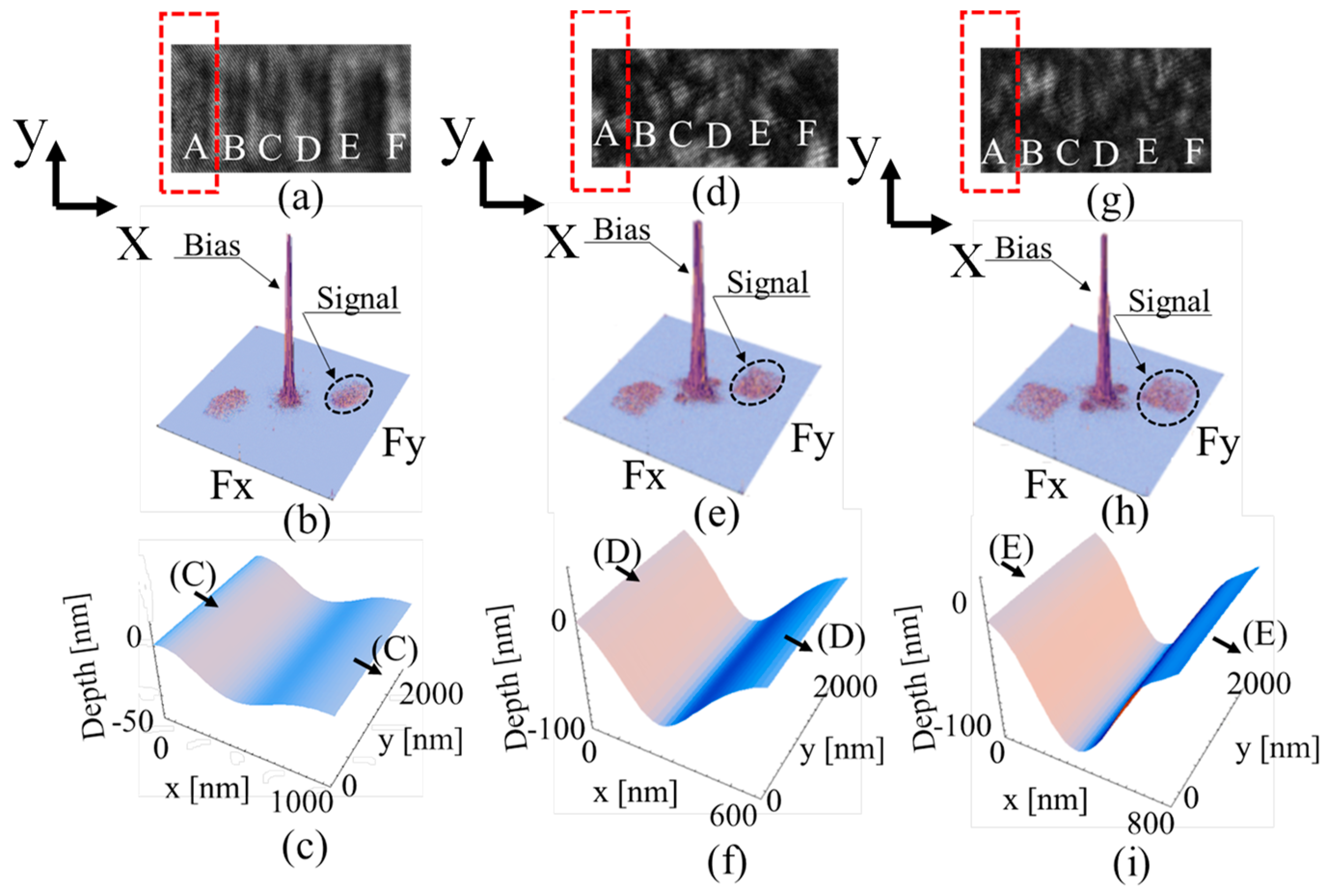
3.3.2. Resolution Enhancement by Scattered Light Illumination When Observing Object Measurements with 20 nm Line Widths
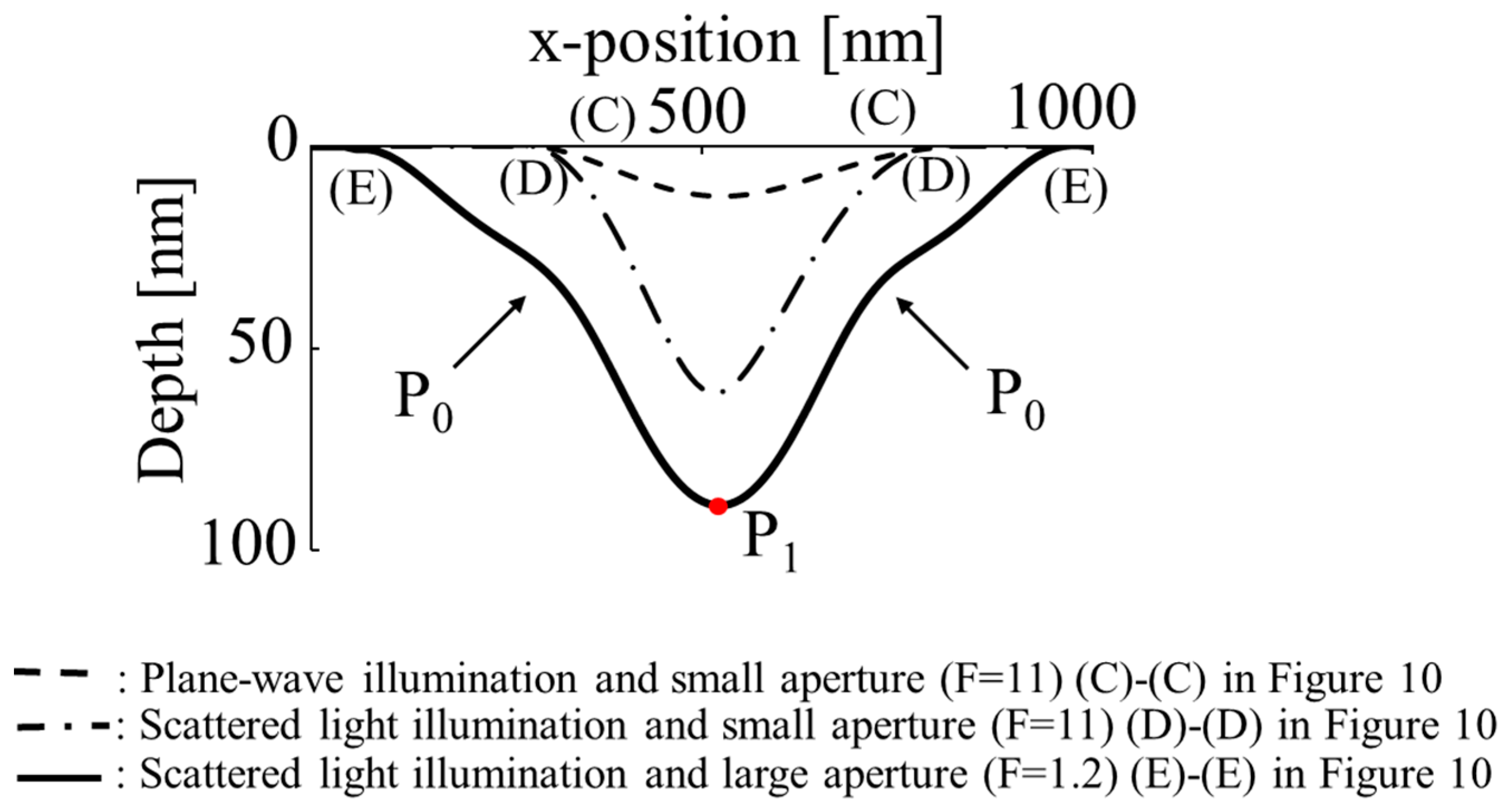
3.3.3. Response to Lateral Resolution Spread of Measurement Results
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 2019; pp. 370–374, 167–177 and 290–292. [Google Scholar]
- Hecht, E. Optics, 4th ed.; Addison Wesley: San Francisco, CA, USA, 2002; pp. 24–31, 149–165, 393–400 and 467–474. [Google Scholar]
- Feynman, P.R. The Feynman Lectures on Physics; Addison-Wesley Publishing Co., Ltd.: Reading, MA, USA, 1989; Chapter 30–33. [Google Scholar]
- Kohler, H. On Abbe’s theory of image formation in the microscope. Opt. Acta: Int. J. Opt. 1981, 28, 1691–1701. [Google Scholar] [CrossRef]
- Chalfie, M.; Tu, Y.; Euskirchen, G.; Ward, W.W.; Prasher, D.C. Green Fluorescent Protein as a Marker for Gene Expression. Science 1994, 263, 802–805. [Google Scholar] [CrossRef] [PubMed]
- Remington, S.J. Green fluorescent protein: A perspective. Protein Sci. 2011, 20, 1509–1519. [Google Scholar] [CrossRef] [PubMed]
- Wustner, D.; Modzel, M.; Lund, F.W.; Lomholt, M.A. Imaging approaches for analysis of cholesterol distribution and dynamics in the plasma membrane. Chem. Phys. Lipids 2016, 199, 106–135. [Google Scholar] [CrossRef] [PubMed]
- Garini, Y.; Vermolen, B.J.; Young, I.T. From micro to nano: Recent advances in high-resolution microscopy. Curr. Opin. Biotechnol. 2005, 16, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Heilemann, M.; van de Linde, S.; Schüttpelz, M.; Kasper, R.; Seefeldt, B.; Mukherjee, A.; Tinnefeld, P.; Sauer, M. Subdiffraction-resolution fluorescence imaging with conventional fluorescent probes. Angew. Chem. Int. Ed. 2008, 47, 6172–6176. [Google Scholar] [CrossRef] [PubMed]
- Heintzman, R.; Ficz, G. Beaking the resolution limit in light microscopy. Brief. Funct. Genom. Proteom. 2006, 5, 289–301. [Google Scholar] [CrossRef] [PubMed]
- Hess, T.S.; Girirajan, P.K.T.; Mason, D.M. Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys 2006, 91, 4258–4272. [Google Scholar] [CrossRef]
- Huang, B. Super-resolution optical microscopy: Multiple choices. Curr. Opin. Chem. Biol. 2010, 14, 10–14. [Google Scholar] [CrossRef]
- Huang, B.; Babcock, H.; Zhuang, X. Breaking the Diffraction Barrier: Super-Resolution Imaging of Cells. Cell 2010, 143, 1047–1058. [Google Scholar] [CrossRef]
- Xu, B.; Liu, L. Developments, applications, and prospects of cryo-electron microscopy. Protein Sci. 2020, 29, 872–882. [Google Scholar] [CrossRef] [PubMed]
- Saibil, H.R. Cryo-EM in molecular and cellular biology. Mol. Cell 2022, 82, 274–284. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Goh, C.; Keeble, J.L.; Qin, J.S.; Roediger, B.; Jain, R.; Wang, Y.; Chew, W.; Weninger, W.; Ng, L. Intravital multiphoton imaging of immune responses in the mouse ear skin. Nat. Protoc. 2012, 7, 221–234. [Google Scholar] [CrossRef] [PubMed]
- Cox, S. Super-resolution imaging in live cells. Dev. Biol. 2015, 401, 175–181. [Google Scholar] [CrossRef] [PubMed]
- Mahecic, D.; Testa, I.; Griffie, J.; Manley, S. Strategies for increasing the throughput of super-resolution microscopies. Curr. Opin. Chem. Biol. 2019, 51, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Chakkarapani, S.K.; Park, G.; Kang, S.H. Base pair distance analysis in single DNA molecule by direct stochastic optical reconstruction microscopy. Chin. Chem. Lett. 2015, 26, 1490–1495. [Google Scholar] [CrossRef]
- Sirohi, R.S. Speckle Metrology; Marcel Dekker: New York, NY, USA, 1993; pp. 99–234. [Google Scholar]
- Cloud, G. Optical Methods of Engineering Analysis; Cambridge University Press: New York, NY, USA, 1995; pp. 395–476. [Google Scholar]
- Malacara, D. Optical Shop Testing; John Wiley &Sons: New York, NY, USA, 1992; pp. 501–652. [Google Scholar]
- Arai, Y. Three-dimensional shape measurement beyond the diffraction limit of lens using speckle interferometry. J. Mod. Opt. 2018, 65, 1866–1874. [Google Scholar] [CrossRef]
- Arai, Y. Role of Phase Information Propagation in the Realisation of Super-Resolution Based on Speckle Interferometry. Photonics 2023, 10, 1306. [Google Scholar] [CrossRef]
- Arai, Y. Factors affecting the measurement resolution of super-resolution techniques based on speckle interferometry. J. Mod. Opt. 2022, 69, 897–910. [Google Scholar] [CrossRef]
- Arai, Y. Three-Dimensional shape measurement beyond diffraction limit for measurement of Dynamic Events. In Progress in Optomechatronic Technologies, Springer Proceedings in Physics; Springer: Singapore, 2019; p. 233. [Google Scholar] [CrossRef]
- Arai, Y. Electronic speckle pattern interferometry based on spatial information using only two sheets of speckle patterns. J. Mod. Opt. 2014, 61, 297–306. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arai, Y. Improved Optics for Super-Resolution Time-Lapse Observations of Biological Phenomenon Using Speckle Interferometry. Photonics 2024, 11, 427. https://doi.org/10.3390/photonics11050427
Arai Y. Improved Optics for Super-Resolution Time-Lapse Observations of Biological Phenomenon Using Speckle Interferometry. Photonics. 2024; 11(5):427. https://doi.org/10.3390/photonics11050427
Chicago/Turabian StyleArai, Yasuhiko. 2024. "Improved Optics for Super-Resolution Time-Lapse Observations of Biological Phenomenon Using Speckle Interferometry" Photonics 11, no. 5: 427. https://doi.org/10.3390/photonics11050427
APA StyleArai, Y. (2024). Improved Optics for Super-Resolution Time-Lapse Observations of Biological Phenomenon Using Speckle Interferometry. Photonics, 11(5), 427. https://doi.org/10.3390/photonics11050427




