Twisted Multi-Cosine Gaussian Schell-Model Arrays and Their Statistical Characteristics
Abstract
1. Introduction
2. Analytic Solutions for Twisted Multi-Cosine Gaussian Schell-Model Arrays
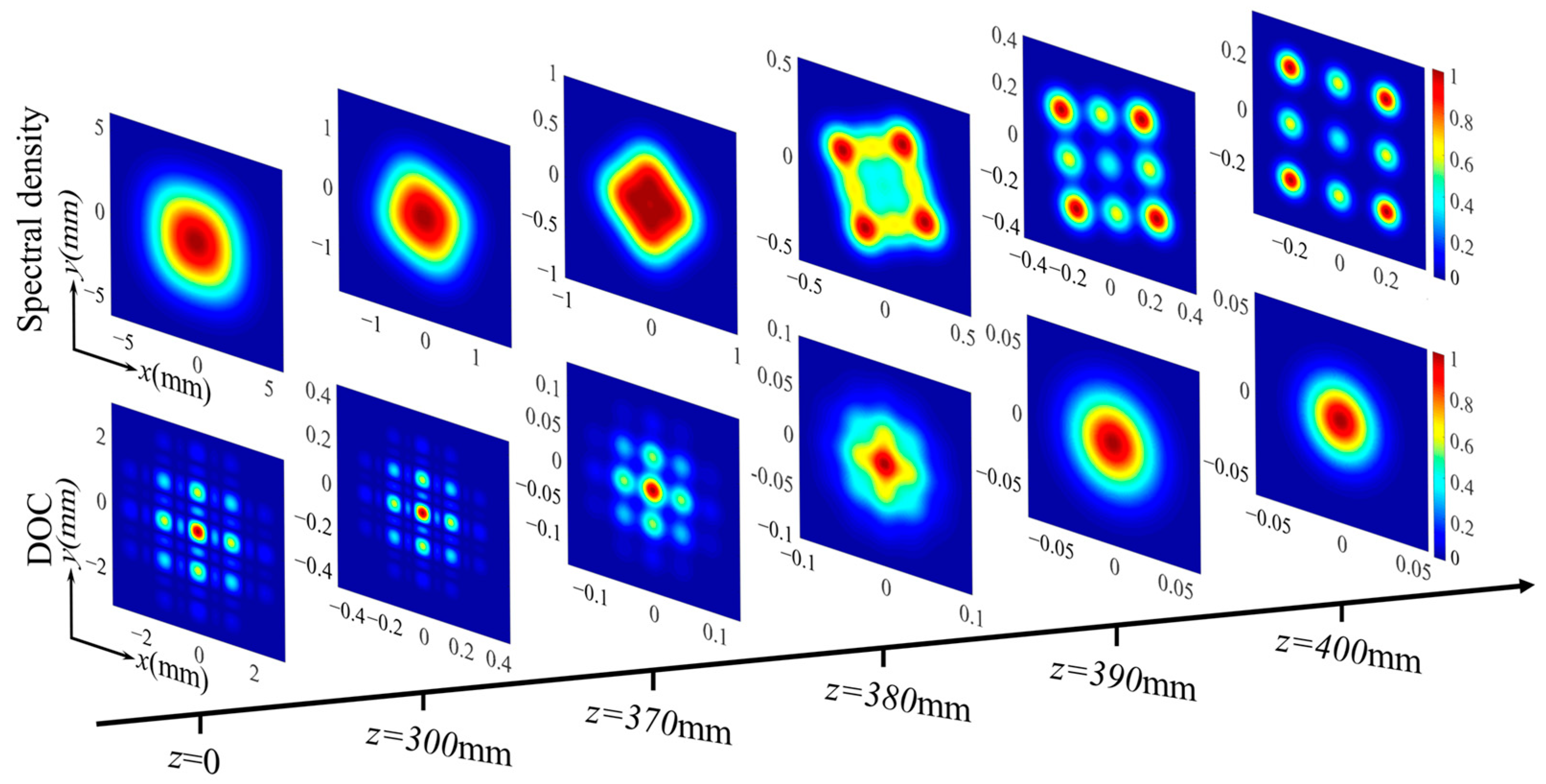
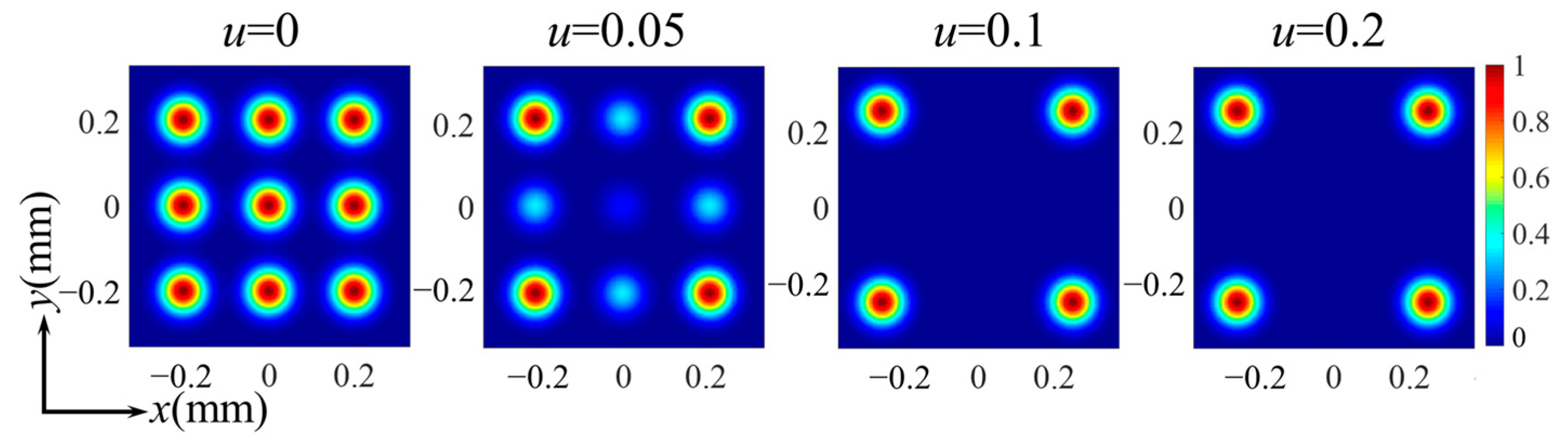
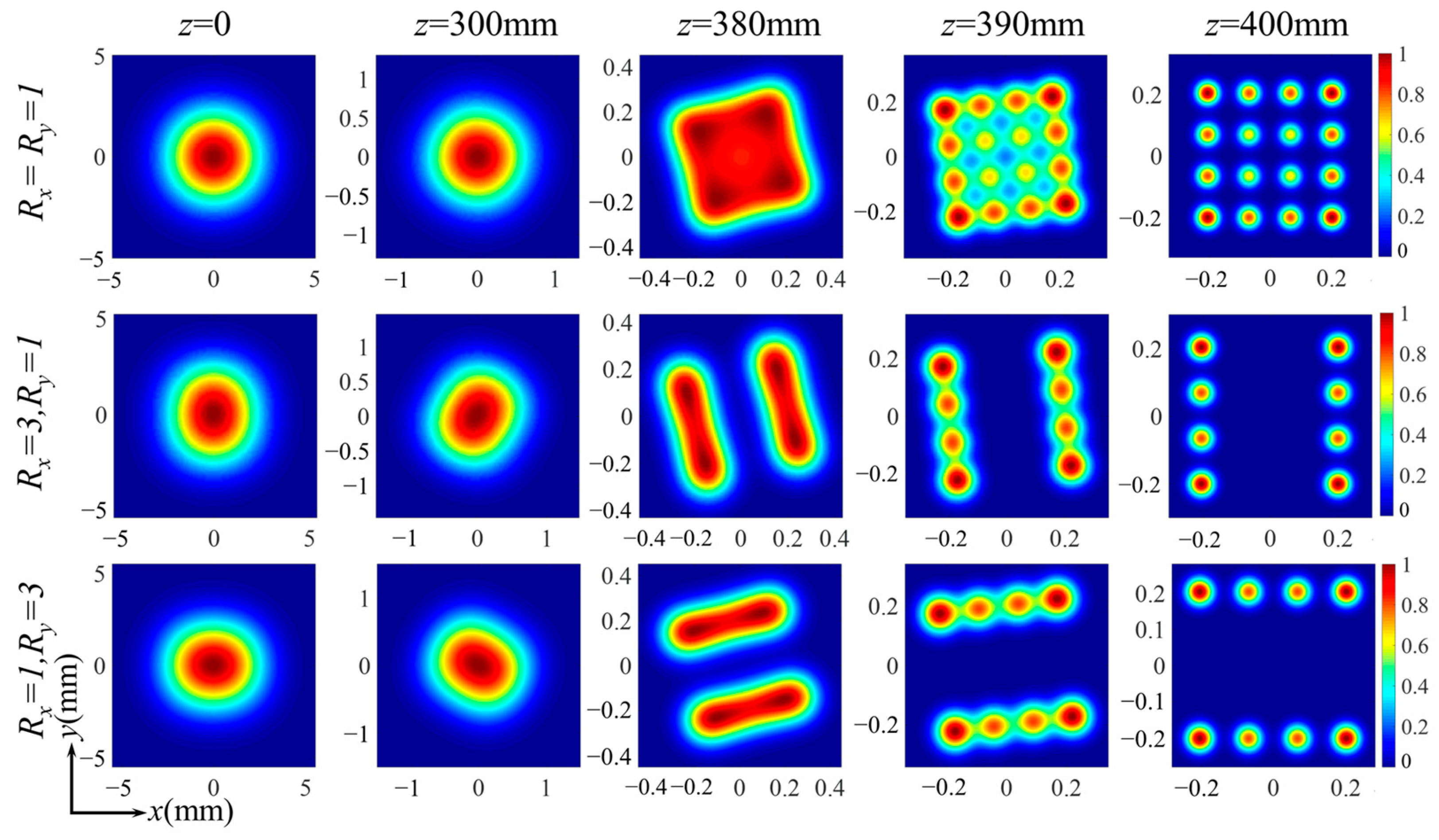
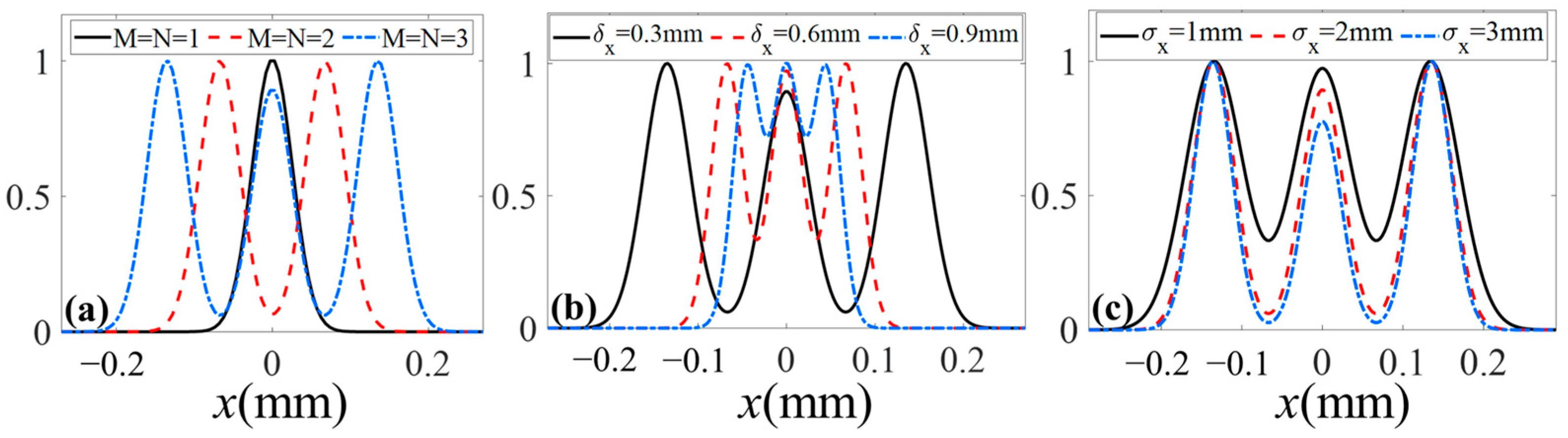
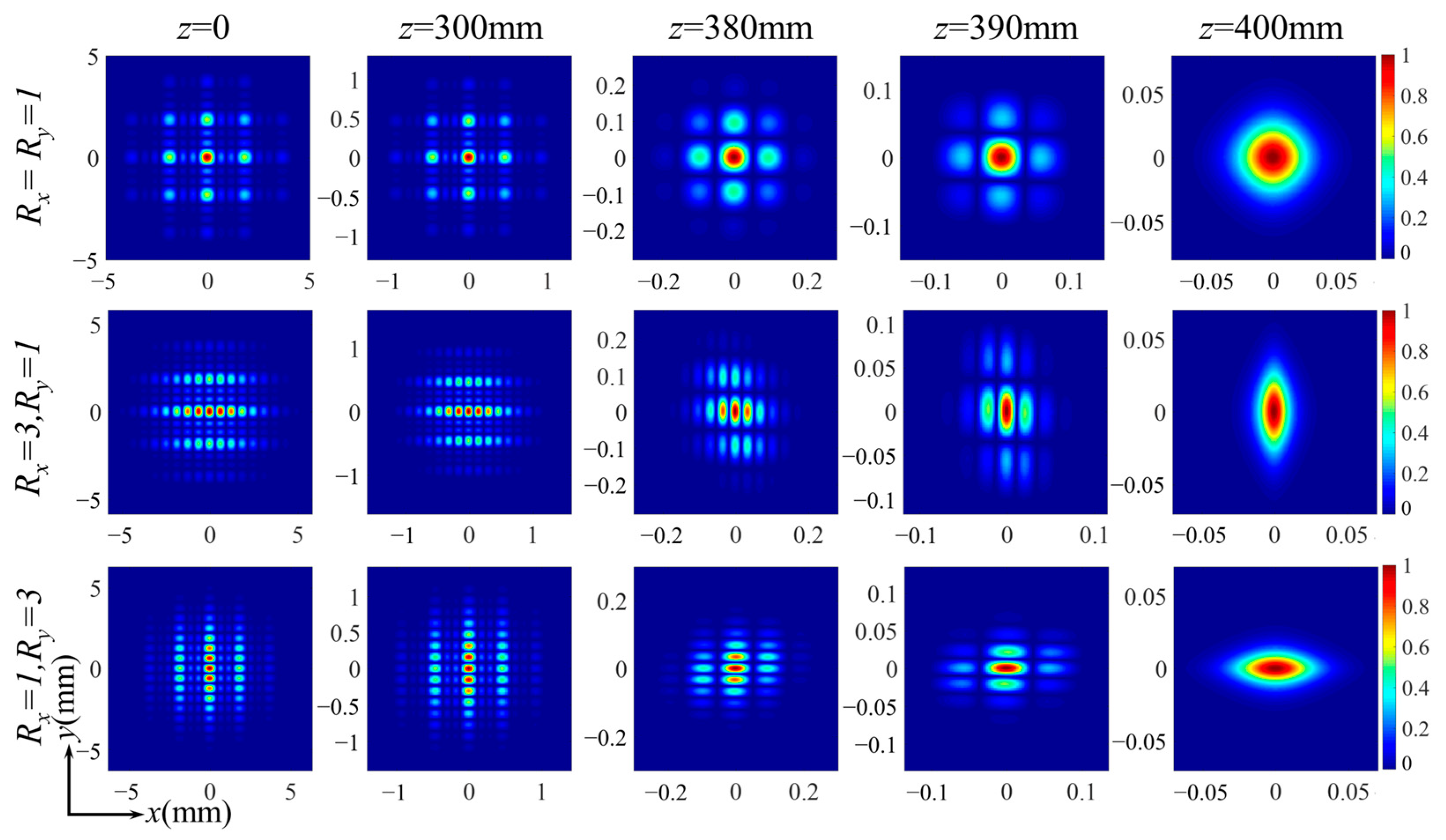
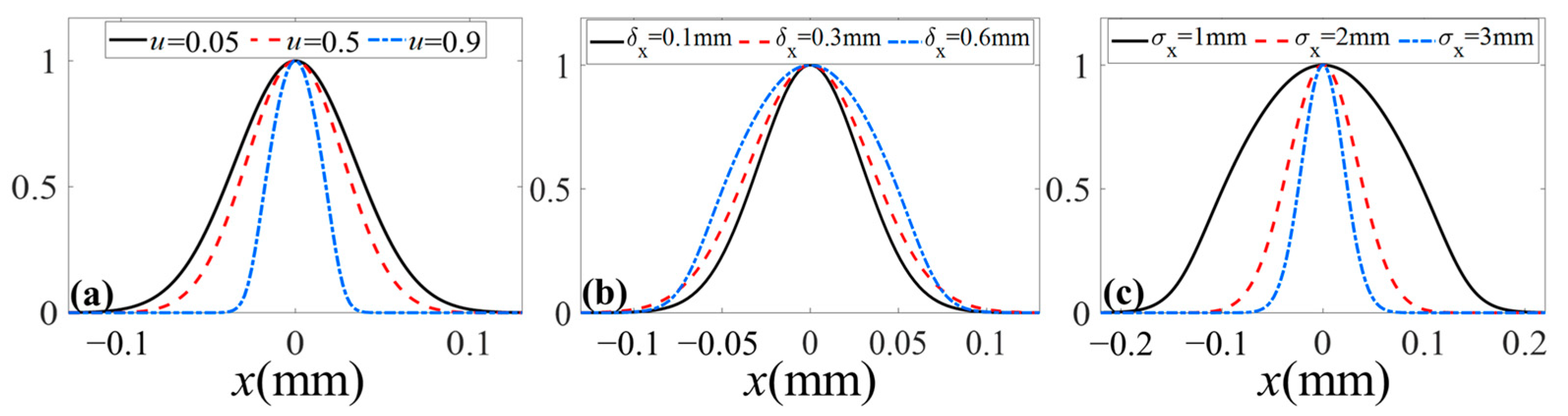
3. Numerical Examples
4. Discussion
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korotkova, O. Random Beams: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Kato, Y.; Mima, K.; Miyanaga, N.; Arinaga, S.; Kitagawa, Y.; Nakatsuka, M.; Yamanaka, A.C. Random phasing of high-power lasers for uniform target acceleration and plasma-instability suppression. Phys. Rev. Lett. 1984, 53, 1057–1060. [Google Scholar] [CrossRef]
- Ferri, F.; Magatti, D.; Gatti, A.; Bache, M.; Brambilla, E.; Lugiato, L.A. High-resolution ghost image and ghost diffraction experiments with thermal light. Phys. Rev. Lett. 2005, 94, 183602. [Google Scholar] [CrossRef] [PubMed]
- Auñón, J.M.; Nieto-Vesperinas, M. Partially coherent fluctuating sources that produce the same optical force as a laser beam. Opt. Lett. 2013, 38, 2869–2872. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.F.; Wang, Z.Y.; Cheng, B.; Wang, Q.Y.; Wu, B.; Shen, X.X.; Lin, Q. Atom cooling by partially spatially coherent lasers. Phys. Rev. A 2013, 88, 023416. [Google Scholar] [CrossRef]
- Wu, G.; Cai, Y. Detection of a semirough target in turbulent atmosphere by a partially coherent beam. Opt. Lett. 2011, 36, 1939–1941. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Dong, Z.; Peng, D.; Chen, Y.; Wang, F.; Cai, Y. Robust Far-Field Optical Image Transmission with Structured Random Light Beams. Phys. Rev. Appl. 2022, 17, 024043. [Google Scholar] [CrossRef]
- Peng, D.; Huang, Z.; Liu, Y.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Optical coherence encryption with structured random light. PhotoniX 2021, 2, 6. [Google Scholar] [CrossRef]
- Simon, R.; Mukunda, N. Twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1993, 10, 95–109. [Google Scholar] [CrossRef]
- Friberg, A.T.; Tervonen, E.; Turunen, J. Interpretation and experimental demonstration of twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1994, 11, 1818–1826. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Eyyuboğlu, H.T.; Baykal, Y. Twist phase-induced reduction in scintillation of a partially coherent beam in turbulent atmosphere. Opt. Lett. 2012, 37, 184–186. [Google Scholar] [CrossRef]
- Tong, Z.; Korotkova, O. Beyond the classical Rayleigh limit with twisted light. Opt. Lett. 2012, 37, 2595–2597. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Zhu, S. Orbital angular moment of a partially coherent beam propagating through an astigmatic ABCD optical system with loss or gain. Opt. Lett. 2014, 39, 1968–1971. [Google Scholar] [CrossRef] [PubMed]
- Wu, G. Propagation properties of a radially polarized partially coherent twisted beam in free space. J. Opt. Soc. Am. A 2016, 33, 345–350. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, H.; Zhao, D. Optical trapping Rayleigh particles with a twist effect. Opt. Laser Eng. 2020, 130, 106101. [Google Scholar] [CrossRef]
- Borghi, R.; Gori, F.; Guattari, G.; Santarsiero, M. Twisted Schell-model beams with axial symmetry. Opt. Lett. 2015, 40, 4504–4507. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M. Devising genuine twisted cross-spectral densities. Opt. Lett. 2018, 43, 595–598. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Random sources for rotating spectral densities. Opt. Lett. 2017, 42, 255–258. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Twisted EM beams with structured correlations. Opt. Lett. 2018, 43, 3905–3908. [Google Scholar] [CrossRef]
- Tian, C.; Zhu, S.; Huang, H.; Cai, Y.; Li, Z. Customizing twisted Schell-model beams. Opt. Lett. 2020, 45, 5880–5883. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, H.; Liu, L.; Chen, Y.; Wang, F.; Cai, Y. Experimental Synthesis and Demonstration of the Twisted Laguerre–Gaussian Schell-Mode Beam. Photonics 2023, 10, 314. [Google Scholar] [CrossRef]
- Zhou, Y.; Cui, Z.; Han, Y. Polarization and coherence properties in self-healing propagation of a partially coherent radially polarized twisted beam. Opt. Express 2022, 30, 23448–23462. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wu, Y.; Zheng, X.; Shi, J.; Luo, Y.; Huang, J.; Deng, D. Particle manipulation with twisted circle Pearcey vortex beams. Opt. Lett. 2023, 48, 3535–3538. [Google Scholar] [CrossRef] [PubMed]
- Fu, G.; Chen, J.; Qi, G.; Wu, Y.; Zhang, X.; Wang, H.; Shi, Y.; Zhao, C.; Jin, S. Generating a hollow twisted correlated beam using correlated perturbations. Opt. Express 2023, 31, 1442–1451. [Google Scholar] [CrossRef]
- Hu, J.; Wei, W.; Sun, Z.; Li, X.; Qian, Y. Customizing twisted structured light beams. Opt. Laser Technol. 2025, 181, 111708. [Google Scholar] [CrossRef]
- Anderson, B.P.; Gustavson, T.L.; Kasevich, M.A. Atom trapping in nondissipative optical lattices. Phys. Rev. A 1996, 53, R3727–R3730. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, M.P.; Paterson, L.; Volke-Sepulveda, K.; Arlt, J.; Sibbet, W.; Dholakia, K. Creation and manipulation of three-dimensional optically trapped structures. Science 2002, 296, 1101–1103. [Google Scholar] [CrossRef]
- MacDonald, M.; Spalding, G.; Dholakia, K. Microfluidic sorting in an optical lattice. Nature 2003, 426, 421–424. [Google Scholar] [CrossRef]
- Mei, Z.; Zhao, D.; Korotkova, O.; Mao, Y. Gaussian Schell-model arrays. Opt. Lett. 2015, 40, 5662–5665. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, D. Random medium model for producing optical coherence lattice. Opt. Express 2017, 25, 25222–25233. [Google Scholar] [CrossRef]
- Mao, Y.; Mei, Z. Random sources generating ring-shaped optical lattice. Opt. Commun. 2016, 381, 222–226. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Optical coherence grids and their propagation characteristics. Opt. Express 2018, 26, 2168–2180. [Google Scholar] [CrossRef] [PubMed]
- Wan, L.; Zhao, D. Twisted Gaussian Schell-model array beams. Opt. Lett. 2018, 43, 3554–3557. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zhao, D. Statistical properties of electromagnetic twisted Gaussian Schell-model array beams during propagation. Opt. Express 2019, 27, 19624–19632. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Huang, H.; Chen, Y.; Wang, H.; Zhu, S.; Li, Z.; Cai, Y. Twisted partially coherent array sources and their transmission in anisotropic turbulence. Opt. Express 2018, 26, 25974–25988. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Yuan, C.; Ji, X.; Wang, T. Ring-shaped twisted Gaussian Schell-model array beams. J. Opt. Soc. Am. A 2020, 37, 444–449. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, M.; Li, H.; Li, X. Twisted sinc-correlation Schell-model array beams. Opt. Express 2023, 31, 26069–26077. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef]
- Gbur, G. Singular Optics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Mandel, L.; Wolf, E. Coherence and Quantum Optics; Springer: Boston, MA, USA, 1973. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Dong, S.; Yuan, P.; Yang, Y.; Zhou, Y.; Li, X. Twisted Multi-Cosine Gaussian Schell-Model Arrays and Their Statistical Characteristics. Photonics 2024, 11, 1139. https://doi.org/10.3390/photonics11121139
Tang M, Dong S, Yuan P, Yang Y, Zhou Y, Li X. Twisted Multi-Cosine Gaussian Schell-Model Arrays and Their Statistical Characteristics. Photonics. 2024; 11(12):1139. https://doi.org/10.3390/photonics11121139
Chicago/Turabian StyleTang, Miaomiao, Shijie Dong, Pengju Yuan, Yunzhe Yang, Yujie Zhou, and Xinzhong Li. 2024. "Twisted Multi-Cosine Gaussian Schell-Model Arrays and Their Statistical Characteristics" Photonics 11, no. 12: 1139. https://doi.org/10.3390/photonics11121139
APA StyleTang, M., Dong, S., Yuan, P., Yang, Y., Zhou, Y., & Li, X. (2024). Twisted Multi-Cosine Gaussian Schell-Model Arrays and Their Statistical Characteristics. Photonics, 11(12), 1139. https://doi.org/10.3390/photonics11121139




