A Micro-Mach–Zehnder Interferometer Temperature Sensing Design Based on a Single Mode–Coreless–Multimode–Coreless–Single Mode Fiber Cascaded Structure
Abstract
1. Introduction
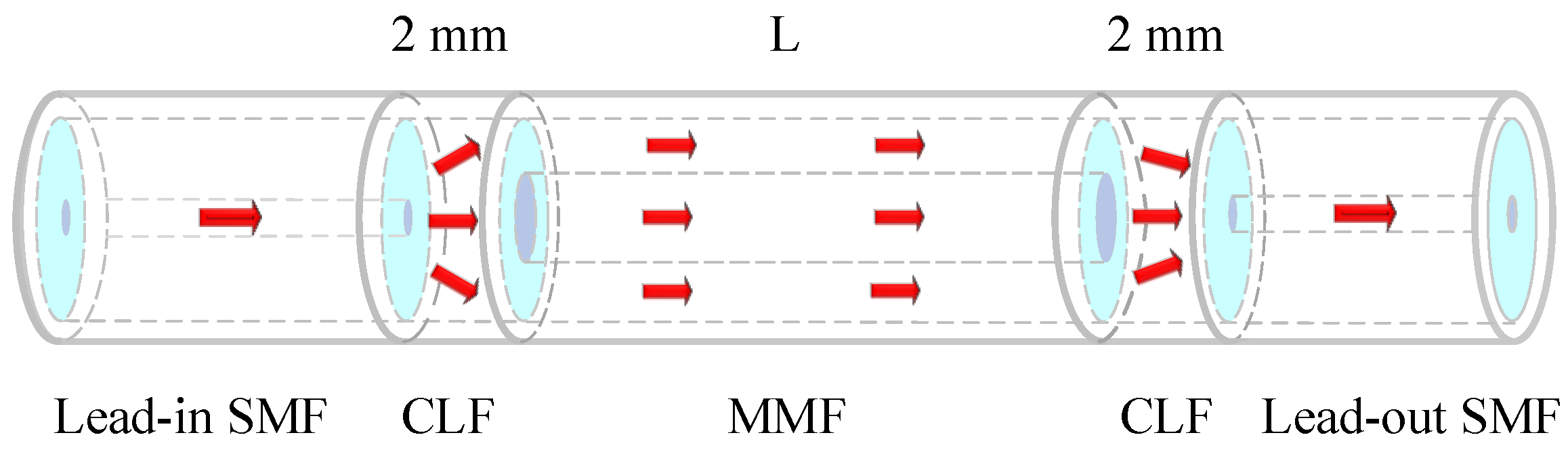
2. Structure and Principle of the Sensor Head
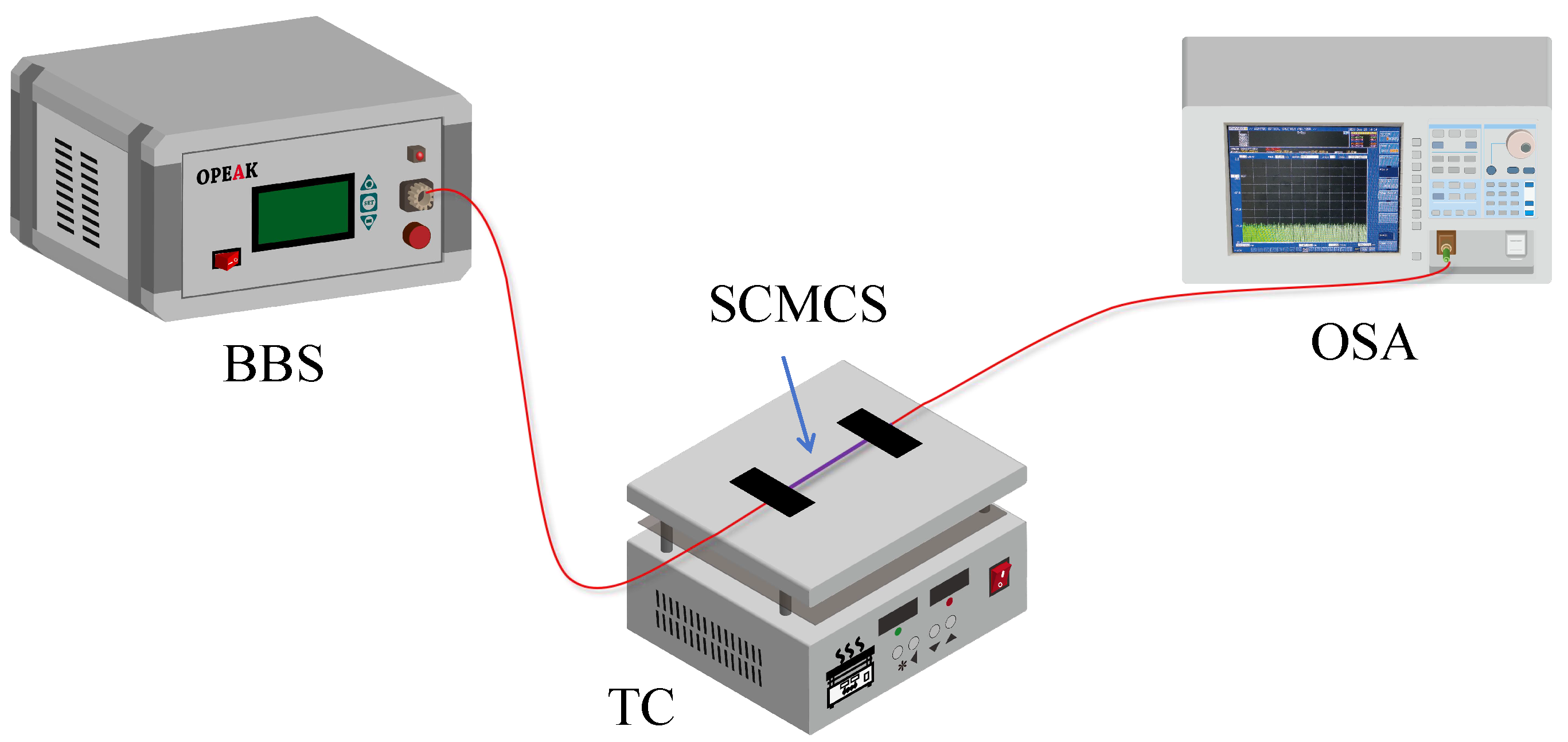
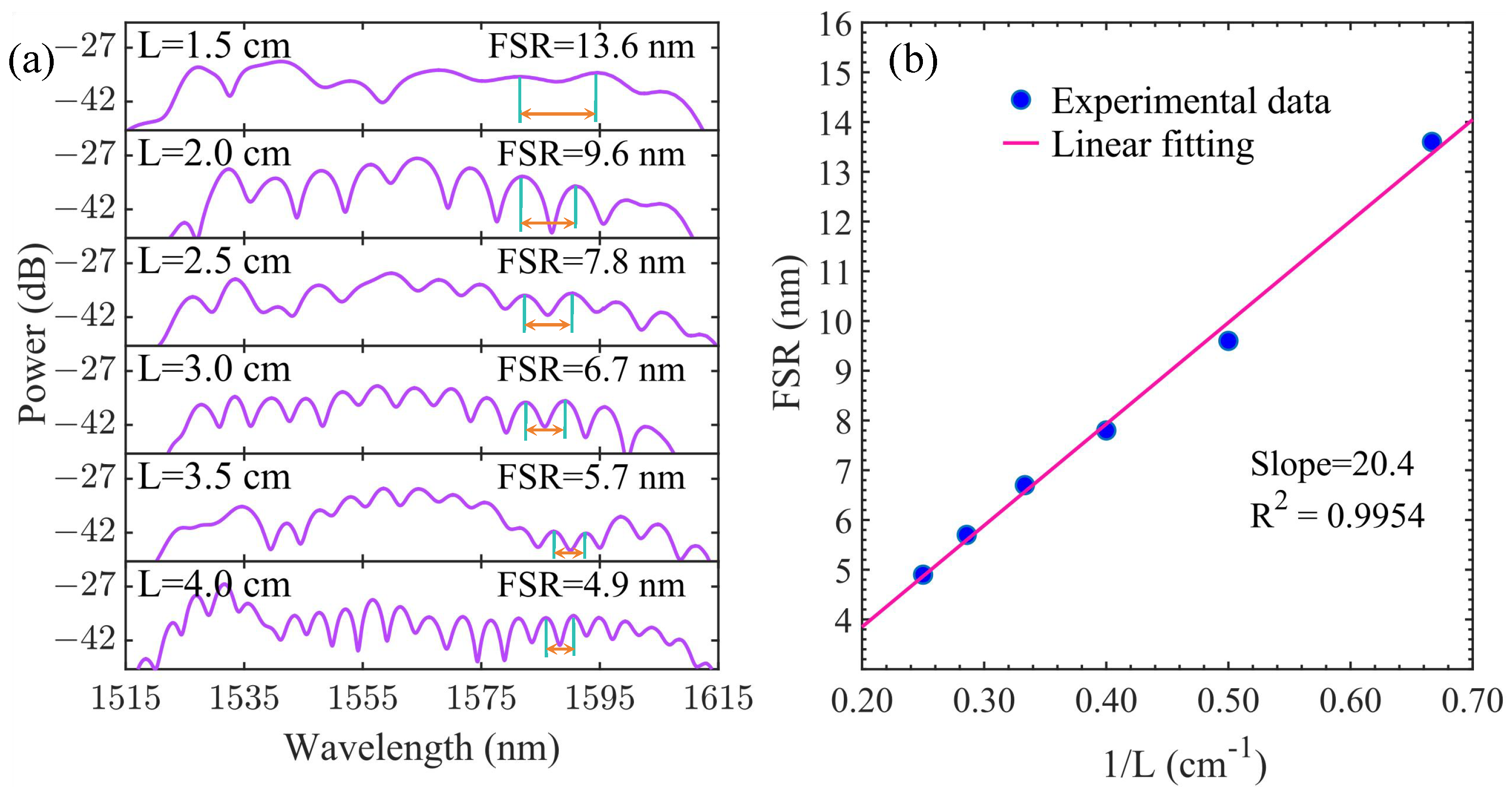
3. Experiments and Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z.D.; Liu, L.; Liu, Z.H.; Zhang, Y.; Zhang, Y.X. Surface-plasmon-resonance-based optical-fiber temperature sensor with high sensitivity and high figure of merit. Opt. Lett. 2017, 42, 2948–2951. [Google Scholar] [CrossRef] [PubMed]
- Jauregui-Vazquez, D.; Korterik, J.P.; Offerhaus, H.L.; Rojas-Laguna, R.; Alvarez-Chavez, J.A. Strain optical fiber sensor with modified sensitivity based on the vernier effect. Instrum. Sci. Technol. 2023, 51, 421–434. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Abu Bakar, M.H.; Anas, S.B.A.; Mahdi, M.A.; Yaacob, M.H. Optical fiber sensor network integrating SAC-OCDMA and cladding modified optical fiber sensors coated with nanomaterial. Opt. Fiber Technol. 2022, 70, 102875. [Google Scholar] [CrossRef]
- Jiang, B.Q.; Zhou, K.M.; Wang, C.L.; Zhao, Y.H.; Zhao, J.L.; Zhang, L. Temperature-calibrated high-precision refractometer using a tilted fiber Bragg grating. Opt. Express 2017, 25, 25910–25918. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Zuo, Y.W.; Zhou, K.M.; Yang, Q.; Hu, X.; Jiang, Y. Low Acoustic Frequency Sensing Based on Ghost Mode of Small Angle Tilted Fiber Bragg Grating. J. Light. Technol. 2023, 42, 2538–2543. [Google Scholar] [CrossRef]
- Tian, J.; Zuo, Y.W.; Hou, M.J.; Jiang, Y. Magnetic field measurement based on a fiber laser oscillation circuit merged with a polarization-maintaining fiber Sagnac interference structure. Opt. Express 2021, 29, 8763–8769. [Google Scholar] [CrossRef] [PubMed]
- Pizzaia, J.P.L.; Silva, R.L.; Leal, A.G.; Castellani, C.E.S. Temperature sensor based on an erbium-doped fiber Sagnac interferometer. Appl. Opt. 2022, 61, 2352–2356. [Google Scholar] [CrossRef] [PubMed]
- Ge, Q.; Zhu, J.H.; Cui, Y.Y.; Zhang, G.; Wu, X.Q.; Li, S.L.; Wang, H.S.; Yu, B.L. Fiber optic temperature sensor utilizing thin PMF based Sagnac loop. Opt. Commun. 2022, 502, 127417. [Google Scholar] [CrossRef]
- Lin, W.H.; Shao, L.Y.; Liu, Y.B.; Bandyopadhyay, S.; Liu, Y.H.; Xu, W.J.; Liu, S.Q.; Hu, J.; Vai, M.I. Temperature Sensor Based on Fiber Ring Laser with Cascaded Fiber Optic Sagnac Interferometers. IEEE Photonics J. 2021, 13, 7100512. [Google Scholar] [CrossRef]
- Yang, X.L.; Liu, M.Y.; Song, H.; Zhu, S.Q.; Wu, Y.H. Vibration resistance FBG temperature sensor fabrication and its application in the motor for hydraulic pump. Measurement 2022, 205, 112141. [Google Scholar] [CrossRef]
- Wang, X.Y.; Sun, X.Y.; Hu, Y.W.; Zeng, L.; Liu, Q.S.; Duan, J. Highly-sensitive fiber Bragg grating temperature sensors with metallic coatings. Optik 2022, 262, 169337. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, X.; Li, K.; Du, D.J.; Zheng, M.; Niu, Q.; Yang, Y.; Zhou, Q.; Sun, T.; Grattan, K.T.V. Real-Time Battery Temperature Monitoring Using FBG Sensors: A Data-Driven Calibration Method. IEEE Sens. J. 2022, 22, 18639–18648. [Google Scholar] [CrossRef]
- Mollah, M.A.; Islam, S.M.R.; Yousufali, M.; Abdulrazak, L.F.; Hossain, M.B.; Amiri, I.S. Plasmonic temperature sensor using D-shaped photonic crystal fiber. Results Phys. 2020, 16, 102966. [Google Scholar] [CrossRef]
- Abbasi, M.; Soroosh, M.; Namjoo, E. Polarization-insensitive temperature sensor based on liquid filled photonic crystal fiber. Optik 2018, 168, 342–347. [Google Scholar] [CrossRef]
- Liu, D.J.; Wu, Q.; Mei, C.; Yuan, J.H.; Xin, X.J.; Mallik, A.K.; Wei, F.F.; Han, W.; Kumar, R.; Yu, C.X.; et al. Hollow Core Fiber Based Interferometer for High-Temperature (1000 °C) Measurement. J. Light. Technol. 2018, 36, 1583–1590. [Google Scholar] [CrossRef]
- Deng, H.C.; Jiang, X.W.; Huang, X.X.; Chen, M.; Yang, H.Y.; Cheng, Y.; Teng, C.A.X.; Xu, R.H.; Yuan, L.B. A Temperature Sensor Based on Composite Optical Waveguide. J. Light. Technol. 2022, 40, 2663–2669. [Google Scholar] [CrossRef]
- Yan, X.; Wei, L.; Fu, R.; Cheng, T.L. Highly sensitive temperature sensor based upon a multimode interference structure filled with an ethanol-glycerol solution. Instrum. Sci. Technol. 2022, 51, 465–477. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.J.; Zhang, Y.X.; Liu, Z.H.; Yang, X.H.; Zhang, J.Z.; Yang, J.; Yuan, L.B. Simultaneous measurement of temperature and refractive index based on a hybrid surface plasmon resonance multimode interference fiber sensor. Appl. Opt. 2020, 59, 1225–1229. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.S.; Pua, C.H.; Harun, S.W.; Ahmad, H. Temperature-sensitive dual-segment polarization maintaining fiber Sagnac loop mirror. Opt. Laser Technol. 2010, 42, 377–381. [Google Scholar] [CrossRef]
- Osman, S.S.; Salim, M.A.M.; Sahidan, N.S.; Bakhtiar, H.; Krishnan, G.; Othman, M.H.D.; Rahman, M.A.; Ismail, A.F.; Yahya, N. Comparison of Fiber Bragg Grating based on SMF and MMF over Temperature Sensitivity. Senai Malays. 2019, 1484, 012014. [Google Scholar] [CrossRef]
- Chaudhary, V.S.; Kumar, D.; Mishra, R.; Sharma, S. Twin core photonic crystal fiber for temperature sensing. Mater. Today Proc. 2019, 33, 2289–2292. [Google Scholar] [CrossRef]
- Ma, L.; Kang, Z.X.; Qi, Y.H.; Jian, S.S. Fiber-optic temperature sensor based on a thinner no-core fiber. Optik 2015, 126, 1044–1046. [Google Scholar] [CrossRef]
- Xin, Y.; Dong, X.Y.; Meng, Q.Q.; Qi, F.; Zhao, C.L. Alcohol-filled side-hole fiber Sagnac interferometer for temperature measurement. Sensors Actuators A-Phys. 2013, 193, 182–185. [Google Scholar] [CrossRef]
- Razali, N.F.; Abu Bakar, M.H.; Tamchek, N.; Yaacob, M.H.; Mahdi, M.A. Temperature Sensitivity Comparison between Bare FBG and Buffered FBG. In Proceedings of the 2014 IEEE 5th International Conference on Photonics (ICP), Kuala Lumpur, Malaysia, 2–4 September 2014; pp. 36–37. [Google Scholar]
- Yang, S.; Rong, Q.Z.; Sun, H.; Zhang, J.; Liang, L.; Xu, Q.F.; Zhan, S.C.; Du, Y.Y.; Feng, D.; Qiao, X.G.; et al. High temperature probe sensor with high sensitivity based on Michelson interferometer. Acta Phys. Sin. 2013, 62, 084218. [Google Scholar] [CrossRef]
- Hatta, A.M.; Rajan, G.; Semenova, Y.; Farrell, G. SMS fibre structure for temperature measurement using a simple intensity-based interrogation system. Electron. Lett. 2009, 45, 1069–1070. [Google Scholar] [CrossRef]
- Noor, S.; Harun, S.W.; Ahmad, H.; Muhammad, A.R. Multimode interference based fiber-optic sensor for temperature measurement. J. Phys. Conf. Ser. 2018, 1151, 012023. [Google Scholar] [CrossRef]
- Wu, Q.; Hatta, A.M.; Wang, P.F.; Semenova, Y. Use of a Bent Single SMS Fiber Structure for Simultaneous Measurement of Displacement and Temperature Sensing. IEEE Photonics Technol. Lett. 2011, 23, 130–132. [Google Scholar] [CrossRef]
- Wang, K.; Dong, X.C.; Kienle, P.; Fink, M.; Kurz, W.; Köhler, M.H.; Jakobi, M.; Koch, A.W. Optical Fiber Sensor for Temperature and Strain Measurement Based on Multimode Interference and Square-Core Fiber. Micromachines 2021, 12, 1239. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.X.; Wang, Q.A.; Zhao, F.; Meng, B.; Qu, S.L. Optimal design and fabrication of SMS fiber temperature sensor for liquid. Opt. Commun. 2010, 283, 3149–3152. [Google Scholar] [CrossRef]
- Shao, M.; Cao, Z.W.; Gao, H.; Fu, H.W.; Qiao, X.G. High-sensitive and temperature-immune curvature sensor based on bitaper sandwiching in SMS fiber structure. Opt. Commun. 2023, 540, 129501. [Google Scholar] [CrossRef]
- Lian, X.K.; Wu, Q.; Farrell, G.; Shen, C.Y.; Ma, Y.Q.; Semenova, Y.L.Y. Discrete Self-Imaging in Small-Core Optical Fiber Interferometers. J. Light. Technol. 2019, 37, 1873–1884. [Google Scholar] [CrossRef]
- Fu, X.H.; Xie, H.Y.; Yang, C.Q.; Zhang, S.Y.; Fu, G.W.; Bi, W.H. Research on the temperature sensing characteristics of triple cladding quartz specialty fiber based on cladding mode resonance. Acta Phys. Sin. 2016, 65, 024211. [Google Scholar]
- Liu, F.; Wei, S.P.; Li, B.; Tan, Y.X.; Guo, X.; Fu, X.H. A novel fast response and high precision water temperature sensor based on Fiber Bragg Grating. Optik 2023, 289, 171257. [Google Scholar] [CrossRef]
- Ahmad, H.; Zulkhairi, A.S.; Azzuhri, S.R. Temperature sensor and fiber laser based on optical microfiber knot resonator. Optik 2018, 154, 294–302. [Google Scholar] [CrossRef]
- Li, C.X.; Liu, Y.; Qu, S.L.; Chen, M. Temperature fiber sensor without cross sensitivity based on the multi-thin-no-thin-multi fiber coated with PDMS. J. Phys. D-Appl. Phys. 2021, 54, 455101. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, D.; Lu, P.; Sun, Q.; Yang, W.; Wang, S.; Liu, L.; Ni, W. High sensitivity optical fiber strain sensor using twisted multimode fiber based on SMS structure. Opt. Commun. 2017, 405, 416–420. [Google Scholar] [CrossRef]
- Novais, S.; Ferreira, M.S.; Pinto, J.L. Relative Humidity Fiber Sensor Based on Multimode Interferometer Coated with Agarose-Gel. Coatings 2018, 8, 453. [Google Scholar] [CrossRef]
- He, Y.; Yang, H.; Lim, K.; Ahmad, H.; Feng, Z.; Zhang, P.; Tian, Q.; Lu, K.; Han, Z.; Liu, J. Discriminative measurement for temperature and humidity using hollow-core Fabry-Pérot interferometer. Opt. Fiber Technol. 2019, 53, 102027. [Google Scholar] [CrossRef]
- Li, X.; Chen, N.K.; Xi, L.X.; Zhang, H.; Zhang, X.G.; Zhang, W.B.; Tang, X.F. Micro-fiber Mach-Zehnder interferometer based on ring-core fiber. Opt. Express 2019, 27, 34603–34610. [Google Scholar] [CrossRef]
- Wu, Y.Q.; Yan, D.; Chen, N.K.; Grattan, K.T.V.; Rahman, B.M.A.; Li, X.; Tian, Z.; Zhang, L.Q.; Zhang, X.; Zhang, X.G.; et al. High sensitivity micro-fiber Mach-Zehnder interferometric temperature sensors with a high index ring layer. Opt. Express 2019, 27, 34248–34258. [Google Scholar] [CrossRef]
- Roriz, P.; Silva, S.; Frazao, O.; Novais, S. Optical Fiber Temperature Sensors and Their Biomedical Applications. Sensors 2020, 20, 2113. [Google Scholar] [CrossRef] [PubMed]
- Miliou, A. In-Fiber Interferometric-Based Sensors: Overview and Recent Advances. Photonics 2021, 8, 265. [Google Scholar] [CrossRef]
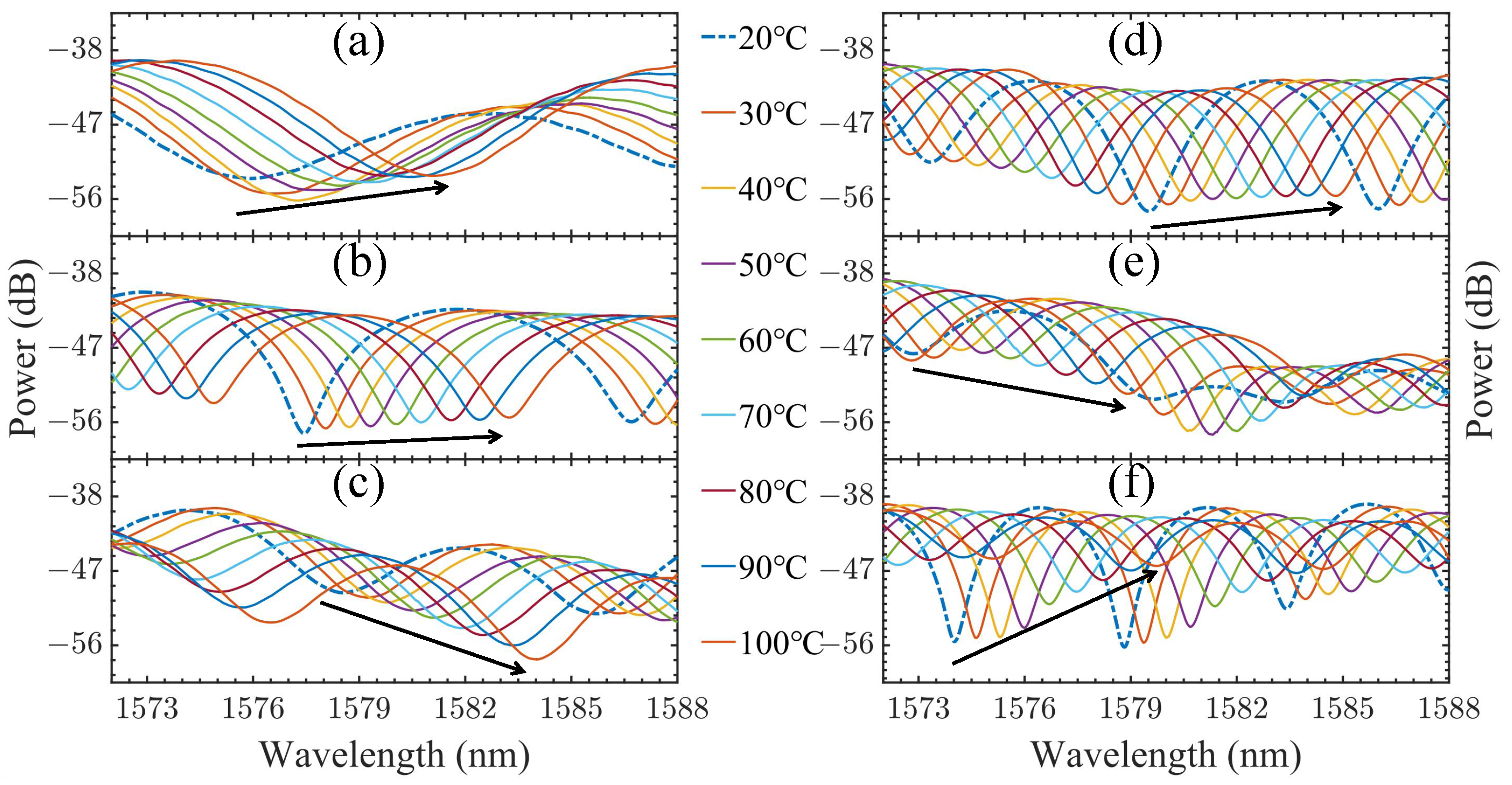
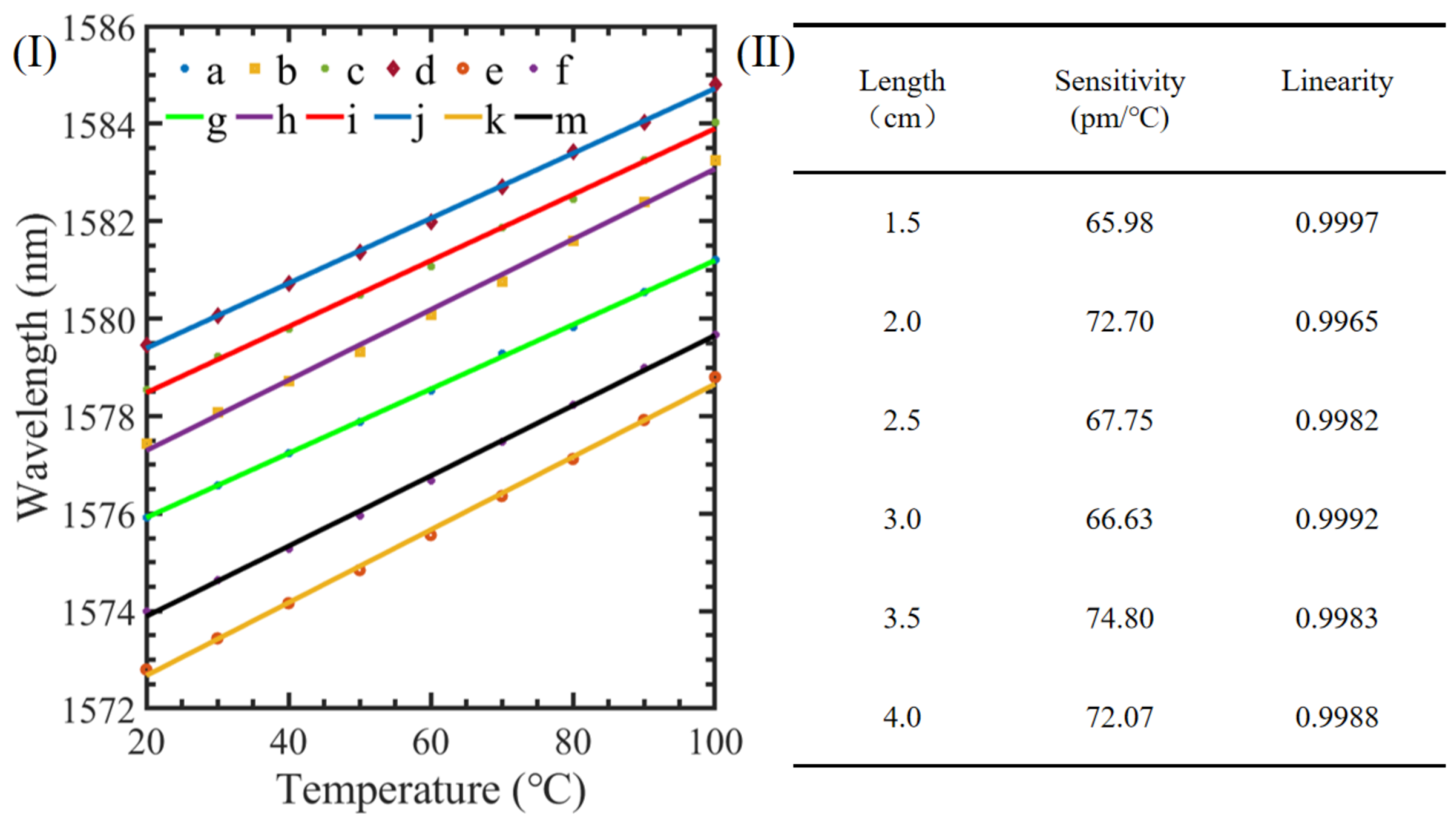
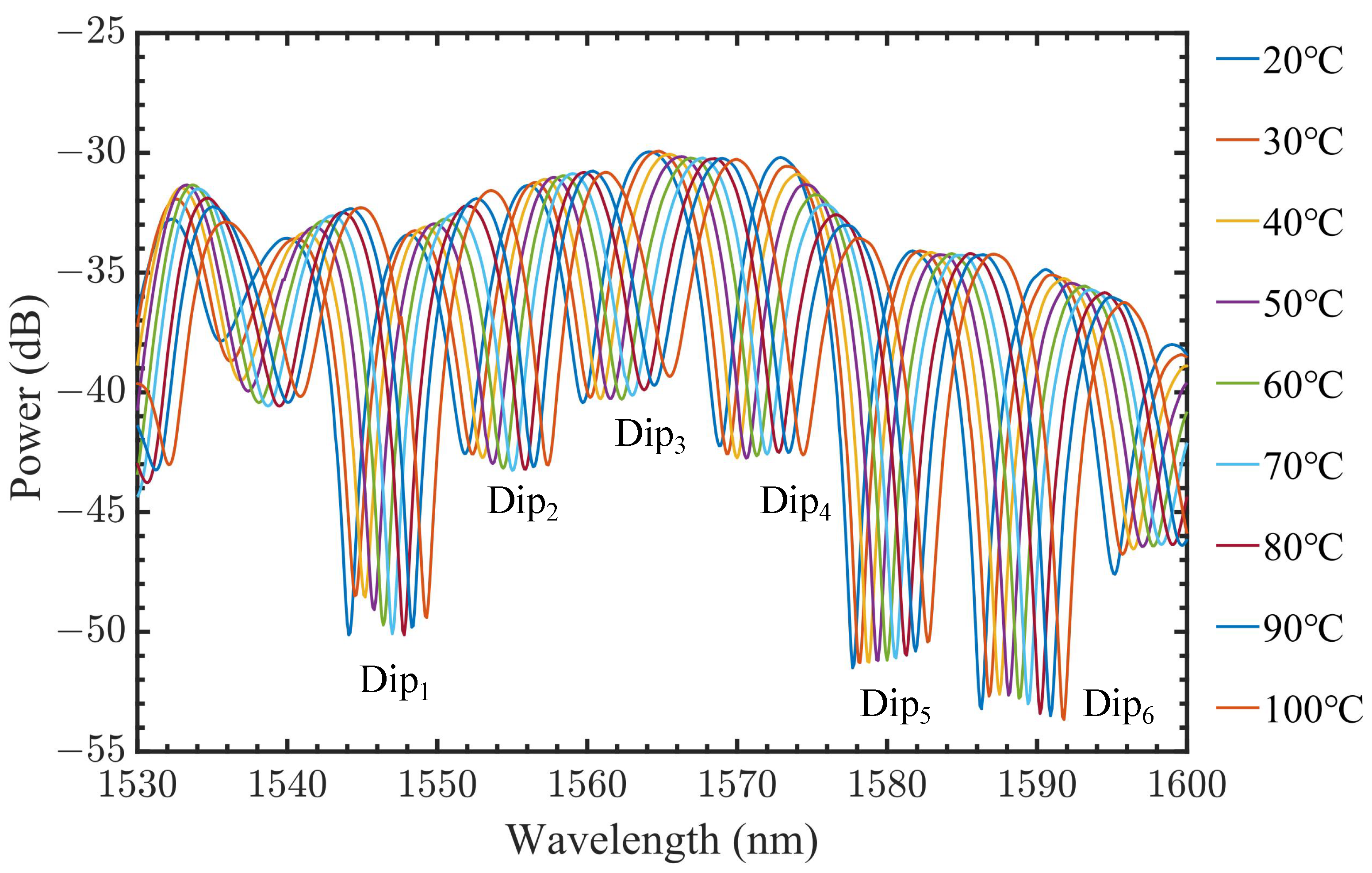
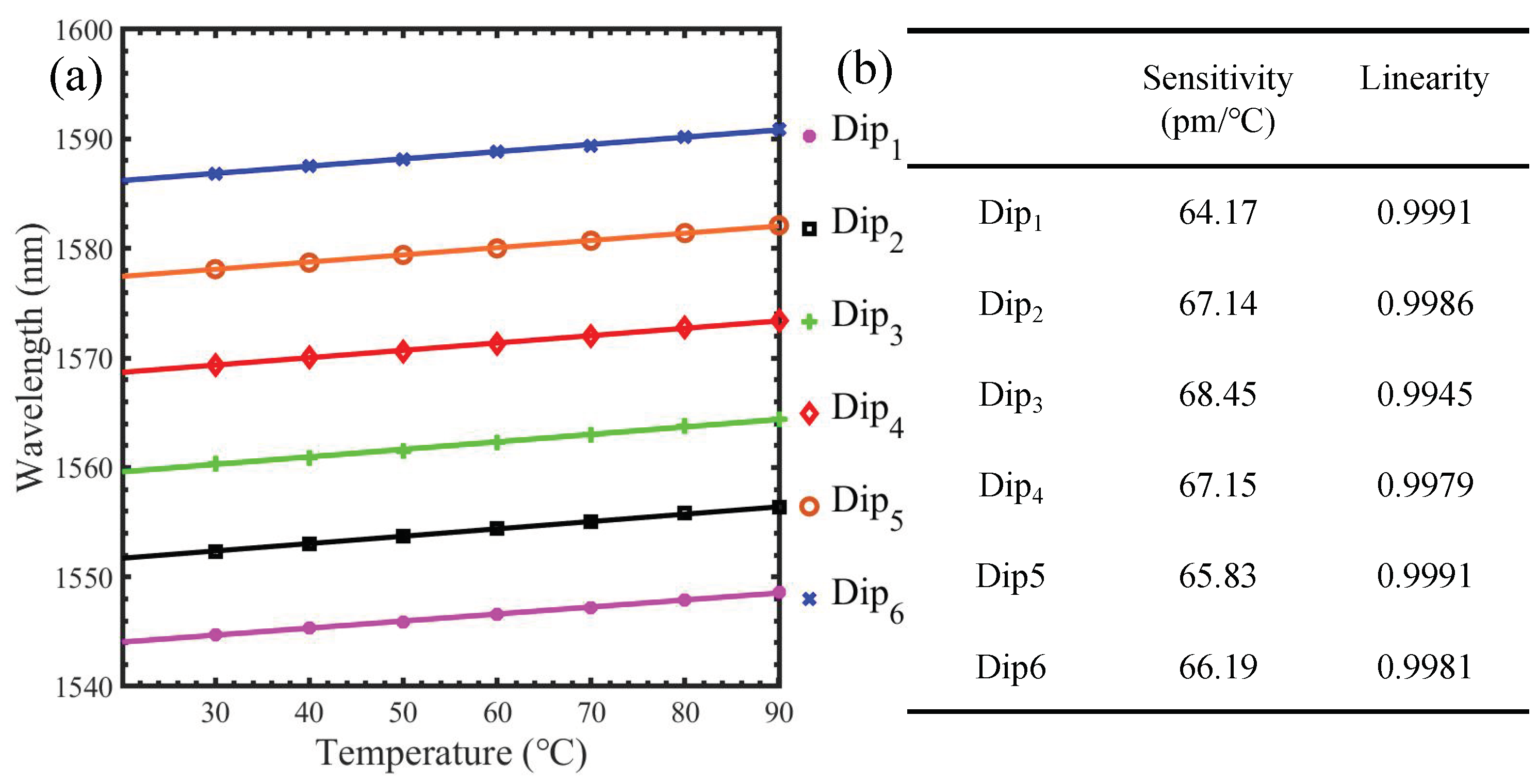

| Temperature (°C) | Trough When L = 1.5 cm (nm) | Trough When L = 2.0 cm (nm) | Trough When L = 2.5 cm (nm) | Trough When L = 3.0 cm (nm) | Trough When L = 3.5 cm (nm) | Trough When L = 4.0 cm (nm) |
|---|---|---|---|---|---|---|
| 20 | 1575.92 | 1577.44 | 1578.55 | 1579.46 | 1572.8 | 1574 |
| 30 | 1576.58 | 1578.08 | 1579.23 | 1580.06 | 1573.44 | 1574.64 |
| 40 | 1577.24 | 1578.72 | 1579.78 | 1580.72 | 1574.16 | 1575.28 |
| 50 | 1577.89 | 1579.32 | 1580.48 | 1581.36 | 1574.84 | 1575.96 |
| 60 | 1578.52 | 1580.08 | 1581.08 | 1581.98 | 1575.56 | 1576.68 |
| 70 | 1579.28 | 1580.76 | 1581.86 | 1582.7 | 1576.36 | 1577.48 |
| 80 | 1579.82 | 1581.6 | 1582.46 | 1583.42 | 1577.12 | 1578.24 |
| 90 | 1580.54 | 1582.4 | 1583.24 | 1584.02 | 1577.92 | 1579 |
| 100 | 1581.21 | 1583.24 | 1584.02 | 1584.8 | 1578.8 | 1579.68 |
| Sensing Structure | Temperature (°C) | Sensitivity (pm/°C) | Length (mm) | Reference |
|---|---|---|---|---|
| Triple cladding quartz specialty fiber | 35∼95 | 73.34 | 5, 10, 20 | [33] |
| Gallium alloy sensitivity-enhanced FBG | 5∼30 | 30 | — | [34] |
| Optical microfiber knot resonator | 27∼95 | 14.5 | Diameter = 1.3 | [35] |
| MMF-TCF-NCF-TCF-MMF | 35∼90 | 65.24 | 25 | [36] |
| SMF-MMF-SMF | 15∼75 | 29.33 | 44 | [37] |
| A thinner no-core fiber | −30∼100 | 38.7 | 33.7–35.1 | [22] |
| SMF-NCF | 10∼70 | 13.6 | 30 | [38] |
| SMF-HCF-PCF | 25∼70 | 10.64 | 1229 | [39] |
| This work | 20∼100 | 72 | 20–40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Tian, J.; Hu, X.; Tian, J.; He, Q. A Micro-Mach–Zehnder Interferometer Temperature Sensing Design Based on a Single Mode–Coreless–Multimode–Coreless–Single Mode Fiber Cascaded Structure. Photonics 2024, 11, 363. https://doi.org/10.3390/photonics11040363
Yang Q, Tian J, Hu X, Tian J, He Q. A Micro-Mach–Zehnder Interferometer Temperature Sensing Design Based on a Single Mode–Coreless–Multimode–Coreless–Single Mode Fiber Cascaded Structure. Photonics. 2024; 11(4):363. https://doi.org/10.3390/photonics11040363
Chicago/Turabian StyleYang, Qing, Jing Tian, Xiao Hu, Jiajun Tian, and Qiqi He. 2024. "A Micro-Mach–Zehnder Interferometer Temperature Sensing Design Based on a Single Mode–Coreless–Multimode–Coreless–Single Mode Fiber Cascaded Structure" Photonics 11, no. 4: 363. https://doi.org/10.3390/photonics11040363
APA StyleYang, Q., Tian, J., Hu, X., Tian, J., & He, Q. (2024). A Micro-Mach–Zehnder Interferometer Temperature Sensing Design Based on a Single Mode–Coreless–Multimode–Coreless–Single Mode Fiber Cascaded Structure. Photonics, 11(4), 363. https://doi.org/10.3390/photonics11040363




