High-Efficiency Dynamic Three-Dimensional Topography Measurement Using the Phase Shift Generation Method
Abstract
1. Introduction
2. Basic Theory
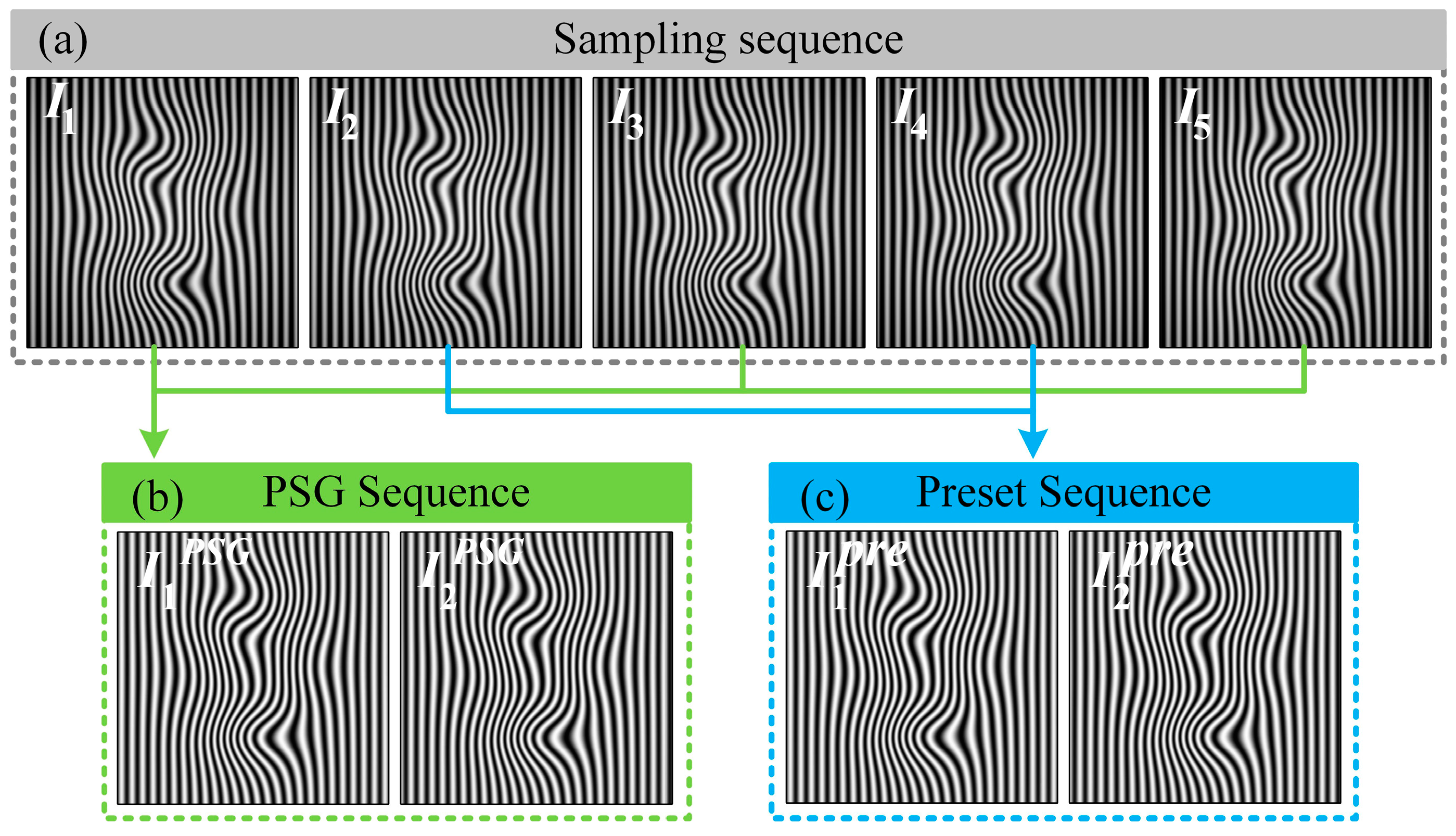
2.1. PSG Method
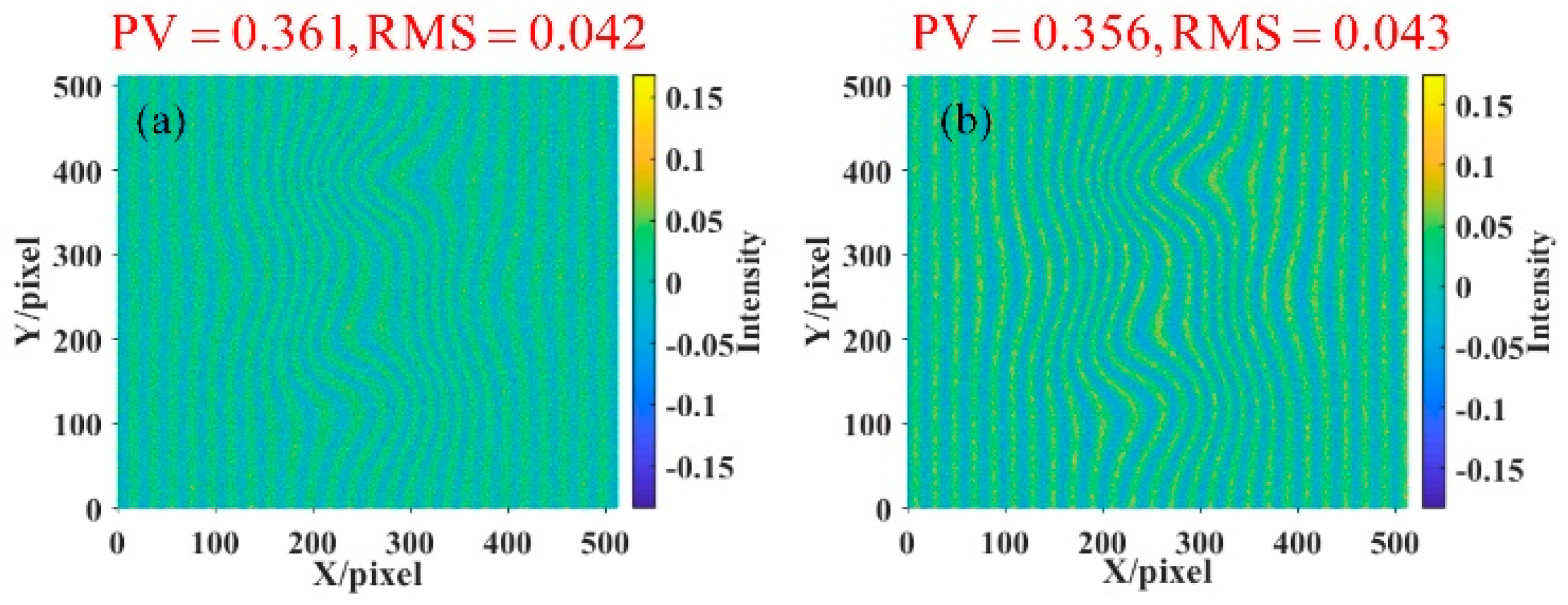
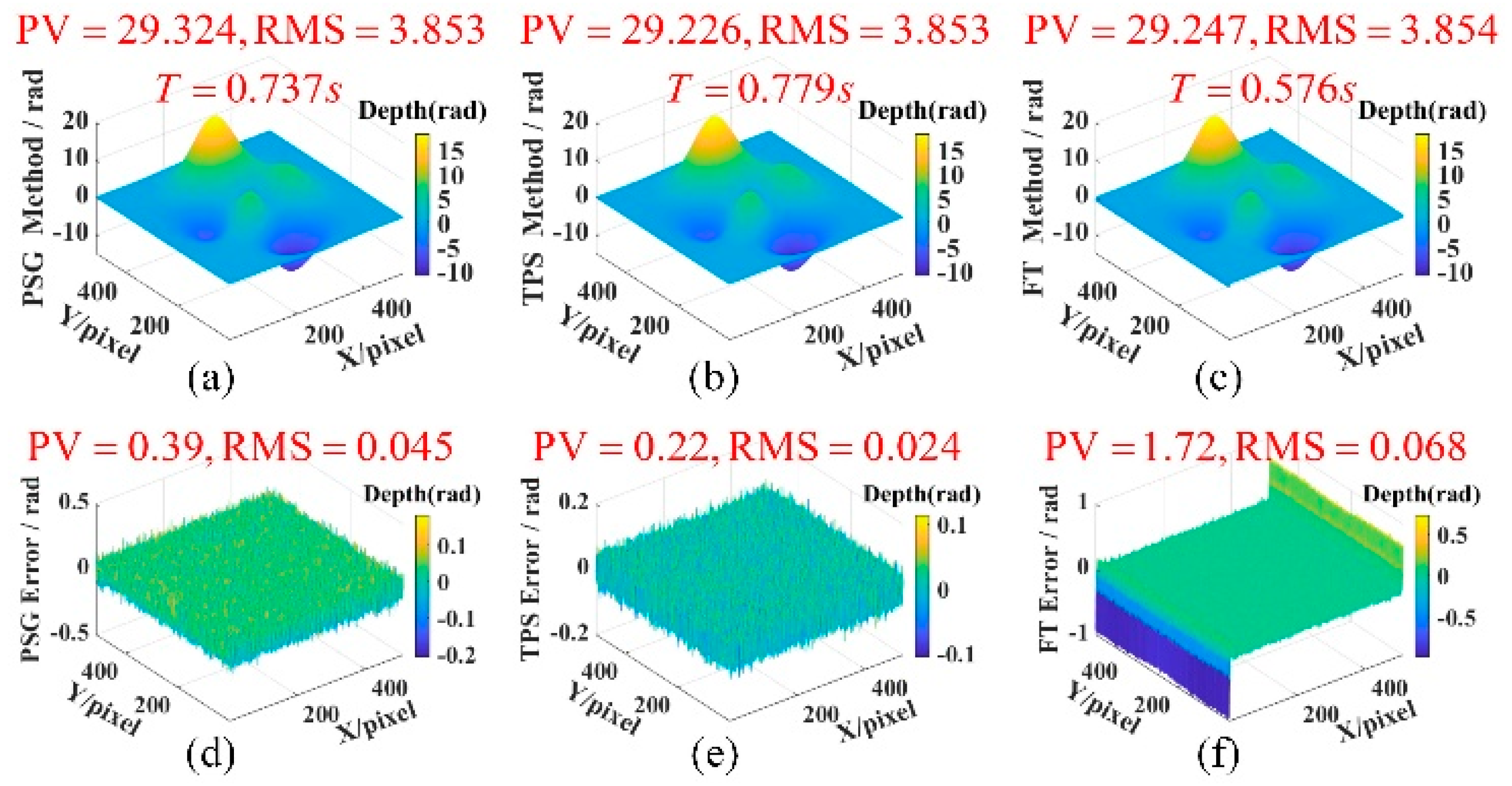
2.2. Simulation Analysis
3. Experiment Results
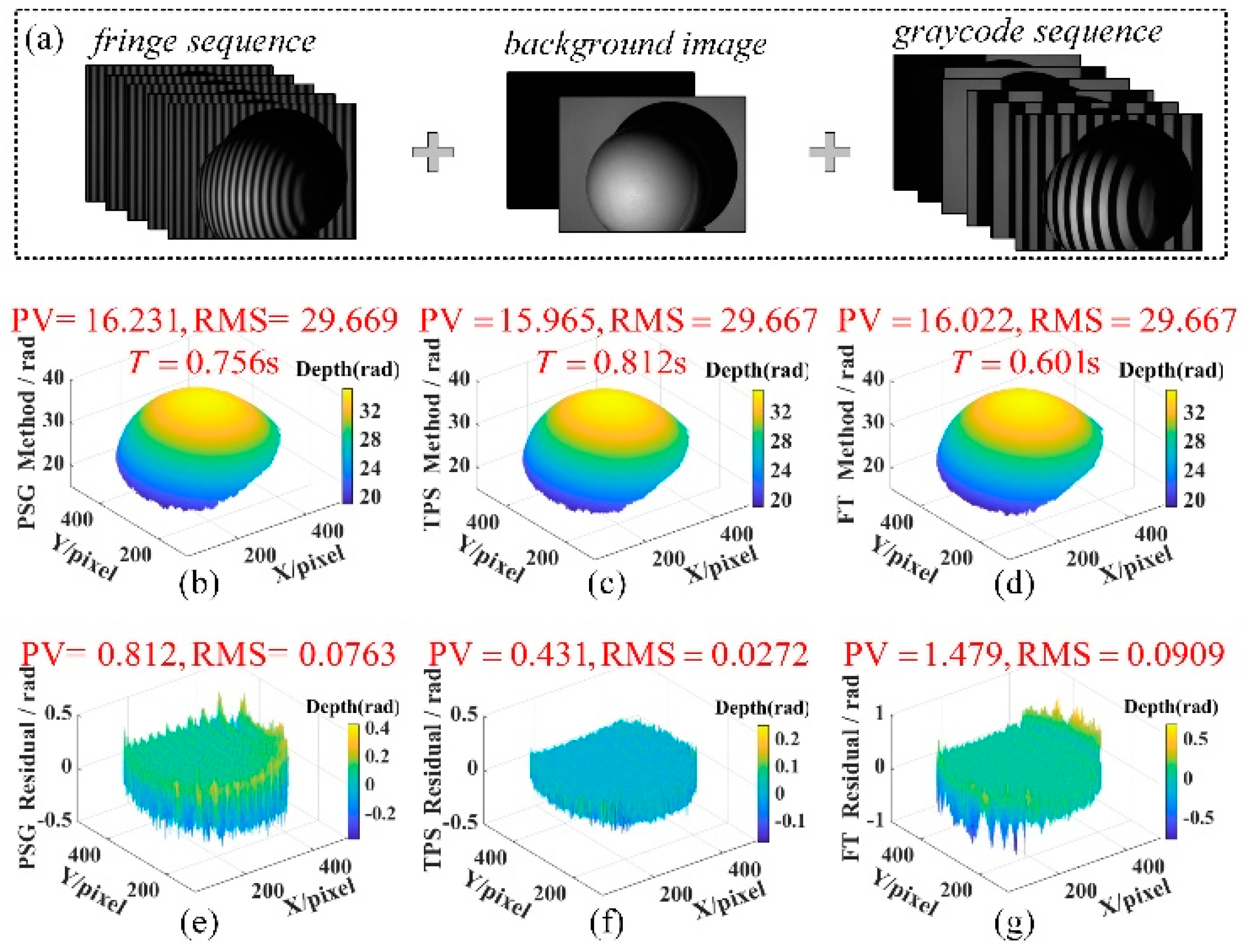
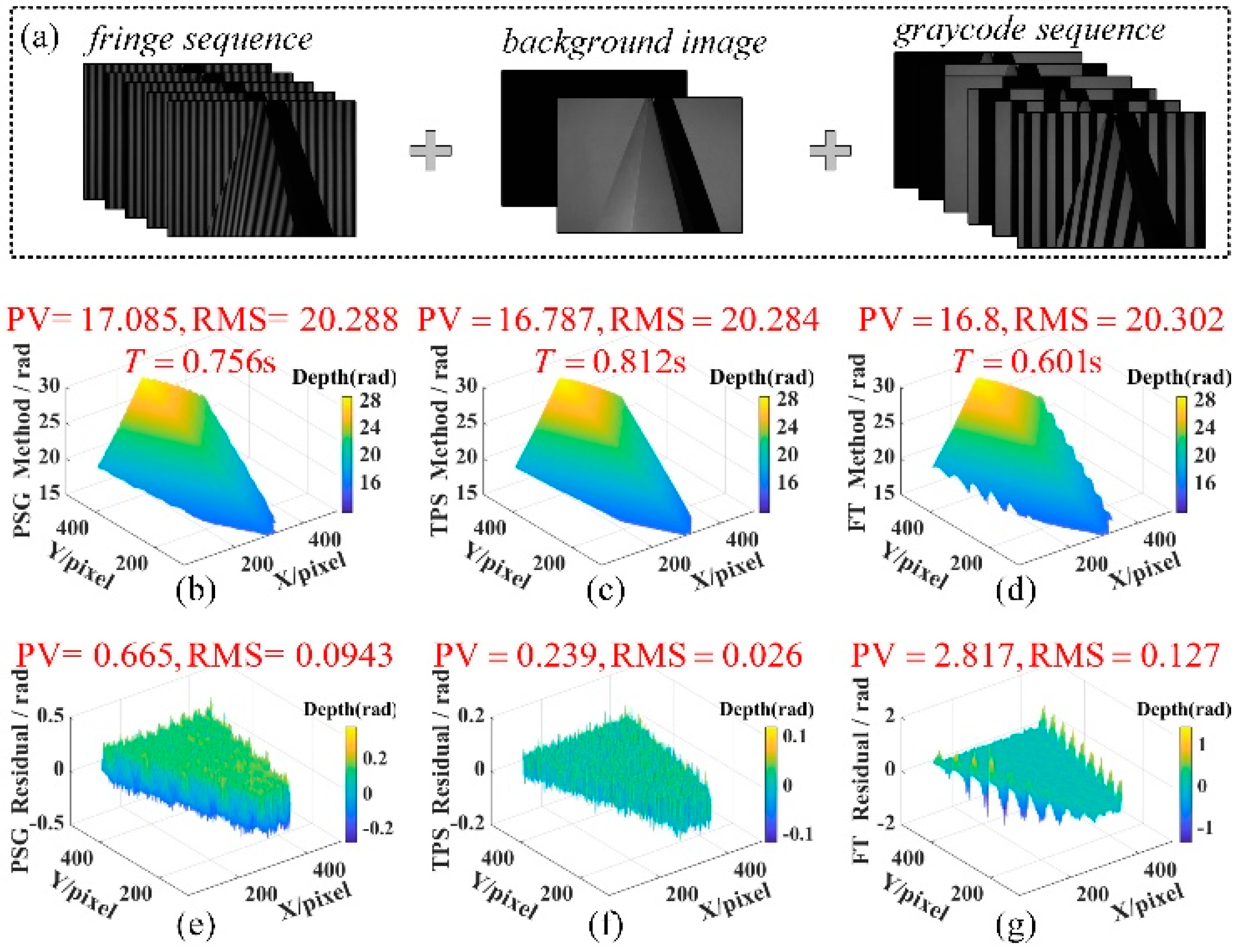
3.1. Static Scene Test
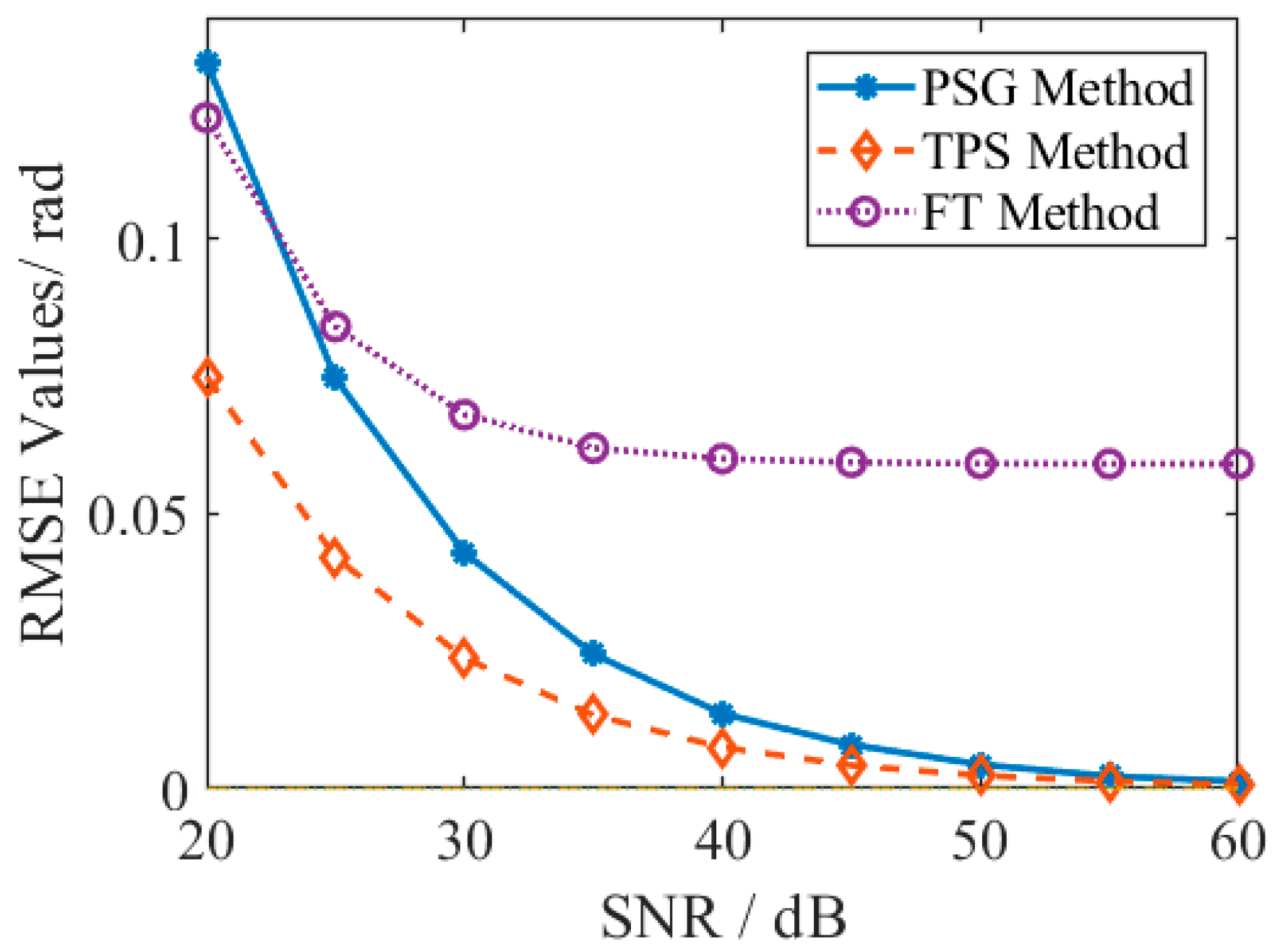
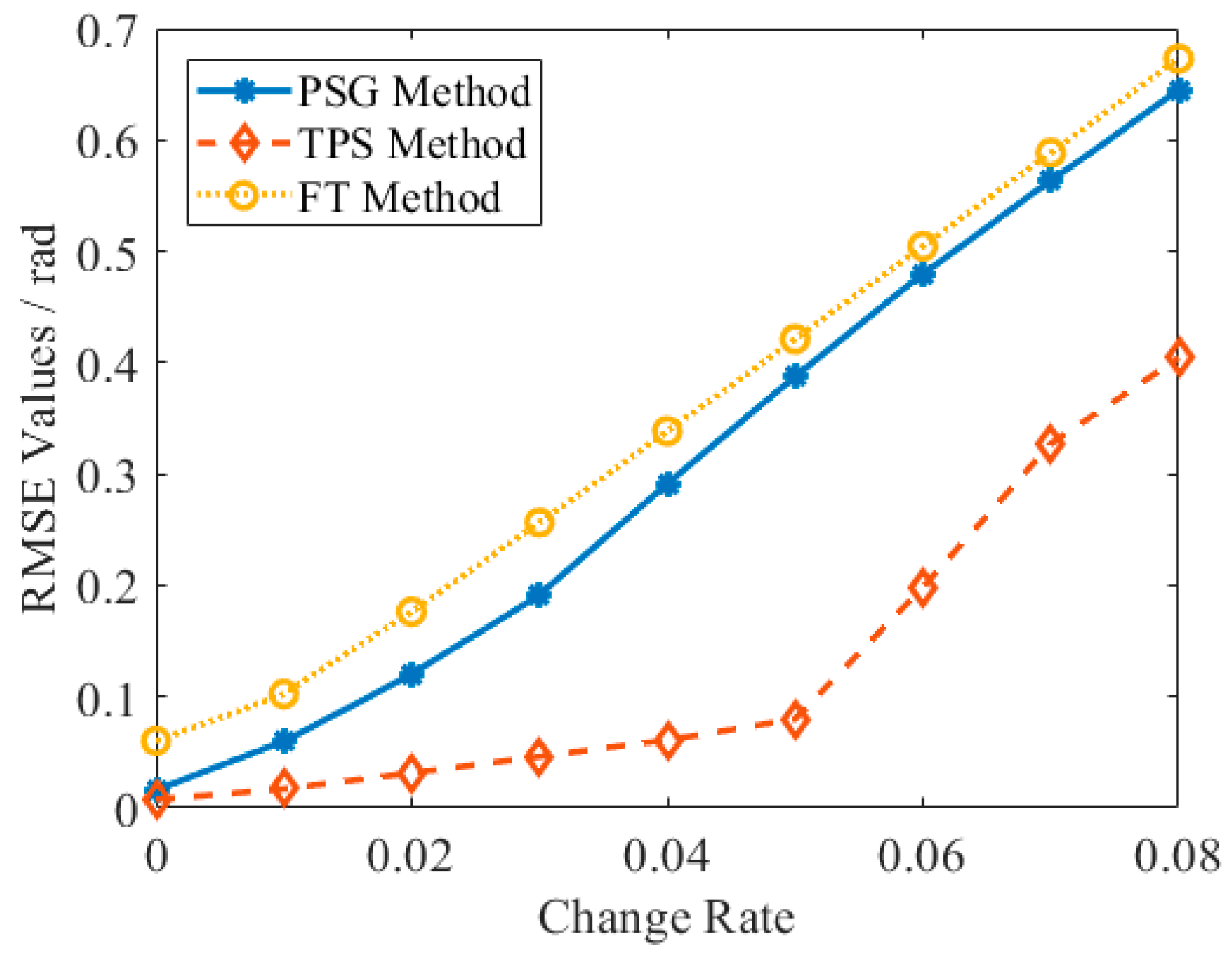
3.2. Accuracy and Efficiency Analysis
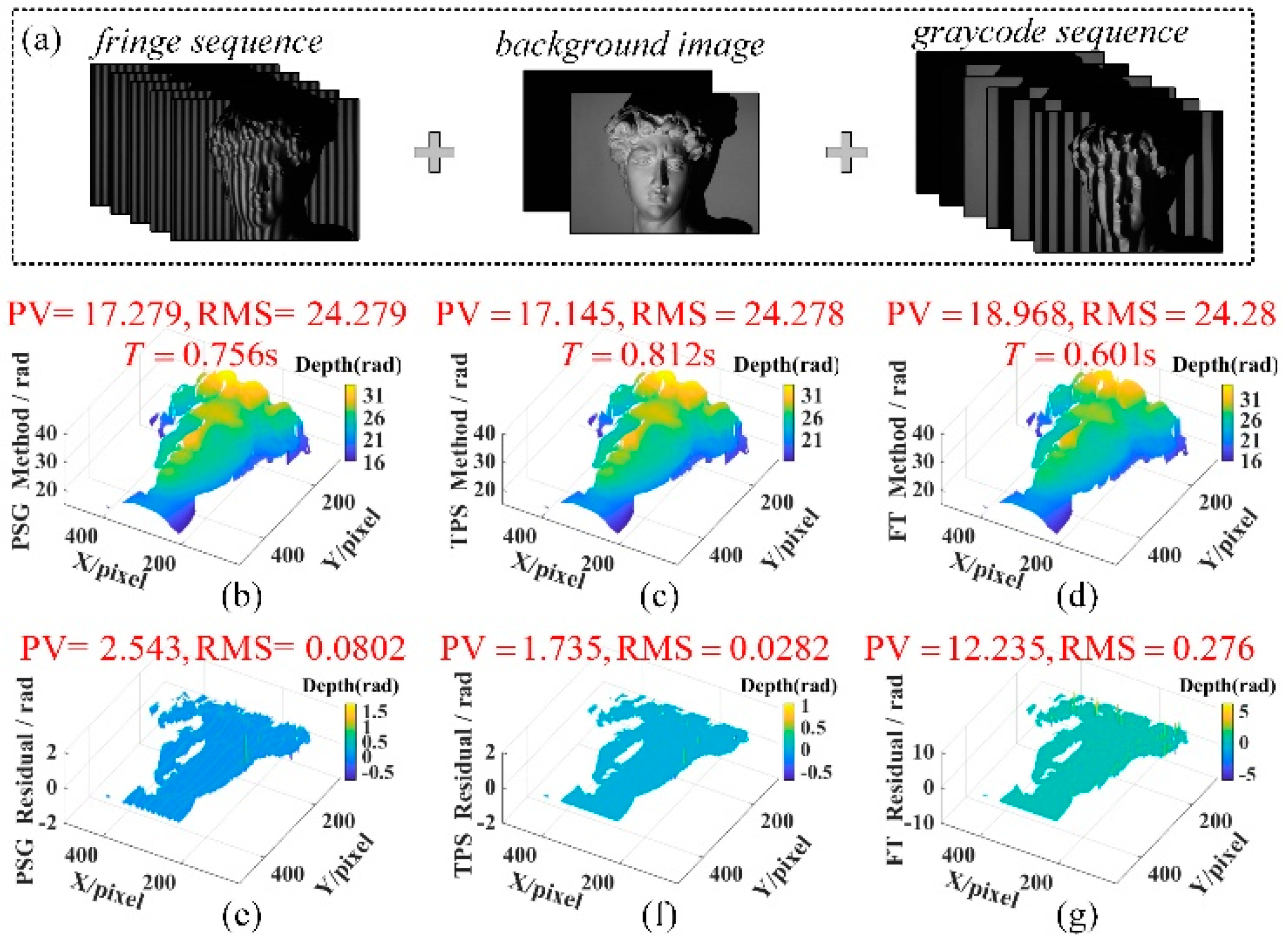
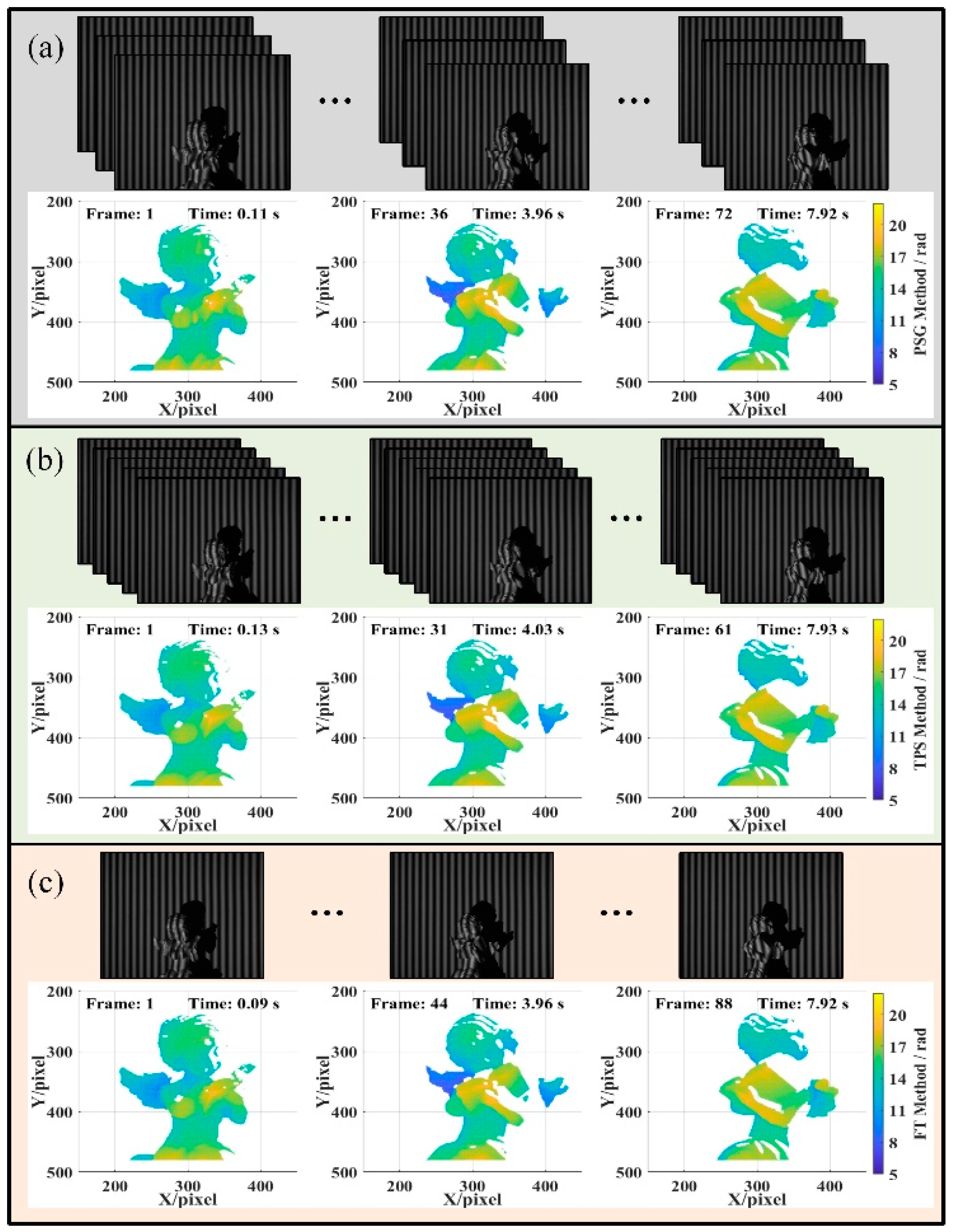
3.3. Dynamic Scene Test
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zuo, C.; Feng, S.J.; Huang, L.; Tao, T.Y.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Laser Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Lyu, N.Q.; Yu, H.T.; Han, J.; Zheng, D.L. Structured light-based underwater 3-d reconstruction techniques: A comparative study. Opt. Laser Eng. 2023, 161, 107344. [Google Scholar] [CrossRef]
- Lv, S.Z.; Kemao, Q. Modeling the measurement precision of fringe projection profilometry. Light-Sci. Appl. 2023, 12, 257. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Tao, T.Y.; Feng, S.J.; Huang, L.; Asundi, A.; Chen, Q. Micro fourier transform profilometry (μFTP): 3D shape measurement at 10,000 frames per second. Opt. Laser Eng. 2018, 102, 70–91. [Google Scholar] [CrossRef]
- Feng, S.; Zuo, C.; Chen, Q. High-speed 3D measurements at 20,000 Hz with deep convolutional neural networks. In Optical Metrology and Inspection for Industrial Applications VI; Han, S., Yoshizawa, T., Zhang, S., Chen, B., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 11189. [Google Scholar]
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Laser Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Flores, J.L.; Stronik, M.; Muñoz, A.; Garcia-Torales, G.; Ordoñes, S.; Cruz, A. Dynamic 3D shape measurement by iterative phase shifting algorithms and colored fringe patterns. Opt. Express 2018, 26, 12403–12414. [Google Scholar] [CrossRef] [PubMed]
- Pagès, J.; Salvi, J.; Collewet, C.; Forest, J. Optimised de bruijn patterns for one-shot shape acquisition. Image Vis. Comput. 2005, 23, 707–720. [Google Scholar] [CrossRef]
- Morita, H.; Yajima, K.; Sakata, S. Reconstruction of Surfaces of 3-D Objects by M-Array Pattern Projection Method. In International Conference on Computer Vision; IEEE Computer Society: Washington, DC, USA, 1998. [Google Scholar]
- Zhou, P.; Zhu, J.P.; Jing, H.L. Optical 3-D surface reconstruction with color binary speckle pattern encoding. Opt. Express 2018, 26, 3452–3465. [Google Scholar] [CrossRef]
- Zhong, F.Q.; Kumar, R.; Quan, C.G. RGB laser speckles based 3D profilometry. Appl. Phys. Lett. 2019, 114, 201104. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Xu, B.; Lau, D.L.; Zhu, C.; Liu, K. Correcting projector lens distortion in real time with a scale-offset model for structured light illumination. Opt. Express 2022, 30, 24507–24522. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yau, S.T. High-resolution, real-time 3d absolute coordinate measurement based on a phase-shifting method. Opt. Express 2006, 14, 2644–2649. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.J.; Xu, Y.P.; Zhang, C.L.; Tang, J.F.; Tang, D.; Kong, C.; Jin, J. An optimized error compensation method for phase measurement profilometry. Photonics 2023, 10, 1036. [Google Scholar] [CrossRef]
- Zheng, D.L.; Da, F.P.; Kemao, Q.; Seah, H.S. Phase-shifting profilometry combined with gray-code patterns projection: Unwrapping error removal by an adaptive median filter. Opt. Express 2017, 25, 4700–4713. [Google Scholar] [CrossRef] [PubMed]
- Lv, S.Z.; Tang, D.W.; Zhang, X.J.; Yang, D.Y.; Deng, W.J.; Qian, K.M. Fringe projection profilometry method with high efficiency, precision, and convenience: Theoretical analysis and development. Opt. Express 2022, 30, 33515–33537. [Google Scholar] [CrossRef]
- Zappa, E.; Busca, G. Static and dynamic features of fourier transform profilometry: A review. Opt. Laser Eng. 2012, 50, 1140–1151. [Google Scholar] [CrossRef]
- Kemao, Q. Two-dimensional windowed fourier transform for fringe pattern analysis: Principles, applications and implementations. Opt. Laser Eng. 2007, 45, 304–317. [Google Scholar] [CrossRef]
- Gao, W.J.; Huyen, N.T.T.; Loi, H.S.; Kemao, Q. Real-time 2d parallel windowed fourier transform for fringe pattern analysis using graphics processing unit. Opt. Express 2009, 17, 23147–23152. [Google Scholar] [CrossRef] [PubMed]
- Ming, Z.; Qian, K.M. Multicore implementation of the windowed fourier transform algorithms for fringe pattern analysis. Appl. Opt. 2015, 54, 587–594. [Google Scholar]
- Xu, Y.J.; Gao, F.; Jiang, X.Q. A brief review of the technological advancements of phase measuring deflectometry. Photonix 2020, 1, 14. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, P.S. High-resolution, real-time three-dimensional shape measurement. Opt. Eng. 2006, 45, 123601. [Google Scholar]
- Liu, K.; Wang, Y.C.; Lau, D.L.; Hao, Q.; Hassebrook, L.G. Dual-frequency pattern scheme for high-speed 3-D shape measurement. Opt. Express 2010, 18, 5229–5244. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.C.; Liu, K.; Hao, Q.; Lau, D.L.; Hassebrook, L.G. Period coded phase shifting strategy for real-time 3-D structured light illumination. IEEE Trans. Image Process. 2011, 20, 3001–3013. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Towers, C.E.; Towers, D.P. Time efficient color fringe projection system for 3D shape and color using optimum 3-frequency selection. Opt. Express 2006, 14, 6444–6455. [Google Scholar] [CrossRef] [PubMed]
- Ayubi, G.A.; Ayubi, J.A.; Di Martino, J.M.; Ferrari, J.A. Pulse-width modulation in defocused three-dimensional fringe projection. Opt. Lett. 2010, 35, 3682–3684. [Google Scholar] [CrossRef]
- Guo, H.; Huang, P.S. Absolute phase technique for the fourier transform method. Opt. Eng. 2009, 48, 043609. [Google Scholar] [CrossRef]
- Qian, J.M.; Tao, T.Y.; Feng, S.J.; Chen, Q.; Zuo, C. Motion-artifact-free dynamic 3D shape measurement with hybrid fourier-transform phase-shifting profilometry. Opt. Express 2019, 27, 2713–2731. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.B.; Wu, Z.J.; Li, Y.Y.; Liu, Y.H.; Zhang, Q.C. Real-time 3d shape measurement with dual-frequency composite grating and motion-induced error reduction. Opt. Express 2020, 28, 26882–26897. [Google Scholar] [CrossRef]
- Zhong, C.; Gao, Z.; Wang, X.; Shao, S.; Gao, C. Structured light three-dimensional measurement based on machine learning. Sensors 2019, 19, 3229. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Q.; Zuo, C.; Feng, S. High-speed high dynamic range 3D shape measurement based on deep learning. Opt. Laser Eng. 2020, 134, 106245. [Google Scholar] [CrossRef]
- Yu, H.T.; Chen, X.Y.; Zhang, Z.; Zuo, C.; Zhang, Y.; Zheng, D.L.; Han, J. Dynamic 3-D measurement based on fringe-to-fringe transformation using deep learning. Opt. Express 2020, 28, 9405–9418. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.J.; Zuo, C.; Tao, T.Y.; Hu, Y.; Zhang, M.L.; Chen, Q.; Gu, G.H. Robust dynamic 3-D measurements with motion-compensated phase-shifting profilometry. Opt. Laser Eng. 2018, 103, 127–138. [Google Scholar] [CrossRef]
- Lu, L.; Jia, Z.Y.; Luan, Y.S.; Xi, J.T. Reconstruction of isolated moving objects with high 3d frame rate based on phase shifting profilometry. Opt. Commun. 2019, 438, 61–66. [Google Scholar] [CrossRef]
- Feng, S.; Zuo, C.; Yin, W.; Gu, G.; Chen, Q. Micro deep learning profilometry for high-speed 3D surface imaging. Opt. Laser Eng. 2019, 121, 416–427. [Google Scholar] [CrossRef]
- Qian, J.M.; Feng, S.J.; Li, Y.X.; Tao, T.Y.; Han, J.; Chen, Q.; Zuo, C. Single-shot absolute 3D shape measurement with deep-learning-based color fringe projection profilometry. Opt. Lett. 2020, 45, 1842–1845. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Guo, W.; Zhang, Q. High-speed three-dimensional shape measurement based on shifting gray-code light. Opt. Express 2019, 27, 22631–22644. [Google Scholar] [CrossRef]
- Zhang, S. High-speed 3d shape measurement with structured light methods: A review. Opt. Laser Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zuo, C.; Guo, W.B.; Tao, T.Y.; Zhang, Q.C. High-speed three-dimensional shape measurement based on cyclic complementary gray-code light. Opt. Express 2019, 27, 1283–1297. [Google Scholar] [CrossRef]
- Servin, M.; Padilla, M.; Garnica, G.; Paez, G. Design of nonlinearly spaced phase-shifting algorithms using their frequency transfer function. Appl. Opt. 2019, 58, 1134–1138. [Google Scholar] [CrossRef]
- Servin, M.; Padilla, M.; Garnica, G.; Paez, G. Fourier spectra for nonuniform phase-shifting algorithms based on principal component analysis. Opt. Express 2019, 27, 25861–25871. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Q.; Liu, Y.; Zhu, F.; Hou, J.; Xiong, F.; Zhang, Y. High-Efficiency Dynamic Three-Dimensional Topography Measurement Using the Phase Shift Generation Method. Photonics 2024, 11, 364. https://doi.org/10.3390/photonics11040364
Deng Q, Liu Y, Zhu F, Hou J, Xiong F, Zhang Y. High-Efficiency Dynamic Three-Dimensional Topography Measurement Using the Phase Shift Generation Method. Photonics. 2024; 11(4):364. https://doi.org/10.3390/photonics11040364
Chicago/Turabian StyleDeng, Qinyuan, Yangyi Liu, Fashi Zhu, Jie Hou, Fei Xiong, and Yan Zhang. 2024. "High-Efficiency Dynamic Three-Dimensional Topography Measurement Using the Phase Shift Generation Method" Photonics 11, no. 4: 364. https://doi.org/10.3390/photonics11040364
APA StyleDeng, Q., Liu, Y., Zhu, F., Hou, J., Xiong, F., & Zhang, Y. (2024). High-Efficiency Dynamic Three-Dimensional Topography Measurement Using the Phase Shift Generation Method. Photonics, 11(4), 364. https://doi.org/10.3390/photonics11040364




