Advances in Optical Fiber Speckle Sensing: A Comprehensive Review
Abstract
1. Introduction
2. Brief Historical Background and Terminology
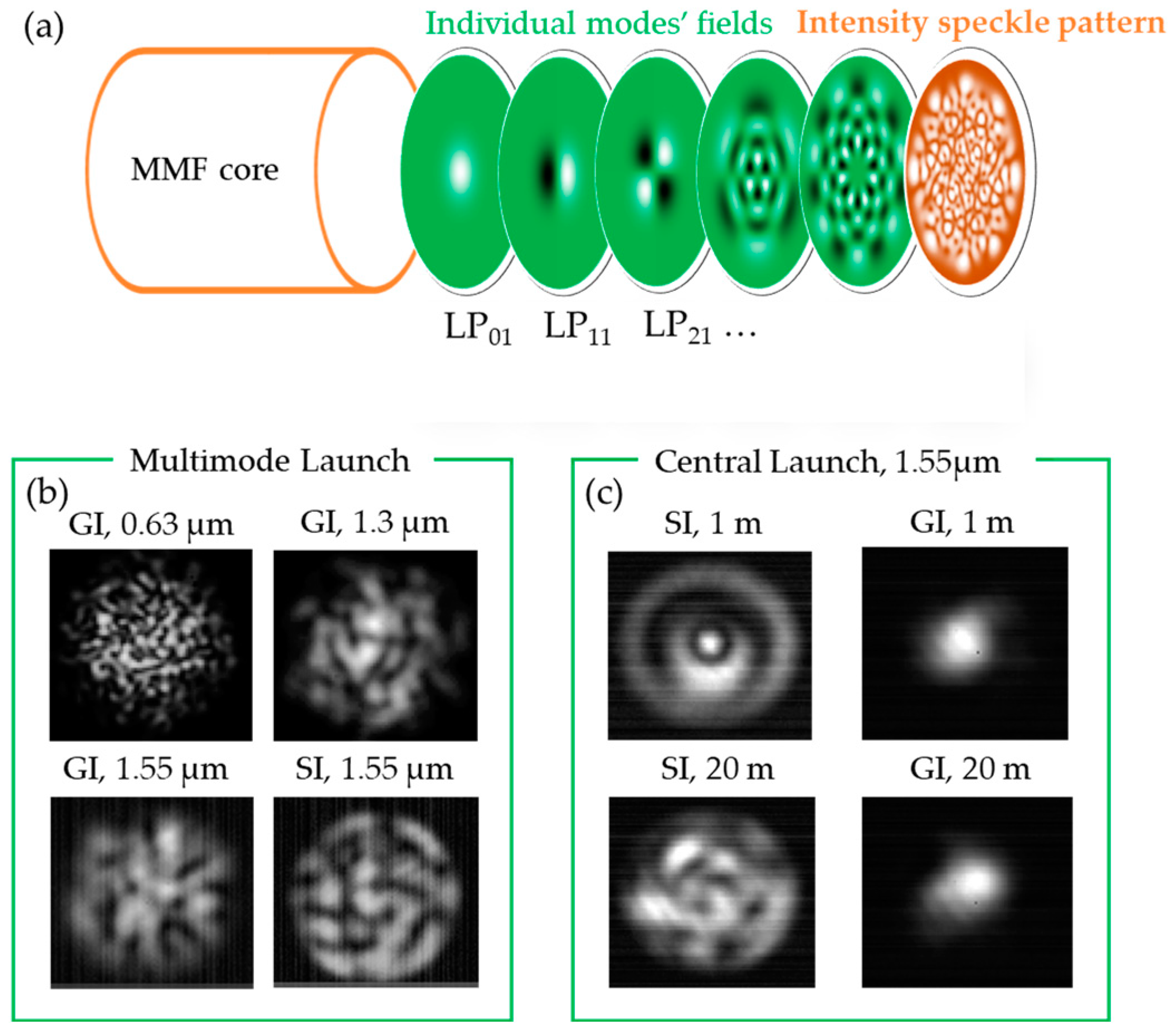
3. Fundamentals of Optical Fiber Speckle Sensing
4. Signal Processing and Data Analysis
4.1. Intensity Approach
4.2. Correlation Approach
4.3. Machine Learning Approach
4.4. Spectral Domain Approach
5. Sensing Applications
6. Challenges and Future Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Theodosiou, A.; Kalli, K. Recent trends and advances of fibre Bragg grating sensors in CYTOP polymer optical fibres. Opt. Fiber Technol. 2020, 54, 102079. [Google Scholar] [CrossRef]
- Mizuno, Y.; Theodosiou, A.; Kalli, K.; Liehr, S.; Lee, H.; Nakamura, K. Distributed polymer optical fiber sensors: A review and outlook. Photonics Res. 2021, 9, 1719–1733. [Google Scholar] [CrossRef]
- Sabri, N.; Aljunid, S.A.; Salim, M.S.; Ahmad, R.B.; Kamaruddin, R. Toward Optical Sensors: Review and Applications. J. Phys. Conf. Ser. 2013, 423, 012064. [Google Scholar] [CrossRef]
- Poeggel, S.; Tosi, D.; Duraibabu, D.; Leen, G.; McGrath, D.; Lewis, E. Optical Fibre Pressure Sensors in Medical Applications. Sensors 2015, 15, 17115–17148. [Google Scholar] [CrossRef] [PubMed]
- Leal-Junior, A.G.; Diaz, C.A.; Avellar, L.M.; Pontes, M.J.; Marques, C.; Frizera, A. Polymer Optical Fiber Sensors in Healthcare Applications: A Comprehensive Review. Sensors 2019, 19, 3156. [Google Scholar] [CrossRef] [PubMed]
- Xiao, G.; Guo, H.; Mrad, N.; Rocha, B.; Sun, Z. Towards the simultaneous monitoring of load and damage in aircraft structures using fiber Bragg grating sensors. In Proceedings of the OFS2012 22nd International Conference on Optical Fiber Sensors, Beijing, China, 14–19 October 2012; Volume 8421, p. 8421BD-8421BD–4. [Google Scholar] [CrossRef]
- Theodosiou, A.; Komodromos, M.; Kalli, K. Carbon cantilever beam health inspection using a polymer fiber bragg grating array. J. Light. Technol. 2017, 36, 986–992. [Google Scholar] [CrossRef]
- André, P.; Varum, H.; Antunes, P.; Ferreira, L.; Sousa, M. Monitoring of the concrete curing process using plastic optical fibers. Measurement 2012, 45, 556–560. [Google Scholar] [CrossRef]
- Theodosiou, A.; Savva, P.; Mendoza, E.; Petrou, M.F.; Kalli, K. In-Situ Relative Humidity Sensing for Ultra-High-Performance Concrete Using Polymer Fiber Bragg Gratings. IEEE Sens. J. 2021, 21, 16086–16092. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Theodosiou, A.; Diaz, C.R.; Marques, C.; Pontes, M.J.; Kalli, K.; Frizera, A. Simultaneous measurement of axial strain, bending and torsion with a single fiber bragg grating in cytop fiber. J. Light. Technol. 2019, 37, 971–980. [Google Scholar] [CrossRef]
- Leal-junior, A.G. Polymer Optical Fiber Sensors for Healthcare Devices: From Material Analysis to Practical Applications. Ph.D. Thesis, Digital Repository of the Universidade Federal do Espírito Santo, Vitória, Brasil, 2018; p. 201. [Google Scholar]
- Domingues, M.F.; Tavares, C.; Leitão, C.; Frizera-Neto, A.; Alberto, N.; Marques, C.; Radwan, A.; Rodriguez, J.; Postolache, O.; Rocon, E.; et al. Insole optical fiber Bragg grating sensors network for dynamic vertical force monitoring. J. Biomed. Opt. 2017, 22, 091507. [Google Scholar] [CrossRef]
- Chiavaioli, F.; Baldini, F.; Tombelli, S.; Trono, C.; Giannetti, A. Biosensing with optical fiber gratings. Nanophotonics 2017, 6, 663–679. [Google Scholar] [CrossRef]
- Pospori, A.; Webb, D.J. Stress Sensitivity Analysis of Optical Fiber Bragg Grating-Based Fabry–Pérot Interferometric Sensors. J. Light. Technol. 2017, 35, 2654–2659. [Google Scholar] [CrossRef]
- Teng, C.; Min, R.; Zheng, J.; Deng, S.; Li, M.; Hou, L.; Yuan, L. Intensity-Modulated Polymer Optical Fiber-Based Refractive Index Sensor: A Review. Sensors 2021, 22, 81. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Hayashi, N.; Mizuno, Y.; Nakamura, K. Slope-Assisted Brillouin Optical Correlation-Domain Reflectometry Using Polymer Optical Fibers with High Propagation Loss. J. Light. Technol. 2017, 35, 2306–2310. [Google Scholar] [CrossRef]
- Theodosiou, A.; Kalli, K. All-in-Fiber Cladding Interferometric and Bragg Grating Components Made via Plane-by-Plane Femtosecond Laser Inscription. J. Light. Technol. 2019, 37, 4864–4871. [Google Scholar] [CrossRef]
- Efendioglu, H.S. A Review of Fiber-Optic Modal Modulated Sensors: Specklegram and Modal Power Distribution Sensing. IEEE Sens. J. 2017, 17, 2055–2064. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Rademacher, G.; Luís, R.S. Space-division multiplexing for optical fiber communications. Optica 2021, 8, 1186–1203. [Google Scholar] [CrossRef]
- Ukil, A.; Braendle, H.; Krippner, P. Distributed Temperature Sensing: Review of Technology and Applications. IEEE Sens. J. 2012, 12, 885–892. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, C.; Liu, K.; Jiang, J.; Yang, D.; Pan, G.; Pu, Z.; Liu, T. Distributed Optical Fiber Sensors Based on Optical Frequency Domain Reflectometry: A review. Sensors 2018, 18, 1072. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Theodosiou, A.; Min, R.; Casas, J.; Diaz, C.R.; Dos Santos, W.M.; Pontes, M.J.; Siqueira, A.A.G.; Marques, C.; Kalli, K.; et al. Quasi-Distributed Torque and Displacement Sensing on a Series Elastic Actuator’s Spring Using FBG Arrays Inscribed in CYTOP Fibers. IEEE Sens. J. 2019, 19, 4054–4061. [Google Scholar] [CrossRef]
- Sanders, W.C. Basic Principles of Nanotechnology; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Theodosiou, A.; Komodromos, M.; Kalli, K. Accurate and Fast Demodulation Algorithm for Multipeak FBG Reflection Spectra Using a Combination of Cross Correlation and Hilbert Transformation. J. Light. Technol. 2017, 35, 3956–3962. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera-Neto, A.; Marques, C.; Pontes, M.J. Measurement of Temperature and Relative Humidity with Polymer Optical Fiber Sensors Based on the Induced Stress-Optic Effect. Sensors 2018, 18, 916. [Google Scholar] [CrossRef]
- Bilro, L.; Alberto, N.; Pinto, J.L.; Nogueira, R. Optical Sensors Based on Plastic Fibers. Sensors 2012, 12, 12184–12207. [Google Scholar] [CrossRef]
- Wu, S.; Yin, S.; Yu, F.T.S. Sensing with fiber specklegrams. Appl. Opt. 1991, 30, 4468–4470. [Google Scholar] [CrossRef]
- Wu, S.; Yin, S.; Rajan, S.; Yu, F.T.S. Multichannel sensing with fiber specklegrams. Appl. Opt. 1992, 31, 5975–5983. [Google Scholar] [CrossRef]
- Takahara, H. Visibility of speckle patterns: Effect of the optical guide length in coherent light. Appl. Opt. 1976, 15, 609–610. [Google Scholar] [CrossRef]
- Crosignani, B.; Daino, B.; Di Porto, P. Speckle-pattern visibility of light transmitted through a multimode optical fiber. J. Opt. Soc. Am. 1976, 66, 1312–1313. [Google Scholar] [CrossRef]
- Kingsley, S.; Davies, D. Multimode optical-fibre phase modulators and discriminators: I-theory. Electron. Lett. 1978, 14, 322–324. [Google Scholar] [CrossRef]
- Layton, M.R.; Bucaro, J.A. Optical fiber acoustic sensor utilizing mode-mode interference. Appl. Opt. 1979, 18, 666–670. [Google Scholar] [CrossRef]
- Bucaro, J.A.; Dardy, H.D.; Carome, E.F. Optical fiber acoustic sensor. Appl. Opt. 1977, 16, 1761–1762. [Google Scholar] [CrossRef]
- Kotov, O.; Chapalo, I.; Medvedev, A. Mode-Mode Interference Sensor with Increasing Number of Modes along the Multimode Optical Fiber; SPIE Optical Engineering + Applications: San Diego, CA, USA, 2014; p. 92030B. [Google Scholar] [CrossRef]
- Chapalo, I.; Theodosiou, A.; Kalli, K.; Kotov, O. Multimode Fiber Interferometer Based on Graded-Index Polymer CYTOP Fiber. J. Light. Technol. 2020, 38, 1439–1445. [Google Scholar] [CrossRef]
- Kotov, O.I.; Kosareva, L.I.; Liokumovich, L.B.; Markov, S.I.; Medvedev, A.V.; Nikolaev, V.M. Multichannel signal detection in a multimode optical-fiber interferometer: Ways to reduce the effect of amplitude fading. Tech. Phys. Lett. 2000, 26, 844–848. [Google Scholar] [CrossRef]
- Spillman, W.B.; Kline, B.R.; Maurice, L.B.; Fuhr, P.L. Statistical-mode sensor for fiber optic vibration sensing uses. Appl. Opt. 1989, 28, 3166–3176. [Google Scholar] [CrossRef]
- Petrov, A.; Bisyarin, M.; Kotov, O.I. Broadband intermodal fiber interferometer for sensor application: Fundamentals and simulator. Appl. Opt. 2022, 61, 6544–6552. [Google Scholar] [CrossRef]
- Petrov, A.V.; E Chapalo, I.; I Kotov, O. Theoretical analysis of averaging methods for intermodal fiber interferometer. J. Phys. Conf. Ser. 2019, 1326, 012023. [Google Scholar] [CrossRef]
- Petrov, A.; Chapalo, I.; Kotov, O. Intermodal Fiber Interferometer with Scanning Laser and Correlation Signal Processing: An Experimental Study; Springer: Cham, Switzerland, 2021; pp. 307–316. [Google Scholar]
- Mehta, A.; Mohammed, W.; Johnson, E.G. Multimode interference-based fiber-optic displacement sensor. IEEE Photonics Technol. Lett. 2003, 15, 1129–1131. [Google Scholar] [CrossRef]
- Wu, Q.; Qu, Y.; Liu, J.; Yuan, J.; Wan, S.-P.; Wu, T.; He, X.-D.; Liub, B.; Liuc, D.; Ma, Y.; et al. Singlemode-Multimode-Singlemode Fiber Structures for Sensing Applications—A Review. IEEE Sens. J. 2021, 21, 12734–12751. [Google Scholar] [CrossRef]
- Wang, K.; Dong, X.; Kohler, M.H.; Kienle, P.; Bian, Q.; Jakobi, M.; Koch, A.W. Advances in Optical Fiber Sensors Based on Multimode Interference (MMI): A Review. IEEE Sens. J. 2021, 21, 132–142. [Google Scholar] [CrossRef]
- Wang, K.; Mizuno, Y.; Dong, X.; Kurz, W.; Koehler, M.; Kienle, P.; Lee, H.; Jakobi, M.; Koch, A.W. Multimode optical fiber sensors: From conventional to machine learning-assisted. Meas. Sci. Technol. 2024, 35, 022002. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, H.; Wang, X.; Farrell, G.; Brambilla, G. A Review of Multimode Interference in Tapered Optical Fibers and Related Applications. Sensors 2018, 18, 858. [Google Scholar] [CrossRef] [PubMed]
- Guzmán-Sepúlveda, J.R.; Guzmán-Cabrera, R.; Castillo-Guzmán, A.A. Optical Sensing Using Fiber-Optic Multimode Interference Devices: A Review of Nonconventional Sensing Schemes. Sensors 2021, 21, 1862. [Google Scholar] [CrossRef] [PubMed]
- Frazão, O.; Silva, S.O.; Viegas, J.; Ferreira, L.A.; Araújo, F.M.; Santos, J.L. Optical fiber refractometry based on multimode interference. Appl. Opt. 2011, 50, E184–E188. [Google Scholar] [CrossRef]
- Wang, P.; Brambilla, G.; Ding, M.; Semenova, Y.; Wu, Q.; Farrell, G. Investigation of single-mode–multimode–single-mode and single-mode–tapered-multimode–single-mode fiber structures and their application for refractive index sensing. J. Opt. Soc. Am. B 2011, 28, 1180–1186. [Google Scholar] [CrossRef]
- Kumar, A.; Varshney, R.K.; Antony, C.S.; Sharma, P. Transmission characteristics of SMS fiber optic sensor structures. Opt. Commun. 2003, 219, 215–219. [Google Scholar] [CrossRef]
- Donlagic, D.; Culshaw, B. Microbend sensor structure for use in distributed and quasi-distributed sensor systems based on selective launching and filtering of the modes in graded index multimode fiber. J. Light. Technol. 1999, 17, 1856–1868. [Google Scholar] [CrossRef]
- Gowar, J. Optical Communication Systems; Prentice/Hall International: London, UK, 1984. [Google Scholar]
- Gloge, D. Weakly Guiding Fibers. Appl. Opt. 1971, 10, 2252–2258. [Google Scholar] [CrossRef]
- Kotov, O.I.; Bisyarin, M.A.; Chapalo, I.E.; Petrov, A.V. Simulation of a multimode fiber interferometer using averaged characteristics approach. J. Opt. Soc. Am. B 2018, 35, 1990–1999. [Google Scholar] [CrossRef]
- Hallam, A. Mode Control in Multimode Optical Fiber and Its Applications; Aston University: Birmingham, UK, 2007. [Google Scholar]
- Chapalo, I.; Petrov, A.; Bozhko, D.; Bisyarin, M.A.; Kotov, O.I. Averaging Methods for a Multimode Fiber Interferometer: Experimental and Interpretation. J. Light. Technol. 2020, 38, 5809–5816. [Google Scholar] [CrossRef]
- Cabral, T.D.; Fujiwara, E.; Warren-Smith, S.C.; Ebendorff-Heidepriem, H.; Cordeiro, C.M.B. Multimode exposed core fiber specklegram sensor. Opt. Lett. 2020, 45, 3212–3215. [Google Scholar] [CrossRef]
- Taylor, H. Bending effects in optical fibers. J. Light. Technol. 1984, 2, 617–628. [Google Scholar] [CrossRef]
- Kosareva, L.I.; Kotov, O.I.; Liokumovich, L.B.; Markov, S.I.; Medvedev, A.V.; Nikolaev, V.M. Two mechanisms of phase modulation in multimode fiber-optic interferometers. Tech. Phys. Lett. 2000, 26, 70–74. [Google Scholar] [CrossRef]
- Kotov, O.I.; Liokumovich, G.B.; Markov, S.I. Registration of Influence on Optical Fiber by Mode-Mode Interference; Lasers for Measurements and Information Transfer: St. Petersburg, Russia, 2004; pp. 91–102. [Google Scholar]
- Berdagué, S.; Facq, P. Mode division multiplexing in optical fibers. Appl. Opt. 1982, 21, 1950–1955. [Google Scholar] [CrossRef] [PubMed]
- Chapalo, I.; Petrov, A.; Bozhko, D.; Bisyarin, M.; Kotov, O. Methods of signal averaging for a multimode fiber interferometer: An experimental study. In Optical Sensors 2019; SPIE Optics + Optoelectronics: Prague, Czech Republic, 2019; p. 110282Q. [Google Scholar] [CrossRef]
- Marcuse, D. Light Transmission Optics; Van Nostrand Reinhold Company: New York, NY, USA, 1982. [Google Scholar]
- Rawson, E.G.; Goodman, J.W.; Norton, R.E. Frequency dependence of modal noise in multimode optical fibers. J. Opt. Soc. Am. 1980, 70, 968–976. [Google Scholar] [CrossRef]
- Kotov, O.I.; Chapalo, I.E.; Petrov, A.V. Signals of an intermodal fiber interferometer induced by laser frequency modulation. Tech. Phys. Lett. 2016, 42, 11–14. [Google Scholar] [CrossRef]
- Kotov, O.; Chapalo, I. Signal-to-Noise Ratio for Mode-Mode Fiber Interferometer; SPIE Optical Metrology: Munich, Germany, 2017; p. 1032945. [Google Scholar] [CrossRef]
- Petrov, A.; Chapalo, I.E.; Bisyarin, M.; Kotov, O.I. Intermodal fiber interferometer with frequency scanning laser for sensor application. Appl. Opt. 2020, 59, 10422–10431. [Google Scholar] [CrossRef] [PubMed]
- Redding, B.; Popoff, S.M.; Cao, H. All-fiber spectrometer based on speckle pattern reconstruction. Opt. Express 2013, 21, 6584–6600. [Google Scholar] [CrossRef] [PubMed]
- Lomer, M.; Rodriguez-Cobo, L.; Revilla, P.; Herrero, G.; Madruga, F.; Lopez-Higuera, J.M. Speckle POF Sensor for Detecting Vital Signs of Patients. In Proceedings of the OFS2014 23rd International Conference on Optical Fiber Sensors, Santander, Spain, 2–6 June 2014; p. 91572I. [Google Scholar] [CrossRef]
- Rodríguez-Cuevas, A.; Peña, E.R.; Rodríguez-Cobo, L.; Lomer, M.; López-Higuera, J.M. Low-cost fiber specklegram sensor for noncontact continuous patient monitoring. J. Biomed. Opt. 2017, 22, 037001. [Google Scholar] [CrossRef] [PubMed]
- Dhall, A.; Chhabra, J.; Aulakh, N. Intrusion detection system based on speckle pattern analysis. Exp. Tech. 2005, 29, 25–31. [Google Scholar] [CrossRef]
- Kotov, O.I.; Kosareva, L.I.; Liokumovich, L.B.; Markov, S.I.; Medvedev, A.V.; Nikolaev, V.M. Multichannel signal detection in a multimode optical-fiber interferometer: Reducing the effect of spurious signals. Tech. Phys. Lett. 2000, 26, 991–995. [Google Scholar] [CrossRef]
- Szustakowski, M.; Ciurapiński, W.; Życzkowski, M.; Wróbel, J.; Dulski, R.; Markowskia, P. Security–orientated Plastic Optical Fiber sensor in Modalmetric Configuration. Procedia Eng. 2012, 47, 916–923. [Google Scholar] [CrossRef]
- Rodriguez-Cobo, L.; Lomer, M.; Lopez-Higuera, J.-M. Fiber Specklegram-Multiplexed Sensor. J. Light. Technol. 2015, 33, 2591–2597. [Google Scholar] [CrossRef]
- Pan, K.; Uang, C.-M.; Cheng, F.; Yu, F.T.S. Multimode fiber sensing by using mean-absolute speckle-intensity variation. Appl. Opt. 1994, 33, 2095–2098. [Google Scholar] [CrossRef] [PubMed]
- Lujo, I.; Klokoc, P.; Komljenovic, T.; Sipus, Z. Measuring structural vibrations with a multimode fiber optical sensor. In Proceedings of the 2007 19th International Conference on Applied Electromagnetics and Communications (ICECom), Dubrovnik, Croatia, 24–26 September 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Fujiwara, E.; Ri, Y.; Wu, Y.T.; Fujimoto, H.; Suzuki, C.K. Evaluation of image matching techniques for optical fiber specklegram sensor analysis. Appl. Opt. 2018, 57, 9845–9854. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.T.S.; Zhang, J.; Pan, K.; Zhao, D.; Ruffin, P.B. Fiber vibration sensor that uses the speckle contrast ratio. Opt. Eng. 1995, 34, 236–239. [Google Scholar] [CrossRef]
- Kulchin, Y.N.; Vitrik, O.B.; Lantsov, A.D. Correlation method for processing speckles of signals from single-fibre multimode interferometers by using charge-coupled devices. Quantum Electron. 2006, 36, 339–342. [Google Scholar] [CrossRef]
- Yu, F.T.S.; Wen, M.; Yin, S.; Uang, C.-M. Submicrometer displacement sensing using inner-product multimode fiber speckle fields. Appl. Opt. 1993, 32, 4685–4689. [Google Scholar] [CrossRef]
- Kulchin, Y.N.; Vitrik, O.B.; Lantsov, A.D. Correlation processing of signals of a single-fibre multimode interferometer upon excitation of few modes during measurements of deformation effects. Quantum Electron. 2008, 38, 56–58. [Google Scholar] [CrossRef]
- Fujiwara, E.; dos Santos, M.F.M.; Suzuki, C.K. Optical fiber specklegram sensor analysis by speckle pattern division. Appl. Opt. 2017, 56, 1585–1590. [Google Scholar] [CrossRef]
- Rodriguez-Cobo, L.; Lomer, M.; Cobo, A.; Lopez-Higuera, J.M. Optical fiber strain sensor with extended dynamic range based on specklegrams. Sens. Actuators A Phys. 2013, 203, 341–345. [Google Scholar] [CrossRef]
- Kulchin, Y.N.; Obukh, V.F. Spatial filtering of radiation from a multimode waveguide in determination of hydroacoustic pressures. Sov. J. Quantum Electron. 1986, 16, 424–426. [Google Scholar] [CrossRef]
- A Bykovskiĭ, Y.; Vitrik, O.B.; Kulchin, Y.N. Amplitude spatial filtering in the processing of signals from a single-fiber multimode interferometer. Sov. J. Quantum Electron. 1990, 20, 1288–1290. [Google Scholar] [CrossRef]
- Kamshilin, A.A.; Jaaskelainen, T.; Kulchin, Y.N. Adaptive correlation filter for stabilization of interference-fiber-optic sensors. Appl. Phys. Lett. 1998, 73, 705–707. [Google Scholar] [CrossRef]
- Potton, R.J. Adaptive spatial filtering using photochromic glass. Meas. Sci. Technol. 1999, 10, 1315–1318. [Google Scholar] [CrossRef]
- Newaz, A.; Faruque, O.; Al Mahmud, R.; Sagor, R.H.; Khan, M.Z.M. Machine-Learning-Enabled Multimode Fiber Specklegram Sensors: A Review. IEEE Sens. J. 2023, 23, 20937–20950. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.; Qin, Q.; Tan, Z.; Wang, M.; Yan, F. Bending recognition based on the analysis of fiber specklegrams using deep learning. Opt. Laser Technol. 2020, 131, 106424. [Google Scholar] [CrossRef]
- Li, G.; Liu, Y.; Qin, Q.; Zou, X.; Wang, M.; Ren, W. Feature Extraction Enabled Deep Learning From Specklegram for Optical Fiber Curvature Sensing. IEEE Sens. J. 2022, 22, 15974–15984. [Google Scholar] [CrossRef]
- Lu, S.; Tan, Z.; Li, G.; Jingya, Y. A Sensitized Plastic Fiber Sensor for Multi-Point Bending Measurement Based on Deep Learning. IEEE Photonics J. 2021, 13, 8600107. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, Z. 2D tactile sensor based on multimode interference and deep learning. Opt. Laser Technol. 2020, 136, 106760. [Google Scholar] [CrossRef]
- Pal, D.; Agadarov, S.; Beiderman, Y.; Beiderman, Y.; Kumar, A.; Zalevsky, Z. Non-invasive blood glucose sensing by machine learning of optic fiber-based speckle pattern variation. J. Biomed. Opt. 2022, 27, 097001. [Google Scholar] [CrossRef]
- Chen, P.; You, C.; Ding, P. Event classification using improved salp swarm algorithm based probabilistic neural network in fiber-optic perimeter intrusion detection system. Opt. Fiber Technol. 2020, 56, 102182. [Google Scholar] [CrossRef]
- Cuevas, A.R.; Fontana, M.; Rodriguez-Cobo, L.; Lomer, M.; Lopez-Higuera, J.M. Machine Learning for Turning Optical Fiber Specklegram Sensor into a Spatially-Resolved Sensing System. Proof of Concept. J. Light. Technol. 2018, 36, 3733–3738. [Google Scholar] [CrossRef]
- Gao, H.; Hu, H. Spatially-resolved bending recognition based on a learning-empowered fiber specklegram sensor. Opt. Express 2023, 31, 7671–7683. [Google Scholar] [CrossRef] [PubMed]
- Wei, M.; Tang, G.; Liu, J.; Zhu, L.; Liu, J.; Huang, C.; Zhang, J.; Shen, L.; Yu, S. Neural Network Based Perturbation-Location Fiber Specklegram Sensing System Towards Applications With Limited Number of Training Samples. J. Light. Technol. 2021, 39, 6315–6326. [Google Scholar] [CrossRef]
- Markvart, A.A.; Liokumovich, L.B.; Ushakov, N.A. Simultaneous measurement of strain and bend with a fiber optic SMS structure. In Proceedings of the Optical Fiber Sensors Conference 2020 Special Edition, Washington, DC, USA, 8–12 June 2020; p. W4.57. [Google Scholar] [CrossRef]
- Markvart, A.A.; Liokumovich, L.B.; Ushakov, N.A. Fiber Optic SMS Sensor for Simultaneous Measurement of Strain and Curvature. Tech. Phys. Lett. 2022, 48, 34. [Google Scholar] [CrossRef]
- Galarza, M.; Perez-Herrera, R.A.; Leandro, D.; Judez, A.; López-Amo, M. Spatial-frequency multiplexing of high-sensitivity liquid level sensors based on multimode interference micro-fibers. Sens. Actuators A Phys. 2020, 307, 111985. [Google Scholar] [CrossRef]
- Rota-Rodrigo, S.; Lopez-Aldaba, A.; Perez-Herrera, R.A.; Bautista, M.d.C.L.; Esteban, O.; Lopez-Amo, M. Simultaneous Measurement of Humidity and Vibration Based on a Microwire Sensor System Using Fast Fourier Transform Technique. J. Light. Technol. 2016, 34, 4525–4530. [Google Scholar] [CrossRef]
- Cardona-Maya, Y.; Del Villar, I.; Socorro, A.B.; Corres, J.M.; Matias, I.R.; Botero-Cadavid, J.F. Wavelength and Phase Detection Based SMS Fiber Sensors Optimized With Etching and Nanodeposition. J. Light. Technol. 2017, 35, 3743–3749. [Google Scholar] [CrossRef]
- Petrov, A.; Kotov, O.; Golovchenko, A. Measurement of External Impact by an Intermodal Fiber Interferometer with Spectral Interrogation and Fourier Transform of Output Signals. In Proceedings of the 2023 International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersbourg, Russia, 20–21 October 2023; pp. 406–409. [Google Scholar] [CrossRef]
- Theodosiou, A. Adaptive Refractive Index Measurements via Polymer Optical Fiber Speckle Pattern Analysis. IEEE Sens. J. 2024, 24, 287–291. [Google Scholar] [CrossRef]
- Leung, C.-Y.; Chang, I.-F.; Hsu, S. Fiberoptic Line-Sensing System for Perimeter Protection Against Intrusion. In Optical Fiber Sensors; Optica Publishing Group: Tokyo, Japan, 1986; p. 54. [Google Scholar] [CrossRef]
- Leng, J.; Asundi, A. NDE of smart structures using multimode fiber optic vibration sensor. NDT E Int. 2002, 35, 45–51. [Google Scholar] [CrossRef]
- Wang, J.-J.; Yan, S.-C.; Xu, F. Speckle-based fiber sensor for temperature measurement. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Wang, J.-J.; Yan, S.-C.; Ruan, Y.-P.; Xu, F.; Lu, Y.-Q. Fiber-Optic Point-Based Sensor Using Specklegram Measurement. Sensors 2017, 17, 2429. [Google Scholar] [CrossRef] [PubMed]
- Musin, F.; Mégret, P.; Wuilpart, M. Fiber-Optic Surface Temperature Sensor Based on Modal Interference. Sensors 2016, 16, 1189. [Google Scholar] [CrossRef] [PubMed]
- Regez, B.; Sayeh, M.; Mahajan, A.; Figueroa, F. A novel fiber optics based method to measure very low strains in large scale infrastructures. Measurement 2009, 42, 183–188. [Google Scholar] [CrossRef]
- Fujiwara, E.; da Silva, L.E.; Marques, T.H.R.; Cordeiro, C.M.B. Polymer optical fiber specklegram strain sensor with extended dynamic range. Opt. Eng. 2018, 57, 116107. [Google Scholar] [CrossRef]
- Fujiwara, E.; Wu, Y.T.; dos Santos, M.F.M.; Schenkel, E.A.; Suzuki, C.K. Development of a tactile sensor based on optical fiber specklegram analysis and sensor data fusion technique. Sens. Actuators A Phys. 2017, 263, 677–686. [Google Scholar] [CrossRef]
- Garcia-Valenzuela, A.; Tabib-Azar, M. Fiber-optic force and displacement sensor based on speckle detection with 0.1 nN and 0.1 Å resolution. Sens. Actuators A Phys. 1993, 36, 199–208. [Google Scholar] [CrossRef]
- Wang, X.; Song, L.; Wang, X.; Lu, S.; Li, J.; Zhang, P.; Fang, F. An Ultrasensitive Fiber-End Tactile Sensor With Large Sensing Angle Based on Specklegram Analysis. IEEE Sens. J. 2023, 23, 30394–30402. [Google Scholar] [CrossRef]
- Kinet, D.; Wuilpart, M.; Reginster, M.; Caucheteur, C.; Musin, F. Cost-effective optical fiber gas leakage detector around buried pipelines. In Optical Sensing and Detection V; SPIE Photonics Europe: Strasbourg, France, 2018; p. 1068018. [Google Scholar] [CrossRef]
- Ramprasad, B.; Bai, T.R. Speckle-based fibre-optic current sensor. Opt. Laser Technol. 1984, 16, 156–159. [Google Scholar] [CrossRef]
- Wang, B.; Fu, J.Y.; Liu, Y.; Guo, R.; Yu, F.T.S. Displacement Sensing with Hetero-Core Fiber Specklegram. In Proceedings of the Optical Science and Technology, the SPIE 49th Annual Meeting, Denver, CO, USA, 2–6 August 2004; p. 164. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Q.; Liu, H.-H.; Tan, Z.-W.; Wang, M.-G. Investigation of an image processing method of step-index multimode fiber specklegram and its application on lateral displacement sensing. Opt. Fiber Technol. 2018, 46, 48–53. [Google Scholar] [CrossRef]
- Chen, W.; Feng, F.; Chen, D.; Lin, W.; Chen, S.-C. Precision non-contact displacement sensor based on the near-field characteristics of fiber specklegrams. Sens. Actuators A Phys. 2019, 296, 1–6. [Google Scholar] [CrossRef]
- Osório, J.H.; Cabral, T.D.; Fujiwara, E.; Franco, M.A.; Amrani, F.; Delahaye, F.; Gérôme, F.; Benabid, F.; Cordeiro, C.M. Displacement sensor based on a large-core hollow fiber and specklegram analysis. Opt. Fiber Technol. 2023, 78, 103335. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Li, S.; Wang, X.; Zhang, P.; Lu, S.; Yu, D.; Zheng, Y.; Song, L.; Fang, F. A reflective multimode fiber vector bending sensor based on specklegram. Opt. Laser Technol. 2024, 170, 110235. [Google Scholar] [CrossRef]
- Warren-Smith, S.C.; Kilpatrick, A.D.; Wisal, K.; Nguyen, L.V. Multimode optical fiber specklegram smart bed sensor array. J. Biomed. Opt. 2022, 27, 067002. [Google Scholar] [CrossRef] [PubMed]
- Bennett, A.; Beiderman, Y.; Agdarov, S.; Beiderman, Y.; Hendel, R.; Straussman, B.; Zalevsky, Z. Monitoring of vital bio-signs by analysis of speckle patterns in a fabric-integrated multimode optical fiber sensor. Opt. Express 2020, 28, 20830–20844. [Google Scholar] [CrossRef] [PubMed]
- Markvart, A.; Kulik, D.; Petrov, A.; Liokumovich, L.; Ushakov, N. Pulse Wave Measurement Using Fiber-Optic Intermodal Interferometric Sensor. In International Youth Conference on Electronics, Telecommunications and Information Technologies: Proceedings of the YETI 2021, St. Petersburg, Russia; Springer: Berlin/Heidelberg, Germany, 2022; pp. 429–436. [Google Scholar]
- Pang, Y.-N.; Liu, B.; Liu, J.; Wan, S.-P.; Wu, T.; Yuan, J.; Xin, X.; He, X.-D.; Wu, Q. Singlemode-Multimode-Singlemode Optical Fiber Sensor for Accurate Blood Pressure Monitoring. J. Light. Technol. 2022, 40, 4443–4450. [Google Scholar] [CrossRef]
- Zhao, F.; Lin, W.; Guo, P.; Hu, J.; Liu, S.; Yu, F.; Zuo, G.; Wang, G.; Liu, H.; Chen, J.; et al. Demodulation of DBR Fiber Laser Sensors With Speckle Patterns. IEEE Sens. J. 2023, 23, 26022–26030. [Google Scholar] [CrossRef]
- Lin, W.; Liu, B.; Liu, H.; Yang, C.; Zhang, H. Fibre-optic salinity sensor based on multimode fibre specklegram analysis. Meas. Sci. Technol. 2021, 32, 115110. [Google Scholar] [CrossRef]
- Fujiwara, E.; da Silva, L.E.; Cabral, T.D.; de Freitas, H.E.; Wu, Y.T.; Cordeiro, C.M.d.B. Optical Fiber Specklegram Chemical Sensor Based on a Concatenated Multimode Fiber Structure. J. Light. Technol. 2019, 37, 5041–5047. [Google Scholar] [CrossRef]
- Mu, G.; Liu, Y.; Qin, Q.; Tan, Z.; Li, G.; Wang, M.; Yan, F. Refractive Index Sensing Based on the Analysis of D-Shaped Multimode Fiber Specklegrams. IEEE Photonics Technol. Lett. 2020, 32, 485–488. [Google Scholar] [CrossRef]
- Arı, F.; Şerbetçi, H.; Navruz, I. Tapered fiber optic refractive index sensor using speckle pattern imaging. Opt. Fiber Technol. 2023, 79, 103366. [Google Scholar] [CrossRef]
- Al Zain, M.; Karimi-Alavijeh, H.; Moallem, P.; Khorsandi, A.; Ahmadi, K. A High-Sensitive Fiber Specklegram Refractive Index Sensor With Microfiber Adjustable Sensing Area. IEEE Sens. J. 2023, 23, 15570–15577. [Google Scholar] [CrossRef]
- Cai, L.; Wang, M.; Zhao, Y. Investigation on refractive index sensing characteristics based on multimode fiber specklegram. Meas. Sci. Technol. 2023, 34, 015125. [Google Scholar] [CrossRef]
- Guo, P.; Peng, X.; Li, J.; Zhou, Z.; Hu, J.; Xue, C.; Hu, J.; Li, J.; Dang, H.; Chen, J.; et al. Refractive Index Detection of Liquid Analyte in Broad Range Using Multimode Fiber Speckle Sensor. In Proceedings of the 2022 Asia Communications and Photonics Conference (ACP), Shenzhen, China, 5–8 November 2022; pp. 1981–1983. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, W.; Zhao, F.; Liu, Y.; Sun, J.; Hu, J.; Li, J.; Chen, J.; Zhang, X.; Vai, M.I.; et al. A Multimode Microfiber Specklegram Biosensor for Measurement of CEACAM5 through AI Diagnosis. Biosensors 2024, 14, 57. [Google Scholar] [CrossRef] [PubMed]
- Feng, F.; Chen, W.; Chen, D.; Lin, W.; Chen, S.-C. In-situ ultrasensitive label-free DNA hybridization detection using optical fiber specklegram. Sens. Actuators B Chem. 2018, 272, 160–165. [Google Scholar] [CrossRef]
- Inalegwu, O.C.; Ii, R.E.G.; Huang, J. A Machine Learning Specklegram Wavemeter (MaSWave) Based on a Short Section of Multimode Fiber as the Dispersive Element. Sensors 2023, 23, 4574. [Google Scholar] [CrossRef]
- Tan, H.; Li, B.; Crozier, K.B. Optical fiber speckle spectrometer based on reversed-lens smartphone microscope. Sci. Rep. 2023, 13, 12958. [Google Scholar] [CrossRef] [PubMed]
- Redding, B.; Alam, M.; Seifert, M.; Cao, H. High-resolution and broadband all-fiber spectrometers. Optica 2014, 1, 175. [Google Scholar] [CrossRef]
- Jamali, R.; Nazari, F.; Ghaffari, A.; Velu, S.K.P.; Moradi, A.-R. Speckle tweezers for manipulation of high and low refractive index micro-particles and nano-particle loaded vesicles. Nanophotonics 2021, 10, 2915–2928. [Google Scholar] [CrossRef]
- Volpe, G.; Kurz, L.; Callegari, A.; Volpe, G.; Gigan, S. Speckle optical tweezers: Micromanipulation with random light fields. Opt. Express 2014, 22, 18159–18167. [Google Scholar] [CrossRef]
- Moslehi, B.; Goodman, J.W.; Rawson, E.G. Bandwidth estimation for multimode optical fibers using the frequency correlation function of speckle patterns. Appl. Opt. 1983, 22, 995–999. [Google Scholar] [CrossRef]
- Ahn, T.-J.; Moon, S.; Kim, S.; Oh, K.; Kim, D.Y.; Kobelke, J.; Schuster, K.; Kirchhof, J. Frequency-domain intermodal interferometer for the bandwidth measurement of a multimode fiber. Appl. Opt. 2006, 45, 8238–8243. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Sakr, H.; Hayes, J.R.; Fokoua, E.R.N.; Ding, M.; Poletti, F.; Richardson, D.J.; Slavík, R. Hollow-core fiber with stable propagation delay between −150 °C and +60 °C. Opt. Lett. 2023, 48, 763–766. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.H.; Kumar, C.J.; Somnath, B.; Kumar, G.P. Multi-Fiber Optic 2d-Array Device for Sensing and Localizing Environment Perturbation Using Speckle Image Processing. US6590194B2, 27 March 2001. [Google Scholar]
- Thompson, D.; Joshua, G.; Keenan, R. Fiber-Optic Mat Sensor. US7532781B2, 19/772007, 12 May 2009. [Google Scholar]
- Kotov, O.I.; Chapalo, I.E.; Medvedev, A.V. Dependence of the signal of a multimode fiber-optic interferometer on the mode power distribution. Tech. Phys. Lett. 2014, 40, 509–512. [Google Scholar] [CrossRef]
- Kotov, O.I.; Chapalo, I.E. External impact localization in a distributed intermodal fiber interferometer. Tech. Phys. Lett. 2015, 41, 1139–1142. [Google Scholar] [CrossRef]
- Kotov, O.; Chapalo, I. Mode-Mode Fiber Interferometer with Impact Localization Ability; SPIE Photonics Europe: Brussels, Belgium, 2016; p. 98992J. [Google Scholar] [CrossRef]
- Chapalo, I.; Kotov, O.; Petrov, A. Dual-wavelength one-directional multimode fiber interferometer with impact localization ability. In Optical Sensing and Detection V; SPIE Photonics Europe: Strassburg, France, 2018; p. 106801V. [Google Scholar] [CrossRef]
- Chapalo, I.; Theodosiou, A.; Kalli, K.; Kotov, O. Multimode fiber interferometer with embedded long period grating. In Seventh European Workshop on Optical Fibre Sensors; In Proceedings of the Seventh European Workshop on Optical Fibre Sensors; Limassol, Cyprus, 1–4 October 2019, p. 111990Q. [CrossRef]
- Chapalo, I.; Chah, K.; Gusarov, A.; Ioannou, A.; Pospori, A.; Nan, Y.-G.; Kalli, K.; Mégret, P. Gamma-radiation enhancement of sensing properties of FBGs in a few-mode polymer CYTOP fiber. Opt. Lett. 2023, 48, 1248–1251. [Google Scholar] [CrossRef]
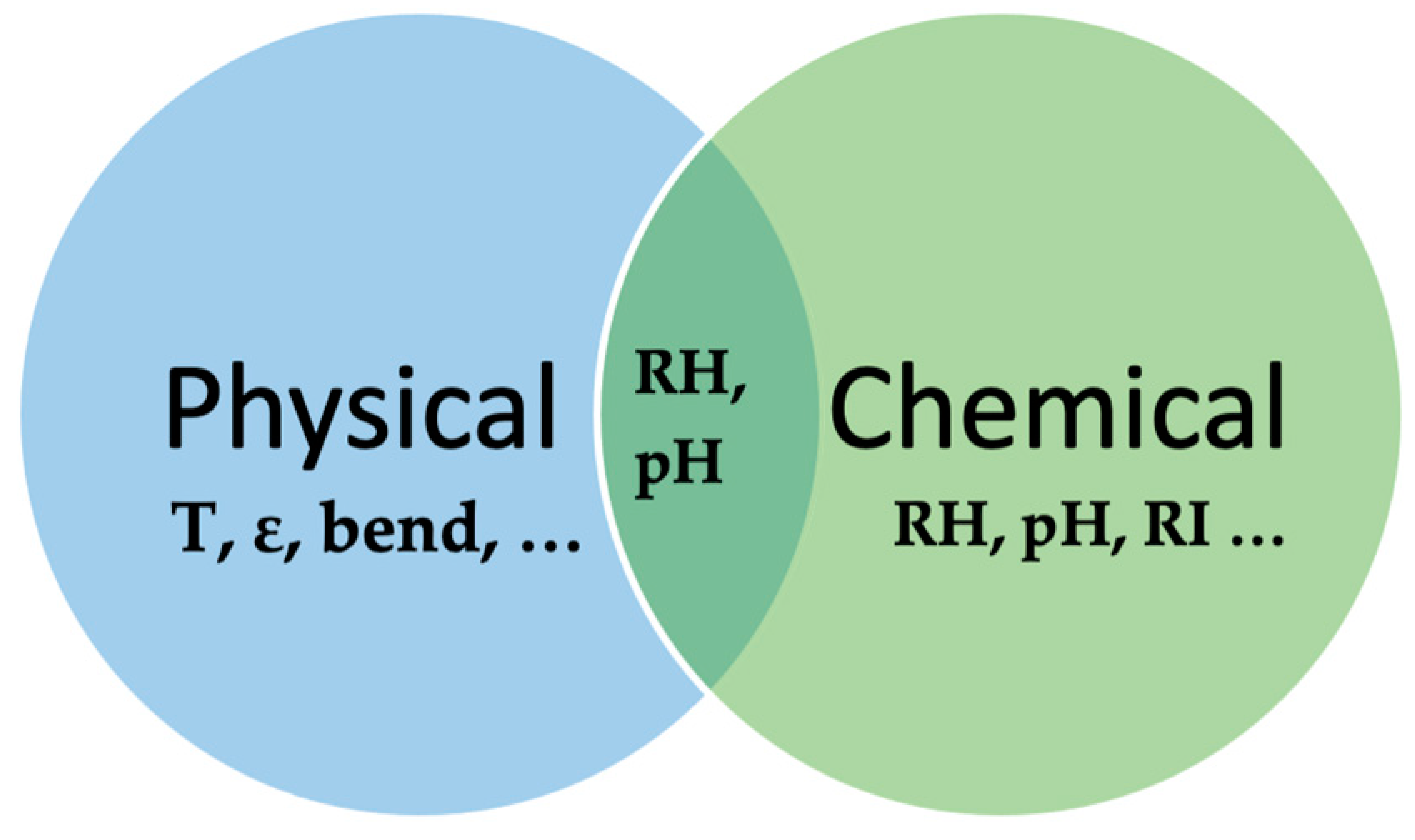
| Group A—Physical | Group B—Chemical |
|---|---|
| Strain | Refractive index |
| Temperature | Relative Humidity |
| Pressure | Gas sensing |
| Curvature | pH |
| Vibrations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chapalo, I.; Stylianou, A.; Mégret, P.; Theodosiou, A. Advances in Optical Fiber Speckle Sensing: A Comprehensive Review. Photonics 2024, 11, 299. https://doi.org/10.3390/photonics11040299
Chapalo I, Stylianou A, Mégret P, Theodosiou A. Advances in Optical Fiber Speckle Sensing: A Comprehensive Review. Photonics. 2024; 11(4):299. https://doi.org/10.3390/photonics11040299
Chicago/Turabian StyleChapalo, Ivan, Andreas Stylianou, Patrice Mégret, and Antreas Theodosiou. 2024. "Advances in Optical Fiber Speckle Sensing: A Comprehensive Review" Photonics 11, no. 4: 299. https://doi.org/10.3390/photonics11040299
APA StyleChapalo, I., Stylianou, A., Mégret, P., & Theodosiou, A. (2024). Advances in Optical Fiber Speckle Sensing: A Comprehensive Review. Photonics, 11(4), 299. https://doi.org/10.3390/photonics11040299







