Abstract
To overcome the limitation of dynamic reciprocity, a new method for designing broadband on-chip optical isolators is proposed and demonstrated based on saturated gain, which is able to support simplex and duplex operation modes. By connecting a saturated gain waveguide to an appropriate linear loss waveguide, broadband isolation is predicted and proved theoretically through saturated gain-induced non-reciprocal transmission. The proposed isolator is numerically demonstrated with an operating band of 59 nm and an isolation ratio of −20 dB at the central wavelength of 1550 nm. It is noteworthy that when the current pump changes, the isolator still works well and keeps the high isolation ratio at a different input power. The footprint of the whole device is 465 μm × 0.35 μm which satisfies the requirement of photonic integrated circuits. The proposed isolator, with the combined advantages of compact footprint, broadband, duplex operation and high isolation, can enable on-chip unidirectional transmission and complex topological routing designation.
1. Introduction
Non-reciprocity is a remarkable physical phenomenon, which provides abundant applications in the photonics industry [1,2,3,4,5,6,7,8], especially on-chip photonics. The photonic isolator is one of the biggest concerns in non-reciprocal on-chip photonic devices due to wide applications of integrated backscatter eliminating and complex communication topology construction in photonics. To implement on-chip isolation, three well-known non-reciprocal phenomena have been investigated extensively as solutions, including nonlinear optical (NLO) effects [9,10,11,12,13], magneto-optical (MO) effects [14,15,16,17,18,19,20,21,22] and the time-dependent optical (TDO) system [23,24,25]. The NLO effects usually provide two schemes, which are optically induced transparency [8] and optical bistability [9,10]. The former exploits four-wave mixing in micro-ring which leads to the narrow operation band. The latter is seriously limited by dynamic reciprocity [26], and hence, the isolator function cannot be constructed when a forward signal transmits through the system, which means the duplex operation modes cannot be supported. The MO effects are also actualized by two schemes. One is an MO micro-ring [12], which is not only a narrow operation band device but also requires complex manufactured technology. The other is the MO-induced reciprocal loss waveguide [14,18], which is limited by its large size for on-chip photonics. The TDO system demands a very high modulation frequency. Therefore, although numerous pieces of research focus on optical isolators, there is still a lack of a small-sized scheme holding not only a wide operating band but also supporting duplex workings and keeping a high isolation rate.
In this paper, we propose and demonstrate that saturated gain can be a new solution to implement non-reciprocal transmission, which is a fabrication-friendly, duplex work supporting, wide operating band and relatively small-sized scheme. Table 1 shows the comparison between current schemes and the saturated gain-induced non-reciprocal transmission proposed in this paper.

Table 1.
Characteristics of the current schemes and proposed scheme.
In this work, we utilize the broadband saturated gain of a semiconductor optical amplifier (SOA) waveguide to construct a non-reciprocal propagation area, and then compensate the power change with an appropriate linear loss waveguide which is designed as a hybrid surface plasmon polariton (SPP) waveguide [27]. The designed isolator supports duplex operation mode in a 59 nm operating band, and the isolation rate is as high as −20 dB, while the whole size of the device is as small as 465 μm × 0.35 μm.
2. Non-Reciprocal Transmission in Saturated Gain Waveguide
There is an important property of non-reciprocal transmission in a saturated gain waveguide. When light only inputs to one port of the waveguide with different powers (simplex operation mode), the output powers are identical after propagating over a long enough distance. The model of saturated gain is described in [28,29,30,31] as
where P is the power of light propagating in the saturated gain waveguide, Ps is the saturated parameter, G0 is the gain coefficient for small signals, and α is the linear loss of the waveguide. Figure 1 shows the relationship between G and P. The zero point of the G–P curve is defined as cut-off power Pc, which can be expressed as
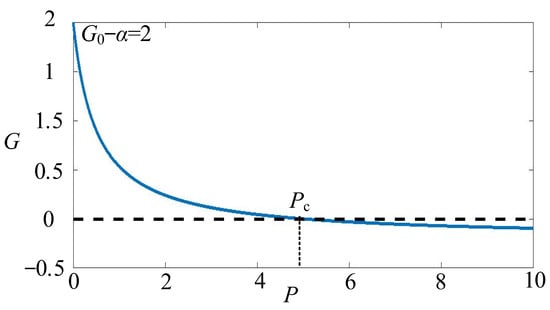
Figure 1.
Blue line: Relation between the gain coefficient G and light power P. Pc is the cut-off power. Parameters of this case. The result is simulated with G0 = 2.2, Ps = 0.5, and α = 0.2. Dotted: G = 0.
When the power of the input light P is higher (lower) than Pc, the gain coefficient G is smaller (greater) than zero, and then P is going to decrease (increase) to Pc. It can be found that the gain coefficient G convergences to zero as shown in Figure 2a,b after a long enough propagating distance, and the output power P convergences to Pc which corresponds to the zero-gain coefficient.
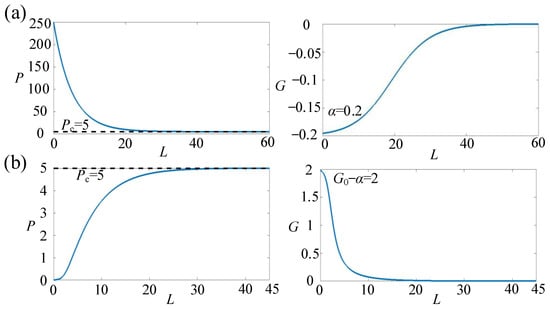
Figure 2.
Blue line: Theoretical curves of functions P(L) and G(L) when the input power is (a) lower and (b) higher than Pc. Dotted: Pc = 5.
When light signals are input into both of the two ports of a waveguide (duplex operation mode), Equation (1) is changed as
where P1 and P2 are the power of light signals input from the right and left ports, respectively. In addition, P1 and P2 satisfy the following relations and conditions:
Assuming that Lw is long enough to meet the boundary conditions, the solutions can be obtained by combining Equations (3)–(5) as
Evidently, the sum of the input power at the right port and the output power at the left port is equal to the sum of the output power at the right port and the input power at the left port, and the value is exactly equal to Pc.
3. Isolator Model
Using the saturated gain model, we propose a sketchy model, supporting both the simplex and duplex operation modes, and then investigate the relationship between device size and performance. Exploiting the preceding demonstrations of Equations (1)–(6), the property of a saturated gain waveguide can be summed up as the illustration in Figure 3a. Po1 is the output power of PH, and Po2 is the output power of PL, where PH >> PL, and Po1 ≈ Po2 ≈ PH ≈ Pc. Connecting a linear loss element to the saturated gain waveguide, the isolator model is obtained as shown in Figure 3b.
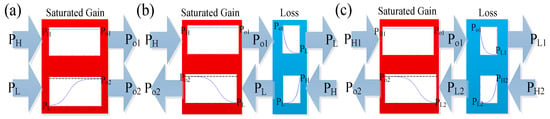
Figure 3.
(a) Saturated gain property, (b) schematic diagram of simplex operating mode and (c) duplex operating mode. PH >> PL, Po1 ≈ Po2 ≈ PH ≈ Pc.
In the simplex operating mode, only one of the two ports of the device allows for the input of light signals. As shown in Figure 3b, when the light transmits from the left side to the right side, and its power is as high as PH ≈ Pc, the power can only be gained a little and becomes Po1 because of the saturated gain property; then, it decays to PL << PH after transmitting through the additional loss element. By contrast, if light with power PH is input from the right side, its power will decay to PL first, and then grow to Po2 which is very close to PH.
In the duplex operating mode, both of the two ports are inputs as shown in Figure 3c, it can be understood that PH1 + Po2 = PL2 + Po1 = Pc in terms of Equation (6). If PH1 = Pc, it is clear that Po2 = Pc/2 >> PL1. The isolation for backward signals is kept when the forward signals are transmitted through it. It should be noted that the operating power of duplex mode is half that of simplex in the same device.
The above discussion is based on the theory demonstrated in Equations (4) and (5), a theory that demands enough waveguide length. Here, a more detailed analysis is given to demonstrate how long that required length is. The design isolation ratio of the isolator r is defined as
where TL is the transmission of input from the left and TR is the transmission of input from the right. Firstly, we discuss the simplex operation mode. The P–L curve of a saturated gain waveguide for small signal input is plotted in Figure 4a in accordance with the numerical solution of
and the “enough amount of length” of the saturated gain waveguide can be found in Figure 4a as Lt1, which considers the output power tolerance as t × Pc. Connecting a linear loss waveguide which decays the input power from Pc to rsPc (rs is the isolation ratio of simplex operation mode), the asymmetric transmission phenomenon can be observed in Figure 4b,c.
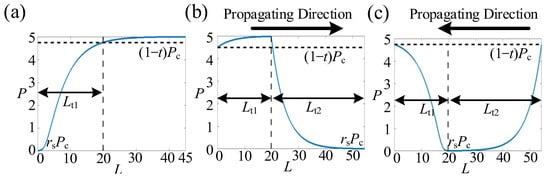
Figure 4.
Blue line: Simulated results of propagation properties of the saturated gain waveguide (a), the proposed isolator when signals transmit forward (b) and backward (c).
Next, we discuss the duplex operation mode. Similar to the simplex operation mode, the P–L curve of the saturated gain waveguide is also needed to find the “enough amount of length” Lt2 as shown in Figure 5a. Further, connecting a linear loss waveguide which decays the input power from Pc to rdPc/2 (rd is the isolation ratio of duplex), the P–L curve becomes Figure 5b for different propagating directions, and the asymmetric transmission can be observed. It should be noted that the main difference between simplex and duplex is the operation power. The operation power of duplex is half of that in simplex. Comparing simplex operation mode with duplex operation mode in the same system, it can be found that their operation powers are different. The operation power of duplex changed to Pc/2, which is half that of the simplex operation mode.
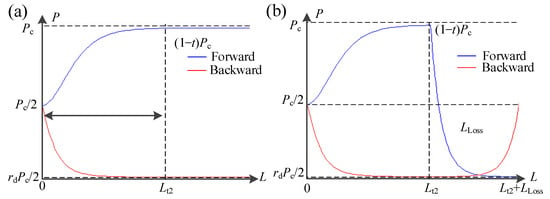
Figure 5.
Simulated results of propagation properties of (a) the saturated gain waveguide and (b) connecting a linear loss waveguide in the isolator working at duplex mode.
4. Device Designing
Then, we give a practical design of an on-chip optical isolator in accordance with the model described in Figure 3. The design is made up of an SOA waveguide covered by metal, which provides saturated gain with a linear loss α fitting the mathematical model in Equation (1). Figure 6a exhibits the schematic of our design. The isolator consists of two parts, the gain part and the loss part. The cross-sections of the two parts are the same, shown in Figure 6b, while the lengths and pump currents are different. For the gain part, the length is LSOA = 450 μm, and the pump current is 90 mA, corresponding to the parameters Ps = 3.41 mW and G0 = 0.3 μm−1 at 1.55 μm operation wavelength [19,20,21,22]. For the loss part, the length is only LD = 15 μm, and no pump is utilized in it. Figure 6b shows the layer structure of the cross-section of the proposed design. It can be seen that the SOA waveguide is an SPP waveguide consisting of a metal layer (exploited as an electrode), a p-type InP layer, an n-type InP layer and an InGaAsP quantum well layer [18]. It should be noted that the parameters Ps and G0 are of the material, not of the SPP mode employed as shown in Figure 6c. The effective index of the SPP mode is 3.03 + i0.0176, and the decayed coefficient α is 0.1426 μm−1 in terms of the imaginary effective index 0.0197. Meanwhile, the Ps and G0 become 3.5365 mW and 0.1687 μm−1, respectively, and the cut-off power Pc is 643 μW. Accordingly, it can be calculated using Equation (8) and the FDTD method or the Runge–Kutta method that 15 μm LD provides a bidirectional 20 dB decay to make the 643 μW input power decay to 6.43 μW; additionally, the 450 μm LSOA ensures the 6.43 μW low-power signal increases back to 643 μW, and the 643 μW signal maintains its power, which realizes non-reciprocal transmission.
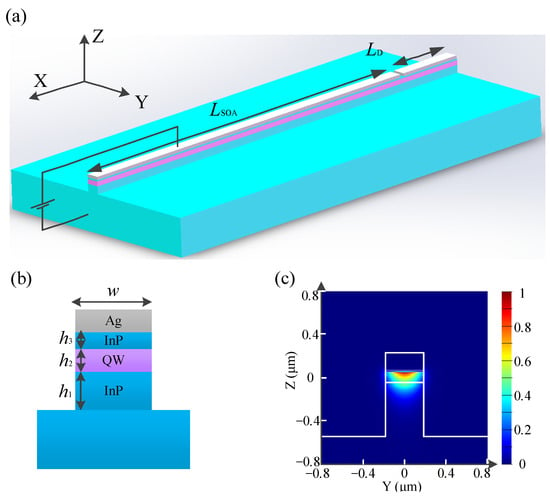
Figure 6.
(a) Schematic of the isolator, LSOA = 450 μm, LD = 15 μm. (b) Layer structure of SOA waveguide, h1 = 0.5 μm, h2 = 0.2 μm, h3 = 0.01 μm, w = 0.35 μm. (c) Normalized electrical field distribution of fundamental TM mode. The length of SOA LSOA and loss part LD are designed to support an on-chip optical isolator with a 643 μW input power and 20 dB isolation rate. LD = 15 μm provides a bidirectional 20 dB decay to make 643 μW input power decay to 6.43 μW. LSOA = 450 μm ensures the 6.43 μW low-power signal increases back to 643 μW, and the 643 μW signal maintains its power.
According to Equation (8) and the parameters (α, Ps and G0), the solid blue line in Figure 7a can be calculated numerically. It is clear that a 6.43 μW signal increases to 642.5 μW (99.92% of Pc) after propagating a 450 μm distance. The finite-difference time-domain (FDTD) [32,33] result (the red dashed line) also fits the analytical solution (calculated using Equations (4) and (5) with original code) as shown in Figure 7a. Meanwhile, if a signal with a power of 643 μW is input, the P–L curve changes to Figure 7b. Connecting a 15 μm loss waveguide with the SOA mentioned above, the function of an isolator can be realized; the P–L curves (signal inputs from the left and right), similar to Figure 4b,c, are given in Figure 8a,b, respectively.
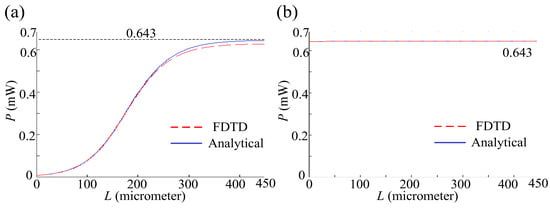
Figure 7.
FDTD-simulated and analytical results of relation between P and L when a signal with (a) 6.43 μW and (b) 643 μW inputs power. Black dotted lines: P = 0.643.
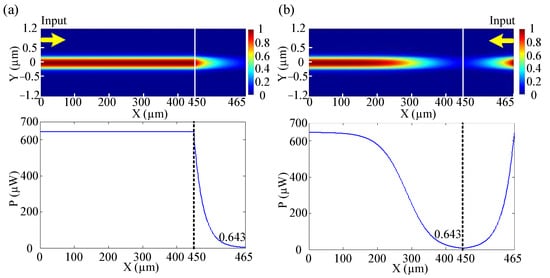
Figure 8.
Blue lines: Conditions when light is input (a) from right to left and (b) from left to right. Dotted lines: X = 450.
Our design also supports broadband operation. Exploiting the broadband gain spectrum of the SOA, we have calculated the broadband transmission characteristics of the SOA when the input power is 643 μW and 6.43 μW in Figure 9a. Combining with the transmission spectrum of the loss part, Figure 9 can be obtained to illustrate the output power spectrum of both directions of the isolator and the spectrum of the isolating factor, F, expressed by Pout/Pin. Further, considering F > 99 as a criterion, the bandwidth of the isolator is calculated to be as broad as 59 nm. All the results are simulated.
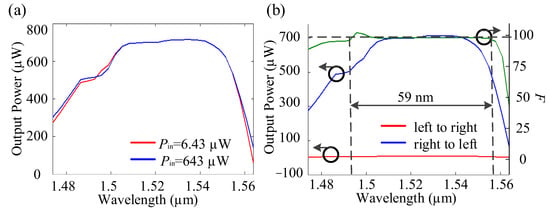
Figure 9.
(a) Simulated broadband transmission characteristic of the SOA. (b) Simulated broadband transmission and isolating factor of the whole device.
It has already been pointed out in Figure 5 that duplex operation mode exhibits lower operation power compared to simplex, so it is important to find an effective way to adjust operation power. The pump current is the key to controlling operation power. The operation power varies with the pump current of the gain part. Figure 10a gives the relation between P and L of the SOA with different pump currents at 1.55 μm, and the corresponding operation power can be calculated in Figure 10b. If we change the operation mode from simplex to duplex, and hope to maintain operation power, we can increase pump currents to fit it.
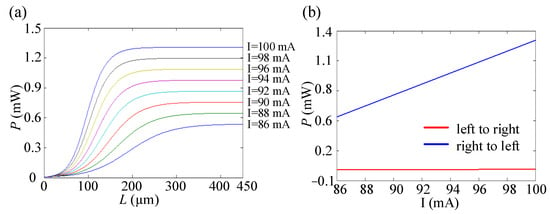
Figure 10.
(a) P–L curves of the SOA with different pump currents. (b) Operation power of the isolator with different pump currents. All the curves are simulated using FDTD.
5. Conclusions
In summary, we have proposed a novel method of designing the broadband optical isolator based on nonlinear gain, and the fundamental theory of the isolator is completely demonstrated. With the guidance of this theory, we have designed a broadband optical isolator working at a wide wavelength scope, from 1.500 μm to 1.559 μm. In addition, the isolator works at different powers with the same isolated factor, 100, when the current pump is changed. Moreover, the length of the whole device is only 465 μm, and the footprint area is as small as 465 μm × 0.35 μm. The size of the device satisfies the requirement of the application of photonic integrated circuits, and in particular, it can be applied to eliminate integrated backscatter, protect the source and construct complex communication topology in photonic integration.
Author Contributions
Conceptualization, M.X.; methodology, H.T.; software, H.D. and M.W.; validation, H.T. and H.D.; writing—original draft preparation, M.X.; writing—review and editing, M.X.; project administration, M.X.; funding acquisition, M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Basic Research Program of Shaanxi, grant number 2022JQ-634; the Scientific Research Plan of Shaanxi Education Department, grant number 22JK0301 and the Natural Science Basic Research Program of Shaanxi, grant number 2022JQ-175.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ma, H.; He, Z.; Hotate, K. Reduction of backscattering induced noise by carrier suppression in waveguide-type optical ring resonator. J. Light. Technol. 2011, 29, 85–90. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, L. Nonreciprocal thermal photonics for energy conversion and radiative heat transfer. Phys. Rev. Appl. 2022, 18, 027001. [Google Scholar] [CrossRef]
- Shui, T.; Yang, W.X.; Cheng, M.T.; Lee, R.K. Optical nonreciprocity and nonreciprocal photonic devices with directional four-wave mixing effect. Opt. Express 2022, 30, 6284–6299. [Google Scholar] [CrossRef] [PubMed]
- Ehlers, P.; Silander, I.; Wang, J.; Foltynowicz, A.; Axner, O. Fiber-laser-based noise-immune cavity-enhanced optical heterodyne molecular spectrometry incorporating an optical circulator. Opt. Lett. 2014, 39, 279–282. [Google Scholar] [CrossRef]
- Wang, X.; Hao, R.; Fan, P.; Hu, L.; Ye, B.; Zou, Y.; Jin, S. Effective enhancement of the non-Hermitian corner skin effect in reciprocal photonic crystals. Opt. Lett. 2024, 49, 554–557. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Zhang, S.; Qi, J.; Bo, F.; Li, H. Faraday rotation in nonreciprocal photonic time-crystals. Appl. Phys. Lett. 2023, 122, 051703. [Google Scholar] [CrossRef]
- Mimbs, J.W.; O’Donnell, M.; Miller, J.G.; Sobel, B.E. Detection of cardiomyopathic changes induced by doxorubicin based on quantitative analysis of ultrasonic backscatter. Am. J. Cardiol. 1981, 47, 1056–1060. [Google Scholar] [CrossRef]
- Dong, C.; Shen, Z.; Zou, C.; Zhang, Y.; Fu, W.; Guo, G. Non-reciprocal light storage in a silica microsphere. In Proceedings of the 2015 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2015; pp. 1–2. [Google Scholar]
- Zheng, Y.; Yang, J.; Shen, Z.; Cao, J.; Chen, X.; Liang, X.; Wan, W. Optically induced transparency in a micro-cavity. Light Sci. Appl. 2016, 5, e16072. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, X.; Hua, S.; Yang, C.; Wen, J.; Jiang, L.; Li, G.; Wang, G.; Xiao, M. Parity–time symmetry and variable optical isolation in active-passive-coupled microresonators. Nat. Photonics 2014, 8, 524–529. [Google Scholar] [CrossRef]
- Ahmed, W.; Farhat, M.; Staliunas, K.; Zhang, X.; Wu, Y. Machine learning for knowledge acquisition and accelerated inverse-design for non-Hermitian systems. Commun. Phys. 2023, 6, 2. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.; Fan, S.; Nori, F.; Bender, C.; Yang, L. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Shen, Z.; Dong, C.; Chen, Y.; Xiao, Y.; Sun, F.; Guo, G. Compensation of the Kerr effect for transient optomechanically induced transparency in a silica microsphere. Opt. Lett. 2016, 41, 1249–1252. [Google Scholar] [CrossRef] [PubMed]
- Bi, L.; Hu, J.; Jiang, P.; Kim, D.; Dionne, G.; Kimerling, L.; Ross, C. On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nat. Photonics 2011, 5, 758–762. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Siddharth, A.; Wang, R.; Blésin, T.; He, J.; Kippenberg, T.; Bhave, S. Magnetic-free silicon nitride integrated optical isolator. Nat. Photonics 2021, 15, 828–836. [Google Scholar] [CrossRef]
- Kittlaus, E.; Jones, W.; Rakich, P.; Otterstrom, N.; Muller, R.; Rais-Zadeh, M. Electrically driven acousto-optics and broadband non-reciprocity in silicon photonics. Nat. Photonics 2021, 15, 43–52. [Google Scholar] [CrossRef]
- Wang, C.; Fu, Z.; Mao, W.; Qie, J.; Stone, A.; Yang, L. Non-Hermitian optics and photonics: From classical to quantum. Adv. Opt. Photonics 2023, 15, 442–523. [Google Scholar] [CrossRef]
- Fujita, J.; Levy, M.; Osgood Jr, R.; Wilkens, L.; Dötsch, H. Waveguide optical isolator based on Mach–Zehnder interferometer. Appl. Phys. Lett. 2000, 76, 2158–2160. [Google Scholar] [CrossRef]
- Vanwolleghem, M.; Gogol, P.; Beauvillain, P.; Van Parys, W.; Baets, R. Design and optimization of a monolithically integratable InP-based optical waveguide isolator. JOSA B 2007, 24, 94–105. [Google Scholar] [CrossRef]
- Van Parys, W.; Moeyersoon, B.; Van Thourhout, D.; Baets, R.; Vanwolleghem, M.; Dagens, B.; Decobert, J.; Le Gouezigou, O.; Make, D.; Lagae, L. Transverse magnetic mode non reciprocal propagation in an amplifying AlGaInAs/InP optical waveguide isolator. Appl. Phys. Lett. 2006, 88, 071115. [Google Scholar] [CrossRef]
- Qin, J.; Deng, L.; Xie, J.; Tang, T.; Bi, L. Highly sensitive sensors based on magneto-optical surface plasmon resonance in Ag/CeYIG heterostructures. AIP Adv. 2015, 5, 017118. [Google Scholar] [CrossRef]
- Shui, K.; Nie, L.; Zhang, Y.; Peng, B.; Xie, J.; Deng, L.; Bi, L. Design of a compact waveguide optical isolator based on multimode interferometers using magneto-optical oxide thin films grown on silicon-on-insulator substrates. Opt. Express 2016, 24, 12856–12867. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photonics 2009, 3, 91–94. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, Y.; Chen, Y.; Zou, C.; Xiao, Y.; Zou, X.; Sun, F.; Guo, G.; Dong, C. Experimental realization of optomechanically induced non-reciprocity. Nat. Photonics 2016, 10, 657–661. [Google Scholar] [CrossRef]
- Galiffi, E.; Tirole, R.; Yin, S.; Li, H.; Vezzoli, S.; Huidobro, P.; Silveirinha, M.; Sapienza, R.; Alù, A.; Pendry, J. Photonics of time-varying media. Adv. Photonics 2022, 4, 014002. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, Z.; Fan, S. Limitations of nonlinear optical isolators due to dynamic reciprocity. Nat. Photonics 2015, 9, 388–392. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Dutta, N.K.; Wang, Q. Semiconductor Optical Amplifiers; World Scientific Press: Singapore, 2013. [Google Scholar]
- Sugawara, M.; Mukai, K.; Nakata, Y.; Ishikawa, H.; Sakamoto, A. Effect of homogeneous broadening of optical gain on lasing spectra in self-assembled InxGa1-xAs/GaAs quantum dot lasers. Phys. Rev. B 2000, 61, 7595. [Google Scholar] [CrossRef]
- Durhuus, T.; Mikkelsen, B.; Stubkjaer, K. Detailed Dynamic Model for Semiconductor Optical Amplifiers and Their Crosstalk and Intermodulation Distortion. J. Light. Technol. 1992, 10, 1056–1065. [Google Scholar] [CrossRef]
- Connelly, M.J. Semiconductor Optical Amplifiers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sullivan, D.M. Electromagnetic Simulation Using the FDTD Method; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Available online: www.photond.com (accessed on 1 October 2020).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).