The Spiral Spectrum of a Laguerre–Gaussian Beam Carrying the Cross-Phase Propagating in Weak-to-Strong Atmospheric Turbulence
Abstract
1. Introduction
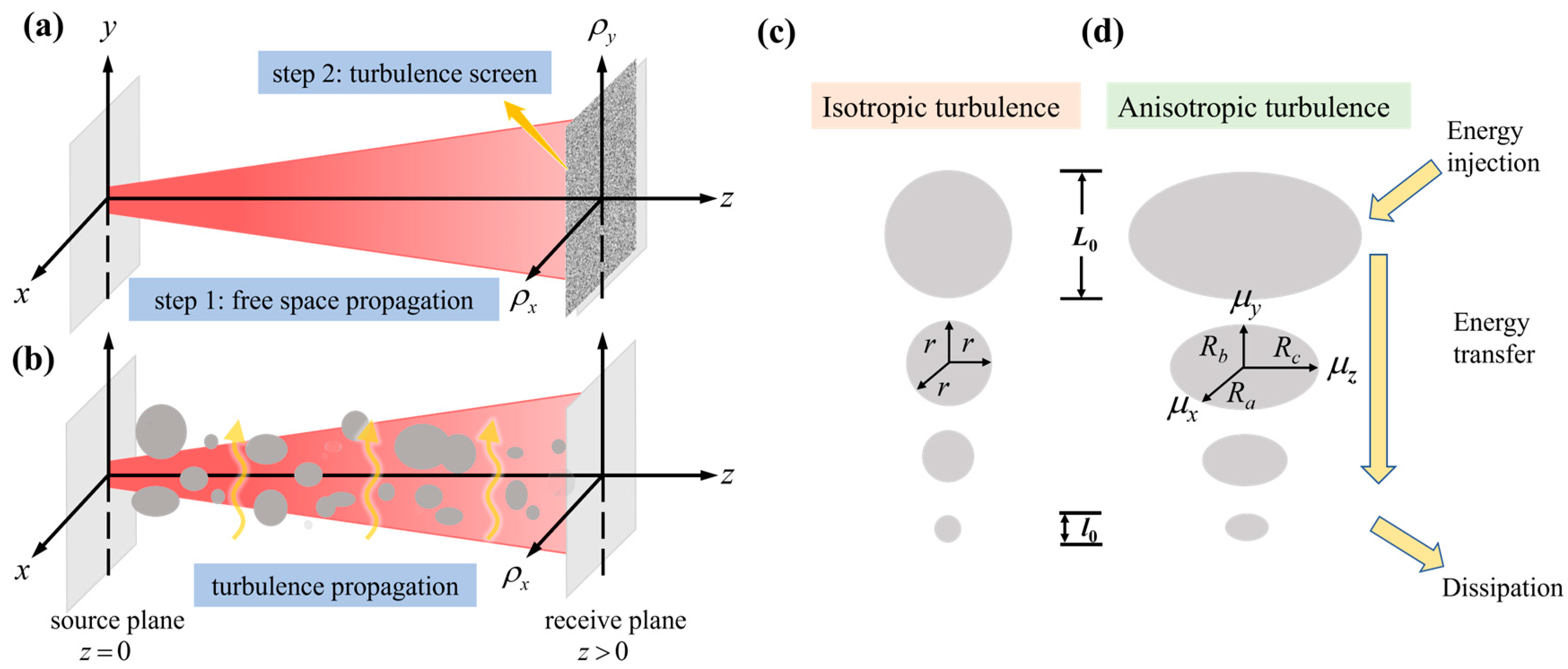
2. Propagation of a Laguerre–Gaussian Beam Carrying the Cross-Phase in Atmospheric Turbulence
3. Numerical Results
3.1. Spiral Spectrum of an LG Beam Carrying the Cross-Phase in the Source Plane
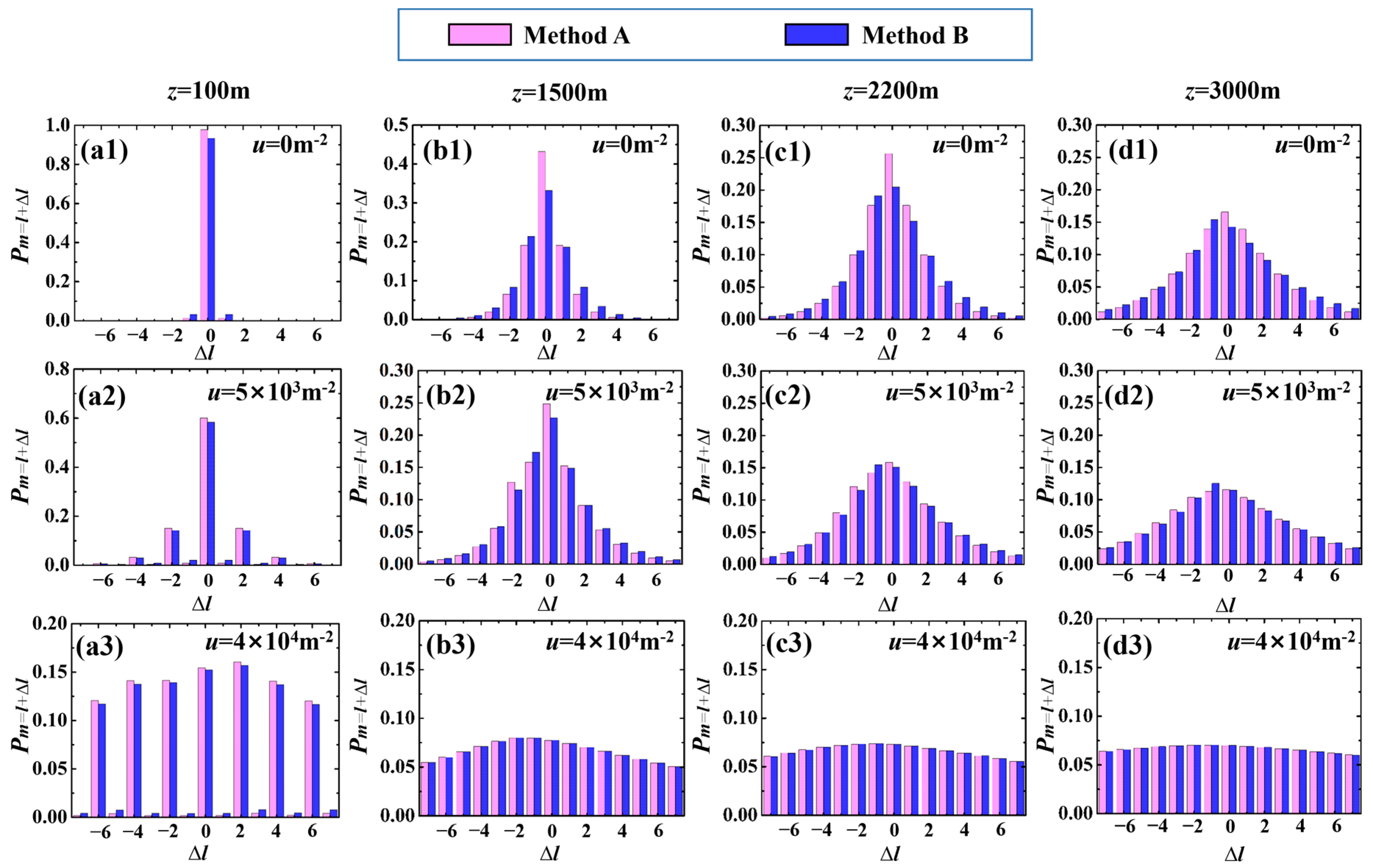
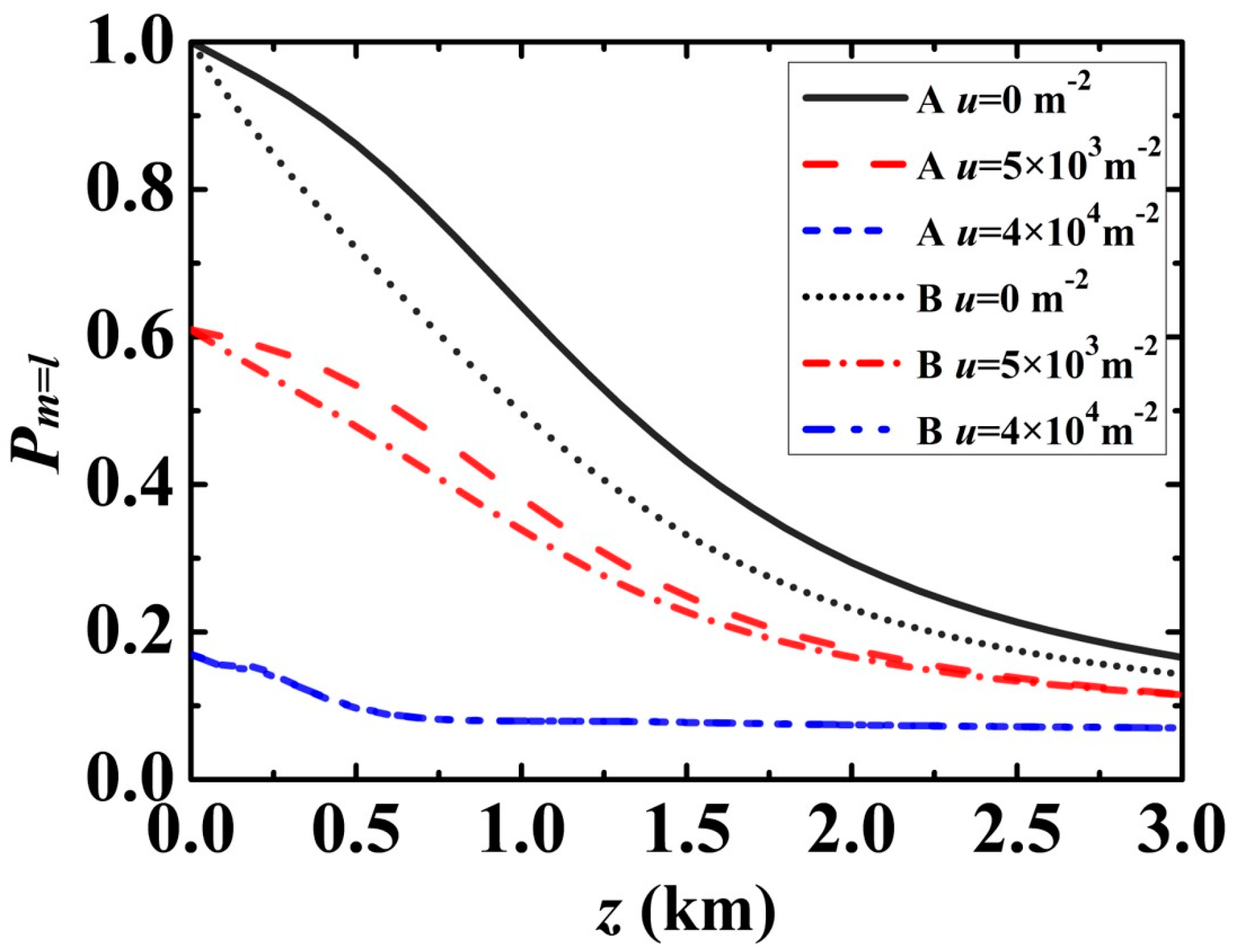
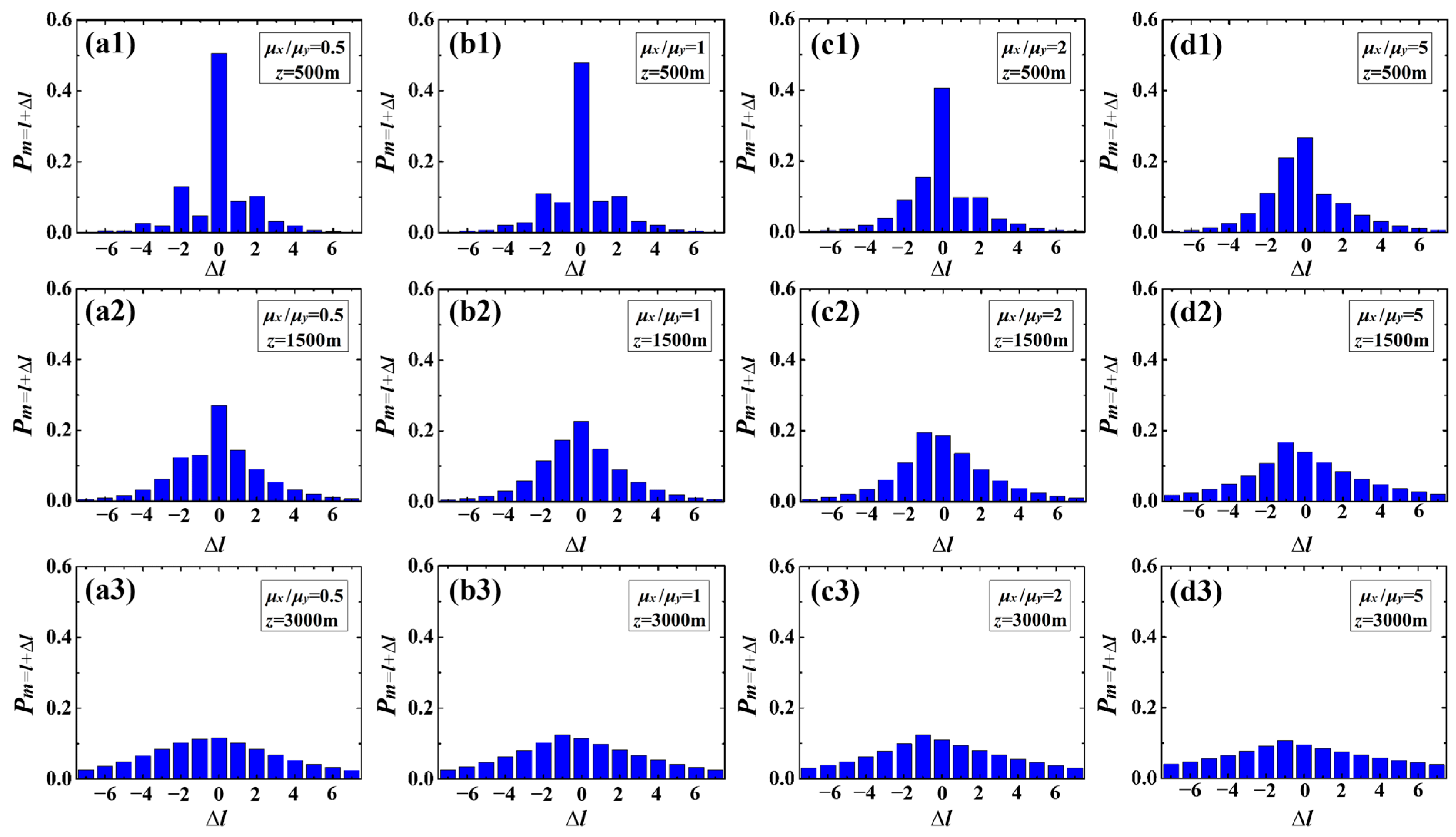
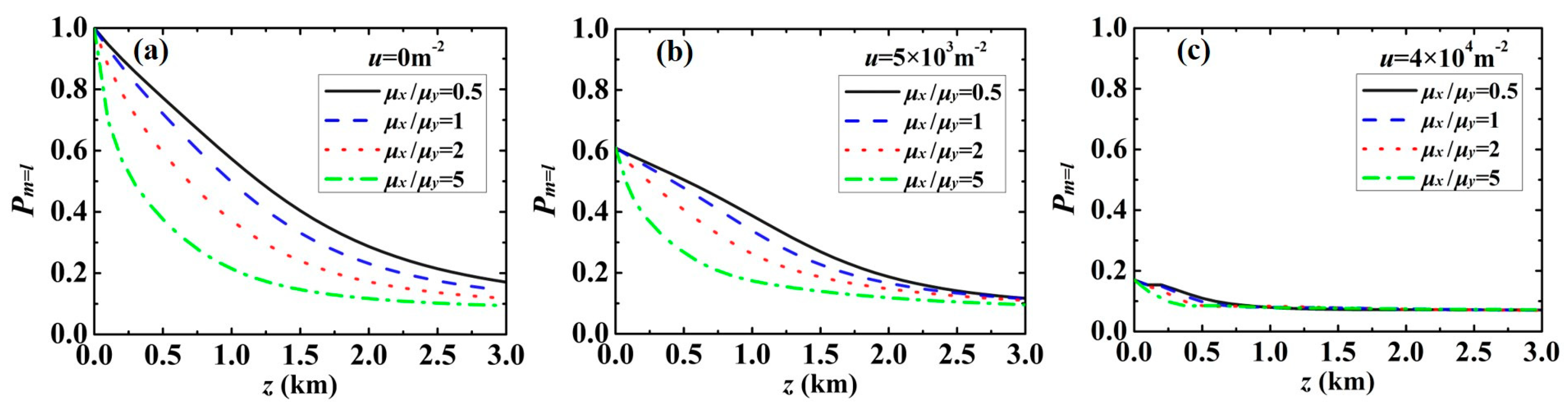
3.2. Spiral Spectrum of an LG Beam Carrying the Cross-Phase in Weak-to-Strong Anisotropic Atmospheric Turbulence
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gbur, G. Singular Optics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 11, 8185–8189. [Google Scholar] [CrossRef]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh Criterion Limit with Optical Vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef]
- Qiu, X.; Li, F.; Zhang, W.; Zhu, Z.; Chen, L. Spiral phase contrast imaging in nonlinear optics: Seeing phase objects using invisible illumination. Optica 2018, 5, 208–212. [Google Scholar] [CrossRef]
- He, H.; Friese, M.E.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 1995, 75, 826–829. [Google Scholar] [CrossRef]
- Paterson, L.; MacDonald, M.P.; Arlt, J.; Sibbett, W.; Bryant, P.E.; Dholakia, K. Controlled rotation of optically trapped microscopic particles. Science 2001, 292, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ren, Y.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Kong, L.; Zhang, W.; Li, P.; Guo, X.; Zhang, J.; Zhang, F.; Zhao, J.; Zhang, X. High capacity topological coding based on nested vortex knots and links. Nat. Commun. 2022, 13, 2705. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Chremmos, I.; Chen, Y.; Zhang, Y.; Yu, S. Arbitrary Multiplication and Division of the Orbital Angular Momentum of Light. Phys. Rev. Lett. 2020, 124, 213901. [Google Scholar] [CrossRef] [PubMed]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Wang, Z.; Liao, P.; Li, L.; Xie, G.; Huang, H.; Zhao, Z.; Yan, Y.; Ahmed, N.; Willner, A.; et al. Experimental characterization of a 400 Gbit/s orbital angular momentum multiplexed free-space optical link over 120 m. Opt. Lett. 2016, 41, 622–625. [Google Scholar] [CrossRef]
- Wang, A.; Zhu, L.; Wang, L.; Ai, J.; Chen, S.; Wang, J. Directly using 8.8-km conventional multi-mode fiber for 6-mode orbital angular momentum multiplexing transmission. Opt. Express 2018, 26, 10038–10047. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photon. 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, G.; Lavery, M.P.J.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z.; et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 4876. [Google Scholar] [CrossRef]
- Lei, T.; Zhang, M.; Li, Y.; Jia, P.; Liu, G.N.; Xu, X.; Li, Z.; Min, C.; Lin, J.; Yu, C.; et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 2015, 4, e257. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Li, S.; Zhao, Y.; Du, J.; Zhu, L. Orbital angular momentum and beyond in free-space optical communications. Nanophotonics 2022, 11, 645–680. [Google Scholar] [CrossRef]
- Paterson, C. Atmospheric turbulence and orbital angular momentum of single photons for optical communication. Phys. Rev. Lett. 2005, 94, 153901. [Google Scholar] [CrossRef] [PubMed]
- Anguita, J.A.; Neifeld, M.A.; Vasic, B.V. Turbulence-induced channel crosstalk in an orbital angular momentum-multiplexed free-space optical link. Appl. Opt. 2008, 47, 2414–2429. [Google Scholar] [CrossRef] [PubMed]
- Tyler, G.A.; Boyd, R.W. Influence of atmospheric turbulence on the propagation of quantum states of light carrying orbital angular momentum. Opt. Lett. 2009, 34, 142–144. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Hu, Z.; Wang, S.; Zhu, Y. Influence of random media on orbital angular momentum quantum states of optical vortex beams. Phys. Rev. A 2022, 105, 053513. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, S.; Zhang, J.; Ou, J.; Tang, H. Spiral spectrum of Laguerre–Gaussian beam propagation in non-Kolmogorov turbulence. Opt. Commun. 2013, 303, 38–41. [Google Scholar] [CrossRef]
- Yu, L.; Hu, B.; Zhang, Y. Intensity of vortex modes carried by Lommel beam in weak-to-strong non-Kolmogorov turbulence. Opt. Express 2017, 25, 19538. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, X.; Zhao, C.; Wang, F.; Gbur, G.; Cai, Y. Spiral spectrum of a Laguerre-Gaussian beam propagating in anisotropic non-Kolmogorov turbulent atmosphere along horizontal path. Opt. Express 2019, 27, 25342–25356. [Google Scholar] [CrossRef]
- Li, P.; Liu, S.; Peng, T.; Xie, G.; Gan, X.; Zhao, J. Spiral autofocusing Airy beams carrying power-exponent-phase vortices. Opt. Express 2014, 22, 7598. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, L.; Xie, J.; Zhang, D.; Lv, Q.; Guo, L. Spiral spectrum of high-order elliptic Gaussian vortex beams in a non-Kolmogorov turbulent atmosphere. Opt. Express 2021, 29, 16056. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, X.; Gao, J.; Zhang, Y.; Zhao, F. Probability density of the orbital angular momentum mode of Hankel-Bessel beams in an atmospheric turbulence. Opt. Express 2014, 22, 7765. [Google Scholar] [CrossRef]
- Chen, C.; Yang, H.; Tong, S.; Lou, Y. Changes in orbital-angular-momentum modes of a propagated vortex Gaussian beam through weak-to-strong atmospheric turbulence. Opt. Express 2016, 24, 6959–6975. [Google Scholar] [CrossRef]
- Fu, S.; Gao, C. Influences of atmospheric turbulence effects on the orbital angular momentum spectra of vortex beams. Photonics Res. 2016, 4, 1–4. [Google Scholar] [CrossRef]
- Elder, H.F.; Sprangle, P. Mode power spectrum for Laguerre–Gauss beams in Kolmogorov turbulence. Opt. Lett. 2022, 47, 3447–3450. [Google Scholar] [CrossRef]
- Chen, C.; Yang, H. Characterizing the radial content of orbital-angular-momentum photonic states impaired by weak-to-strong atmospheric turbulence. Opt. Express 2016, 24, 19713–19727. [Google Scholar] [CrossRef]
- Lv, H.; Ren, C.; Liu, X. Orbital angular momentum spectrum of partially coherent vortex beams in slant atmospheric turbulence. Infrared Phys. Technol. 2020, 105, 103181. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, J.; Wang, A.; Lv, W.; Zhu, L.; Li, S.; Wang, J. Demonstration of data-carrying orbital angular momentum-based underwater wireless optical multicasting link. Opt. Express 2017, 25, 28743–28751. [Google Scholar] [CrossRef]
- Fang, X.; Yang, H.; Yao, W.; Wang, T.; Zhang, Y.; Gu, M.; Xiao, M. High-dimensional orbital angular momentum multiplexing nonlinear holography. Adv. Photonics 2021, 3, 015001. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J. Simultaneous generation of multiple orbital angular momentum (OAM) modes using a single phase-only element. Opt. Express 2015, 23, 26221–26233. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Yuan, X.C.; Tao, S.H.; Burge, R.E. Collinear superposition of multiple helical beams generated by a single azimuthally modulated phase-only element. Opt. Lett. 2005, 30, 3266–3268. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhao, Q.; Liu, L.; Liu, Y.; Rosales-Guzmán, C.; Qiu, C. Manipulation of Orbital-Angular-Momentum Spectrum Using Pinhole Plates. Phys. Rev. Appl. 2019, 12, 064007. [Google Scholar] [CrossRef]
- Fu, S.; Shang, Z.; Hai, L.; Huang, L.; Lv, Y.; Gao, C. Orbital angular momentum comb generation from azimuthal binary phases. Adv. Photonics Nexus 2022, 1, 016003. [Google Scholar] [CrossRef]
- Liang, G.; Wang, Q. Controllable conversion between Hermite Gaussian and Laguerre Gaussian modes due to cross phase. Opt. Express 2019, 27, 10684–10691. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Controllable rotating Gaussian Schell-model beams. Opt. Lett. 2019, 44, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Wang, C.; Liu, T.; Wang, Z.; Yin, C.; Qiu, S.; Li, Z.; Wu, H. Polygonal shaping and multi-singularity manipulation of optical vortices via high-order cross-phase. Opt. Express 2020, 28, 26257–26266. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Li, Z.; Monfared, Y.E.; Liang, C.; Wang, F.; Hoenders, B.J.; Cai, Y.; Ma, P. Flexible autofocusing properties of ring Pearcey beams by means of a cross phase. Opt. Lett. 2021, 46, 70–73. [Google Scholar]
- Simon, R.; Mukunda, N. Twist phase in Gaussian-beam optics. J. Opt. Soc. Am. A 1998, 15, 2373–2382. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Wang, F.; Cai, Y.; Liang, C.; Korotkova, O. Robust far-field imaging by spatial coherence engineering. Opto-Electron. Adv. 2021, 4, 210027. [Google Scholar] [CrossRef]
- Klug, A.; Peters, C.; Forbes, A. Robust structured light in atmospheric turbulence. Adv. Photonics 2023, 5, 016006. [Google Scholar] [CrossRef]
- Diouf, M.; Lin, Z.; Harling, M.; Krishna, K.; Toussaint, K.C. Interferometric phase stability from Gaussian and space–time light sheets. Optica 2023, 10, 1161. [Google Scholar] [CrossRef]
- Diouf, M.; Lin, Z.; Harling, M.; Toussaint, K.C. Demonstration of speckle resistance using space–time light sheets. Sci. Rep. 2022, 12, 14064. [Google Scholar] [CrossRef]
- Yura, H.T. Mutual Coherence Function of a Finite Cross Section Optical Beam Propagating in a Turbulent Medium. Appl. Opt. 1972, 11, 1399–1406. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Peng, D.; Huang, Z.; Liu, Y.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Optical coherence encryption with structured random light. PhotoniX 2021, 2, 6. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, H.; Xie, G.; Ahmed, N.; Yan, Y.; Erkmen, B.I.; Chandrasekaran, N.; Lavery, M.P.; Steinhoff, N.K.; Tur, M.; et al. Atmospheric turbulence effects on the performance of a free space optical link employing orbital angular momentum multiplexing. Opt. Lett. 2013, 38, 4062–4065. [Google Scholar] [CrossRef]
- Zhu, Z.; Janasik, M.; Fyffe, A.; Hay, D.; Zhou, Y.; Kantor, B.; Winder, T.; Boyd, R.W.; Leuchs, G.; Shi, Z. Compensation-free high-dimensional free-space optical communication using turbulence-resilient vector beams. Nat. Commun. 2021, 12, 1666. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, G.; Liu, Y.; Wang, H.; Hoenders B., J.; Liang, C.; Cai, Y.; Zeng, J. Robust measurement of orbital angular momentum of a partially coherent vortex beam under amplitude and phase perturbations. Opto-Electron. Sci. 2024, 3, 240001. [Google Scholar] [CrossRef]
- Vallone, G.; D’Ambrosio, V.; Sponselli, A.; Slussarenko, S.; Marrucci, L.; Sciarrino, F.; Villoresi, P. Free-space quantum key distribution by rotation-invariant twisted photons. Phys. Rev. Lett. 2014, 113, 060503. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Lu, X.; Liu, L.; Zhu, X.; Zhao, C.; Cai, Y. Simultaneous measurement of the radial and azimuthal mode indices of a higher-order partially coherent vortex beam based on phase detection. Opt. Lett. 2019, 44, 3881–3884. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, C.L.; Shao, Y.; Zeng, J.; Konijnenberg, A.P.; Zhu, X.; Popov, S.; Urbach, P.; Cai, Y. Phase detection of coherence singularities and determination of the topological charge of a partially coherent vortex beam. Appl. Phys. Lett. 2019, 114, 201106. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Q.; Zeng, J.; Cai, Y.; Liang, C. Measurement of optical coherence structures of random optical fields using generalized Arago spot experiment. Opto-Electron. Sci. 2023, 2, 220024. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, X.; Gao, J.; Zhao, X.; Zhan, Q.; Cai, Y.; Zhao, C. Coherence phase spectrum analyzer for a randomly fluctuated fractional vortex beam. Photonics Res. 2024, 12, 33. [Google Scholar] [CrossRef]
- Wang, H.; Zhan, Z.; Hu, F.; Meng, Y.; Liu, Z.; Fu, X.; Liu, Q. Intelligent optoelectronic processor for orbital angular momentum spectrum measurement. PhotoniX 2023, 4, 9. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, Z.; Li, R.; Xu, D.; Zhang, H.; Cai, Y.; Zeng, J. The Spiral Spectrum of a Laguerre–Gaussian Beam Carrying the Cross-Phase Propagating in Weak-to-Strong Atmospheric Turbulence. Photonics 2024, 11, 148. https://doi.org/10.3390/photonics11020148
Li Y, Zhang Z, Li R, Xu D, Zhang H, Cai Y, Zeng J. The Spiral Spectrum of a Laguerre–Gaussian Beam Carrying the Cross-Phase Propagating in Weak-to-Strong Atmospheric Turbulence. Photonics. 2024; 11(2):148. https://doi.org/10.3390/photonics11020148
Chicago/Turabian StyleLi, Yunxiao, Zhao Zhang, Ruyi Li, Dong Xu, Hao Zhang, Yangjian Cai, and Jun Zeng. 2024. "The Spiral Spectrum of a Laguerre–Gaussian Beam Carrying the Cross-Phase Propagating in Weak-to-Strong Atmospheric Turbulence" Photonics 11, no. 2: 148. https://doi.org/10.3390/photonics11020148
APA StyleLi, Y., Zhang, Z., Li, R., Xu, D., Zhang, H., Cai, Y., & Zeng, J. (2024). The Spiral Spectrum of a Laguerre–Gaussian Beam Carrying the Cross-Phase Propagating in Weak-to-Strong Atmospheric Turbulence. Photonics, 11(2), 148. https://doi.org/10.3390/photonics11020148





