Next Article in Journal
High-Power Terahertz Photonic Crystal Surface-Emitting Laser with High Beam Quality
Previous Article in Journal
The Spiral Spectrum of a Laguerre–Gaussian Beam Carrying the Cross-Phase Propagating in Weak-to-Strong Atmospheric Turbulence
Previous Article in Special Issue
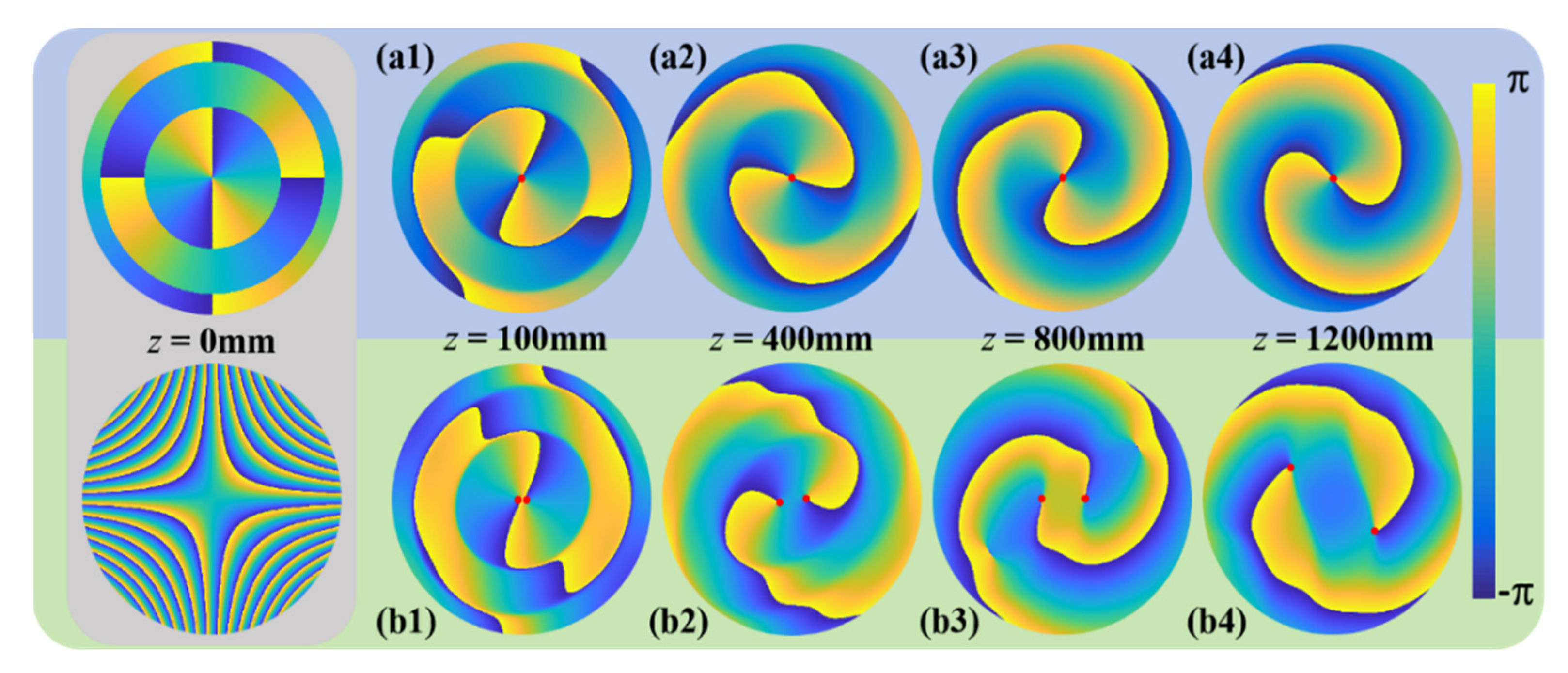
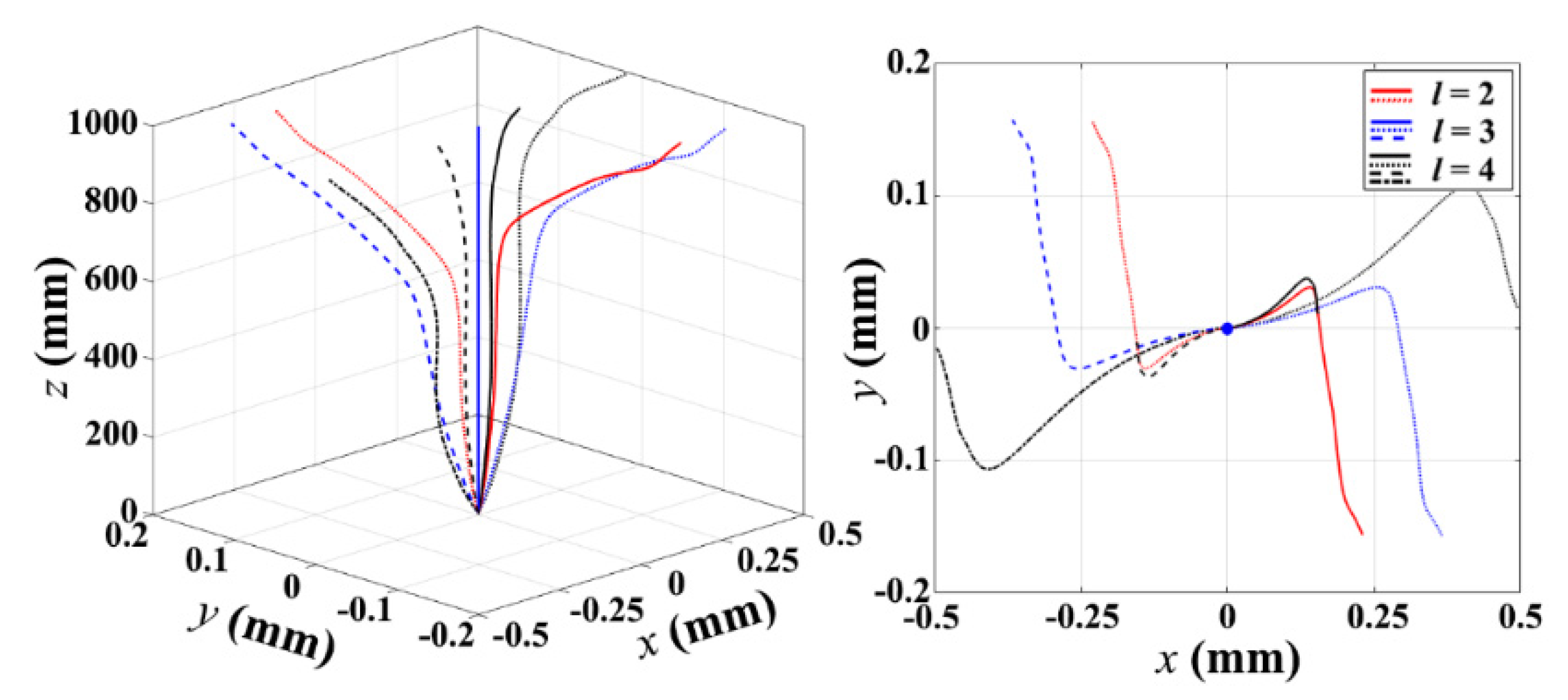
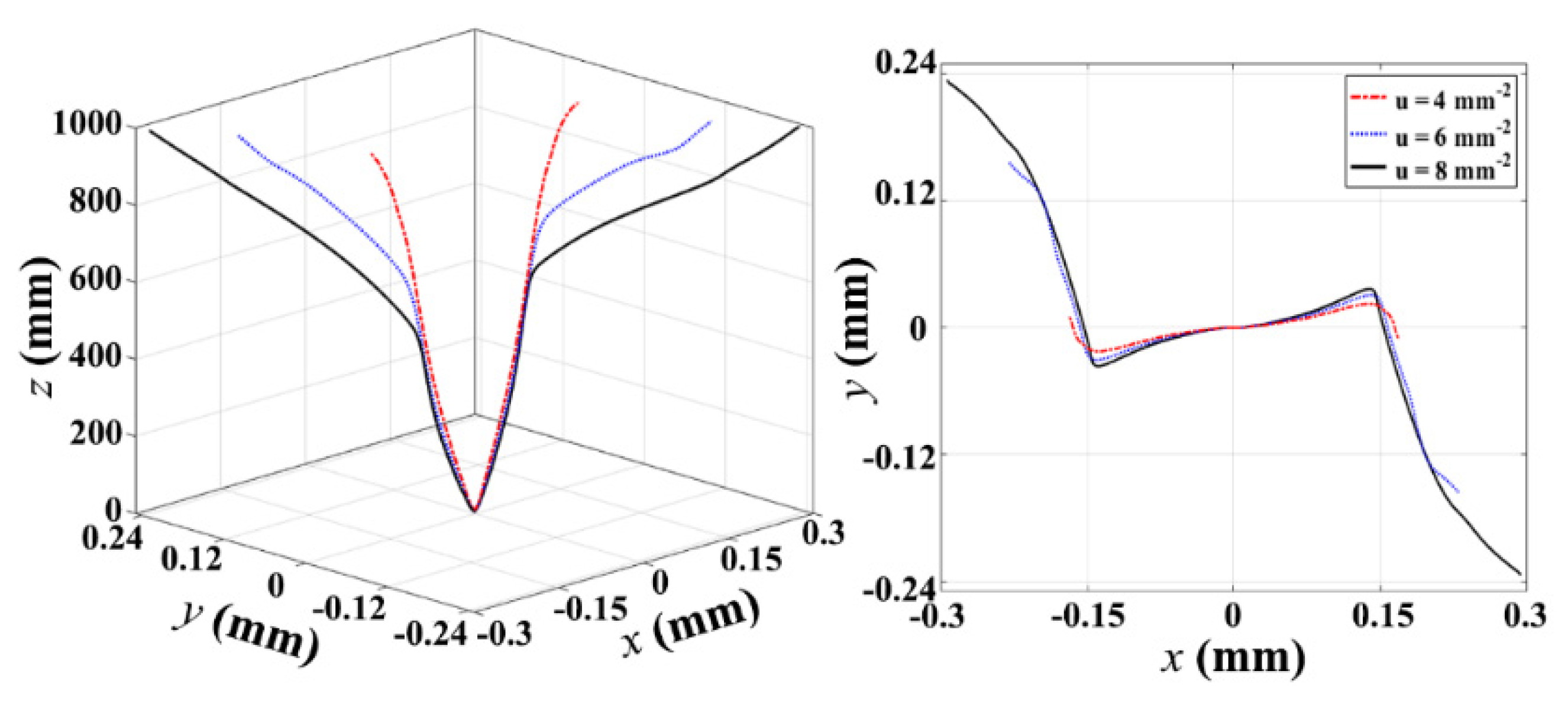
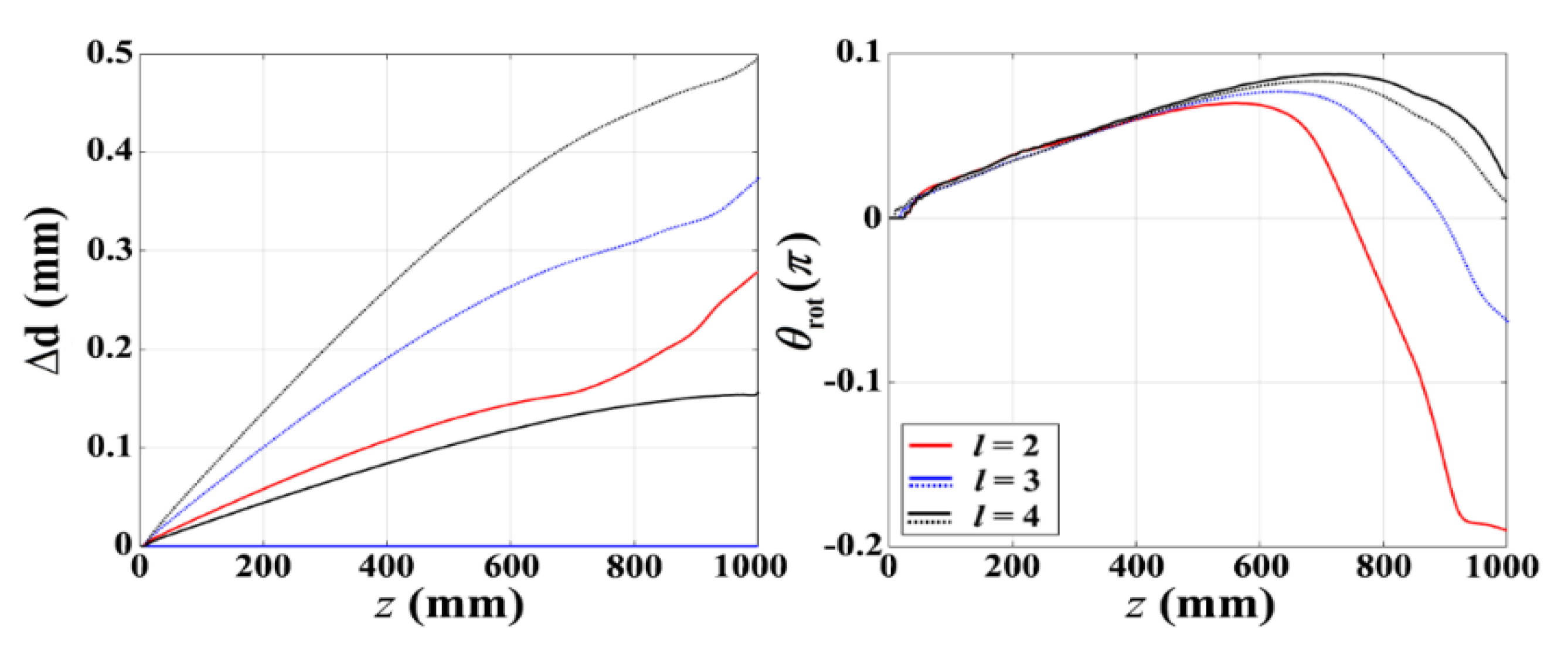
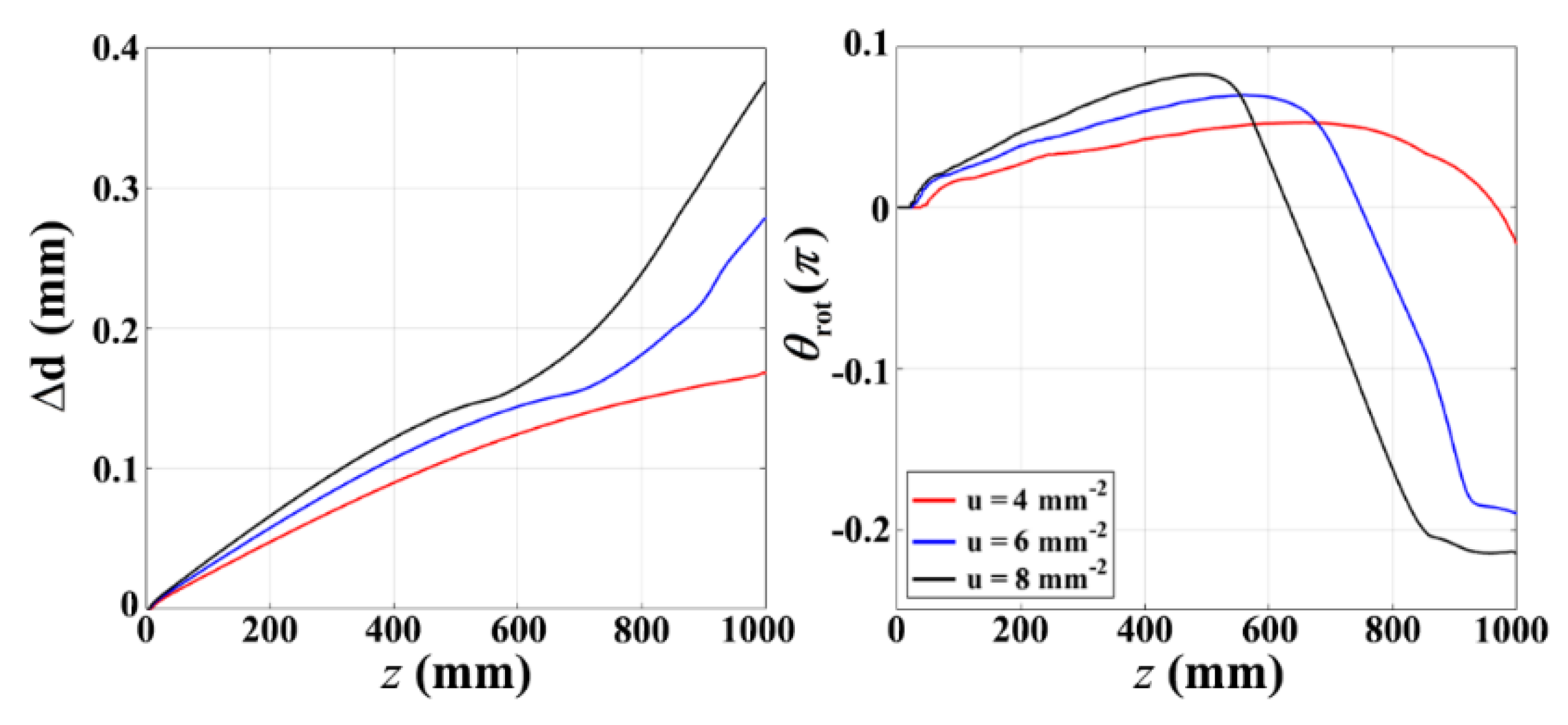
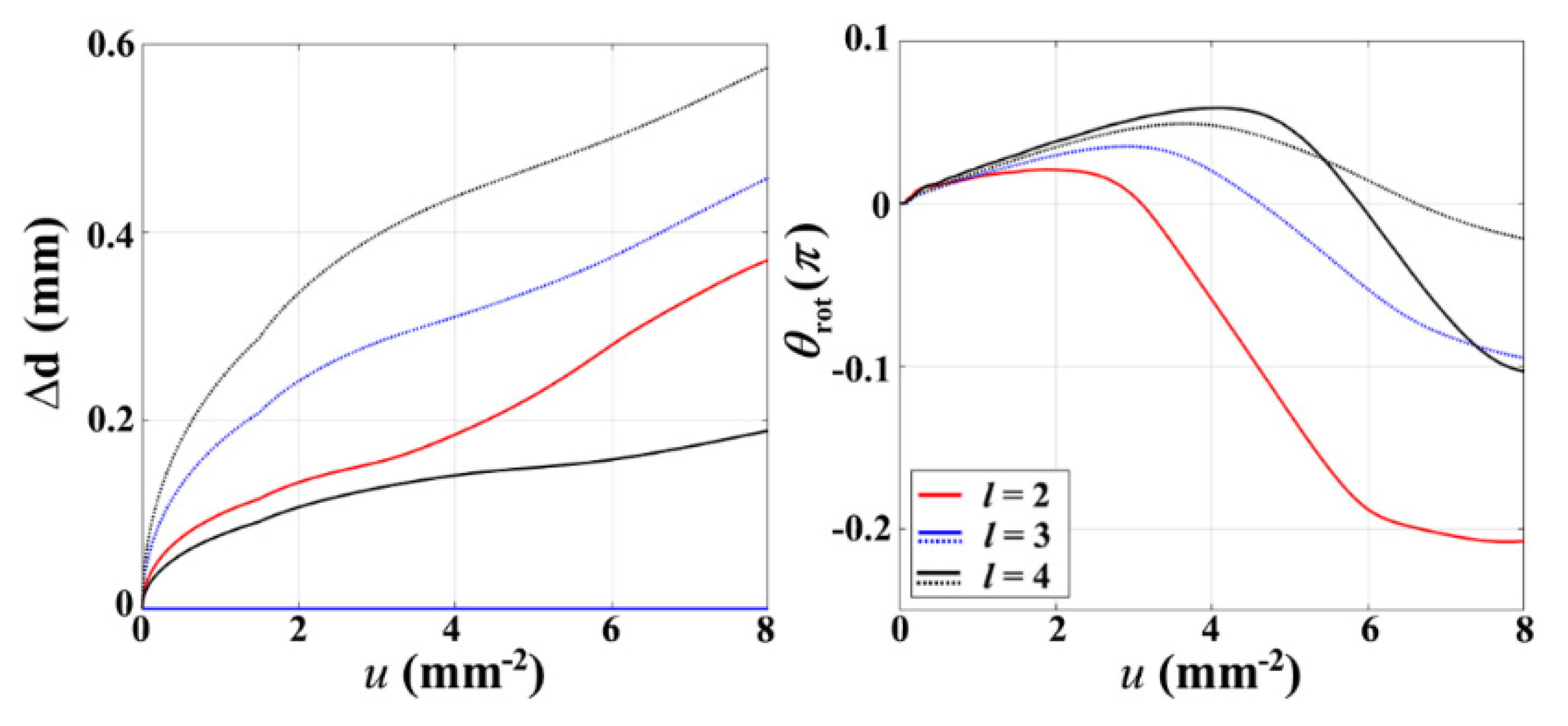
Numerical Analysis and Verification of Off-Axis Double Vortex Beams
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 11
Issue 2
10.3390/photonics11020149
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

Evolution of the Phase Singularity of an Orbital Angular Momentum Beam with an Astigmatism Phase

by
Chunhao Liang
1,2,
Cuiling Zheng
1,2,
Xinru Lian
1,2,
Qian Chen
1,2,
Yaru Gao
1,2,*,
Jinsong Liu
1,2,
Yangjian Cai
1,2 and
Jun Zeng
1,2,*
1
Shandong Provincial Engineering and Technical Center of Light Manipulation & Shandong Provincial Key Laboratory of Optics and Photonics Devices, School of Physics and Electronics, Shandong Normal University, Jinan 250014, China
2
Collaborative Innovation Center of Light Manipulations and Applications, Shandong Normal University, Jinan 250358, China
*
Authors to whom correspondence should be addressed.
Photonics 2024, 11(2), 149; https://doi.org/10.3390/photonics11020149
Submission received: 8 January 2024 / Revised: 25 January 2024 / Accepted: 1 February 2024 / Published: 5 February 2024
(This article belongs to the Special Issue Coherence Manipulation, Propagation and Applications of Vortex Beam)
Browse Figures
Versions Notes

Abstract

In this study, we explore the impact of the astigmatism phase on the evolution of the phase singularity of an orbital angular momentum (OAM) beam propagating through free space. The results demonstrate that the high-order phase singularity dispersed into a cluster of individual unit phase singularities owing to the astigmatism phase. The number of singularities equaled the topological charge of the OAM beam. By adjusting the astigmatism phase, we could manipulate and control the evolution of the phase singularities, including their displacements and rotation angles. These findings offer significant prospects for customizing 3D vortex lines, optical topologies, and applications involving topological charge measurement, information encoding, and transfer.
Keywords: phase singularity; astigmatism phase; orbital angular momentum beam phase singularity; astigmatism phase; orbital angular momentum beam

Share and Cite

MDPI and ACS Style

Liang, C.; Zheng, C.; Lian, X.; Chen, Q.; Gao, Y.; Liu, J.; Cai, Y.; Zeng, J. Evolution of the Phase Singularity of an Orbital Angular Momentum Beam with an Astigmatism Phase. Photonics 2024, 11, 149. https://doi.org/10.3390/photonics11020149

AMA Style

Liang C, Zheng C, Lian X, Chen Q, Gao Y, Liu J, Cai Y, Zeng J. Evolution of the Phase Singularity of an Orbital Angular Momentum Beam with an Astigmatism Phase. Photonics. 2024; 11(2):149. https://doi.org/10.3390/photonics11020149

Chicago/Turabian Style

Liang, Chunhao, Cuiling Zheng, Xinru Lian, Qian Chen, Yaru Gao, Jinsong Liu, Yangjian Cai, and Jun Zeng. 2024. "Evolution of the Phase Singularity of an Orbital Angular Momentum Beam with an Astigmatism Phase" Photonics 11, no. 2: 149. https://doi.org/10.3390/photonics11020149

APA Style

Liang, C., Zheng, C., Lian, X., Chen, Q., Gao, Y., Liu, J., Cai, Y., & Zeng, J. (2024). Evolution of the Phase Singularity of an Orbital Angular Momentum Beam with an Astigmatism Phase. Photonics, 11(2), 149. https://doi.org/10.3390/photonics11020149

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop