Enhancing Alignment Accuracy in Laser Wireless Power Transmission Systems Using Integrated Target Detection and Perturbation-Observation Method

Abstract

This paper introduces a high-precision alignment method for laser wireless power transmission (LWPT) systems, integrating neural network-based target detection with a perturbation-observation technique. The objective is to enhance the alignment accuracy between the laser spot and the photovoltaic array, thereby improving energy transfer efficiency. The method’s key feature is its ability to achieve these results without requiring additional optical components, simplifying system design. Continual assessment and adjustment based on real-time output power data ensure optimal alignment, maximizing the photovoltaic array power output. Experimental results demonstrated that the proposed method achieved an initial alignment precision with pixel errors below 3%, translating to a physical error of approximately 7 mm. Fine-tuning through the perturbation-observation method further optimized the alignment, resulting in a photovoltaic array power output of 98.70% of its maximum potential. This hybrid approach provides a reliable solution for boosting the performance of LWPT systems, offering significant potential for practical applications.

1. Introduction

Wireless power transmission (WPT) enables non-contact power supply through energy conversion [1]. WPT technology offers several advantages, including enhanced security, improved flexibility, convenience, and user-friendliness [2,3]. It is widely used in electric vehicles [4], portable electronics [5,6], and Internet of Things devices [7] to resolve conflicts between energy demand and portability. To extend the transmission distance, laser wireless power transmission (LWPT) has emerged as a promising method, attracting attention for its capability in long-distance power transmission [8]. The LWPT system uses focused laser beams to transmit energy [9]. This technology eliminates the need for physical connectors, making it particularly suitable for remote or challenging environments [10]. It is useful for powering spacecraft, remote sensors, and unmanned aerial vehicles [11], where traditional power supply methods may be less practical.

Precision alignment in LWPT systems is crucial for maximizing power transmission performance [12]. In optical communication systems, the receiving end must be covered by a light beam and accurately aligned to achieve optimal information transmission rates [13]. Similarly, in LWPT systems, the beam must be precisely matched with the photovoltaic (PV) array. Misalignment can lead to damage to the PV array due to the high power density. A precise alignment method is essential for achieving high power transmission efficiency [14].

Currently, there are two main approaches for aligning LWPT systems [15], as shown in Figure 1. One method is mainly based on optical principles, using lenses, reflectors, and photoelectric devices such as quadrant photodetectors [16]. In this setup, mirrors are placed at the center or edge of the PV array [17], while quadrant photodetectors are aligned coaxially with the beam expander [15]. Alignment can start with initial positioning using a global positioning system (GPS), followed by laser scanning. When the laser beam irradiates the PV array, part of the beam is reflected back and detected by the quadrant photodetector. This allows for dynamic tracking based on feedback from the reflected light. This method is effective for optical communication systems. However, it is less commonly used in power transmission. The additional optical components will introduce energy loss, which reduces power transmission efficiency.

In contrast, image-based aligning techniques use visual sensors to obtain real-time positional information of the target [18]. Image processing algorithms analyze the target’s coordinates and adjust the laser beam direction accordingly. This method does not require additional optical components at the receiver. It relies entirely on image processing for alignment and tracking. The implementation of this method requires high-precision visual sensors and fast, accurate image processing algorithms. Additionally, its performance can be adversely affected by external light conditions, potentially leading to instability in tracking accuracy [19].

In the early stages of research on LWPT, many studies employed reflectors to achieve precise alignment. In 1997, Tohoku University used germanium mirrors and quadrant photodetectors for alignment [20]. Similarly, in 2002, a German study utilized steering mirrors and reflective films to enhance alignment accuracy [21]. By 2007, Kawashima’s team at Kinki University achieved long-term automatic tracking with a corner-cube reflector, maintaining alignment precision within ±1 cm over 50 m [16,17]. In 2017, the University of Washington conducted a study combining acoustic and optical techniques for smartphone charging alignment [6]. Although these methods ensured alignment accuracy through structural design, they present several challenges. The reflection of the power beam, while helpful for positioning, causes energy loss because the laser spot does not fully match the PV array. Moreover, additional optical components also complicate both the transmitter and receiver systems.

Advances in Artificial Intelligence, such as neural networks and target detection, offer new alternatives for aligning LWPT systems. These innovative approaches use neural network-based target detection for beam alignment. They simplify system design and reduce system complexity. More recent methods include Kanazawa University’s 2020 approach using infrared light emitting diodes (LEDs) for target recognition [19]. In China, advancements include Shandong Aerospace’s 2014 Acquisition, Pointing and Tracking (APT) system for multi-beam tracking [22], a 2019 unmanned aerial vehicle (UAV) tracking system with GPS and beacon light [23], and Three Gorges University’s 2020 beacon-free tracking using improved Kalman filtering [24]. In 2021, Sichuan University developed fuzzy PID controllers to enhance tracking precision [25]. The use of neural network-based target detection in LWPT systems introduces a simpler structural design but increases algorithm complexity. Beacon-based methods [19] help precisely locate the PV array but add complexity to the receiver. In contrast, beacon-free approaches [24] reduce hardware demands but require more advanced detection algorithms to maintain previse alignment.

Recent advancements have introduced several alignment techniques to improve precision. Studies have explored methods such as depth cameras and computer vision for dynamic safety systems (2024) [12,18], and two-stage beam alignment using optical power feedback (2023) [15]. Other works detail self-alignment methods for free space optical communication (FSOC) in small mobile platforms (2022) [26] and Artificial Intelligence (AI)-based algorithms for adaptive optical beam alignment in 5G-over free space optics systems (2021) [14]. Additionally, a tactical beam alignment method using voice coil motor-based scanning and quadrant photodiode (QPD) feedback has been proposed (2022) [27]. The above alignment methods have demonstrated their effectiveness and high alignment accuracy.

While those studies effectively improve alignment accuracy, they often require additional auxiliary devices, such as quadrant detectors [15], power meters [14,15], laser rangefinders [12], infrared LED markers [19], and large-area photodetectors [26]. This research aims to maintain precise beam alignment without increasing system complexity. The method leverages the operational characteristics of the PV array in the LWPT system. It uses PV array voltage and current data to assist in precise alignment. The data have been overlooked in previous LWPT alignment methods. This alignment approach draws on research related to maximum power point tracking (MPPT). In MPPT, the PV array is perturbed to operate at the maximum power point voltage (u_mpp). Similarly, in the alignment system, the laser spot position is perturbed to ensure the PV array operates under maximum irradiance.

This paper presents an effective laser beam alignment approach that combines neural network-based target detection with a perturbation-observation technique, effectively eliminating the need for additional auxiliary devices like mirrors or detectors. The method uses image recognition to initially align the laser spot with the photovoltaic array, followed by fine-tuning through perturbation-observation. The method achieves alignment by continuously adjusting the gimbal’s azimuth and pitch angles based on power changes in the PV array. It requires only an image sensor at the transmitter. The method requires transmission of the PV array data from the receiver to the transmitter controller. Notably, the energy control in LWPT systems already requires PV array data, so no additional data measurement or communication requirements are added. Additionally, this method can achieve precise alignment even if the initial alignment is relatively poor, as long as the laser beam irradiates the PV array. Subsequent adjustments can refine the alignment, thereby reducing the requirements for image sensing and target recognition algorithms.

2. Proposed Alignment Method for Laser Wireless Power Transmission System

This chapter introduces the proposed alignment method, which integrates neural network-based target detection with a perturbation-observation technique. It begins by outlining the overall framework of the alignment approach, followed by a detailed explanation of the initial alignment using neural network target detection. Finally, it discusses the precision alignment achieved through the perturbation-observation method. The content of this chapter establishes the principles and functionalities of the proposed method, essential for enhancing alignment accuracy in LWPT systems.

2.1. Overall Architecture

This section outlines the comprehensive structure of the proposed alignment method for LWPT systems, divided into two primary phases: initial alignment using neural network-based target detection and fine-tuning using a perturbation-observation technique.

Initial alignment is achieved using neural network-based target detection. A charge coupled device (CCD) camera captures images of the PV array and the laser spot, which are processed to determine the pixel positions of both the PV array and the laser spot. The system then calculates the required gimbal movements to align the laser spot with the center of the PV array. This method eliminates the need for auxiliary beacon lights or additional optical components, simplifying the alignment process and reducing system complexity. Through this initial alignment, the laser beam can be irradiated onto the PV array. The initial alignment method lays the foundation for laser wireless power transmission.

Once the laser spot is roughly aligned, the system enters the fine-tuning phase using the perturbation-observation method. This technique adjusts the gimbal’s azimuth and pitch angles by monitoring variations in the PV array’s output power, similar to MPPT methods. The MPPT technique is used to optimize the output power of solar PV systems and laser PV systems. The output power of PV cells is influenced by factors such as light intensity, temperature, and load characteristics. Therefore, the maximum power point (MPP) of the PV array varies under different environmental conditions. The core of MPPT technology is to dynamically adjust the operating point of the PV array to keep it as close as possible to the MPP (u_mpp), thereby maximizing energy conversion efficiency. By applying a similar principle, the alignment method continuously adjusts the laser spot position to ensure the PV array operates at its maximum power output, enhancing the overall efficiency of the LWPT system.

Continual assessment and adjustment based on real-time output power data ensures optimal alignment, maximizing power output. This approach enhances alignment precision and ensures stability and robustness under varying operational conditions. Since the perturbation-observation method utilizes data already collected for LWPT system power control, it does not introduce additional sensors, maintaining system simplicity while achieving high alignment accuracy.

In summary, the neural network-based target detection ensures initial alignment. The perturbation-observation method refines the alignment. This combination provides a comprehensive and effective approach to enhance alignment accuracy. It ensures maximum energy transfer efficiency while keeping the system simple and robust.

2.2. Initial Alignment via Neural Network-Based Target Detection

This section introduces the method of achieving initial alignment of the laser spot with the PV array using a neural network-based target detection model. Recent advancements in deep neural networks (DNNs) have enabled significant progress in computer vision tasks such as image classification and object detection. Among these, YOLOv5 (You Only Look Once version 5) is a prominent one-stage object detection model that directly predicts object classes and locations, making it highly efficient for real-time applications. PP-LCNet (PaddlePaddle Lightweight Convolutional Network) is optimized for high inference speed on Intel central processing unit (CPU) platforms, leveraging features such as the H-Swish activation function, squeeze-and-excitation (SE) modules for enhanced accuracy, and the use of 5 × 5 convolutional layers to improve model performance.

To balance model accuracy and computational efficiency, particularly in CPU-based deployments, this research adopts the lightweight PP-LCNet backbone for the YOLOv5 model, as shown in Figure 2. PPLCNet-YOLOv5 is a hybrid deep learning model that combines the PP-LCNet and YOLOv5 architectures. This model is designed to achieve high accuracy and efficiency in target detection, particularly in the CPU-based platform. PP-LCNet serves as the backbone of the model, providing feature extraction capabilities. The neck and head components of YOLOv5 are retained to perform target detection, including bounding box prediction and class classification. The combination leverages the efficiency of PP-LCNet and the detection accuracy of YOLOv5 to create a model that is both lightweight and effective.

In the proposed method, images captured by the CCD camera are processed through this neural network to identify and locate the PV array and laser spot within the image. The system calculates the necessary gimbal adjustments. It aligns the laser spot with the PV array’s center. This completes the initial alignment without needing auxiliary beacon lights or additional optical components. This approach ensures high accuracy in the initial positioning of the laser spot, setting the stage for the subsequent fine-tuning phase.

2.3. Precision Alignment via Perturbation-Observation Method

In LWPT systems, precise alignment between the laser spot and the PV array is critical for maximizing system efficiency. The primary goal is to ensure optimal alignment, allowing for maximum power output with minimal energy loss. Alignment efficiency quantifies how well the laser spot overlaps with the PV array; ideally, perfect alignment results in 100% efficiency, meaning no energy is wasted. However, practical limitations such as gimbal accuracy, mechanical play, and oscillations, along with nonlinear and time-varying characteristics of the medium and photoelectric devices, often lead to less than perfect alignment.

Given the challenges of precise alignment, especially after the initial positioning, this section proposes the use of a perturbation-observation method inspired by MPPT techniques commonly employed in photovoltaic systems. Following the initial alignment phase, where the laser spot is roughly aligned with the PV array, this method refines the alignment.

The process involves adjusting the gimbal’s horizontal and vertical angles based on real-time feedback from the PV array’s power output P_PV, as shown in Functions (1)–(3). Small, deliberate perturbations $\delta \theta$ are made to the gimbal’s position, and the resulting changes in output power are observed. If the power output increases, the adjustment direction is deemed correct, and further adjustments are made in the same direction. Conversely, if the power output decreases, the direction is reversed.

$$P_{\mathrm{P}\mathrm{V}}\left(k\right)=u_{\mathrm{P}\mathrm{V}}\left(k\right)i_{\mathrm{P}\mathrm{V}}\left(k\right)$$

(1)

$$\theta \left(k+1\right)=\theta \left(k\right)+\delta \theta$$

(2)

$$\left\{\begin{array}{c}if:P_{\mathrm{P}\mathrm{V}}\left(k+1\right)\ge P_{\mathrm{P}\mathrm{V}}\left(k\right),\delta \theta =a;\\ if:P_{\mathrm{P}\mathrm{V}}\left(k+1\right)<P_{\mathrm{P}\mathrm{V}}\left(k\right),\delta \theta =-a;\end{array}\right.$$

(3)

In Functions (1) and (2), $P_{\mathrm{P}\mathrm{V}}\left(k\right)$ represents the instantaneous power output of the photovoltaic array at time step $k$, which is calculated as the product of PV voltage $u_{\mathrm{P}\mathrm{V}}\left(k\right)$ and current $i_{\mathrm{P}\mathrm{V}}\left(k\right)$. The gimbal angle $\theta \left(k+1\right)$ is updated at time step $k+1$ according to the step size $\delta \theta$, where $a$ and $-a$ denote positive and negative step sizes, respectively. These procedures govern the alignment process, ensuring that the gimbal angle is adjusted towards maximizing the instantaneous power output of the PV array. The termination conditions for the iteration are as follows: reaching the preset power level and the number of consecutive round-trip oscillations.

These rules ensure that the gimbal angle is adjusted towards increasing the PV array’s instantaneous power output. The choice of step size $a$ affects both alignment speed and precision. Larger step sizes accelerate the alignment process but may cause overshooting or oscillations; smaller step sizes improve precision but prolong alignment time.

This iterative process continues until the system converges on optimal alignment, ensuring the laser spot achieves the best possible overlap with the PV array. The implementation of the perturbation-observation method is illustrated in the flowcharts provided in Figure 3. Initially, the method completes the rough alignment using the laser spot position control strategy, as discussed previously. It then measures the PV array’s initial power output and begins the perturbation process, adjusting the gimbal angles incrementally.

In the fixed-step laser alignment algorithm, the step size is crucial for alignment accuracy. A large step size can cause oscillations around the ideal position, leading to alignment errors. A smaller step size reduces oscillations and improves accuracy but increases alignment time due to sensor and transmission delays.

To balance accuracy and speed, a variable-step laser alignment algorithm is proposed, as shown in Figure 4. This method is similar to the fixed-step algorithm described above but adjusts the step size based on the initial power relative to a threshold. After initial alignment using image processing, if the initial PV array output power $P_{PV}\left(0\right)$ is below 50% of the threshold power $P_{\mathrm{t}}$, the variable-step method is applied for smaller-step alignment.

$$\left\{\begin{array}{c}if:P_{\mathrm{P}\mathrm{V}}\left(0\right)\ge {0.5P}_{\mathrm{t}},\left|\delta \theta \right|=a_1;\\ if:P_{\mathrm{P}\mathrm{V}}\left(0\right)<{0.5P}_{\mathrm{t}},\left|\delta \theta \right|=a_2;\end{array}\right.$$

(4)

The variable-step laser alignment algorithm improves upon the fixed-step approach by dynamically adjusting the step size. Based on the initial alignment, measure the power of the PV array at this time $P_{PV}\left(0\right)$. The gimbal angle $\theta \left(k+1\right)$ is updated at time step $k+1$ according to the step size $\delta \theta$, where $a_1$ and $a_2$ denote small and large step sizes, respectively. These rules allow for faster convergence when the PV array output is close to the maximum power point, while maintaining high precision during the initial alignment phase.

The method is designed to be simple yet effective, relying on data already necessary for the system’s power regulation, making it a practical solution for enhancing alignment accuracy. This approach addresses the limitations of image-based methods, which can struggle with precision when the laser spot and PV array are nearly aligned. Continuous optimization based on actual power output ensures that the laser spot is always positioned for maximum energy transfer.

In summary, the perturbation-observation method provides a robust and efficient means of fine-tuning laser alignment in LWPT systems, enhancing system efficiency, and maintaining stable performance under varying conditions.

3. Alignment Experiment Results

In this chapter, we focus on the experimental validation of the alignment methods introduced in Chapter 2. Our goal is to demonstrate the effectiveness and precision of these techniques. The chapter starts with an overview of the experimental platform setup. This is followed by detailed experiments on initial alignment, utilizing neural network-based target detection, and fine-tuning alignment through the perturbation-observation method. The results from these experiments offer crucial insights into the accuracy and reliability of the proposed alignment strategies.

3.1. Experimental Setup

To address the challenges of capture, aiming, and tracking in LWPT systems, an experimental platform was constructed based on an existing research setup, as shown in Figure 5a. This platform primarily comprises a CCD image sensor, a two-degree-of-freedom gimbal, an X-Z translation stage, a central processor (intel-CPU), and other supporting equipment, as illustrated in Figure 5.

The CCD image sensor captures images of the receiver, including the laser spot and PV array, and transmits these images to the central processor for processing. The central processor, a portable Intel Core i7-12700H 2.30GHz laptop, processes the captured images and uses the proposed neural network to identify the laser spot and PV array. Using the Hough transform, the centers of the laser spot and PV array are determined, enabling the system to calculate the relative positions and derive the necessary gimbal angle and speed control parameters. These parameters are subsequently converted into gimbal motor control signals (pulse count and frequency) by an STM32 processor and transmitted via a serial bus.

The two-degree-of-freedom gimbal consists of a rotation platform, a tilt platform, stepper motors, motor drivers, and a stepper motor controller (STM32). The STM32 controller receives the motor control signals. It generates the corresponding pulses and sends them to the motor drivers. The motor drivers regulate the voltage and current supplied to the stepper motor windings (A+, A−, B+, B−). This ultimately controls the rotation angle of the motors. The mechanical reduction structure further refines the gimbal’s actual rotation angle.

Additionally, the X-Z translation stage, along with its associated components, such as X and Z-axis stages, stepper motors, drivers, and a controller (PC), is used to adjust the position of the PV array and the heat dissipation plate mounted on the translation stage. This setup enables the evaluation of the proposed method’s alignment performance under various conditions.

3.2. Initial Alignment Experiment Using Neural Network-Based Target Detection

In this section, we describe the initial alignment experiment employing the PPLCNet-YOLOv5 network model. This model was specifically designed to detect and localize the laser spot and PV array within captured images. The input images, sized at 640 × 480 × 3 pixels, were resized to 640 × 640 × 3 before being processed through a series of convolutional layers. These layers included standard convolution blocks, depth-wise separable convolutions, and feature enhancement layers, resulting in high-dimensional feature maps for precise object detection.

For this experiment, data were collected using a video recording of the laser spot moving across the PV array. A total of 1512 images were extracted from the video at intervals of 10 frames. These images were manually annotated using the labelImg tool, with objects classified as either “PV” (photovoltaic array) or “Spot” (laser spot). The annotated dataset was then divided into a training set and a test set in a 9:1 ratio.

The PPLCNet-YOLOv5 model was trained on this dataset using the PyTorch 2.0.1 framework, with Python 3.9 as the development language. The training process involved 200 epochs with a batch size of 8, using a stochastic gradient descent optimizer, and the results are shown in Figure 6. The learning rate was dynamically adjusted throughout the training to optimize model performance. This setup enabled the effective detection and initial alignment of the laser spot with the PV array, setting the stage for further fine-tuning.

Using the PPLCNet-YOLOv5 model to directly detect the test video (containing a moving photovoltaic array and a moving laser spot), the detection results can be seen as shown in Figure 7. When the laser spot is located within the photovoltaic array region, it can be considered that a portion of the laser spot overlaps with the photovoltaic array. By using image processing methods, the position of the laser spot can be identified. The flowchart of the circle detection method is illustrated in Figure 8. The PV array’s region was segmented and processed for grayscale conversion, thresholding, and circle detection, yielding the fitted center coordinates.

Following the proposed alignment algorithm for the LWPT demonstration platform, the experiment was designed to validate the effectiveness of the neural network-based detection method. First, the stepper motor control program was developed and uploaded to the STM32 processor, enabling it to convert the gimbal displacement angles received from the upper computer into stepper motor control signals, thus facilitating gimbal movement. Subsequently, a Python program interfaced with the camera captured real-time images, which were fed into the trained PPLCNet-YOLOv5 detection network. This network identified the positions of the PV array and the laser spot, and the corresponding displacement angle for the gimbal was calculated using a coordinate transformation algorithm. The upper computer then sent displacement commands to the STM32, directing the gimbal to move towards the target position. The stepper motor’s stair-step control method allowed for small, incremental movements in both horizontal and vertical directions. This approach enabled the collection of fine-grained data within a small area, improving the accuracy of the coordinate transformation model’s calibration.

Figure 9 illustrates the results of an alignment experiment conducted both before and after the gimbal movement. Initially, as shown in Figure 9a, the laser spot was positioned below and to the left of the PV array. The image was processed by the detection algorithm, as depicted in Figure 9b, where bounding boxes for the PV array and the laser spot were generated. Circle detection then provided the center coordinates of the PV array and the laser spot, which were used to calculate the required gimbal displacement angle. After executing the movement, the final alignment result is shown in Figure 9d.

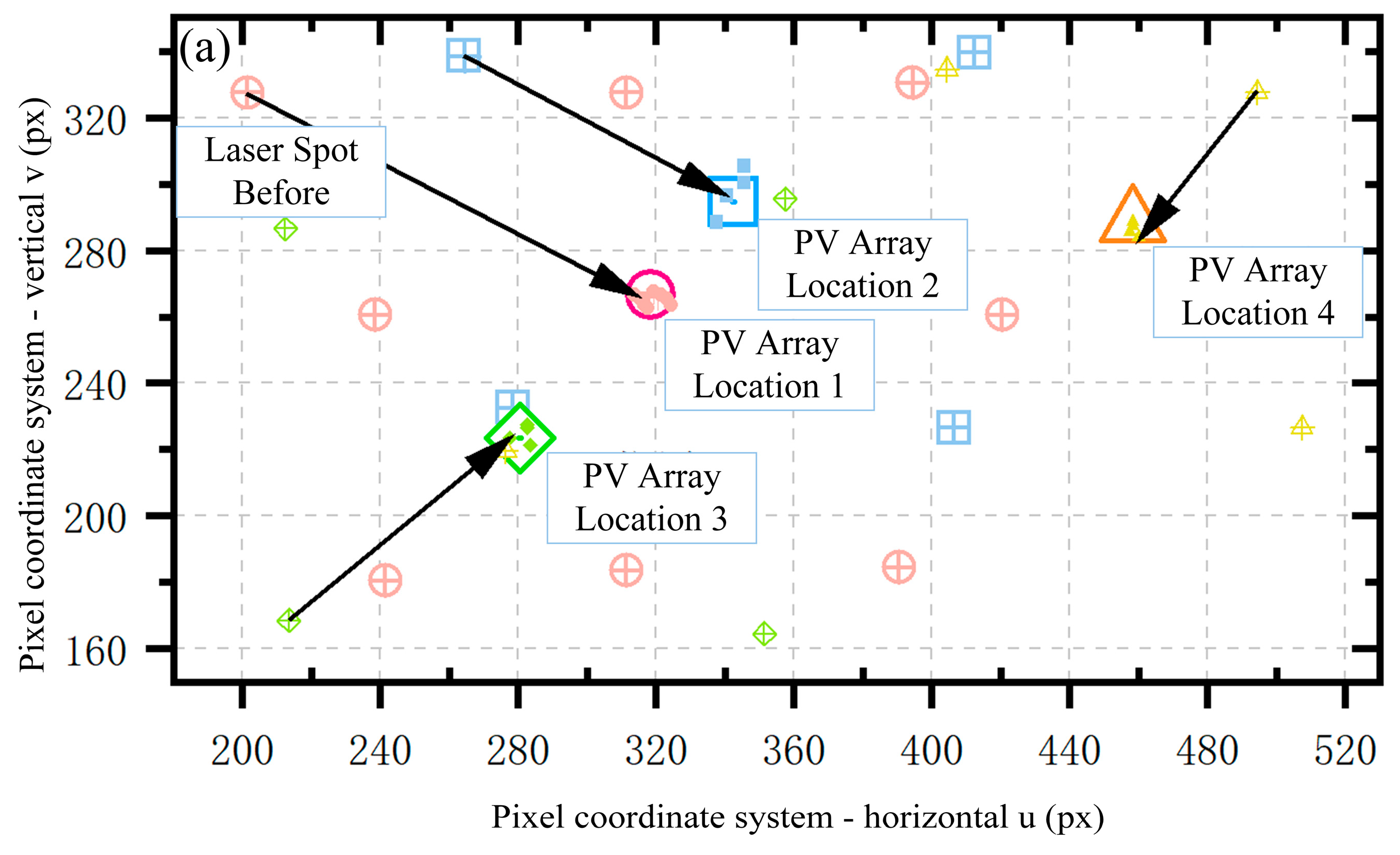
Multiple experiments were conducted with the PV array fixed in four different positions, generating a series of data as shown in

Table 1. Experimental results of alignment based on neural network target detection.

	Before				Rotation Angle		After		Error
	PV		Spot		Rotate	Pitch	NewSpot		Level	Vertical
	upv	vpv	uspot	vspot	α	β	upv1	vpv1	δu	δv
1	318.5	266.5	238.5	260.5	−3	0	317.5	266.5	−0.31	0.00
2			420.5	260.5	3.7	−0.2	317.5	262.5	−0.31	−1.52
3			311.5	327.5	−0.2	2.2	319.5	265.5	0.31	−0.38
4			311.5	183.5	−0.2	−3	319.5	265.5	0.31	−0.38
5			241.5	180.5	−2.8	−3.1	319.5	267.5	0.31	0.37
6			394.5	330.5	2.8	2.2	320.5	263.5	0.63	−1.14
7			201.5	327.5	−4.4	2.3	316.5	265.5	−0.63	−0.38
8			390.5	184.5	2.7	−3.1	320.5	263.5	0.63	−1.14
9	342.5	294.5	278.5	232.5	−2.3	−2.2	337.5	288.5	−1.46	−2.08
10			412.5	339.5	2.6	1.5	345.5	304.5	0.88	3.28
11			264.5	338.5	−2.9	1.7	345.5	300.5	0.88	2.00
12			406.5	226.5	2.4	−2.6	340.5	296.5	−0.58	0.67
13	280.5	223.5	213.5	168.5	−2.5	−1.9	283.5	221.5	1.07	−0.90
14			357.5	295.5	2.8	2.5	282.5	227.5	0.71	1.76
15			212.5	286.5	−2.5	2.3	277.5	223.5	−1.07	0.00
16			351.5	164.5	2.5	−2.3	282.5	226.5	0.71	1.32
17	458.5	288.5	276.5	219.5	−6.7	−2.4	460	284	0.33	−1.58
18			494.5	327.5	1.3	1.4	457.5	285.5	−0.22	−1.05
19			404.5	334.5	−2	1.7	458.5	288.5	0.00	0.00
20			507.5	226.5	1.8	−2.3	458.5	287.5	0.00	−0.35

. The table presents the pre-alignment pixel coordinates of the PV array and laser spot centers, the calculated displacement, the post-alignment laser spot center, and the horizontal and vertical alignment errors derived from the data. The alignment experiment showed that the pixel alignment errors were 0.57% horizontally and 1.02% vertically, demonstrating the efficacy of the proposed initial alignment method.

Based on the data presented in Table 1, the laser spot’s displacement toward the photovoltaic (PV) array and the corresponding error distribution were plotted, as illustrated in Figure 10. In Figure 10a, the centers of the four PV arrays are marked along with a 3% error zone. The initial positions of the laser spots, represented by hollow shapes, correspond to the same color as the solid shapes, indicating the final positions after alignment. Figure 10b depicts the horizontal and vertical errors observed during the alignment experiments.

Analyzing the experimental data and visual representations, it is evident that while some alignment errors exist, the average error varies depending on the PV array’s position. This variation is due to the non-uniform displacement on the target plane when the gimbal rotates by the same angle. Overall, the alignment errors are minor and remain within an acceptable range, demonstrating the effectiveness of the proposed alignment method.

3.3. Fine-Tuning Alignment Experiment Using Perturbation-Observation Method

In this section, we validate the efficiency of the optimal laser alignment algorithm proposed in Chapter 2 through a series of experiments. The algorithm was implemented on the built experiment platform, and the results were analyzed to demonstrate its effectiveness. In one of the fixed-step alignment experiments, the laser input current was set to 1.5 A, corresponding to an output optical power of approximately 8 W. When the laser beam fully covered the PV array, the array received an irradiance of around 890 W/m², with a fixed operating voltage of 7 V, yielding a maximum power output about 3.0 W. Therefore, the threshold power was set at 3.0 W.

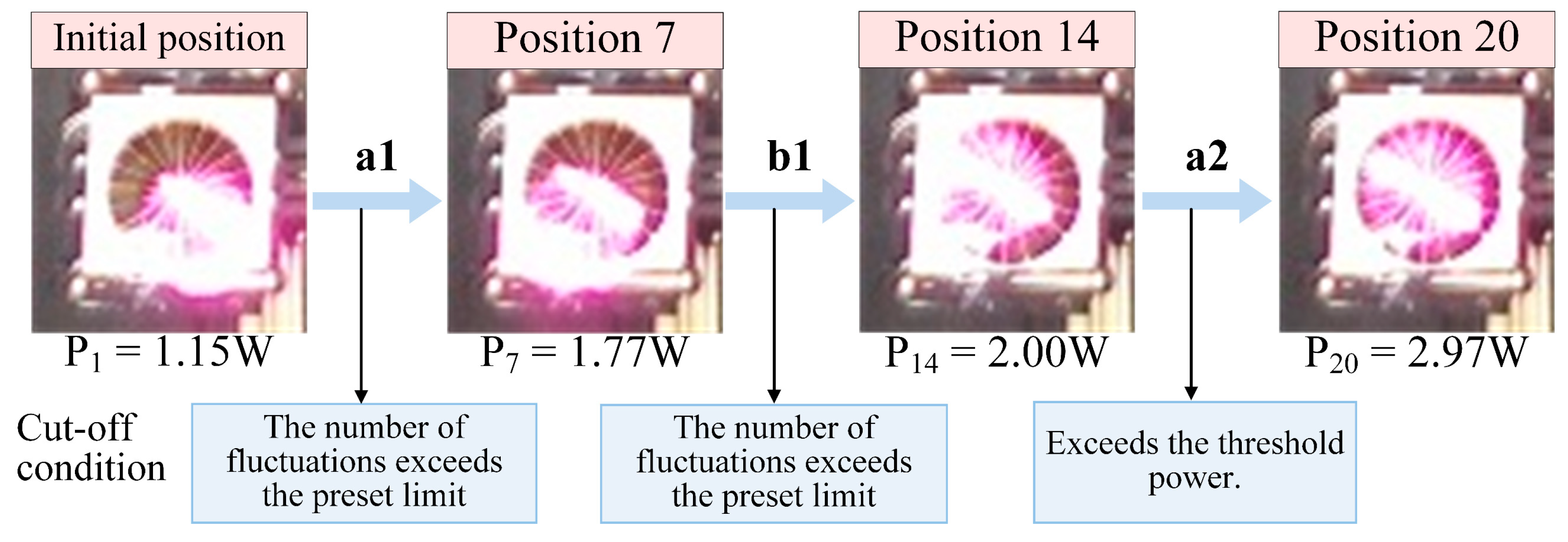
As shown in Figure 11, the laser spot initially appeared in the upper left corner of the PV array, with an initial power output of 0.79 W. The fixed-step size was set to 0.1°. The fixed-step laser alignment algorithm first adjusted the gimbal’s horizontal orientation, progressively moving the spot closer to the center. After two horizontal adjustments, the algorithm switched to vertical adjustments, making two more adjustments before stopping.

For comparison, the variable-step laser alignment algorithm was also implemented and tested, as shown in Figure 12. In this experiment, the laser spot started in the lower right corner of the PV array, with an initial power output of 1.15 W. The threshold power was again set at 3.0 W, with the large and small step sizes set at 0.1° and 0.03°, respectively. Horizontal adjustments with large steps were performed first, followed by vertical adjustments. After the large-step adjustments were completed, small-step adjustments were applied, eventually resulting in a power output exceeding the threshold, indicating that the optimal alignment was achieved.

Voltage, current, and power data were collected after each displacement, and the corresponding curves are presented in Figure 13. To ensure maximum power output, the PV array’s operating voltage was maintained at 7 V. The actual measured voltages from the PV array sensor ranged from 6.86 V to 7.17 V, with an average of approximately 7.07 V and a standard deviation of 0.089 V. The higher measured voltage compared to the preset value of 7 V is primarily due to the internal resistance of the connecting wires, which causes a slight voltage drop. This internal resistance is small, leading to a minor voltage difference, approximately 1/100 of the rated value, and can be considered negligible. Other possible causes of voltage fluctuations include the precision of the DC voltage sensor (approximately 0.5%) and the ripple in the laser power (approximately 0.5%).

The current and power output of the PV array increased as the gimbal adjustments progressed, with noticeable fluctuations towards the end of both horizontal and vertical adjustments. These fluctuations were influenced by the algorithm’s settings, which terminated the adjustments if the number of direction changes exceeded two.

The variable-step algorithm consistently outperformed the fixed-step method, achieving higher alignment precision and maximizing the PV array’s power output. When the laser input current was increased to 2 A, the variable-step method achieved an alignment rate close to 100%, compared to the lower alignment efficiency of the fixed-step method.

Table 2. Experimental results of alignment based on perturbation-observation method.

	Before				Regulate		After	Result
	Laser Diode		Relative Position		Threshold	Step	PV Power	Alignment Rate
	ilaser	Plaser	δu	δv	Pt	n	Pout	Po/Pt
1	1.5 A 8 W		left	up	3.0 W	19	2.90 W	96.67%
2			left	down		10	2.95 W	98.33%
3			right	up		12	3.00 W	100.00%
4			right	down		33	2.91 W	97.00%
5	1.7 A 12 W		left	up	4.3 W	28	4.23 W	98.37%
6			left	down		22	4.28 W	99.53%
7			right	up		32	4.10 W	95.35%
8			right	down		22	4.21 W	97.91%
9	1.9 A 17 W		left	up	5.6 W	27	5.58 W	99.64%
10			left	down		20	5.60 W	100.00%
11			right	up		35	5.40 W	96.43%
12			right	down		20	5.58 W	99.64%
13	2.1 A 22 W		left	up	7.3 W	29	7.29 W	99.86%
14			left	down		18	7.30 W	100.00%
15			right	up		25	7.18 W	98.36%
16			right	down		23	7.29 W	99.86%
17	2.3 A 26 W		left	up	9.0 W	28	8.78 W	97.56%
18			left	down		31	9.02 W	100.00%
19			right	up		26	8.96 W	99.56%
20			right	down		33	9.08 W	100.00%

shows the results under different laser input currents and different relative positions. The data demonstrate that the variable-step alignment algorithm not only achieves higher precision but also optimizes the energy received by the PV array, leading to maximum PV array power output.

Furthermore, the algorithm’s robustness was tested by manually perturbing the laser spot position and using the variable-step alignment method to realign. The results, as shown in Table 2, confirm that the algorithm consistently achieves optimal alignment, with an average alignment rate of 98.70%. While only two step sizes were used in this experiment, adding more steps or reducing the smaller step size could further enhance alignment precision, albeit at the cost of increased time and complexity.

4. Discussion

The experiments conducted validate the effectiveness of the proposed alignment method, which combines neural network-based target detection with a perturbation-observation technique. The initial alignment phase successfully detected the relative positions of the PV array and the laser spot, allowing for precise calculation of the gimbal’s rotation and tilt angles. The resulting alignment achieved horizontal and vertical pixel average errors of 0.57% and 1.02%, respectively, translating to a physical error of approximately 7 mm on the experimental platform. The detection process achieved a frame rate of 5 FPS, demonstrating efficient real-time processing within the constraints of the system.

Following the initial alignment, the perturbation-observation method was employed to fine-tune the alignment. By introducing small adjustments to the gimbal angles and observing the resulting changes in the PV array’s output power, the system was able to iteratively refine the laser spot’s position. The final alignment accuracy was limited by the smallest gimbal adjustment step, set at 0.3° (approximately 3 mm). Despite potential fluctuations in laser power due to ripple effects (ranging from 0.5% to 1%), the system effectively achieved a high degree of alignment, with the PV array averaging outputting 98.70% of its maximum historical power.

The initial alignment using the PPLCNet-YOLOv5 neural network achieves a detection speed of approximately 3–5 FPS, with the total initial alignment time being around 0.3 s. The precision alignment via the perturbation-observation method involves multiple iterations, with the time taking longer than the initial alignment. In one example, it took 20 steps to reach the optimal alignment point, with each step including data collection, wireless communication, and gimbal adjustment. The method is primarily suitable for static or quasi-static conditions. Fine adjustments based on PV array information can improve alignment accuracy and adapt to target position disturbances. To enhance the speed, optimizations such as using faster GPUs, reducing PV array power detection intervals, and increasing gimbal movement speed can be implemented. However, for highly dynamic targets, significant interference may cause mismatches in the perturbation-observation method, leading to alignment failures. For high-dynamic scenarios, it may be possible to use a tracking algorithm based on Kalman filter to predict the target position and achieve tracking of highly dynamic targets.

The neural network-based detection method eliminates the need for additional optical components such as mirrors or photodetectors, making it particularly suitable for LWPT applications. The two-step alignment process, leveraging the PPLCNet-YOLOv5 architecture, achieves initial pixel errors below 3%, corresponding to a physical error of approximately 7 mm. During fine-tuning, the perturbation-observation method ensures precise alignment, maximizing the PV array’s power output close to its theoretical maximum. These findings demonstrate the robustness and efficiency of the proposed alignment method, making it a viable solution for enhancing the accuracy and effectiveness of LWPT systems.

5. Conclusions

This paper introduced and validated a laser alignment method for LWPT systems, integrating a neural network-based target detection approach with a perturbation-observation technique. The proposed method demonstrated significant advantages over traditional approaches by achieving initial alignment with minimal pixel errors, which corresponded to an acceptable physical alignment accuracy of approximately 7 mm on the experimental platform. Subsequent fine-tuning using the perturbation-observation method further enhanced alignment precision, resulting in a photovoltaic array power output of 98.70% of its historical maximum.

The results of this research highlight the effectiveness and efficiency of the two-step alignment process, which not only simplifies the system design by eliminating the need for additional optical components, but also achieves high alignment accuracy. Moreover, the robust performance of the method under varying operational conditions underscores its potential for practical application in LWPT systems. This innovative alignment strategy offers a reliable solution for enhancing energy transfer efficiency and overall system performance, paving the way for advanced implementations in the field of wireless power transmission.