Analysis of Randomization Capacity in Quantum Noise Randomized Cipher System

Abstract

We propose and verify a method for analyzing the randomization capacity in a 160 km quantum noise randomized cipher system with different data modulation formats. The randomization capacity is defined as the difference in mutual information between Alice and Bob while the randomization level is at 0 and at its maximum, under the condition of error-free transmission. Our experimental analysis examines the capacity of quantum noise randomized cipher systems under different optical signal-to-noise ratios for each modulation format. Additionally, we analyze the noise masking values while the randomization reaches its capacity. The experimental results indicate that the binary phase shift-keying-based quantum noise randomized cipher system achieves the highest randomization capacity and highest noise masking value.

1. Introduction

Physical-layer security in optical networks is crucial as they face threats that may disrupt services or allow access to confidential data without authorization [1]. The quantum key distribution (QKD) is proposed as a method to stand against these threats [2]. Although QKD can provide unconditional physical-layer security, it suffers from technical imperfections, which pose great challenges to the rates of key generation and transmission distances. QKD has seen breakthroughs in extending secure transmission distances [3] and increasing secret key rates [4]. However, these schemes still require complex equipment to achieve. Compared to QKD, quantum secure direct communication (QSDC) has the advantage of immediacy, as it does not require key establishment before information transmission [5]. Yet, its practical application is limited by the current technological constraints of quantum memory and quantum repeaters. Quantum digital signatures (QDSs) offer a promising approach for the future of digital signatures and data integrity [6,7]. Nevertheless, implementing QDSs requires advanced quantum communication infrastructure, including stable QKD systems and controlled quantum networks. Quantum noise stream cipher (QNSC) is proposed to overcome these challenging implementation difficulties [8,9,10,11,12,13,14,15,16]. It allows high transmission rates and long distances since the encoding and decoding are performed in digital signal processing (DSP). The security is protected by the quantum noise in the transmission system. Many experiments have been reported for different modulation formats in QNSC, such as phase shift-key (PSK) [8], quadrature amplitude modulation (QAM) [9,10,11,12] and intensity modulation (IM) [9,10,11].

To further enhance the security of QNSC, the technique of quantum noise randomized cipher (QNRC) has been developed. It increases the noise masking by applying randomization in the QNSC symbol. There have been reports of both theoretical and experimental studies related to the QNRC system [14,15,16,17,18,19,20,21,22]. Recently, the randomization scheme driven by optical temporal scrambling has been proposed [14]. Moreover, applying a chaotic system as a random source is also an effective method to enhance the QNRC [15,16,17,18,19]. All these schemes need a pseudo/true-random number generator as a randomization source for QNRC. Although randomization has shown advantages in enhancing the security of QNRC, existing studies have pointed out that high levels of randomization may significantly decrease transmission performance. Moreover, existing studies have rarely analyzed the limiting capacity of randomization under various conditions. Therefore, it is essential to conduct a quantitative capacity analysis of randomization in QNRC to determine the maximal level of randomization that can ensure both high security and high transmission performance.

In this paper, we propose a capacity analysis method for randomization in QNRC and verify it in 160 km BPSK/QNRC, QPSK/QNRC and 16QAM/QNRC transmission systems. Compared to existing methods, our approach offers unique advantages in analyzing randomization capacity: it enables quantification of system randomization capacity across different modulation formats and optical signal-to-noise ratios, thereby assessing the maximum level of randomization that ensures both high security and transmission performance. Experimental results demonstrate that the BPSK-based 2^M QNRC system has the best capacity performance for randomization. And a higher M leads to a lower capacity. Moreover, BPSK has the highest value of noise masking while the system’s randomization level reaches its capacity.

In the following sections, this paper provides a structured analysis of the randomization capacity in QNRC systems. Section 2 introduces the principle of QNRC, explaining the encryption schemes and randomization techniques utilized for different data modulation formats. In Section 3, we present a detailed mathematical framework for calculating randomization capacity across various modulation schemes, including BPSK, QPSK, 16QAM and IM. Section 4 describes the experimental setup used to evaluate QNRC performance over a 160 km optical fiber link and discusses the results, highlighting the security and randomization capacity trade-offs under different conditions. Finally, Section 5 concludes the paper by summarizing key findings and suggesting future directions.

2. Principle of QNRC

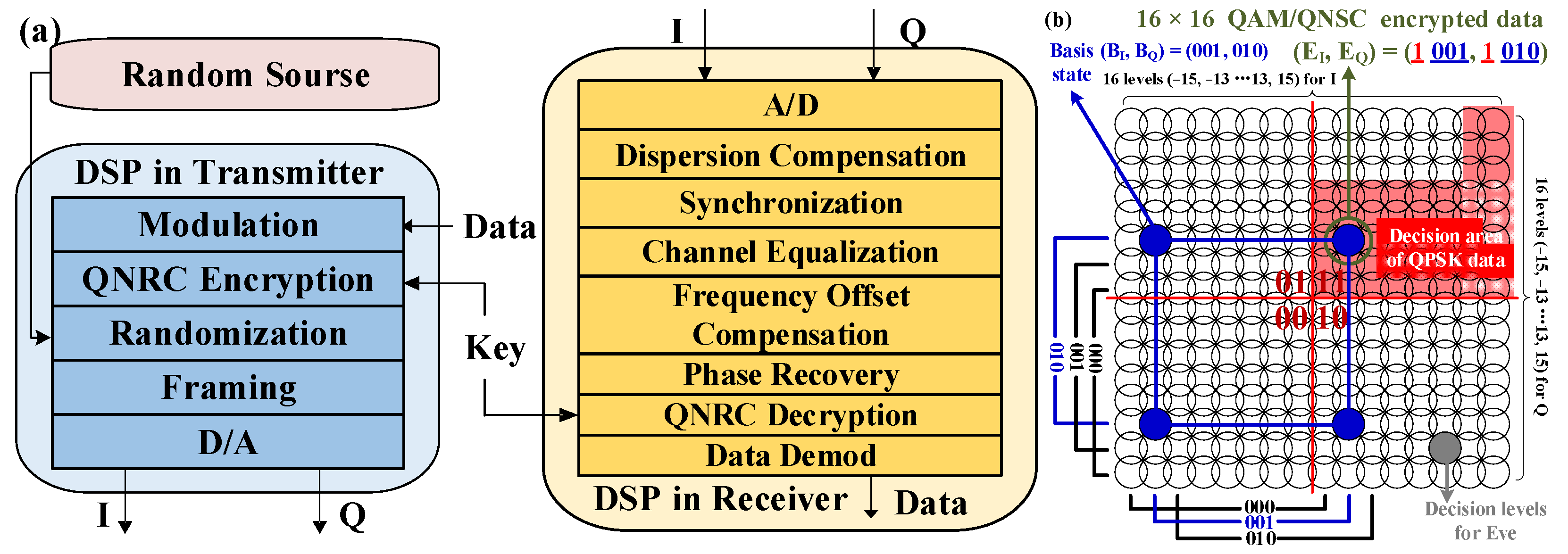
Figure 1 shows the DSP module in QNRC at the transmitter and receiver. For QPSK/QNRC and 16QAM/QNRC, the original data stream is firstly mapped into QPSK or 16QAM symbols at the transmitter. Secondly, the randomized signal is encrypted into QAM format with QNRC. In detail, the encrypted QAM is, respectively, generated by 1-bit QPSK or 2-bit 16QAM signal xor M-bit basis (which uses keys generated by pseudo-random number generator (PRNG) and is pre-synchronized by Alice and Bob) in I and Q modes. The encryption rule is also shared by Alice and Bob. The modulation format of such encrypted data is 2^M × 2^M QAM. The mapping rule of QNRC is natural binary mapping instead of gray mapping. Therefore, 2-bit or 4-bit (I + Q) is hidden in one encrypted QAM symbol and the correct decision level of the signal for Eve is covered with quantum noise. Similarly, BPSK or IM symbols can also be encrypted into 2^M BPSK/QNRC or 2^M IM/QNRC symbols. As an example, the constellation of 16 × 16 QAM/QNRC is shown in Figure 1b, where QPSK (1 bit for I and Q, respectively) data are encrypted by using $2\times 2^3$ basis states (3 bits for I and Q, respectively). We use 2-bit information data $S_I=0$, $S_Q=1$ and 6-bit basis $B_I=\left(b_{I3}{b}_{I2}{b}_{I1}\right)=001$, $B_Q=\left(b_{Q3}{b}_{Q2}{b}_{Q1}\right)=010$ to generate 8-bit encrypted data $E_I=\left(S_I\oplus b_{I2}{b}_{I1}, B_I\right)=1001$, $E_Q=\left(S_Q\oplus b_{Q2}{b}_{Q1}, B_Q\right)=1010$. The encrypted binary information $E_I$ and $E_Q$ are converted into decimal constellation levels $L_I$ and $L_Q$. Then, we apply scrambling to $L_I$ and $L_Q$ as follows: $\left(L_I\prime ,L_Q\prime \right)=\left(L_I+i,L_Q+q\right)$, where $i$ and $q$ are randomized perturbations with a standard deviation of $\gamma$. Meanwhile, $i$ and $q$ are determined based on random numbers from a random source. Similarly, this disturbance manifests in the phase for BPSK and in the optical intensity for IM. Our previous work demonstrated an integrating key distribution scheme based on the physical layer of optical fibers. The generated keys have been proven to exhibit good randomness, which can be used as a random source for QNRC [23,24,25]. Finally, training sequences and pilots are inserted into randomized I/Q signals for transmission.

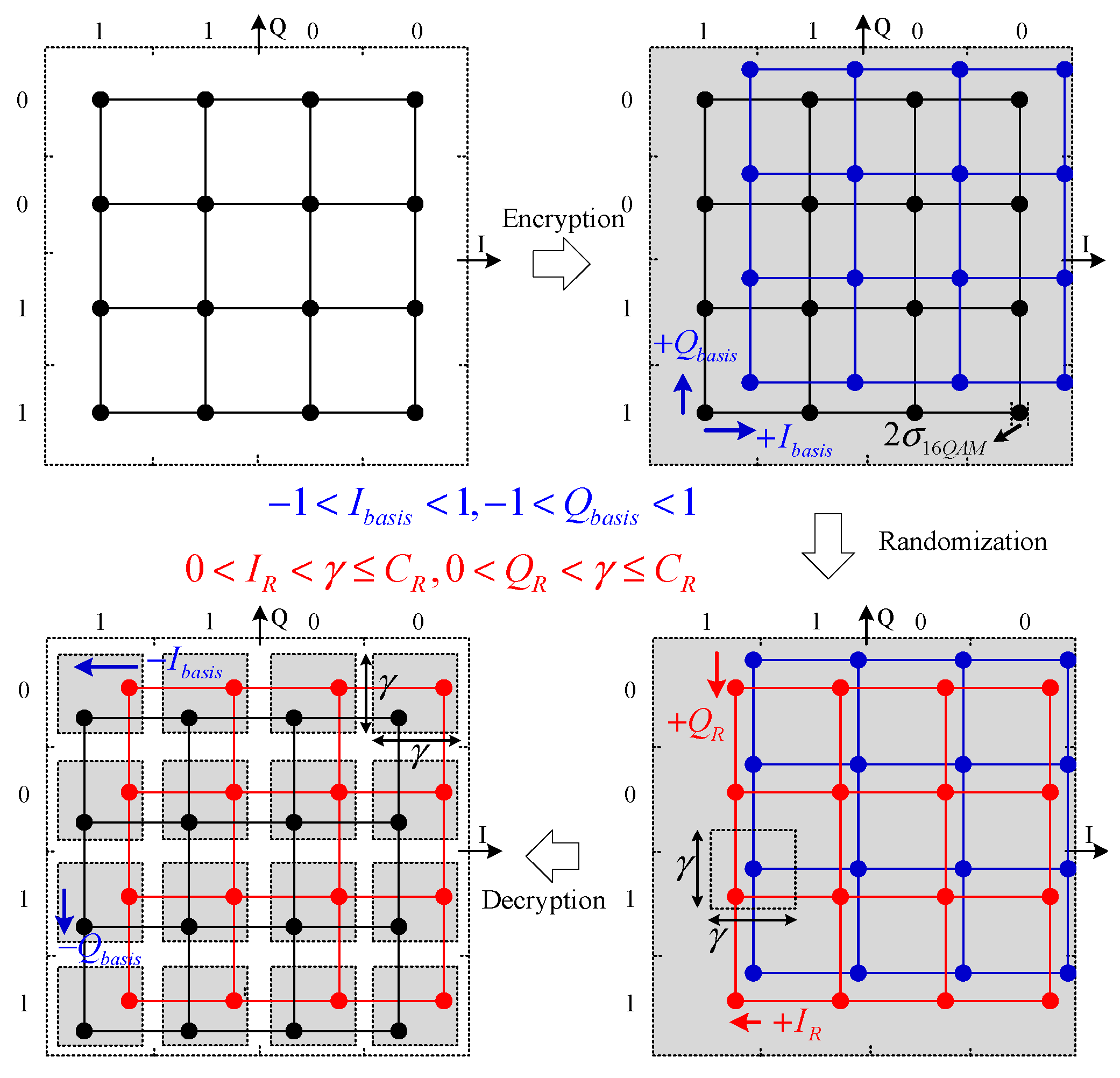
Figure 2 shows the principle of randomization in QNRC for different data modulation. The blue and pink areas represent the noise masking range before and after randomization, respectively. The effect of randomization directly appears as the increase in the noise masking and the decrease in Bob’s receiver performance. Nevertheless, Bob can receive the data correctly as long as γ is below a critical level. This fact leads us to the motivation of capacity analysis of randomization.

3. Randomization Capacity

The capacity of randomization (C_R) is defined as the difference in mutual information between Alice and Bob between $\gamma =0$ and maximal γ. The value of maximal γ is obtained when the bit error rate (BER) of Bob reaches the forward error correction (FEC) threshold P_th. The specific calculation method of mutual information in BPSK and IM (N-level) is shown in Equations (1) and (2).

$$I_0\left(y;x\right)=H\left(y\right)-H\left(\left.y\right|x\right),$$

(1)

$$I_{th}\left(y;x\right)=H\left(y\right)+P_{th}{\log }_2{P}_{th}+\left(1-P_{th}\right){\log }_2\left(1-P_{th}\right),$$

(2)

where x is the data from Alice before transmission, y is the data received by Bob. C_R is related to I₀ and I_th based on Equations (1) and (2). I₀ represents the mutual information between Alice and Bob without randomization. A higher value of I indicates better system transmission performance, which is influenced by factors such as system noise and optical fiber nonlinearity. Meanwhile, I_th represents the mutual information between Alice and Bob with randomization while BER reaches P_th. The value of I_th depends on P_th. It can be observed that the C_R of the system increases as the system transmission performance improves or a more powerful FEC algorithm with a higher threshold P_th is employed. C_R for BPSK and IM is as Equation (3) to Equation (5).

$$H\left(y\right)=-{\displaystyle \sum _{y=0}^{1}P\left(y\right)}{\log }_{2}P\left(y\right),$$

(3)

$$H\left(y\left|x\right.\right)=-{\displaystyle \sum _{x=0}^1{\displaystyle \sum _{y=0}^{1}P\left(x\right)}P\left(y\left|x\right.\right){\log }_{2}P\left(y\left|x\right.\right)},$$

(4)

$$C_R={\left[I_0\left(y;x\right)-I_{th}\left(y;x\right)\right]}_{P\left(x\right)={\displaystyle \frac{1}{N}}},$$

(5)

Similarly, the calculation methods of mutual information and C_R in QPSK and 16QAM (N × N-level), are given, respectively, by Equation (6) to Equation (10).

$$I_0\left(y_I,y_Q;x_I,x_Q\right)=H\left(y_I,y_Q\right)-H\left(\left.y_I,y_Q\right|x_I,x_Q\right),$$

(6)

$$I_{th}\left(y_I,y_Q;x_I,x_Q\right)=H\left(y_I,y_Q\right)+P_{th}^2{\log }_2{P}_{th}^2+{\left(1-P_{th}\right)}^2{\log }_2{\left(1-P_{th}\right)}^2+2P_{th}\left(1-P_{th}\right){\log }_2{P}_{th}\left(1-P_{th}\right),$$

(7)

$$H\left(y_I,y_Q\right)=-{\displaystyle \sum _{y_I=0}^1{\displaystyle \sum _{y_Q=0}^{1}P\left(y_I,y_Q\right)}{\log }_{2}P\left(y_I,y_Q\right)},$$

(8)

$$H\left(y_I,y_Q\left|x_I,x_Q\right.\right)=-{\displaystyle \sum _{x_I=0}^1{\displaystyle \sum _{x_Q=0}^1{\displaystyle \sum _{y_I=0}^1{\displaystyle \sum _{y_Q=0}^{1}P\left(x_I,x_Q\right)}}}}P\left(y_I,y_Q\left|x_I,x_Q\right.\right){\log }_{2}P\left(y_I,y_Q\left|x_I,x_Q\right.\right),$$

(9)

$$C_R={\left[I_0\left(y_I,y_Q;x_I,x_Q\right)-I_{th}\left(y_I,y_Q;x_I,x_Q\right)\right]}_{P\left(x_I,x_Q\right)={\displaystyle \frac{1}{N^2}}},$$

(10)

3.1. C_R in BPSK/QNRC

The principle of QNRC differs when data modulation is varied. Hence, the calculation method of C_R is also different for QNRC in different data modulations. Figure 3 shows the principle of BPSK-based QNRC. Data are encrypted by rotating the phase of BPSK with θ_basis. After encryption, the constellation becomes a high-order PSK signal. Subsequently, a truly random phase randomization of θ_R is added to the signal. The range of randomization is γ and it has a maximum value of C_R. The randomization increases in the noise masking. In the receiver, only θ_basis is subtracted with the pre-shared key. And the effect of randomization decreases Bob’s receiver performance.

The noise masking Γ is commonly considered as an evaluation index of security in the QNRC system. In 2^M BPSK/QNRC, the average phase noise $\Delta \overline{\Phi }$ is defined as Equation (11). The Γ_BPSK is given as Equation (12).

$$\Delta \overline{\Phi }=\sqrt{{\displaystyle \frac{1}{2^M}}{\displaystyle \sum _{n=1}^{2^M}\Delta {\Phi }_n^2}},$$

(11)

$${\Gamma }_{BPSK}=\left(\Delta \overline{\Phi }+\gamma \right)/\Delta \theta ,\Delta \theta =\pi /2^{M-1},$$

(12)

The calculation of the bit error ratio for the M-th bit position is as Equation (13). The M-th bit has the lowest bit error rate among 1-st to M-th bits in the 2^M BPSK/QNRC symbol. It is used for data transmission [10].

$$R_{M-BPSK}={\displaystyle \frac{1}{2^{M-1}}}{\displaystyle \sum _{i=0}^{\begin{array}{l}{2}^{M-2}\\ -1\end{array}}\left\{\frac{1}{2}erfc\left[\frac{\sin \left(i\cdot \pi /2^{M-1}\right)}{\sqrt{2}\Delta \overline{\Phi }/2}\right]\right\}},$$

(13)

Appling R_M-BPSK in Equation (5), C_R in BPSK/QNRC is shown as follows:

$$C_{R-BPSK}=R_{M-BPSK}{\log }_2{R}_{M-BPSK}+\left(1-R_{M-BPSK}\right){\log }_2\left(1-R_{M-BPSK}\right)-P_{th}{\log }_2{P}_{th}-\left(1-P_{th}\right){\log }_2\left(1-P_{th}\right),$$

(14)

3.2. C_R in QPSK/QNRC

Figure 4 shows the principle of QPSK-based QNRC. Data are encrypted by translating the amplitude of QPSK with I_basis and Q_basis in the I/Q channel, respectively. After encryption, the constellation becomes a high-order QAM signal. Subsequently, a truly random amplitude randomization of I_R and Q_R is added to the signal in the I/Q channel. In the receiver, only I_basis and Q_basis are subtracted with the pre-shared key.

In QPSK/QNRC, we define the average noise standard deviation ${\overline{\sigma }}_{QPSK}$ as Equation (15). The Γ for each channel of 2^M × 2^M QPSK/QNRC (I or Q) is given as Equation (16).

$${\overline{\sigma }}_{QPSK}=\sqrt{{\displaystyle \frac{1}{2\times 4}}{\displaystyle \sum _{n=1}^4\left({\sigma }_{I,n}^2+{\sigma }_{Q,n}^2\right)}},$$

(15)

$${\Gamma }_{QPSK}=2\left({\overline{\sigma }}_{QPSK}+\gamma \right)/\Delta ,\Delta =2/\left(2^M-1\right),$$

(16)

The calculation of the bit error ratio for M-th bit position in 2^M × 2^M QPSK/QNRC symbol (I or Q) is as Equation (17) [10].

$$R_{M-QPSK}={\displaystyle \frac{1}{2^{M-1}}}{\displaystyle \sum _{h=0}^{\begin{array}{l}{2}^{M-1}\\ -1\end{array}}\left[\frac{1}{2}erfc\left(\frac{2^M-1-2h}{\sqrt{2}{\Gamma }_{QPSK}}\right)\right]},$$

(17)

Hence, in terms of Equation (10), C_R in 2^M × 2^M QPSK/QNRC is shown as follows:

$$\begin{array}{l}{C}_{R-QPSK}=R_{M-QPSK}^2{\log }_2{R}_{M-QPSK}^2+{\left(1-R_{M-QPSK}\right)}^2{\log }_2{\left(1-R_{M-QPSK}\right)}^2+2R_{M-QPSK}\left(1-R_{M-QPSK}\right){\log }_2{R}_{M-QPSK}\left(1-R_{M-QPSK}\right)\\ -P_{th}^2{\log }_2{P}_{th}^2-{\left(1-P_{th}\right)}^2{\log }_2{\left(1-P_{th}\right)}^2-2P_{th}\left(1-P_{th}\right){\log }_2{P}_{th}\left(1-P_{th}\right),\end{array}$$

(18)

3.3. C_R in 16QAM/QNRC

Figure 5 shows the principle of 16QAM-based QNRC. The operation of encryption, decryption and randomization by translating the amplitude is similar to that of QPSK/QNRC. Yet, the encrypted data represents 16QAM instead of QPSK.

Similar to 2^M × 2^M QPSK/QNSC, the average noise standard deviation and Γ in 2^M × 2^M 16QAM/QNRC are as shown in Equations (19) and (20).

$${\overline{\sigma }}_{16QAM}=\sqrt{{\displaystyle \frac{1}{2\times 16}}{\displaystyle \sum _{n=1}^{16}\left({\sigma }_{I,n}^2+{\sigma }_{Q,n}^2\right)}},$$

(19)

$${\Gamma }_{16QAM}=2\left({\overline{\sigma }}_{16QAM}+\mathsf{\gamma }\right)/\mathsf{\Delta },\mathsf{\Delta }=2/\left(2^M-1\right),$$

(20)

In 2^M × 2^M 16QAM/QNRC, M-th and M − 1-th bit in each symbol of the I/Q channel is used for data transmission. Their bit error ratios are shown in Equation (21) and Equation (22), respectively.

$$R_{M-16QAM}={\displaystyle \frac{1}{2^{M-1}}}{\displaystyle \sum _{h=0}^{\begin{array}{l}{2}^{M-1}\\ -1\end{array}}\left[\frac{1}{2}erfc\left(\frac{2^M-1-2h}{\sqrt{2}{\Gamma }_{16QAM}}\right)\right]},$$

(21)

$$R_{M-1-16QAM}={\displaystyle \frac{1}{2^{M-1}}}{\displaystyle \sum _{h=0}^{\begin{array}{l}{2}^{M-2}\\ -1\end{array}}\left\{{\displaystyle \sum _{j=0}^1\left[{\displaystyle \sum _{i=1}^{3-2j}{\left(-1\right)}^{i+1}\frac{1}{2}erfc\left(\frac{i{2}^{M-1}-1-2h}{\sqrt{2}{\Gamma }_{16QAM}}\right)}+{\displaystyle \sum _{i=1}^{2j}{\left(-1\right)}^{i+1}\frac{1}{2}erfc\left(\frac{i{2}^{M-1}-1-2h}{\sqrt{2}{\Gamma }_{16QAM}}\right)}\right]}\right\}},$$

(22)

While $\overline{R}=\left(R_{M-16QAM}+R_{M-1-16QAM}\right)/2$, as Equation (10), C_R in 2^M × 2^M 16QAM/QNRC is calculated as follows:

$$\begin{array}{l}{C}_{R-16QAM}={\overline{R}}^2{\log }_2{\overline{R}}^2+{\left(1-\overline{R}\right)}^2{\log }_2{\left(1-\overline{R}\right)}^2+2\overline{R}\left(1-\overline{R}\right){\log }_2\overline{R}\left(1-\overline{R}\right)-P_{th}^2{\log }_2{P}_{th}^2-{\left(1-P_{th}\right)}^2{\log }_2{\left(1-P_{th}\right)}^2\\ -2P_{th}\left(1-P_{th}\right){\log }_2{P}_{th}\left(1-P_{th}\right),\end{array}$$

(23)

3.4. C_R in IM/QNRC

Figure 6 shows the principle of IM-based QNRC. Data are encrypted by adjusting the intensity with P_basis. After encryption, the constellation becomes a high-order IM signal. Subsequently, a truly random intensity randomization of P_R is added to the signal. In the receiver, only the P_basis is subtracted with the pre-shared key.

The average noise standard deviation and Γ in 2^M IM/QNRC are as shown in Equations (24) and (25).

$${\overline{\sigma }}_{IM}=\sqrt{{\displaystyle \frac{1}{2^M}}{\displaystyle \sum _{n=1}^{2^M}{\sigma }_n^2}},$$

(24)

$${\Gamma }_{IM}={\displaystyle \frac{\left(2^M-1\right)\left(r+1\right)}{r-1}}\left({\overline{\sigma }}_{IM}+\gamma \right),$$

(25)

$r=P_{2^M}/P_1$ and P_m is the intensity level of 2^M IM/QNRC (1 ≤ m ≤ 2^M). The calculation of the bit error ratio for the M-th bit position in the 2^M IM/QNRC symbol is as Equation (26). Hence, as claimed by Equation (5), C_R in 2^M IM/QNRC is shown as Equation (27).

$$R_{M-IM}={\displaystyle \frac{1}{2^{M-1}}}{\displaystyle \sum _{h=0}^{\begin{array}{l}{2}^{M-1}\\ -1\end{array}}\left[\frac{1}{2}erfc\left(\frac{2^M-1-2h}{\sqrt{2}{\Gamma }_{IM}}\right)\right]},$$

(26)

$$C_{R-IM}=R_{M-IM}{\log }_2{R}_{M-IM}+\left(1-R_{M-IM}\right){\log }_2\left(1-R_{M-IM}\right)-P_{th}{\log }_2{P}_{th}-\left(1-P_{th}\right){\log }_2\left(1-P_{th}\right),$$

(27)

4. Experiment Setup and Results Analysis

Figure 7 shows the experiment setup of 2^M BPSK/QNRC, 2^M IM/QNRC, 2^M × 2^M QPSK/QNRC, and 2^M × 2^M 16QAM/QNRC. At the transmitter, the data are converted by an arbitrary waveform generator (AWG) to an electrical signal at the sampling rate of 10-GSa/s and a digital analog converter (DAC) of 12 bits. An external cavity laser (ECL) sends a beam at 1550 nm with 6 dBm power into an electro-optical converter. For BPSK/QNRC, QPSK/QNRC, and 16QAM/QNRC, the electro-optical conversion is achieved by an I/Q modulator. While an intensity modulator is used in the electro-optical conversion of IM/QNRC. After the variable optical attenuator (VOA), the signal is loaded onto the 160 km (80 km × 2) standard single-mode fiber (SSMF) with an attenuation of 0.2 dB/km.

At the receiver, the received OSNR is measured by an optical spectrum analyzer. The received optical signal is amplified into 0 dBm, and then transformed into an electrical signal by an optical-electro converter. For BPSK/QNRC, QPSK/QNRC, and 16QAM/QNRC, the optical-electro conversion is achieved by a coherent receiver which is combined with a local oscillator. While in IM/QNRC, a photoelectric detector is used for optical-electro conversion. The received electrical signals are captured by a digital oscilloscope.

Figure 8a shows the C_R in QNRC (M = 8) with different data modulation for OSNR from 1 dB to 25 dB. In our QNRC system with M = 8, higher OSNR values lead to higher C_R values. The soft-decision FEC (SD-FEC) with low-density parity-check codes we used has a threshold P_th of 4 ×10⁻². Consequently, the maximum achievable C_R in our system is 0.242. This value can be further improved by using a more powerful SD-FEC algorithm. However, it will increase the computational complexity of the receiver. For BPSK, QPSK, 16QAM, IM (r = 3) and IM (r = 2) data modulations, the C_R exceeds 0 at OSNR values of above 0, 6, 10, 14 and 17 dB, respectively. Moreover, the C_R reaches 0.242 at OSNR values of above 7, 13, 17, 21 and 24 dB, respectively. These results suggest that BPSK modulation provides the best capacity performance for randomization compared to other data modulations in the QNRC system with M = 8.

Figure 8b illustrates the C_R performance of 2^M × 2^M 16QAM/QNRC for various OSNR values. For M = 6, 7, 8, 9 and 10, the C_R exceeds 0 at OSNR values of above 5, 8, 10, 12, and 12 dB, respectively. Additionally, the C_R reached 0.242 at OSNR values of above 12, 14, 17, 19, and 20 dB for M = 6, 7, 8, 9 and 10, respectively. Meanwhile, C_R increases as the increase in OSNR and a higher M leads to a lower C_R value. This result is due to the increased complexity of the QAM modulation scheme at higher values of M, which makes the transmission more susceptible to noise and impairments.

Figure 9a presents the values of Γ for QNRC (M = 8) when the system reaches C_R at different OSNR levels. Despite the increase in OSNR, the value of Γ remained relatively stable when the system achieved C_R. However, the choice of data modulation scheme has a significant impact on the value of Γ when the system reaches C_R. For instance, we found that Γ was 283.68, 54.76, 48.49, 134.34, and 142.34 for BPSK, IM (r = 2), IM (r = 3), 16QAM and QPSK while $OSNR=10 \mathrm{dB}$, respectively. These findings demonstrate that BPSK has the highest value of Γ when the randomization reaches C_R. It is worth noting that the value of Γ provides a useful metric for evaluating the security of QNRC [9].

Figure 9b shows the Γ and 1-DFP for QPSK/QNRC (M = 8) with or without randomization in different OSNR. Detection failure probability (DFP) refers to the probability that Eve (an eavesdropper) fails to detect the QNRC symbol that is masked by noise. This measure is often used to evaluate the security level of QNRC systems [8,9,10,11,12,13,14,15,16,17,18]. The calculation method for the DFP of QPSK/QNRC is presented in Equation (28).

$$DFP=1-\left\{1-\left[{\displaystyle \frac{2^M-1}{2^M}}erfc\left({\displaystyle \frac{1}{\sqrt{2}{\Gamma }_{QPSK}}}\right)\right]\right\}$$

(28)

It can be observed that the noise masking number, Γ, for QPSK/QNRC decreases as OSNR increases. This is due to the fact that high OSNR diminishes the effectiveness of noise masking, thereby compromising the security of the system [9,20]. However, the introduction of randomization raises the value of Γ. When the level of randomization reaches the system’s tolerance C_R, for OSNR is 15 dB, Γ increases from 4.56 to 48.60. Meanwhile, 1 − DFP decreases from 3.19 × 10⁻² to 4.47 × 10⁻⁴. The results indicate that the introduction of randomization increases the probability of Eve failing to detect the QNRC symbols, thereby enhancing the security of the QNRC system.

5. Conclusions

In this article, we propose a randomization capacity analysis method for QNRC and verify it in 160 km BPSK/QNRC, QPSK/QNRC, 16QAM/QNRC, and IM/QNRC transmission systems. The experimental results demonstrate that the BPSK-based 2^M QNRC system performs best in terms of capacity performance for randomization. Our findings also suggest that higher modulation orders (M) of QNRC lead to lower capacity, highlighting the trade-off between security and randomization capacity. Additionally, we show that BPSK has the highest value of Γ, which indicates that it is the most secure and effective modulation scheme for randomization when the system reaches its capacity limit. However, this randomization method also has certain limitations. For example, as the modulation order increases (such as with a higher M value), the randomization capacity decreases. This is because higher-order modulation formats are more sensitive to noise and system impairments under complex transmission conditions. For future research, further exploration could focus on enhancing QNRC systems with advanced error correction techniques to improve capacity and security in higher-order modulation schemes. Additionally, investigating alternative randomization sources, such as quantum-based random number generators, may provide increased randomness and robustness [26,27].