Simple Direct Measurement of the Orbital Stokes Parameters in Structured Vortex Beams
Abstract
1. Introduction
2. The Second-Order Intensity Moment Matrix
2.1. Preliminary Theoretical Background
2.2. Stokes Representation
2.3. Mapping onto the Orbital Poincar é Sphere
3. Direct Measurement of the Orbital Stokes Parameters
3.1. Choosing the Measurement of the Third Orbital Stokes Parameter
3.2. The Reciprocity Effect Between the OAM and the Cross-Matrix Element
3.3. The Experiment
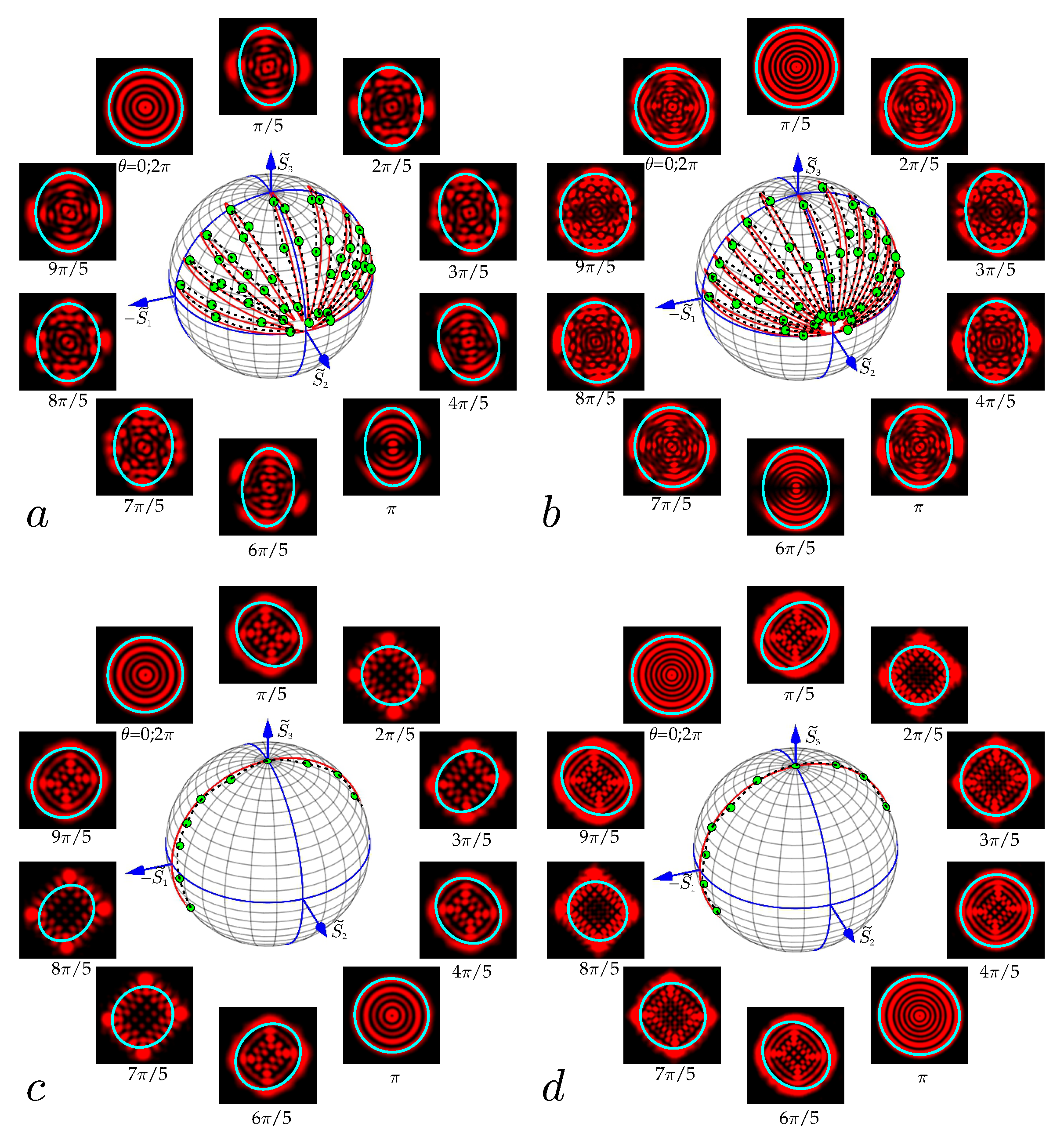
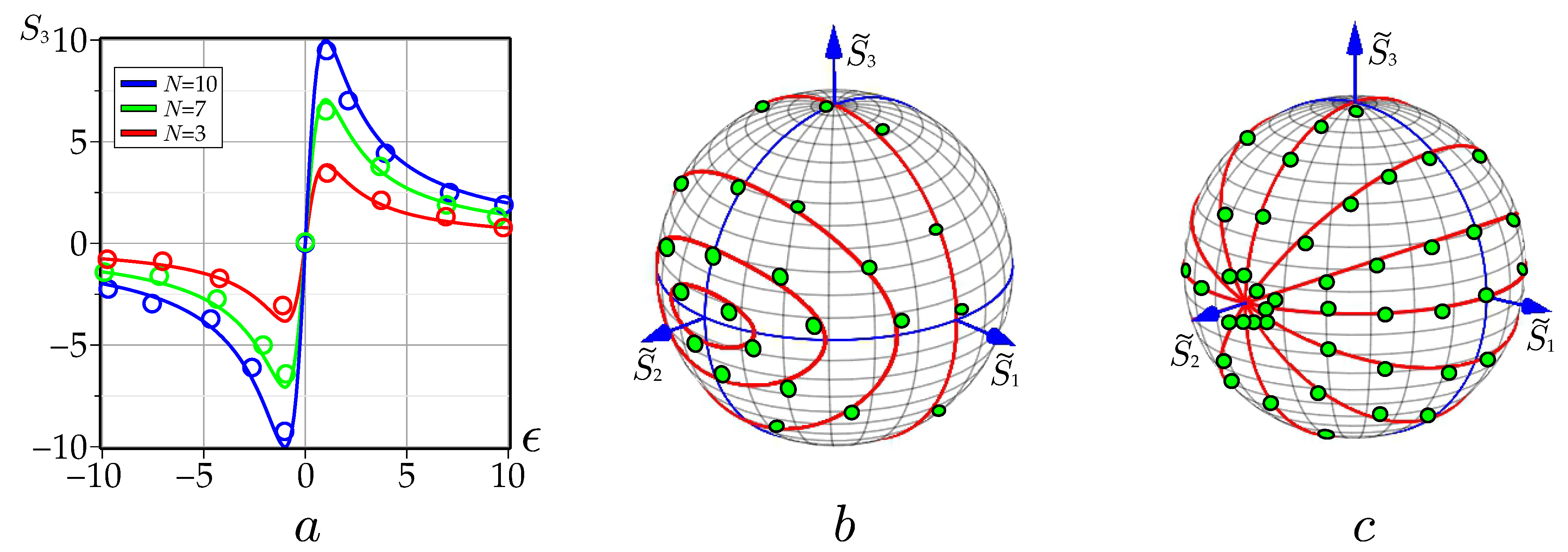
3.4. Structured sLG Beams and Their Asymptotics
3.5. Binomial Vortex Beams
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, C.; Shen, Y.; Forbes, A. Towards higher-dimensional structured light. Light. Sci. Appl. 2022, 11, 205. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A.; de Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, X.; Naidoo, D.; Fu, X.; Forbes, A. Structured ray-wave vector vortex beams in multiple degrees of freedom from a laser. Optica 2020, 7, 820–831. [Google Scholar] [CrossRef]
- Forbes, A.; Dudley, A.; McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photon. 2016, 8, 200–227. [Google Scholar] [CrossRef]
- Padgett, M.J. Orbital angular momentum 25 years on [Invited]. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef]
- Gbur, G.J. Singular Optics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; p. 563. [Google Scholar]
- Piccirillo, B.; Slussarenko, S.; Marrucci, L.; Santamato, E. Directly measuring mean and variance of infinite-spectrum observables such as the photon orbital angular momentum. Nat. Commun. 2015, 6, 8606. [Google Scholar] [CrossRef]
- Suprano, A.; Zia, D.; Polino, E.; Giordani, T.; Innocenti, L.; Paternostro, M.; Ferraro, A.; Spagnolo, N.; Sciarrino, F. Enhanced detection techniques of orbital angular momentum states in the classical and quantum regimes. New J. Phys. 2021, 23, 073014. [Google Scholar] [CrossRef]
- Fatkhiev, D.M.; Butt, M.A.; Grakhova, E.P.; Kutluyarov, R.V.; Stepanov, I.V.; Kazanskiy, N.L.; Khonina, S.N.; Lyubopytov, V.S.; Sultanov, A.K. Recent Advances in Generation and Detection of Orbital Angular Momentum Optical Beams—A Review. Sensors 2021, 21, 4988. [Google Scholar] [CrossRef]
- Deng, D.; Lin, M.; Li, Y.; Zhao, H. Precision Measurement of Fractional Orbital Angular Momentum. Phys. Rev. Appl. 2019, 12, 014048. [Google Scholar] [CrossRef]
- Wei, H.; Xue, X.; Leach, J.; Padgett, M.J.; Barnett, S.M.; Franke-Arnold, S.; Yao, E.; Courtial, J. Simplified measurement of the orbital angular momentum of single photons. Opt. Commun. 2003, 223, 117–122. [Google Scholar] [CrossRef]
- Mohammadi, S.M.; Daldorff, L.K.S.; Forozesh, K.; Thide, B.; Bergman, J.E.S.; Isham, B.; Karlsson, R.; Carozzi, T.D. Orbital angular momentum in radio: Measurement methods. Radio Sci. 2010, 45, RS4007. [Google Scholar] [CrossRef]
- Kulkarni, G.; Sahu, R.; Magana-Loaiza, O.S.; Boyd, R.W.; Jha, A.K. Single-shot measurement of the orbital-angular-momentum spectrum of light. Nat. Commun. 2017, 8, 1054. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y. Rays, waves, SU(2) symmetry and geometry: Toolkits for structured light. J. Opt. 2021, 23, 124004. [Google Scholar] [CrossRef]
- Dennis, M.R.; Alonso, M.A. Swings and roundabouts: Optical Poincaré spheres for polarization and Gaussian beams. Phil. Trans. R. Soc. A. 2017, 375, 20150441. [Google Scholar] [CrossRef]
- Padgett, M.J.; Courtial, J. Poincaré-sphere equivalent for light beams containing orbital angular momentum. Opt. Lett. 1999, 24, 430–432. [Google Scholar] [CrossRef]
- Shen, Y.; Meng, Y.; Fu, X.; Gong, M. Hybrid topological evolution of multi-singularity vortex beams: Generalized nature for helical-Ince–Gaussian and Hermite–Laguerre–Gaussian modes. J. Opt. Soc. Am. A 2019, 36, 578–587. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Z.; Fu, X.; Naidoo, D.; Forbes, A. SU(2) Poincaré sphere: A generalized representation for multidimensional structured light. Phys. Rev. A 2020, 102, 031501(R). [Google Scholar] [CrossRef]
- Calvo, G.F. Wigner representation and geometric transformations of optical orbital angular momentum spatial modes. Opt. Lett. 2005, 30, 1207–1209. [Google Scholar] [CrossRef]
- Tang, F.; Zhang, D.; Chen, L. Nontrivial evolution and geometric phase for an orbital angular momentum qutrit. Opt. Express 2024, 32, 21200–21215. [Google Scholar] [CrossRef]
- Agarwal, G.S. SU(2) structure of the Poincaré sphere for light beams with orbital angular momentum. J. Opt. Soc. Am. A 1999, 16, 2914–2916. [Google Scholar] [CrossRef]
- Schwinger, J.; Biedenharn, L.C.; Van Dam, H. Quantum Theory of Angular Momentum, 1st ed.; Academic Press: New York, NY, USA, 1965; p. 229. [Google Scholar]
- Abramochkin, E.G.; Volostnikov, V.G. Generalized Gaussian beams. J. Opt. A: Pure Appl. Opt. 2004, 6, S157–S161. [Google Scholar] [CrossRef]
- Bastiaans, M.J. Wigner distribution function and its application to first-order optics. J. Opt. Soc. Am. 1979, 69, 1710–1716. [Google Scholar] [CrossRef]
- Alieva, T.; Bastiaans, M.J. Evolution of the vortex and the asymmetrical parts of orbital angular momentum in separable first-order optical systems. Opt. Lett. 2004, 29, 1587–1589. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.-P. Geometric phase for twisted light. Opt. Express 2023, 31, 10287–10296. [Google Scholar] [CrossRef]
- Alieva, T.; Bastiaans, M.J. Phase-space rotations and orbital Stokes parameters. Opt. Lett. 2009, 34, 410–412. [Google Scholar] [CrossRef]
- Volyar, A.; Bretsko, M. Mapping structured Laguerre–Gaussian beam states onto the orbital Poincaré sphere in the form of controllable spatial trajectories. J. Opt. Soc. Am. A 2024, 41, 1648–1655. [Google Scholar] [CrossRef]
- Nemes, G.; Siegman, A.E. Measurement of all ten second-order moments of an astigmatic beam by the use of rotating simple astigmatic (anamorphic) optics. J. Opt. Soc. Am. A 1994, 11, 2257–2264. [Google Scholar] [CrossRef]
- Eppich, A.; Gao, C.; Weber, H. Determination of the ten second order intensity moments. Opt. Laser Technol. 1998, 30, 337–340. [Google Scholar] [CrossRef]
- Nemes, G.; Serna, J. Laser Beam Characterization with use of Second Order Moments: An Overview. In DPSS (Diode Pumped Solid State) Lasers: Applications and Issues; 17 of OSA Trends in Optics and Photonics; Optica Publishing Group: Washington, DC, USA, 1998; p. MQ2. [Google Scholar]
- ISO 11146-2:2021; Lasers and Laser-Related Equipment—Test Methods for Laser Beam Widths, Divergence Angles and Beam Propagation Ratios—Part 2: General Astigmatic Beams. ISO: Geneva, Switzerland, 2021.
- Bekshaev, A.Y.; Soskin, M.S.; Vasnetsov, M.V. Optical vortex symmetry breakdown and decomposition of the orbital angular momentum of light beams. J. Opt. Soc. Am. A 2003, 20, 1635–1643. [Google Scholar] [CrossRef]
- Letsch, A.; Giesen, A. Characterization of general astigmatic laser beams. Proc. SPIE 2006, 6101, 610117. [Google Scholar]
- Alperin, S.N.; Niederriter, R.D.; Gopinath, J.T.; Siemens, M.E. Quantitative measurement of the orbital angular momentum of light with a single, stationary lens. Opt. Lett. 2016, 41, 5019–5022. [Google Scholar] [CrossRef] [PubMed]
- Bastiaans, M.J. Wigner Distribution in Optics. In Phase-Space Optics: Fundamentals and Applications; Testorf, M., Hennelly, B., Ojeda-Castaneda, J., Eds.; McGraw-Hill: New York, NY, USA, 2009; pp. 1–44. [Google Scholar]
- Bastiaans, M.J.; Alieva, T. First-order optical systems with unimodular eigenvalues. J. Opt. Soc. Am. A 2006, 23, 1875–1883. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Testorf, M.; Hennelly, B.; Ojeda-Castaneda, J. Phase-Space Optics: Fundamentals and Applications: Fundamentals and Applications., 1st ed.; McGraw Hill Professional: New York, NY, USA, 2009; p. 416. [Google Scholar]
- Volyar, A.; Abramochkin, E.; Akimova, Y.; Bretsko, M. Control of the orbital angular momentum via radial numbers of structured Laguerre–Gaussian beams. Opt. Lett. 2022, 47, 2402–2405. [Google Scholar] [CrossRef]
- Alieva, T.; Camara, A.; Bastiaans, M.J. Beam mapping on the orbital Poincaré sphere. Proc. SPIE 2011, 8011, 801160. [Google Scholar]
- Eppich, B. Laser Beam Characterization; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Bekshaev, A.Y.; Soskin, M.S.; Vasnetsov, M.V. Transformation of higher-order optical vortices upon focusing by an astigmatic lens. Opt. Commun. 2004, 241, 237–247. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge: Cambridge, UK, 1999; p. 952. [Google Scholar]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Astigmatic transforms of an optical vortex for measurement of its topological charge. Appl. Opt. 2017, 56, 4095–4104. [Google Scholar] [CrossRef]
- Volyar, A.; Abramochkin, E.; Egorov, Y.; Bretsko, M.; Akimova, Y. Fine structure of perturbed Laguerre–Gaussian beams: Hermite–Gaussian mode spectra and topological charge. Appl. Opt. 2020, 59, 7680–7687. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; van der Veen, H.E.L.O.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Van Enk, S.J. Geometric phase, transformations of gaussian light beams and angular momentum transfer. Opt. Commun. 1993, 102, 59–64. [Google Scholar] [CrossRef]
- Volyar, A.; Abramochkin, E.; Bretsko, M.; Akimova, Y. Engineering Orbital Angular Momentum in Structured Beams in General Astigmatic Systems via Symplectic Matrix Approach. Photonics 2024, 11, 191. [Google Scholar] [CrossRef]
- Volyar, A.; Bretsko, M.; Khalilov, S.; Akimova, Y. Structurally Stable Astigmatic Vortex Beams with Super-High Orbital Angular Momentum (ABCD Matrix Approach). Photonics 2023, 10, 1048. [Google Scholar] [CrossRef]
- Volyar, A.V.; Bretsko, M.V.; Khalilov, S.I.; Akimova, Y.E. Orbital angular momentum burst control in astigmatic structured beams in ABCD-matrix transforms. Comp. Opt. 2024, 48, 171–179. [Google Scholar] [CrossRef]
- Goldstein, D.H. Polarized Light, Revised and Expanded, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003; p. 680. [Google Scholar]
- Volyar, A.V.; Abramochkin, E.; Bretsko, M.V.; Akimova, Y.E.; Egorov, Y.A. Can the radial number of vortex modes control the orbital angular momentum? Comput. Opt. 2022, 46, 853–863. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A. Orbital angular momentum of paraxial propagation-invariant laser beams. J. Opt. Soc. Am. A 2022, 39, 1061–1065. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Vortex Hermite–Gaussian laser beams. Opt. Lett. 2015, 40, 701–704. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volyar, A.; Bretsko, M.; Khalilov, S.; Akimova, Y. Simple Direct Measurement of the Orbital Stokes Parameters in Structured Vortex Beams. Photonics 2024, 11, 1095. https://doi.org/10.3390/photonics11111095
Volyar A, Bretsko M, Khalilov S, Akimova Y. Simple Direct Measurement of the Orbital Stokes Parameters in Structured Vortex Beams. Photonics. 2024; 11(11):1095. https://doi.org/10.3390/photonics11111095
Chicago/Turabian StyleVolyar, Alexander, Mikhail Bretsko, Server Khalilov, and Yana Akimova. 2024. "Simple Direct Measurement of the Orbital Stokes Parameters in Structured Vortex Beams" Photonics 11, no. 11: 1095. https://doi.org/10.3390/photonics11111095
APA StyleVolyar, A., Bretsko, M., Khalilov, S., & Akimova, Y. (2024). Simple Direct Measurement of the Orbital Stokes Parameters in Structured Vortex Beams. Photonics, 11(11), 1095. https://doi.org/10.3390/photonics11111095






