Interference Generation of a Reverse Energy Flow with Varying Orbital and Spin Angular Momentum Density
Abstract
1. Introduction
2. Theoretical Background
3. Analytics and Numerical Illustrations for Two Point Sources
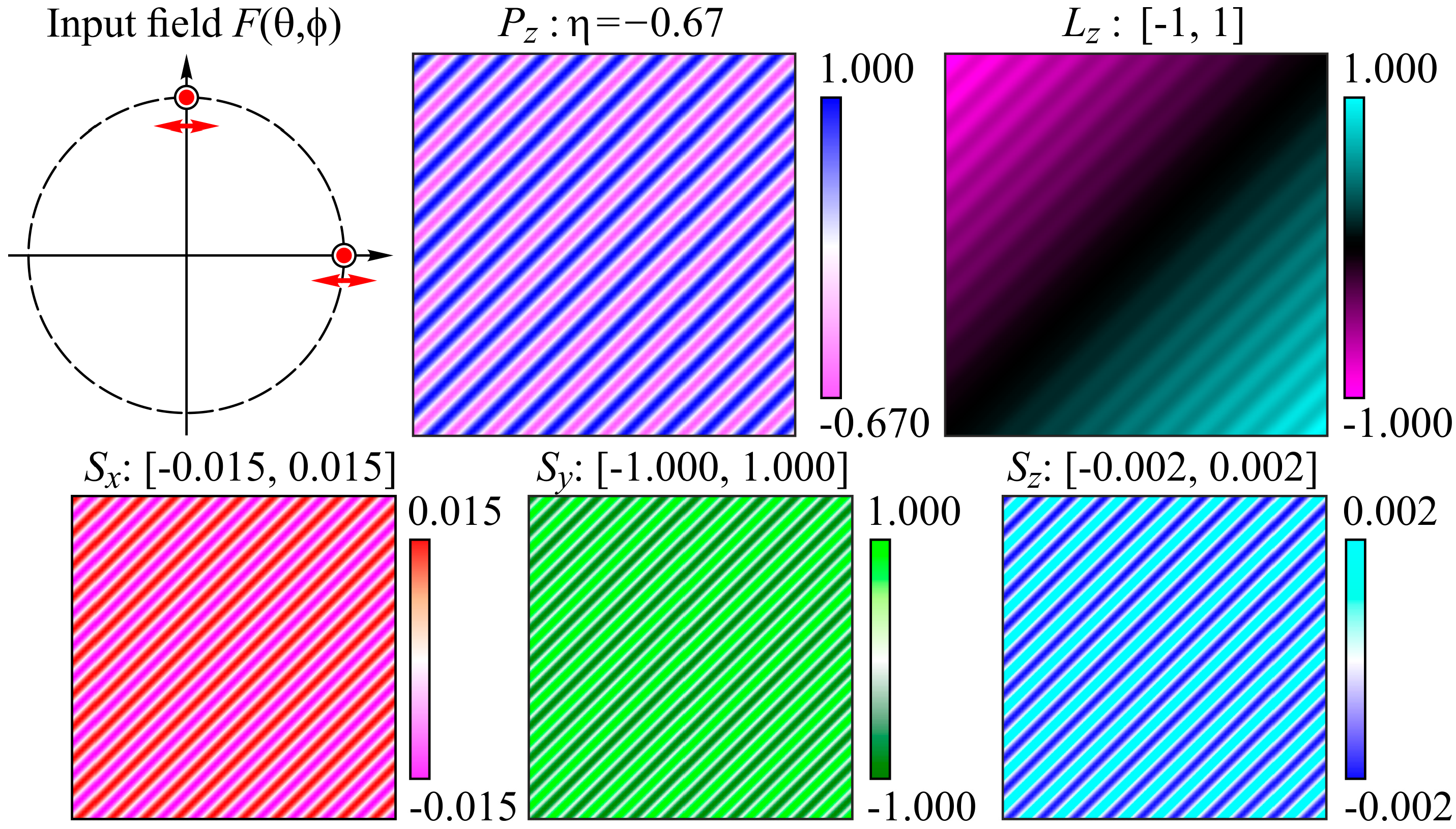
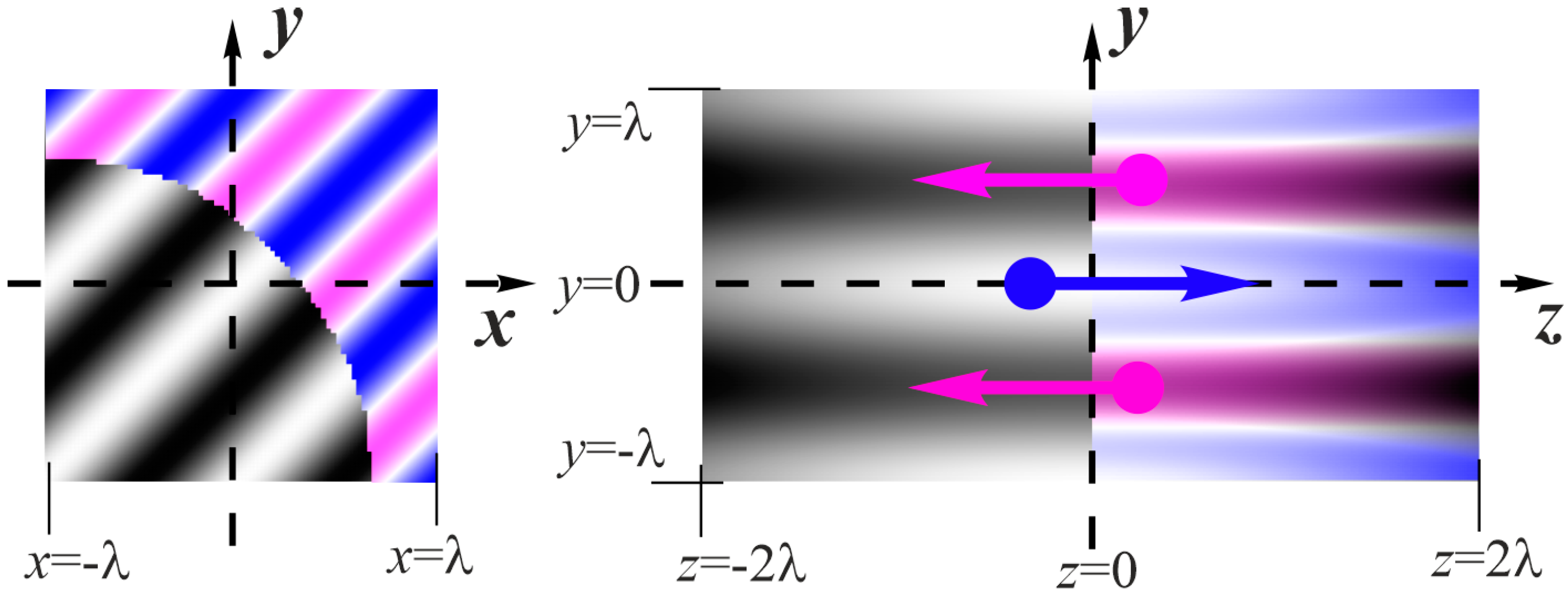
3.1. A Single Point Source
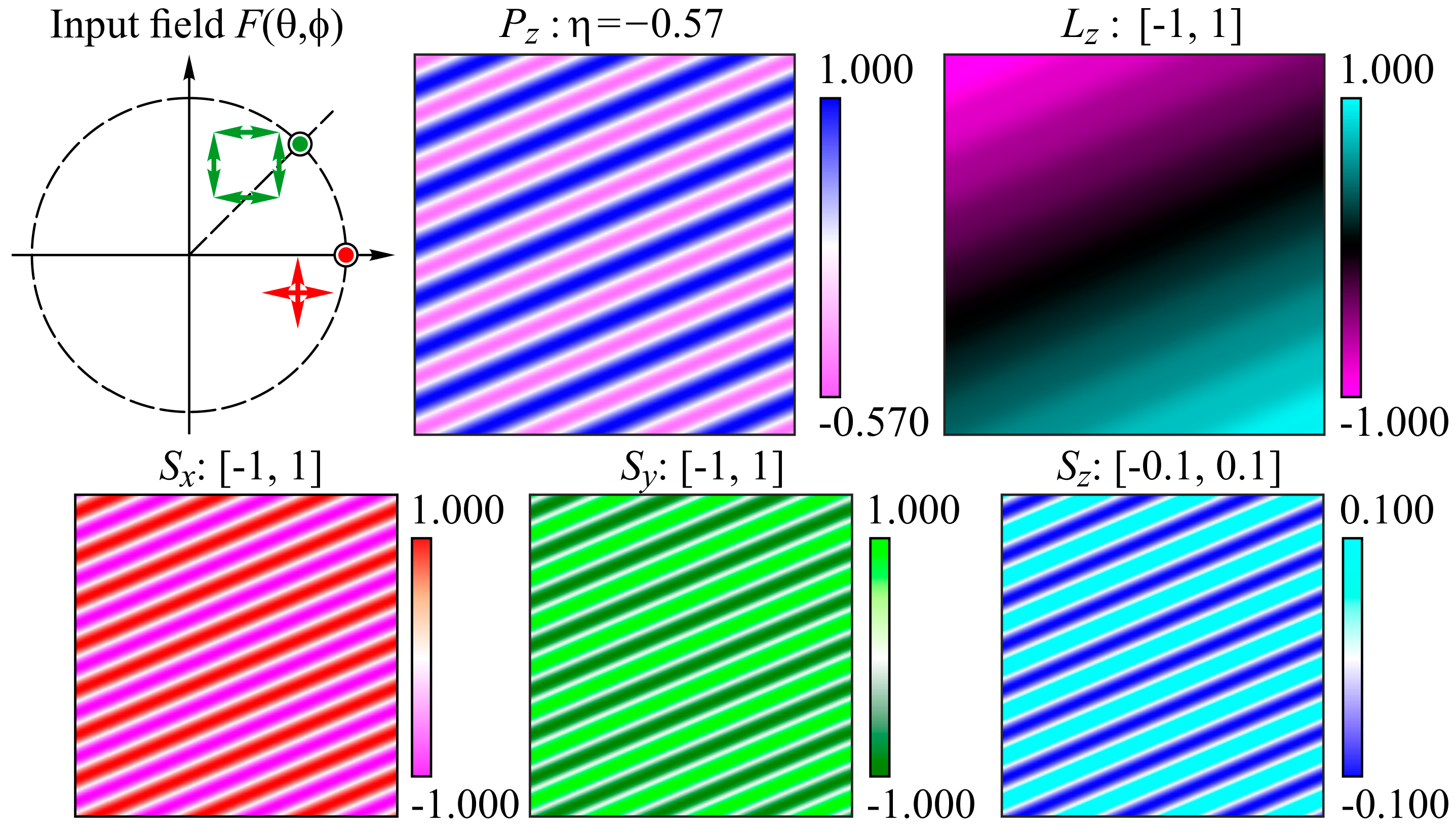
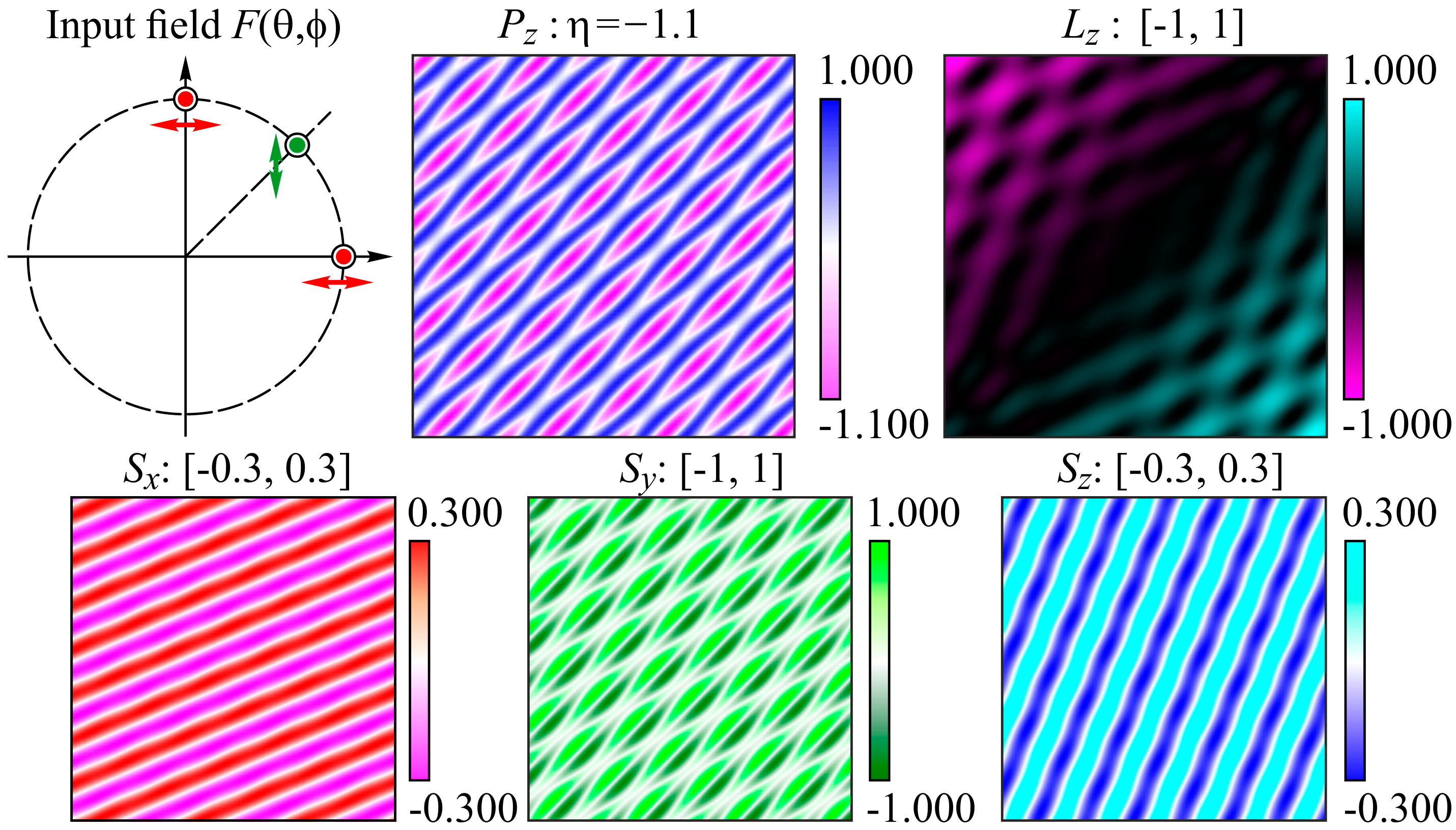
3.2. Two Point Sources
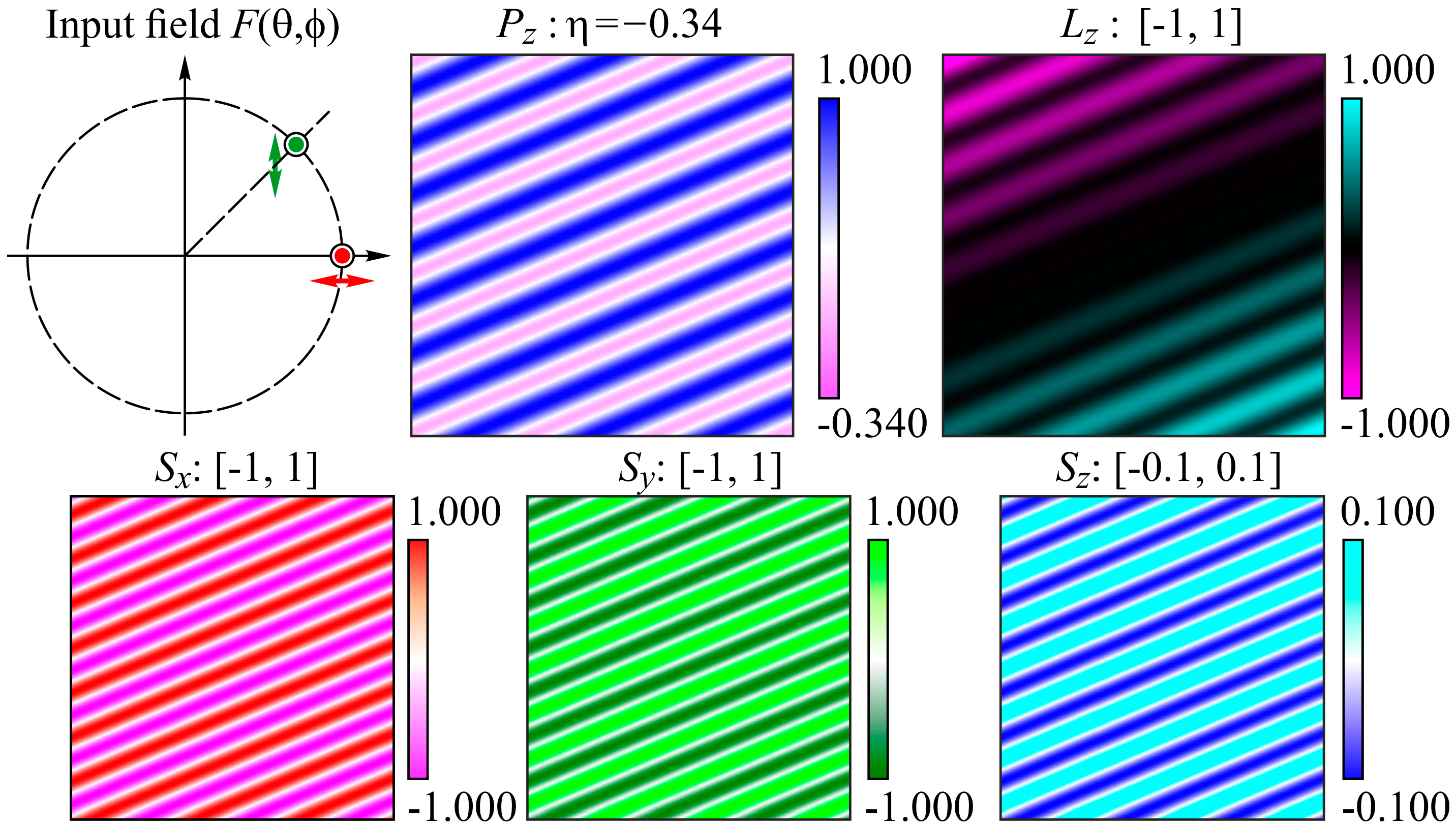
3.3. Proportional Relationships of Polarization Coefficients
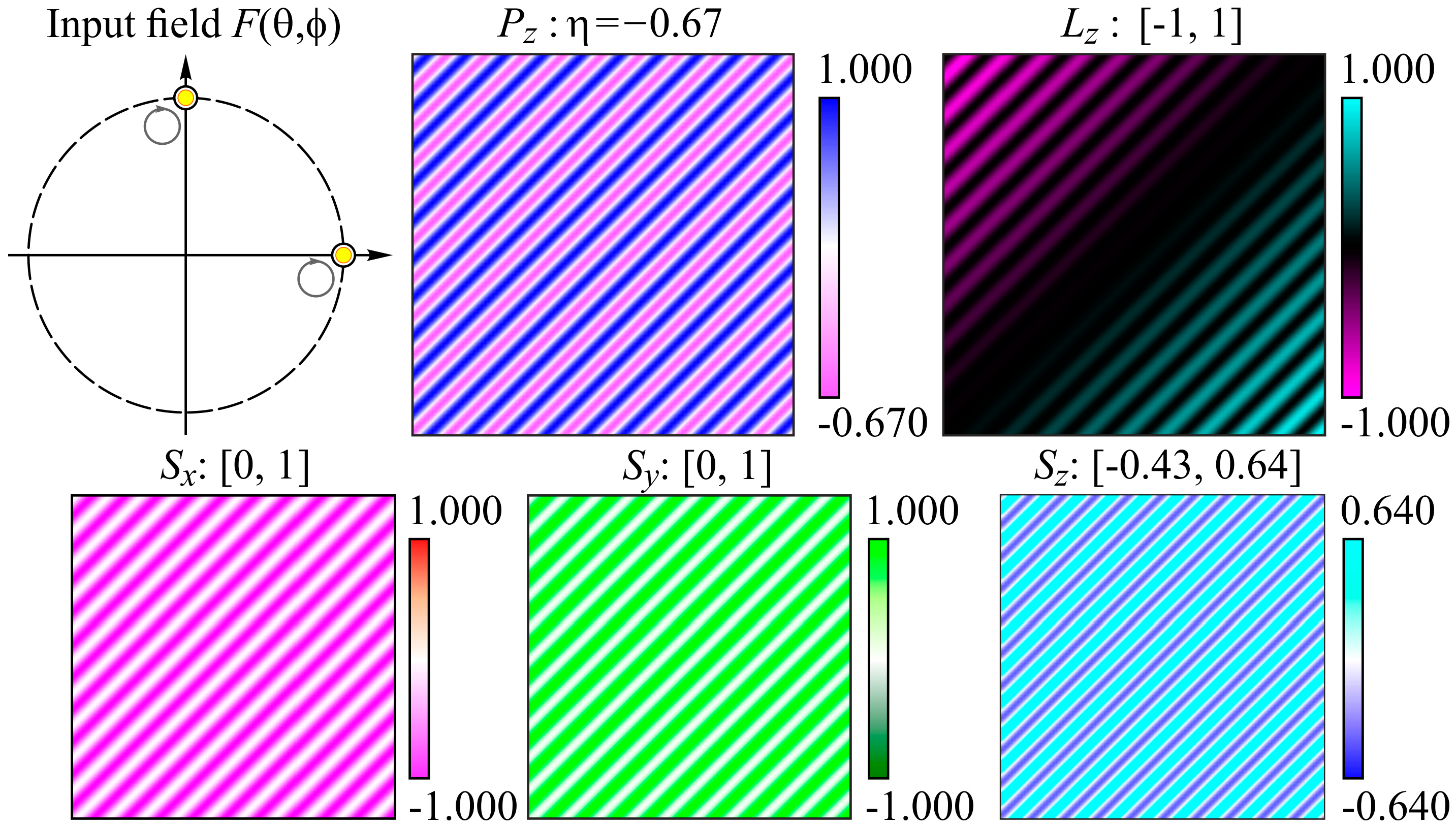
3.4. Orthogonal States of Polarization
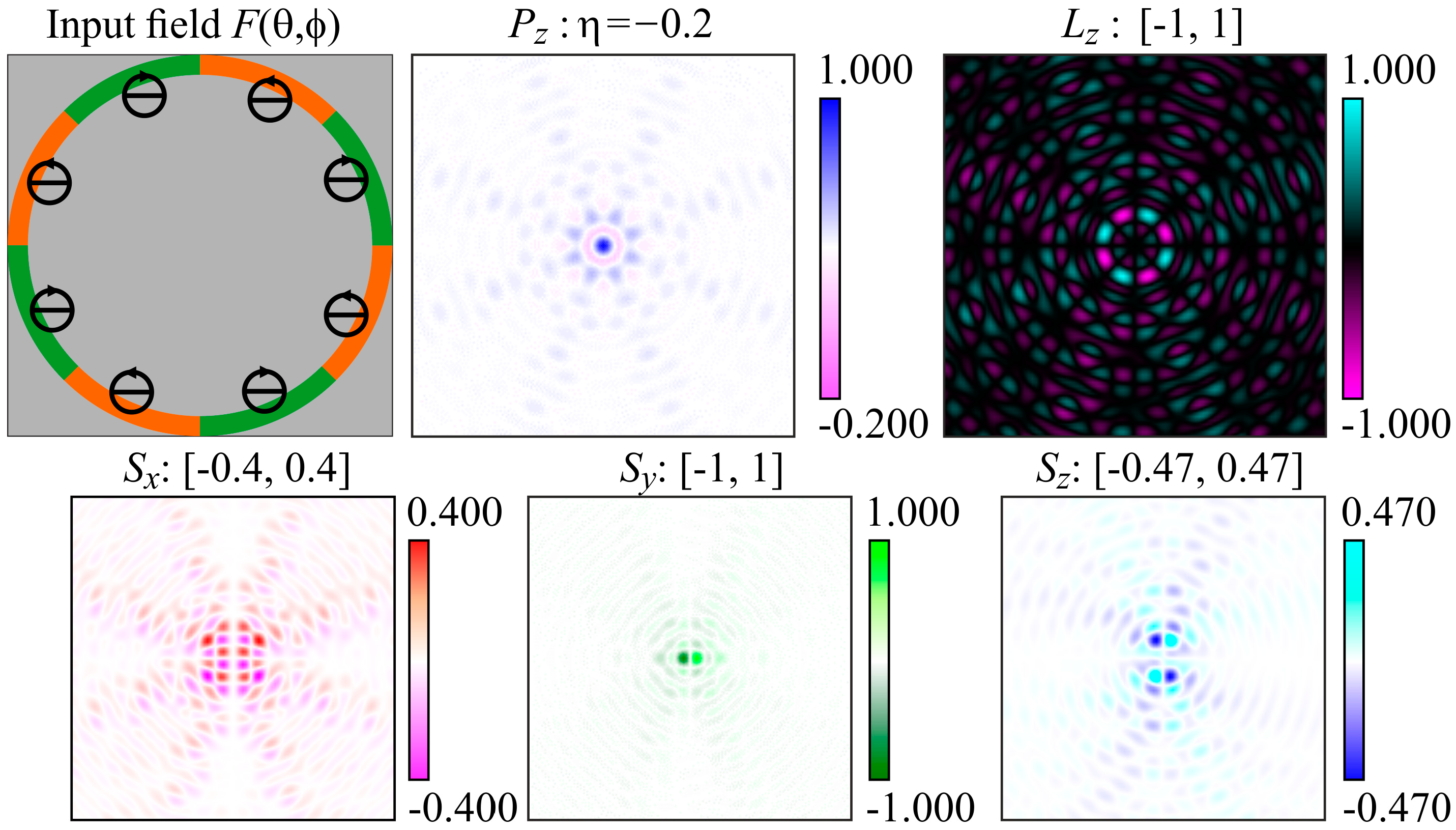
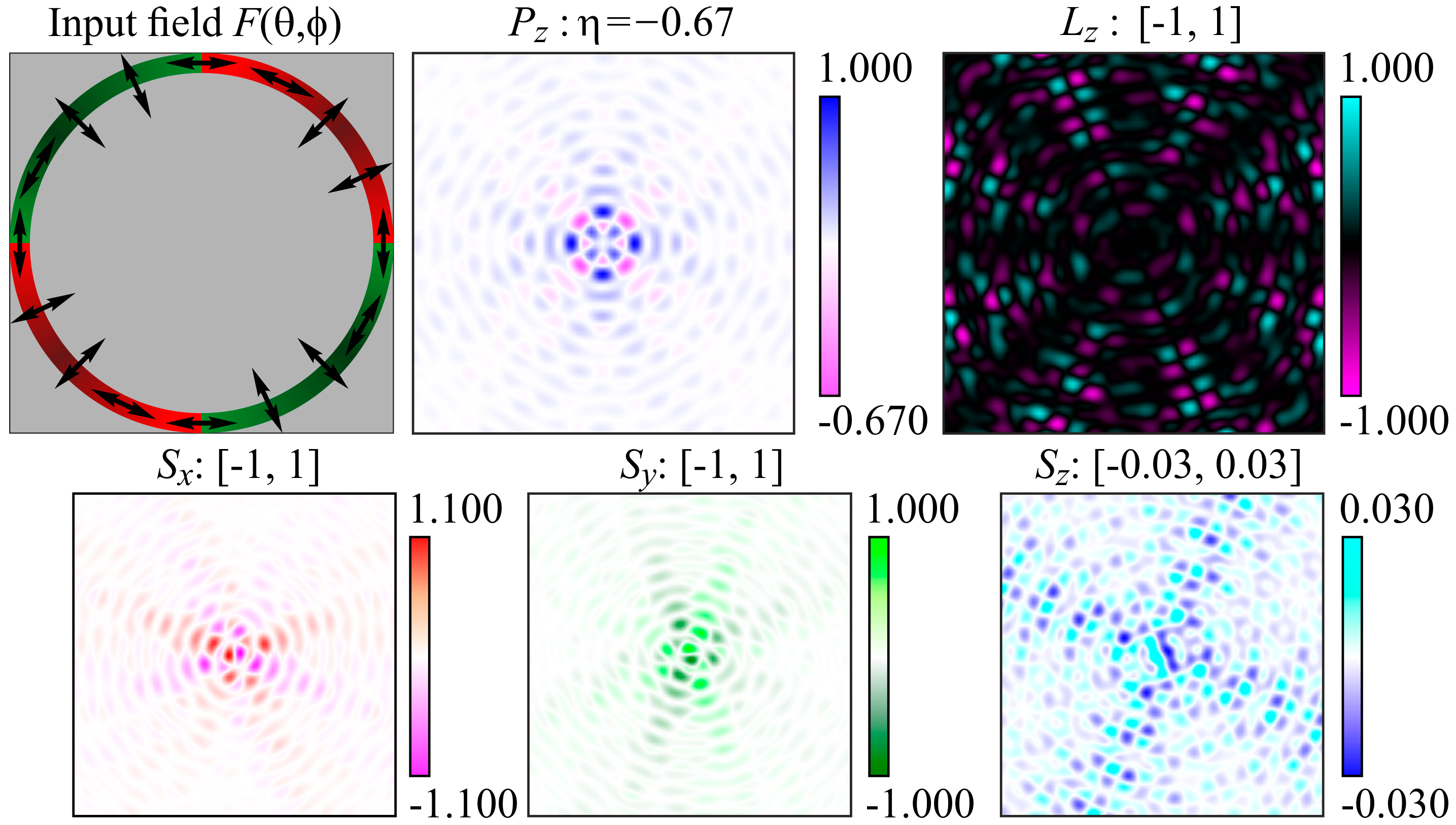
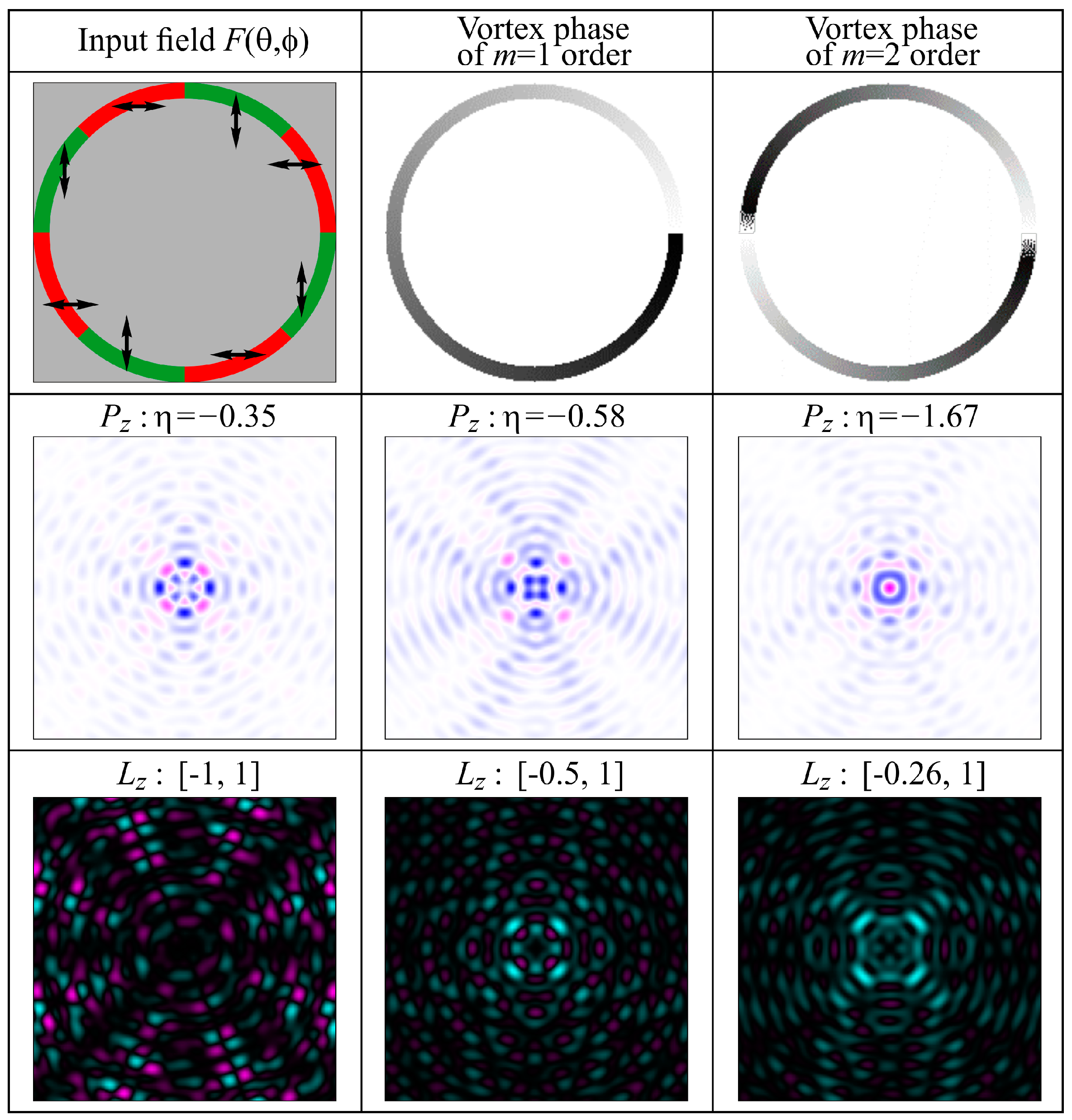
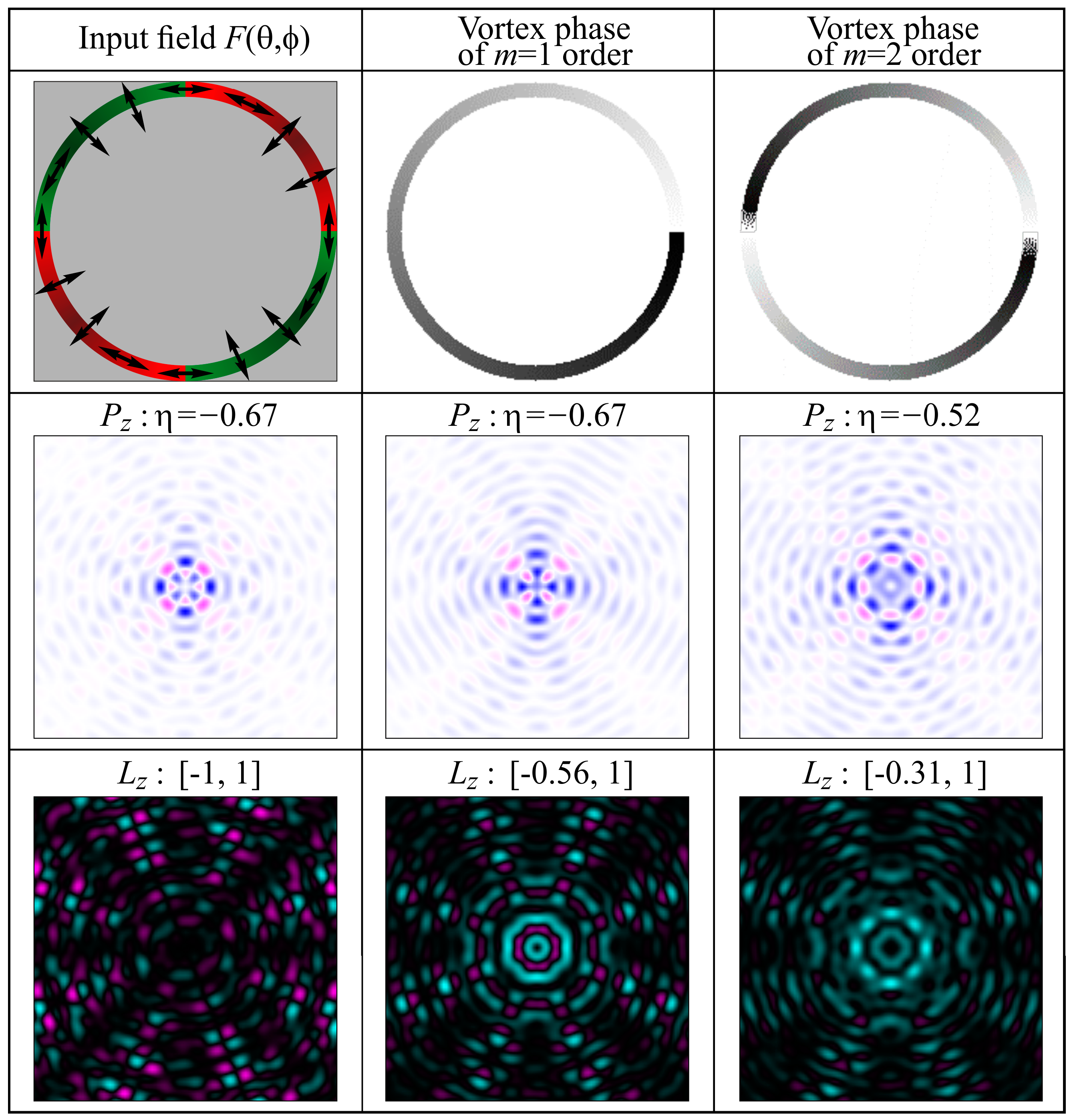
4. Interference Formation of Reverse Flow in Different Configurations of Point Light Sources
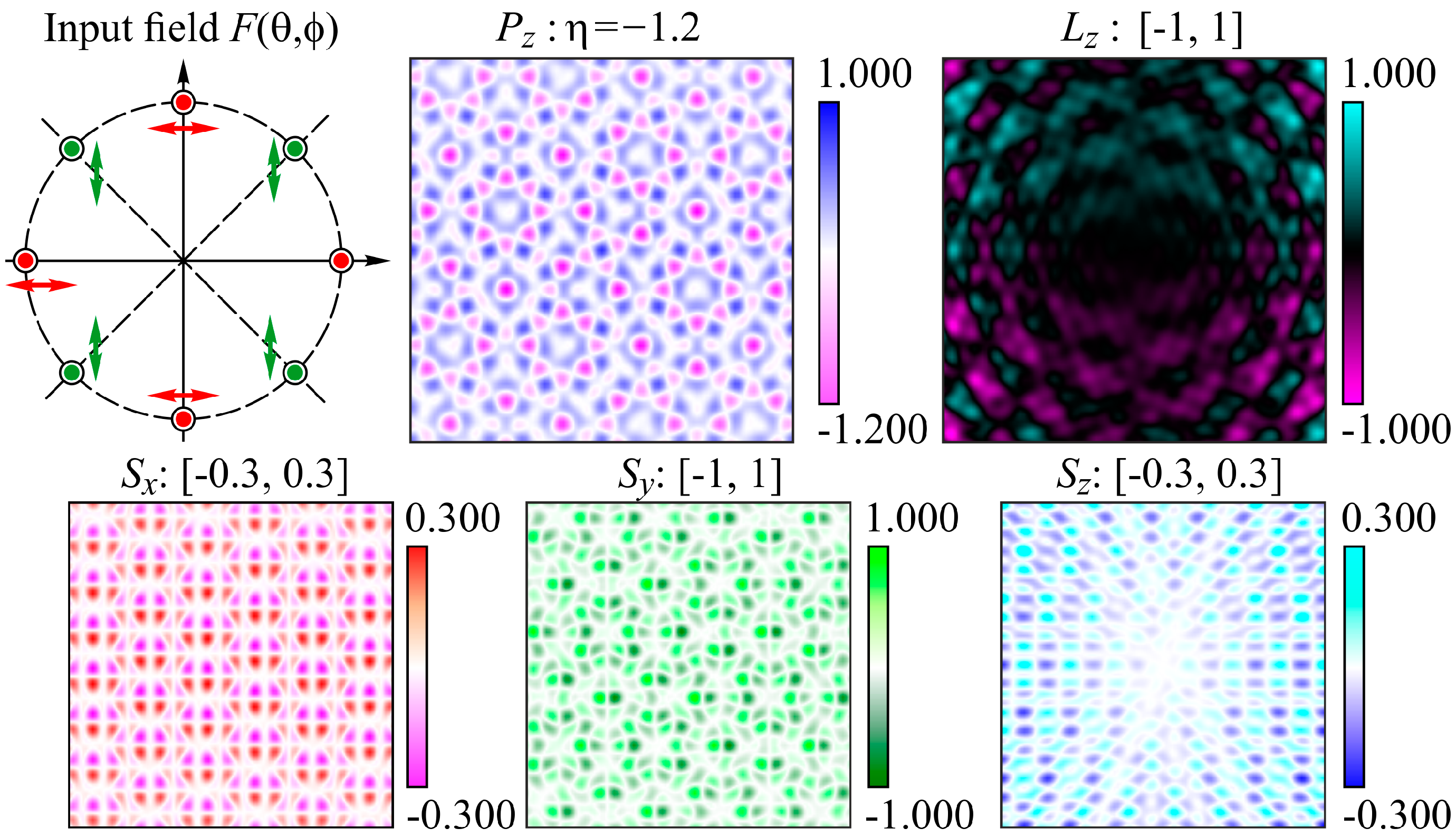
4.1. Three Point Light Sources
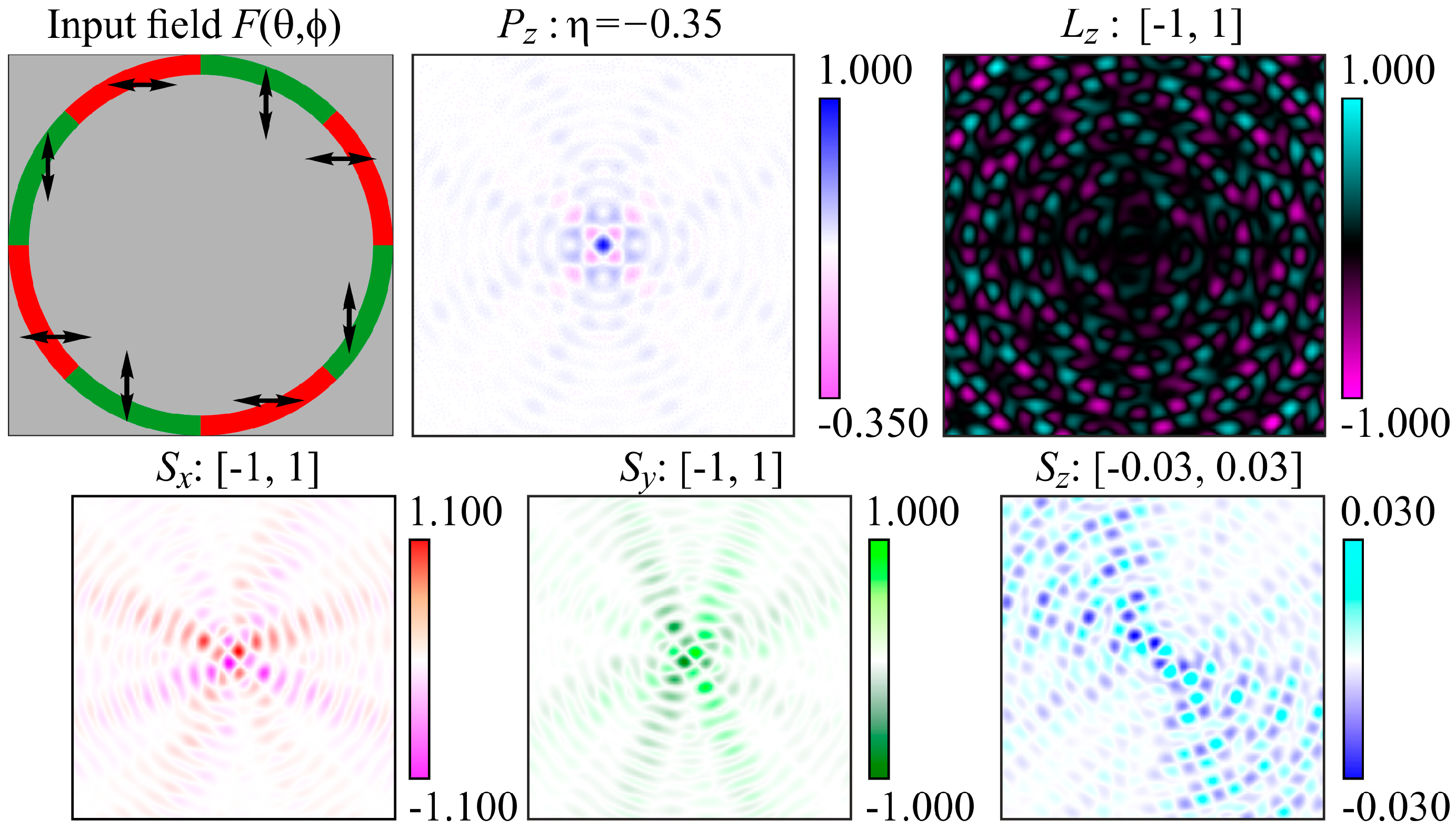
4.2. Segmented Annular-Shaped Polarization-Phase Elements
5. Discussion
5.1. Two Sources
5.2. Three Sources
5.3. Four Sources
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Andrews, D.L. Structured Light and Its Applications: An Introduction to Phase Structured Beams and Nanoscale Optical Forces; Academic Press: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T. Roadmap on structured light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Rosales-Guzman, C.; Ndagano, B.; Forbes, A. A review of complex vector light fields and their applications. J. Opt. 2018, 20, 123001. [Google Scholar] [CrossRef]
- Forbes, A. Structured light from lasers. Laser Photonics Rev. 2019, 13, 1900140. [Google Scholar] [CrossRef]
- Forbes, A.; de Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Angelsky, O.V.; Bekshaev, A.Y.; Hanson, S.G.; Zenkova, C.Y.; Mokhun, I.I.; Zheng, J. Structured light: Ideas and concepts. Front. Phys. 2020, 8, 114. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Z.; Fu, X.; Khan, A.; Zhao, S.; Gao, Y.; Jie, Y.; He, W.; Li, X.; Liu, Q.; et al. Evolution on spatial patterns of structured laser beams: From spontaneous organization to multiple transformations. Adv. Photonics Nexus 2023, 2, 024001. [Google Scholar] [CrossRef]
- Soskin, M.S.; Vasnetsov, M.V. Singular optics. Prog. Opt. 2001, 42, 219–276. [Google Scholar] [CrossRef]
- Gbur, G.J. Singular Optics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Kuchmizhak, A.A.; Gurbatov, S.O.; Juodkazis, S.; Khonina, S.N.; Kul’chin, Y.N. Phase singularities and optical vortices in photonics. Phys. Usp. 2022, 192, 841–866. [Google Scholar] [CrossRef]
- Angelsky, O.V.; Bekshaev, A.Y.; Vasnetsov, M.V.; Zenkova, C.Y.; Maksimyak, P.P.; Jun, Z. Optical phase singularities: Physical nature, manifestations and applications. Front. Phys. 2022, 10, 1060787. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Chapin, S.C.; Germain, V.; Dufresne, E.R. Automated trapping, assembly, and sorting with holographic optical tweezers. Opt. Express 2006, 14, 13095–13100. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Viloria, I.; Nodar, Á.; Molezuelas-Ferreras, M.; Olmos-Trigo, J.; Cifuentes, Á.; Martínez, M.; Varga, M.; Molina-Terriza, G. On-axis optical trapping with vortex beams: The role of the multipolar decomposition. ACS Photonics 2024, 11, 626–633. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, N.; Yuan, X.-C. High-volume optical vortex multiplexing and de-multiplexing for free-space optical communication. Opt. Express 2011, 19, 482–492. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Butt, M.A. Spatial-light-modulator-based multichannel data transmission by vortex beams of various orders. Sensors 2021, 21, 2988. [Google Scholar] [CrossRef]
- Furhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef]
- Anand, V.; Khonina, S.; Kumar, R.; Dubey, N.; Reddy, A.N.K.; Rosen, J.; Juodkazis, S. Three-dimensional incoherent imaging using spiral rotating point spread functions created by double-helix beams. Nanoscale Res. Lett. 2022, 17, 37. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Shvedov, V.G.; Krolikowski, W.; Rode, A.V. Materials processing with a tightly focused femtosecond laser vortex pulse. Opt. Lett. 2010, 35, 3417–3419. [Google Scholar] [CrossRef]
- Ambrosio, A.; Marrucci, L.; Borbone, F.; Roviello, A.; Maddalena, P. Light-induced spiral mass transport in azo-polymer films under vortex-beam illumination. Nat. Commun. 2012, 3, 989. [Google Scholar] [CrossRef] [PubMed]
- Nivas, J.J.J.; Allahyari, E.; Cardano, F.; Rubano, A.; Fittipaldi, R.; Vecchione, A.; Paparo, D.; Marrucci, L.; Bruzzese, R.; Amoruso, S. Vector vortex beams generated by q-plates as a versatile route to direct fs laser surface structuring. Appl. Surf. Sci. 2019, 471, 1028–1033. [Google Scholar] [CrossRef]
- Porfirev, A.; Khonina, S.; Kuchmizhak, A. Light–matter interaction empowered by orbital angular momentum: Control of matter at the micro-and nanoscale. Progr. Quantum Electron. 2023, 88, 100459. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Milione, G. Vector Beams for Fundamental Physics and Applications. Ph.D. Thesis, CUNY, New York, NY, USA, June 2016. Available online: https://academicworks.cuny.edu/gc_etds/1267 (accessed on 9 October 2024).
- Skoulas, E.; Manousaki, A.; Fotakis, C.; Stratakis, E. Biomimetic surface structuring using cylindrical vector femtosecond laser beams. Sci. Rep. 2017, 7, 45114. [Google Scholar] [CrossRef]
- Bautista, G.; Kakko, J.-P.; Dhaka, V.; Zang, X.; Karvonen, L.; Jiang, H.; Kauppinen, E.; Lipsanen, H.; Kauranen, M. Nonlinear microscopy using cylindrical vector beams: Applications to three-dimensional imaging of nanostructures. Opt. Express 2017, 25, 12463–12468. [Google Scholar] [CrossRef]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef]
- Syubaev, S.A.; Zhizhchenko, A.Y.; Pavlov, D.V.; Gurbatov, S.O.; Pustovalov, E.V.; Porfirev, A.P.; Khonina, S.N.; Kulinich, S.A.; Rayappan, J.B.B.; Kudryashov, S.I.; et al. Plasmonic nanolenses produced by cylindrical vector beam printing for sensing applications. Sci. Rep. 2019, 9, 19750. [Google Scholar] [CrossRef]
- Li, Z.X.; Ruan, Y.P.; Chen, P.; Tang, J.; Hu, W.; Xia, K.Y.; Lu, Y.Q. Liquid crystal devices for vector vortex beams manipulation and quantum information applications. Chin. Opt. Lett. 2021, 19, 112601. [Google Scholar] [CrossRef]
- Ishitobi, H.; Nakamura, I.; Kobayashi, T.A.; Hayazawa, N.; Sekkat, Z.; Kawata, S.; Inouye, Y. Nanomovement of azo polymers induced by longitudinal fields. ACS Photonics 2014, 1, 190–197. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Khonina, S.N.; Ivliev, N.A.; Meshalkin, A.; Achimova, E.A.; Forbes, A. Writing and reading with the longitudinal component of light using carbazole-containing azopolymer thin films. Sci. Rep. 2022, 12, 3477. [Google Scholar] [CrossRef] [PubMed]
- Porfirev, A.P.; Khonina, S.N.; Ivliev, N.A.; Porfirev, D.P.; Kazanskiy, N.L. Stacked polarizing elements for controlling parameters of surface relief gratings written in photosensitive materials. Sensors 2024, 24, 1166. [Google Scholar] [CrossRef] [PubMed]
- Poynting, J.H. On the transfer of energy in the electromagnetic field. Proc. R. Soc. Lond. 1883, 36, 186–187. [Google Scholar] [CrossRef]
- Allen, L.; Padgett, M.J. The Poynting vector in Laguerre–Gaussian beams and the interpretation of their angular momentum density. Opt. Commun. 2000, 184, 67–71. [Google Scholar] [CrossRef]
- Hu, B.Y.-K. Introducing electromagnetic field momentum. Eur. J. Phys. 2012, 33, 873. [Google Scholar] [CrossRef][Green Version]
- Mörée, G.; Leijon, M. Comparison of Poynting’s vector and the power flow used in electrical engineering. AIP Adv. 2022, 12, 085219. [Google Scholar] [CrossRef]
- Simpson, N.B.; Dholakia, K.; Allen, L.; Padgett, M.J. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef]
- Stewart, A.M. Angular momentum of light. J. Mod. Opt. 2005, 52, 1145–1154. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Banzer, P.; Neugebauer, M.; Aiello, A.; Marquardt, C.; Lindlein, N.; Bauer, T.; Leuchs, G. The photonic wheel—Demonstration of a state of light with purely transverse angular momentum. J. Eur. Opt. Soc. 2013, 8, 6. [Google Scholar] [CrossRef]
- Aiello, A.; Banzer, P.; Neugebauer, M.; Leuchs, G. From transverse angular momentum to photonic wheels. Nat. Photonics 2015, 9, 789–795. [Google Scholar] [CrossRef]
- Marrucci, L.; Karimi, E.; Slussarenko, S.; Piccirillo, B.; Santamato, E.; Nagali, E.; Sciarrino, F. Spin-to-orbital conversion of the angular momentum of light and its classical and quantum applications. J. Opt. 2011, 13, 064001. [Google Scholar] [CrossRef]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photonics 2014, 8, 543–549. [Google Scholar] [CrossRef]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary spin-to-orbital angular momentum conversion of light. Science 2017, 358, 896–901. [Google Scholar] [CrossRef]
- Shi, P.; Du, L.; Yuan, X. Structured spin angular momentum in highly focused cylindrical vector vortex beams for optical manipulation. Opt. Express 2018, 26, 23449–23459. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P. Harnessing of inhomogeneously polarized Hermite–Gaussian vector beams to manage the 3D spin angular momentum density distribution. Nanophotonics 2021, 2021 11, 697–712. [Google Scholar] [CrossRef]
- Albaladejo, S.; Marqués, M.I.; Laroche, M.; Sáenz, J.J. Scattering forces from the curl of the spin angular momentum of a light field. Phys. Rev. Lett. 2009, 102, 113602. [Google Scholar] [CrossRef]
- Marqués, M.I.; Saénz, J.J. Scattering forces and electromagnetic momentum density in crossed circularly polarized standing waves. Opt. Lett. 2012, 37, 2787–2789. [Google Scholar] [CrossRef]
- Ruffner, D.B.; Grier, D.G. Optical forces and torques in nonuniform beams of light. Phys. Rev. Lett. 2012, 108, 173602. [Google Scholar] [CrossRef]
- Du, J.; Yuen, C.H.; Li, X.; Ding, K.; Du, G.; Lin, Z.; Chan, C.T.; Ng, J. Tailoring optical gradient force and optical scattering and absorption force. Sci. Rep. 2017, 7, 18042. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Volotovskiy, S.G.; Ivliev, N.A.; Podlipnov, V.V. Influence of optical forces induced by paraxial vortex Gaussian beams on the formation of a microrelief on carbazole-containing azopolymer films. Appl. Opt. 2020, 59, 9185–9194. [Google Scholar] [CrossRef] [PubMed]
- Aiello, A.; Lindlein, N.; Marquardt, C.; Leuchs, G. Transverse angular momentum and geometric spin hall effect of light. Phys. Rev. Lett. 2009, 103, 100401. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Yan, S.; Yao, B.; Liang, Y.; Zhang, P. Spinning and orbiting motion of particles in vortex beams with circular or radial polarizations. Opt. Express 2016, 24, 20604–20612. [Google Scholar] [CrossRef] [PubMed]
- Emile, O.; Emile, J. Energy, linear momentum, and angular momentum of light: What do we measure? Ann. Phys. 2018, 530, 1800111. [Google Scholar] [CrossRef]
- Pan, Y.; Gao, X.Z.; Zhang, G.L.; Li, Y.; Tu, C.; Wang, H.T. Spin angular momentum density and transverse energy flow of tightly focused kaleidoscope-structured vector optical fields featured. APL Photonics 2019, 4, 096102. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Orbital angular momentum of twisted light: Chirality and optical activity. J. Phys. Photonics 2021, 3, 022007. [Google Scholar] [CrossRef]
- Yang, S.H.; Naaman, R.; Paltiel, Y.; Parkin, S.S.P. Chiral spintronics. Nat. Rev. Phys. 2021, 3, 328–343. [Google Scholar] [CrossRef]
- Zhang, Z.; Mei, W.; Cheng, J.H.; Tan, Y.; Dai, Z.; Ling, X. Revisiting vortex generation in the spin-orbit interactions of refraction and focusing of light. Phys. Rev. A 2022, 106, 063520. [Google Scholar] [CrossRef]
- Khonina, S.N.; Golub, I. Vectorial spin Hall effect of light upon tight focusing. Opt. Lett. 2022, 47, 2166–2169. [Google Scholar] [CrossRef]
- Porfirev, A.; Khonina, S.; Ustinov, A.; Ivliev, N.; Golub, I. Vectorial spin-orbital Hall effect of light upon tight focusing and its experimental observation in azopolymer films. Opto-Electron. Sci. 2023, 2, 230014. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Sun, J.; Frantz, J.; Shalaev, M.I.; Walasik, W.; Pandey, A.; Myers, J.D.; Bekele, R.Y.; Tsukernik, A.; Sanghera, J.S.; et al. Reconfiguring structured light beams using nonlinear metasurfaces. Opt. Express 2018, 26, 30930–30943. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Crozier, K.B. Metasurfaces 2.0: Laser-integrated and with vector field control. APL Photonics 2021, 6, 080902. [Google Scholar] [CrossRef]
- Khonina, S.N.; Butt, M.A.; Kazanskiy, N.L. A review on reconfigurable metalenses revolutionizing flat optics. Adv. Optical Mater. 2023, 12, 2302794. [Google Scholar] [CrossRef]
- Passilly, N.; de Saint Denis, R.; Aït-Ameur, K.; Treussart, F.; Hierle, R.; Roch, J.-F. Simple interferometric technique for generation of a radially polarized light beam. J. Opt. Soc. Am. A 2005, 22, 984–991. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Fomchenkov, S.A.; Porfirev, A.P. Formation of hybrid higher-order cylindrical vector beams using binary multi-sector phase plates. Sci. Rep. 2018, 8, 14320. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, Z.; Ding, J.; Wang, H.-T. Single ultra-high-definition spatial light modulator enabling highly efficient generation of fully structured vector beams. Appl. Opt. 2019, 58, 6591–6596. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Hu, X.-B.; Selyem, A.; Moreno-Acosta, P.; Franke-Arnold, S.; Ramos-Garcia, R.; Forbes, A. Polarisation-insensitive generation of complex vector modes from a digital micromirror device. Sci. Rep. 2020, 10, 10434. [Google Scholar] [CrossRef]
- Baliyan, M.; Shikder, A.; Nishchal, N.K. Generation of structured light beams by dual phase modulation with a single spatial light modulator. Phys. Scr. 2023, 98, 105528. [Google Scholar] [CrossRef]
- Yu, F.; Li, P.; Shen, H.; Mathur, S.; Lehr, C.-M.; Bakowsky, U.; Mücklich, F. Laser interference lithography as a new and efficient technique for micropatterning of biopolymer surface. Biomaterials 2005, 26, 2307–2312. [Google Scholar] [CrossRef]
- Lai, N.D.; Liang, W.P.; Lin, J.H.; Hsu, C.C.; Lin, C.H. Fabrication of two- and three-dimensional periodic structures by multiexposure of two-beam interference technique. Opt. Express 2005, 13, 9605–9611. [Google Scholar] [CrossRef] [PubMed]
- Vala, M.; Homola, J. Multiple beam interference lithography: A tool for rapid fabrication of plasmonic arrays of arbitrary shaped nanomotifs. Opt. Express 2016, 24, 15656–15665. [Google Scholar] [CrossRef] [PubMed]
- Rebollar, E.; Castillejo, M.; Ezquerra, T.A. Laser induced periodic surface structures on polymer films: From fundamentals to applications. Eur. Polym. J. 2015, 73, 162–174. [Google Scholar] [CrossRef]
- Uesugi, Y.; Miwa, T.; Kadoguchi, N.; Kozawa, Y.; Sato, S. Multi-beam ultrafast laser processing of free-standing nanofilms. Appl. Phys. A 2023, 129, 101. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P.; Karpeev, S.V. Analysis of the polarization distribution and spin angular momentum of the interference field obtained by co-planar beams with linear and circular polarization. Photonics 2024, 11, 478. [Google Scholar] [CrossRef]
- Vaveliuk, P.; Martinez-Matos, O. Negative propagation effect in nonparaxial Airy beams. Opt. Express 2012, 20, 26913–26921. [Google Scholar] [CrossRef]
- Novitsky, A.; Qiu, C.-W.; Wang, H. Single gradientless light beam drags particles as tractor beams. Phys. Rev. Lett. 2011, 107, 203601. [Google Scholar] [CrossRef]
- Nalimov, A.G.; Stafeev, S.S.; Kotlyar, V.V. Optical force acting on a particle in a reverse energy flow near the focus of a gradient lens. J. Opt. 2020, 22, 115001. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Nalimov, A.G.; Kovalev, A.A.; Porfirev, A.P. Experimental investigation of the energy backflow in the tight focal spot. Comput. Opt. 2020, 44, 864–871. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G. Energy backflow in the focus of a light beam with phase or polarization singularity. Phys. Rev. A 2019, 99, 033840. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Degtyarev, S.A. Inverse energy flux of focused radially polarized optical beams. Phys. Rev. A 2018, 98, 043823. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Tang, M.; Li, X. Controlled negative energy flow in the focus of a radial polarized optical beam. Opt. Express 2020, 28, 18607–18615. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Ustinov, A.V. Increased reverse energy flux area when focusing a linearly polarized annular beam with binary plates. Opt. Lett. 2019, 44, 2008–2011. [Google Scholar] [CrossRef] [PubMed]
- Stafeev, S.S.; Kotlyar, V.V. Elongation of the area of energy backflow through the use of ring apertures. Opt. Commun. 2019, 450, 67–71. [Google Scholar] [CrossRef]
- Ustinov, A.V.; Khonina, S.N.; Porfirev, A.P. Formation of inverse energy flux in the case of diffraction of linearly polarized radiation by conventional and generalized spiral phase plates. Photonics 2021, 8, 283. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Ustinov, A.V.; Kirilenko, M.S.; Kazanskiy, N.L. Tailoring of inverse energy flow profiles with vector Lissajous beams. Photonics 2022, 9, 121. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G.; Kovalev, A.A.; Porfirev, A.P. Mechanism of formation of an inverse energy flow in a sharp focus. Phys. Rev. A 2020, 101, 033811. [Google Scholar] [CrossRef]
- Saari, P.; Besieris, I. Backward energy flow in simple four-wave electromagnetic fields. Eur. J. Phys. 2021, 42, 055301. [Google Scholar] [CrossRef]
- Khonina, S.N.; Golub, I. Breaking the symmetry to structure light. Opt. Lett. 2021, 46, 2605–2608. [Google Scholar] [CrossRef]
- Mansuripur, M. Certain computational aspects of vector diffraction problems. J. Opt. Soc. Am. A 1989, 6, 786–805. [Google Scholar] [CrossRef]
- Guo, H.; Chen, J.; Zhuang, S. Vector plane wave spectrum of an arbitrary polarized electromagnetic wave. Opt. Express 2006, 14, 2095–2100. [Google Scholar] [CrossRef] [PubMed]
- Ciattoni, A.; Crosignani, B.; Porto, P.D. Vectorial analytical description of propagation of a highly non paraxial beam. Opt. Commun. 2002, 202, 17–20. [Google Scholar] [CrossRef]
- Li, J.; Zhu, S.; Lu, B. The rigorous electromagnetic theory of the diffraction of vector beams by a circular aperture. Opt. Commun. 2009, 282, 4475–4480. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kharitonov, S.I. An analog of the Rayleigh–Sommerfeld integral for anisotropic and gyrotropic media. J. Mod. Opt. 2013, 60, 814–822. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Kovalyov, A.A.; Volotovsky, S.G. Near-field propagation of vortex beams: Models and computation algorithms. Opt. Mem. Neural Netw. 2014, 23, 50–73. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1959, 253, 358–379. [Google Scholar] [CrossRef]
- Helseth, L.E. Optical Vortices in Focal Regions. Opt. Commun. 2004, 229, 85–91. [Google Scholar] [CrossRef]
- Wu, G.; Lou, Q.; Zhou, J. Analytical vectorial structure of hollow Gaussian beams in the far field. Opt. Express 2008, 16, 6417–6424. [Google Scholar] [CrossRef]
- Zhou, G. The analytical vectorial structure of a nonparaxial Gaussian beam close to the source. Opt. Express 2008, 16, 3504–3514. [Google Scholar] [CrossRef]
- Volyar, A.V.; Shvedov, V.G.; Fadeeva, T.A. The Structure of a Nonparaxial Gaussian Beam near the Focus: II. Optical Vortices. Opt. Spectrosc. 2001, 90, 93–100. [Google Scholar] [CrossRef]
- Mitri, F.G. Superposition of nonparaxial vectorial complex-source spherically focused beams: Axial Poynting singularity and reverse propagation. Phys. Rev. A 2016, 94, 023801. [Google Scholar] [CrossRef]
- Felsen, L.B. Complex-Source-Point-Solutions of the Field Equations and Their Relation to the Propagation and Scattering of Gaussian Beams. In Symposia Matematica, Instituto Nazionale di Alta Matematica XVIII; Academic Press: London, UK, 1976; pp. 39–56. [Google Scholar]
- Norris, A.N. Complex point-source representation of real point sources and the Gaussian beam summation method. J. Opt. Soc. Am. A 1986, 3, 2005–2010. [Google Scholar] [CrossRef]
- Bekshaev, A.Y.; Bliokh, K.Y.; Nori, F. Transverse spin and momentum in two-wave interference. Phys. Rev. X 2015, 5, 011039. [Google Scholar] [CrossRef]
- Xu, X.; Nieto-Vesperinas, M. Azimuthal imaginary Poynting momentum density. Phys. Rev. Lett. 2019, 123, 233902. [Google Scholar] [CrossRef]
- Khonina, S.N.; Degtyarev, S.A.; Ustinov, A.V.; Porfirev, A.P. Metalenses for the generation of vector Lissajous beams with a complex Poynting vector density. Opt. Express 2021, 29, 18651–18662. [Google Scholar] [CrossRef]
- Bekshaev, A. Dynamical characteristics of electromagnetic field under conditions of total internal reflection. J. Opt. 2018, 20, 045604. [Google Scholar] [CrossRef]
- Holbourn, A. Angular momentum of circularly polarised light. Nature 1936, 137, 31. [Google Scholar] [CrossRef]
- Garcés-Chávez, V.; McGloin, D.; Padgett, M.J.; Dultz, W.; Schmitzer, H.; Dholakia, K. Observation of the transfer of the local angular momentum density of a multiringed light beam to an optically trapped particle. Phys. Rev. Lett. 2003, 91, 093602. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, Y.; Zhu, Z.; Rui, G.; Cui, Y.; Gu, B. Theoretical investigation on asymmetrical spinning and orbiting motions of particles in a tightly focused power-exponent azimuthal-variant vector field. Opt. Express 2018, 26, 4318–4329. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Transverse spin of a surface polariton. Phys. Rev. A 2012, 85, 061801. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Transverse and longitudinal angular momenta of light. Phys. Rep. 2015, 592, 1–38. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P. Vector Lissajous laser beams. Opt. Lett. 2020, 45, 4112–4115. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Alonso, M.A.; Ostrovskaya, E.A.; Aiello, A. Angular momenta and spin-orbit interaction of nonparaxial light in freespace. Phys. Rev. A 2010, 82, 063825. [Google Scholar] [CrossRef]
- Zhu, W.G.; She, W.L. Transverse angular momentum and transverse barycenter shift of a focused light field due to nonuniform input angular momentum. Opt. Lett. 2014, 39, 1337–1340. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-wave-front laser-beams produced with a spiral phase plate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Berry, M.V. Optical currents. J. Opt. A-Pure Appl. Opt. 2009, 11, 094001. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G.; Kovalev, A.A. Formation of the reverse flow of energy in a sharp focus. Comput. Opt. 2019, 43, 714–722. [Google Scholar] [CrossRef]
- Barber, P.W. Scattering and absorption efficiencies for nonspherical dielectric objects-biological models. IEEE Trans. Biomed. Eng. 1978, BME-25, 155–159. [Google Scholar] [CrossRef]
- Maruo, S.; Takaura, A.; Saito, Y. Optically driven micropump with a twin spiral microrotor. Opt. Express 2009, 17, 18525–18532. [Google Scholar] [CrossRef]
- Rodrigo, P.J.; Kelemen, L.; Palima, D.; Alonzo, C.A.; Ormos, P.; Glückstad, J. Optical microassembly platform for constructing reconfigurable microenvironments for biomedical studies. Opt. Express 2009, 17, 6578–6583. [Google Scholar] [CrossRef]




| 2 points | –1 | |||||
| 3 points | –1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ustinov, A.V.; Porfirev, A.P.; Khonina, S.N. Interference Generation of a Reverse Energy Flow with Varying Orbital and Spin Angular Momentum Density. Photonics 2024, 11, 962. https://doi.org/10.3390/photonics11100962
Ustinov AV, Porfirev AP, Khonina SN. Interference Generation of a Reverse Energy Flow with Varying Orbital and Spin Angular Momentum Density. Photonics. 2024; 11(10):962. https://doi.org/10.3390/photonics11100962
Chicago/Turabian StyleUstinov, Andrey V., Alexey P. Porfirev, and Svetlana N. Khonina. 2024. "Interference Generation of a Reverse Energy Flow with Varying Orbital and Spin Angular Momentum Density" Photonics 11, no. 10: 962. https://doi.org/10.3390/photonics11100962
APA StyleUstinov, A. V., Porfirev, A. P., & Khonina, S. N. (2024). Interference Generation of a Reverse Energy Flow with Varying Orbital and Spin Angular Momentum Density. Photonics, 11(10), 962. https://doi.org/10.3390/photonics11100962






