Abstract
Multi-channel holographic metasurfaces have great potential for applications in wireless communications and radar. However, geometric phase-based multichannel metasurface units often have complex phase spectra, making the design of holographic metasurfaces complex and time-consuming. To address this challenge, we propose a dynamic attention mixer-based residual network to streamline the optimization and design of a multi-channel holographic metasurface unit. We conduct validation using multi-channel metasurface units, with a training set mean squared error (MSE) of 0.003 and a validation set MSE of 0.4. Additionally, we calculate the mean absolute error (MAE) for the geometric parameters θ1 and θ2 of the backward-predicted metasurface units in the validation set, which are 0.2° and 0.6°, respectively. Compared to traditional networks, our method achieves robust learning outcomes without the need for extensive datasets and provides accurate results even in complex electromagnetic responses. It is believed that the method presented in this paper is also applicable to the design of other artificial materials or multifunctional metasurfaces.
1. Introduction
Metasurfaces are two-dimensional artificial electromagnetic materials composed of arrays of meta-atoms that exhibit a high degree of freedom in manipulating electromagnetic (EM) waves [1]. As the two-dimensional counterpart of metamaterials, metasurfaces exhibit exceptional physical properties that are not found in conventional materials. This enables the flexible regulation of electromagnetic properties [2,3,4]. Owing to the flexible modulation of EM waves, metasurfaces have spawned a number of enchanting applications, such as perfect absorbers [5,6], cloaking devices [7,8], planar meta-lens [9,10] and meta-holograms [11,12]. The capacity of metasurface holography to reconstruct wavefronts has generated considerable interest, with the technology opening new avenues for microwave and optical devices [13,14]. Many fascinating works are springing up, which have greatly enriched the design and application of holograms. The conventional techniques for the design of metasurfaces frequently necessitate a trial-and-error optimization process [15], which is dependent on the designer’s empirical extrapolation of the electromagnetic response of the meta-atom and is a time-consuming endeavor [16]. In order to enhance the design efficiency, the researchers endeavored to address these issues through the utilization of optimization algorithms, including reinforcement learning algorithms [17] and particle swarm optimization algorithms [18]. Nevertheless, these algorithms often encounter difficulties in converging towards the global optimal solution.
In recent years, machine learning has emerged as a prominent area of research, rapidly attracting significant attention from the academic community. Deep learning, a branch of machine learning, has demonstrated its powerful expressions and predictive capabilities, quickly becoming a focal point in the field of artificial intelligence. Its applications span diverse domains, including image classification [19], behavioral prediction [20] and natural language processing [21]. Naturally, due to its strong data-learning capabilities, deep learning has also been introduced into the design of metasurfaces, such as multi-band absorbers [22], metasurface lenses [23], and holograms [24]. For hologram learning, the most common methods are applied at the microstructural level, encompassing both forward and inverse design of metasurface units. That is, the EM response can be directly inferred from the unit structure. Conversely, the geometrical parameters can be derived from the EM responses [25,26]. In the event of encountering more intricate EM spectra, it becomes necessary to increase the number of nodes and layers within the network to fit these complex response spectra. However, this approach of enlarging the network size inevitably leads to increased computational complexity, extended runtime, and heightened resource utilization pressure. Recently, Jiafu Wang et al. [27] have used residual networks to learn the complex amplitude responses of metasurfaces, thereby achieving the learning of metasurface holography. However, there are problems of low learning efficiency and slow learning speed for the structure design of the meta-atoms. Moreover, when designing multi-channel metasurface holography [28], the geometric parameters that control the phase in different bands are interdependent, which has the effect of reducing the accuracy of the design and increasing the complexity of the metasurface unit. Moreover, due to the complexity of the data, it is often necessary to increase the number of network layers to learn these deep relationships.
To address these challenges, this paper proposes a dynamic attention mixer-based residual network (DAMR) architecture for the inverse design of metasurface units. The prediction units are arranged into an array using the angular spectral diffraction algorithm to realize the holographic reconstruction verification. This approach allows for the rapid prediction of structural parameters from electromagnetic responses, offering a promising solution for the fast and precise design of metasurface units. Furthermore, a novel DAMR is introduced, which integrates a long short-term memory module, a dynamic attention mechanism, and parallel mixer modules within the residual module by using the dynamic attention mechanism to assign different weights to different frequency bands, effectively decreasing the crosstalk issues between bands, and employs an LSTM module along with parallel mixers to enhance feature extraction and accelerate the training process. Compared to traditional residual modules, the proposed approach not only enhances the feature extraction process but also facilitates the capture of the temporal sequence relationship of the input electromagnetic responses. This is achieved through the incorporation of a long short-term memory module and a dynamic attention mechanism, which enables the accurate prediction of the structural parameters of the metasurface unit. Subsequently, the simulated dataset of the unit is obtained for training, the mean squared error (MSE) of the validation dataset stabilizes below 0.4, and the mean absolute error (MAE) for the two structural parameters is less than 0.6°. We also conducted simulation tests on the predicted units in the validation set and compared them with the true phases, calculating the average absolute phase error of 3.16°. Furthermore, the peak signal-to-noise ratio (PSNR) is introduced to evaluate the quality of holographic images, with PSNR values of 40.8 dB and 29.156 dB for “V” and “L”, respectively, confirming high-resolution images. This method can not only be applied to multi-channel holographic metasurfaces but can also be extended to the design of multi-polarization, multi-wavelength metasurface devices in the future, enabling rapid design and prediction.
2. Structure and Methodology
The inverse design schematic diagram of dual-band metasurface holographic based on the DAMR network is illustrated in Figure 1. Here, a multi-channel metasurface holographic unit based on multiple annular resonators is designed, which manipulates circularly polarized waves based on the principle of geometric phase [29,30]. Dual-band phase control is achieved by adjusting the rotation angle of the resonators. The meta-atoms are simulated using full-wave simulation software in order to obtain electromagnetic (EM) response curves, which are used to build a dataset for training DAMR networks. The acquired dataset comprises the phase curves and geometric parameters of the elements. The data samples are employed for the purpose of training the network, with the objective of obtaining the predicted metasurface elements. Subsequently, the target image is phase-encoded to obtain the encoded array and the predicted unit is arranged according to the encoded array to obtain the predicted dual-channel holographic images.
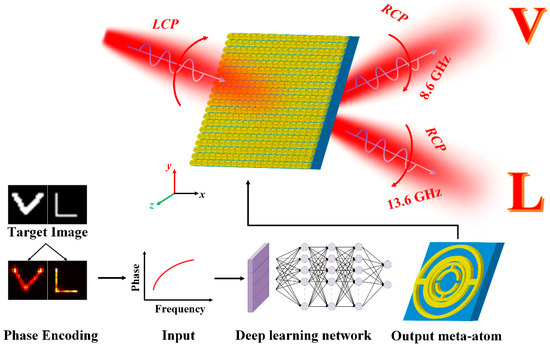
Figure 1.
The inverse design of dual-band metasurface holography by controlling phase based on the deep learning network.
To verify the reliability of the network, a dual-channel metasurface unit based on transmission modes is designed in this study, which consists of a metal layer and a substrate, as shown in Figure 2. The metal layer includes an improved double C-slot resonator (MDCSR) and a double C-open slot resonator (DCOSR). The metal layer is made of copper metal, with a thickness of t = 0.035 mm. The substrate is made of F4B (εr = 2.2, tanδ = 0.001) dielectric material, with a thickness of h = 2 mm. Figure 2a demonstrates the front view of the metasurface structure, where r1 = 5.7 mm, r2 = 4 mm, r3 = 3 mm, r4 = 2 mm, w1 = 0.5 mm, w2 = 0.8 mm, w3 = 0.4 mm, w4 = 0.4 mm, d1 = 0.9 mm, d2 = 0.4 mm, and d3 = 0.4 mm. In order to obtain the 2π phase variation and provide full-wave front control, the PB phase is employed to manipulate the phase shift of the circularly polarized wave.
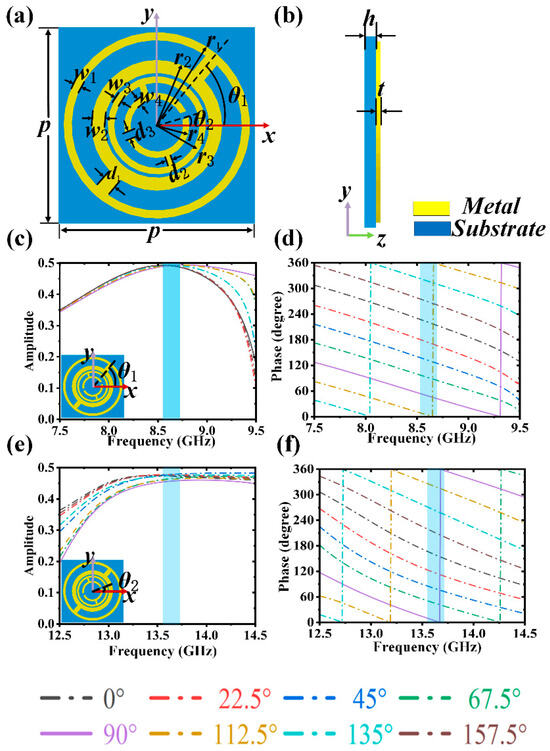
Figure 2.
Schematic diagram of the metasurface element structure and the propagation characteristics under LCP wave incidence. (a) The front view of the metasurface unit structure. (b) The side view of the metasurface unit structure. (c,d) The transmission amplitude and phase shift at 8.6 GHz with varying rotation angles θ1. (e,f) The transmission amplitude and phase shift at 13.6 GHz with varying rotation angles θ2. The blue shaded area represents uniform phase variation.
When a meta-atom is rotated by an angle of θ and illuminated with right circularly polarized (RCP) and left circularly polarized (LCP) waves (/), the RCP and LCP components of the transmissive wave can be expressed as [31] Equation (1):
where t0 and te are the complex amplitude coefficients of the linearly polarized incident wave along the two principal axis directions of the anisotropic meta-atoms. From Equation (1), it can be observed that the metasurface is capable of generating cross-polarization components carrying additional phase shifts (±2θ) under circular polarization illumination. By rotating the meta-atoms from 0 to π, the 2π phase coverage can be achieved.
To characterize the performance of the proposed dual-band meta-atoms, numerical simulations are carried out using the commercial electromagnetic simulation software CST Microwave Studio (2020). The x and y boundary conditions are set to periodic boundaries, while the z direction is set to an open boundary. LCP wave is vertically incident from the top metal layer onto the substrate, while RCP wave is transmitted through the structure in the transmission mode. As illustrated in Figure 2c–f, when the rotation angle θ1 (θ2) of the resonator is varied from 0 to π in increments of π/8, the amplitude of the metasurface elements at f1 = 8.6 GHz (f2 = 13.6 GHz) exceeds 0.45, approaching the theoretical maximum of 0.5 [32,33]. At this point, the phase shift of the metasurface element achieves full phase coverage close to 2π. Therefore, by adjusting the values of θ1 and θ2, higher transmission efficiency and 2π phase shift are achieved at frequencies f1 = 8.6 GHz and f2 = 13.6 GHz, allowing to achieve 2-bit phase encoding with the designed meta-atom. By rotating the angles θ1 and θ2 of the MDCSR and DCOSR, respectively, the corresponding phases of the two resonators could be changed, enabling arbitrary phase modulation at the two operating frequencies.
3. The Design of Reverse Network Structure
Since cross-coupled interference is difficult to achieve independent control and precise design, it is challenging to flexibly control the phase response of the two frequency bands by adjusting the rotation angles of the two resonators. As the two rotation angles θ1 and θ2 rotate, the different parameters result in phase differences and mutual interference between the two frequencies. In order to facilitate the learning of such complex spectral responses, it may be effective to increase the size of the dataset or to enhance the sophistication of the model. However, as the dataset and model depth increase, the learning difficulty and resource occupation also increase. To address this, this paper proposes a dynamic attention mixer-based residual network (DAMR) to learn the correspondence between structural parameters and electromagnetic responses.
In this study, a unique mechanism that integrates dynamic attention with mixers in the residual blocks is introduced to balance the data volume and depth within the network model. As shown in Figure 3, the DAMR network includes an encoder, a residual module, and three fully connected layers. The encoder is meticulously designed and consists of three convolution–pooling–activation modules, each comprising a one-dimensional convolutional layer, a MaxPool layer, and a rectified linear unit (ReLU) activation function. The input channels of the one-dimensional convolutional layer are set to [1, 32, 64] and the output channels are set to [32, 64, 128]. The kernel size and stride of the convolutional operation are set to 3 and 2, respectively, with a padding of 0. The MaxPool operation has a kernel and stride of 2. The encoder performs convolutional operations to extract features and reduces the spatial dimensions of the feature maps using pooling, while the ReLU activation function introduces nonlinearity, enhancing the model’s representation capability.
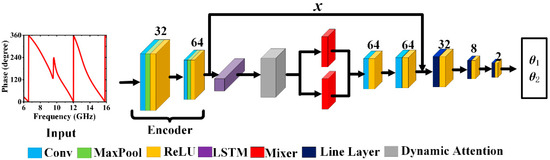
Figure 3.
The network architecture diagram.
The traditional residual module consists of convolutional layers, activation function layers, and a residual skip connection. However, it requires high precision and a large amount of training data, leading to potential issues such as gradient vanishing and exploding during the training process. Therefore, this study proposes an innovative residual module based on a dynamic attention mixer. The residual module includes a long short-term memory (LSTM) module, a dynamic attention module, two parallel mixer modules, two sets of convolution–activation modules, and a residual skip connection. Each mixer module consists of two linear layers with hidden dimensions and two ReLU activation functions. After processing each feature through the LSTM layer, a corresponding hidden state for each piece of data is obtained. These hidden states store the features extracted from the data and include contextual information about the EM spectra. Among these, the final hidden state of the LSTM layer is particularly important, as it represents the ultimate state of the entire EM spectra. Here, the last hidden state is passed to the dynamic attention mechanism, yielding a dynamic attention weight, which indicates the model’s focus on feature points in the phase spectra. Finally, the dynamic attention weight is integrated with the last hidden state of the LSTM layer to form a new state feature, which is then passed to the mixer module for independent mixing operations. The outputs are then aggregated and collectively passed into the convolution–activation modules to extract features from the mixed data. The convolution–activation modules consist of a convolutional layer with a kernel size of 3 and padding of 1, followed by a ReLU activation function to introduce nonlinearity for the mixed input features. Finally, four fully connected layers (FCs) are used for linear transformations and output prediction, with input dimensions of [n*s, 64, 16, 8] (n represents the number of feature channels, s represents the sequence length, both values are obtained from algorithmic computations) and output dimensions of [256, 64, 8, 2]. The dynamic attention mixer residual module enhances the model’s representation capability and adaptability, improving network performance. Although the mixed information is fed to the FC layers, the original information extracted by the encoder is also directly connected to the FC layers to prevent the potential loss of important mixed information. This dual-input strategy ensures that the network retains crucial subtle differences in the input data, contributing to the overall accuracy and effectiveness of the DAMR model.
Since the phase spectrum has a complex data structure, it may meet the jump of 0–360° at the abrupt change. This abrupt phase change seriously interferes with the prediction of the network. To address this issue, preprocessing is performed on the network’s input, removing numerical differences between various parameters [34]. The input data are preprocessed by z-score normalization. Equation (2) is used for preprocessing:
Here, represents the mean of the dataset, and represents the standard deviation of the dataset.
Due to the potential loss of features during the process of summing and averaging by the mixer, in order to extract data features as much as possible, a residual skip connection is added in this study. It concatenates the encoder output with the data processed through the residual block. The residual connection calculation is shown in Equation (3).
In this equation, x represents the input vector, represents the output vector obtained through mixer and convolutional layer operations, and y represents the output vector after the residual connection. High-dimensional features extracted through residual combination are passed to the fully connected layers after being flattened. Finally, the network predicts the geometric parameters for the metasurface unit. The loss function is the mean squared error (MSE) function, which can be represented by Equation (4). The smaller the MSE value, the closer the predicted values are to the true values, indicating higher model accuracy. Furthermore, the performance of parameters θ1 and θ2 is also evaluated by the mean absolute error (MAE) function Equation (5). The smaller the MAE value, the closer the predicted values are to the true values, indicating higher model accuracy.
where yi represents the predicted value, yr represents the true value, and n represents the number of samples. The value of the loss function is used to update the weights of the network through backpropagation. The model is optimized using the Adam optimizer, with an initial learning rate set to 0.001. The Adam optimizer possesses adaptability, allowing for dynamic adjustment of training effectiveness during the optimization process.
The dataset is obtained using the commercial electromagnetic simulation software CST Microwave Studio (2020). The values of θ1 and θ2 range from 0 to 180°, with a sampling interval of 5° (excluding 180°). After generating an additional batch of random angle data and excluding some erroneous data, a total of 1740 units and their corresponding EM responses are collected as the dataset. The input data consist of phase responses from 6–16 GHz, and the output data are the rotation angles of θ1 and θ2. The dataset is divided into a training set and a validation set in a ratio of 90% to 10%, respectively. The training batch size is set to 300, and iterations are performed 10,000 times. The performance of the MSE loss function is shown in Figure 4a, indicating a rapid decrease and convergence of the loss function values for both the training and validation sets. After 2000 iterations, the MSE loss of the model converges to around 1.5 for both the training and validation sets. After 10,000 iterations, the MSE loss of the model converges to 0.003 and 0.4 on the two sets, respectively. Compared with reference [27] (epoch = 2000, MSE = 13), our validation set has a smaller MSE loss after the same 2000 iterations. Additionally, this paper includes the MAE as further validation. As can be observed from Figure 4b,c, after 2000 training iterations, the MAEs for θ1 and θ2 are 0.5° and 0.7°, respectively. After 10,000 training iterations, the MAEs for θ1 and θ2 are 0.2° and 0.6°, respectively.
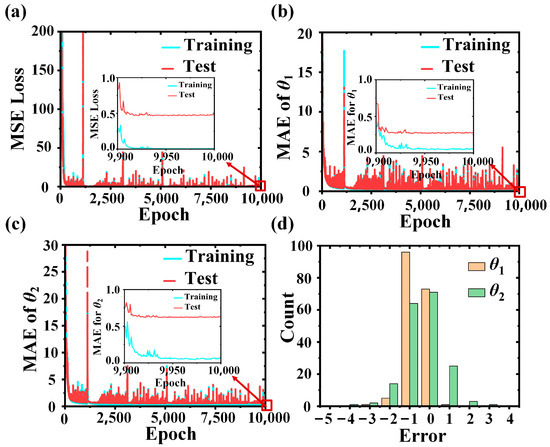
Figure 4.
Statistical plots of MSE, MAE loss, and error for network training. (a) The variation in MSE during training with the DAMR. (b) The change in MAE for θ1 during training. (c) The change in MAE for θ2 during training. (d) The error histogram distribution for θ1 and θ2. The vertical axis represents quantity, and the horizontal axis represents error.
In this study, predictions are made using the well-trained model, and the errors between the predicted and actual values are accumulated and displayed through histograms. Figure 4d indicates that 95% of the data in the validation set have absolute errors concentrated between approximately −1° and 1°, with only a very small number of absolute errors distributed between approximately 1° and 4° as well as between approximately −4° and −1°. The absolute errors follow a Gaussian distribution, which suggests that the network has good predictive capabilities. However, there are some singularities in the training process, which are caused by the stochastic gradient algorithm. The model adopts Adam optimizer, which is adaptive and can dynamically adjust the training effect during the optimization process. As a result, the model can quickly jump out of these singularities, which ensures the robustness of the model. We also conduct simulation tests on the predicted units in the validation set and compare them with the true phases, calculating the average absolute phase error to be 3.16°. This proves that the network has good prediction ability.
4. Results and Discussion
To validate the effectiveness of the network and the dynamic attention mixer, this paper employs multiple networks for comparative experiments under the same conditions: a Resnet network without the addition of a dynamic attention mixer module, a CNN network without any added modules, and a CNN network with an added dynamic attention mixer module (DA-Mixer-CNN), as shown in Table 1. After training each of these networks for 10,000 iterations, the MSE for the Resnet is 1, for the CNN network is 0.8, and for the DA-Mixer-CNN network is 0.6. It can be observed that in the process of learning the complex phase spectrum in the dual-frequency band, the traditional network’s performance is actually not good with a small number of datasets, while the network with the added dynamic attention mixer module has shown certain improvements in both learning efficiency and convergence speed. We also conduct a comparative study with some state-of-the-art (SOTA) networks, such as deep ResNet50 and MSCDNN networks. It can be observed that both MSE and MAE have decreased when learning with the deep ResNet50 network, but the training time is significantly increased. Moreover, it occupies a considerable amount of computational resources. Learning using the MSCDNN network may be affected by singular data in the dataset, resulting in a poor learning effect. This phenomenon may also be associated with the complexity of the phase response. We attempted to manually remove some singular data and found that the loss decreased, indicating that the MSCDNN network still faces some challenges when learning from small datasets.

Table 1.
MSE losses and MAE losses for θ1 and θ2 obtained from different networks training.
As shown in Table 2, several units are randomly selected from the test set and their geometric parameters are predicted using the different networks. It can be seen from the table that the improvement of the network’s learning effect by the Mixer is significant. Furthermore, the proposed DAMR network in this study has shown a substantial improvement compared to traditional networks. This study randomly selected metasurface units and validated the validation set using the DAMR network. The prediction curves shown in Figure 5a–d demonstrate that the predicted results are generally consistent with the actual results. Therefore, under the conditions of a fixed dataset size and network depth, the learning efficiency of the proposed network in this paper remains high.

Table 2.
The performance of different networks in predicting geometric parameters.
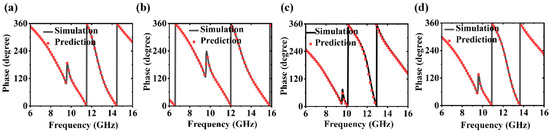
Figure 5.
Result prediction. (a–d) The prediction curves obtained by randomly predicting four units using the DAMR.
In addition, we compare phase errors and dataset sizes in references [27,35,36], with the results shown in Table 3. It can be observed that Ref. [27] has a slightly lower phase error due to its implementation of single-channel holography, which experiences almost no crosstalk in the phase response. In contrast, for multi-channel holographic designs in Ref. [35], it is found that with a small dataset, the 10°phase error is somewhat large. In Ref. [36], a large amount of data are used, resulting in a small phase error of 3.28°, but the increase in the dataset also leads to an increase in training time and computational resources. Our multi-channel holographic design, using a smaller dataset, achieved a small phase error of 3.16°, which fully demonstrates the effectiveness of our network.

Table 3.
Comparison of training epoch, phase errors, and dataset for different designs.
5. Simulation Testing
To further validate the feasibility of the network, we construct a dual-channel metasurface array. As shown in Figure 6a,b, the target images “V” and “L” are discretized into 0 and 1 pixels, and the angular spectral diffraction algorithm [37] is used to encode the phase of the target images. The encoded target images are propagated through diffraction using the diffraction propagation formula, yielding theoretical diffraction images and encoding arrays, with the units arranged in an array configuration. The metasurface array is simulated using the CST Microwave Studio. The number of metasurface units is set to 20 × 20, and the array size is 240 mm × 240 mm. The electromagnetic waves are incident on the metasurface from the top with LCP waves, and the RCP waves are transmitted from the substrate. The reconstruction of “V” and “L” is achieved at a distance of 61 mm from the metasurface at 8.6 GHz and 13.6 GHz, as shown in Figure 6c,d.
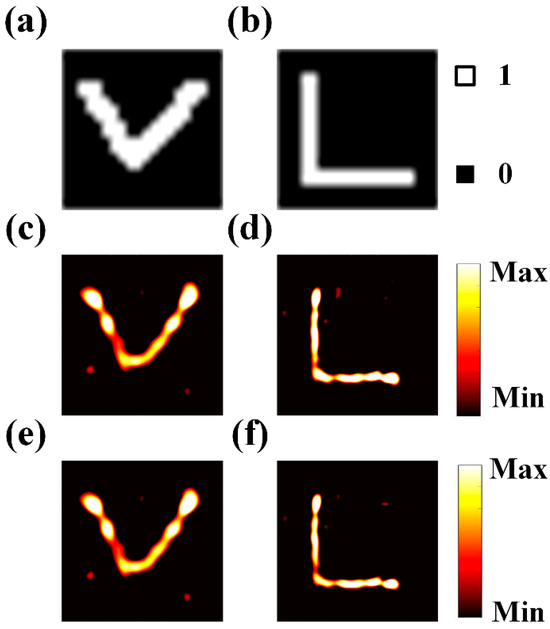
Figure 6.
The inverse design and simulation of the meta-surface. (a,b) The discretized input images “V” and “L”. (c,d) The electric field images of “V” and “L” reconstructed at a distance of 61 mm from the metasurface at frequencies of 8.6 GHz and 13.6 GHz. (e,f) The predicted results of “V” and “L” obtained through network prediction.
Simultaneously, this paper also uses a neural network to predict the metasurface units, obtaining the predicted metasurface structure and performing holographic simulations using the same method. The results are shown in Figure 6e,f. Here, the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) are used for assessing image quality. PSNR is used to compare the difference between the original image and the reconstructed image. SSIM is an index used to assess the similarity between two images based on their luminance, contrast, and structural information, with the formulas for PSNR and SSIM being represented as Equation (6) and Equation (7), respectively.
where the MAXI represents the maximum pixel value and MSE is the mean square error.
Here, μx and μy represent the means of x and y, respectively. σx and σy represent the standard deviations of x and y in sequence. σxy indicates the covariance between x and y. c1 and c2 are constants.
When the PSNR is around 30 dB and the SSIM is greater than 95%, it can be considered that the two images are almost identical [38,39]. In this study, the predicted images for “V” and “L” have PSNR values of 40.8 dB and 29.156 dB, respectively, and SSIM values of 99.6% and 97.8%, respectively.
6. Conclusions
In this paper, a deep learning-based holographic metasurface optimization method is proposed, which is capable of predicting the geometrical parameters of the meta-atom structure to achieve the design of dual-channel holographic metasurfaces. The structural parameters of the metasurface can be rapidly estimated by inputting the target phase response. In comparison to the conventional metasurface design methodology, the optimization network proposed in the article is capable of expediting the scanning and optimization of parameters. This study also introduces an innovative dynamic attention mixer residual module to further extract features, optimize the crosstalk between spectra and reduce dependence on large datasets, which includes an LSTM module, a dynamic attention mechanism, and parallel mixers. The MAE for θ1 and θ2 is below 0.6°, and the errors for the validation set are found to follow a Gaussian distribution, demonstrating high prediction accuracy and reliability of the inverse design. The predicted unit structure is employed for holographic display and is then compared with the holographic image generated from the original unit structure. The PSNR values for “V” and “L” are 40.8 dB and 29.156 dB, respectively, indicating a close match between the predicted and original holographic images. In summary, our proposed deep learning-based multi-channel holographic metasurface unit optimization method can learn complex phase responses with small datasets and still show high learning efficiency, which is conducive to more efficient design and optimization of metasurface devices. It is anticipated that the method will be extended to higher channels in the future, thereby achieving greater efficiency in the de metasurface design.
Author Contributions
Conceptualization, H.Z.; Funding acquisition, L.Z.; Project administration, L.Z.; Supervision, L.Z., L.D., Z.L. and X.D.; Writing—original draft, H.Z.; Writing—review & editing, L.Z. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by the Natural Science Foundation of Heilongjiang Province (Grant No. LH2022F053), National Natural Science Foundation of China (Grant No. 62275063, 62171153), Postdoctoral Research Fund Project of Heilongjiang Province of China (Grant No. LBH-Q21195), and Fundamental Research Funds of Heilongjiang Provincial Universities of China (Grant No. 145209151).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EM | electromagnetic |
| DAMR | dynamic attention mixer-based residual |
| MSE | mean squared error |
| MAE | mean absolute error |
| MDCSR | double C-slot resonator |
| DCOSR | double C-open slot resonator |
| RCP | right circularly polarized |
| LCP | left circularly polarized |
| ReLU | Rectiffed linear unit |
| LSTM | long short-term memory |
| FC | Fully connected layers |
| PSNR | peak signal-to-noise ratio |
| SSIM | structural similarity |
| SOTA | some state of the arts |
References
- Chen, S.; Liu, W.; Li, Z.; Cheng, H.; Tian, J. Metasurface-empowered optical multiplexing and multifunction. Adv. Mater. 2020, 32, e1805912. [Google Scholar] [CrossRef] [PubMed]
- Zeng, C.; Lu, H.; Mao, D.; Du, Y.; Hua, H.; Zhao, W.; Zhao, J. Graphene-empowered dynamic metasurfaces and metadevices. Opto-Electronic Adv. 2022, 5, 200098. [Google Scholar] [CrossRef]
- Gigli, C.; Leo, G. All-dielectric χ(2) metasurfaces: Recent progress. Opto-Electronic Adv. 2022, 5, 210093-1–210093-14. [Google Scholar] [CrossRef]
- Liang, S.; Xu, F.; Li, W.; Yang, W.; Cheng, S.; Yang, H.; Chen, J.; Yi, Z.; Jiang, P. Tunable smart mid infrared thermal control emitter based on phase change material VO2 thin film. Appl. Therm. Eng. 2023, 232, 121074. [Google Scholar] [CrossRef]
- Li, W.; Zhao, W.; Cheng, S.; Zhang, H.; Yi, Z.; Sun, T.; Wu, P.; Zeng, Q.; Raza, R. Tunable metamaterial absorption device based on Fabry–Perot resonance as temperature and refractive index sensing. Opt. Lasers Eng. 2024, 181, 108368. [Google Scholar] [CrossRef]
- Ra’di, Y.; Simovski, C.R.; Tretyakov, S.A. Thin perfect absorbers for electromagnetic waves: Theory, design, and realizations. Phys. Rev. Appl. 2015, 3, 037001. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef]
- Xu, H.X.; Hu, G.; Wang, Y.; Wang, C.; Wang, M.; Wang, S.; Huang, Y.; Genevet, P.; Huang, W.; Qiu, C.-W. Polarization-insensitive 3D conformal-skin metasurface cloak. Light Sci. Appl. 2021, 10, 75. [Google Scholar] [CrossRef]
- Lou, Q.; Chen, Z.N. Sidelobe suppression of metalens antenna by amplitude and phase controllable metasurfaces. IEEE Trans. Antennas Propag. 2021, 69, 6977–6981. [Google Scholar] [CrossRef]
- Yi, Z.; Gaofeng, L.; Zhongquan, W.; Zhihai, Z.; Zhengguo, S.; Gang, C. Recent research progress in optical super-resolution planar meta-lenses. Opto-Electron. Eng. 2021, 48, 210399-1–210399-19. [Google Scholar]
- Zhu, L.; Zhou, W.; Dong, L.; Wu, Q.; Shah, N.; Ding, X. Multifunctional full-space metahologram employing a monolayer phase-encoding metasurface. Phys. Rev. Appl. 2022, 18, 054080. [Google Scholar] [CrossRef]
- Zhu, L.; Wei, J.; Dong, L.; Shang, G.; Shah, N.; Ding, X. Multi-Dimensional Meta-Holography Encrypted by Orbital Angular Momentum, Frequency, and Polarization. Laser Photonics Rev. 2024, 18, 2301362. [Google Scholar] [CrossRef]
- Shang, G.; Wang, Z.; Li, H.; Zhang, K.; Wu, Q.; Burokur, S.N.; Ding, X. Metasurface holography in the microwave regime. Photonics 2021, 8, 135. [Google Scholar] [CrossRef]
- Wan, W.; Gao, J.; Yang, X. Metasurface holograms for holographic imaging. Adv. Opt. Mater. 2017, 5, 1700541. [Google Scholar] [CrossRef]
- So, S.; Badloe, T.; Noh, J.; Bravo-Abad, J.; Rho, J. Deep learning enabled inverse design in nanophotonics. Nanophotonics 2020, 9, 1041–1057. [Google Scholar] [CrossRef]
- Chen, P.; Chen, J.; Yan, H.; Mo, Q.; Xu, Z.; Liu, J.; Zhang, W.; Yang, Y.; Lu, Y. Improving material property prediction by leveraging the large-scale computational database and deep learning. J. Phys. Chem. C 2022, 126, 16297–16305. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, L.; Lanteri, S.; Viquerat, J. Dynamic metasurface control using deep reinforcement learning. Math. Comput. Simul. 2022, 197, 377–395. [Google Scholar] [CrossRef]
- Goudos, S.K.; Sahalos, J.N. Microwave absorber optimal design using multi-objective particle swarm optimization. Microw. Opt. Technol. Lett. 2006, 48, 1553–1558. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Phan, N.; Dou, D.; Wang, H.; Kil, D.; Piniewski, B. Ontology-based deep learning for human behavior prediction with explanations in health social networks. Inf. Sci. 2017, 384, 298–313. [Google Scholar] [CrossRef]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A Survey of the usages of deep learning for natural language processing. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 604–624. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Du, W.; Dong, L.; Wei, J. Optimized design for absorption metasurface based on autoencoder (AE) and BiLSTM-Attention-FCN-Net. Phys Scr. 2024, 99, 036002. [Google Scholar] [CrossRef]
- Dou, K.; Xie, X.; Pu, M.; Li, X.; Ma, X.; Wang, C.; Luo, X. Off-axis multi-wavelength dispersion controlling metalens for multi-color imaging. Opto-Electron. Adv. 2020, 3, 190005. [Google Scholar] [CrossRef]
- Sajedian, I.; Lee, H.; Rho, J. Double-deep Q-learning to increase the efficiency of metasurface holograms. Sci. Rep. 2019, 9, 10899. [Google Scholar] [CrossRef]
- Ma, W.; Liu, Z.; Kudyshev, Z.A.; Boltasseva, A.; Cai, W.; Liu, Y. Deep learning for the design of photonic structures. Nat. Photonics 2021, 15, 77–90. [Google Scholar] [CrossRef]
- Malkiel, I.; Mrejen, M.; Nagler, A.; Arieli, U.; Wolf, L.; Suchowski, H. Plasmonic nanostructure design and characterization via deep learning. Light. Sci. Appl. 2018, 7, 60. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Wang, J.; Fu, X.; Liu, X.; Liu, T.; Chu, Z.; Han, Y.; Qiu, T.; Sui, S.; Qu, S.; et al. Deep-learning-empowered holographic metasurface with simultaneously customized phase and amplitude. ACS Appl. Mater. Interfaces 2022, 14, 48303–48310. [Google Scholar] [CrossRef]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.F.; Wong, P.W.H.; Cheah, K.W.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef]
- Huang, J.; Pogorzelski, R. A Ka-band microstrip reflectarray with elements having variable rotation angles. IEEE Trans. Antennas Propag. 1998, 46, 650–656. [Google Scholar] [CrossRef]
- Bomzon, Z.; Biener, G.; Kleiner, V.; Hasman, E. Space-variant Pancharatnam–Berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 2002, 27, 1141–1143. [Google Scholar] [CrossRef]
- Hsiao, H.H.; Chu, C.H.; Tsai, D.P. Fundamentals and applications of metasurfaces. Small Methods 2017, 1, 1600064. [Google Scholar] [CrossRef]
- Ding, X.; Monticone, F.; Zhang, K.; Zhang, L.; Gao, D.; Burokur, S.N.; De Lustrac, A.; Wu, Q.; Qiu, C.W.; Alù, A. Ultrathin Pancharatnam–Berry metasurface with maximal cross-polarization efficiency. Adv. Mater. 2015, 27, 1195–1200. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Faraon, A. Fundamental limits of ultrathin metasurfaces. Sci. Rep. 2017, 7, srep43722. [Google Scholar] [CrossRef]
- Jiang, L.; Li, X.; Wu, Q.; Wang, L.; Gao, L. Neural network enabled metasurface design for phase manipulation. Opt. Express 2021, 29, 2521–2528. [Google Scholar] [CrossRef] [PubMed]
- Qu, K.; Chen, K.; Hu, Q.; Zhao, J.; Jiang, T.; Feng, Y. Deep-learning-assisted inverse design of dual-spin/frequency metasurface for quad-channel off-axis vortices multiplexing. Adv. Photonics Nexus 2023, 2, 016010. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, X.; Liu, K.; Zhang, H.; Shi, L.; Song, S.; Tang, D.; Guo, Y. Complex-amplitude metasurface design assisted by deep learning. Ann. der Phys. 2022, 534, 202200188. [Google Scholar] [CrossRef]
- Han, C.; Shen, Y. Three-dimensional scene encryption algorithm based on phase iteration algorithm of the angular-spectral domain. IEEE/CAA J. Autom. Sin. 2019, 7, 1074–1080. [Google Scholar] [CrossRef]
- Chen, D.; Sang, X.; Wang, P.; Yu, X.; Gao, X.; Yan, B.; Wang, H.; Qi, S.; Ye, X. Virtual view synthesis for 3D light-field display based on scene tower blending. Opt. Express 2021, 29, 7866–7884. [Google Scholar] [CrossRef]
- Wei, W.; Tang, P.; Shao, J.; Zhu, J.; Zhao, X.; Wu, C. End-to-end design of metasurface-based complex-amplitude holograms by physics-driven deep neural networks. Nanophotonics 2022, 11, 2921–2929. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).