Abstract
The traditional approach to optical design faces limitations as photonic devices grow increasingly complex, requiring advanced functionalities. Recently, machine learning algorithms have gained significant interest for extracting structural designs from customized wavelength spectra, surpassing traditional simulation methods known for their time-consuming nature and resource-demanding computational requirements. This study focuses on the inverse design of a reflectionless multilayer thin-film structure across a specific wavelength region, utilizing a tandem neural network (TNN) approach. The method effectively addresses the non-uniqueness problem in training inverse neural networks. Data generation via the transfer matrix method (TMM) involves simulating the optical behavior of a multilayer structure comprising alternating thin films of silicon dioxide (SiO2) and silicon (Si). This innovative design considers both reflection and absorption properties to achieve near-zero reflection. We aimed to manipulate the structure’s reflectivity by implementing low-index and high-index layers along with Si absorption layers to attain specific optical properties. Our TNN demonstrated an MSE accuracy of less than 0.0005 and a maximum loss of 0.00781 for predicting the desired spectrum range, offering advanced capabilities for forecasting arbitrary spectra. This approach provides insights into designing multilayer thin-film structures with near-zero reflection and highlights the potential for controlling absorption materials to enhance optical performance.
1. Introduction
The pursuit of optical materials and structures that effectively manipulate light propagation has been a foundational endeavor in the field of photonics and optical engineering. By meticulously controlling the film thickness and the properties of materials, thin films can be customized to suit various optical applications [1,2,3]. Moreover, the exploration finds applications in diverse domains, such as the achievement of thin film in solar cells to enhance photovoltaic efficiency [4], the integration of metamaterial elements into thin-film coatings focusing on gas-sensing capabilities, and the potential for enhancing sensor performance for practical applications [5]. Recently, thin-film multilayers with tailored optical properties have shown immense promise for various applications, including TiO2 multilayer thin films for environmental applications [6], heater applications (investigated mainly with sheet resistance and promotion of grain growth in laser annealing) [7], and advanced glazing systems, due to their unique properties and versatility [8].
Designing multilayer thin films presents significant challenges due to the complexity and computational inefficiencies of traditional simulation methods. These methods often suffer from time constraints and high complexity, making them less practical for intricate designs. As a result, machine learning algorithms have garnered considerable attention in photonic research for their potential to overcome these limitations. However, the role and necessity of machine learning in multilayer design remain critical areas of ongoing evaluation and discussion. Researchers investigating techniques have leveraged the power of artificial intelligence to optimize and create structures with desired optical properties using the advantages of deep learning and inverse design machine learning algorithms. The adoption of deep learning in the inverse design of thin films has paved the way for enhancing efficiency and performance in this field. A notable example is the high-precision simulation of nanophotonics using inverse design and artificial neural networks [9]. Another example is the development of a deep generative model that effectively addresses the metamaterial design problem by employing an encoder–decoder architecture to manage the inverse design process [10]. Compared to this reference, our work is advanced by incorporating absorption layers, thereby addressing reflection and absorption simultaneously. Additionally, our study presents a broader application scope with a focus on practical, near-zero reflection design, demonstrating clear improvements in predictive accuracy and practical applicability. A study introduced an inverse design using a 1D convolutional network with a neural adjoint method to predict absorption spectra for metasurface absorbers [11]. These methods are imperative to address the need for improvement in neural networks to tackle the challenges posed by non-uniqueness in complex inverse design. TNN presents distinct advantages over other probability-based neural networks, such as VAE and GAN, in addressing the non-uniqueness of inverse design. Its integration of forward and inverse networks provides real-time feedback, enabling adaptive adjustments during the design process and improving convergence toward optimal solutions. One study presented an inverse design of meta-atoms with high degrees of freedom by integrating deep learning and genetic algorithms [12]. Another notable approach involves the development of TNN, a sophisticated architecture designed to enhance the uniqueness and reliability of the inverse design process [13]. While simpler tasks might be addressed through parameter sweeps, TNN offers distinct advantages for complex, non-linear multilayer designs that go beyond straightforward optimization. TNN has been widely applied in many studies, and TNN has been improved for the inverse design of nanophotonics devices [14]. Moreover, one study presented an innovative approach to the inverse design of a distributed Bragg reflector using deep learning, aiming to manipulate the behavior of light in optical structures [15]. Another approach uses a tandem model with the combination of two neural networks, namely, a mixture density network and a fully connected network, to inversely design thin-film high reflectors [16]. However, implementing a multilayer structure design for these materials could present challenges in both experimental and practical contexts due to the rarity and associated costs of the substances. Researchers have also optimized datasets and hyperparameters during training to better understand and improve the performance of tandem networks. This approach is applied in the design of optical fibers, offering an effective way to design the structure [17]. This approach does not specifically include the consideration of absorption materials in the inverse design process.
Our research focuses on designing practical multilayer thin-film reflectors capable of achieving near-zero reflection. We propose an innovative approach utilizing alternating layers of SiO2 and Si to create low–high refractive index multilayers. Unlike traditional anti-reflective coatings, which prioritize minimizing reflection and maximizing transmittance, our design strategically incorporates the absorption properties of Si layers. This balance between reflectivity and absorption may lead to reduced transmittance but with enhanced overall optical performance. Traditional anti-reflective films depend on precise manual control of layer thickness and interference phase growth, whereas our TNN approach automates the design process. By integrating inverse and forward neural networks, TNN enables faster and more accurate optimization of complex multilayer structures. Additionally, our method includes absorption in the design process, allowing for broader spectral coverage and improved reflection control, which traditional approaches have not explored. We generate data using the TMM numerical simulation method with randomized layer thicknesses, enabling our neural network to design thin-film reflectors for arbitrary reflection spectra, representing a significant advancement in thin-film optics. Specifically, our optimized structure can be used in the design of anti-reflective coatings and photodetectors where precise control of reflectivity and absorption is crucial. Additionally, they can benefit solar cells by enhancing light absorption and can also be applied in advanced coatings for sensors to improve their performance by minimizing signal loss.
2. Data Collection and Simulation
Recognizing the inherent data demands of deep learning models, the data generation employed numerical simulation using TMM to create a dataset of 50,000 unique instances. Each data instance comprised randomly generated thickness values representing the thicknesses of individual layers within the thin-film structure, accompanied by the corresponding reflection spectrum within the wavelength range of 600 to 650 nm, with 1 nm spacing for 51 sampling points. The structural design of the multilayer thin-film reflector featured a five-layer arrangement surrounded by an air medium. These layers alternated between SiO2 and Si materials, as illustrated in Figure 1a. The structure design was constructed to consider practical application, aiming to achieve near-zero reflection through the strategic arrangement of alternating layers. Each layer’s thickness was randomly chosen from 10 to 99 nm. Figure 1b illustrates the inclusion of an imaginary refractive index value of Si. The refractive index of SiO2 was n1 = 1.46, while that of Si was n2 = 3.95 + 0.027i. These parameters were obtained from a refractive index database [18]. Additionally, these values were specifically selected to achieve near-zero reflection for the entire multilayer structure within the specified wavelength range. The TMM method employed for data generation can be summarized as follows.
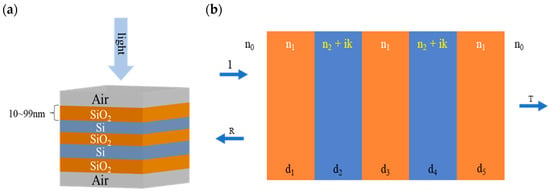
Figure 1.
Structural design of a multilayer thin-film reflector. (a) Schematic of a five-layer thin-film arrangement alternating between SiO2 and Si materials, characterized by reflective indices of 1.46 and 3.95 + 0.027i, respectively, within the wavelength range of 600–650 nm. (b) Structural representation of TMM simulation with n2 as a complex number, and d1, d2, d3, d4, and d5 representing the thicknesses of each layer. The surrounding medium is air; hence, its refractive index is denoted as n0 = 1.
Considering the light incident from layer n − 1 to layer n, the reflection and transmission coefficients for normal incident light are calculated as follows [19] (pp. 124–130):
where is the refractive index of layer n − 1, and is the refractive index of layer n.
In the transfer matrix form,
The phase change after light propagation inside layer n is given by
where wave number , and represents the wavelength of the wave, while and are the refractive index and the thickness of layer n, respectively.
The total transfer matrix for the multilayer structure is represented as
The extraction of the reflection coefficient ‘r’ and transmittance ‘t’ from the total transfer matrix is achieved by
Finally, the reflectivity is calculated as
Following the generation of reflectivity R and corresponding designed structures D using TMM simulation, the data underwent preprocessing for training the neural network model. The input, denoted as X, can be represented as an array (D = [d1,d2,d3,d4,d5]), where each element corresponds to the thickness of a specific layer within the five-layer structure. The output, denoted as Y, is represented as an array (R = [R1,R2,…,R51]), where each element corresponds to the simulated reflectivity spectra. The dataset pairs for the input and output data can be represented as (D1~5, R1~51).
To ensure robust model evaluation and prevent overfitting, the generated dataset was split into the training set comprising 70% of the data, while the remaining 30% was used for testing and validation [20]. Before training the dataset, we ensured the result’s reproducibility by setting the random seed, ensuring that the same sequence of random numbers was generated each time the code was executed. Additionally, the input X was normalized to scale the input features, also known as the Z-score formula [21]. This normalization process ensures that all features contribute equally to the training process and prevents variables with larger scales from dominating the learning process. The normalization formula is given by
where represents the normalized matrix, represents the original matrix, is the mean value of , and σ is the standard deviation of .
3. Tandem Neural Network (TNN)
The TNN architecture comprised two interconnected networks: INN and FNN, as illustrated in Figure 2. FNN, represented by the blue-shaded region, accepted the geometry structures of thin film represented as the vector X (D = [d1,d2,d3,d4,d5]) as input and produced the corresponding reflection spectra responses represented as the vector Y (R = [R1,R2,…,R51]) as output. Conversely, INN generated design parameters as output from an arbitrary spectrum input, effectively mapping design parameters and their responses while addressing non-uniqueness issues where different geometries can yield similar spectra. The network consisted of ten fully connected layers; further details regarding the number of nodes in the hidden layers will be discussed later. Upon completion of training, the learned FNN was integrated with INN to predict a corresponding set of design parameters, updating neural weights based on pre-trained FNN [10], resulting in the predicted spectrum output Y’ and the design parameter set X’ in the intermediate layer. TNN demonstrated remarkable accuracy in generating designs compared to traditional methods, as evidenced by our successful research.
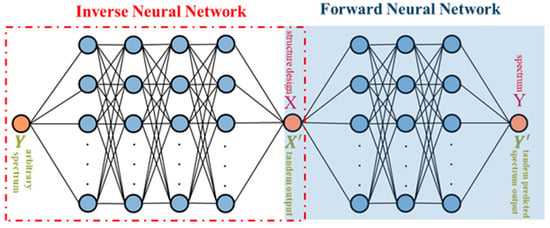
Figure 2.
Architecture of the tandem neural network.
The performance of the neural network was evaluated using the mean squared error (MSE) loss function, a standard metric for regression tasks that measures the accuracy of the predicted reflectivity spectrum. It is mathematically expressed as follows:
where n is the number of samples, and and represent the ground truth and predicted values of the reflectivity spectra, respectively. In the training process, both FNN and TNN models aimed to minimize the MSE loss function, iteratively adjusting parameters (weights) to enhance prediction accuracy and generalization. In a tandem-like structure, forward and inverse neural networks were jointly optimized by linearly combining their loss functions. By adjusting the weights of these combined losses, the model balanced the objectives of forward and inverse training, guiding the optimization process toward achieving precise spectral predictions.
4. Results and Discussion
4.1. Training Forward Neural Network
As we have stated above, FNN was constructed to map the design input D to the output reflectivity spectra R. The training of both FNN and TNN was conducted using Python. The FNN architecture consisted of three dense hidden layers, utilizing leaky ReLU activation functions to introduce non-linearity [22]. The model was compiled using MSE for performance evaluation and the adaptive moment estimation (Adam) optimizer for adjusting its weights as it calculates the adaptive learning rate for each parameter [23]. During training, regularization techniques were implemented in the model to prevent overfitting and enhance the generalization capabilities. Early stopping and learning rate reduction callbacks were employed. This callback monitors a designated quantity, such as the validation loss, and automatically reduces the learning rate if no improvement is observed for a specified number of epochs. Furthermore, a dropout layer with a user-defined dropout rate was incorporated, which randomly deactivates a percentage of neurons during each training iteration [24]. This technique effectively controls the model’s capacity by determining how many steps it can take to fit the training data, thereby mitigating overfitting. The detailed network architecture and hyperparameter settings are presented in Table 1 and were trained for 100 epochs. These hyperparameters were optimized based on the network complexity and fine-tuned through multiple training iterations. The input layer consisted of five neurons, corresponding to the design parameters of the five-layer thin-film structure, while the output layer comprised 51 neurons, representing the reflectivity spectrum.

Table 1.
Hyperparameters of forward deep neural network architecture.
Effective hyperparameter optimization is fundamental, as it significantly influences the network’s training dynamics and its ability to generalize effectively to unseen data. Three model architectures with different hyperparameter configurations were evaluated during the training process. Upon completion of training, three architectures exhibited stable training behavior, and Model 2 achieved the lowest MSE loss, as shown in Figure 3a. The loss function consistently decreased with increasing epochs, indicating effective learning and convergence. After optimizing the hyperparameters, the training and validation processes for MSE loss were visualized in Figure 3b. The results revealed that the validation loss stabilized after approximately 40 epochs of training, suggesting that the model had effectively learned the underlying mapping without overfitting. Here, we observed that the validation loss was lower than the training loss due to regularization techniques and the well-distributed nature of the dataset. This behavior underscores the model’s robustness and its capability to generalize effectively to unseen data. Moreover, it attained an MSE loss of 6.8909 × 10−5 after 100 epochs, demonstrating its high proficiency and accuracy in predicting the reflectivity spectrum, as illustrated in Figure 3c. The blue markers represent the predicted output corresponding to the target indicated by the red line. The close agreement between the predicted and target values underscores the model’s effectiveness in capturing the intricate relationships between the structural design parameters and the corresponding spectral responses. Furthermore, our additional research indicated that the model performed consistently well across a broader wavelength range (400–700 nm) beyond the primary focus, further supporting its versatility and robustness provided in the Appendix A (Figure A1). These results suggest that the trained FNN can contribute to the TNN architecture by providing an accurate output reflectivity spectrum, enabling INN to make predictions of the reflection spectrum for a given structural design.
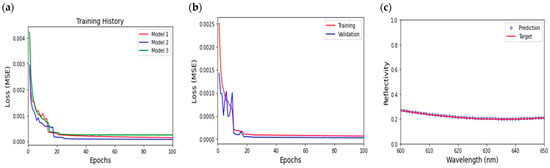
Figure 3.
Training process and result of FNN. (a) Tuning hyperparameters for model training and comparing training loss history. (b) Training and validation performance of Model 2, achieving an MSE loss of 6.8909 × 10−5. (c) The response of FNN prediction for the target reflectivity spectrum.
4.2. Training Tandem Neural Network
The training process involved utilizing a pre-trained model of FNN, which was subsequently evaluated for INN designs using a loss function, followed by iterative updates to the inverse neural weights based on the pre-trained model [11]. Careful monitoring of the validation loss was carried out to ensure potential overfitting of the model during the training process. For TNN, a more complex model than FNN, additional hyperparameters and iterations were considered and fine-tuned using the configurations provided in Table 2 and trained to predict the reflectivity spectrum within the thin-film domain. Dropout layers were implemented for regularization purposes. The hidden layers are responsible for performing non-linear transformations and extracting features from the input data. Similar to FNN training, TNN is equipped with leaky ReLU function and Adam optimizer. Early stopping and learning rate reduction callbacks were implemented to prevent overfitting and enhance convergence. The leaky ReLu in the dense layers can help to address the vanishing gradient problem, leading to faster convergence. Different batch sizes were introduced to enhance time efficiency, considering that excessively large-batch methods may lead to potential degradation in generalization performance [25]. The models were trained on a high-performance computing cluster to accelerate the training process and handle the computational demands of the neural network architectures.

Table 2.
Hyperparameters of tandem deep neural network architecture.
Based on the training results, Model 2 showed the best performance in MSE loss value, achieving less than 0.0005, as shown in Figure 4a. Subsequent analysis focused on visualization of the training and validation performance of Model 2, which achieved an MSE loss of 4.9648 × 10−4 on the validation dataset after 100 epochs, as demonstrated in Figure 4b. The phenomenon of lower validation error occurs due to the model being sufficiently regularized, which prevents overfitting and ensures robust performance on unseen data. The result indicates high accuracy and a capability to achieve near-zero reflectivity values when the target reflectivity is set to zero, as illustrated by Figure 4c. The reflectivity values for the designed structure fell below 0.01, as indicated by the red-dotted line, corresponding to the design parameters (52, 12, 18, 49, and 94 nm). Once TNN is trained, the model directly predicts the optimal thickness needed to achieve zero-reflection. Therefore, further optimization of the thickness is not required. This is further evidenced by comparison with the TMM simulation result for the same layer thicknesses, depicted by the blue markers. Furthermore, Figure 4d demonstrates the MSE error distribution on the validation dataset during the model’s evaluations, with results ideally centered around zero and a minimal spread of 0.1, indicating its robust performance across different samples. The analysis showcases our TNN’s ability to make accurate predictions and adapt to evolving data patterns in addressing complex inverse design challenges. Unlike traditional parameter sweeps, which are computationally intensive and time-consuming due to the need to explore all parameter combinations, our approach significantly enhances efficiency by learning complex, non-linear relationships between design parameters and spectral responses. This allows for rapid convergence on optimal designs. Moreover, TNN’s predictive capabilities offer valuable feedback during the design process, enabling flexible and adaptive adjustments that traditional methods cannot achieve.
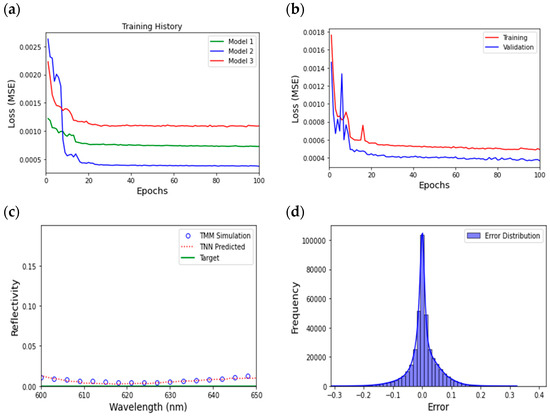
Figure 4.
Training process and result of TNN. (a) Tuning hyperparameters for model training and comparing training loss history. (b) Training and validation performance of Model 2, achieving an MSE loss of 4.9648 × 10−4. (c) The reflectivity spectra of the target and those obtained by TNN and TMM are represented with a green line, a red dashed line, and open circles, respectively. (d) Error distribution of TNN on the validation dataset.
4.3. Visualizing in TMM
Following the TNN-generated design parameters, a five-layer thin-film structure (52, 12, 18, 49, and 94 nm) was simulated using TMM across the spectrum range of 400 to 800 nm. Significant reduction in reflectivity within the targeted wavelength range of 600 to 650 nm was achieved, as illustrated in Figure 5a. This emphasizes the precise prediction of designed multilayer structure by TNN with desired optical properties through strategic placement and material selection in numerical simulation, particularly for absorption layers that govern both absorption and reflection. Figure 5b illustrates the sensitivity of the reflectivity variations to wavelength and the simultaneous changes in inner layer thickness (d2, d3, and d4) of the multilayer structure. Variations in thickness from −2 to 2 nm relative to the reference values were explored, suggesting potential for customized designs by slight adjustments to the layer thickness. A significant correlation between the reflectivity spectrum and inner layer thicknesses was revealed. Decreasing inner layer thicknesses shifted the near-zero reflectivity region towards shorter wavelengths, while increasing thicknesses resulted in a shift towards longer wavelengths. This behavior can be attributed to the influence of varying optical path lengths and their impact on interference effects. The presented analysis showcases the potential of TMM simulation for designing and optimizing multilayer thin-film structures with desired optical properties by exploiting the interplay between layer thicknesses and light reflection. Figure 5c further presents the comparison of reflectivity between the randomly generated structure and after optimization using TNN. It shows a significant reduction in reflectivity, underscoring TNN’s effectiveness in enhancing optical performance compared to the unoptimized structure.
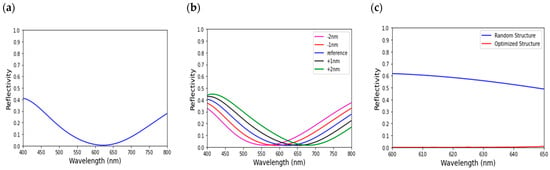
Figure 5.
(a) TMM simulation of the full spectrum range of the thickness resulting from the predicted tandem neural network (52, 12, 18, 49, and 94 nm), demonstrating a significant drop in reflectivity to near zero in the wavelength range of 600–650 nm. (b) Modified structure designs in different wavelength regions. (c) Comparison of reflectivity between the randomly generated structure and after optimization using TNN.
This analysis underscores the potential of TNN architecture in guiding parameter optimization for thin-film reflectors, as it enables the accurate prediction of reflectivity outcomes across specific wavelength ranges. The findings from the TMM simulation further emphasize the intricate relationship between the inclusion of absorption layers and the variation of resulting reflectivity spectra corresponding to the layer thickness, providing valuable insights for the optimization of thin-film designs. Consequently, we have successfully designed a structure that achieves near-zero reflection within the desired wavelength range and provides further insights for achieving near-zero reflection in different wavelength ranges. The design parameters and materials utilized in this study are experimentally feasible, making them suitable for various optical device applications. We have demonstrated the ability to optimize the design structures using the TNN approach while incorporating control over the absorption characteristics for any required wavelength region.
5. Conclusions
In conclusion, this study represents a significant advancement in the inverse design approach for reflectionless multilayer thin-film structures within the specific wavelength range of 600 to 650 nm. By implementing absorption materials in the structure design during the data generation process, we successfully manipulated the reflectivity of the structure to attain desired optical properties, particularly near-zero reflection. This approach has a remarkable capability to accurately predict any spectral response, thereby enabling precise tailoring for near-zero reflection. Furthermore, this work not only provides insights into the designing of such structures but also highlights the potential for controlling absorption within these architectures to enhance optical performance. Importantly, the results pave the way for extending our methodology to tackle more complex multilayer designs in future work as well as broadening the application of our findings to diverse wavelength ranges and material compositions. This research lays the groundwork for optimizing thin-film structures for various desired wavelength regions, thus facilitating innovative applications in optical devices and optical engineering. In future work, we plan to incorporate material dispersion in the design process to further enhance the accuracy and performance, particularly when targeting broader wavelength ranges.
Author Contributions
Conceptualization, H.N.; Validation, S.K.S.; Writing—original draft, S.K.S.; Writing—review & editing, H.N.; Supervision, H.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (NRF-2020R1F1A1074015) and the Biomaterials Specialized Graduate Program through the Korea Environmental Industry and Technology Institute (KEITI), funded by the Ministry of Environment (MOE).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Additional data indicating the model performs consistently well across a broader wavelength range (400–700 nm) beyond the primary focus, further supporting its versatility and robustness.
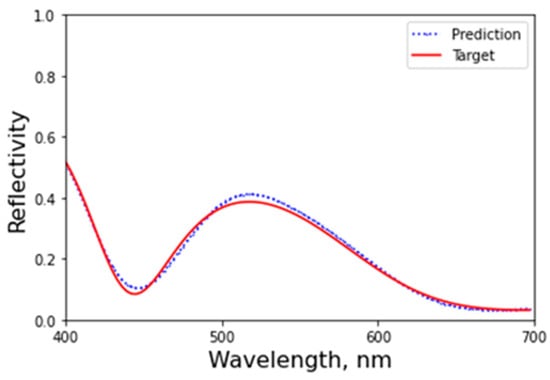
Figure A1.
Expanded performance evaluation of FNN across the 400–700 nm wavelength range.
References
- Whiteside, P.J.D.; Chininis, J.A.; Hunt, H.K. Techniques and Challenges for Characterizing Metal Thin Films with Applications in Photonics. Coatings 2016, 6, 35. [Google Scholar] [CrossRef]
- Li, X.; Yu, X.; Han, Y. Polymer thin films for antireflection coatings. J. Mater. Chem. C Mater. 2013, 1, 2266–2285. [Google Scholar] [CrossRef]
- Rack, P.D.; Holloway, P.H. The structure, device physics, and material properties of thin film electroluminescent displays. Mater. Sci. Eng. R Rep. 1998, 21, 171–219. [Google Scholar] [CrossRef]
- Hsiao, K.J.; Sites, J.R. Electron reflector to enhance photovoltaic efficiency: Application to thin-film CdTe solar cells. Prog. Photovolt. Res. Appl. 2012, 20, 486–489. [Google Scholar] [CrossRef]
- Siciliano, P. Preparation, characterisation and applications of thin films for gas sensors prepared by cheap chemical method. Sens. Actuators B Chem. 2000, 70, 153–164. [Google Scholar] [CrossRef]
- Priya, D.N.; Modak, J.M.; Raichur, A.M. LbL fabricated poly(Styrene Sulfonate)/TiO2 multilayer thin films for environmental applications. ACS Appl. Mater. Interfaces 2009, 1, 2684–2693. [Google Scholar] [CrossRef] [PubMed]
- Li, B.J.; Li, Z.X.; Wang, L.; Huang, L.J. Nanosecond pulsed laser annealing of Cu/Ag/AZO multilayer thin films for performance improvement and transparent heater application. Mater. Sci. Eng. B 2023, 294, 116539. [Google Scholar] [CrossRef]
- Garlisi, C.; Trepci, E.; Li, X.; Al Sakkaf, R.; Al-Ali, K.; Nogueira, R.P.; Zheng, L.; Azar, E.; Palmisano, G. Multilayer thin film structures for multifunctional glass: Self-cleaning, antireflective and energy-saving properties. Appl. Energy 2020, 264, 114697. [Google Scholar] [CrossRef]
- Peurifoy, J.; Shen, Y.; Jing, L.; Yang, Y.; Cano-Renteria, F.; DeLacy, B.G.; Joannopoulos, J.D.; Tegmark, M.; Soljačić, M. Nanophotonic particle simulation and inverse design using artificial neural networks. Sci. Adv. 2018, 4, eaar4206. [Google Scholar] [CrossRef]
- Ma, W.; Cheng, F.; Xu, Y.; Wen, Q.; Liu, Y. Probabilistic Representation and Inverse Design of Metamaterials Based on a Deep Generative Model with Semi-Supervised Learning Strategy. Adv. Mater. 2019, 31, 1901111. [Google Scholar] [CrossRef]
- Li, Z.; Xu, J.; Zhang, L.; Li, Y.; Yang, R.; Fu, Q.; Zhang, F.; Fan, Y. Inverse Design of Dual-Band Optically Transparent Metasurface Absorbers with Neural-Adjoint Method. Ann. Phys. 2023, 535, 2300054. [Google Scholar] [CrossRef]
- Yu, R.; Liu, Y.; Zhu, L. Inverse design of high degree of freedom meta-atoms based on machine learning and genetic algorithm methods. Opt. Express 2022, 30, 35776. [Google Scholar] [CrossRef]
- Liu, D.; Tan, Y.; Khoram, E.; Yu, Z. Training Deep Neural Networks for the Inverse Design of Nanophotonic Structures. ACS Photonics 2018, 5, 1365–1369. [Google Scholar] [CrossRef]
- Xu, X.; Sun, C.; Li, Y.; Zhao, J.; Han, J.; Huang, W. An improved tandem neural network for the inverse design of nanophotonics devices. Opt. Commun. 2021, 481, 126513. [Google Scholar] [CrossRef]
- Head, S.; Hedayati, M.K. Inverse Design of Distributed Bragg Reflectors Using Deep Learning. Appl. Sci. 2022, 12, 4877. [Google Scholar] [CrossRef]
- Unni, R.; Yao, K.; Han, X.; Zhou, M.; Zheng, Y. A mixture-density-based tandem optimization network for on-demand inverse design of thin-film high reflectors. Nanophotonics 2021, 10, 4057–4065. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Ding, J.; Zhao, Y.; Liu, H.; Su, W.; Yang, L.; Tao, G.; Pryamikov, A.; Wang, X.; Mu, H.; et al. Artificial intelligence designer for optical Fibers: Inverse design of a Hollow-Core Anti-Resonant fiber based on a tandem neural network. Results Phys. 2023, 46, 106310. [Google Scholar] [CrossRef]
- Polyanskiy, M.N. Refractiveindex.info database of optical constants. Sci. Data 2024, 11, 94. [Google Scholar] [CrossRef] [PubMed]
- Hecht, E. Optics, 5th ed.; Pearson Education Limited: Essex, UK, 2017; 720p. [Google Scholar]
- Long, Y.; Ren, J.; Li, Y.; Chen, H. Inverse design of photonic topological state via machine learning. Appl. Phys. Lett. 2019, 114, 181105. [Google Scholar] [CrossRef]
- Mare, D.S.; Moreira, F.; Rossi, R. Nonstationary Z-Score measures. Eur. J. Oper. Res. 2017, 260, 348–358. [Google Scholar] [CrossRef]
- He, X.; Cui, X.; Chan, C.T. Constrained tandem neural network assisted inverse design of metasurfaces for microwave absorption. Opt. Express 2023, 31, 40969–40979. [Google Scholar] [CrossRef] [PubMed]
- Nikbakht, S.; Anitescu, C.; Rabczuk, T. Optimizing the neural network hyperparameters utilizing genetic algorithm. J. Zhejiang Univ. Sci. A 2021, 22, 407–426. [Google Scholar] [CrossRef]
- Prechelt, L. Early Stopping—But When? In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar]
- Keskar, N.S.; Nocedal, J.; Tang, P.T.P.; Mudigere, D.; Smelyanskiy, M. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017—Conference Track Proceedings, Toulon, France, 24–26 April 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).