Astronomical Intensity Interferometry
Abstract
1. Introduction
2. Principles of Intensity Interference
2.1. Photon Acquisition and Signal Processing
2.2. Optical Aperture Synthesis
2.3. Comparison of Intensity Interferometry with Other Interferometric Techniques
3. Key Technologies of II
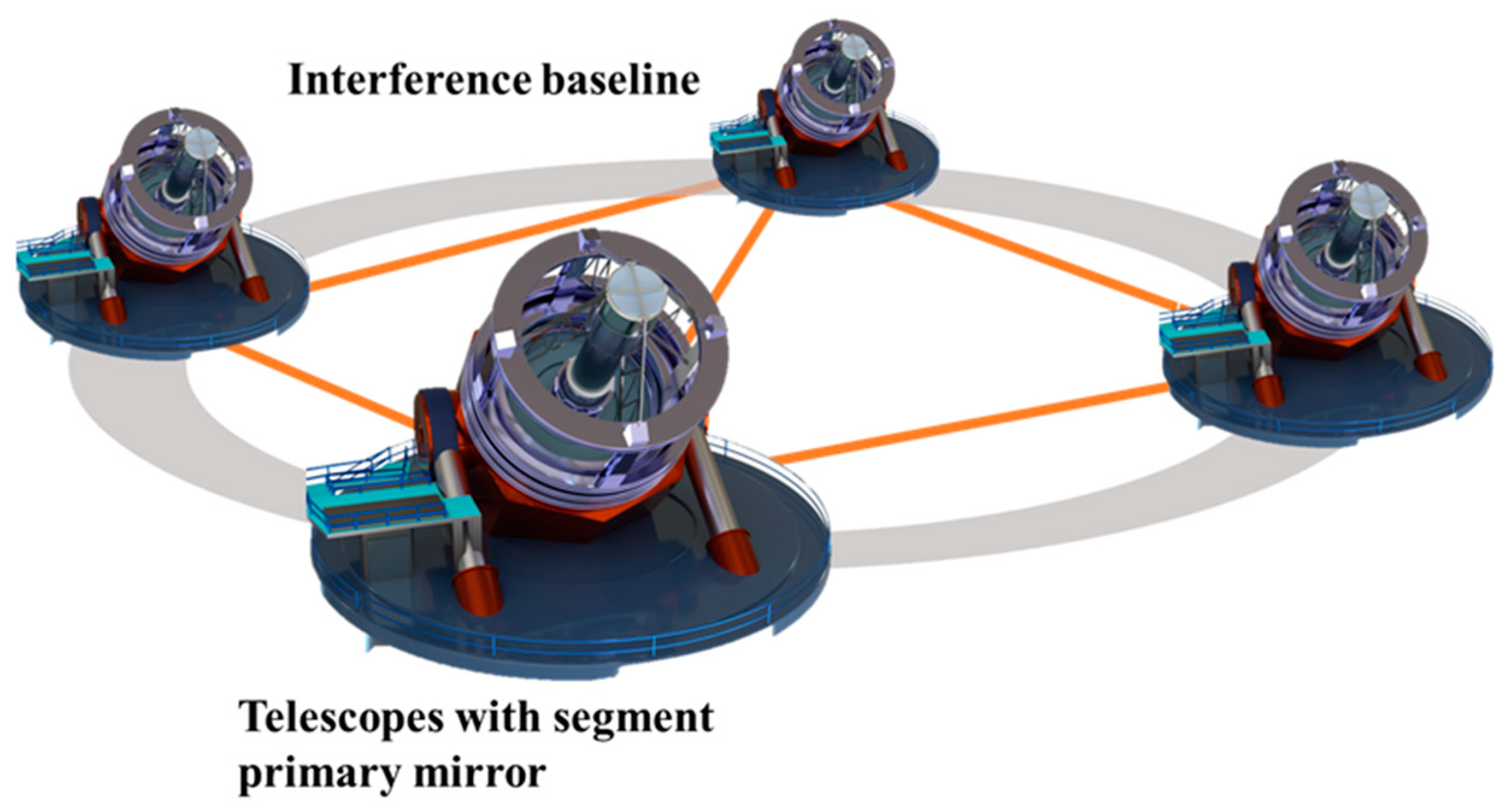
3.1. Design of the System Baseline
3.2. Photon Collection
3.2.1. Telescopes and Optical Systems
3.2.2. Detectors
3.3. Intensity Interferometric Imaging
3.3.1. Phase Reconstruction
3.3.2. Image Reconstruction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mayor, M.; Queloz, D. A Jupiter-mass companion to a solar-type star. Nature 1995, 378, 355–359. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Pathways to Discovery in Astronomy and Astrophysics for the 2020s; National Academies Press: Washington, DC, USA, 2021. [Google Scholar]
- Koch, D.G.; Borucki, W.J.; Webster, L.; Dunham, E.W.; Jenkins, J.M.; Marriott, J.; Reitsema, H.J. Kepler: A space mission to detect earth-class exoplanets. Proc. SPIE 1998, 3356, 599–607. [Google Scholar]
- Jianghui, J.; Haitao, L.; Junbo, Z.; Dong, L.; Liang, F.; Su, W.; Lei, D.; Guo, C.; Fei, L.; Yao, D. Closeby Habitable Exoplanet Survey (CHES): An Astrometry Mission for Probing Nearby Habitable Planets. Chin. J. Space Sci. 2024, 44, 1–22. [Google Scholar]
- Borucki, W.J.; Koch, D.G.; Basri, G.; Batalha, N.; Brown, T.M.; Bryson, S.T.; Caldwell, D.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E. Characteristics of planetary candidates observed by Kepler. II. Analysis of the first four months of data. Astrophys. J. 2011, 736, 19. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R. Transiting exoplanet survey satellite. J. Astron. Telesc. Instrum. Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Ragazzoni, R.; Magrin, D.; Rauer, H.; Pagano, I.; Nascimbeni, V.; Piotto, G.; Piazza, D.; Levacher, P.; Schweitzer, M.; Basso, S. PLATO: A multiple telescope spacecraft for exo-planets hunting. Proc. SPIE 2016, 9904, 731–737. [Google Scholar]
- Tinetti, G.; Drossart, P.; Eccleston, P.; Hartogh, P.; Heske, A.; Leconte, J.; Micela, G.; Ollivier, M.; Pilbratt, G.; Puig, L. The science of ARIEL (atmospheric remote-sensing infrared exoplanet large-survey). Proc. SPIE 2016, 9904, 658–667. [Google Scholar]
- LUVOIR Team. The LUVOIR Mission Concept Study Final Report. arXiv 2019, arXiv:1912.06219. [Google Scholar]
- Gao, M.; Zhao, G.; Gu, Y. Space science and application mission in China’s space station. Bull. Chin. Acad. Sci. 2015, 30, 721–732. [Google Scholar]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Augueres, J.-L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A. Euclid definition study report. arXiv 2011, arXiv:1110.3193. [Google Scholar]
- Green, J.; Schechter, P.; Baltay, C.; Bean, R.; Bennett, D.; Brown, R.; Conselice, C.; Donahue, M.; Fan, X.; Gaudi, B. Wide-field infrared survey telescope (WFIRST) final report. arXiv 2012, arXiv:1208.4012. [Google Scholar]
- Stankus, P.; Nomerotski, A.; Slosar, A.; Vintskevich, S. Two-photon amplitude interferometry for precision astrometry. arXiv 2020, arXiv:2010.09100. [Google Scholar] [CrossRef]
- Chael, A.A.; Johnson, M.D.; Bouman, K.L.; Blackburn, L.L.; Akiyama, K.; Narayan, R. Interferometric imaging directly with closure phases and closure amplitudes. Astrophys. J. 2018, 857, 23. [Google Scholar] [CrossRef]
- Mourard, D.; Blazit, A.; Bonneau, D.; Chevassut, J.; Clausse, J.; Le Bouquin, J.; Maire, J.; Merlin, G.; Rousselet-Perraut, K.; Borgnino, J. Recent progress and future prospects of the GI2T interferometer. Adv. Stellar Interferom. 2006, 6268, 61–71. [Google Scholar]
- Dravins, D. Intensity interferometry: Optical imaging with kilometer baselines. Proc. SPIE 2016, 9907, 128–139. [Google Scholar]
- Brown, R.H.; Jennison, R.; Gupta, M.D. Apparent angular sizes of discrete radio sources: Observations at Jodrell Bank, Manchester. Nature 1952, 170, 1061–1063. [Google Scholar] [CrossRef]
- Brown, R.H.; Twiss, R.Q. Correlation between photons in two coherent beams of light. Nature 1956, 177, 27–29. [Google Scholar] [CrossRef]
- Hanbury Brown, R.; Davis, J.; Allen, L.; Rome, J. The stellar interferometer at Narrabri Observatory-II. The angular diameters of 15 stars. Mon. Not. R. Astron. Soc. 1967, 137, 393. [Google Scholar] [CrossRef]
- Hanbury Brown, R.; Davis, J.; Allen, L. The angular diameters of 32 stars. Mon. Not. R. Astron. Soc. 1974, 167, 121–136. [Google Scholar] [CrossRef]
- Karl, S.; Richter, S.; von Zanthier, J. Photon counting intensity interferometry in the blue at a 0.5 m telescope. RAS Tech. Instrum. 2024, 3, 66–72. [Google Scholar] [CrossRef]
- Norris, B.; Bland-Hawthorn, J. Astrophotonics: The rise of integrated photonics in astronomy. arXiv 2019, arXiv:1909.10688. [Google Scholar] [CrossRef]
- Kuruoglu, E.E.; Baccigalupi, C. Applications of signal processing in astrophysics and cosmology. EURASIP J. Appl. Sign. Process. 2005, 2005, 985049. [Google Scholar]
- Hofmann, W.; CTA Consortium. The Cherenkov telescope array–status. J. Phys. Conf. Ser. 2017, 1792, 1. [Google Scholar]
- Karl, S.; Zmija, A.; Richter, S.; Vogel, N.; Malyshev, D.; Zink, A.; Michel, T.; Anton, G.; von Zanthier, J.; Funk, S. Comparing different approaches for stellar intensity interferometry. Mon. Not. R. Astron. Soc. 2022, 512, 1722–1729. [Google Scholar] [CrossRef]
- Matsuo, H. Far-infrared intensity interferometry for high angular resolution imaging. Proc. SPIE 2020, 11443, 286–295. [Google Scholar]
- Bland-Hawthorn, J.; Leon-Saval, S.G. Astrophotonics: Molding the flow of light in astronomical instruments. Opt. Express 2017, 25, 15549–15557. [Google Scholar] [CrossRef]
- Schulz-DuBois, E.O. High-resolution intensity interferometry by photon correlation. J. Phys. 1983, 6, 6–27. [Google Scholar]
- Spolon, A.; Fiori, M.; Zampieri, L.; Landoni, M. Towards image synthesis with photon counting stellar intensity interferometry. Proc. SPIE 2024, 12996, 206–214. [Google Scholar]
- Brown, R.H.; Twiss, R.Q. A new type of interferometer for use in radio astronomy. Philos. Mag. 1954, 45, 663–682. [Google Scholar] [CrossRef]
- Hanbury Brown, R.; Twiss, R.Q. A test of a new type of stellar interferometer on Sirius. In A Source Book in Astronomy and Astrophysics, 1900–1975; Harvard University Press: Cambridge, MA, USA, 1979; pp. 8–12. [Google Scholar]
- Glauber, R.J. Coherent and incoherent states of the radiation field. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Davis, J.; Tango, W.; Booth, A.; Brummelaar, T.T.; Minard, R.; Owens, S. The Sydney University Stellar Interferometer—I. The instrument. Mon. Not. R. Astron. Soc. 1999, 303, 773–782. [Google Scholar] [CrossRef]
- Bachor, H.-A.; Ralph, T.C. A Guide to Experiments in Quantum Optics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Loudon, R. The Quantum Theory of Light; OUP Oxford: Oxford, UK, 2000. [Google Scholar]
- Mandel, L. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Foellmi, C. Intensity interferometry and the second-order correlation function in astrophysics. Astron. Astrophys. 2009, 507, 1719–1727. [Google Scholar] [CrossRef]
- Shih, Y. An Introduction to Quantum Optics: Photon and Biphoton Physics; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Dravins, D.; LeBohec, S.; Jensen, H.; Nuñez, P.D.; CTA Consortium. Optical intensity interferometry with the Cherenkov Telescope Array. Astropart. Phys. 2013, 43, 331–347. [Google Scholar] [CrossRef]
- Taylor, G.B.; Carilli, C.L.; Perley, R.A. Synthesis Imaging in Radio Astronomy II. 1999, Volume 180. Available online: https://leo.phys.unm.edu/~gbtaylor/astr423/s98book.pdf (accessed on 20 August 2024).
- Thompson, A.R.; Moran, J.M.; Swenson, G.W. Interferometry and Synthesis in Radio Astronomy; Springer Nature: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Creech-Eakman, M.J.; Romero, V.; Payne, I.; Haniff, C.; Buscher, D.; Aitken, C.; Anderson, C.; Bakker, E.; Coleman, T.; Dahl, C. Magdalena Ridge Observatory Interferometer: Advancing to first light and new science. Proc. SPIE 2010, 7734, 72–82. [Google Scholar]
- Glindemann, A. Principles of Stellar Interferometry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Labeyrie, A.; Lipson, S.G.; Nisenson, P. An Introduction to Optical Stellar Interferometry; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Saha, S.K. Aperture Synthesis: Methods and Applications to Optical Astronomy; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Haniff, C. An introduction to the theory of interferometry. New Astron. Rev. 2007, 51, 565–575. [Google Scholar] [CrossRef]
- van Cittert, P.H. Die wahrscheinliche Schwingungsverteilung in einer von einer Lichtquelle direkt oder mittels einer Linse beleuchteten Ebene. Physica 1934, 1, 201–210. [Google Scholar] [CrossRef]
- Zernike, F. The concept of degree of coherence and its application to optical problems. Physica 1938, 5, 785–795. [Google Scholar] [CrossRef]
- Consortium, T.C. Design Concepts for the Cherenkov Telescope Array. arXiv 2010, arXiv:1008.3703. [Google Scholar]
- Lipson, A.; Lipson, S.G.; Lipson, H. Optical Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Nair, R.; Tsang, M. Far-field superresolution of thermal electromagnetic sources at the quantum limit. Phys. Rev. Lett. 2016, 117, 190801. [Google Scholar] [CrossRef]
- Lawson, P. Principles of Long Baseline Stellar Interferometry; JPL: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Abuter, R.; Accardo, M.; Amorim, A.; Anugu, N.; Avila, G.; Azouaoui, N.; Benisty, M.; Berger, J.-P.; Blind, N.; Bonnet, H. First light for GRAVITY: Phase referencing optical interferometry for the Very Large Telescope Interferometer. Astron. Astrophys. 2017, 602, A94. [Google Scholar]
- Event Horizon Telescope Collaboration. First M87 event horizon telescope results. I. The shadow of the supermassive black hole. arXiv 2019, arXiv:1906.11238. [Google Scholar]
- Rotondo, F. Imaging with Amplitude and Intensity Interferometers; Institute for Defense Analyses: Alexandria, VA, USA, 2004. [Google Scholar]
- Bojer, M.; Huang, Z.; Karl, S.; Richter, S.; Kok, P.; von Zanthier, J. A quantitative comparison of amplitude versus intensity interferometry for astronomy. New J. Phys. 2022, 24, 043026. [Google Scholar] [CrossRef]
- Rayleigh. XXXI. Investigations in optics, with special reference to the spectroscope. Philos. Mag. J. Sci. 1879, 8, 261–274. [Google Scholar] [CrossRef]
- Michalet, X.; Weiss, S. Using photon statistics to boost microscopy resolution. Proc. Natl. Acad. Sci. USA 2006, 103, 4797–4798. [Google Scholar] [CrossRef]
- Beckers, J. Techniques for high angular resolution astronomical imaging. In Instrumentation for Large Telescopes; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Abeysekara, A.; Benbow, W.; Brill, A.; Buckley, J.; Christiansen, J.; Chromey, A.; Daniel, M.; Davis, J.; Falcone, A.; Feng, Q. Demonstration of stellar intensity interferometry with the four VERITAS telescopes. Nat. Astron. 2020, 4, 1164–1169. [Google Scholar] [CrossRef]
- Kim, D.; Choi, H.; Brendel, T.; Quach, H.; Esparza, M.; Kang, H.; Feng, Y.-T.; Ashcraft, J.N.; Ke, X.; Wang, T. Advances in optical engineering for future telescopes. Opto-Electron. Adv. 2021, 4, 210040–210041. [Google Scholar] [CrossRef]
- Ziad, A. Review of the outer scale of the atmospheric turbulence. Proc. SPIE 2016, 9909, 545–556. [Google Scholar]
- Dravins, D.; Lagadec, T. Stellar intensity interferometry over kilometer baselines: Laboratory simulation of observations with the Cherenkov Telescope Array. Proc. SPIE 2014, 9146, 298–315. [Google Scholar]
- Dravins, D.; Lagadec, T.; Nuñez, P.D. Optical aperture synthesis with electronically connected telescopes. Nat. Commun. 2015, 6, 6852. [Google Scholar] [CrossRef]
- Leisawitz, D.; Amatucci, E.; Allen, L.; Arenberg, J.; Armus, L.; Battersby, C.; Bauer, J.; Beaman, B.G.; Bell, R.; Beltran, P. Origins Space Telescope: Baseline mission concept. J. Astron. Telesc. Instrum. Syst. 2021, 7, 011002. [Google Scholar] [CrossRef]
- LeBohec, S.; Adams, B.; Bond, I.; Bradbury, S.; Dravins, D.; Jensen, H.; Kieda, D.B.; Kress, D.; Munford, E.; Nuñez, P.D. Stellar intensity interferometry: Experimental steps toward long-baseline observations. Proc. SPIE 2010, 7734, 468–479. [Google Scholar]
- Lacour, S.; Eisenhauer, F.; Gillessen, S.; Pfuhl, O.; Woillez, J.; Bonnet, H.; Perrin, G.; Lazareff, B.; Rabien, S.; Lapeyrere, V. Reaching micro-arcsecond astrometry with long baseline optical interferometry—Application to the GRAVITY instrument. Astron. Astrophys. 2014, 567, A75. [Google Scholar] [CrossRef]
- Ireland, M.J. Long-baseline space interferometry for astrophysics: A forward look at scientific potential and remaining technical challenges. Proc. SPIE 2020, 11446, 329–337. [Google Scholar]
- Borra, E.F. A novel type of very long baseline astronomical intensity interferometer. Mon. Not. R. Astron. Soc. 2013, 436, 1096–1101. [Google Scholar] [CrossRef][Green Version]
- Tuthill, P.G. The narrabri stellar intensity interferometer: A 50th birthday tribute. Proc. SPIE 2014, 9146, 101–107. [Google Scholar]
- Ong, R.; CTA Consortium. Cherenkov telescope array: The next generation Gamma-ray observatory. Proc. Int. Astron. Union 2018, 301, 1071. [Google Scholar]
- Gueta, O. The Cherenkov Telescope Array: Layout, design and performance. arXiv 2021, arXiv:2108.04512. [Google Scholar]
- Ferrini, F.; Wild, W. The Cherenkov Telescope Array Observatory comes of age. ESO Messenger 2020, 180, 3–8. [Google Scholar]
- Holder, J.; Acciari, V.; Aliu, E.; Arlen, T.; Beilicke, M.; Benbow, W.; Bradbury, S.; Buckley, J.; Bugaev, V.; Butt, Y. Status of the VERITAS Observatory. arXiv 2008, arXiv:0810.0474. [Google Scholar]
- Punch, M. Results from Observations of AGNs with the H.E.S.S. Telescope System and Future Plans. In Exploring the Cosmic Frontier: Astrophysical Instruments for the 21st Century; Springer: Berlin/Heidelberg, Germany, 2007; pp. 175–178. [Google Scholar]
- Ohm, S.; Wagner, S.; HESS Collaboration. Current status and operation of the HESS array of imaging atmospheric Cherenkov telescopes. Nucl. Instrum. Methods Phys. Res. A 2023, 1055, 168442. [Google Scholar] [CrossRef]
- Holder, J. Atmospheric Cherenkov gamma-ray telescopes. In The WSPC Handbook of Astronomical Instrumentation: Volume 5: Gamma-Ray and Multimessenger Astronomical Instrumentation; World Scientific: Singapore, 2021; pp. 117–136. [Google Scholar]
- Vercellone, S.; CTA Consortium. The next generation Cherenkov Telescope Array observatory: CTA. Nucl. Instrum. Methods Phys. Res. Sect. A 2014, 766, 73–77. [Google Scholar] [CrossRef]
- Barrio, J.; CTA Consortium. Status of the large size telescopes and medium size telescopes for the Cherenkov Telescope Array observatory. Nucl. Instrum. Methods Phys. Res. A 2020, 952, 161588. [Google Scholar] [CrossRef]
- Bradascio, F. Status of the Medium-Sized Telescopes for the Cherenkov Telescope Array Observatory. arXiv 2023, arXiv:2310.02127. [Google Scholar]
- Le Bohec, S.; Daniel, M.; De Wit, W.; Hinton, J.; Jose, E.; Holder, J.; Smith, J.; White, R. Stellar intensity interferometry with air Cherenkov telescope arrays. New Astron. Rev. 2008, 984, 205–215. [Google Scholar]
- Abe, S.; Abhir, J.; Acciari, V.; Aguasca-Cabot, A.; Agudo, I.; Aniello, T.; Ansoldi, S.; Antonelli, L.; Arbet Engels, A.; Arcaro, C. Performance and first measurements of the MAGIC stellar intensity interferometer. Mon. Not. R. Astron. Soc. 2024, 529, 4387–4404. [Google Scholar] [CrossRef]
- Nigro, C.; Hassan, T.; Olivera-Nieto, L. Evolution of data formats in very-high-energy gamma-ray astronomy. Universe 2021, 7, 374. [Google Scholar] [CrossRef]
- Singh, K. Gamma-ray astronomy with the imaging atmospheric Cherenkov telescopes in India. J. Astrophys. Astron. 2022, 43, 3. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, G.; Wen, L.; Wang, Y. A new optical model for photomultiplier tubes. Eur. Phys. J. C 2022, 82, 329. [Google Scholar] [CrossRef]
- Wang, B.; Mu, J. High-speed Si-Ge avalanche photodiodes. PhotoniX 2022, 3, 8. [Google Scholar] [CrossRef]
- Lai, O.; Guerin, W.; Vakili, F.; Kaiser, R.; Rivet, J.P.; Fouché, M.; Labeyrie, G.; Chabé, J.; Courde, C.; Samain, E. Intensity interferometry revival on the Côte d’Azur. Proc. SPIE 2018, 10701, 599–610. [Google Scholar]
- Zhong, J.; Tian, L.; Varma, P.; Waller, L. Nonlinear optimization algorithm for partially coherent phase retrieval and source recovery. IEEE Trans. Comput. Imaging 2016, 2, 310–322. [Google Scholar] [CrossRef]
- Osherovich, E. Numerical methods for phase retrieval. arXiv 2012, arXiv:1203.4756. [Google Scholar]
- Shechtman, Y.; Eldar, Y.C.; Cohen, O.; Chapman, H.N.; Miao, J.; Segev, M. Phase retrieval with application to optical imaging: A contemporary overview. IEEE Signal Process. Mag. 2015, 32, 87–109. [Google Scholar] [CrossRef]
- Hu, C.; Han, S. On ghost imaging studies for information optical imaging. Appl. Sci. 2022, 12, 10981. [Google Scholar] [CrossRef]
- Yatabe, K.; Ishikawa, K.; Oikawa, Y. Simple, flexible, and accurate phase retrieval method for generalized phase-shifting interferometry. J. Opt. Soc. Am. A 2016, 34, 87–96. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, B.; Morrison, G.R.; Vila-Comamala, J.; Guizar-Sicairos, M.; Robinson, I.K. Phase retrieval by coherent modulation imaging. Nat. Commun. 2016, 7, 13367. [Google Scholar] [CrossRef]
- Rivenson, Y.; Zhang, Y.; Günaydın, H.; Teng, D.; Ozcan, A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light Sci. Appl. 2018, 7, 17141. [Google Scholar] [CrossRef]
- Wang, K.; Song, L.; Wang, C.; Ren, Z.; Zhao, G.; Dou, J.; Di, J.; Barbastathis, G.; Zhou, R.; Zhao, J. On the use of deep learning for phase recovery. Light Sci. Appl. 2024, 13, 4. [Google Scholar] [CrossRef]
- Brown, R.H.; Twiss, R. Interferometry of the intensity fluctuations in light IV. A test of an intensity interferometer on Sirius A. Proc. R. Soc. Lond. A Math. Phys. Sci. 1958, 248, 222–237. [Google Scholar]
- Brown, R.H.; Twiss, R.Q. Interferometry of the intensity fluctuations in light-I. Basic theory: The correlation between photons in coherent beams of radiation. Proc. R. Soc. Lond. A Math. Phys. Sci. 1957, 242, 300–324. [Google Scholar]
- Brown, R.H. The Intensity Interferometer: Its Application to Astronomy; Academic Press: London, UK, 1974. [Google Scholar]
- Zampieri, L.; Naletto, G.; Barbieri, C.; Barbieri, M.; Verroi, E.; Umbriaco, G.; Favazza, P.; Lessio, L.; Farisato, G. Intensity interferometry with Aqueye+ and Iqueye in Asiago. Proc. SPIE 2016, 9907, 140–153. [Google Scholar]
- Zampieri, L.; Naletto, G.; Burtovoi, A.; Fiori, M.; Barbieri, C. Stellar intensity interferometry of Vega in photon counting mode. Mon. Not. R. Astron. Soc. 2021, 506, 1585–1594. [Google Scholar] [CrossRef]
- Acciari, V.; Bernardos, M.; Colombo, E.; Contreras, J.; Cortina, J.; De Angelis, A.; Delgado, C.; Díaz, C.; Fink, D.; Mariotti, M. Optical intensity interferometry observations using the MAGIC Imaging Atmospheric Cherenkov Telescopes. Mon. Not. R. Astron. Soc. 2020, 491, 1540–1547. [Google Scholar] [CrossRef]
- Klaucke, P.M.; Pellegrino, R.A.; Weiss, S.A.; Horch, E.P. Toward an imaging capability with the Southern Connecticut Stellar Interferometer. Proc. SPIE 2020, 11446, 415–426. [Google Scholar]
- Monnier, J.D. Phases in interferometry. New Astron. Rev. 2007, 51, 604–616. [Google Scholar] [CrossRef]
- Thiébaut, É.; Young, J. Principles of image reconstruction in optical interferometry: Tutorial. J. Opt. Soc. Am. A 2017, 34, 904–923. [Google Scholar] [CrossRef]
- Thiébaut, É. Principles of image reconstruction in interferometry. Eur. Astron. Soc. Publ. Ser. 2013, 59, 157–187. [Google Scholar] [CrossRef]
- Nuñez, P.D.; LeBohec, S.; Kieda, D.; Holmes, R.; Jensen, H.; Dravins, D. Stellar intensity interferometry: Imaging capabilities of air Cherenkov telescope arrays. Proc. SPIE 2010, 7734, 458–467. [Google Scholar]
- Nunez, P.D.; Holmes, R.; Kieda, D.; LeBohec, S. High angular resolution imaging with stellar intensity interferometry using air Cherenkov telescope arrays. Mon. Not. R. Astron. Soc. 2012, 419, 172–183. [Google Scholar] [CrossRef]
- Danilova, M.; Dvurechensky, P.; Gasnikov, A.; Gorbunov, E.; Guminov, S.; Kamzolov, D.; Shibaev, I. Recent theoretical advances in non-convex optimization. In High-Dimensional Optimization and Probability: With a View Towards Data Science; Springer: Berlin/Heidelberg, Germany, 2022; pp. 79–163. [Google Scholar]
- Liu, Z.; Shen, X.; Liu, H.; Yu, H.; Han, S. Lensless Wiener–Khinchin telescope based on second-order spatial autocorrelation of thermal light. Chin. Opt. Lett. 2019, 17, 091101. [Google Scholar] [CrossRef]
- Chu, C.; Liu, Z.; Chen, M.; Shao, X.; Situ, G.; Zhao, Y.; Han, S. Wide-spectrum optical synthetic aperture imaging via spatial intensity interferometry. Opto-Electron. Adv. 2023, 6, 230017. [Google Scholar] [CrossRef]
- Thiébaut, É. Image reconstruction with optical interferometers. New Astron. Rev. 2009, 53, 312–328. [Google Scholar] [CrossRef]

| Technique | Advantages | Disadvantages | Resolution | Representative Achievements |
|---|---|---|---|---|
| Amplitude Interferometry | Achieves high resolution through phase synchronization; especially effective in radio wavelengths and for weak signal detection (e.g., VLBI). | Requires precise phase synchronization; especially challenging in optical wavelengths due to atmospheric and instrumental instabilities. | High resolution, but limited in optical wavelengths due to phase synchronization issues. | VLTI, Keck Interferometer, LBTI |
| Intensity Interferometry | Does not rely on phase information; suitable for large baselines and high-frequency optical wavelengths; modern detector technology enhances signal processing efficiency, especially for high-angular-resolution observations. | Weaker signal, particularly under low photon flux conditions; limited by photon degeneracy effects; less advantageous for short baselines. | Achieves very high resolution under large baseline conditions, especially effective for small angular separations. | NSII, CTA, AGIS |
| Aperture Synthesis | Combines multiple telescopes into an effective aperture, simulating a large telescope to achieve extremely high angular resolution (e.g., EHT). | Requires complex synchronization and data processing; expensive infrastructure; especially challenging for high-frequency and precise calibration tasks. | Extremely high resolution, scalable with baseline length, ideal for imaging extreme astronomical objects. | VLA, ALMA, LBTI, VLBI |
| Abbreviation | Number of Apertures | Aperture Diameter | Longest Baseline |
|---|---|---|---|
| NSII | 2 | 6.5 m | 188 m |
| VERITAS | 4 | 12 m | 109 m |
| HESS | 4 | 10.4 m | 120 m |
| MAGIC | 2 | 17 m | 82 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, S.; An, Q.; Zhang, W.; Hu, J.; Wang, L. Astronomical Intensity Interferometry. Photonics 2024, 11, 958. https://doi.org/10.3390/photonics11100958
Yi S, An Q, Zhang W, Hu J, Wang L. Astronomical Intensity Interferometry. Photonics. 2024; 11(10):958. https://doi.org/10.3390/photonics11100958
Chicago/Turabian StyleYi, Shufei, Qichang An, Wenyi Zhang, Jincai Hu, and Liang Wang. 2024. "Astronomical Intensity Interferometry" Photonics 11, no. 10: 958. https://doi.org/10.3390/photonics11100958
APA StyleYi, S., An, Q., Zhang, W., Hu, J., & Wang, L. (2024). Astronomical Intensity Interferometry. Photonics, 11(10), 958. https://doi.org/10.3390/photonics11100958





