Research on Tracking Control Technology Based on Fuzzy PID in Underwater Optical Communication
Abstract
1. Introduction
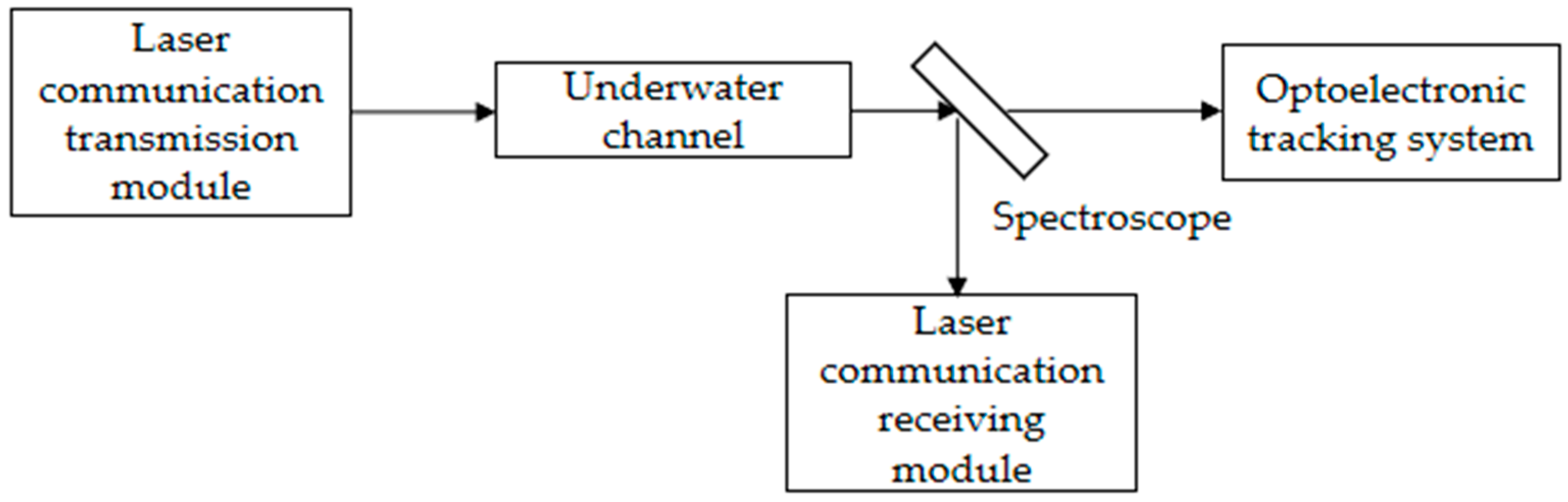
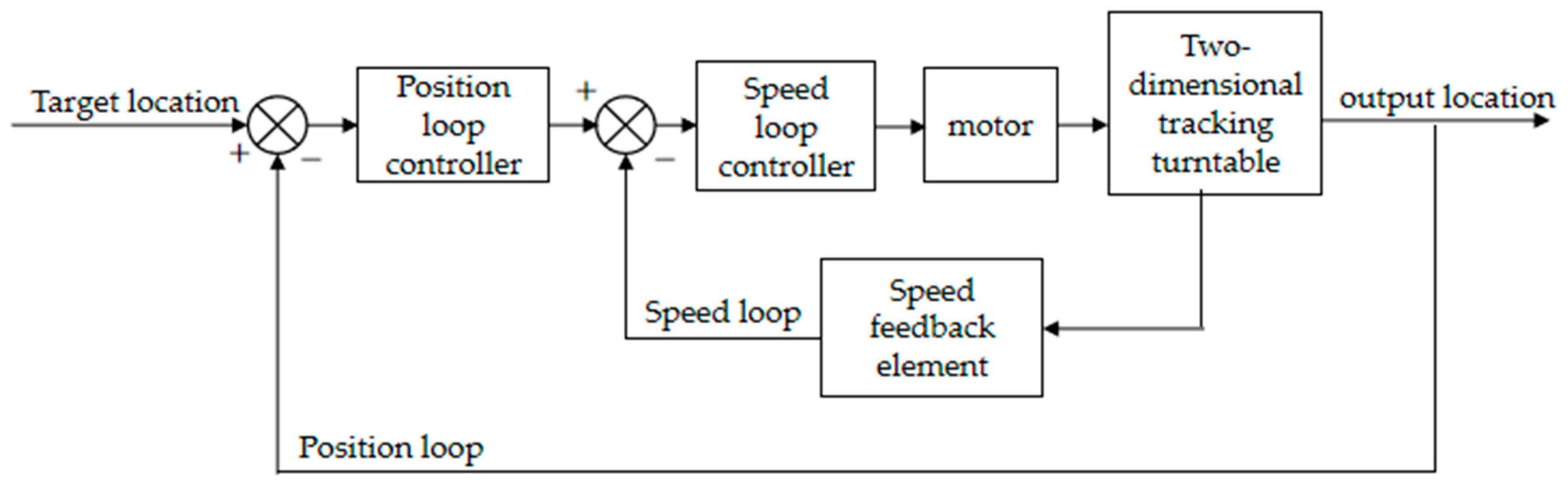
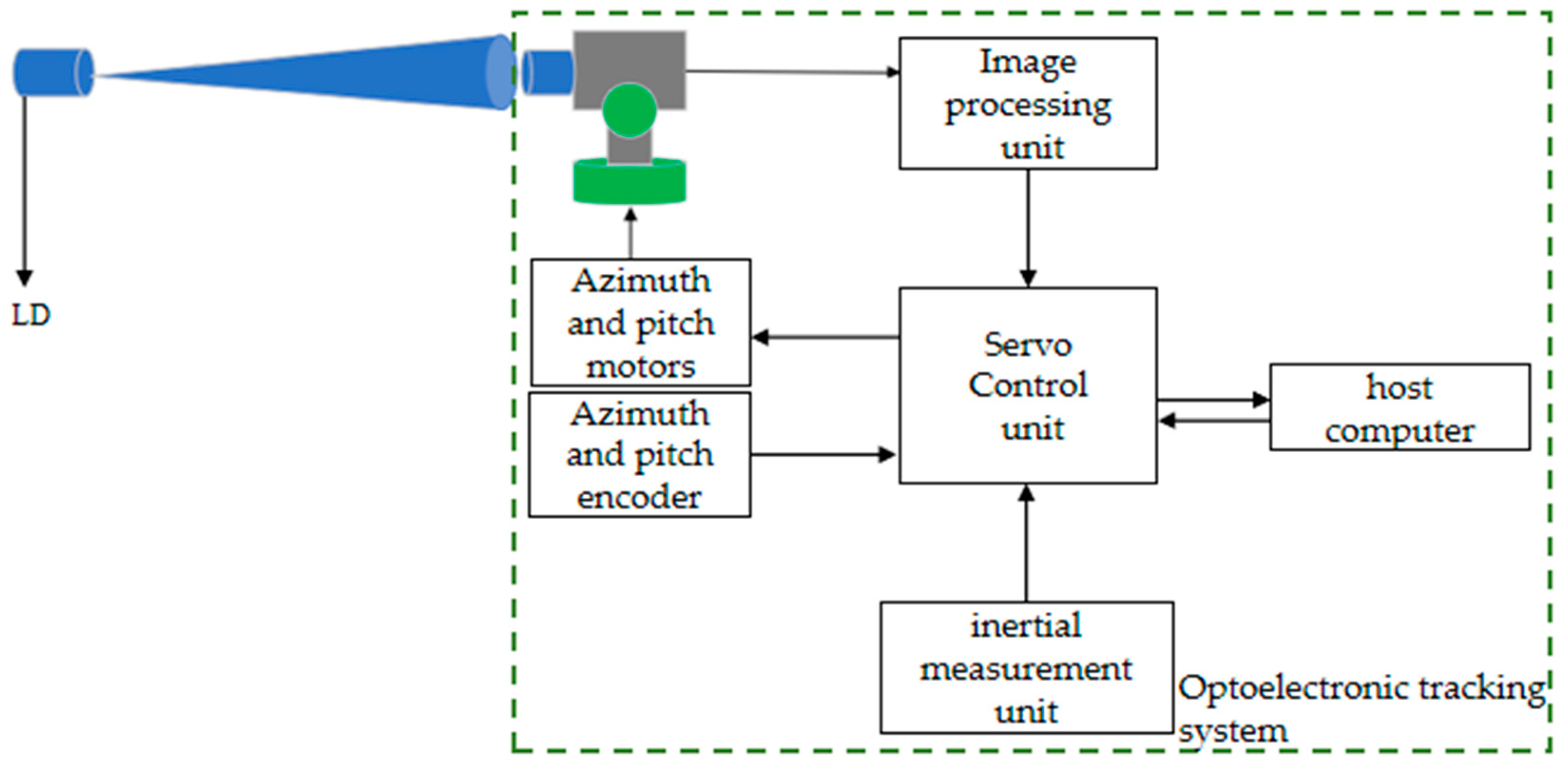
2. Servo Control Principle of UWLC
3. Design and Simulation of Adaptive Fuzzy PID Algorithm Based on Underwater Disturbance
3.1. Underwater Disturbance Analysis
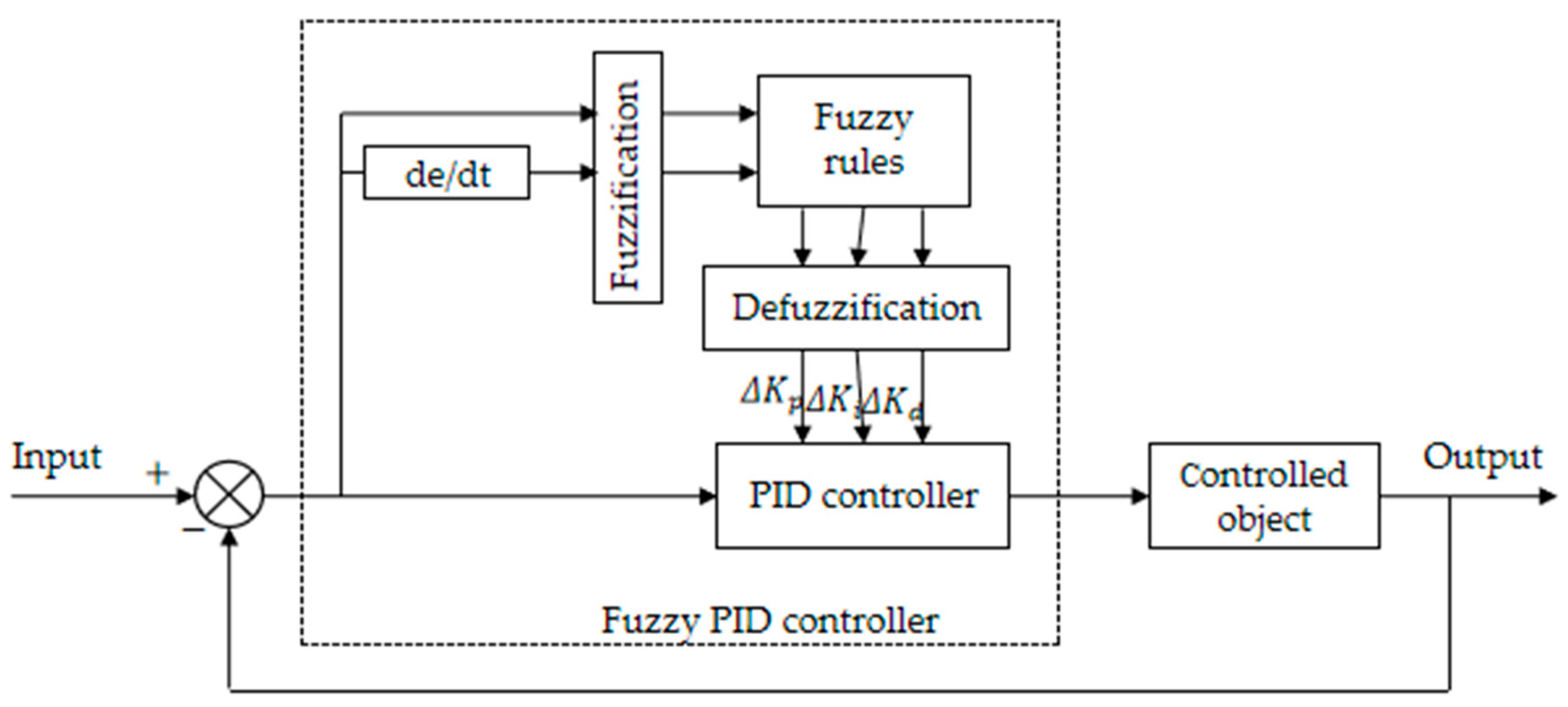
3.2. Design of Adaptive Fuzzy PID Algorithm
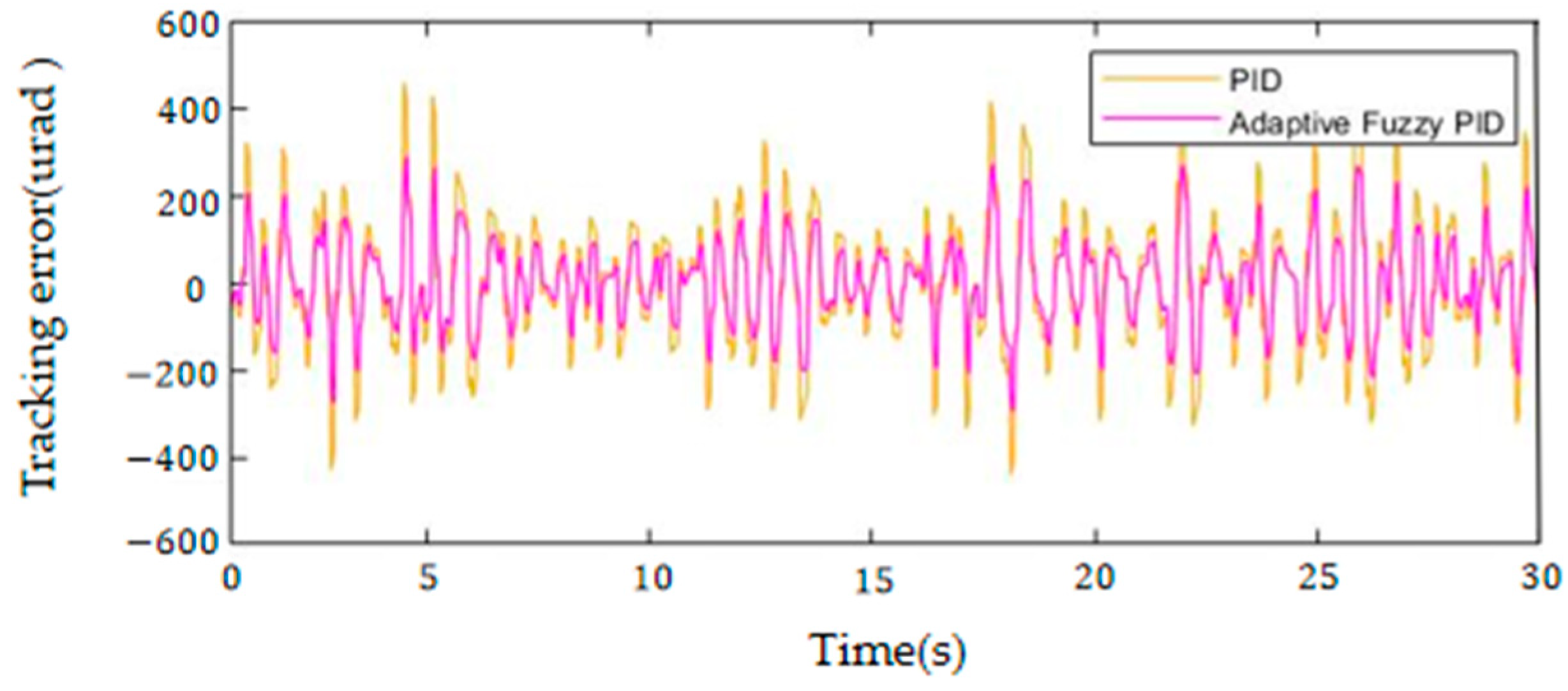
3.3. Simulation Verification
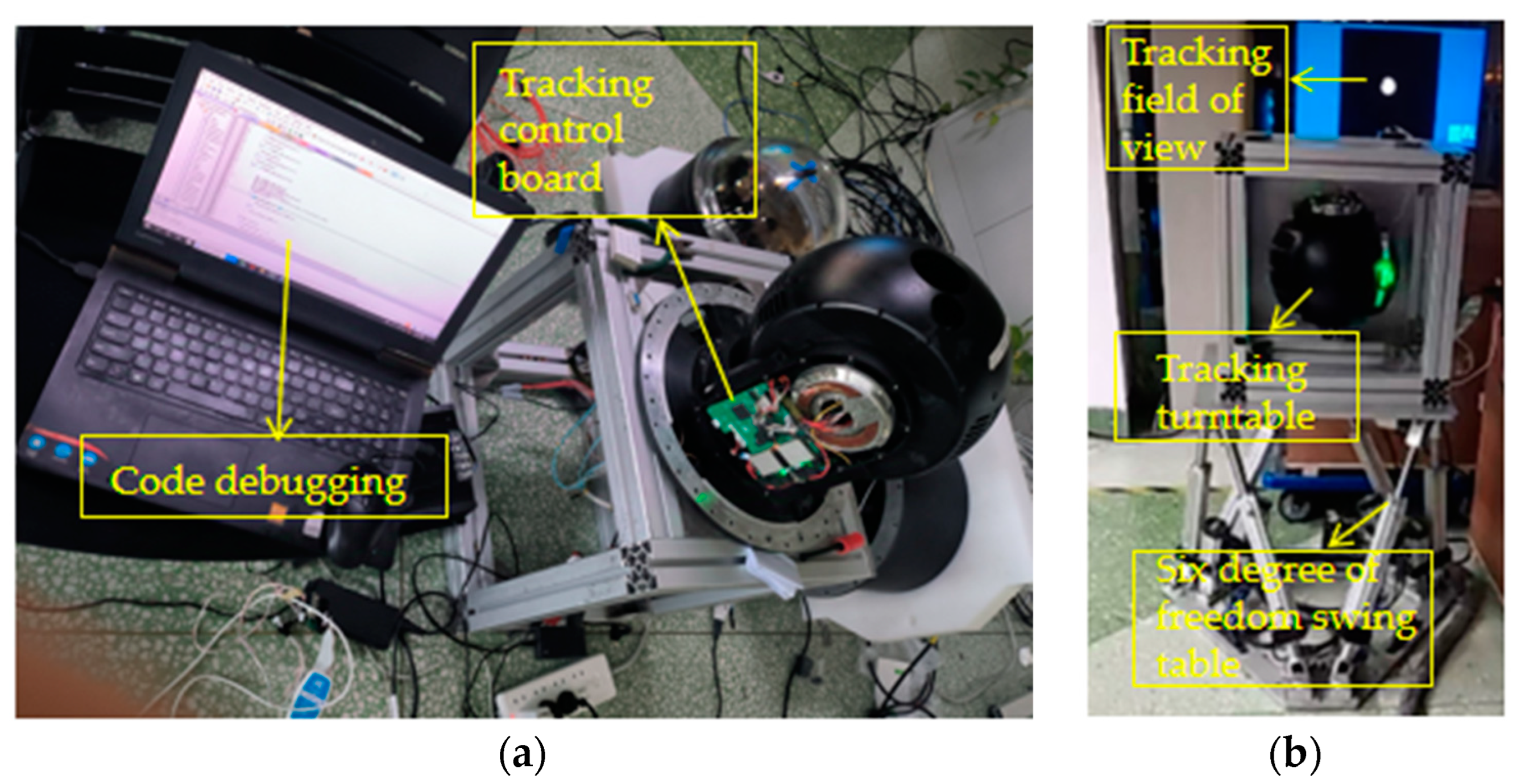
4. Experimental Verification
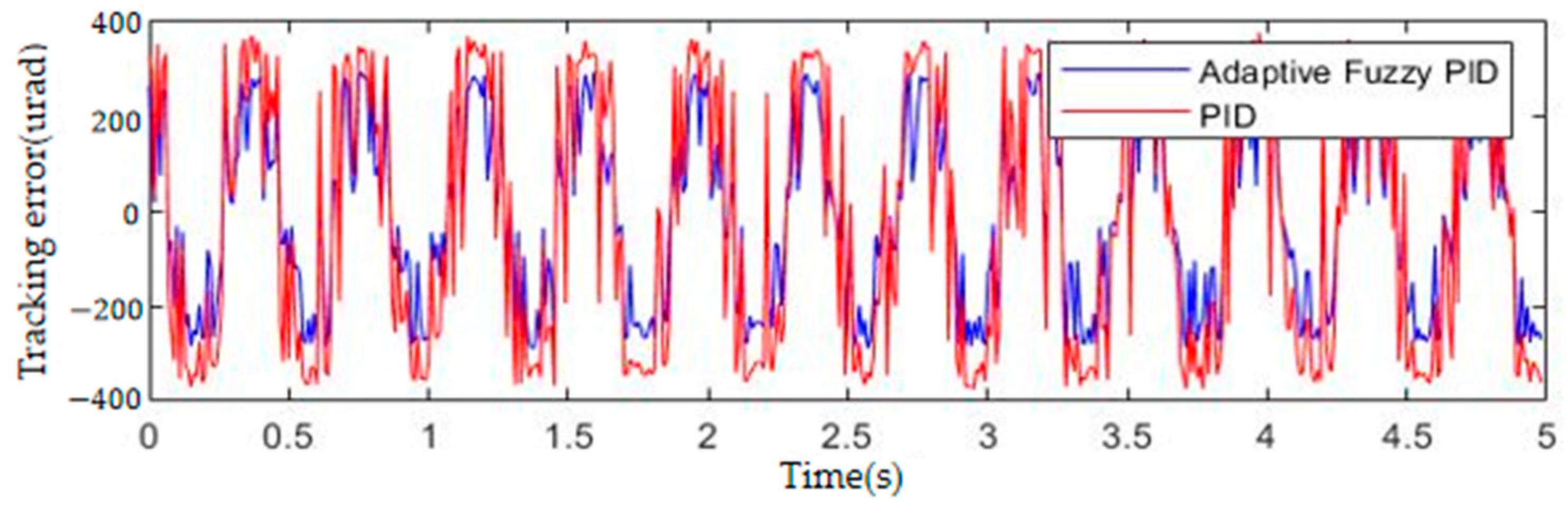
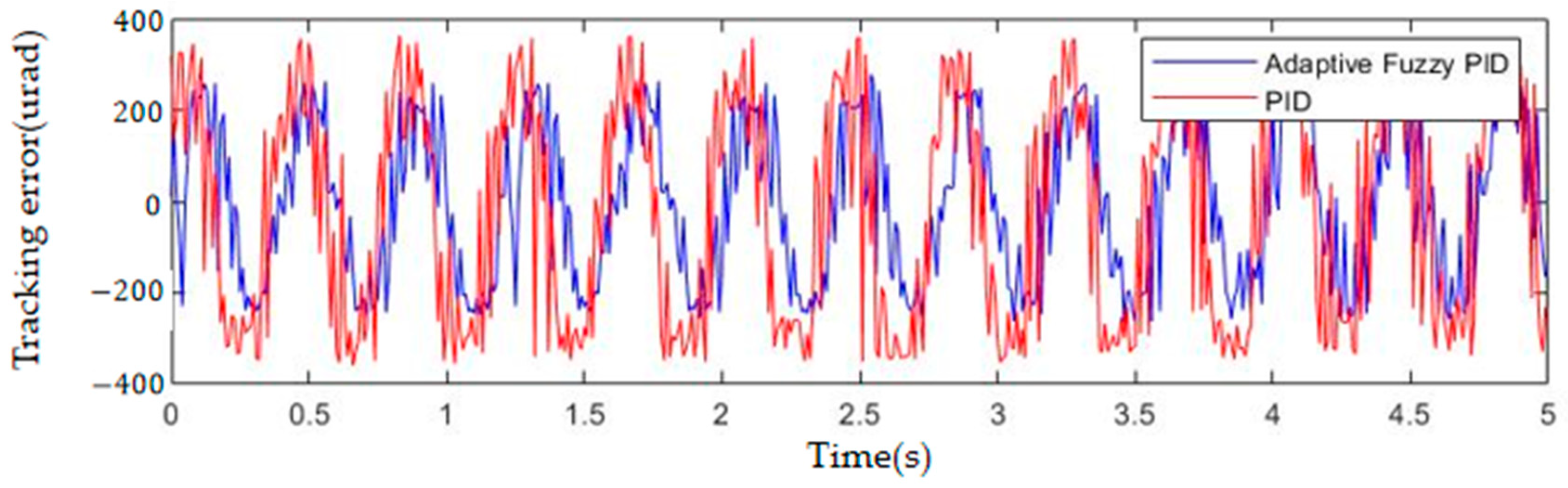
4.1. Tracking Experiment
4.2. Communication Experiment
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Kou, H.; Niu, X.; Wang, C.; Zhang, L.; Li, H. Development of Deep-Sea Underwater Technology and Equipment. Strateg. Study CAE 2024, 26, 1–14. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, M.; Wang, X.; Ren, X. Design and Implementation of More Than 50m Real-Time Underwater Wireless Optical Communication System. J. Light. Technol. 2022, 40, 3654–3668. [Google Scholar] [CrossRef]
- Oubei, H.M.; Shen, C.; Kammoun, A.; Zedini, E.; Park, K.-H.; Sun, X.; Liu, G.; Kang, C.H.; Ng, T.K.; Alouini, M.-S.; et al. Light based underwater wireless communications. Jpn. J. Appl. Phys. 2018, 57, 08PA06. [Google Scholar] [CrossRef]
- Williams, A.J.; Laycock, L.L.; Griffith, M.S.; McCarthy, A.G.; Rowe, D.P. Acquisition and Tracking for Underwater Optical Communications. Proceedings 2017, 10437, 1043707. [Google Scholar]
- Shan, X. Research on Laser Guidance and Docking Technology of AUV. Master’s Thesis, Zhejiang University, Hangzhou, China, 2018. [Google Scholar]
- Ramavath, P.N.; Udupi, S.A.; Krishnan, P. High-speed and reliable Underwater Wireless Optical Communication system using Multiple-Input Multiple-Output and channel coding techniques for IoUT applications. Opt. Commun. 2020, 461, 125229. [Google Scholar] [CrossRef]
- Li, J.; Ye, D.; Fu, K.; Wang, L.; Piao, J.; Wang, Y. Single-photon detection for MIMO underwater wireless optical communication enabled by arrayed LEDs and SiPMs. Opt. Express 2021, 29, 25922–25944. [Google Scholar] [CrossRef]
- Huang, X.; Yang, F.; Song, J. Hybrid LD and LED-based Underwater Optical Communication: State-of-the-art, Opportunities, Challenges, And Trends. Chin. Opt. Lett. 2019, 17, 100002. [Google Scholar] [CrossRef]
- Solanki, P.B.; Al-Rubaiai, M.; Tan, X. Extended Kalman filter-based active alignment control for LED optical communication. IEEE/ASME Trans. Mechatron. 2018, 23, 1501–1511. [Google Scholar] [CrossRef]
- Deng, X. Research on Photoelectric Tracking Control System for Underwater Laser Communication. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar]
- Wang, J.; Zhang, P.; Zhao, Y.; Liu, C.; Liu, R.; Du, Y.; Tong, S. Underwater Wireless Optical Dynamic Communication Technology and Experimental Research. Acta Photonica Sin. 2023, 52, 1106001. [Google Scholar]
- Liu, H.; Yang, Y.; Yin, Y.; Zhang, J.; Li, S. Alignment Control Algorithm of Underwater LD Communication Based on EKF. Acta Photonica Sin. 2020, 49, 0406003. [Google Scholar] [CrossRef]
- Gao, X.; Ke, F.; Zou, W.; Yu, X.; Yuan, J. Servo Control of Fast Steering Mirror Based on Fuzzy Control Strategy. Acta Armamentarii 2020, 41, 1529–1538. [Google Scholar]
- Zheng, Z. Research and Implementation of APT System for Underwater Wireless Optical Communication. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar]
- Dong, X. Study on Structural Reliability of Offshore Platform Under Wave Action. Master’s Thesis, Wuhan Institute of Technology, Wuhan, China, 2022. [Google Scholar]
- Li, G. Research on Submersible, Motor and Propeller Match Strategy of Autonomous Underwater Vehicle Effected by Marine Disturbance. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Zhang, D.; Yan, J.; Zhao, B.; Zhu, K. PMM simulation experiment of full appended submarine. Period. Ocean Univ. China 2023, 53, 98–109. [Google Scholar]
- Hu, T.; Shen, L.; Cao, J.; Dong, W.; Ning, J. Disturbance compensation and neural network fuzzy control of electric servo mechanism. Electr. Mach. Control 2023, 27, 10–20. [Google Scholar]








| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB | PB | PM | PM | PS | ZO | ZO |
| NM | PB | PB | PM | PS | PS | ZO | NS |
| NS | PM | PM | PS | PS | ZO | NS | NS |
| ZO | PM | PS | PS | ZO | NS | NS | NM |
| PS | PS | PS | ZO | NS | NS | NM | NM |
| PM | PS | ZO | NS | NS | NM | NB | NB |
| PB | ZO | ZO | NM | NM | NM | NB | NB |
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | NB | NB | NM | NM | NS | ZO | ZO |
| NM | NB | NB | NM | NS | NS | ZO | ZO |
| NS | NM | NM | NS | NS | ZO | PS | PS |
| ZO | NM | NS | NS | ZO | PS | PS | PM |
| PS | ZO | NS | ZO | ZO | PS | PM | PB |
| PM | ZO | ZO | ZO | PS | PM | PB | PB |
| PB | ZO | ZO | PS | PS | PM | PB | PB |
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PS | NS | NB | NB | NB | NM | PS |
| NM | PS | NS | NB | NM | NM | NS | ZO |
| NS | ZO | NS | NM | NM | NS | NS | ZO |
| ZO | ZO | ZO | NS | NS | NS | ZO | ZO |
| PS | PM | ZO | ZO | ZO | ZO | ZO | PM |
| PM | PB | NS | PS | PS | PS | PS | PB |
| PB | PB | PM | PM | PM | PS | PS | PB |
| Communication Distance/m | Communication Rate/Mbps | Error Rate |
|---|---|---|
| 50 | 10 | 2.3 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, D.; Liu, Y.; Fu, J.; Teng, Y.; Qian, Y.; Wang, G.; Gu, S.; Liu, T.; Xi, W. Research on Tracking Control Technology Based on Fuzzy PID in Underwater Optical Communication. Photonics 2024, 11, 957. https://doi.org/10.3390/photonics11100957
Guan D, Liu Y, Fu J, Teng Y, Qian Y, Wang G, Gu S, Liu T, Xi W. Research on Tracking Control Technology Based on Fuzzy PID in Underwater Optical Communication. Photonics. 2024; 11(10):957. https://doi.org/10.3390/photonics11100957
Chicago/Turabian StyleGuan, Dongliang, Yang Liu, Jingyi Fu, Yunjie Teng, Yang Qian, Gongtan Wang, Sen Gu, Tongyu Liu, and Wang Xi. 2024. "Research on Tracking Control Technology Based on Fuzzy PID in Underwater Optical Communication" Photonics 11, no. 10: 957. https://doi.org/10.3390/photonics11100957
APA StyleGuan, D., Liu, Y., Fu, J., Teng, Y., Qian, Y., Wang, G., Gu, S., Liu, T., & Xi, W. (2024). Research on Tracking Control Technology Based on Fuzzy PID in Underwater Optical Communication. Photonics, 11(10), 957. https://doi.org/10.3390/photonics11100957




