1. Introduction
There are many areas where it is important to focus light to as small a focal spot as possible. These include applications in microscopy [
1], especially confocal and multiphoton microscopy (in both biomedical and industrial applications, such as surface profiling) [
2], laser micromachining [
3], laser materials processing [
4], optical data storage [
5], optical microlithography, near-field optics, high-power lasers and plasma physics, laser trapping and cooling [
6], the physics of light/atom interactions [
7], and cavity quantum electrodynamics [
8].
For tight focusing of light, it is important to consider nonparaxial effects in focusing: we can no longer assume that
as in paraxial theory; but more importantly polarization effects become very important. There have been many papers over the last few decades that have discussed these effects. Broadly, these papers can be divided into two rather separate subdisciplines that are obviously related, but tend to have their own literature: the first, which is the main topic of this paper, is focusing by a lens of high numerical aperture (NA) with a hard-edged aperture (
with
the semi-angular aperture and
n the refractive index of the immersion medium, so that
). The second is the generalization of the theory of optical beam propagation, usually without a hard-edged aperture, to the nonparaxial case [
9,
10,
11,
12]. The aim of the present paper is to clarify some significant issues about the relative performance of different cases, especially different polarization conditions, and to summarize the results for various different cases. In particular, we have unified the normalizations for all cases, and presented comparisons for the area and volume of the focal spot. These comparisons, which include plots of the variations in focal intensity, area, and volume with NA, should prove useful for specification and design of focusing systems.
The structure of the paper is as follows. First, we review the two limiting cases of the paraxial case and the case of a complete spherical field of steradians. Then, we discuss the effects of the amplitude weighting of the illumination field. For investigating the effects of polarization, we first consider the case of a Bessel beam. We discuss briefly the generalization of the Gaussian beam to the nonparaxial regime. Then, we consider focusing by a lens of high NA. Finally, we discuss the case of so-called 4Pi focusing, that approximates a complete spherical field.
2. The Paraxial Case
For paraxial focusing, usually we can consider the scalar case. (Cases where we cannot include the focusing of fields with polarization vortices [
13,
14], but in this paper we consider only focal spots with a bright centre, as opposed to a dark focus such as a doughnut or bottle beam [
13,
14,
15,
16,
17].) For the paraxial scalar case, we have the simple well-known result that the amplitude in the focal plane is the Fourier transform of the angular spectrum of plane waves, given by the amplitude in the front focal plane of the lens (the entrance pupil). This is the paraxial form of the Debye approximation. If the aperture stop is not situated in the front focal plane, then we must take into account the Fresnel number of the optical system, but in this paper we do not consider this case [
18]. The focal spot (the point spread function, or PSF) for a uniformly illuminated circular pupil is given by the Airy disk. By the scaling theorem of Fourier transforms, the size of the focal spot is inversely proportional to the size of the aperture stop. It is also proportional to the wavelength of the light in the immersion medium, so the size of the focal spot is proportional to
. The amplitude weighting of the amplitude in the entrance pupil affects the size of the focal spot. If the amplitude is concentrated near the optical axis, the focal spot is broadened, but the strength of the side lobes (outer rings) is decreased, a process called apodization. On the contrary, if the amplitude is concentrated near the edge of the pupil, the focal spot is smaller, but the side lobes are stronger. These are sometimes called super-resolving filters, but for simplicity, in this paper we use the term apodization to apply to both cases. Several different optimum conditions have been identified (some of the terms are defined in the following two paragraphs):
Here, the Strehl ratio
S is the intensity at the focal point, normalized by the maximum of the corresponding Airy disk. The signal concentration factor
F is the ratio of the intensity at the focus to the
focused power (i.e., not the power
incident on the filter) [
28,
31]. For the paraxial case, this is a measure of the strength of the focal intensity relative to the side lobe level, which is important in many applications. For applications where the efficiency is most important,
S is the more important parameter, but often a laser of higher power can be used. We have
, where
for a pure phase filter, and
for an amplitude filter.
The radius of the first zero of the focal spot, normalized by that of the Airy disk, is
, where
G is called the gain [
23]. The parabolic width of the central lobe, normalized by that of the Airy disk, is
, where we call
the transverse gain [
31]. We would expect that if the shape of the central lobe is approximately constant, then
. An advantage of defining
, rather than
G, is that the parabolic width can be expressed simply in terms of the moments of the pupil, which can be calculated without having to evaluate the PSF every time. On the other hand, to determine
G, the focal field must be evaluated. This distinction becomes important for the high-NA case, when computation of the focused field is time consuming.
is also defined so that it is possible to take negative values, corresponding to a minimum in intensity at the focus, but in this case
G is imaginary.
The principle of the so-called super-resolving filters was rediscovered under the name of superoscillations [
32]. This has resulted in numerous publications, many of which do not mention the extensive old work of Wilkins, Toraldo di Francia, Barakat, Frieden, Boivin, and many others [
20,
21,
22,
23,
25,
26,
27,
28].
4. Effect of Amplitude Weighting of the Illumination Field
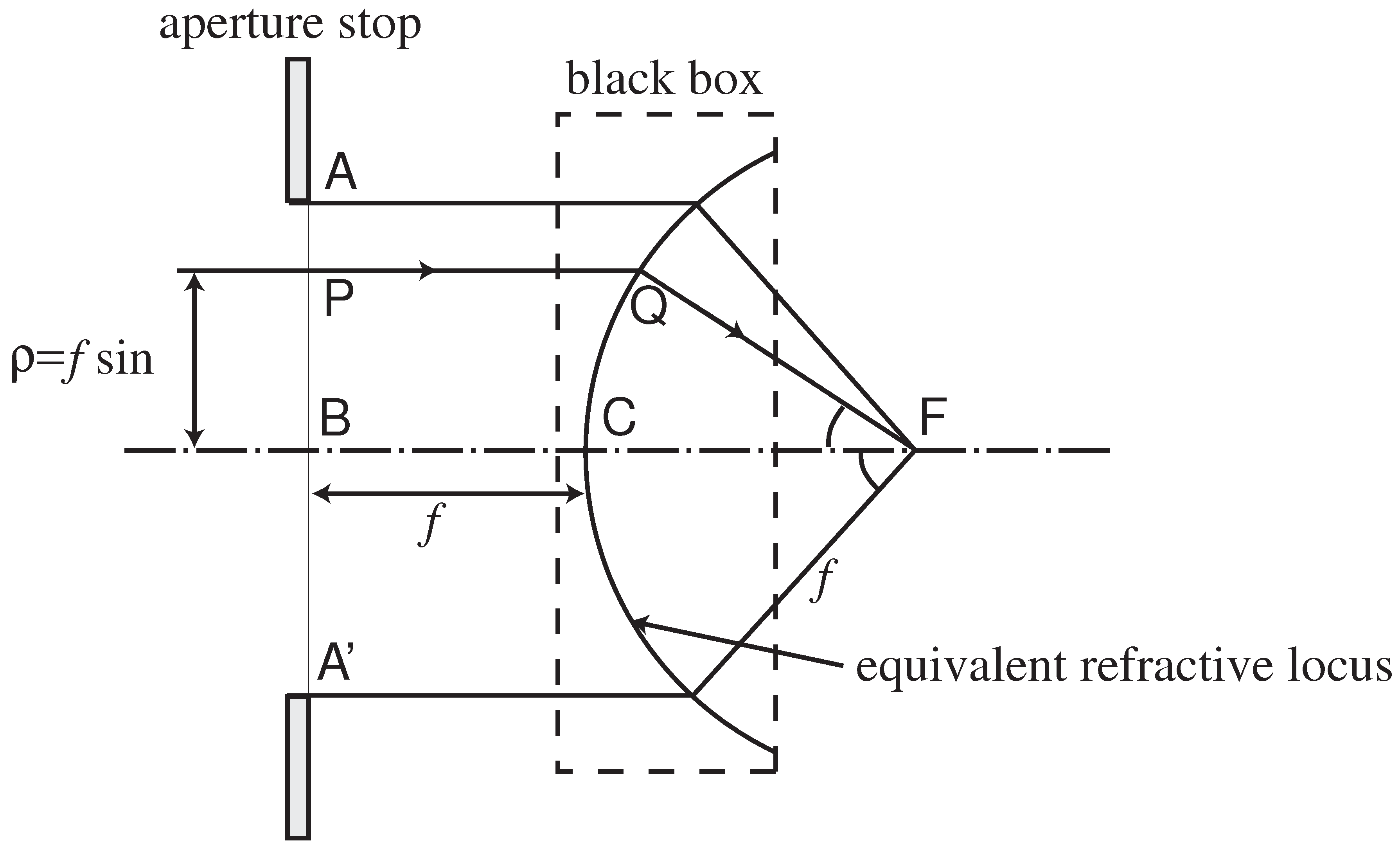
Now, we consider focusing by high-NA lenses with different values of NA. Our model of a high-NA, infinity-tube-length lens is shown in
Figure 2. The lens is considered as a black box, i.e., we do not consider the actual optical elements within it. Focusing is described by a surface called the equivalent refractive locus, which is the surface formed by the intersection of ingoing rays, assumed parallel, and outgoing rays, which are focused onto the focal point [
41]. Note that the equivalent refractive locus is not a real interface, but just a conceptual surface. Hence, it is incorrect to apply Fresnel’s transmission coefficients to this surface. For a system satisfying the sine condition, the surface is spherical. If, in addition, there are no aberrations, it is called an aplanatic system. The radius of the sphere is equal to the focal length
f. The aperture stop (the entrance pupil) is situated a distance
f in front of the equivalent refractive locus. The outgoing rays are equivalent to an angular spectrum of plane waves incident on the focal region. The range of angles of this angular spectrum is limited by the size of the aperture stop. The field in the focal region is thus calculated by integrating vectorially over this angular spectrum of plane waves [
42,
43]. The amplitude weighting
of the angular spectrum of plane waves incident on the focus for a system satisfying the sine condition is
[
42,
43].
The exit pupil, the virtual image of the aperture stop within the lens, is situated at minus infinity. It is also infinitely large, so that Debye’s condition, which requires the Fresnel number to be very large, is automatically satisfied [
44]. The model for the lens considered here is much the same as described by Richards and Wolf [
43]. However, they do not show an aperture stop in their system. Effectively, they are therefore analysing the case of a converging spherical wave incident on an aperture, which is the exit pupil of the system. In order for the Debye approximation to be valid, the Fresnel number of the system must be very large, which will usually be the case for practical high-NA systems.
We also want to point out that if Richards and Wolf’s method is used to calculate the focal distribution, the axial optical coordinate they propose (
) is not the best choice for a high-NA system [
43]. A better choice is
, which matches the shape of the spherical defocused wavefront [
34,
45].
In earlier papers, we have considered focusing by optical systems obeying different focusing conditions, including the sine condition (aplanatic), Herschel condition, Helmholtz condition, and for a paraboloidal mirror [
46,
47,
48]. These different conditions alter the shape of the equivalent refractive locus, and therefore, the amplitude weighting
of the angular spectrum of plane waves incident on the focus. The Herschel condition has an angular spectrum with a uniform angular distribution, and gives perfect axial imaging. (Note that the term ‘perfect’ here is the conventional term, but refers to geometrical optics, and does not imply that the system does not suffer from diffraction effects. Perhaps ‘ideal’ is a better description.) For the Helmholtz condition, the equivalent refractive locus is flat, corresponding to a planar surface, and this case is important because it applies for a planar diffractive optics element, or planar optics. For a paraboloidal mirror the surface is a paraboloid.
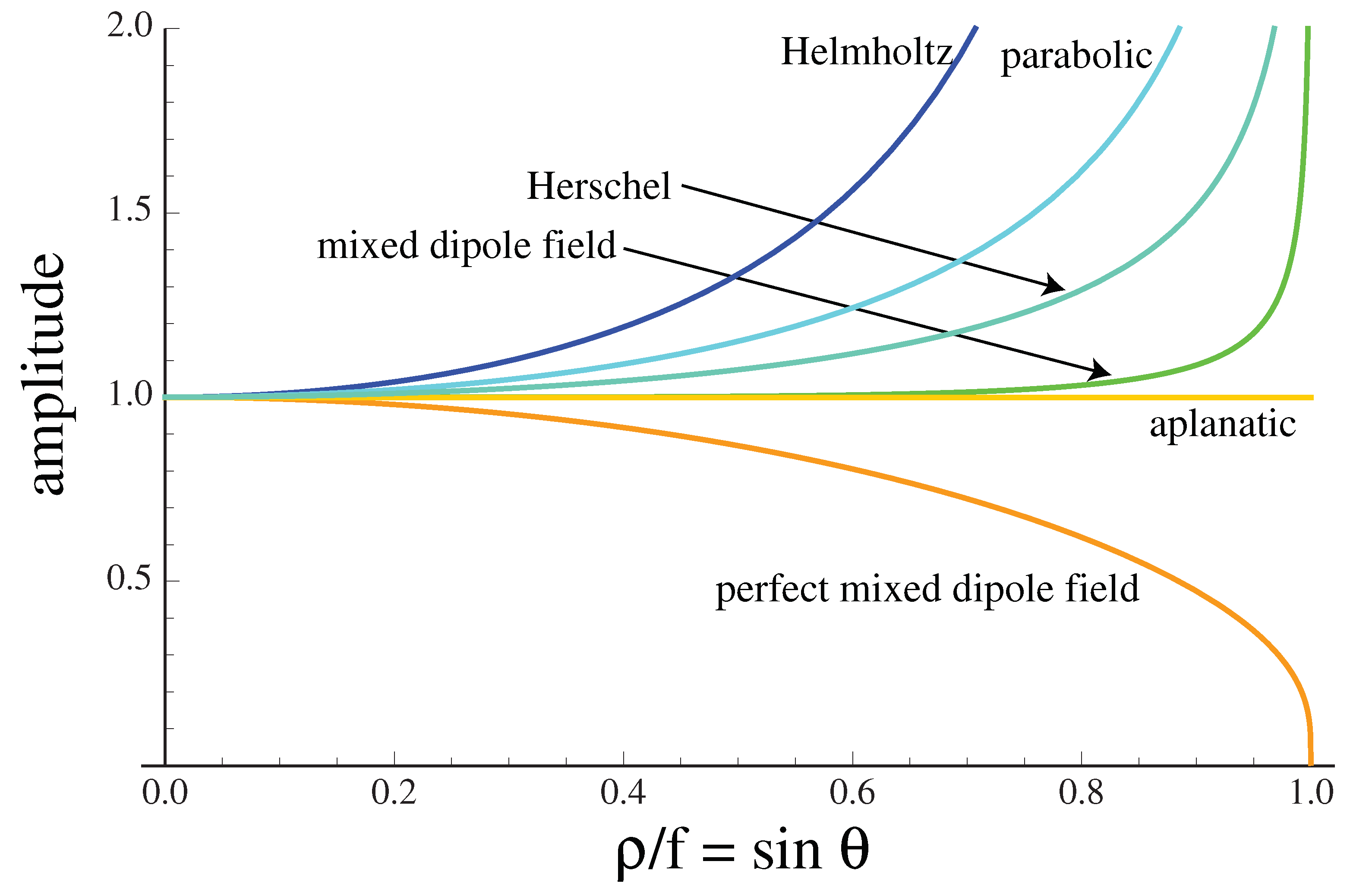
The different conditions are thus equivalent to illuminating an aplanatic system with plane waves with different variations of amplitude strength with distance from the axis,
, with
f the focal length and
the direction of the component of the angular spectrum relative to the axis, and therefore, can be used to explore the effects of apodization. These input plane wave amplitudes
are illustrated in
Figure 3. Most of the different conditions are thus equivalent to illuminating with a plane wave that is stronger near the edge of the aperture. We also show the field that needs to be incident on an aplanatic system to generate a mixed-dipole field for the vectorial case (see
Section 3.2). Note that the aplanatic case gives a good approximation to the mixed-dipole field for moderate values of NA. Further, we show the case of a so-called perfect mixed-dipole field, which is seen to drop off in amplitude away from the axis (also see
Section 4.2). For any input, we can generate the perfect version of the wave by multiplying by
. We explain the significance of the perfect fields later in this section. The amplitudes of
that we must put into an aplanatic system to attain focusing that is the same for the different conditions are as follows:
Aplanatic: , ;
Mixed-dipole field: , ;
Herschel condition: , ;
Helmholtz condition: , ;
Paraboloidal mirror: , ;
Perfect mixed dipole: , .
So far, we have discussed focusing of a plane wave onto the focal point. The same model also applies to the case of collimating light from a point source [
46]. Some papers have erroneously claimed that these two arrangements behave differently from one another, but by Helmholtz’s principle of reciprocity, the arrows on the rays in
Figure 2 can be simply reversed. However, care must be taken when changing the integration variable. For a system satisfying the sine condition,
, so
, and therefore,
. As
, we then have
, and we see that the factor
has moved from the numerator to the denominator.
4.1. Scalar Case
We define
F as the ratio of the intensity at the focus to the focused power, normalized by the maximum achievable value, which is for a complete spherical focused field with a uniform angular spectrum. This can be calculated directly from the moments of the pupil, avoiding the necessity to calculate the focused field [
47]. We have
where
is the pupil function (angular spectrum) expressed in terms of
.
It is easy to show from Schwarz’s inequality that for the scalar case F is maximized, for any value of , for a uniform angular spectrum (Herschel condition), and then, . For the different conditions:
Scalar Helmholtz condition:
Scalar paraboloidal mirror:
For the Herschel case, for a complete sphere, . For a complete hemisphere and uniform angular illumination, . For an aplanatic scalar system, for , ; for a Helmholtz system, as the input power diverges in this case; and for a paraboloidal mirror, .
We also introduce the parameter
, which is the ratio of the intensity at the focus to the integrated intensity in the focal plane [
47]. For the scalar case,
4.2. Vectorial Case
For the vectorial case, in general we must use a vectorial pupil function [
48,
49]. The angular spectrum is vectorial, and must be multiplied by the corresponding angular weighting
, if necessary. For the case of illumination of the front focal plane by a linearly polarized wave,
It is found from Schwarz’s inequality that for the vectorial case the mixed-dipole field maximizes the total energy density at the focus, for a given power input, for any NA [
38]. The mixed-dipole field corresponds to the field of an electric dipole and a magnetic dipole, oriented at right angles to each other, and in this case
.
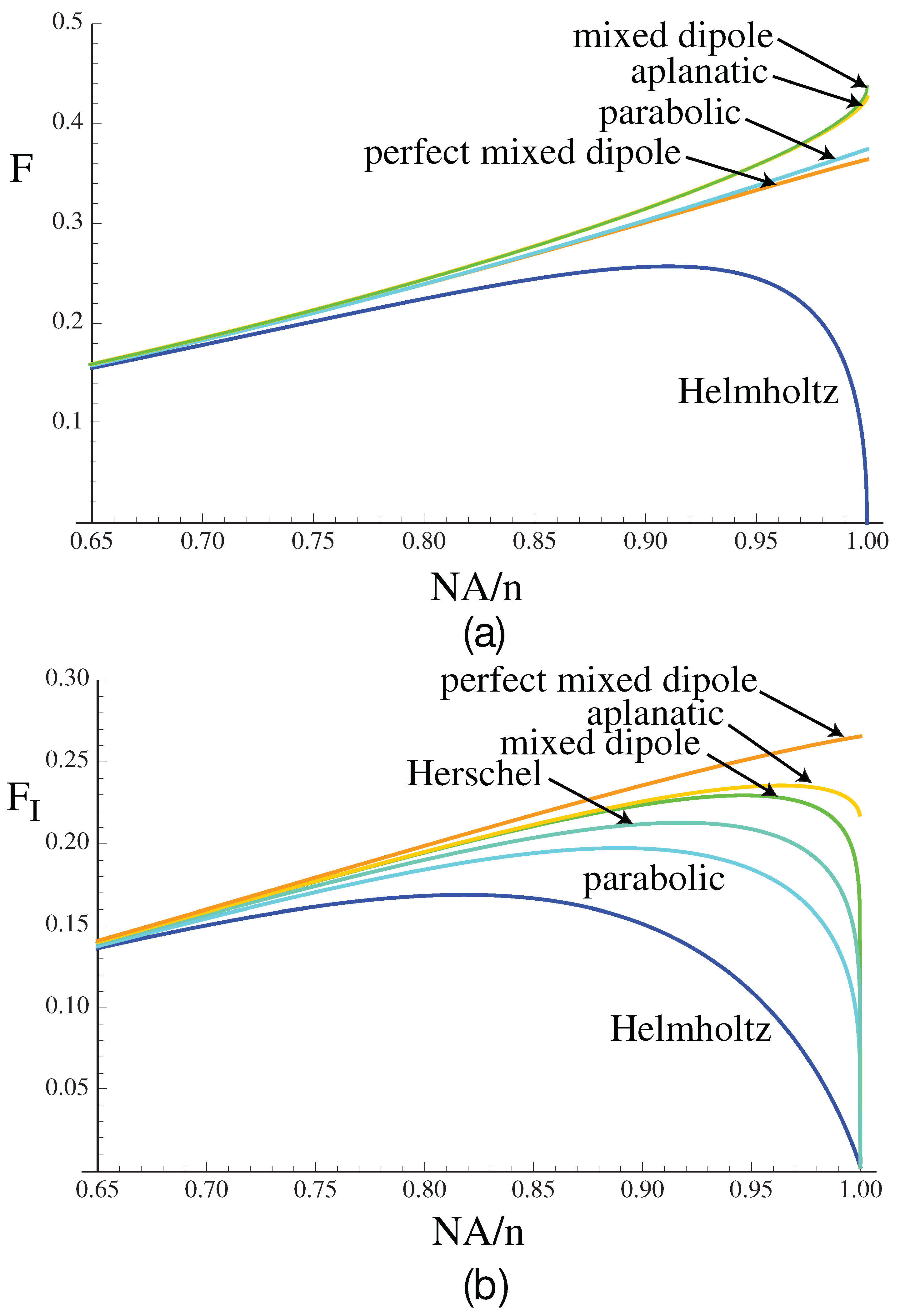
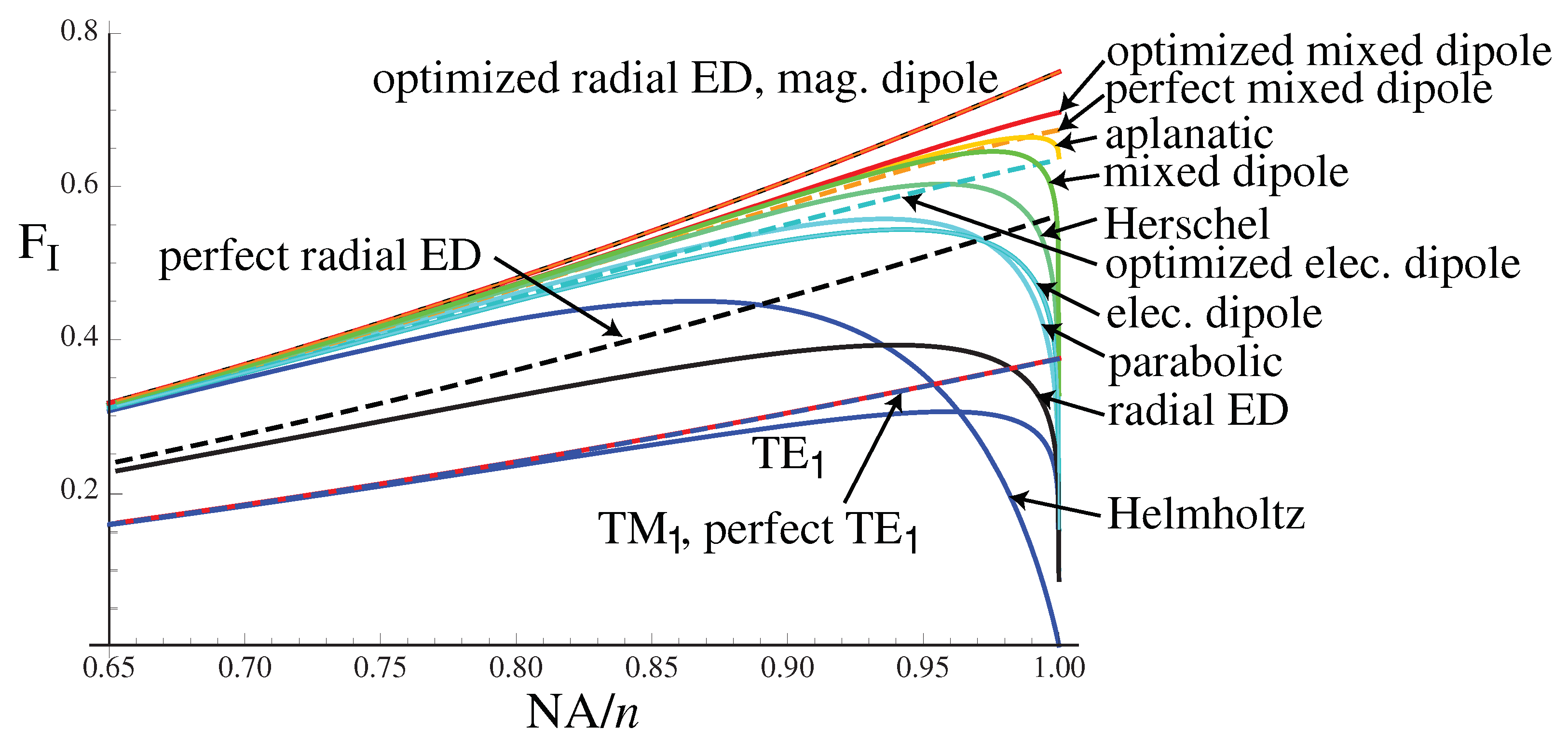
Figure 4a shows the variation in
F, defined now as the ratio of the electric energy density at the focus to the focused power, this time normalized by the maximum achievable value for linearly polarized illumination and for a complete spherical focused field. The values are plotted against NA. The mixed-dipole field produces the highest
F for any linearly polarized input. The Herschel case is not shown in
Figure 4a: it is slightly lower than the curve for the aplanatic case. For
,
for the mixed-dipole field,
for the aplanatic case,
for the Herschel case, and
for the paraboloidal mirror [
38]. The maximum possible
F that can be achieved (over a complete sphere) is
, as half of the total energy density is electric energy density. It might be surprising that the mixed-dipole field does so well for illumination over only a hemisphere, as only half of the total energy density is in the electric form, but this is explained by the directional (forward propagating) nature of the mixed-dipole field. In the multipole expansion, the electric and magnetic energy densities at the focus, resulting from the electric and magnetic dipole terms, are still equal, but both are larger than half what they would be for a complete sphere. All the curves behave similarly for low NA, and then, at high NA, the Helmholtz case in particular falls off significantly, partly as a result of the strong weighting at high incidence angles, but also the strong longitudinal field component in the focal region. It is interesting to note that the shape of the curves looks quite different when plotted against NA rather than the angle
, as has been presented previously [
38].
We have for F for linearly polarized illumination:
These compare with
for the scalar case. Zumofen et al. considered scattering of a focused wave by a point-like dipole [
50]. They showed that the scattering ratio
is equal to our
. For illumination over a hemisphere (
), as the point dipole scatters isotropically, half of the scattered intensity is backscattered and half is forward-scattered, and
is therefore the proportion of the backscattered power. For the mixed-dipole case in particular,
of the power is therefore backscattered, which is the upper bound for focused linearly polarized light. An identical fraction is forward-scattered, which interferes destructively with the incident power, so that the overall transmittance is
. These results can be generalized for the arbitrary aperture
, giving for the proportion of backscattered power
; for forward-propagating light
; and for sideways scattering
. These three components add together to give unity, agreeing with conservation of energy.
As for the scalar case, we also introduce the parameter
, which is the ratio of the electric energy density at the focus to the integrated electric energy density in the focal plane [
47]. For the vectorial case, again we must in general use a vectorial pupil function [
49].
Figure 4b shows the variation in
with NA for different pupil weightings.
is normalized so that it equals
F for the paraxial case. (In our earlier paper, for the scalar case the normalization was different [
47].) It can be shown (again using Schwarz’s inequality) that for linearly polarized input,
is maximized for the so-called
perfect mixed-dipole field, which tends to
for
[
48]. All the other curves in
Figure 4b fall off at high values of NA. The aplanatic case performs quite well for
, exhibiting a maximum value of 0.236 for
, as well as for
F. For the mixed-dipole case,
has a maximum value of 0.230 at
. The concept of the perfect wave was introduced by Stamnes [
51]. However, it has been criticized on the grounds that integrated intensity is not proportional to power because of directional effects [
52]. Our view is that this parameter is useful, as it compares the electric energy density at the focus with the strength of the side lobes in the focal plane. Like
F,
can be calculated directly from the pupil function, because integrated intensity, even though it is not the same as power, satisfies a conservation law for propagation in free space [
52]. We might call
F the power concentration factor, and
the integrated energy concentration factor.
The parameters
F and
are measures of the strength of focusing, but an alternative approach to specifying performance is to consider the parabolic width of the central focused lobe, which can also be calculated directly from the moments of the pupil [
31]. We define the gains
, and
so that close to the focal point the normalized electric energy density is [
48]
The gains have been normalized so that for a complete spherical scalar field, when the intensity is
, they become unity. The parabolic variation gives a reasonably accurate prediction of the full width at half maximum (FWHM) of the focused spot. The limitations of this approximation, and its statistical interpretation, were discussed by Larkin [
53]. The parabolic approximation is determined by pupil moments up to second order, and always predicts a smaller value than the true FWHM. Typically, for practical non-confocal intensity PSFs the parabolic approximation is about
smaller than the true value, and
smaller for Bessel beams, so a better approximation can be obtained simply by a constant scaling. A much better approximation can be achieved by using moments up to the fourth order [
53]. The parabolic approximation also cannot predict the Rayleigh two-point resolution, as the sum of two parabolas is always a parabola. A fourth-order treatment predicts the two-point resolution for the Airy disk to be just
smaller than the true value.
The area of the focal spot, defined in terms of the FWHM of the parabolic approximation to the intensity in the central lobe, in general elliptical, is
where
. The volume of the ellipsoidal focal spot is
For circularly polarized illumination, rather than linear polarization, when the focal spot is cylindrically symmetric, we have
where
is the cylindrical radius, and
and where
and
are the gains for the corresponding linearly polarized case. The area of the focal spot in this case can be written as
This expression gives close to the same value as Equation (
16) if the focal spot is approximately symmetric, as the geometric mean of
,
,
, is approximately equal to the arithmetic mean,
, but for a distorted focal spot they can give significantly different values. This also alters the values for the volume of the focal spot for the circularly polarized case,
:
For the scalar case, the minimum area for uniform focusing by a single lens (Herschel) at
is
and the minimum volume is
. Interestingly, for uniform scalar focusing over more than a hemisphere, the minimum area of
is reached at
[
47].
Expressions for
, and
for various different cases have been given in our previous papers [
47,
48,
54,
55,
56,
57].
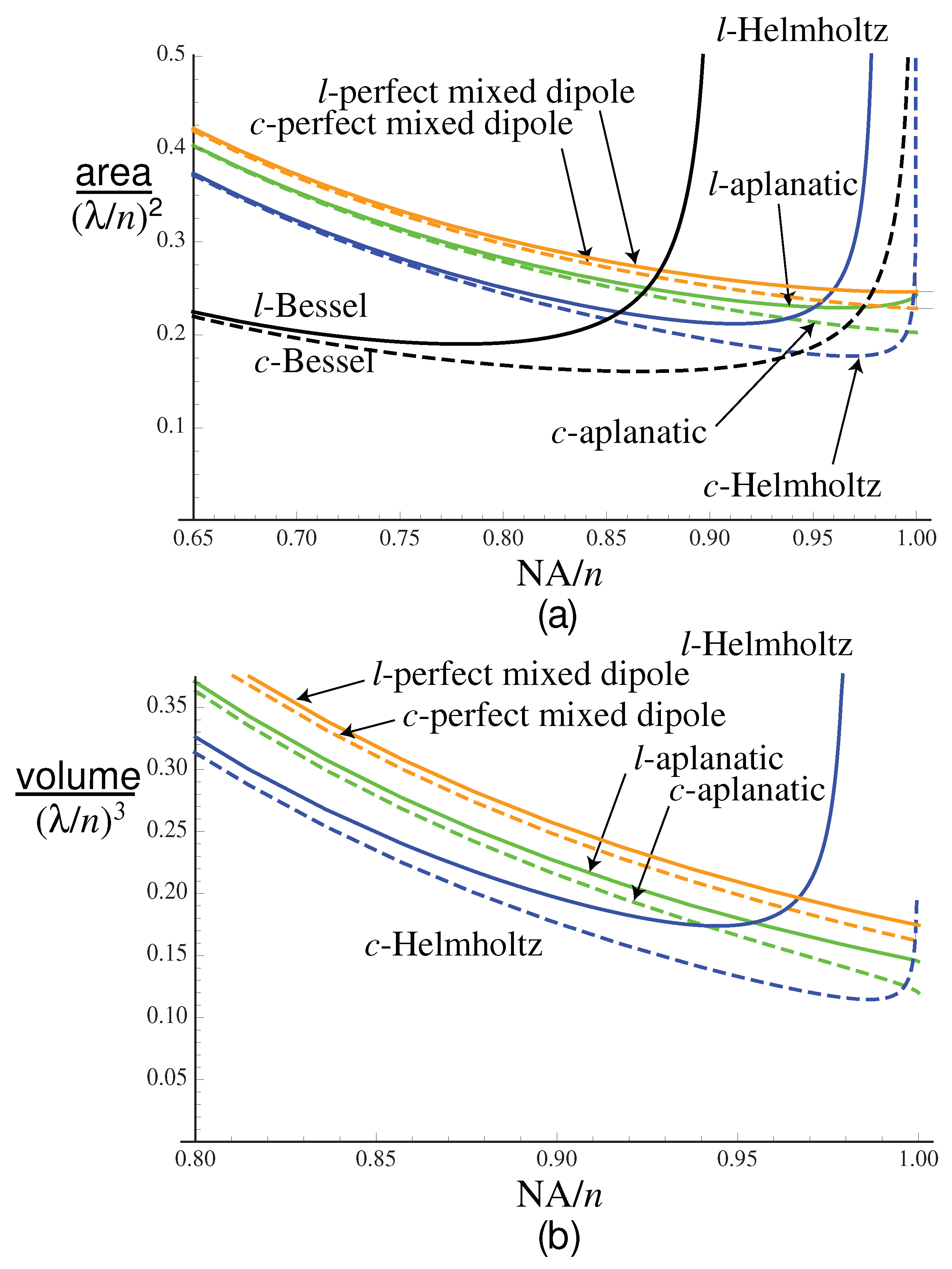
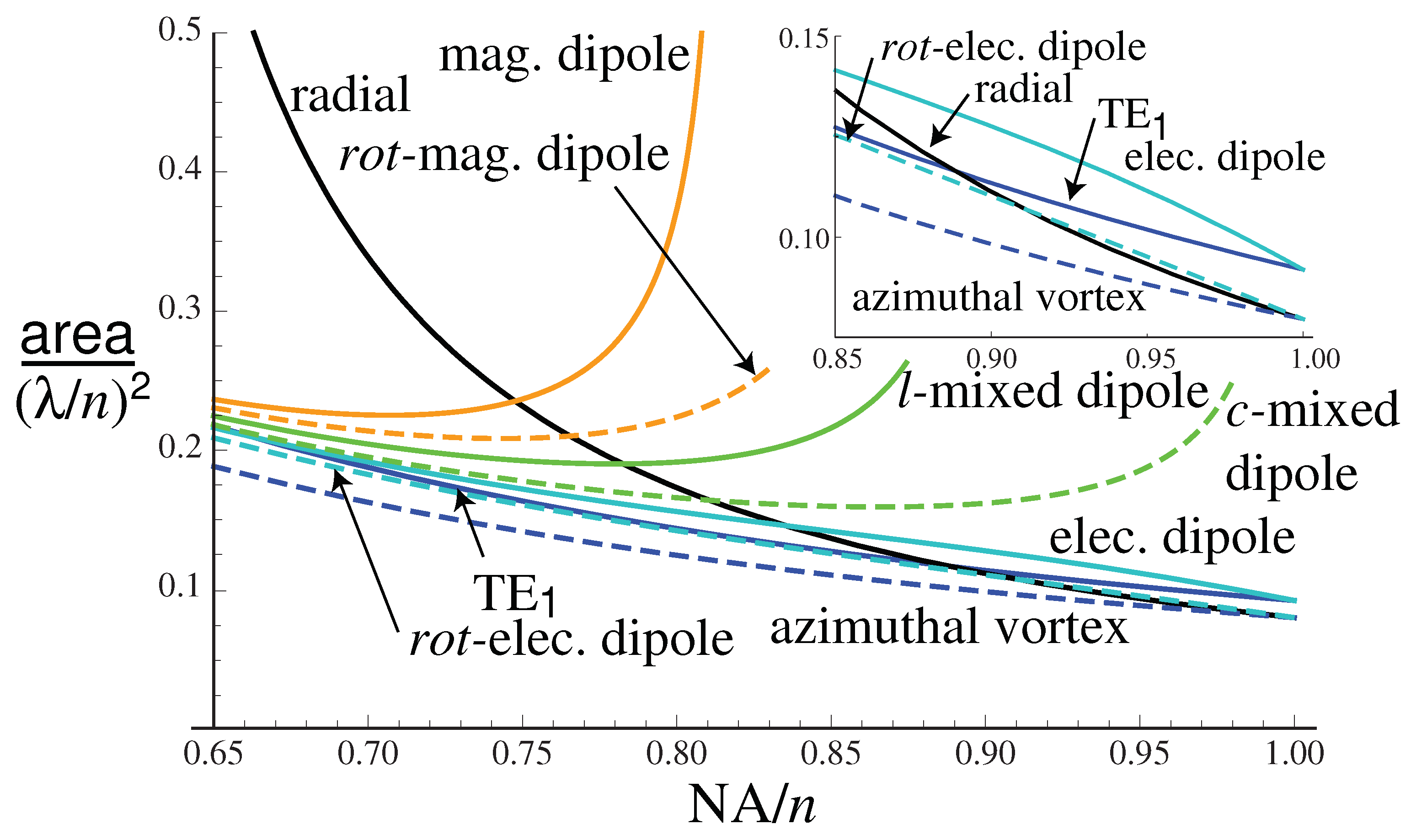
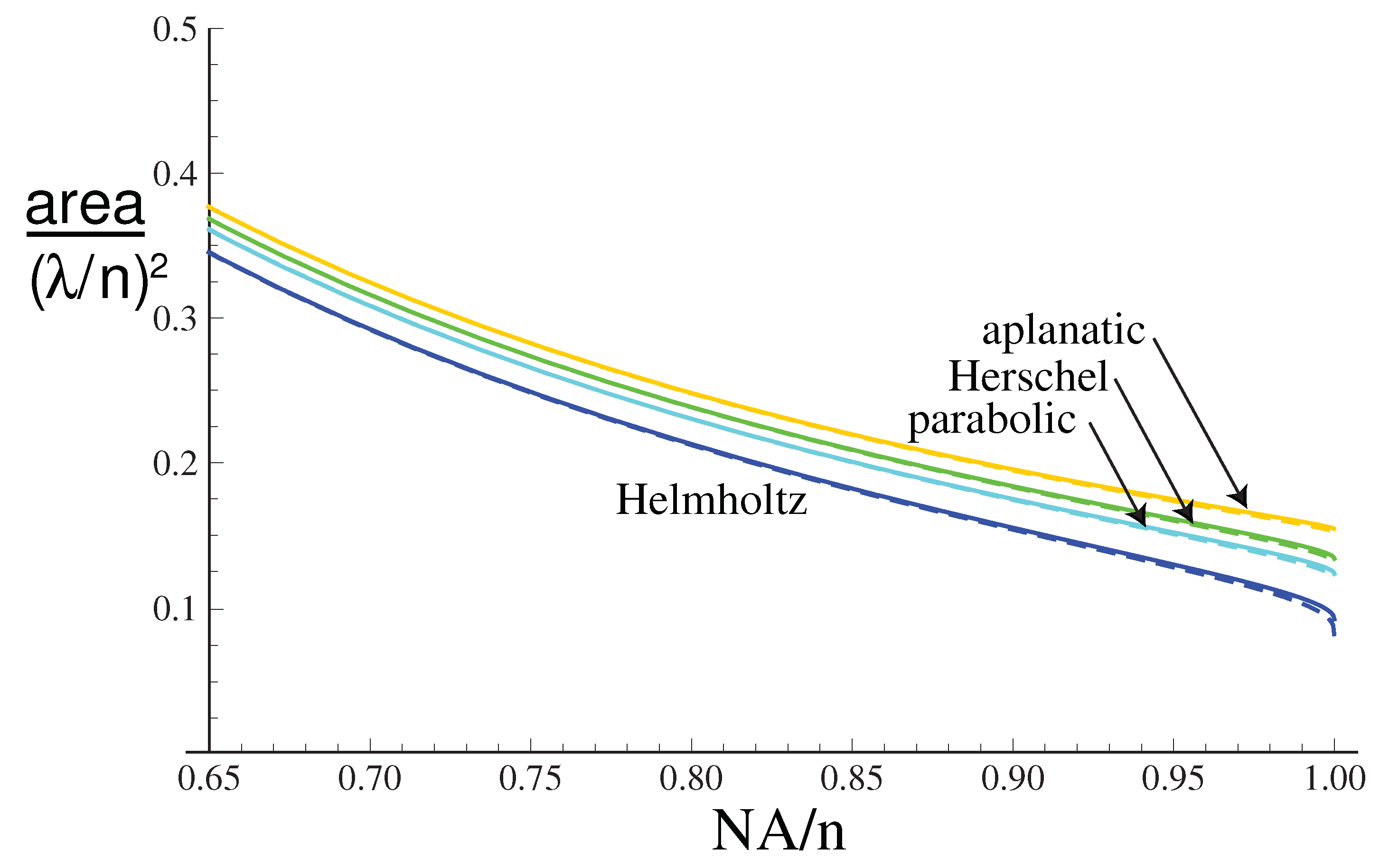
Figure 5a shows the area of the focal spot for some different cases of linearly polarized or circular polarized illumination. The focal spot in general has a smaller area for the circular polarized cases than the linearly polarized cases, which follows from the inequality
. For the linearly polarized case, it has been observed that the focal spot can split into two peaks for high NAs, thus limiting how high an NA can be used [
36]. This limitation is not present for the circularly polarized case, but nevertheless the area of the focal spot fails to reduce in size for high NA. For the different apodizations considered, for linearly polarized illumination, the focal spot is smallest for the Helmholtz condition and
, when the area is
. For circularly polarized illumination, the size of the focal spot for the aplanatic case monotonically decreases with NA, but not for linearly polarized illumination. A smaller spot can be achieved using Helmholtz weighting and circular polarization, reaching a smallest size of
at
.
5. Effects of Polarization: The Bessel Beam
The Bessel beam is an important example of a propagationally invariant beam, meaning that the shape and cross-section of the beam does not change with distance, i.e., it has an infinite depth of field, as was pointed out in Ref. [
58]. However, it has been known for much longer that for scalar waves a beam with a Bessel function
amplitude cross-section can be generated by a pupil that is a narrow annular ring [
59,
60,
61,
62,
63,
64]. In our early (1978) paper on Bessel beams, we called this a
-ring [
58]. That the Bessel function
was a mode in free space for the scalar wave equation was discussed by Rayleigh [
65]. In Ref. [
64], an experimental image of an extended object formed using a lens with a narrow annular aperture was presented. For some reason, papers by Durnin et al. are often cited although they were published much later than these cited references, and others [
66]. Perhaps this was because of the somewhat sensationalistic and misleading terms used: non-diffracting or diffraction-free. Misleading because propagationally invariant beams do diffract, but the diffraction of the central lobe is balanced by inward diffraction from the side lobes.
A conical prism acts as an axicon, and generates an approximation to a Bessel beam [
67,
68]. A diffractive axicon, which is like a zone plate but with equally spaced rings, also gives an approximation to a Bessel beam [
69]. The Bessel beam has the narrowest central lobe for any pupil filter that is real and non-negative. However, the side lobes are strong. In fact, a Bessel beam is not actually physically realizable as there is an infinite amount of power in the side lobes, so that the parameters
F and
are both zero. This situation is not as bad as it may seem, as other waves such as plane waves and spherical waves are also not physically realizable, but nevertheless they are useful concepts.
Physically realizable approximations to Bessel beams include the Bessel–Gauss beam, which is a paraxial beam that can be considered as an integration of inclined Gaussian beams with their axes on a cone and their waists at the apex of the cone [
58,
70]. Although Bessel beams are valid for the nonparaxial case, Gaussian beams are fundamentally a paraxial concept, and there are different ways to extend them, and therefore, Bessel–Gauss beams, to the nonparaxial case [
71,
72,
73,
74]. Another approximation to the Bessel beam is that formed from an annular pupil of finite width (a circular slit) [
61]. Yet another is a binary phase filter that produces an approximation to a Bessel beam over a finite axial range [
75,
76].
When polarization is considered, an important case is that of a lens with a narrow annular pupil illuminated by a linearly polarized wave [
36,
77]. After focusing, this forms a mixed-dipole wave [
36]. The variation in the area of the focal spot of electric energy density with NA is plotted in
Figure 6, labelled
l-mixed dipole. At the axis, the field is transversely linearly polarized. For high NA, longitudinal and cross-polarization terms with
- and
-dependence, respectively, are introduced, which enlarge the beam in one transverse direction, making it not cylindrically symmetric. As the NA is increased, eventually (at a value of
) the intensity exhibits two offset maxima, with a saddle between [
36]. The area according to the parabolic approximation is then undefined. Although the electric energy density is not cylindrically symmetric, the total energy density is cylindrically symmetric. The same transversely polarized Bessel beam with a cylindrically symmetric total energy density (but not electric energy density) was investigated by Mishra [
78]. His expressions simplify and reduce to our expressions upon introducing the double angle
, where
is the azimuthal angle, and using the identity
(as in Equation (
22) with
) [
36].
An alternative case is when the annular pupil is illuminated with a circularly polarized wave. In
Figure 6, this is labelled as
c-mixed dipole. On the axis, the field is transverse and circularly polarized. The focal spot is symmetric and the double spot tends to be averaged out. For high NA, the
c-mixed dipole gives a smaller area focal spot than the linearly polarized,
l-mixed-dipole, case. The focal spot for a linearly polarized Bessel beam is smallest for
, with an area of
, and for a circularly polarized Bessel beam it is
for
. These areas compare with the parabolic approximation for the area of a scalar Bessel beam for
, which is
.
The mixed-dipole field can be considered as the sum of an electric dipole field and a magnetic dipole field. For low NA, the electric, magnetic, and mixed-dipole fields behave identically, but as the NA is increased the electric dipole field gives rise to a concentration of electric energy density, and a smaller focal spot (
Figure 6) [
40,
79]. The magnetic dipole field, on the other hand, gives a concentration of magnetic energy density, and the electric energy density becomes weaker and spread out. For a magnetic dipole oriented along the
y-axis, the field component
everywhere. Similarly, for an electric dipole oriented along the
x-axis, the field component
everywhere. The electric and magnetic dipole fields can be taken together as a basis for generating a continuous set of different polarization distributions. The normalized electric energy density is [
55]
where
,
, and
D is a parameter which is equal to 1 for an electric dipole field, 0 for a mixed-dipole field, and –1 for a magnetic dipole field. Note that for
, the terms in
, corresponding to the
y component of the electric field, vanish.
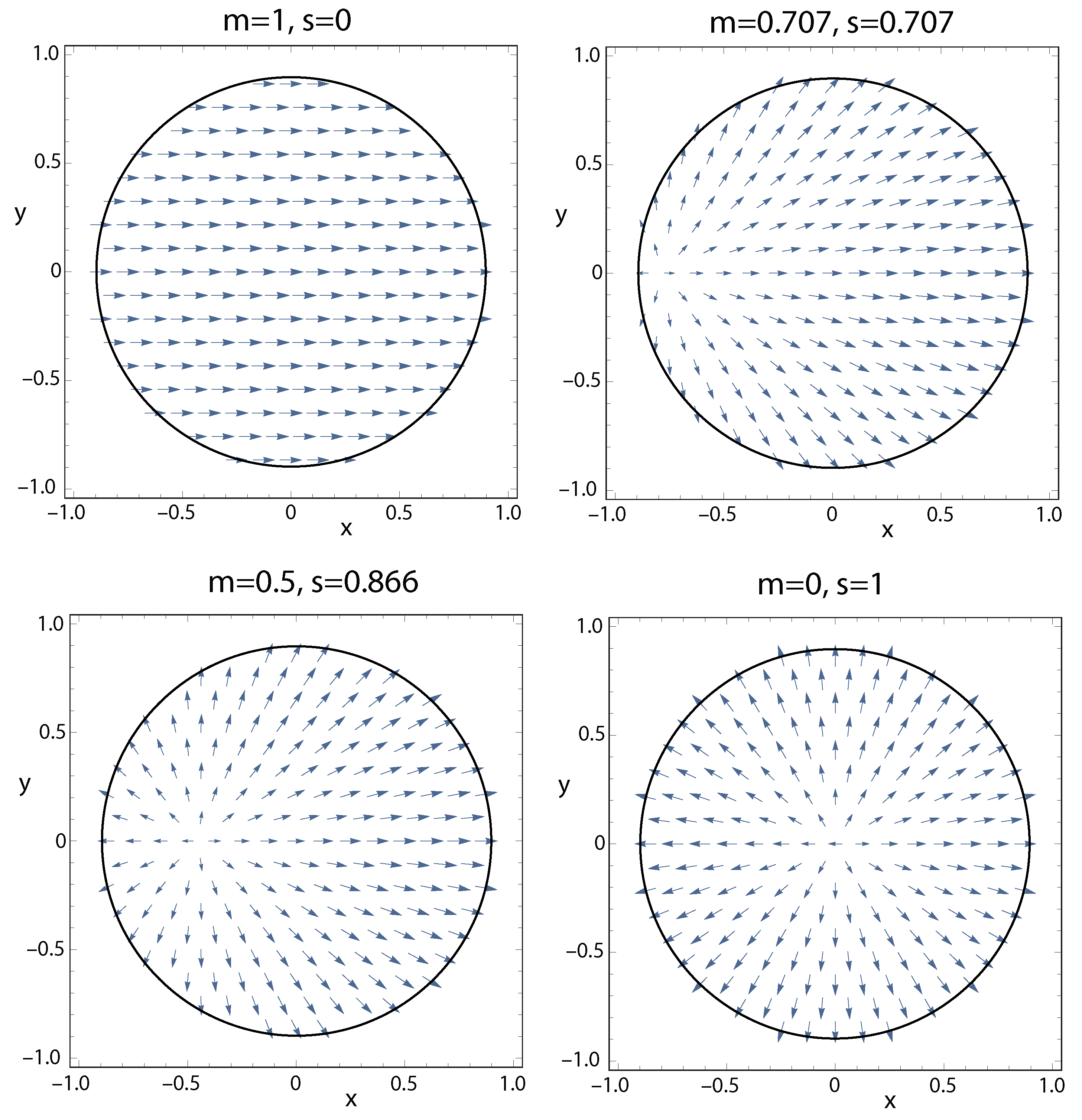
The polarization on the reference sphere, as shown in
Figure 1 for the different cases, can be written as
The focal spot of the electric dipole field is asymmetric, but a symmetric version can be generated by summing in phase quadrature two beams rotated by
with respect to each other, which is equivalent to the field of a rotating electric dipole (
.-electric dipole) [
56,
57]. This is analogous to the symmetric
c-mixed-dipole field, produced by summing in phase quadrature two linearly polarized beams to give circularly polarized illumination.
.-electric dipole polarization corresponds to illuminating an annular pupil with elliptically polarized light, where the ellipticity varies from circularly polarized for
, to azimuthally polarized for
. The major axis of the ellipse rotates around the annulus, equivalent to a phase vortex of unity charge. The polarization on the reference sphere, in analogy with
Figure 1, is now given by
The corresponding areas of the focal spot are labelled as
rot.-elec. dipole and
rot.-mag. dipole in
Figure 6, and are smaller than for the fixed-dipole cases. To our knowledge, this distinction for the cross-sectional areas has not been described previously.
The term in
in Equation (
22) does not contribute to the parabolic approximation to the size of the focal spot. However, the
in Equation (
25) does increase the area of the focal spot. The terms in
in both equations vanish if
, and the electric field is then purely transverse,
, i.e., it is a transverse electric (TE) field of azimuthal mode number unity,
. In a similar way,
corresponds to a transverse magnetic field,
,
. The mixed-dipole field in the annular region of
k-space is equal to the sum of a
field and a
field, so the
and
fields can be taken as an alternative basis to generate the set of polarization distributions, either fixed or rotating [
55]. The rotating TE field,
-
, corresponds to an azimuthal field with a phase vortex (phase singularity of unity charge), labelled azimuthal vortex in
Figure 6 [
10,
13,
14,
56,
57,
80]. It can be generated experimentally using a liquid crystal modulator as a polarization rotator, which introduces the required phase vortex automatically [
81]. The area of azimuthal vortex is smaller than that of
. It is interesting to note that the rotating and stationary versions of mixtures of electric and magnetic dipole fields tend to give similar focal areas for low NA, except for the case of the azimuthal vortex and
cases, which actually become more different from the linear polarized cases at low NAs, because the input polarization is completely different. The
cases are not shown in
Figure 6, as the spot sizes are outside of the range of the plot.
Another polarization distribution that has received much attention is radial polarization. If an annular pupil is illuminated with a radially polarized beam, equivalent to
, the resulting Bessel beam exhibits a purely longitudinal electric field along the axis [
82,
83,
84,
85,
86]. The normalized electric energy density is [
86]
The area of the focal spot is also shown in
Figure 6. For intermediate values of NA the area is large as a result of the strong radial electric field component, but at high NA the spot becomes smaller than the other polarization distributions, except for the azimuthal vortex, which is smaller except at
, where they become equal in size. For
,
,
is negative, corresponding to an intensity minimum on the axis. At
, the radial case, the azimuthal vortex, and
c-ED all become equal to the scalar Bessel beam, with
and area
. An expanded view of the behaviour at high NA is shown in the inset of
Figure 6. The area for the radial polarization case is smaller than for
for values of
.
7. Focusing by a High-NA Lens: Effect of Polarization
For focusing of a lens with a circular pupil, in general we can control the amplitude, phase, and polarization of the illumination beam. In
Section 4, we found that for linearly polarized illumination and any value of NA, the value of
F (defined for electric energy density at the focus) is maximized for the mixed-dipole field, and
is maximized for the perfect mixed-dipole field. An aplanatic lens illuminated with a uniform linearly polarized plane wave behaves in a similar way to the mixed-dipole field, but the values of
F and
are slightly reduced.
In
Section 5, we showed that the area of the focal spot for a Bessel beam can be made smaller than that for the mixed-dipole field by altering the input polarization, because the effects of polarization cross-components can be reduced. We would also expect that this process would increase the value of
F for a complete pupil. In fact, we can show that for a transverse electric field at the focal point, the value of
F is maximized for an electric dipole field, by specification of the correct input polarization and also magnitude.
is maximized for a perfect electric dipole field, where the far field is the electric dipole field multiplied by
. From
Figure 7a, it is seen that
F is higher for the electric dipole case than the aplanatic (linearly polarized illumination) case. For the electric dipole and perfect electric cases, respectively,
F is given by [
40,
55]
On the other hand, for the magnetic dipole case,
The input electric field polarization can be alternatively expanded into a basis of
and
components, giving a vectorial pupil
, with
. For
,
, and for
,
. For general combinations of electric and magnetic dipole fields
as a basis, this vectorial pupil becomes
. Then,
F and
are given in terms of moments of the pupil [
55]:
The constant multiplier for F has been chosen so that , with for a complete electric dipole field, . The constant multiplier for gives for small angles. For linearly polarized input, , and for the mixed-dipole field in particular, . For electric dipole polarization (ED), , and for magnetic dipole polarization (MgD), . For perfect , , .
For
,
while for
,
Figure 7 shows the variation in
F and
with NA for various different polarization conditions. For
, all the curves, except for the perfect cases, drop at high values of NA. By Schwarz’s inequality,
is maximized for the perfect electric dipole field, giving a value 9/32
for a hemispherical focused field,
. For perfect
,
for
. The maximum values for other cases are as follows: electric dipole, 0.238 at
(
); magnetic dipole, 0.199 at
(
; and
, 0.153 at
(
).
If the electric field at the focal point is longitudinal rather than transverse, the value of
F is maximized for radially polarized illumination such that, after focusing, the field matches that of an axially oriented electric dipole [
40,
54,
96], i.e., its amplitude varies as
, which we label as radial ED in
Figure 7a. This behaviour is consistent with our understanding that, as a result of reciprocity, a receiving antenna has the same gain as a radiating antenna. Radial ED corresponds to the
mode. The value of
F is small for low NA because the field strength of an axially oriented dipole is small near the axis, and
F only becomes higher than that of the aplanatic case for the extreme case of
. For radial ED,
F is given by [
40]
The maximum value of is 0.194 at (). There is also a case, corresponding to azimuthal polarization, but we do not consider this further as the focal field is zero. For mixtures of and , with or without a phase difference, the electric energy density at the focus is also reduced.
For radially polarized illumination, the corresponding expressions for
in terms of the pupil
are
By Schwarz’s inequality, these are maximized by
and
, corresponding to radial ED and perfect radial ED, respectively. For perfect radial ED, after focusing the field varies as
, and
for
. Unfortunately, some of our previous papers have not been consistent in the normalization of the expressions and plots for
[
54,
55,
57]. For both the electric dipole and radial ED cases, for
(a hemisphere),
, which is half the value for a complete sphere, so the scattering ratio for a point-like dipole scatterer is
, and the incident light is completely back-reflected [
50].
The behaviour of
F is related to the multipole (spherical harmonic) analysis of the focused field. The far field can be expanded as a multipole expansion, and the field in the focal region can then be determined by summing over the fields of the multipoles, appearing as pairs of sinks and sources [
8,
35,
97,
98]. This computational approach is very efficient for high NAs, with the series converging very quickly, and is particularly amenable for the calculation of scattering and trapping forces [
97]. Hoang et al. considered the different polarization distributions discussed in this paper, and calculated the strength of the low-order multipole components [
98]. The ratios of the strengths of the magnetic dipole and the quadrupole terms to the electric dipole term are measures of the degradation of the focal spot relative to true dipole focusing, as only the low-order terms have significant value in the focal region. These ratios are plotted against NA in
Figure 8. For a tight focus we require these ratios to be as small as possible, which is best satisfied for the electric dipole and
cases.
The parameters
, and
can also be expressed in terms of moments of the pupil [
54,
55]. For the radial case, in Ref. [
54],
and moments
are introduced. Then,
For a focal electric field in the
x-direction, defining
,
in the same way [
55],
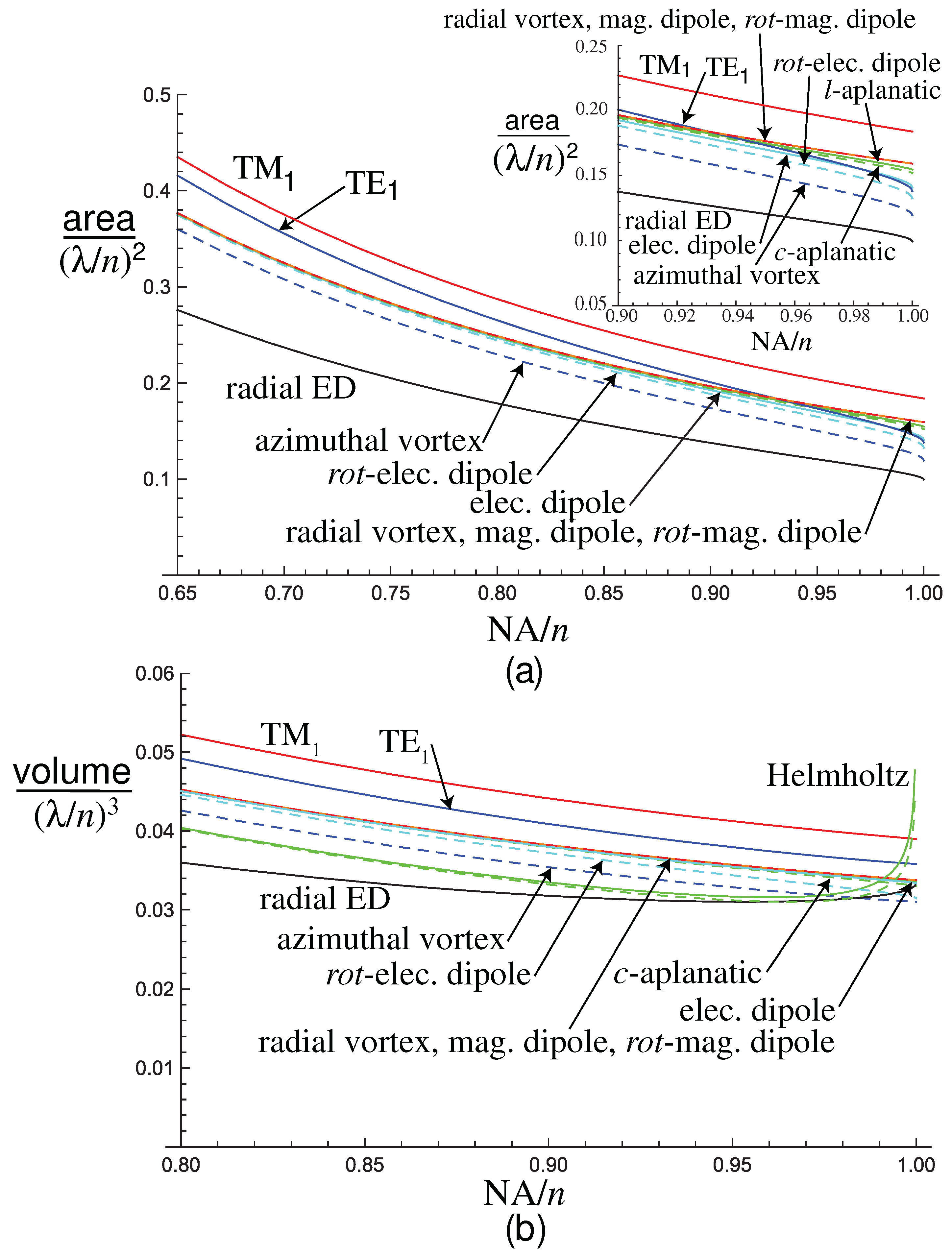
The area of the focal spot for the different cases is shown in
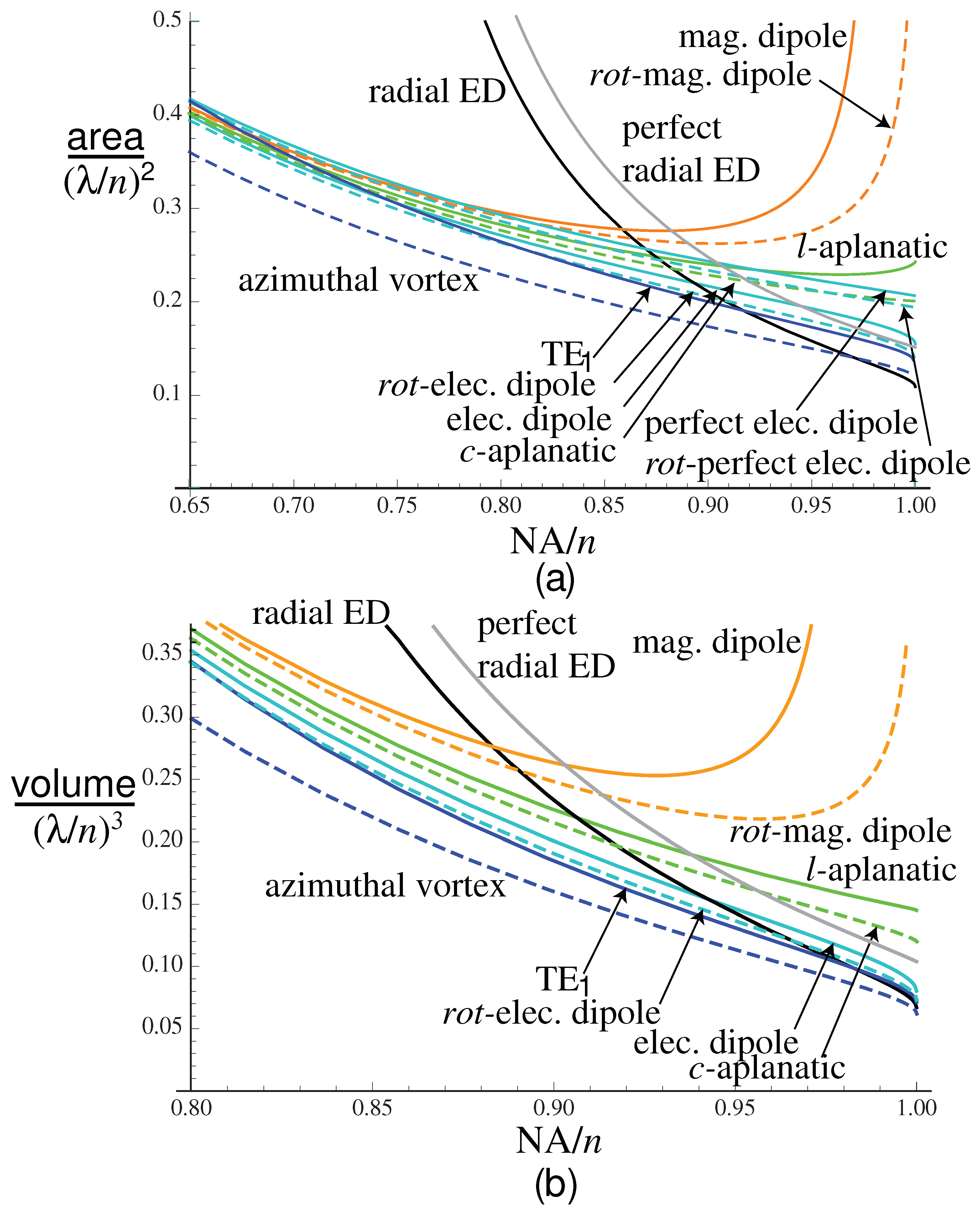
Figure 9a. The radial ED case has a large area at intermediate values of NA as a result of the transverse electric field, but at high NA the area can be smaller than most of the other cases shown [
99,
100,
101,
102]. For
,
,
is negative, corresponding to an intensity minimum at the focus [
54]. It might be thought that obstructing these low angles of incidence by using an annular pupil would result in improved overall performance, but we find that this always results in lower values of
F and
. The azimuthal vortex (
-
) always has the smallest area for
. At
, the radial ED case gives an area of
, and the azimuthal vortex gives
. These are both smaller than for a paraxial scalar Airy disk at the same NA, which gives
. All the cases with a transverse field behave similarly at low NA, except for
and azimuthal vortex. Interestingly, the
and azimuthal vortex cases do not even tend to the same area as each other for low NA, as
does not become a uniform illumination even for low NA. The focal volume is smallest for the azimuthal vortex for any NA (
Figure 9b).
For cases when there is a transverse electric field at the focus, the electric dipole polarization results in the highest electric energy density at the focus. The small focal spot for
and azimuthal vortex can be partly explained by the difference in the pupil weighting as compared with the electric dipole field. More generally, we can consider the pupil to be made up of rings, each with polarization as in
Section 5, and with amplitude strength that can be set. Increasing the contribution from the outer parts of the pupil can decrease the area of the focal spot, as we had in
Figure 5a [
102,
103]. We chose a pupil weighting
, with
j a constant, while retaining the balance between the
and
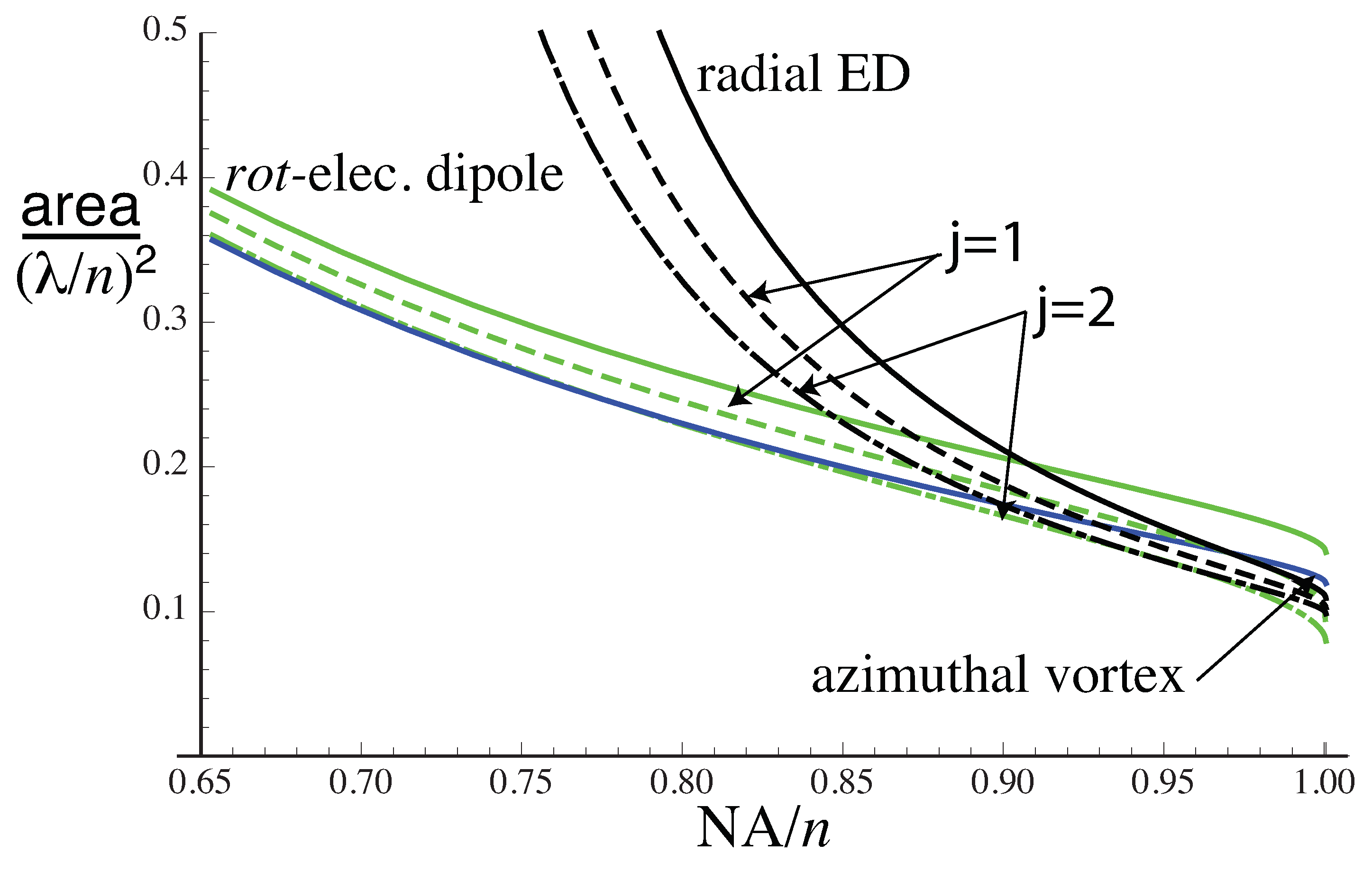
components for an electric dipole field. The resulting focal areas for the rotating electric dipole case for
are shown in
Figure 10. The focal area becomes equal to that of azimuthal vortex for
for
, and
for
. The corresponding variations in
F are shown in
Figure 11. The values of
F are greater than that for azimuthal vortex (or TE) for
0.98 for
, and <0.94 for
. So, for
,
rot-electric dipole with
gives a smaller spot and lower power in the side lobes than azimuthal vortex. This behaviour occurs because a higher proportion of the energy density is in the form of electric energy density. For
, the area of the focal spot is
and
for
, respectively, compared with
for no weighting.
In
Figure 12, we compare the variation in normalized electric energy density in the focal plane for a lens of
for rotating electric dipole polarization and weighting
, with azimuthal vortex polarization. This was calculated by integrating over the angular spectrum [
55]. We see that for
the size of the central lobe is virtually the same as for azimuthal vortex, but the first side lobe is much weaker, which is an advantage for two-point resolution. This is because the relative strength of the electric dipole component for azimuthal vortex polarization is weaker than for electric dipole polarization. Experimental generation of the rotating electric dipole polarization is more complicated than for azimuthal vortex, but an interferometric method could be used [
104], as the field for a particular zone of the lens corresponds to the superposition of two circularly polarized waves, one with a phase vortex, of relative strength that depends on the zone, as in Equation (
24).
Pupil weighting can also be applied to other polarization distributions. In
Figure 10 and
Figure 11, we also show the result of weighting the radial ED polarization by
. We chose this weighting as it reduces the paraxial contributions to the field, thus reducing the parasitic transverse electric field in the focal region. We can see that
gives a good overall performance for high NAs. For
, the area of the focal spot is
and
for
, respectively, compared with
for no weighting.
8. 4Pi Focusing
In
Section 7, we considered focusing by a high-NA lens, with a maximum
of unity, corresponding to focusing over a hemisphere of
steradians, while in
Section 3 we discussed focusing over a complete sphere of
steradians. For an angular semi-aperture greater than
radians, the expressions given for
F are still valid (except for the aplanatic case, which is limited to
). For an electric dipole wave,
has a maximum value of 1.032 at
. For azimuthal vortex,
has a maximum value of 1.125 at
. For a radial electric dipole wave,
has a maximum value of 1.264 at
. For scattering of an electric dipole wave by a point-like dipole, the expression given in
Section 4 for the fraction of forward-propagating power (
) is also still valid. This has its maximum value of unity when
and
, as shown in
Figure 13. By ‘forward propagating’, here we mean within the extended cone of the illumination. Power is still conserved, so that the total outgoing power is equal to the ingoing power, and thus, the outgoing power that is not in the forward direction, comprising backscattering (back into the cone of illumination) and sideways scattering, is
. For
, the incident light is completely backscattered [
50]. As
increases above
to
, the fraction of power propagating in the forward direction increases from 0 to 1, while the remaining outgoing fraction decreases from 1 to 0 (see
Figure 13). The concepts of scattering ratio
and cross-section are not really meaningful for
. For excitation of a two-level quantum system, Lindlein et al. have noted that [
7]:
“The radiant intensity should be as close as possible to a dipole radiation in order to have a similar field distribution as in the emission process.”
8.1. 4Pi Focusing with Two Opposing Lenses
Now, we consider focusing using two opposing high-NA lenses, which together can approximate a complete sphere, an arrangement that is called 4Pi focusing [
105]. The fields of the two lenses interfere to give a standing wave pattern in the longitudinal direction. Such an arrangement has been used in 4Pi microscopy, where the axial resolution is much improved. We presented a conference paper in August 1990 describing this basic technique, and presenting three-dimensional transfer functions for 4Pi illumination [
106]. Similar arrangements have been used for optical trapping [
107], and also for study of light/atom interactions. The geometry is similar to an optical cavity (open resonator), and in order to produce a small focal spot the resonator must be of the nearly concentric type. In
Section 6, we discussed nonparaxial Gaussian beams, which can exhibit different polarization distributions. For the mixed-dipole field, two counter-propagating beams interfere so that the magnetic (or electric) energy density at the focus can cancel out for particular values of the relative phase [
90]. Other papers have considered beams of other polarization distributions, such as the electric dipole type [
108].
In order to generate a compact field distribution, we require the polarization of the far field produced by the two lenses to approximate to an electric dipole field, with the electric dipole oriented in either the transverse direction,
x or rotating, or the longitudinal,
z, direction. Note that if a single deep paraboloidal mirror is used with linearly polarized illumination, the polarization matches the mixed-dipole field, not the electric dipole field. On the other hand, a single deep paraboloid can be used with radial polarization [
7,
102,
103,
109,
110], as we discuss in
Section 9. With two lenses and linearly polarized illumination, we can approximate to an electric dipole field for the correct phase relationship between the two fields. Changing the relative phase by
can give an approximation to a magnetic dipole field, with a zero in electric energy density at the focal point. With two lenses and radially polarized illumination [
109], a longitudinal electric dipole field can be approximated for the correct relative phase, while for a change in phase of we can approximate to a longitudinal electric quadrupole field.
An interesting feature is that for 4Pi focusing resulting in an approximation to a transverse electric dipole field, the longitudinal field component cancels out, so that the focal spot is better behaved at high NAs than for focusing by a single lens [
111]. For the case of Bessel beams, the terms in
cancel, and we then have, for the electric energy density variation,
or for the rotating case,
On the contrary, for the case of 4Pi focusing of radially polarized Bessel beams, the transverse fields cancel out, and we are left with just the simple term
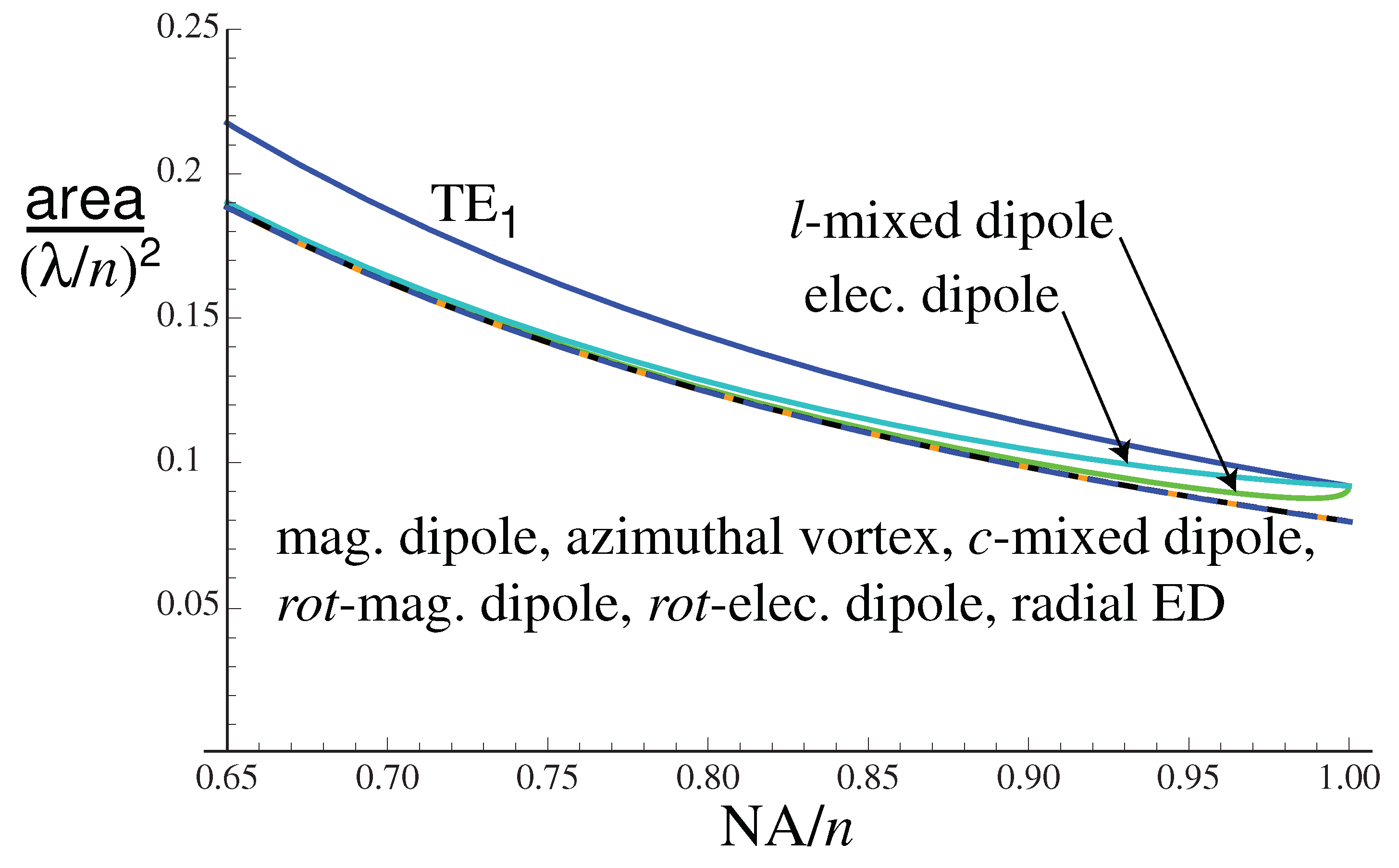
The area of the central lobe of the Bessel beam for different polarization distributions is shown in
Figure 14. The area for a variety of different polarizations is found to be the same: magnetic dipole, azimuthal vortex, circular polarized mixed dipole, rotating magnetic dipole, rotating electric dipole, and radial ED. This is because the
term in Equations (
36) and (
37) does not affect the parabolic width of the beam. The other cases, linear mixed dipole, electric dipole, and TE, all exhibit larger areas as a result of the
term in Equation (
36).
For 4Pi focusing with high-NA lenses, similar effects occur. The value of
F is simply twice that for focusing by a single lens, as was presented in
Figure 4a and
Figure 7a, as the intensity at the focus is increased by a factor of four while the power is doubled. The behaviour of
is not so straightforward, however, and can be calculated by considering the components of the pupil function giving rise to a transverse or longitudinal field for the cases of transverse and longitudinal electric dipole fields, respectively. [
55]. Then, we have, for a transverse electric field at the focus,
For a longitudinal electric field at the focus,
The results for
are illustrated in
Figure 15. Because of the cancellation of some field components in the focal plane, it is no longer the case that
behaves like
F for small convergence angles. Unlike the case of the single lens, the perfect mixed-dipole case (as defined for a single lens) does not now give the highest value of
at a particular NA for linearly or circularly polarized illumination. In fact, we can establish, using Schwarz’s inequality, that the optimum solution for linearly or circularly polarized is for
. The corresponding curve is shown in
Figure 15.
The value of
can be made higher by using some different polarization distributions, as also shown in
Figure 15. We find that the value is greatest for the magnetic dipole case. We can also find from Schwarz’s inequality that there is an optimum radially polarized case, for
, which gives the same result for
as the magnetic dipole case. There is another optimum solution that results from Schwarz’s inequality, the optimized electric dipole solution, with
,
, giving a slightly greater
(but only
greater) than a perfect electric dipole (not shown in
Figure 15).
For the scalar 4Pi case, the minimum area is the same as for a single lens (). The minimum volume is , i.e., half that for a single lens.
For 4Pi, the odd moments
and moments
, and even moments
are zero as they cancel, whereas the other components reinforce one another [
111]. The area of the focal spot is slightly smaller for circular polarized illumination than for linear polarized illumination, but the difference is very small (
Figure 16). This difference is caused by the presence of cross-polarization in the linear polarized case, the longitudinal polarization having cancelled for the 4Pi configuration. By comparison, the difference for a single lens, as in
Figure 5, is much larger, and is mainly caused by longitudinal polarization. The effect of apodization is also stronger, as the limitation of NA set by the dominance of longitudinal polarization is absent.
In
Figure 17a, we show the area of the focal spot for 4Pi focusing for different polarization distributions. The smallest spot is achieved for radial ED illumination (area
for
). The transverse polarization has completely cancelled in the focal plane, leaving pure axial polarization. Then, the next smallest areas are for the
c- Helmholtz (area
for
), azimuthal vortex (area
for
), and rotating electric dipole (area
for
) cases. Many of the other cases have similar widths to each other, but not exactly, as can be seen more clearly from the magnified inset in
Figure 17a. The areas for radial vortex, mag. dipole, and
rot-mag. dipole, are identical. Radial vortex corresponds to radially polarized illumination with a vortex of charge unity, the rotating version of
, which gives a transverse circularly polarized electric field at the focal point [
13,
14]. In contrast, for focusing by a single lens,
and radial vortex give focal spots that separate into two peaks for NAs greater than
and
, respectively.
In
Figure 17b, we show the focal volume for 4Pi focusing for different polarization distributions. It is interesting to note that the volume does not change very much with NA. This can be explained by the observation that the gains for 4Pi focusing satisfy
, so that a decrease in the transverse widths is accompanied by an increase in the axial length [
111]. This is most noticeable for radial ED, which exhibits a small increase in focal volume at the highest NAs. The minimum volume of
is achieved at an NA of 0.952, which corresponds to close to a spherical focal spot [
110]. The volumes for radial vortex, mag. dipole, and
rot-mag. dipole, are identical, and for
l-aplanatic, electric dipole, and
c-aplanatic the volumes are also very similar. Azimuthal vortex gives the smallest focal volume for
0.98. Electric dipole and radial ED give the same volume (
) for
, as they are both equivalent to the field of an electric dipole. For linear or circular polarization focused by a planar lens (
l- or
c-Helmholtz), the minimum volume is
at
or
at
. At a value
, the focal volumes are
(radial ED),
(
c-Helmholtz),
(azimuthal vortex), and
(
rot.-ED). All these volumes are much smaller than those for a single lens, as in
Figure 9.
8.2. 4Pi Focusing with a Mirror
A paraboloidal mirror can be used to achieve values of convergence angle
greater than
, so a single mirror can be used to achieve values of
greater than
[
7,
37,
110]. An infinite mirror would be necessary to achieve
, but there is also a singularity for this value, and so, here we assume a mirror with
, for
. In
Figure 18, we show the value of
F as a function of
for a paraboloidal mirror for different input waves. For a radially polarized ED wave as input (grey line),
F reaches a maximum value of
for
. If the input is a uniform radially polarized plane wave (magenta line), the optimum is
, for
. For a radially polarized plane wave (blue line), where the amplitude varies as proportional to the cylindrical radius,
F has a maximum value of
, for
. In
Figure 18, we also show the case of direct focusing of a radial ED wave for
for comparison (cyan line), for which
F tends to unity for
.
9. Focused Field in an Arbitrary Orientation
For some applications it is desired to focus light tightly, with the electric field at the focus oriented in an arbitrary direction [
112,
113,
114,
115]. For example, we might want to investigate scattering or fluorescence from an oriented structure. In a similar way, emission from an oriented molecule, after collimation, will have a characteristic field distribution. The study of fluorescence polarization gives information on the orientation of fluorescent molecules [
116,
117], and fluorescence polarization can be observed from single isolated molecules [
118,
119,
120]. An important application in super-resolution microscopy is identifying the orientation of a fluorescent molecule to improve localization precision [
121].
In order to couple light efficiently into an electric field in a transverse (
x) direction, the polarization after focusing should ideally be the same as the far field of an electric dipole placed at the focus: ED polarization [
40]. Then, the electric field of the illuminating plane wave is given by [
40,
55,
56]
The factor at the front is cancelled out by the aplanatic apodization factor of a lens that satisfies the sine condition. Similarly, for an electric field at the focus oriented along the
y-axis we have
For an electric field at the focus oriented in the axial direction, we should illuminate with radially polarized light [
40,
99,
100,
101],
To illuminate with the electric field at the focus oriented in an arbitrary direction with direction cosines
, the illumination field should be the sum
where
are the values of
F (Strehl ratios, electric energy density at the focus for a constant input power) for transverse or axial electric dipole waves, respectively, which are given in Equations (
27) and (
32) [
40].
This illumination field can be generated in practice using a liquid crystal light modulator used as a polarization rotator. Note that a phase change produced by rotation of polarization then needs to be cancelled out [
81], and so, three modulators, or passes through a modulator, are needed to control polarization, phase, and modulus, starting from a linearly polarized input beam. The required input to the modulator can be calculated in Cartesian coordinates
using the following equations [
49,
122]:
The required illuminating electric field is shown in
Figure 19 for various different orientations in the azimuthal
plane.
It is seen from
Figure 7 that the excitation of an axial dipole is comparatively inefficient for practical numerical apertures. This suggests that using a simple plane-polarized input to generate the transverse field, mixed with the radial beam in appropriate proportion, is an alternative strategy for lower numerical apertures.
10. Discussion
Focusing of linearly polarized light with a high-NA lens usually results in a focal spot that is larger than predicted by paraxial optics. This effect, which results mainly from parasitic cross-polarization terms, is especially important for Bessel beams. It is well established that the size of the focal spot can be decreased by using radially polarized illumination, resulting in a strong longitudinal field component in the focal region. However, some applications require a transverse electric field. For this case, electric dipole polarization gives a small focal spot, and maximizes the electric energy density at the focal point for a fixed input power, giving a value that is higher than using radial polarization for any aperture smaller than a complete hemisphere.
Another parameter we consider in this paper is , the electric energy density at the focus for a fixed integrated intensity in the focal plane. This is a measure of the intensity at the focus compared with the strength of the sidelobes.
We also considered the size of the focal spot, based on the FWHM of a parabolic approximation. Transverse electric () gives a smaller central lobe area even than radial polarization for values of NA less than 0.92. Azimuthal polarization with a vortex, the rotationally symmetric version of , gives the smallest focal spot for NA less than 0.97. Azimuthal vortex gives the smallest focal volume for any value of NA. Azimuthal vortex, rotating electric dipole (the rotationally symmetric version of electric dipole polarization), and polarizations all give Bessel beams with smaller area than radial polarization, with azimuthal vortex being the smallest.
The product of F and the focal spot area is a measure of the power in the central lobe. Simple apodization, by reducing the strength of the angular spectrum at higher angles of incidence, reduces the value of F, increases the area of the focal spot, and may increase the value of as the side lobes are decreased in strength. This effect can be seen by comparing the perfect mixed-dipole case with the mixed-dipole case. On the other hand, increasing the strength of the angular spectrum at higher angles, increases F, decreases the area of the focal spot, and may decrease the value of as the side lobes are increased in strength.
The cross-sectional areas and values of
F and
for
(
for oil;
for water) are summarized in
Table 1. We find that for
F, in order of decreasing value, are the electric dipole, aplanatic, perfect electric dipole, and perfect mixed-dipole cases. For
, we have in decreasing order of value the perfect electric dipole, perfect mixed-dipole, electric dipole, and aplanatic cases. Note that no radial polarization cases appear here, as the assumed high value of NA is still not high enough. For focal area, in increasing order of area we have azimuthal vortex, radial electric dipole,
, rotating electric dipole, and electric dipole. Rotating electric dipole appears in all three lists. So, there is a compromise in terms of performance in terms of these different parameters, azimuthal vortex and radial electric dipole have small areas, but also smaller
F and
.
For 4Pi focusing, radial electric dipole polarization gives the smallest area of focal spot, and achieves close to a spherical focal volume at an
of about 0.95 [
109]. For
, the area of the focal spot for 4Pi is 1.3 times smaller than for a single lens, while the focal volume is 4.6 times smaller.
For a transverse electric field at the focus, rotating electric dipole and aplanatic cases give good overall performance. The aplanatic case performs well for 4Pi because the parasitic cross-components of polarization cancel on 4Pi focusing [
111].
c-Helmholtz gives a small focal volume, but
F is not very high. Optimum forms for maximizing
for the 4Pi cases of electric dipole, mixed-dipole, and radial polarizations were presented.
From Refs. [
7,
8,
50], for excitation of isolated atoms or scattering by small structures, the most important parameter is the intensity at the focus, given by
F. For imaging of sparse samples, including localization microscopy, this is also the case. This conclusion is in agreement with that of Stallinga et al., who particularly investigated localization microscopy [
123]. This argument seems to not favour the use of pupil (superoscillation) masks, as the value of
F is dramatically reduced by even a small improvement in focal spot size.
On the other hand, if the sample is not sparse, transverse imaging within the focal plane may be improved by choosing a high value of or by decreasing the focal area. Rotating electric dipole still seems to be the best overall option in this case, or radial ED if a longitudinal field is required.