Real-Time Simulation of Clear Sky Background Radiation in Gas Infrared Remote Sensing Monitoring
Abstract
1. Introduction
2. Materials and Methods
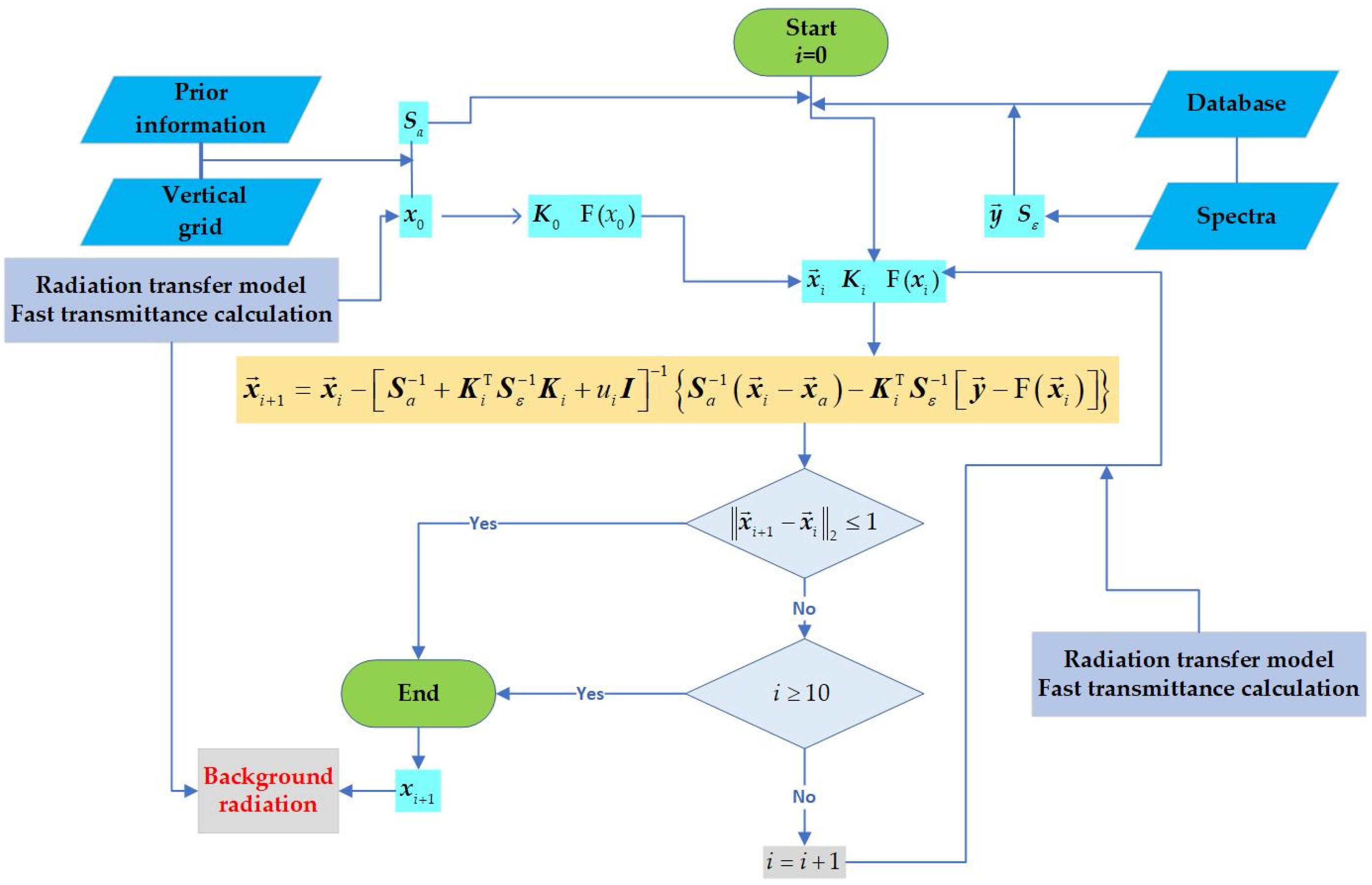
2.1. Retrieval Strategy
2.2. Vertical Grid
2.3. Prior Information
2.4. Spectrum and Radiation Transfer Model
2.4.1. Spectrum to Be Retrieved
2.4.2. Simplified Radiation Transfer Model
- In the radiation transfer model, the atmosphere is assumed to be in thermodynamic equilibrium, allowing us to use the Planck intensity as the source function in accordance with Kirchhoff’s law.
- The atmosphere is considered to be plane-parallel, implying that the radiance or intensity varies only in the vertical direction.
2.4.3. Fast Transmittance Calculation
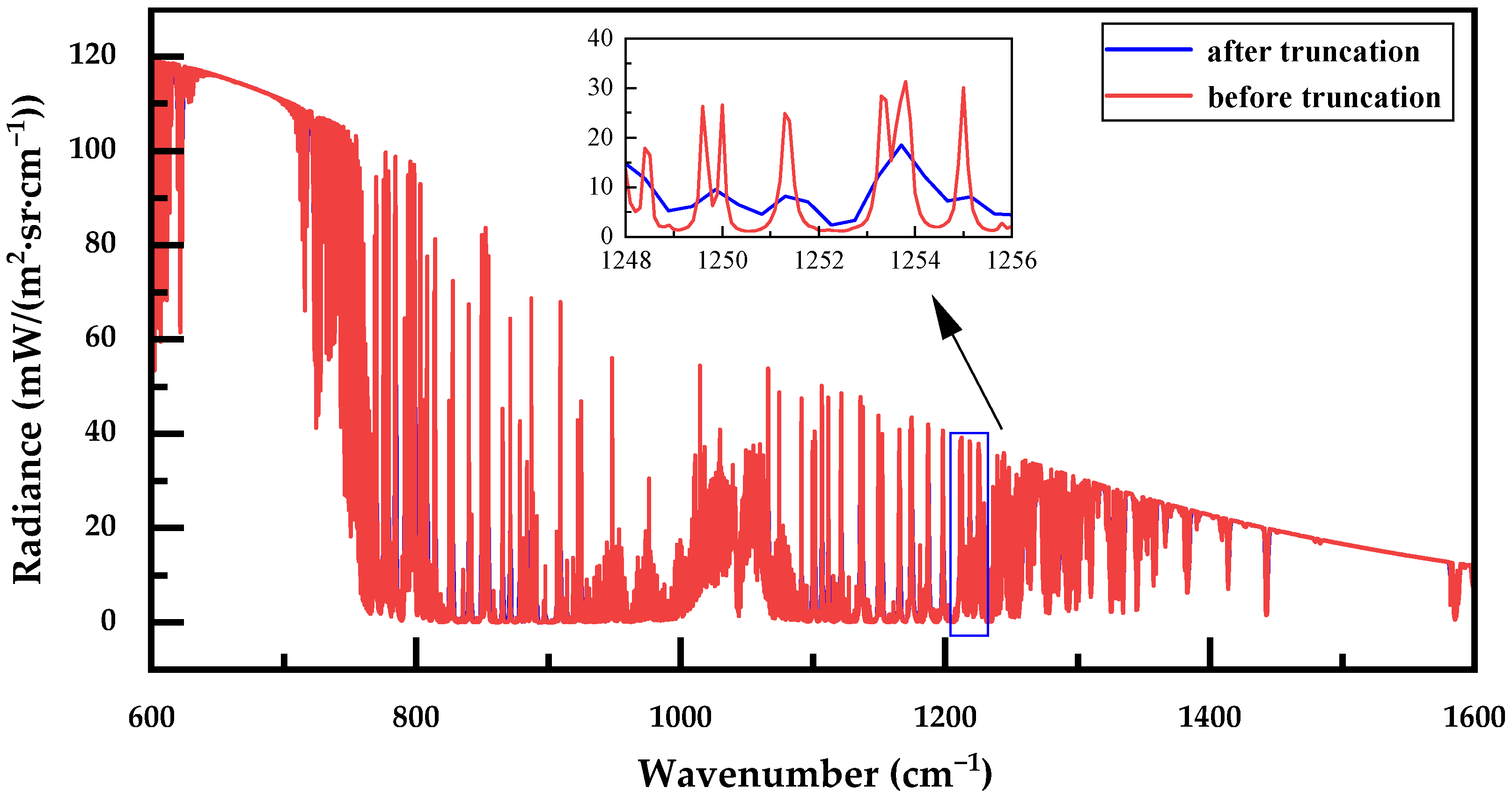
2.4.4. Simulated Spectra Correction
3. Results and Analysis
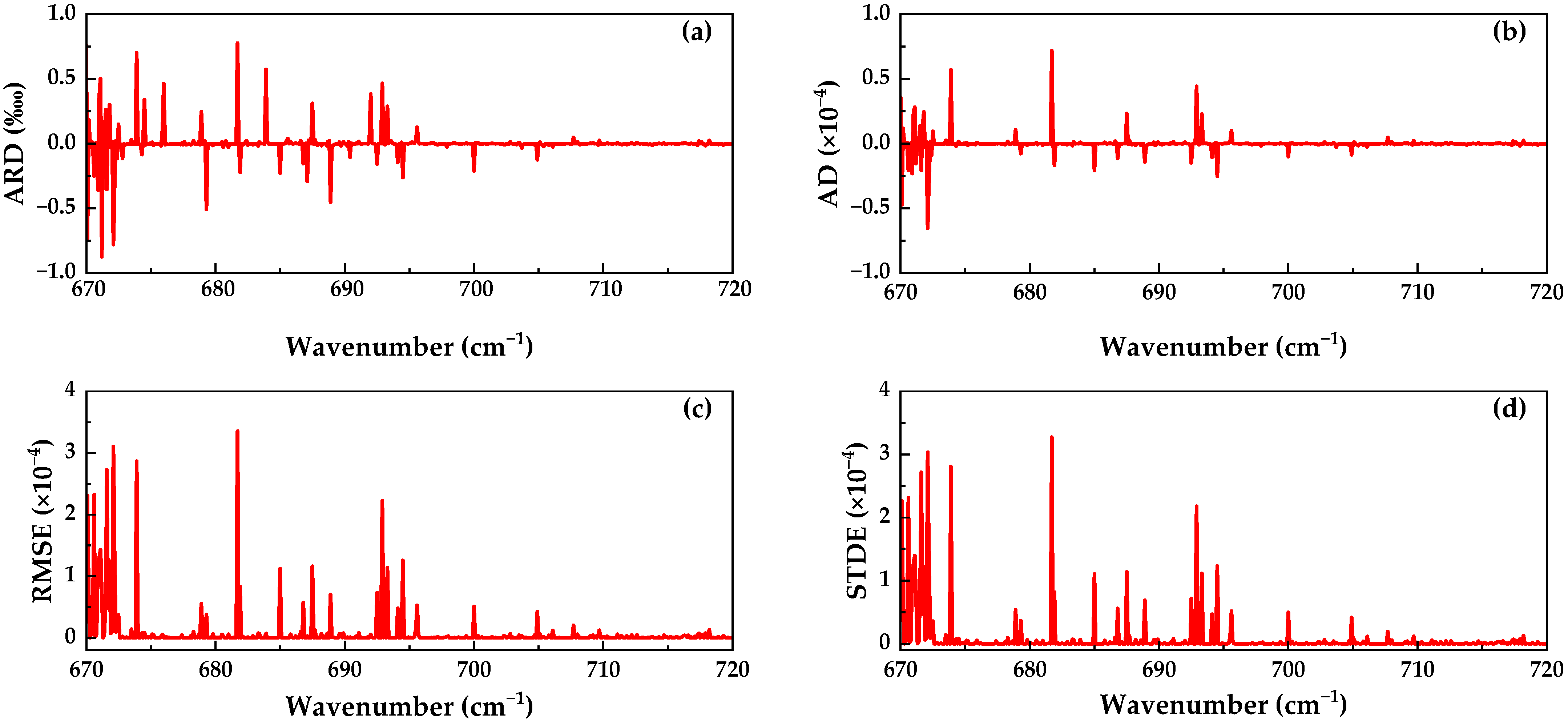
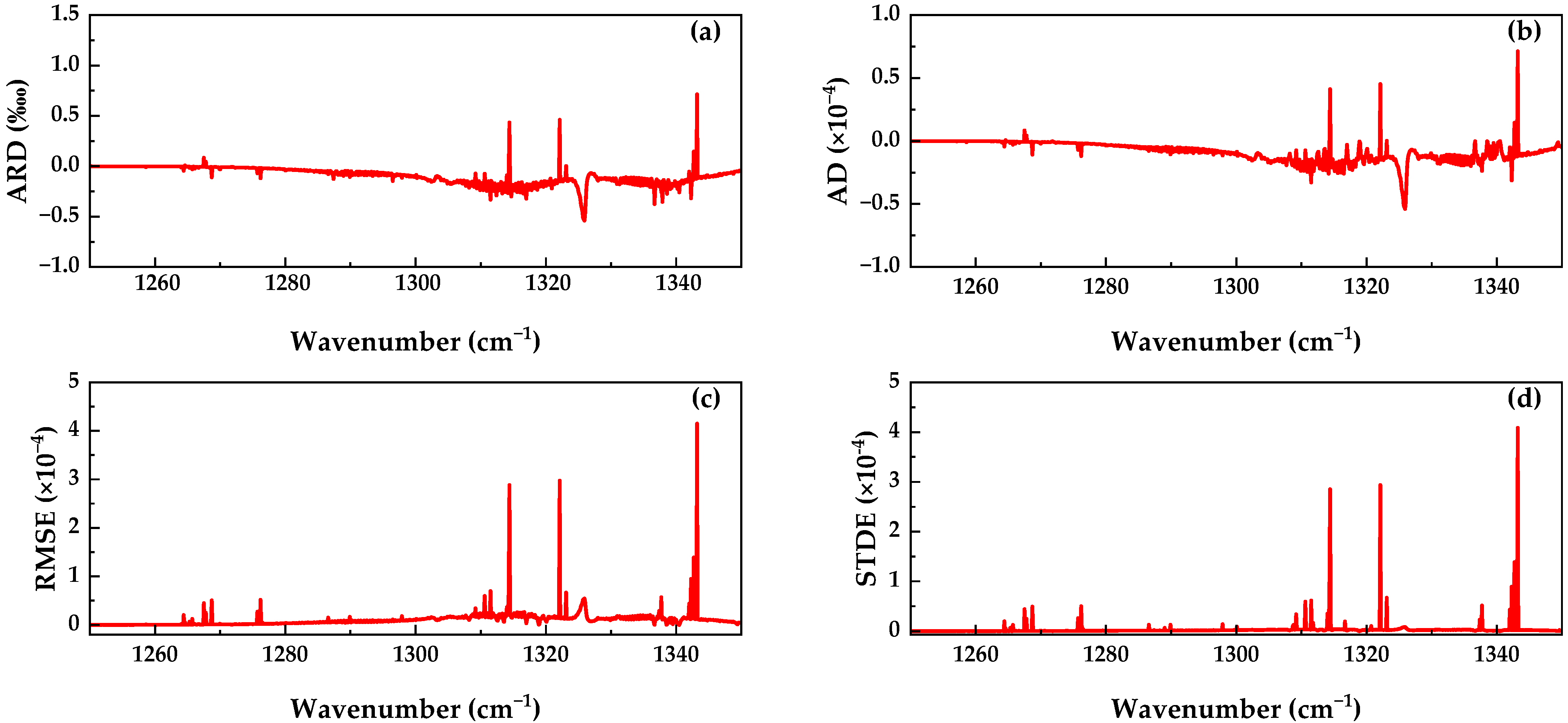
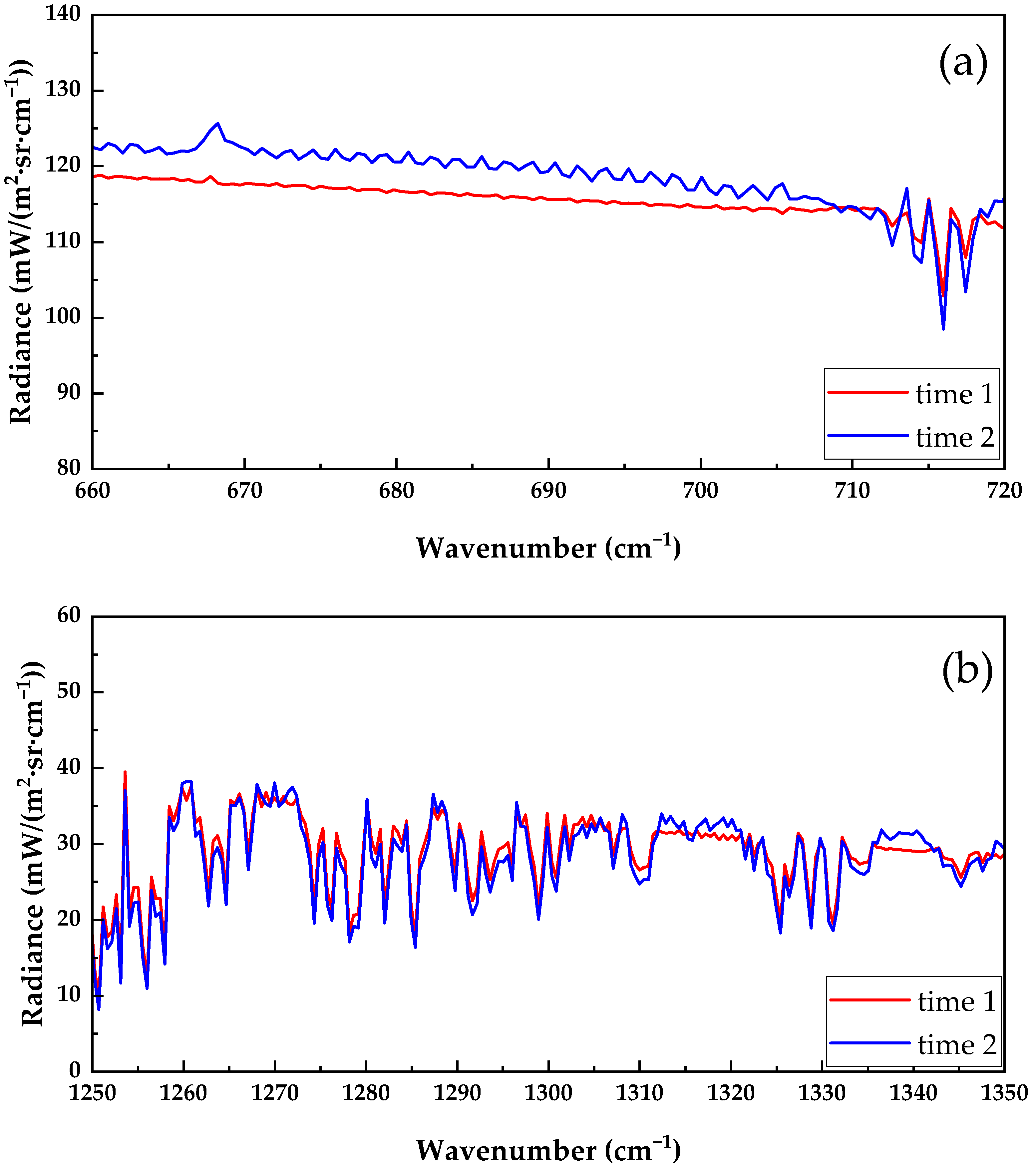
3.1. Assessment of Rapid Transmittance Calculation Accuracy
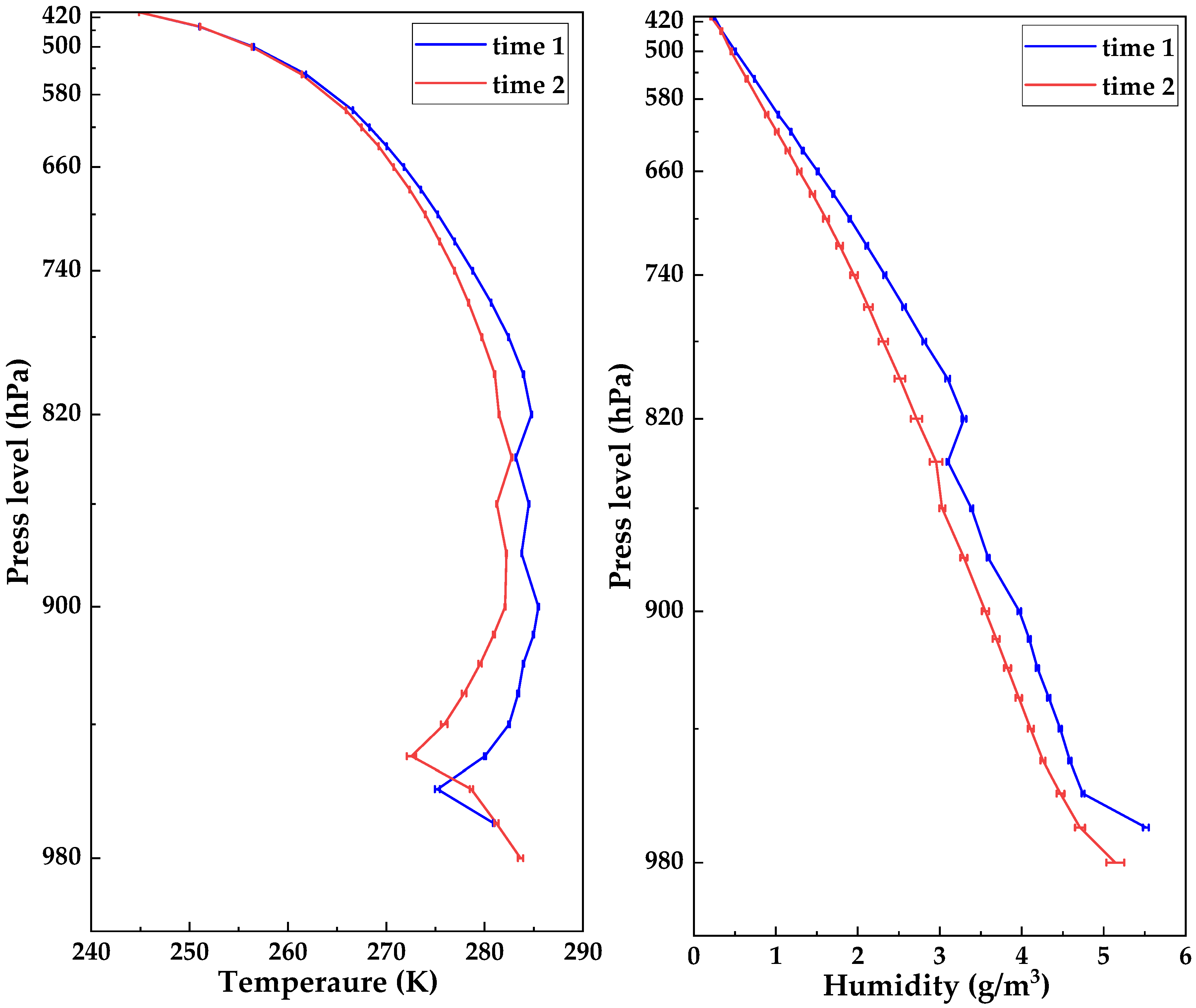
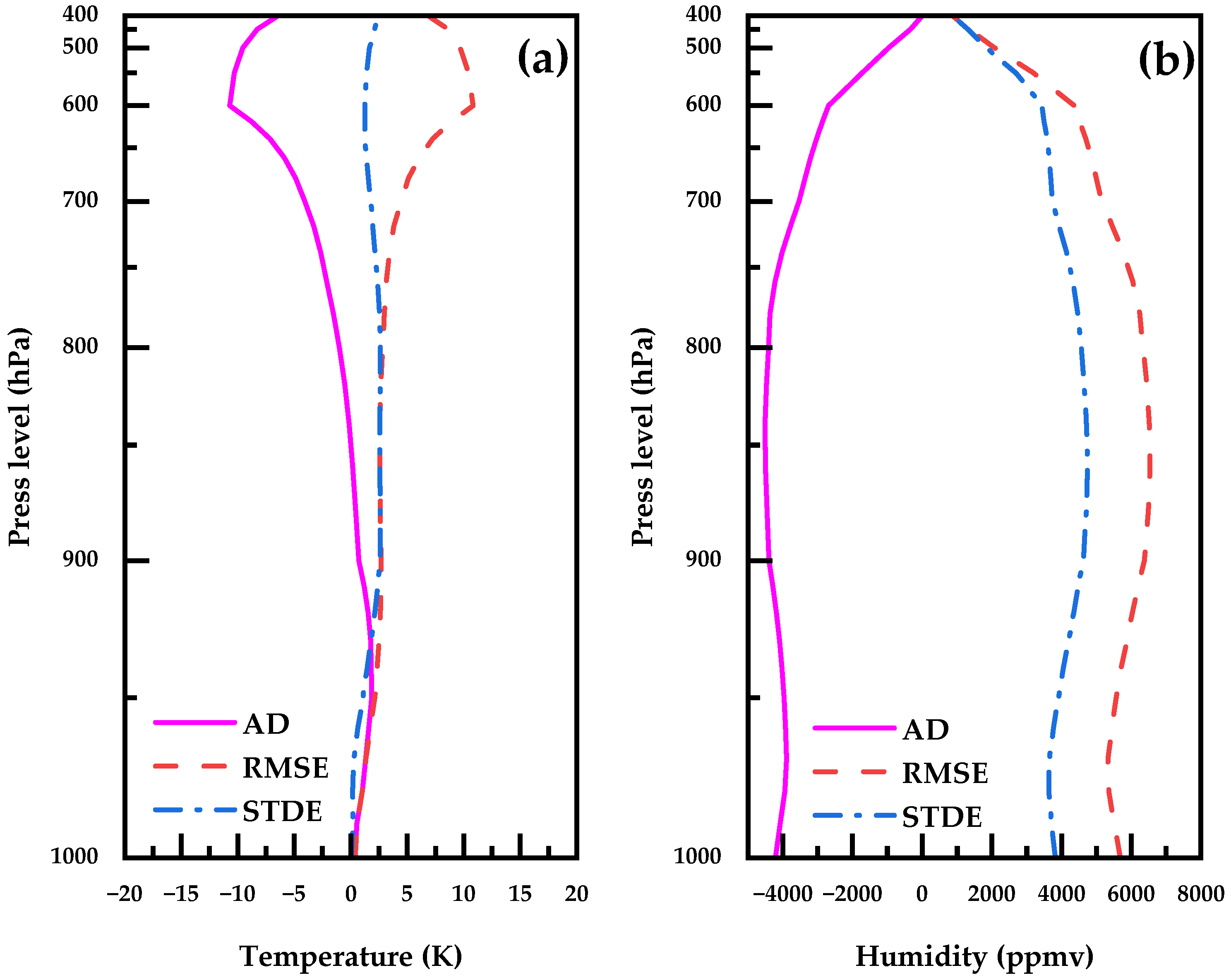
3.2. Evaluation of Temperature and Humidity Profile Retrieval Accuracy
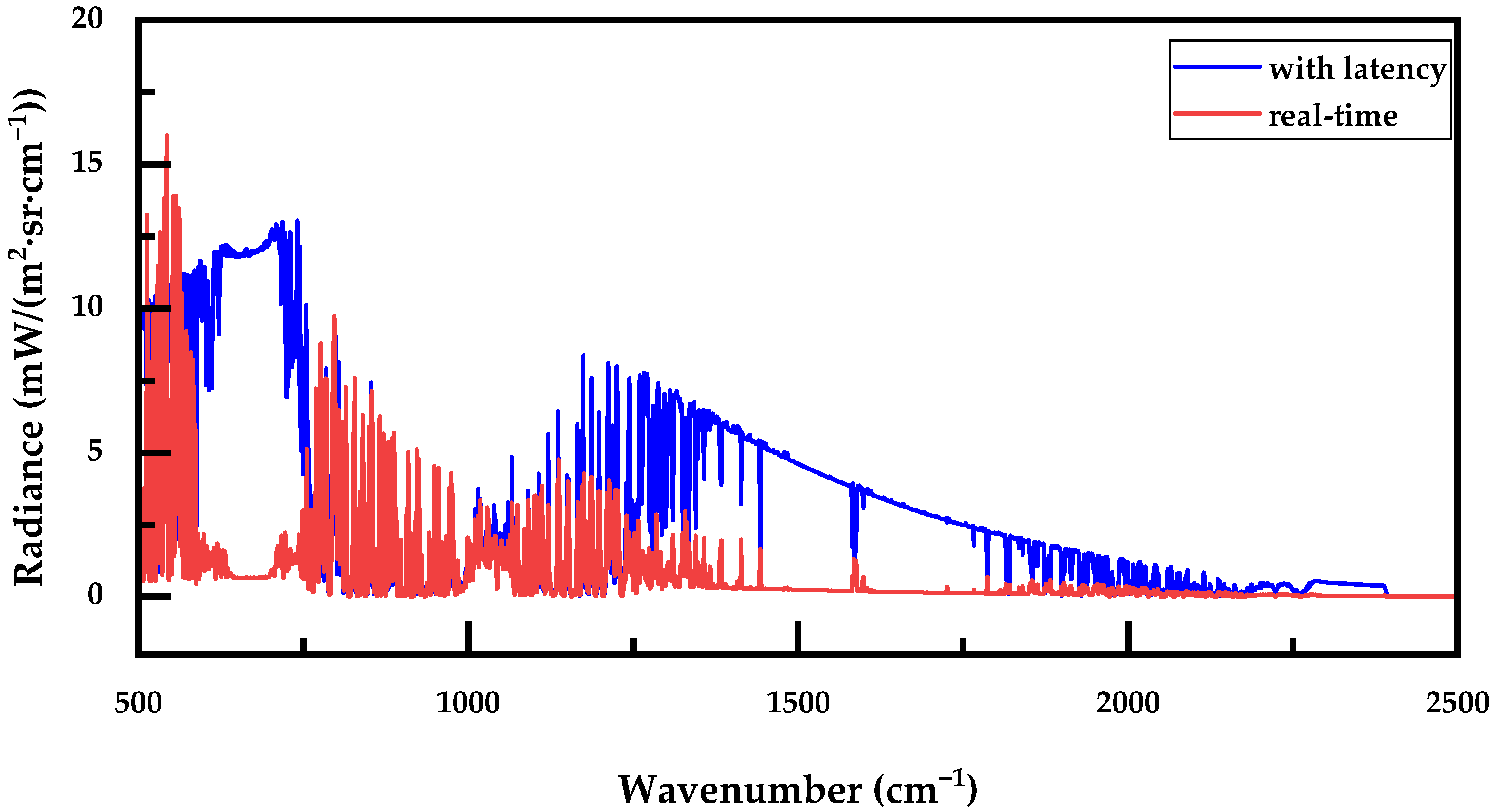
3.3. Evaluation of Sky Background Radiation Simulations
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| P | H | CO2 | CH4 | CO (×10−1) | N2O (×10−1) | HNO3 (×10−3) | NH3 (×10−3) | NO (×10−3) | NO2 (×10−3) | O2 (×105) | SO2 (×10−3) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 50 | 402.78 | 1.94 | 1.96 | 3.25 | 1.08 | 4.23 | 1.59 | 7.55 | 21.11 | 4.51 |
| 990 | 150 | 402.74 | 1.93 | 1.85 | 3.25 | 1.19 | 3.80 | 1.38 | 6.59 | 21.11 | 4.00 |
| 980 | 300 | 402.70 | 1.93 | 1.74 | 3.25 | 1.08 | 3.38 | 1.17 | 5.63 | 21.11 | 3.49 |
| 970 | 420 | 402.67 | 1.93 | 1.63 | 3.25 | 1.19 | 2.95 | 0.96 | 4.67 | 21.11 | 2.98 |
| 960 | 530 | 402.63 | 1.92 | 1.52 | 3.25 | 1.30 | 2.52 | 0.75 | 3.71 | 21.12 | 2.48 |
| 950 | 600 | 402.59 | 1.92 | 1.41 | 3.25 | 1.40 | 2.09 | 0.55 | 2.75 | 21.12 | 1.97 |
| 940 | 710 | 402.55 | 1.92 | 1.30 | 3.25 | 1.51 | 1.66 | 0.34 | 1.79 | 21.12 | 1.46 |
| 930 | 810 | 402.51 | 1.91 | 1.19 | 3.25 | 1.62 | 1.23 | 0.13 | 0.83 | 21.12 | 0.95 |
| 920 | 900 | 402.50 | 1.91 | 1.17 | 3.25 | 1.54 | 1.14 | 0.11 | 0.73 | 21.12 | 0.87 |
| 910 | 1000 | 402.49 | 1.91 | 1.14 | 3.25 | 1.46 | 1.05 | 0.09 | 0.62 | 21.12 | 0.79 |
| 900 | 1100 | 402.47 | 1.91 | 1.11 | 3.25 | 1.38 | 0.95 | 0.07 | 0.51 | 21.12 | 0.71 |
| 880 | 1280 | 402.45 | 1.91 | 1.06 | 3.25 | 1.23 | 0.77 | 0.04 | 0.29 | 21.13 | 0.54 |
| 860 | 1460 | 402.44 | 1.90 | 1.02 | 3.25 | 1.09 | 0.67 | 0.03 | 0.23 | 21.13 | 0.47 |
| 840 | 1660 | 402.43 | 1.90 | 0.99 | 3.25 | 0.95 | 0.57 | 0.02 | 0.17 | 21.13 | 0.39 |
| 820 | 1860 | 402.42 | 1.90 | 0.96 | 3.25 | 0.83 | 0.49 | 0.02 | 0.12 | 21.14 | 0.33 |
| 800 | 2080 | 402.42 | 1.90 | 0.94 | 3.25 | 0.73 | 0.43 | 0.01 | 0.11 | 21.14 | 0.29 |
| 780 | 2280 | 402.42 | 1.89 | 0.91 | 3.25 | 0.63 | 0.36 | 0.01 | 0.09 | 21.14 | 0.25 |
| 760 | 2500 | 402.44 | 1.89 | 0.90 | 3.25 | 0.56 | 0.31 | 0.01 | 0.07 | 21.15 | 0.22 |
| 740 | 2720 | 402.46 | 1.89 | 0.88 | 3.25 | 0.49 | 0.26 | 0.01 | 0.07 | 21.15 | 0.19 |
| 720 | 2940 | 402.49 | 1.89 | 0.86 | 3.25 | 0.42 | 0.22 | 0.01 | 0.06 | 21.16 | 0.16 |
| 700 | 3180 | 402.54 | 1.89 | 0.85 | 3.25 | 0.38 | 0.18 | 0.01 | 0.05 | 21.16 | 0.14 |
| 680 | 3420 | 402.59 | 1.89 | 0.84 | 3.26 | 0.33 | 0.15 | 0.01 | 0.05 | 21.17 | 0.12 |
| 660 | 3650 | 402.64 | 1.89 | 0.82 | 3.26 | 0.29 | 0.12 | 0.01 | 0.04 | 21.17 | 0.10 |
| 640 | 3900 | 402.69 | 1.88 | 0.81 | 3.26 | 0.27 | 0.10 | 0.01 | 0.04 | 21.17 | 0.09 |
| 620 | 4150 | 402.74 | 1.88 | 0.80 | 3.26 | 0.24 | 0.08 | 0.01 | 0.04 | 21.18 | 0.07 |
| 600 | 4420 | 402.79 | 1.88 | 0.80 | 3.26 | 0.23 | 0.07 | 0.01 | 0.04 | 21.18 | 0.06 |
| 550 | 5120 | 402.92 | 1.88 | 0.78 | 3.26 | 0.20 | 0.04 | 0.01 | 0.04 | 21.19 | 0.04 |
| 500 | 5860 | 403.04 | 1.88 | 0.77 | 3.26 | 0.19 | 0.03 | 0.01 | 0.04 | 21.20 | 0.03 |
| 450 | 6670 | 403.09 | 1.88 | 0.77 | 3.26 | 0.23 | 0.02 | 0.01 | 0.05 | 21.20 | 0.02 |
| 400 | 7550 | 403.07 | 1.87 | 0.77 | 3.26 | 0.27 | 0.02 | 0.02 | 0.06 | 21.21 | 0.02 |
| 350 | 8540 | 402.96 | 1.87 | 0.76 | 3.26 | 0.32 | 0.02 | 0.03 | 0.07 | 21.21 | 0.02 |
| 300 | 9630 | 402.74 | 1.87 | 0.75 | 3.26 | 0.36 | 0.02 | 0.04 | 0.09 | 21.21 | 0.02 |
| 250 | 10,880 | 402.37 | 1.86 | 0.71 | 3.25 | 0.45 | 0.01 | 0.06 | 0.11 | 21.21 | 0.02 |
| 200 | 12,380 | 401.78 | 1.85 | 0.62 | 3.23 | 0.63 | 0.01 | 0.08 | 0.12 | 21.22 | 0.02 |
| 175 | 13,250 | 401.45 | 1.83 | 0.55 | 3.22 | 0.75 | 0.01 | 0.08 | 0.13 | 21.22 | 0.02 |
| 150 | 14,230 | 401.14 | 1.82 | 0.47 | 3.19 | 0.89 | 0.01 | 0.09 | 0.13 | 21.23 | 0.02 |
| 125 | 15,350 | 400.93 | 1.81 | 0.39 | 3.17 | 1.04 | 0.00 | 0.10 | 0.16 | 21.23 | 0.02 |
| 100 | 16,720 | 400.64 | 1.79 | 0.31 | 3.12 | 1.35 | 0.00 | 0.13 | 0.21 | 21.23 | 0.03 |
| 75 | 18,410 | 399.67 | 1.73 | 0.21 | 2.99 | 2.25 | 0.00 | 0.17 | 0.33 | 21.23 | 0.07 |
| 50 | 20,850 | 396.89 | 1.55 | 0.13 | 2.55 | 5.01 | 0.00 | 0.27 | 0.69 | 21.23 | 0.09 |
| 30 | 24,090 | 394.46 | 1.32 | 0.15 | 1.88 | 7.71 | 0.00 | 0.62 | 1.91 | 21.23 | 0.02 |
| 25 | 25,250 | 394.04 | 1.25 | 0.16 | 1.67 | 7.85 | 0.00 | 0.85 | 2.65 | 21.22 | 0.02 |
| 20 | 26,720 | 393.69 | 1.17 | 0.17 | 1.42 | 7.35 | 0.00 | 1.27 | 3.85 | 21.22 | 0.02 |
| 15 | 28,600 | 393.45 | 1.07 | 0.19 | 1.12 | 5.91 | 0.00 | 2.04 | 5.70 | 21.22 | 0.02 |
| 10 | 31,320 | 393.32 | 0.96 | 0.22 | 0.79 | 3.55 | 0.00 | 3.37 | 8.10 | 21.22 | 0.02 |
| 7 | 33,800 | 393.31 | 0.88 | 0.26 | 0.57 | 1.92 | 0.00 | 4.59 | 9.39 | 21.22 | 0.01 |
| 5 | 36,160 | 393.33 | 0.81 | 0.31 | 0.42 | 0.96 | 0.00 | 5.67 | 9.72 | 21.22 | 0.01 |
| 4 | 37,840 | 393.34 | 0.76 | 0.34 | 0.35 | 0.59 | 0.00 | 6.38 | 9.51 | 21.22 | 0.01 |
| 3 | 40,000 | 393.35 | 0.70 | 0.38 | 0.27 | 0.29 | 0.00 | 7.14 | 9.00 | 21.22 | 0.02 |
| 2 | 43,100 | 393.33 | 0.60 | 0.44 | 0.18 | 0.09 | 0.00 | 7.72 | 7.92 | 21.22 | 0.03 |
References
- Capodaglio, A.G. Developments and Issues in Renewable Ecofuels and Feedstocks. Energies 2024, 17, 3560. [Google Scholar] [CrossRef]
- Wu, M.; Liu, W.; Ma, Z.; Qin, T.; Chen, Z.; Zhang, Y.; Cao, N.; Xie, X.; Chi, S.; Xu, J.; et al. Global Trends in the Research and Development of Petrochemical Waste Gas from 1981 to 2022. Sustainability 2024, 16, 5972. [Google Scholar] [CrossRef]
- Zhao, Q.; Nie, X.X.; Luo, D.; Wang, J.; Li, Q.R.; Chen, W. An Effective Method for Gas-Leak Area Detection and Gas Identification with Mid-Infrared Image. Photonics 2022, 9, 992. [Google Scholar] [CrossRef]
- Rodriguez-Conejo, M.A.; Melendez, J.; Barber, R.; Garrido, S. Design of an Infrared Imaging System for Robotic Inspection of Gas Leaks in Industrial Environments. Int. J. Adv. Robot. Syst. 2015, 12, 23. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Xu, L.; Xu, H.Y.; Shen, X.C.; Deng, Y.S.; Xu, H.Y.; Liu, J.G.; Liu, W.Q. Three-dimensional reconstruction of a leaking gas cloud based on two scanning FTIR remote-sensing imaging systems. Opt. Express 2022, 30, 25581–25596. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.Y.; Xu, L.; Shen, X.C.; Jin, L.; Xu, H.Y.; Deng, Y.S.; Liu, J.G.; Liu, W.Q. Reconstruction of a leaking gas cloud from a passive FTIR scanning remote-sensing imaging system. Appl. Opt. 2021, 60, 9396–9403. [Google Scholar] [CrossRef] [PubMed]
- Donato, P.; Barres, O.; Sausse, J.; Taquet, N. Advances in 3-D infrared remote sensing gas monitoring. Application to an urban atmospheric environment. Remote Sens. Environ. 2016, 175, 301–309. [Google Scholar] [CrossRef]
- Kastek, M.; Piatkowski, T.; Trzaskawka, P. Infrared Imaging Fourier Transform Spectrometer as the Stand-Off Gas Detection System. Metrol. Meas. Syst. 2011, 18, 607–620. [Google Scholar] [CrossRef]
- Stremme, W.; Krueger, A.; Harig, R.; Grutter, M. Volcanic SO2 and SiF4 visualization using 2-D thermal emission spectroscopy–Part 1: Slant-columns and their ratios. Atmos. Meas. Tech. 2012, 5, 275–288. [Google Scholar] [CrossRef]
- Kang, R.Y.; Liatsis, P.; Kyritsis, D.C. Emission Quantification via Passive Infrared Optical Gas Imaging: A Review. Energies 2022, 15, 3304. [Google Scholar] [CrossRef]
- Wu, S.P.; Zhong, X.; Qu, Z.; Wang, Y.H.; Li, L.; Zeng, C.L. Infrared Gas Detection and Concentration Inversion Based on Dual-Temperature Background Points. Photonics 2023, 10, 490. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Xu, L.; Shen, X.C.; Shu, S.Q.; Xu, H.Y.; Deng, Y.S.; Xu, H.Y.; Liu, J.G.; Liu, W.Q. Inversion method of target gas cloud transmittance based on atmospheric profile synthesis background. Acta Phys. Sin. 2023, 72, 033201. [Google Scholar] [CrossRef]
- Knuteson, R.; Revercomb, H.; Best, F.; Ciganovich, N.; Dedecker, R.; Dirkx, T.; Ellington, S.; Feltz, W.; Garcia, R.; Howell, H.; et al. Atmospheric Emitted Radiance Interferometer. Part I: Instrument Design. J. Atmos. Ocean. Technol. 2004, 21, 1763–1776. [Google Scholar] [CrossRef]
- Knuteson, R.; Revercomb, H.; Best, F.; Ciganovich, N.; Dedecker, R.; Dirkx, T.; Ellington, S.; Feltz, W.; Garcia, R.; Howell, H.; et al. Atmospheric Emitted Radiance Interferometer. Part II: Instrument Performance. J. Atmos. Ocean. Technol. 2004, 21, 1777–1789. [Google Scholar] [CrossRef]
- Zhao, H.J.; Ma, X.H.; Jia, G.R.; Mi, Z.Y.; Ji, H.L. Synergistic Retrieval of Temperature and Humidity Profiles from Space-Based and Ground-Based Infrared Sounders Using an Optimal Estimation Method. Remote Sens. 2022, 14, 5256. [Google Scholar] [CrossRef]
- Löhnert, U.; Turner, D.D.; Crewell, S. Ground-Based Temperature and Humidity Profiling Using Spectral Infrared and Microwave Observations. Part I: Simulated Retrieval Performance in Clear-Sky Conditions. J. Appl. Meteorol. Climatol. 2009, 48, 1017–1032. [Google Scholar] [CrossRef]
- Smith, W.L.; Feltz, W.E.; Knuteson, R.O.; Revercomb, H.E.; Woolf, H.M.; Howell, H.B. The retrieval of planetary boundary layer structure using ground-based infrared spectral radiance measurements. J. Atmos. Ocean. Technol. 1999, 16, 323–333. [Google Scholar] [CrossRef]
- Feltz, W.F.; Smith, W.L.; Knuteson, R.O.; Revercomb, H.E.; Woolf, H.M.; Howell, H.B. Meteorological applications of temperature and water vapor retrievals from the ground-based Atmospheric Emitted Radiance Interferometer (AERI). J. Appl. Meteorol. 1998, 37, 857–875. [Google Scholar] [CrossRef]
- Rodgers, C. Optimal Methods for Non-linear Inverse Problems. In Inverse Methods for Atmospheric Sounding: Theory and Practice; Taylor, F.W., Ed.; World Scientific: London, UK, 2000; Volume 2, pp. 81–99. [Google Scholar]
- Zhou, X.H.; Liang, Y.; Wang, X.M.; Zhou, L.C. Comparison of saturation vapor pressure formulas. J. Liaoning Tech. Univ. 2007, 26, 331–333. [Google Scholar]
- Liou, K. Thermal Infrared Radiation Transfer in the Atmosphere. In An Introduction to Atmospheric Radiation, 2nd ed.; Dmowska, R., Holton, J.R., Rossby, H.T., Eds.; Academic Press: San Diego, CA, USA, 2002; Volume 84, pp. 122–127. [Google Scholar]
- Kochanov, R.V.; Gordon, I.; Rothman, L.; Wcisło, P.; Hill, C.; Wilzewski, J. HITRAN Application Programming Interface (HAPI): A comprehensive approach to working with spectroscopic data. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 15–30. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Pressure Levels from 1940 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.bd0915c6?tab=overview (accessed on 23 June 2024).

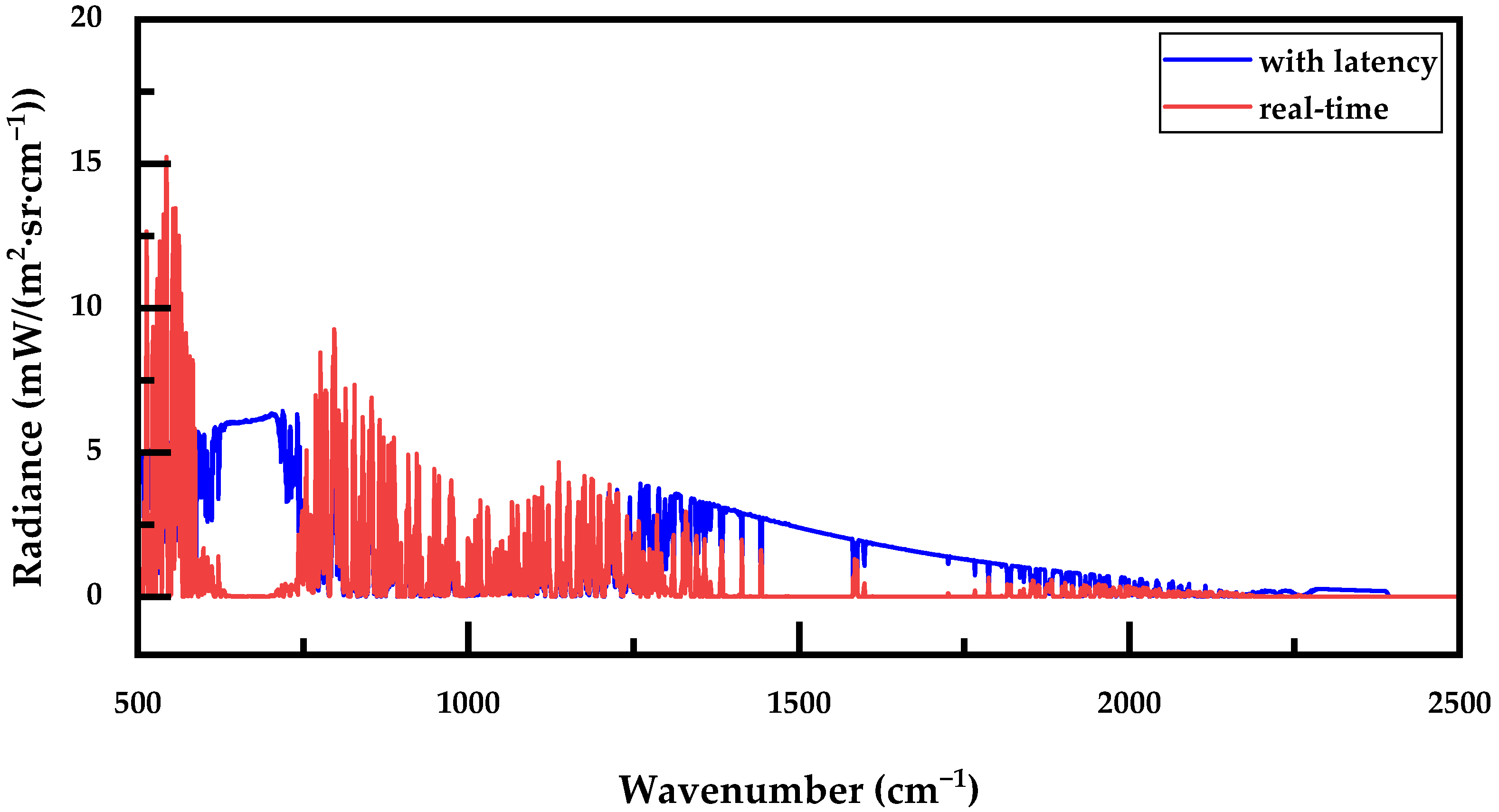
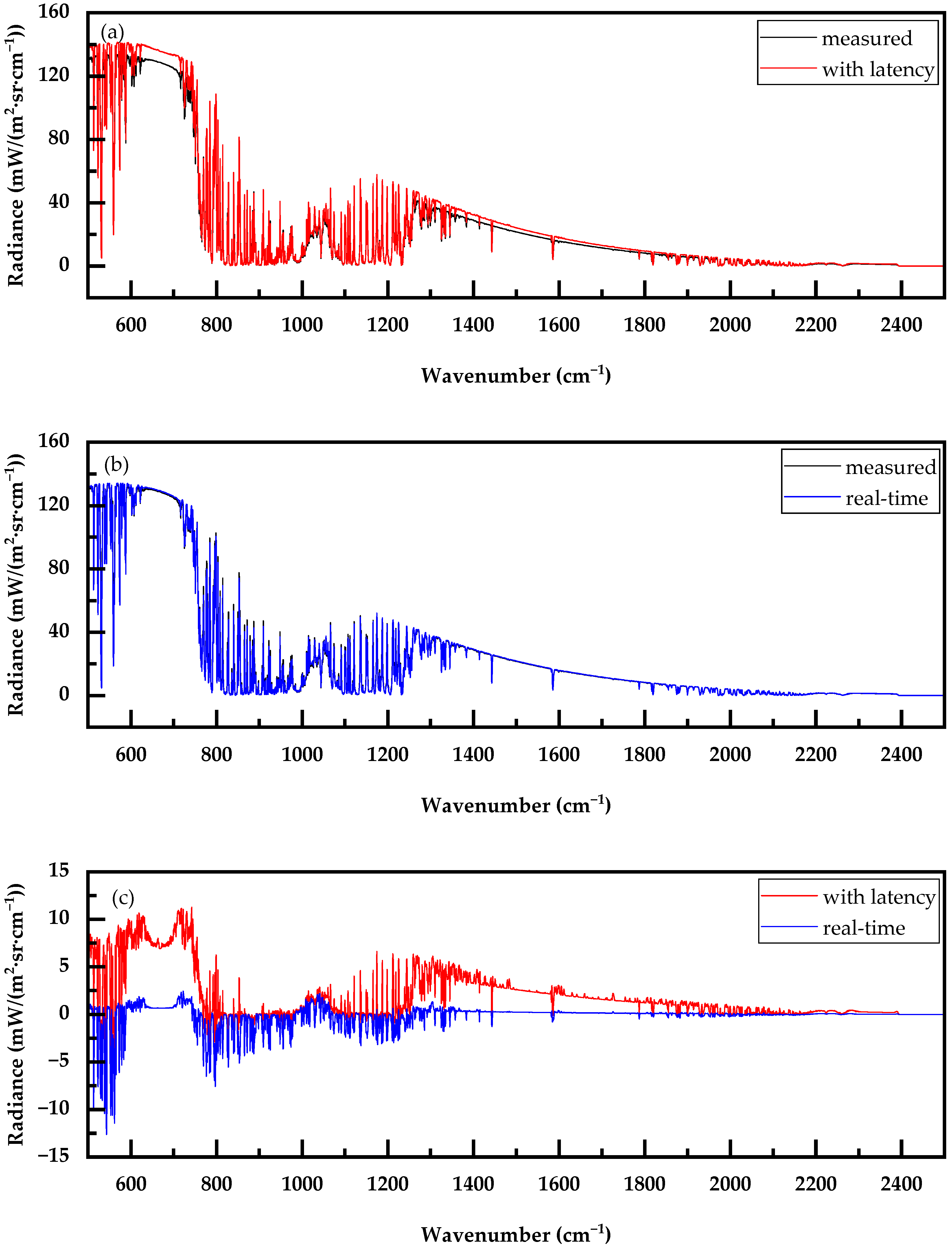
| 1000 | 950 | 900 | 800 | 700 | 600 | 350 | 150 | 30 | 7 |
| 990 | 940 | 880 | 780 | 680 | 550 | 300 | 125 | 25 | 5 |
| 980 | 930 | 860 | 760 | 660 | 500 | 250 | 100 | 20 | 4 |
| 970 | 920 | 840 | 740 | 640 | 450 | 200 | 75 | 15 | 3 |
| 960 | 910 | 820 | 720 | 620 | 400 | 175 | 50 | 10 | 2 |
| Temperature (K) | Pressure (hPa) | Gas Concentrations (ppmv) | |
|---|---|---|---|
| 270.1 | 1000 | CO2: 400 | O2: 210000 |
| 272.3 | 900 | H2O: 10000 | NH3: 0.0042 |
| 274.5 | 800 | CH4: 1.90 | NO: 0.0016 |
| 276.7 | 700 | CO: 0.20 | NO2: 0.0060 |
| 278.9 | 600 | N2O: 0.33 | SO2: 0.0045 |
| O3: 0.03 | HNO3: 0.0011 | ||
| Total Time Taken (s) | ||
|---|---|---|
| Calculation Bands (cm−1) | HAPI | Interpolation Method |
| 672–715 | 898 | 37.5 |
| 1250–1350 | 1151 | 35 |
| 500–2500 | 3118 | 37.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, S.; Liu, J.; Xu, L.; Wang, Y.; Deng, Y.; Sun, Y. Real-Time Simulation of Clear Sky Background Radiation in Gas Infrared Remote Sensing Monitoring. Photonics 2024, 11, 904. https://doi.org/10.3390/photonics11100904
Shu S, Liu J, Xu L, Wang Y, Deng Y, Sun Y. Real-Time Simulation of Clear Sky Background Radiation in Gas Infrared Remote Sensing Monitoring. Photonics. 2024; 11(10):904. https://doi.org/10.3390/photonics11100904
Chicago/Turabian StyleShu, Shengquan, Jianguo Liu, Liang Xu, Yuhao Wang, Yasong Deng, and Yongfeng Sun. 2024. "Real-Time Simulation of Clear Sky Background Radiation in Gas Infrared Remote Sensing Monitoring" Photonics 11, no. 10: 904. https://doi.org/10.3390/photonics11100904
APA StyleShu, S., Liu, J., Xu, L., Wang, Y., Deng, Y., & Sun, Y. (2024). Real-Time Simulation of Clear Sky Background Radiation in Gas Infrared Remote Sensing Monitoring. Photonics, 11(10), 904. https://doi.org/10.3390/photonics11100904






