The Arago–Poisson Spot: New Applications for an Old Concept
Abstract
1. Introduction
2. Results
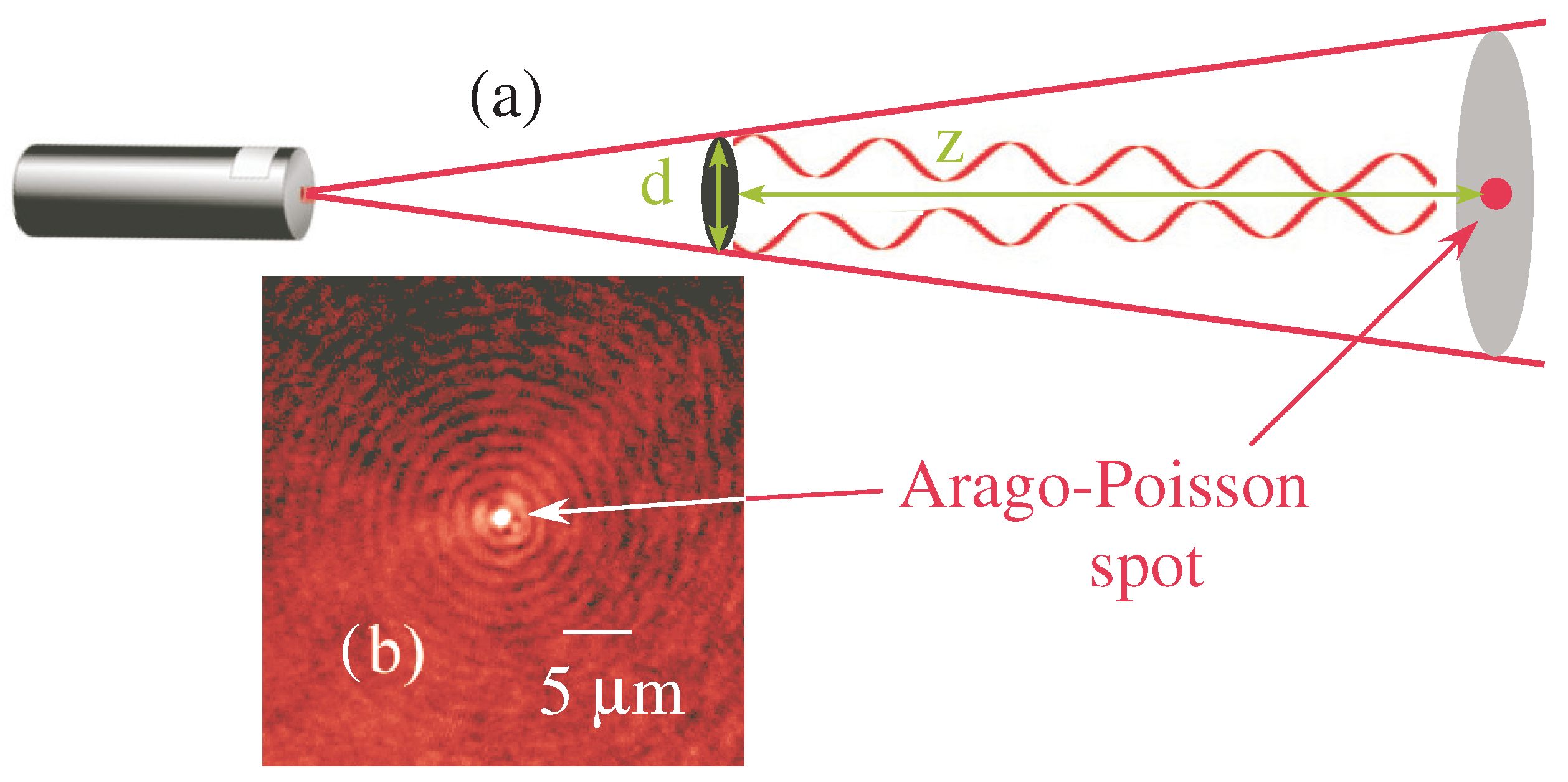
2.1. Theoretical Considerations
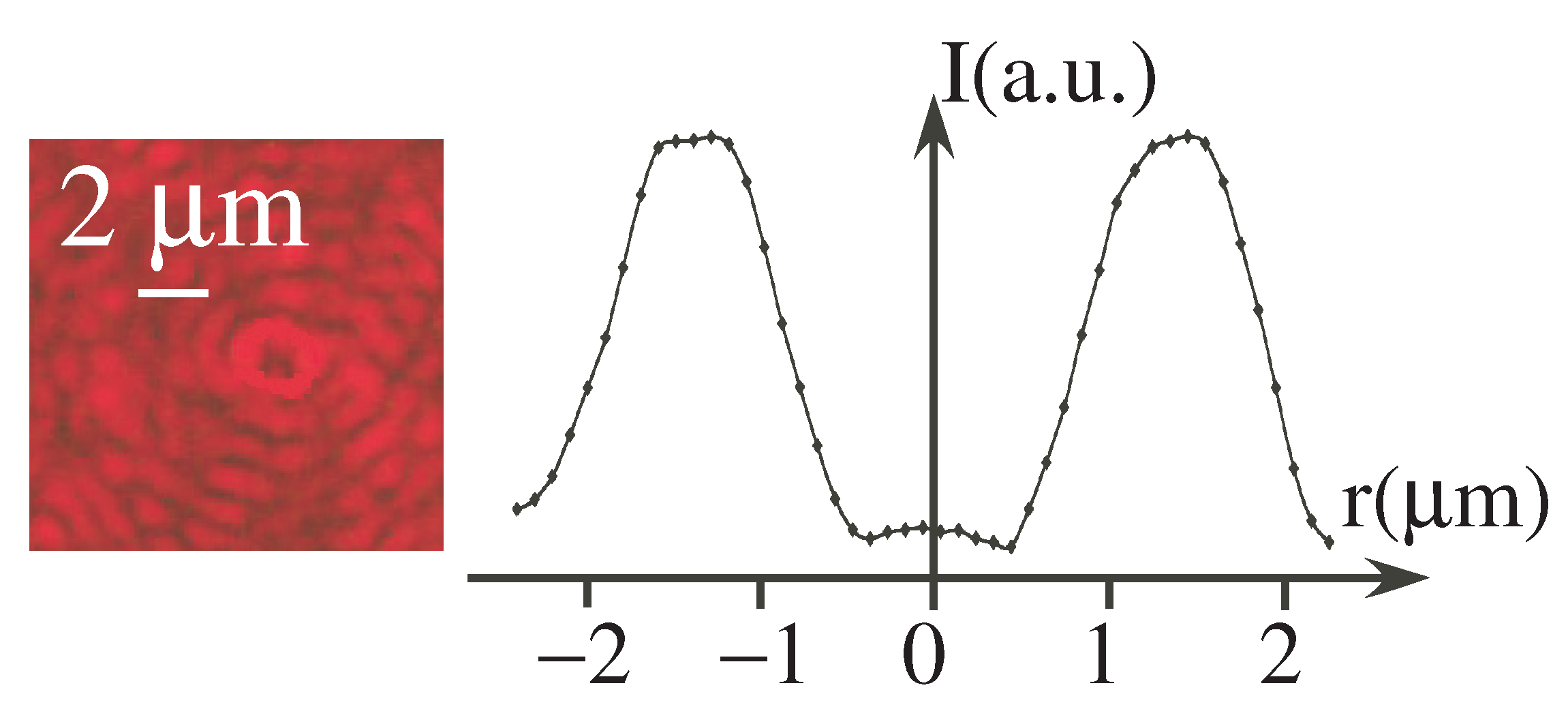
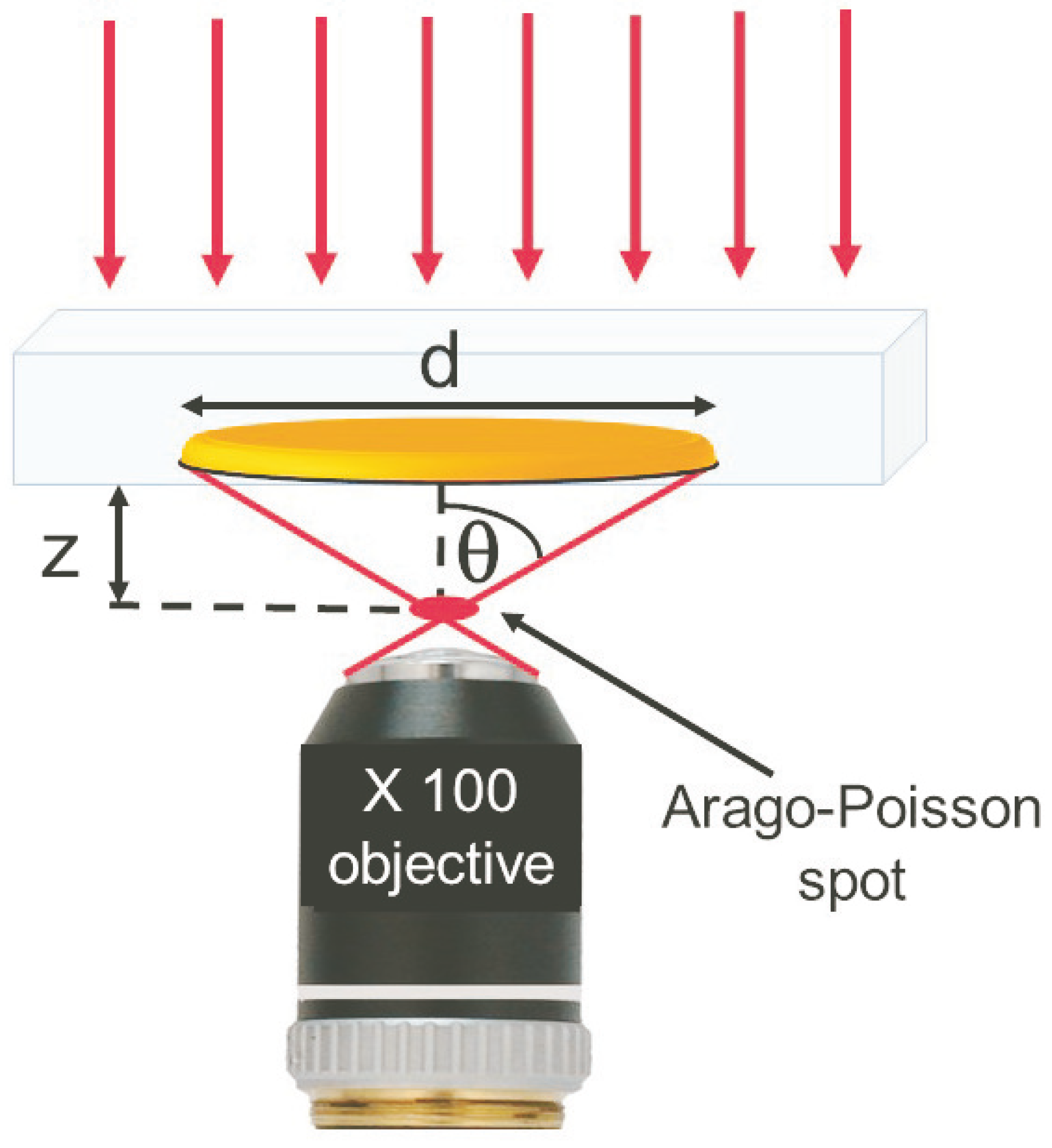
2.2. Experiments
2.3. Properties
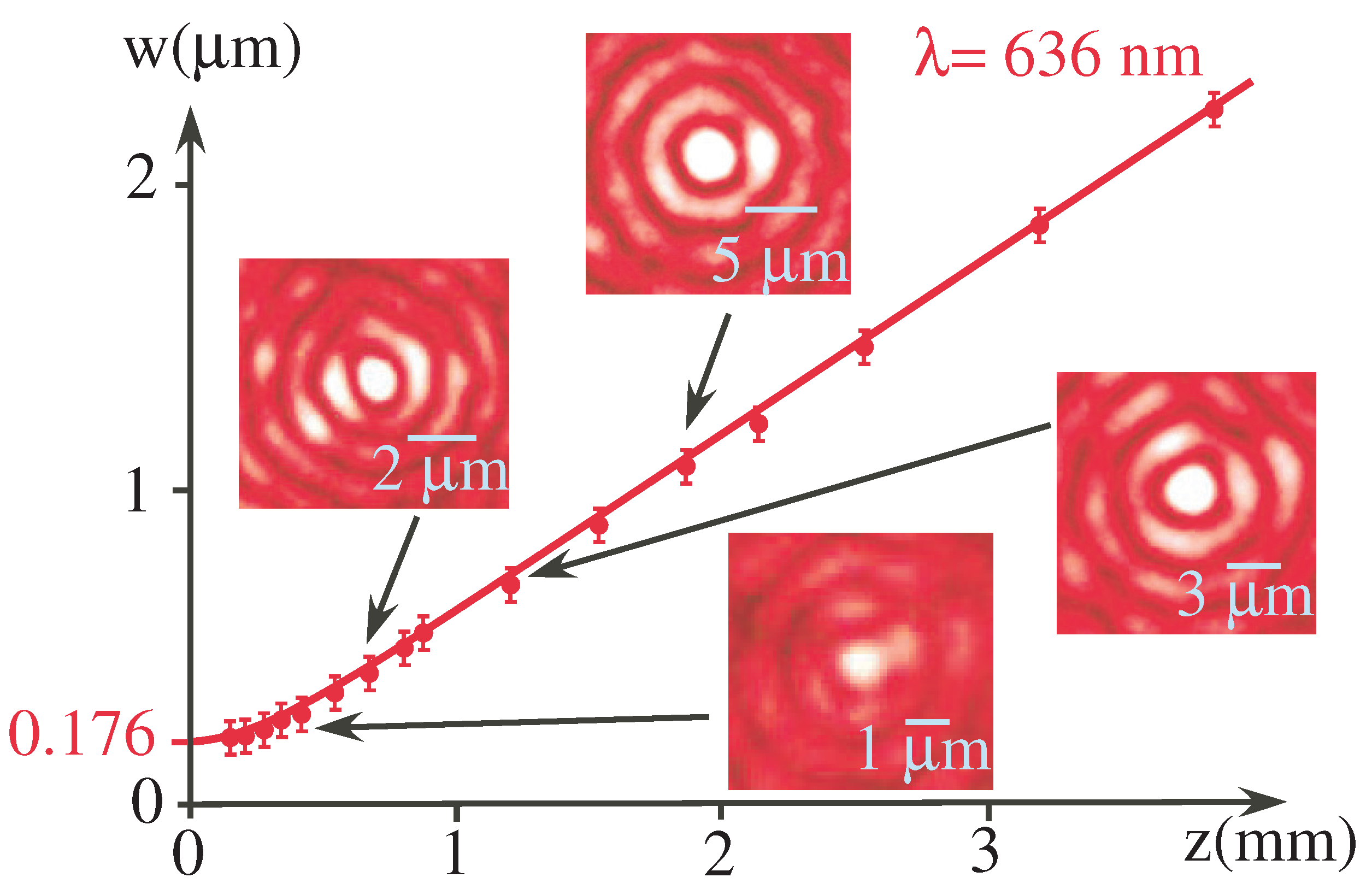
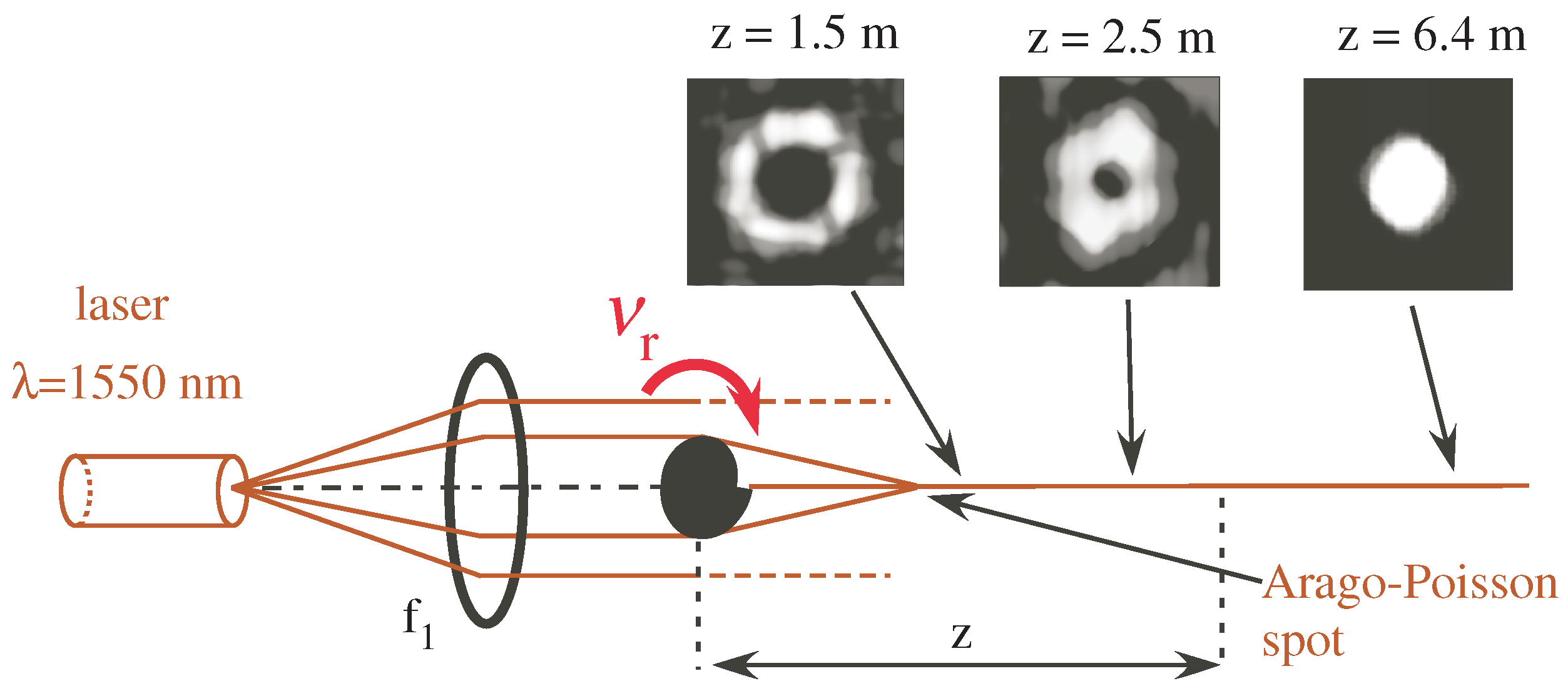
2.3.1. Ultimate Arago–Poisson Beam Size
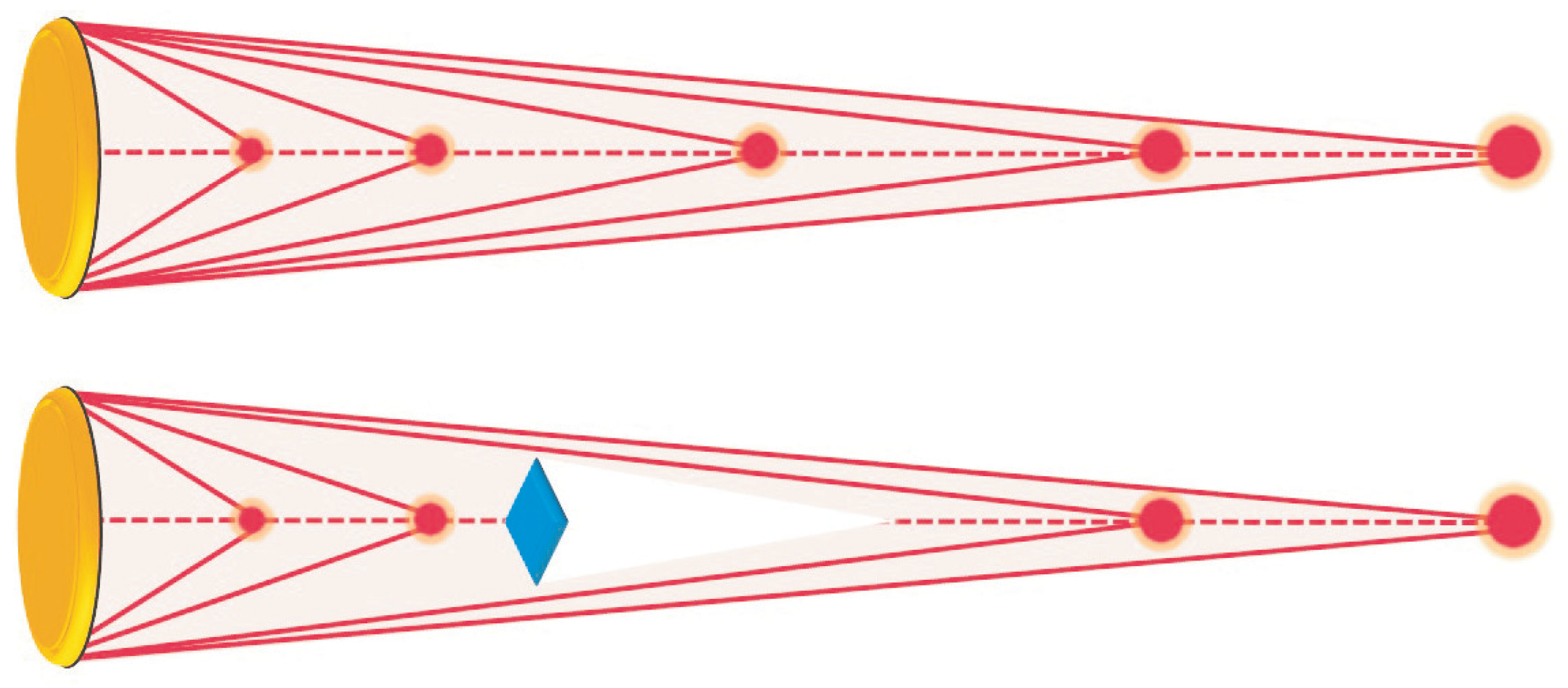
2.3.2. Self-Healing and Nondiffractive Properties
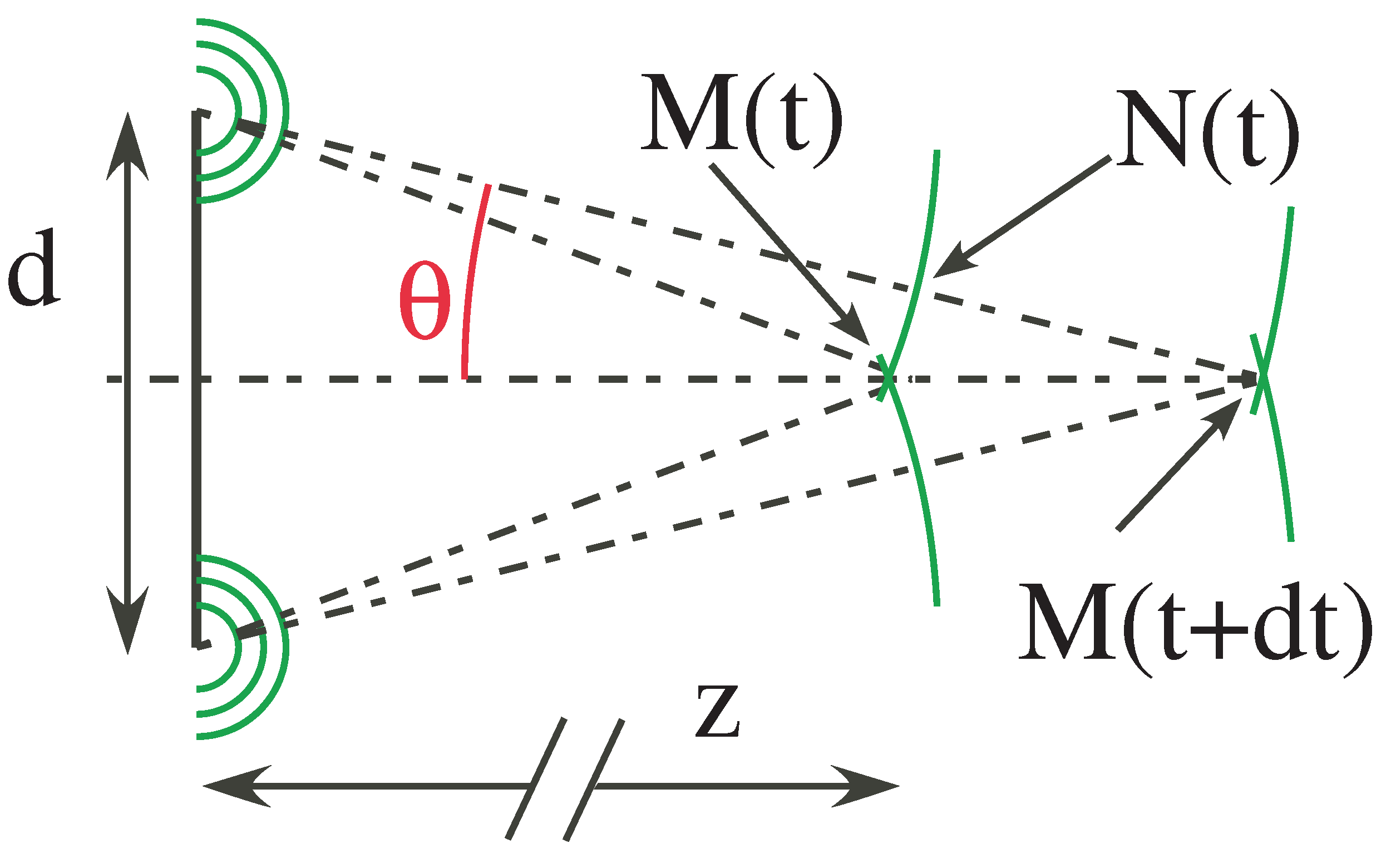
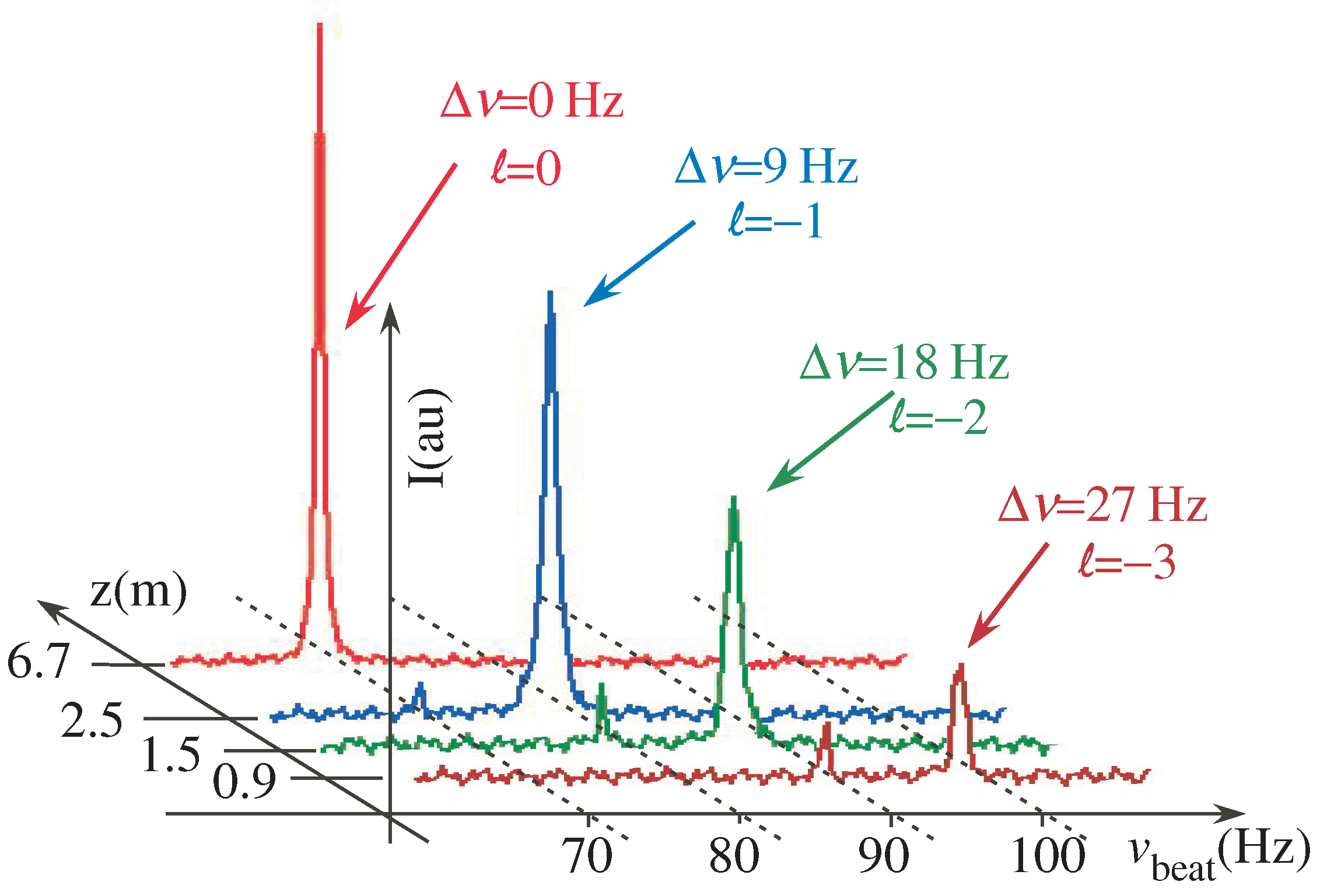
2.3.3. Faster-Than-Light Properties
3. Discussion
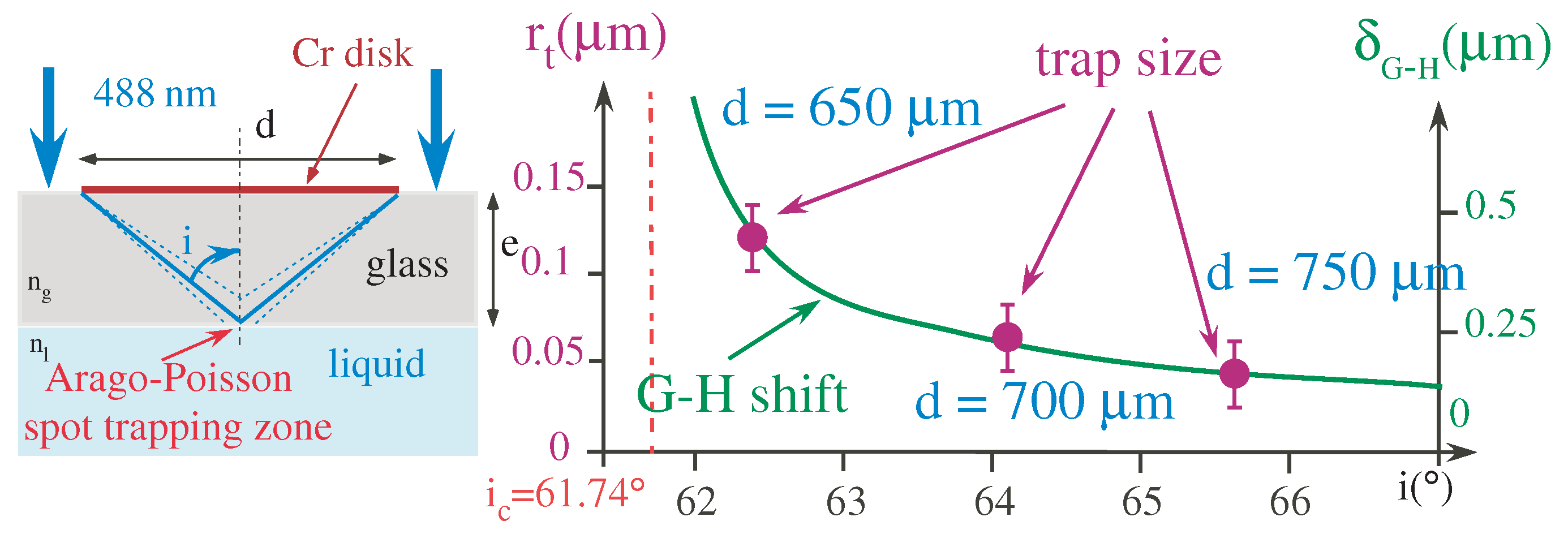
3.1. Particle Trapping
3.2. Changing Nature of the Arago–Poisson Spot and Application to Signal Addressing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bertrand, J. Eloge Historique de Léon Foucault: Lu Dans la Séance Publique Annuelle du 6 Février 1882; Institut de France: Paris, France, 1882. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Hecht, E. Optics, 5th ed.; Pearson: London, UK, 2015. [Google Scholar]
- Aspect, A. From Huygens’ waves to Einstein’s photons: Weird light. C. R. Phys. 2017, 18, 498–503. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Herndon, VA, USA, 1986. [Google Scholar]
- Chauvat, D.; Emile, O.; Brunel, M.; Le Floch, A. Direct measurement of the central fringe velocity in Young-type experiments. Phys. Lett. A 2002, 295, 78–80. [Google Scholar] [CrossRef]
- Chauvat, D.; Emile, O.; Brunel, M.; Le Floch, A. Huygens’ principle and Young’s experiment in the propagation of light beams. Am. J. Phys. 2003, 71, 1196–1198. [Google Scholar] [CrossRef]
- Piksarv, P.; Bowlan, P.; Lohmus, M.; Valtna-Lukner, H.; Trebino, R.; Saari, P. Diffraction of ultrashort Gaussian pulses within the framework of boundary diffraction wave theory. J. Opt. 2011, 14, 015701. [Google Scholar] [CrossRef]
- Kim, M.S.; Scharf, T.; Etrich, C.; Rockstuhl, C.; Peter, H.H. Longitudinal-differential interferometry: Direct imaging of axial superluminal phase propagation. Opt. Lett. 2012, 37, 305–307. [Google Scholar] [CrossRef] [PubMed]
- Xiafukaiti, A.; Lagrosas, N.; Shiina, T. Exploration for adequate non-diffractive beam generation in dense scattering media. Sci. Rep. 2022, 12, 8824. [Google Scholar] [CrossRef] [PubMed]
- Emile, O.; Emile, J. Experimental analysis of submicrometer optical intensity distributions after an opaque disk. Appl. Opt. 2020, 59, 1678–1683. [Google Scholar] [CrossRef]
- Evans, P.; Rogers, K.; Chan, J.; Rogers, J.; Dicken, A. High intensity X-ray diffraction in transmission mode employing an analog of Poisson’s spot. Appl. Phys. Lett. 2010, 97, 204101. [Google Scholar] [CrossRef]
- Macaulay, E.J.; Hartmann, W.M.; Rakerd, B. The acoustical bright spot and mislocalization of tones by human listeners. J. Acoust. Soc. Am. 2010, 127, 1440–1449. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, X. Poisson-Arago spot for gravitational waves. Sci. China Phys. Mech. Astron. 2021, 64, 120462. [Google Scholar] [CrossRef]
- Reisinger, T.; Patel, A.A.; Reingruber, H.; Fladischer, K.; Ernst, W.E.; Bracco, G.; Smith, H.I.; Holst, B. Poisson’s spot with molecules. Phys. Rev. A 2009, 79, 053823. [Google Scholar] [CrossRef]
- Eder, S.; Reisinger, T.; Greve, M.; Bracco, G.; Holst, B. Focusing of a neutral helium beam below one micron. New J. Phys. 2012, 14, 073014. [Google Scholar] [CrossRef][Green Version]
- Sommerfeld, A. Lectures on Theoretical Physics: Optics; Academic Press: Cambridge, MA, USA, 1954; Volume 4. [Google Scholar]
- Dauger, D.E. Simulation and study of Fresnel diffraction for arbitrary two-dimensional apertures. Comput. Phys. 1996, 10, 591–604. [Google Scholar] [CrossRef]
- Horváth, Z.; Bor, Z. Diffraction of short pulses with boundary diffraction wave theory. Phys. Rev. E 2001, 63, 026601. [Google Scholar] [CrossRef]
- Harvey, J.E.; Forgham, J.L. The spot of Arago: New relevance for an old phenomenon. Am. J. Phys. 1984, 52, 243–247. [Google Scholar] [CrossRef]
- Fischer, P.; Skelton, S.E.; Leburn, C.G.; Streuber, C.T.; Wright, E.M.; Dholakia, K. The dark spots of Arago. Opt. Express 2007, 15, 11860–11873. [Google Scholar] [CrossRef]
- Emile, O.; Voisin, A.; Niemiec, R.; de Lesegno, B.V.; Pruvost, L.; Ropars, G.; Emile, J.; Brousseau, C. Dark zone in the centre of the Arago-Poisson diffraction spot of a helical laser beam. EPL 2013, 101, 54005. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Barnett, S.M.; Babiker, M.; Padgett, M.J. Optical orbital angular momentum. Phil. Trans. R. Soc. A 2017, 375, 20150444. [Google Scholar] [CrossRef]
- Papathanasopoulos, A.; Rahmat-Samii, Y. Fundamentals of Orbital Angular Momentum Beams. In Electromagnetic Vortices; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; Chapter 1; pp. 1–32. [Google Scholar]
- Hebri, D.; Rasouli, S.; Dezfouli, A.M. Theory of diffraction of vortex beams from structured apertures and generation of elegant elliptical vortex Hermite-Gaussian beams. J. Opt. Soc. Am. A 2019, 36, 839–852. [Google Scholar] [CrossRef]
- Emile, O.; Emile, J.; Tabuteau, H. Nanoscale optical trap for fluorescent nanoparticles. EPL 2020, 129, 58001. [Google Scholar] [CrossRef]
- Girard, C.; Dereux, A. Near-field optics theories. Rep. Prog. Phys. 1996, 59, 657. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V. Very compact focal spot in the near-field of the fractional axicon. Opt. Commun. 2017, 391, 24–29. [Google Scholar] [CrossRef]
- Huang, F.M.; Zheludev, N.I. Super-Resolution without Evanescent Waves. Nano Lett. 2009, 9, 1249–1254. [Google Scholar] [CrossRef]
- Khonina, S.N.; Golub, I. Engineering the smallest 3D symmetrical bright and dark focal spots. J. Opt. Soc. Am. A 2013, 30, 2029–2033. [Google Scholar] [CrossRef]
- Quabis, S.; Dorn, R.; Eberler, M.; Glöckl, O.; Leuchs, G. Focusing light to a tighter spot. Opt. Commun. 2000, 179, 1–7. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966. [Google Scholar] [CrossRef]
- Yen, A. Rayleigh or Abbe? Origin and naming of the resolution formula of microlithography. J. Micro/Nanolithogr. MEMS 2020, 19, 040501. [Google Scholar] [CrossRef]
- Harland, M.; Khonina, S.N.; Golub, I. Enlightening Arago–Poisson spot using structured light. Appl. Opt. 2021, 60, 7432–7436. [Google Scholar] [CrossRef]
- Mestre, M.; Diry, F.; Viaris de Lesegno, B.; Pruvost, L. Cold atom guidance by a holographically-generated Laguerre-Gaussian laser mode. Eur. Phys. J. D 2010, 57, 87. [Google Scholar] [CrossRef]
- Carrat, V.; Cabrera-Gutiérrez, C.; Jacquey, M.; Tabosa, J.W.; de Lesegno, B.V.; Pruvost, L. Long-distance channeling of cold atoms exiting a 2D magneto-optical trap by a Laguerre—Gaussian laser beam. Opt. Lett. 2014, 39, 719–722. [Google Scholar] [CrossRef]
- McGloin, D.; Dholakia, K. Bessel beams: Diffraction in a new light. Contemp. Phys. 2005, 46, 15–28. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Karpeev, S.V.; Butt, M.A. Bessel beam: Significance and applications—A progressive review. Micromachines 2020, 11, 997. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli Jr, J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499. [Google Scholar] [CrossRef]
- Cox, A.; D’Anna, J. Constant-axial-intensity nondiffracting beam. Opt. Lett. 1992, 17, 232–234. [Google Scholar] [CrossRef]
- Ren, Y.X.; He, H.; Tang, H.; Wong, K.K. Non-diffracting light wave: Fundamentals and biomedical applications. Front. Phys. 2021, 9, 698343. [Google Scholar] [CrossRef]
- Paterson, C.; Smith, R. Higher-order Bessel waves produced by axicon-type computer-generated holograms. Opt. Commun. 1996, 124, 121–130. [Google Scholar] [CrossRef]
- Tiwari, S.K.; Mishra, S.R.; Ram, S.P.; Rawat, H.S. Generation of a Bessel beam of variable spot size. Appl. Opt. 2012, 51, 3718–3725. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Ye, J.S.; Feng, S.F.; Wang, X.K.; Han, P.; Sun, W.F.; Zhang, Y.; Zhang, X.C. Generation of long-distance stably propagating Bessel beams. OSA Contin. 2021, 4, 1223–1233. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.T.; Ye, J.S.; Feng, S.F.; Wang, X.K.; Han, P.; Sun, W.F.; Zhang, Y. Generation of stable propagation Bessel beams and axial multifoci beams with binary amplitude filters. J. Opt. Soc. Am. A 2023, 40, 1425–1433. [Google Scholar] [CrossRef] [PubMed]
- Zhi, Z.; Na, Q.; Xie, Q.; Chen, B.; Li, Y.; Liu, X.; Li, X.; Wang, L.; Lo, G.; Song, J. On-chip generation of Bessel—Gaussian beam via concentrically distributed grating arrays for long-range sensing. Light Sci. Appl. 2023, 12, 92. [Google Scholar] [CrossRef]
- Fahrbach, F.O.; Simon, P.; Rohrbach, A. Microscopy with self-reconstructing beams. Nat. Photonics 2010, 4, 780–785. [Google Scholar] [CrossRef]
- Vettenburg, T.; Dalgarno, H.I.; Nylk, J.; Coll-Lladó, C.; Ferrier, D.E.; Čižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-sheet microscopy using an Airy beam. Nat. Methods 2014, 11, 541–544. [Google Scholar] [CrossRef]
- Planchon, T.A.; Gao, L.; Milkie, D.E.; Davidson, M.W.; Galbraith, J.A.; Galbraith, C.G.; Betzig, E. Rapid three-dimensional isotropic imaging of living cells using Bessel beam plane illumination. Nat. Methods 2011, 8, 417–423. [Google Scholar] [CrossRef]
- Liu, J.T.; Glaser, A.K.; Bera, K.; True, L.D.; Reder, N.P.; Eliceiri, K.W.; Madabhushi, A. Harnessing non-destructive 3D pathology. Nat. Biomed. Eng. 2021, 5, 203–218. [Google Scholar] [CrossRef]
- Suchand Sandeep, C.; Khairyanto, A.; Aung, T.; Vadakke Matham, M. Bessel Beams in Ophthalmology: A Review. Micromachines 2023, 14, 1672. [Google Scholar] [CrossRef]
- Garcés-Chávez, V.; McGloin, D.; Melville, H.; Sibbett, W.; Dholakia, K. Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam. Nature 2002, 419, 145–147. [Google Scholar] [CrossRef]
- Chu, X. Analytical study on the self-healing property of Bessel beam. Eur. Phys. J. D 2012, 66, 259. [Google Scholar] [CrossRef]
- Aiello, A.; Agarwal, G.S. Wave-optics description of self-healing mechanism in Bessel beams. Opt. Lett. 2014, 39, 6819–6822. [Google Scholar] [CrossRef] [PubMed]
- Grunwald, R.; Bock, M. Needle beams: A review. Adv. Phys. X 2020, 5, 1736950. [Google Scholar] [CrossRef]
- Shen, Y.; Pidishety, S.; Nape, I.; Dudley, A. Self-healing of structured light: A review. J. Opt. 2022, 24, 103001. [Google Scholar] [CrossRef]
- Mphuthi, N.; Botha, R.; Forbes, A. Are Bessel beams resilient to aberrations and turbulence? J. Opt. Soc. Am. A 2018, 35, 1021–1027. [Google Scholar] [CrossRef]
- Valtna-Lukner, H.; Bowlan, P.; Lõhmus, M.; Piksarv, P.; Trebino, R.; Saari, P. Direct spatiotemporal measurements of accelerating ultrashort Bessel-type light bullets. Opt. Express 2009, 17, 14948–14955. [Google Scholar] [CrossRef]
- Courvoisier, F.; Stoian, R.; Couairon, A. Ultrafast laser micro-and nano-processing with nondiffracting and curved beams: Invited paper for the section: Hot topics in ultrafast lasers. Opt. Laser Technol. 2016, 80, 125–137. [Google Scholar] [CrossRef]
- Mugnai, D.; Ranfagni, A.; Ruggeri, R. Observation of superluminal behaviors in wave propagation. Phys. Rev. Lett. 2000, 84, 4830. [Google Scholar] [CrossRef]
- Tian, S.; Xia, X.; Sun, W.; Li, W.; Li, J.; Gu, C. Large-scale ordered silicon microtube arrays fabricated by Poisson spot lithography. Nanotechnology 2011, 22, 395301. [Google Scholar] [CrossRef]
- Jung, Y.; Vacic, A.; Sun, Y.; Hadjimichael, E.; Reed, M.A. Mapping of near field light and fabrication of complex nanopatterns by diffraction lithography. Nanotechnology 2012, 23, 045301. [Google Scholar] [CrossRef] [PubMed]
- Kaemtner, D.; Prenting, J. Straight Line Reference System (SLRS) for the Adjustment of the X-ray Free-electron Laser (XFEL) at DESY. In Proceedings of the 9th International Workshop on Accelerator Alignment (IWAA), Stanford Linear Accelerator Center (SLAC), Menlo Park, CA, USA, 26–29 September 2006. [Google Scholar]
- Luo, T.; He, Z.; Cheng, H.; Zuo, T.; Xiao, S.; Lu, S.; Ke, Z.; Ma, N.; Wang, T.; Liang, J.; et al. A new laser-based alignment method for the multi-slits VSANS in high precision. Nucl. Instrum. Methods A 2021, 1010, 165526. [Google Scholar] [CrossRef]
- He, Z.; Wang, T.; Wang, X.; Lu, S.; Liu, H.; Li, X.; Men, L.; Ma, N.; Ke, Z.; Liang, J.; et al. A new laser-based monitoring method for the cryomodule components alignment. Meas. Sci. Technol. 2022, 33, 075201. [Google Scholar] [CrossRef]
- Niewiem, W.; Polak, K.; Dusek, M.; Mergelkuhl, D.; Gayde, J.C.; Wieser, A.; Sulc, M. Variation of Structured Laser Beam pattern and optimization for an alignment reference line creation. Opt. Express 2023, 31, 43307–43322. [Google Scholar] [CrossRef]
- Erbschloe, D.R. The Spot of Arago and Its Role in Aberration Analysis. Master’s Thesis, University of New Mexico, Albuquerque, NM, USA, 1983. [Google Scholar]
- Ovryn, B.; Hovenac, E.A. Coherent forward scattering particle-image velocimetry: Application of Poisson’s spot for velocity measurements in fluids. In Proceedings of the SPIE: Optical Diagnostics in Fluid and Thermal Flow, SPIE, Orlando, FL, USA, 13–14 April 1993; Volume 2005, pp. 338–348. [Google Scholar]
- Vanderbei, R.J. Eliminating Poisson’s spot with linear programming. In Proceedings of the Operations Research and Cyber-Infrastructure; Springer: Berlin/Heidelberg, Germany, 2009; pp. 455–467. [Google Scholar]
- Lyot, B. The study of the solar corona and prominences without eclipses (George Darwin Lecture, 1939). Mon. Not. R. Astron. Soc. 1939, 99, 580. [Google Scholar]
- Kuchner, M.J.; Traub, W.A. A coronagraph with a band-limited mask for finding terrestrial planets. Astrophys. J. 2002, 570, 900. [Google Scholar] [CrossRef]
- Guyon, O.; Pluzhnik, E.; Kuchner, M.; Collins, B.; Ridgway, S. Theoretical limits on extrasolar terrestrial planet detection with coronagraphs. Astrophys. J. Suppl. 2006, 167, 81. [Google Scholar] [CrossRef]
- Cash, W. Analytic modeling of starshades. Astrophys. J. 2011, 738, 76. [Google Scholar] [CrossRef][Green Version]
- Soto, G.J.; Savransky, D.; Morgan, R. Analytical model for starshade formation flying with applications to exoplanet direct imaging observation scheduling. J. Astron. Telesc. Instrum. Syst. 2021, 7, 021209. [Google Scholar] [CrossRef]
- Cocks, F.; Watkins, S.; Walker, M.; Lutz, T.; Sussingham, J. A High-Resolution Solar Telescope Using Dark-Lens Diffractive Optics. Sol. Phys. 2001, 198, 211–222. [Google Scholar] [CrossRef]
- Cash, W. The Aragoscope: Ultra-High Resolution Optics at Low Cost; Technical Report; NASA: Washington, DC, USA, 2014. [Google Scholar]
- Lotz, J.E.; Koekemoer, A.; Coe, D.; Grogin, N.; Capak, P.; Mack, J.; Anderson, J.; Avila, R.; Barker, E.; Borncamp, D.; et al. The Frontier Fields: Survey design and initial results. Astrophys. J. 2017, 837, 97. [Google Scholar] [CrossRef]
- Robertson, B.E. Galaxy formation and reionization: Key unknowns and expected breakthroughs by the james webb space telescope. Ann. Rev. Astron. Astrophys. 2022, 60, 121–158. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Neuman, K.C.; Block, S.M. Optical trapping. Rev. Sci. Instrum. 2004, 75, 2787–2809. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.H.; Maragò, O.M.; Volpe, G. Optical Tweezers: Principles and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Bustamante, C.J.; Chemla, Y.R.; Liu, S.; Wang, M.D. Optical tweezers in single-molecule biophysics. Nat. Rev. Methods Primers 2021, 1, 25. [Google Scholar] [CrossRef] [PubMed]
- Spesyvtseva, S.E.S.; Dholakia, K. Trapping in a material world. ACS Photonics 2016, 3, 719–736. [Google Scholar] [CrossRef]
- Almaas, E.; Brevik, I. Radiation forces on a micrometer-sized sphere in an evanescent field. J. Opt. Soc. Am. B 1995, 12, 2429–2438. [Google Scholar] [CrossRef]
- Yoon, Y.Z.; Cicuta, P. Optical trapping of colloidal particles and cells by focused evanescent fields using conical lenses. Opt. Express 2010, 18, 7076–7084. [Google Scholar] [CrossRef] [PubMed]
- Emile, O.; Emile, J.; Tabuteau, H. 2-D evanescent trapping of colloids in the vicinity of a micrometer waveguide. EPL 2017, 116, 64003. [Google Scholar] [CrossRef]
- Novotny, L.; Bian, R.X.; Xie, X.S. Theory of nanometric optical tweezers. Phys. Rev. Lett. 1997, 79, 645. [Google Scholar] [CrossRef]
- Volpe, G.; Quidant, R.; Badenes, G.; Petrov, D. Surface plasmon radiation forces. Phys. Rev. Lett. 2006, 96, 238101. [Google Scholar] [CrossRef]
- Juan, M.L.; Righini, M.; Quidant, R. Plasmon nano-optical tweezers. Nat. Photonics 2011, 5, 349–356. [Google Scholar] [CrossRef]
- Kotsifaki, D.G.; Chormaic, S.N. Plasmonic optical tweezers based on nanostructures: Fundamentals, advances and prospects. Nanophotonics 2019, 8, 1227–1245. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Y.; Su, W.; Zhang, Y.; Liu, Z.; Yang, X.; Zhang, J.; Yang, J.; Yuan, L. Super-low-power optical trapping of a single nanoparticle. Opt. Lett. 2019, 44, 5165–5168. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, G.; Sasanelli, N.; Armenise, M.N.; Ciminelli, C. Nanoscale Optical Trapping by Means of Dielectric Bowtie. Photonics 2022, 9, 425. [Google Scholar] [CrossRef]
- Emile, O.; Emile, J. Nanometer optical trap based on stimulated emission in evanescence of a totally reflected Arago spot: Nanometer optical trap for fluorescent nanoparticles. Eur. Phys. J. E 2020, 43, 68. [Google Scholar] [CrossRef] [PubMed]
- Haugland, R.P. The handbook: A Guide to Fluorescent Probes and Labeling Technologies; Molecular Probes: Eugene, OR, USA, 2005. [Google Scholar]
- Floch, A.L.; Emile, O.; Ropars, G.; Agrawal, G.P. Dynamics and detection of the Newton-Wigner time delays at interfaces using a swivelling method. Sci. Rep. 2017, 7, 9083. [Google Scholar] [CrossRef] [PubMed]
- Emile, O.; Le Meur, M.; Emile, J. Light angular momentum of a plane wave diffracted by a two-dimensional object. Phys. Rev. A 2014, 89, 013846. [Google Scholar] [CrossRef]
- Emile, O.; Emile, J. Rotation of millimeter-sized objects using ordinary light. Opt. Lett. 2016, 41, 211–214. [Google Scholar] [CrossRef]
- Emile, J.; Tabuteau, H.; Emile, O. Rotation of a floating hydrophobic disk: Influence of line tension. Soft Matter 2018, 14, 3829–3833. [Google Scholar] [CrossRef]
- Emile, O.; Emile, J. Rotational Doppler Effect: A Review. Ann. Phys. 2023, 535, 2300250. [Google Scholar] [CrossRef]
- Emile, O.; Emile, J. Frequency changes during the propagation of a light beam. EPL 2022, 139, 35001. [Google Scholar] [CrossRef]
- Hall, J.L. Nobel Lecture: Defining and measuring optical frequencies. Rev. Mod. Phys. 2006, 78, 1279. [Google Scholar] [CrossRef]
- Stenholm, S. Foundations of Laser Spectroscopy; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Chebotayev, V.; Letokhov, V. Nonlinear narrow optical resonances induced by laser radiation. Prog. Quantum Electron. 1975, 4, 111–206. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emile, O.; Emile, J. The Arago–Poisson Spot: New Applications for an Old Concept. Photonics 2024, 11, 55. https://doi.org/10.3390/photonics11010055
Emile O, Emile J. The Arago–Poisson Spot: New Applications for an Old Concept. Photonics. 2024; 11(1):55. https://doi.org/10.3390/photonics11010055
Chicago/Turabian StyleEmile, Olivier, and Janine Emile. 2024. "The Arago–Poisson Spot: New Applications for an Old Concept" Photonics 11, no. 1: 55. https://doi.org/10.3390/photonics11010055
APA StyleEmile, O., & Emile, J. (2024). The Arago–Poisson Spot: New Applications for an Old Concept. Photonics, 11(1), 55. https://doi.org/10.3390/photonics11010055




