Abstract
In order to deal with the chromatic dispersion-induced power fading issue for short-reach direct-detection optical fiber communication applications, such as the ever-increasing data-center interconnections (DCIs), optical filed recovery is intensively being under investigation. To date, various direct detection schemes capable of optical field recovery have been proposed, including the Kramers–Kronig (KK) receiver, asymmetric self-coherence detection (ASCD) receiver, carrier-assisted differential detection receiver (CADD), Stokes vector receiver (SVR), and carrier-free phase-retrieval (CF-PR) receiver. Among those, the CF-PR receiver attracts lots of research attention because it can circumvent the requirement of a strong continuous-wave (CW) optical carrier for the beating with the signal. Generally, the CF-PR receiver consists of only two single-ended photodiodes (PDs) and one dispersive element, for the field recovery of the quadrature amplitude modulation (QAM) signals. Based on the theoretical and experimental studies reported so far, this paper reviews the latest progress of CF-PR receivers designed for high-speed optical short-reach transmission links.
1. Introduction
With the large-scale application of cloud computing, artificial intelligence, Internet of things (IoT), and other network applications, we have witnessed an exponential growth of data traffic, which stimulates the anticipation for high-speed, large-capacity fiber optical communication systems. Coherent detection technology can realize multi-dimensional optical signal detection, allowing for linear transmission impairments to be solved by the receiver-side (Rx) digital signal processing (DSP) algorithm; thus, the high-speed, large-capacity long-distance optical fiber communication transmission can be realized. While coherent detection constitutes the preferred solution for medium-reach to long-reach transmissions, the lasers with high power, narrow linewidths, and high wavelength stability used in coherent detection systems are not suitable for cost-sensitive and power-sensitive short-reach links such as data center interconnections (DCIs). At present, short-reach optical communications are still dominated by intensity modulation direct detection (IM/DD) systems, which employ only one single-ended photodiode (PD) at the Rx in comparison with coherent detection, reducing hardware costs and power consumption [1]. However, IM/DD lacks the key capability of optical field recovery, and can only obtain the signal intensity information, which greatly limits the transmission data rate of the IM/DD system. In order to increase the transmission data rate, the order of pulse amplitude modulation (PAM) must be increased, but the increase in the PAM order often leads to the serious deterioration of the receiver sensitivity. Additionally, the chromatic dispersion (CD) is a transmission damage that induces power fading for IM/DD systems, limiting the transmission distance [2,3,4,5,6,7,8,9,10,11,12,13].
In order to adapt to the receiver requirements of short-reach optical communication with low cost, low power consumption, and high receiver sensitivity characteristics, reconstructing the optical signal field from the intensity measurement of the optical signal has attracted intensive attention. In recent years, self-coherence detection schemes have been proposed to reconstruct complex-valued signals in single-polarization systems by using direct detection, including the Kramers–Kronig (KK) [14,15,16,17] receiver, asymmetric self-coherence detection (ASCD) receiver [18], carrier-assisted differential detection receiver (CADD) [19], and the Stokes vector receiver (SVR) [20]. These self-coherent schemes need to insert a continuous-wave (CW) optical carrier along with the modulated optical signal. Consequently, the optical field of the modulated signal at the Rx can be reconstructed using the beat term between the signal and the CW carrier based on direct detection. However, direct detection introduces signal-to-signal beat interference (SSBI) [21,22,23], which results in the poor performance of these self-coherent receivers. The KK receiver can suppress SSBI using the KK relationship, but in order to meet the minimum phase condition of the KK algorithm, only single sideband (SSB)-modulated optical signals can be used, thus reducing the electrical spectral efficiency (ESE) by half. In addition, the KK operation adds a non-negligible computational complexity, especially considering the high oversampling rate required. SVR and CADD receivers are proposed to enhance the ESE of the system, which can reconstruct the field of double-sided band (DSB) signals, but both schemes require at least three single-ended PDs and one optical hybrid, which results in complex hardware configurations. For ASCD receivers, optical bandpass filters (OBPF) with sharp responses are required to eliminate the SSBI, which places strict requirements on receiver hardware. Generally, the carrier-to-signal-power ratio (CSPR) is defined as the power ratio between the CW carrier and the modulated signal, determining the SSBI mitigation capability. At least 6, 7, and 10 dB CSPR for KK, CADD and ASCD receivers are needed to guarantee the optimal performance. However, due to the saturation of erbium-doped fiber amplifiers (EDFAs), the aforementioned high CSPR will limit the number of wavelength division multiplexing (WDM) channels. More details about the comparison of these self-coherence detection schemes can be found in [24,25].
The polarization division multiplexing (PDM) can double the capacity and spectral efficiency (SE) of a single-polarization direct-detection system [26]. For PDM coherence detection, the signal can be divided into two orthogonal polarization state outputs using the polarization beam splitter (PBS). On the other hand, the local oscillator (LO) at the Rx allows for the state of polarization (SOP) to be well aligned with the PBS and equally split. Thus, reconstructing a replica of both polarized signals is possible and polarization demultiplexing can be accomplished in the digital domain, whereas in the self-coherent systems described above, the optical CW carrier is added at the transmitter, acting as the equivalent of LO, and undergoes random polarization rotation in the fiber link [27,28,29,30,31,32]. Therefore, evenly splitting the CW carrier using PBS without active polarization control is no longer guaranteed. The above random carrier splitting phenomenon is called carrier fading, which is different from the power fading effect caused by the CD in IM/DD systems [32]. One solution to avoid carrier fading [33,34,35,36,37,38,39] is to add two spaced orthogonal carriers on either side of the signal, but during polarization demultiplexing, OBPFs with sharp edges are needed to remove the unwanted orthogonal carriers [33]. In addition, polarization multiplexing quadrature amplitude modulation (QAM) signals can be received using the Jones space scheme [40], but polarization recovery needs to be performed after signal field recovery (SFR). However, under unpredictable polarization changes, the SFR of the signal cannot operate stably. In order to improve the stability, a joint polarization multiplexing self-coherent detection and reception scheme combining SVR and KK is proposed [41,42]. The CSPR of this scheme is about 10 dB, and at least six single-ended PDs and one optical hybrid are needed at the Rx. The high sampling rate also brings higher requirements of the devices.
Recently, carrier-free phase-retrieval (CF-PR) receivers [43,44,45,46,47] have been widely studied to circumvent the requirement of a strong CW optical carrier, and the full optical field information of DSB signal can be reconstructed by the multiple intensity measurements after PD detection by running an iterative PR algorithm. The most obvious advantage of utilizing CF-PR is that there is no need to insert a strong CW carrier to co-propagate with the information-bearing signal at the transmitter, which usually means a higher spectral efficiency (a guard band is essential for the insertion of the optical CW carrier) and simplified transmitter configuration. In this paper, we provide an overview of the principles and challenges of CF-PR receivers, with special attention on the advances in reducing the complexity of the iterative PR algorithm, reducing receiver-side sampling rate, and recovering polarization/space division multiplexed QAM signals. In Section 2, we briefly introduce the principle and challenges of the CF-PR scheme, and in Section 3, we present various performance-enhanced CF-PR receivers in detail. Finally, we summarize the results and look forward to the future development of CF-PR receiver systems.
2. Principle of CF-PR Receivers
Compared with the self-coherent phase reconstruction scheme with the aid of a strong CW carrier, the CF-PR receiver based on the modified Gerchberg–Saxton (MGS) [48,49,50,51,52,53,54,55,56,57,58,59,60,61] algorithm consists of only two single-ended PDs and one dispersive element, which could recover the full-field information of the optical QAM signal without relying on any optical carrier. Theoretically, the CF-PR receiver can retrieve the phase of arbitrary QAM signals, and transmission impairments such as CD can be mitigated after phase retrieval [47]. As shown in Figure 1, the received QAM signal is divided into two parts, one part is directly detected using a PD, and the other part of the QAM signal is firstly passed through a dispersive element and then detected by another PD. The CF-PR algorithm is generally utilized to recover the full optical field from two intensity measurements, and , where and are the undispersed signal and the dispersed signal at the Rx, respectively. We set and for the ease of discussion. Without considering the nonlinearity of optical fiber, the undispersed signal after standard single-mode fiber (SSMF) transmission, and the dispersed signal after both SSMF and the dispersive element transmission can be expressed as
where is the output signal of the transmitter side (Tx), is the convolution operation, and represent the complex transfer functions resulting from the use of SSMF links and the dispersive element, respectively. represents the transmitted complex-valued data symbols, T is the symbol duration, and represents the basic pulse waveform of the transmitter. The frequency response of and can be expressed as
where stands for the Fourier transform function, is the laser center wavelength, is the speed of light propagation in a vacuum, and and are the cumulative CD value originating from the SSMF link and the cumulative CD value of the dispersive element, respectively. The solution for optical field recovery is to run an iterative CF-PR algorithm and iterate out the phase of the signal so that it satisfies the following condition:
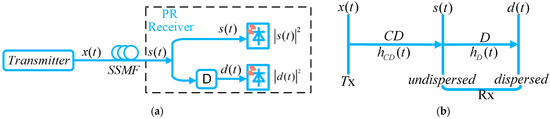
Figure 1.
(a) Schematic of the transmission system using the CF-PR receiver; (b) the relationship of the signals at different planes.
After the projection, by adding additional CD, the signal intensities are decorrelated and thus the signal phase can be retrieved when the reconstructed signal intensities on all projection planes are consistent with the measurements. However, CF-PR receivers often need a dispersive element with a large CD to ensure the phase recovery accuracy and reduce the number of iteration times of the CF-PR algorithm [46]. We should note that the requirement of the larger CD can be significantly relaxed if higher symbol rate signals are applied. Additionally, because the CF-PR algorithm is implemented in a block-wise manner with a block size of , and handles the signal propagation and shaping in the frequency domain using the classical radix-2 algorithm for the fast Fourier transform [45,46,47], the CF-PR receiver also suffers from high computational complexity for each iteration when the accumulated CD is large. Moreover, CF-PR algorithms based on MGS are prone to fall into the local minima, which results in a slow convergence with nearly a thousand iterations and reduced PR accuracy. When polarization multiplexing is applied to double the transmission capacity and SE, it is also challenging to recover the polarization multiplexed QAM signals for the CF-PR receiver.
3. Modified CF-PR Receiver Scheme
3.1. Improve the Performance of the CF-PR with a Reduced Number of Iterations and Better Steady Accuracy
This section introduces the research progress on preventing the CF-PR algorithm from being strapped into the local minima, with a reduced number of iterations and better steady PR accuracy, by adding more constraints on the CF-PR algorithm.
3.1.1. Parallel Alternating Projections
The schematic diagram of the CF-PR receiver with parallel alternating projections [45] is shown in Figure 2a. This receiver scheme consists of multiple dispersive elements and PDs to increase the number of intensity measurements. Generally, each dispersive element owes a different amount of dispersion, which changes the received signal strength through its own linear model of dispersion. Figure 2b shows the schematic diagram of the algorithm flow with iterations in each dispersion plane. Assuming that there are dispersion planes in total, the total number of iterations is thus . At each stage, the MGS algorithm iteratively refines the estimation of the complex-valued and its dispersed counterpart , and finally recovers the optical field information of the signal by exploiting the intensity constraints. Because it provides more complementary intensity constraints, the parallel alternating projection scheme can improve the PR performance of the CF-PR receiver.

Figure 2.
(a) Illustration of a phase-retrieval receiver employing parallel alternating projections; (b) schematic of the signal processing flow running the modified GS algorithm over multiple dispersed planes sequentially.
The parallel alternating projection scheme computes the averaged amplitude error between and after each iteration, i.e., as a metric to evaluate the phase recovery error accuracy. When the algorithm completes the iteration of one dispersion plane and moves to the next one, the will first show a peak and then fall sharply, which proves that the parallel alternating projection helps the PR algorithm solve the local minimum issue. Compared with a single alternative projection scheme, the parallel alternating projection scheme has faster convergence speed and higher phase recovery accuracy. We should also mention that the use of more dispersion planes is beneficial for improving the PR performance, but at the cost of more hardware complexity. Experiments have shown that in the case where the dispersion element is composed of 25, 35, and 55 km SSMFs, and the 30Gbaud quadrature phase shift-keying (QPSK) signal is transmitted through a 55 km SSMF. After 2000 iterations, the bit–error ratio (BER) of the CF-PR receiver is stabilized below when the number of dispersion planes is three. When the number of dispersion planes is one, the BER curve of the CF-PR receiver cannot converge [45].
It is worth mentioning that the space–time (ST) diversity scheme is similar to the parallel alternate projection scheme in that time decorrelation and spatial scrambling are employed to decorrelate the signals [62]. The specific implementation process is shown in Figure 3. In this scheme, the complex-valued signal is first split into two tributaries. One tributary is sent into a dispersive element. The other tributary is split equally into N copies, and the N redundant copies are temporally decorrelated by the relative time delays. The N copies are then mixed spatially using a symmetric N-by-N optical coupler. This scheme proves that the utilization of more ST diversity channels increases the convergence speed of the CF-PR algorithm and the receiver tolerance toward the receiver, but at the sacrifice of more hardware complexity.

Figure 3.
Diagram of (a) a CF-PR receiver with ST diversity; (b) field recovery process.
3.1.2. Enhanced CF-PR Algorithms
CF-PR Scheme with Selective Phase Resetting (PR-PR)
The CF-PR scheme with parallel alternating projections improves the PR performance by adding more hardware such as more PDs, which would significantly increase the implementation cost. In contrast, the PR-PR scheme [47], which uses only one dispersive projection, and adopts the MGS algorithm with a selective phase reset, can ensure a faster and accurate phase retrieval performance, as shown in Figure 4. After iterations, the 10-symbol moving average of , which is represented by , is calculated. If , the phase reset procedure is applied to reinitialize the phase information of the signal. The parameter is the acceptable GS error level. The use of helps eliminate error spikes that disturb with convergence, thus avoiding the local minima.

Figure 4.
Schematic representation of the PR-PR process.
Experiment results have shown that after 30Gbaud, QPSK signals are transmitted through a 55 km SSMF and the PR-PR receiver can improve the convergence speed using a phase reset by adaptively updating the acceptable GS error level. Consequently, the PR-PR scheme can realize fast algorithm convergence with less than 200 iterations.
Joint Optimization of CF-PR and Forward Error Correction (FEC) Overheads
Generally speaking, the use of pilot symbols is essential for the PR process to impose additional pilot constraint. The more pilot symbols we utilize, the more accurate the retrieved phase we can obtain when enough iterations for the CF-PR algorithm are used to guarantee the convergency. However, using more pilot symbols could have worse performance than the case with less pilot symbols when not having enough iterations, considering limited complexity and a fixed FEC overhead [63]. It has been reported that the joint optimization of the CF-PR and FEC overheads can enable a higher data rate and significantly reduced number of PR iterations [64]. Figure 5 shows the distribution of CF-PR pilot symbols and FEC overhead. The M here represents the number of bits for the insertion of pilot symbols for the CF-PR and is related to the modulation format. The overall overhead (OH) can be expressed as , where is the overall rate as follows:
where , is the symbol rate, and is the cardinality size of signal constellation. A larger CF-PR overhead indicates a stronger phase information acquisition capability, which ensures the CF-PR algorithm converge fasters and the bit–error rate (BER) after convergence is lower. On the other hand, in order to maintain the same net data rate, an increase in CF-PR pilot overhead also implies a decrease in the FEC overhead, leading to reduced error correction capability. Therefore, at a fixed data rate, overhead allocation between CF-PR and FEC becomes critical to optimize performance. The CF-PR and FEC overhead joint optimization scheme is carried out by optimizing the combination of FEC-OH, PR iteration, and PR pilot OH, at a total OH of 44%. Under the condition of BER < 1 × 10−6, the optical field recovery of 30GBaud QPSK signal after 55 km SSMF transmission is completed, and the total number of PR iterations can be reduced by 66% [64].

Figure 5.
CF-PR pilots overhead vs. FEC overhead.
CF-PR Scheme with Adaptive Intensity Transformation (AIT-PR)
In order to further improve the phase retrieval performance of the PR-PR receiver, an AIT-PR scheme is proposed by imposing an AIT constraint [65,66]. The principle of the AIT-PR receiver is shown in Figure 6. The two measured intensities are transformed adaptively with the current number of iterations. Regarding the QPSK signal, the constant modulus constraint is also included so that the AIT-PR algorithm can converge faster and more accurately.

Figure 6.
Illustration of (a) the carrier-less PR receiver; (b) the intensity transformation process.
The AIT operation can be generally expressed as
Specifically, the measured signal strength is powered by the factor , and is adaptively adjusted at each iteration. is determined by the maximum power factor and attenuation factor , which need optimization to ensure the best PR performance in terms of convergency speed and steady BER performance. The AIT operation can be efficiently implemented using a look-up table (LUT). The flow of the AIT-PR algorithm is shown in Algorithm 1. By utilizing intensity transformation, the PR algorithm can avoid falling into suboptimal solutions, leading to a better convergence performance. By performing CD compensation on the reconstructed signal, it propagates back to Tx. The reconstructed signal is then down-sampled to one sample per symbol (SPS) after being shaped by a root-raised cosine (RRC) filter, and pilot constrained to update the sample phase at the predetermined locations. Due to the constant modulus of the QPSK format, another modulus constraint is applied to force the signal strength to be constant. After being up-sampled by two SPSs, the signal is shaped by another RRC filter. After the signal propagates to the Rx dispersed plane, its strength is constrained by the transformation. Finally, the updated signal is transmitted to the Rx undispersed plane, and the phase of the signal is preserved until the next iteration.
| Algorithm 1 AIT-PR | |
| 1. Initialize 2. | ◊ Initialize phase |
| 3. for from 1 to 4. ◊ AIT | |
| 5. | ◊ Reconstruct the filed |
| 6. | ◊ Propagate back to Tx |
| 7. | ◊ RRC shaping |
| 8. | ◊ Down-sample to 1 SPS |
| 9. | ◊ Pilot constraint |
| 10. | ◊ Modulus constraint |
| 11. | ◊ Up-sample to 2 SPS |
| 12. | ◊ RRC shaping |
| 13. | ◊ To projection plane |
| 14. | ◊ Intensity update |
| 15. | ◊ Propagate back to Rx |
| 16. end for | |
| 17. returns | |
It has been verified that the AIT-PR receiver scheme only requires 50 iterations to numerically reconstruct the 56GBaud QPSK signal after transmitting through an 80 km standard single-mode fiber. And in terms of 20% soft-decision forward error correction (SD-FEC) and 7% hard-decision forward error correction (HD-FEC), the required optical signal-to-noise ratio (OSNR) of the AIT-PR receiver is reduced by 1.95 and 1.89 dB when compared to the PR-PR receiver, respectively.
Weighted Decision-Enhanced PR Receiver with Adaptive Intensity Transformation (WD-AIT-PR)
Hard decisions (HD) can be employed before the pilot symbol insertion to enhance the PR performance [55]. On the other hand, the HD operation can only be applied after a large number of iterations with better pre-convergency to guarantee the correct decisions. In addition, HD-induced errors inevitably limit the PR performance. In this context, the WD-AIT-PR scheme is proposed to improve the PR performance [67,68]. By providing weighted decision feedback, this scheme increases the “pilot” proportion without additional occupation of spectrum efficiency. WD is carried out separately for in-phase and quadrature (I/Q) components of the complex QAM signal. The principle of WD can be expressed as
where and are functions that take the real and imaginary parts, respectively. and are the I/Q components of hard decisions. and are the HD errors of the I/Q components, respectively. The reliability function and can be expressed as
The use of reliability can minimize the impact of decision errors. In addition, is a compressed sigmoid function to increase the effect of reliability value when it is a high value, as well as decrease this effect when it is a low value, as shown below.
where is an integer and is a compression factor in the range of . These two parameters need to be optimized to ensure the best performance of the algorithm. When the condition of is satisfied, WD can be regarded as a hard decision. The algorithm flow of a WD-AIT-PR receiver is shown in Algorithm 2. We first perform CD compensation on the signal after intensity transformation, and in this way, the reconstructed signal is considered as being transmitted back to Tx. After RRC filtering, the signal is down-sampled to one SPS and normalized. After iteration, WD is carried out on the I/Q components of the complex signal, respectively. Afterward, the pilot constraint is applied to update the sampling phase at the predetermined position. After being up-sampled to two SPSs, the signal is then shaped by another RRC filter. After the signal is propagated to the Rx dispersed plane, its strength is constrained by the transformed intensity measurement. Finally, the updated signal is transmitted to the Rx undispersed plane, and the phase of the signal is preserved until the next iteration.
| Algorithm 2 WD-AIT-PR | |
| 1. Initialize 2. | ◊ Initialize phase |
| 3. for from 1 to 4. ◊ AIT | |
| 5. | ◊ Reconstruct the filed |
| 6. | ◊ Propagate back to Tx |
| 7. | ◊ RRC shaping |
| 8. | ◊ Down-sample to 1 SPS |
| 9. | ◊ Normalization |
| 10. if | Introduce WD |
| constraint | |
| end if | |
| 11. | ◊ Pilot constraint |
| 12. | ◊ Up-sample to 2 SPS |
| 13. | ◊ RRC shaping |
| 14. | ◊ To projection plane |
| 15. | ◊ Intensity update |
| 16. 17. end for | ◊ Propagate back to Rx |
| 18. returns | |
After an 80 km SSMF transmission, the WD-AIT-PR receiver shows faster convergence speed and better stable BER performance through numerical reconstruction of the 56GBaud 16QAM signal. With only 70 iterations, the required OSNR was reduced by 0.8 dB, 1.8 dB, and 1.8 dB, respectively, to achieve 7% hard-decision forward error correction (HD-FEC) in comparison with the HD-AIT-PR receiver, by replacing WD with HD, the PR-PR receiver, and the AIT-PR receiver. The enhanced performance of the WD-AIT-PR receiver is also experimentally verified in terms of convergence speed, stable BER performance, and transmission impairment tolerance. Please note that if a strong optical carrier is inserted at the transmitter side along with the information-bearing signal, the PR performance can be improved accordingly with the help of this optical carrier [69,70], but this is out of the scope of this submission, as we focus on carrier-free phase retrieval.
Leveraging Digital Up-Sampling
The CF-PR receiver can reconstruct the full field information of the signal using only the intensity measurements, as is shown in Figure 7. B represents the bandwidth of modulated signals. The bandwidth of the signal , after PD detection becomes twice that of , . Additionally, the amplitude information of , is calculated on the measured intensities by the square root operation, which is a nonlinear operation and broadens the signal spectrum. In addition, the filter roll-off factor used for RRC shaping filtering is non-zero. Therefore, capturing and without frequency clipping requires a sampling rate larger than two SPSs, otherwise the signal will be distorted.

Figure 7.
(a) Concept of the CF-PR process. (b) Bandwidth of signal and its intensity .
The above problems can be solved by increasing the sampling rate. An iterative scheme was proposed to average the interleaved up-sampling symbols to maintain two samples per symbol of the estimated complex signal to achieve faster algorithm convergence [71]. The principle of the scheme is shown in Figure 8, where T is the symbol duration of the signal. Signals and are up-sampled four times, and the sampled symbols are divided into even and odd subsequences , , , . On both projection planes, is duplicated and intensity constraints are applied in an interleaved fashion in order to estimate with two SPSs per iteration. Finally, under the condition that OSNR is 30 dB and RRC filter roll-off factor is 0.01, the optical field recovery of the 30GBaud QPSK signal after transmission over a 55 km SSMF is completed, and the CF-PR receiver using interleaved up-sampling symbols needs only 110 and 250 iterations to reach the 20% and 7% FEC thresholds, respectively.

Figure 8.
CF-PR receiver using interleaved up-sampling symbols.
3.2. Reduce the Complexity of Each PR Iteration
CD compensation (CDC) and simulation (CDE) will introduce high computational complexity for each PR iteration. Compared with traditional single-carrier receivers, a digital subcarrier multiplexing (DSM)-enabled CF-PR is proposed and beneficial for reducing the implementation complexity of the CF-PR process [72], as the lower symbol rate of each subcarrier helps reduce the implementation complexity of multiple CDCs and CDEs during PR iteration [73,74].
The use of DSM means dividing a high baud rate single-carrier signal into several low-baud-rate subcarriers for transmission, and the generation process of the DSM signal is shown in Figure 9. The QAM symbol sequence is generated using the delayed de-correlation sequence, which is divided into streams ( is the number of subcarriers). Each subcarrier signal is first up-sampled to two SPSs. After the signal is filtered through an RRC filter with a roll-off factor of 0.01, each subcarrier signal is up-sampled M times (essentially zero filling in the frequency domain) and shifted to corresponding intermediate frequencies (subcarrier positioning). The DSM signal is finally obtained by multiplexing all subcarrier signals. For single-carrier modulation, the QAM symbol sequence is generated using the delay decorrelation sequence. After the signal is up-sampled to two SPSs, the single-carrier signal is passed through an RRC filter with a roll-off factor of 0.01. In fact, the single-carrier signal can be regarded as a special DSM signal when .

Figure 9.
Generation of DSM signals.
The specific value for reducing the complexity of each PR iteration using a DSM-enabled CF-PR receiver is as follows. The AIT-PR algorithm is implemented in a block-wise manner, with block sizes of and for single-carrier and DSM-enabled receivers, respectively. Assuming that the received signal after analog-to-digital converters (ADC) has two SPS, it requires real multiplications and real adder for each iteration. As shown in Figure 10, as the number of carriers increases, the number of multiplications and additions of CF-PR decreases accordingly. Therefore, the DSM-enabled CF-PR receiver can greatly reduce the algorithm complexity.

Figure 10.
Complexity comparison, in terms of (a) the number of adders; and (b) number of multiplications.
By numerically retrieving the optical field information of 56GBaud DSM signals after transmitting through a 80 km SSMF using QPSK/16QAM/32QAM modulation, it can be found that compared to traditional single-carrier receivers, the DSM-enabled CF-PR receiver has the advantage of reducing the complexity of the CF-PR iteration process. In addition, a DSM-enabled CF-PR receiver has been verified to be the most robust to transmission defects such as laser linewidth and wavelength drift at the transmitter side, time skew and amplitude imbalance between two intensity tributaries at the receiver side. Finally, the superiority of the DSM-enabled CF-PR receiver was experimentally verified by restoring the optical field information of the 25GBaud 16QAM signal after transmission over a 40 km SSMF.
3.3. CF-PR Receiver with Polarization and Spatial Mode Diversity
3.3.1. CF-PR Receiver with Polarization Mode Diversity
Polarization division multiplexing can double the SE in comparison with its single-polarization counterpart. Figure 11 shows the diagram of the receiver architecture for the recovery of a polarization multiplexed QAM signal with intensity measurements only. A PBS separates the polarization-mixed received signal after fiber transmission onto the two polarizations with respect to the PBS axis. Thereafter, the single-polarization CF-PR receiver can reconstruct the full field of the single-polarization QAM signal. To guarantee the full field of polarization multiplexed QAM signal with high accuracy, the estimation of the 2 × 2 fiber transfer matrix is essential [43]. However, the acquisition of the fiber transfer matrix is challenging as the conventional polarization demultiplexing algorithm only works well when the full field of the QAM signals is accurately retrieved.
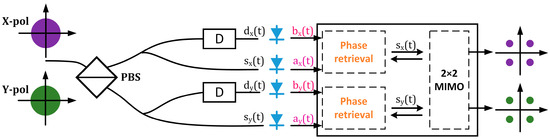
Figure 11.
Schematic of the polarization-diversity CF-PR receiver.
In order to accomplish the polarization demultiplexing in dual-polarization CF-PR receiver, the scheme of using training sequence to estimate the fiber transfer matrix is proposed in [47], as shown in Figure 12. This scheme uses 300 consecutive training symbols to obtain the fiber transfer matrix [75,76,77,78], by multiplying the received training symbols with the pseudo inverse of time-aligned transmitted training symbols. By running the phase retrieval algorithm and channel estimation iteratively, the fiber transfer matrix , containing both the polarization rotation and CD, can be properly recovered. Note that polarization dependent loss and polarization mode dispersion is ignored for simplicity considering the short-reach applications. After removing the CD contribution, , the transfer matrix from polarization rotation can be obtained [43]. After obtaining the transfer matrix, the PR-PR algorithm is used to reconstruct the polarization multiplexed signal in the entire field. Experimental results have shown that the polarization-diversity CF-PR receiver can reconstruct the full field of 30Gbaud dual-polarization QPSK signals after transmitting over a 520 km SSMF, with BERs of and with 10% and 20% pilot symbols, respectively.

Figure 12.
Illustration of the time domain transmission matrix, , estimation (: training sequence, : convolution, : unitary matrix, : estimation of at iteration ).
3.3.2. CF-PR Receiver with Both Polarization and Spatial Mode Diversity
In the absence of any optical carrier, full-field reconstruction of six spatial and polarization modes was achieved using intensity measurements only after 30 km multimode fiber transmission [44]. The three spatial modes are , , and , each with two polarizations. Figure 13 shows the schematic diagram of the receiver architecture for the reception of those spatial and polarization modes. After mode demultiplexing, each spatial and polarization mode is detected by two single ended PDs. The difference between the two intensity measurements lies in the addition of dispersion elements in one path.

Figure 13.
Schematic diagram of the receiver architecture for the full field of the spatial and polarization modes.
Firstly, the 6 × 6 transmission matrix, h, for polarization multiplexing is estimated through a training sequence, followed by the use of PR-PR to recover optical field information, and finally, DSP including 6 × 6 MIMO is performed. Thus, achieving full-field reconstruction of mode and polarization multiplexed signals with six spatial and polarization modes is accomplished.
4. Conclusions
In order to meet the requirements of low cost, low power consumption, and high sensitivity for short-range optical communication receivers, reconstructing the optical signal field from the intensity measurements has attracted widespread attention. The CF-PR receiver is a potential candidate and can reconstruct the full field of QAM signals from two intensity measurements by running an iterative PR algorithm, without the assistance of a strong CW optical carrier. However, the PR algorithm is prone to falling into local minima, slowing low convergence speed, low PR accuracy, and high computational complexity. This article reviews the research progress on how to improve the PR performance, in terms of reducing the iteration number along with the complexity of each iteration, and enhancing the steady BER performance. In addition, we also review the work on polarization and spatial mode diversity CF-PR receivers which can reconstruct the full field of multi-dimensional signals. We should note that there are still some challenges we need to overcome in future studies. For example, the transmission impairments induced from the transceiver such as bandwidth constraint and in-phase/quadrature imbalance degrade the PR performance significantly, which can be reflected by a relatively large BER, above the 7% FEC threshold, in experiments. Additionally, the required number of iterations to guarantee a full PR convergency is still high in terms of practical implementation, and we believe that the utilization of machine learning techniques would play a vital role in further reducing the iteration number because of its strong fitting capability. Finally, the comparison between CF-PR receivers and other self-coherent receivers in terms of performance and hardware configuration requirement is worthy studying.
Author Contributions
Conceptualization, Y.M., X.G. and M.X.; methodology, M.X. and S.F.; software, Y.M. and M.X.; validation, Y.M. and M.X.; formal analysis, C.W., W.C., J.L. (Jilong Li), J.L. (Jianping Li) and G.Z.; investigation, Y.M., M.X. and S.F.; resources, M.X.; data curation, W.C. and M.X.; writing—original draft preparation, Y.M.; writing—review and editing, X.G., Y.Q. and S.F.; supervision, C.W.; project administration, X.G.; funding acquisition, M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Key Research and Development Program of China (2021YFB2900702), the National Natural Science Foundation of China (62075046, U21A20506), and the Guangdong Introducing Innovative and Entrepreneurial Teams of “The Pearl River Talent Recruitment Program” (2021ZT09X044).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time, but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kikuchi, K. Fundamentals of Coherent Optical Fiber Communications. J. Light. Technol. 2016, 34, 157–179. [Google Scholar] [CrossRef]
- Cvijetic, M. Coherent and Nonlinear Lightwave Communications; Artech House: Boston, MA, USA, 2016; ISBN 13-978-0890065907. [Google Scholar]
- Batagelj, B.; Janyani, V.; Tomazic, S. Research challenges in optical communications towards 2020 and beyond. Inf. MIDEM 2014, 44, 177–184. [Google Scholar]
- Ip, E.M.; Kahn, J.M. Fiber Impairment Compensation Using Coherent Detection and Digital Signal Processing. J. Light. Technol. 2009, 28, 502–519. [Google Scholar] [CrossRef]
- Uzunidis, D.; Logothetis, M.; Stavdas, A.; Hillerkuss, D.; Tomkos, I. Fifty Years of Fixed Optical Networks Evolution: A Survey of Architectural and Technological Developments in a Layered Approach. Telecom 2022, 3, 619–674. [Google Scholar] [CrossRef]
- Savory, S.J.; Gavioli, G.; Killey, R.I.; Bayvel, P. Electronic compensation of chromatic dispersion using a digital coherent receiver. Opt. Express 2007, 15, 2120–2126. [Google Scholar] [CrossRef] [PubMed]
- Winzer, J.; Essiambr, R. Advanced Optical Modulation Formats. Proc. IEEE 2006, 94, 952–985. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, X.; Huo, J.; Yu, C.; Lu, C.; Lau, A.P.T. Digital Signal Processing for Short-Reach Optical Communications: A Review of Current Technologies and Future Trends. J. Light. Technol. 2018, 36, 377–400. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Cheng, Z.; Yin, L.; Hu, W. Spectrally sliced heterodyne coherent receiver with halved electrical bandwidth. Chin. Opt. Lett. 2022, 20, 090601-1–090601-6. [Google Scholar] [CrossRef]
- Che, D.; Sun, C.; Shieh, W. Maximizing the spectral efficiency of Stokes vector receiver with optical field recovery. Opt. Express 2018, 26, 28976–28981. [Google Scholar] [CrossRef]
- Gao, Y.; Lau, A.P.T.; Yan, S.; Lu, C. Low-complexity and phase noise tolerant carrier phase estimation for dual-polarization 16-QAM systems. Opt. Express 2011, 22, 21717–21729. [Google Scholar] [CrossRef]
- Faruk, M.S.; Kikuchi, K. Adaptive frequency-domain equalization in digital coherent optical receivers. Opt. Express 2011, 13, 12789–12798. [Google Scholar] [CrossRef] [PubMed]
- Xin, H.; Zhang, K.; Li, L.; He, H.; Hu, W. 50 Gbps PAM-4 Over Up to 80-km Transmission With C-Band DML Enabled by Post-Equalizer. IEEE Photonics Technol. Lett. 2020, 32, 643–646. [Google Scholar] [CrossRef]
- Mecozzi, A.; Antonelli, C.; Shtaif, M. Kramers–Kronig coherent receiver. Optica 2016, 3, 1220–1227. [Google Scholar] [CrossRef]
- Chen, X.; Chandrasekhar, S.; Olsson, S.; Adamiecki, A.; Winzer, P. Impact of O/E front-end frequency response on Kramers-Kronig receivers and its compensation. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; p. Mo3F.5. [Google Scholar]
- Bo, T.; Kim, H. Toward. practical Kramers-Kronig receiver: Resampling, performance, and implementation. J. Light. Technol. 2019, 37, 461–469. [Google Scholar] [CrossRef]
- Patel, R.K.; Alimi, I.A.; Muga, N.J.; Pinto, A.N. Optical signal phase retrieval with low complexity DC-value method. J. Light. Technol. 2020, 38, 4205–4212. [Google Scholar] [CrossRef]
- Li, X.; O’Sullivan, M.; Xing, Z.; Alam, M.; Mousa-Pasandi, E.M.; Plant, V.D. Asymmetric self-coherent detection. Opt. Express 2021, 29, 25412–25427. [Google Scholar] [CrossRef]
- Shieh, W.; Sun, C.; Ji, H. Carrier-assisted differential detection. Light Sci. Appl. 2020, 9, 18. [Google Scholar] [CrossRef]
- Che, D.; Li, A.; Chen, X.; Hu, Q.; Wang, Y.; Shieh, W. Stokes Vector Direct Detection for Linear Complex Optical Channels. J. Light. Technol. 2015, 33, 678–684. [Google Scholar] [CrossRef]
- Peng, W.R.; Wu, X.; Feng, K.M.; Arbab, V.R.; Shamee, B.; Yang, J.Y.; Christen, L.C.; Willner, A.E.; Chi, S. Spectrally efficient direct-detected OFDM transmission employing an iterative estimation and cancellation technique. Opt. Express 2009, 17, 9099–9111. [Google Scholar] [CrossRef]
- Zou, K.; Zhu, Y.; Zhang, F.; Chen, Z. Spectrally efficient terabit optical transmission with Nyquist 64-QAM half-cycle subcarrier modulation and direct detection. Opt. Lett. 2016, 12, 2767–2770. [Google Scholar] [CrossRef]
- Li, Z.; Erkılınç, M.; Shi, K.; Sillekens, E.; Galdino, L.; Thomsen, B.; Bayvel, P.; Killey, R. SSBI mitigation and the Kramers-Kronig scheme in single-sideband direct-detection transmission with receiver-based electronic dispersion compensation. J. Light. Technol. 2017, 35, 1887–1893. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, Z.; Zhu, Y.; Zhang, Y.; Ji, H.; Yang, Y.; Qiao, G.; Liu, L.; Wang, S.; Liang, J. Machine Learning for Self-Coherent Detection Short-Reach Optical Communications. Photonics 2023, 10, 1001. [Google Scholar] [CrossRef]
- Karar, A.S.; Falou, A.R.E.; Barakat, J.M.H.; Gürkan, Z.N.; Zhong, K. Recent Advances in Coherent Optical Communications for Short-Reach: Phase Retrieval Methods. Photonics 2023, 10, 308. [Google Scholar] [CrossRef]
- Che, D.; Shieh, W. Polarization Demultiplexing for Stokes Vector Direct Detection. J. Light. Technol. 2016, 34, 754–760. [Google Scholar] [CrossRef]
- Kikuchi, K. Quantum Theory of Noise in Stokes Vector Receivers and Application to Bit Error Rate Analysis. J. Light. Technol. 2020, 38, 3164–3172. [Google Scholar] [CrossRef]
- Qian, D.; Cvijetic, N.; Hu, J.; Wang, T. 108 Gb/s OFDMA-PON with Polarization Multiplexing and Direct Detection. J. Light. Technol. 2009, 28, 484–493. [Google Scholar] [CrossRef]
- Ji, H.; Li, J.; Li, X.; Dong, S.; Xu, Z.; Su, Y.; Shieh, W. Complementary Polarization-Diversity Coherent Receiver for Self-Coherent Homodyne Detection with Rapid Polarization Tracking. J. Light. Technol. 2022, 40, 2773–2779. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Zhuge, Q.; Hu, W. Dual-Carrier-Assisted Phase Retrieval for Polarization Division Multiplexing. J. Light. Technol. 2022, 40, 7297–7306. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Jiang, H.; Zhuge, Q.; Hu, W. Optical Field Recovery in Jones Space. J. Light. Technol. 2022, 41, 66–74. [Google Scholar] [CrossRef]
- Che, D.; Sun, C.; Shieh, W. Single-Channel 480-Gb/s Direct Detection of POL-MUX IQ Signal Using Single-Sideband Stokes Vector Receiver. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Zhu, Y.; Jiang, M.; Zhang, F. Direct detection of polarization multiplexed single sideband signals with orthogonal offset carriers. Opt. Express 2018, 26, 15887–15898. [Google Scholar] [CrossRef]
- Fukuda, H.; Yamada, K.; Tsuchizawa, T.; Watanabe, T.; Shinojima, H.; Itabashi, S. Silicon photonic circuit with polarization diversity. Opt. Express 2008, 16, 4872–4880. [Google Scholar] [CrossRef] [PubMed]
- Charles, L.; Villeneuve, B.; Zhang, Z.; McGhan, D.; Sun, H.; O’Sullivan, M. WDM performance and PMD tolerance of a coherent 40-Gbit/s dual-polarization QPSK transceiver. J. Light. Technol. 2008, 26, 168–175. [Google Scholar]
- Peng, W.; Feng, K.; Willner, A.E. Direct-detected polarization division multiplexed OFDM systems with self-polarization diversity. In Proceedings of the LEOS 2008—21st Annual Meeting of the IEEE Lasers and Electro-Optics Society, Newport Beach, CA, USA, 9–13 November 2008; pp. 71–72. [Google Scholar]
- Nazarathy, M.; Agmon, A. Doubling direct-detection data rate by polarization multiplexing of 16-QAM without active polarization control. Opt. Express 2013, 26, 31998–32012. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; O’Sullivan, M.; Xing, Z.; Alam, M.S.; Hoang, T.; Xiang, M.; Zhu, M.; Zhang, J.; Elfiky, E.; Plant, D.V. Asymmetric direct detection of orthogonal offset carriers assisted polarization multiplexed single-sideband signals. Opt. Express 2020, 28, 3226–3236. [Google Scholar] [CrossRef]
- Antonelli, C.; Mecozzi, A.; Shtaif, M.; Chen, X.; Chandrasekhar, S.; Winzer, P.J. Polarization multiplexing with the Kramers-Kronig receiver. J. Light. Technol. 2017, 24, 5418–5424. [Google Scholar] [CrossRef]
- Che, D.; Sun, C.; Shieh, W. Direct detection of the optical field beyond single polarization mode. Opt. Express 2018, 26, 3368–3380. [Google Scholar] [CrossRef]
- Hoang, T.M.; Sowailem, Y.S.M.; Zhuge, Q.; Xing, Z.; Morsy-Osman, M.; El-Fiky, E.; Fan, S.; Xiang, M.; Plant, D.V. Single wavelength 480 Gb/s direct detection over 80km SSMF enabled by Stokes vector Kramers Kronig transceiver. Opt. Express 2017, 25, 33534–33542. [Google Scholar] [CrossRef]
- Che, D.; Sun, C.; Shieh, W. Optical field recovery in stokes space. J. Light. Technol. 2019, 37, 451–460. [Google Scholar] [CrossRef]
- Chen, H.; Fontaine, N.K.; Gené, J.M.; Ryf, R.; Neilson, D.T.; Raybon, G. Full-field, carrier-less, polarization diversity, direct detection receiver based on phase retrieval. In Proceedings of the 45th European Conference on Optical Communication (ECOC 2019), Dublin, Ireland, 22–26 September 2019; pp. 1–3. [Google Scholar]
- Chen, H.; Alvarado, Z.; Juan, C.; Huang, H.; Fontaine, N.K.; Ryf, R.; Neilson, D.T.; Amezcua-Correa, R. Mode-Multiplexed Full-Field Reconstruction Using Direct and Phase Retrieval Detection. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Huang, H.; Chen, H.; Huang, Y.; Li, Z.; Zhang, Q.; Fontaine, N.K.; Ryf, R.; Song, Y. Phase Retrieval Receiver using Parallel Alternative Projections for Coherent Communications. In Proceedings of the 2020 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2020; pp. 1–2. [Google Scholar]
- Chen, H.; Huang, H.; Fontaine, N.K.; Ryf, R. Phase retrieval with fast convergence employing parallel alternative projections and phase reset for coherent communications. Opt. Lett. 2020, 45, 1188–1191. [Google Scholar] [CrossRef]
- Chen, H.; Fontaine, N.K.; Gene, J.M.; Ryf, R.; Neilson, D.T.; Raybon, G. Dual Polarization Full-Field Signal Waveform Reconstruction Using Intensity Only Measurements for Coherent Communications. J. Light. Technol. 2020, 38, 2587–2597. [Google Scholar] [CrossRef]
- Dorrer, C. Characterization of nonlinear phase shifts by use of the temporal transport-of-intensity equation. Opt. Lett. 2005, 30, 3237–3239. [Google Scholar] [CrossRef] [PubMed]
- Cuadrado-Laborde, C.; Carrascosa, A.; Pérez-Millán, P.; Díez, A.; Cruz, J.L.; Andres, M.V. Phase recovery by using optical fiber dispersion. Opt. Lett. 2014, 39, 598–601. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, M. A phase retrieval method using dispersion for direct detection of biased QAM signals. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018; pp. 1–2. [Google Scholar]
- Gerchberg, R.W. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Burvall, A.; Lundström, U.; Takman, P.A.C.; Larsson, D.H.; Hertz, H.M. Phase retrieval in X-ray phase-contrast imaging suitable for tomography. Opt. Express 2011, 19, 10359–10376. [Google Scholar] [CrossRef] [PubMed]
- Shechtman, Y.; Eldar, Y.C.; Cohen, O.; Chapman, H.N.; Miao, J.; Segev, M. Phase retrieval with application to optical imaging: A contemporary overview. IEEE Signal Process. Mag. 2015, 32, 87–109. [Google Scholar] [CrossRef]
- Jaganathan, K.; Eldar, Y.C.; Hassibi, B. Phase retrieval: An overview of recent developments. arXiv 2015, arXiv:1510.07713. [Google Scholar]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef]
- Fienup, J.R. Reconstruction of a complex-valued object from the modulus of its Fourier transform using a support constraint. J. Opt. Soc. Am. A 1987, 4, 118–123. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase-retrieval algorithms for a complicated optical system. Appl. Opt. 1993, 32, 1737–1746. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Sivokon, V.P. Phase retrieval from a set of intensity measurements: Theory and experiment. J. Opt. Soc. Am. A 1992, 9, 1515–1524. [Google Scholar] [CrossRef]
- Fatadin, I.; Savory, J.S. Impact of phase to amplitude noise conversion in coherent optical systems with digital dispersion compensation. Opt. Express 2010, 18, 16273–16278. [Google Scholar] [CrossRef] [PubMed]
- Malekiha, M.; Tselniker, I.; Plant, V.D. Chromatic dispersion mitigation in long-haul fiber-optic communication networks by sub-band partitioning. Opt. Express 2015, 23, 32654–32663. [Google Scholar] [CrossRef] [PubMed]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Sierra, A.; Mumtaz, S.; Esmaeelpour, M.; Burrows, E.C.; Essiambre, R.; Winzer, P.J.; et al. Mode-division multiplexing over 96 km of few-mode fiber using coherent 6 × 6 MIMO processing. J. Light. Technol. 2012, 30, 521–531. [Google Scholar] [CrossRef]
- Chen, H.; Fontaine, N.K.; Essiambre, R.; Huang, H.; Mazur, M.; Ryf, R.; Neilson, D.T. Space-Time Diversity Phase Retrieval Receiver. In Proceedings of the 2021 Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 6–10 June 2021; p. Th4D.3. [Google Scholar]
- Smith, B.P.; Farhood, A.; Hunt, A.; Kschischang, F.R.; Lodge, J. Staircase Codes: FEC for 100 Gb/s OTN. J. Light. Technol. 2012, 30, 110–117. [Google Scholar] [CrossRef]
- Chen, B.; Huang, H.; Chen, H.; Lei, Y.; Fontaine, N.K.; Ryf, R.; Zhang, Q.; Song, Y. Joint Optimization of Phase Retrieval and Forward Error Correcting for Direct Detection Receiver. In Proceedings of the 2020 European Conference on Optical Communications (ECOC), Brussels, Belgium, 6–10 December 2020; pp. 1–4. [Google Scholar]
- Xiang, M.; Zhou, P.; Ye, B.; Fu, S.; Xu, O.; Li, J.; Peng, D.; Wang, Y.; Qin, Y. Adaptive intensity transformation-based phase retrieval with high accuracy and fast convergence. Opt. Lett. 2021, 46, 3215–3218. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wu, X.; Sun, L.; Liu, J.; Lau, A.P.T.; Guo, C.; Yu, S.; Lu, C. C-band 120-Gb/s PAM-4 transmission over 50-km SSMF with improved weighted decision-feedback equalizer. Opt. Express 2021, 29, 41622–41633. [Google Scholar] [CrossRef]
- Zhou, P.; Xiang, M.; Zhou, G.; Li, J.; Li, J.; Fu, S.; Qin, Y. Weighted Decision Enhanced Phase-Retrieval Receiver with Adaptive Intensity Transformation. In Proceedings of the 2022 European Conference on Optical Communication (ECOC), Basel, Switzerland, 18–22 September 2022; p. We5.27. [Google Scholar]
- Zhou, P.; Xiang, M.; Cheng, W.; Ma, Y.; Wu, R.; Zhou, G.; Li, J.; Li, J.P.; Zhang, C.; Fu, S.; et al. Weighted Decision Enhanced Phase-Retrieval Receiver with Adaptive Intensity Transformation. J. Light. Technol. 2023, 41, 6208–6217. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Zhuge, Q.; Hu, W. Dual-Polarization Direct Detection with Jones Space Field Recovery. In Proceedings of the 2022 Asia Communications and Photonics Conference (ACP), Shenzhen, China, 5–8 November 2022; pp. 763–767. [Google Scholar]
- Wu, Q.; Zhu, Y.; Zhuge, Q.; Hu, W. Carrier-Assisted Phase Retrieval with Multiple Projections. In Proceedings of the 2022 Asia Communications and Photonics Conference (ACP), Shenzhen, China, 5–8 November 2022; pp. 465–468. [Google Scholar]
- Huang, H.; Chen, H.; Huang, Y.; Fontaine, N.K.; Ryf, R.; Song, Y. Carrier-less phase retrieval receiver leveraging digital up-sampling. Opt. Lett. 2020, 45, 6070–6073. [Google Scholar] [CrossRef]
- Ma, Y.; Xiang, M.; Cheng, W.; Wu, R.; Zhou, P.; Zhou, P.; Li, J.; Li, J.; Fu, S.; Qin, Y. Digital subcarrier multiplexing-enabled carrier-free phase-retrieval receiver. Adv. Photonics Nexus 2023, 2, 046004. [Google Scholar] [CrossRef]
- Huang, H.; Chen, H.; Fontaine, N.K.; Song, Y.; Mazur, M.; Dallachiesa, L.; Veen, D.V.; Houtsma, V.; Ryf, R.; Neilson, D.T. Simplified Phase Retrieval Receiver Employing Transmission Fiber for Alternative Projection. In Proceedings of the 2022 European Conference on Optical Communication (ECOC), Basel, Switzerland, 18–22 September 2022; pp. 1–4. [Google Scholar]
- Madsen, C.K.; Lenz, G.; Bruce, A.J.; Capuzzo, M.A.; Gomez, L.T.; Nielsen, T.N.; Brener, I. Multistage dispersion compensator using ring resonators. Opt. Lett. 1999, 24, 1555–1557. [Google Scholar] [CrossRef]
- Lachowicz, S.; Pfleiderer, H.-J. Fast evaluation of nonlinear functions using FPGAs. Adv. Radio Sci. 2008, 6, 233–237. [Google Scholar] [CrossRef]
- Hu, S.; Zhang, J.; Tang, J.; Jin, W.; Giddings, R.; Qiu, K. Data-Aided Iterative Algorithms for Linearizing IM/DD Optical Transmission Systems. J. Light. Technol. 2021, 39, 2864–2872. [Google Scholar] [CrossRef]
- Zheng, Z.; Cui, N.; Xu, H.; Zhang, X.; Zhang, W.; Xi, L.; Fang, Y.; Li, L. Window-split structured frequency domain kalman equalization scheme for large PMD and ultra-fast RSOP in an optical coherent PDM-QPSK system. Opt. Express 2018, 26, 7211–7226. [Google Scholar] [CrossRef] [PubMed]
- Morsy-Osman, M.; Chagnon, M.; Zhuge, Q.; Xu, X.; E. Mousa-Pasandi, M.; A. El-Sahn, Z.; V. Plant, D. Ultrafast and low overhead training symbol based channel estimation in coherent M-QAM single-carrier transmission systems. Opt. Express 2012, 20, B171–B180. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).